高一数学测试题—向量的加减法.doc
高一数学向量的加法与减法练习

向量的加法与减法练习【课内四基达标】一、选择题1. □ABCD 中, -+等于( ) A.B.C.D.2.D 、E 、F 分别是△ABC 三边AB 、BC 、CA 的中点,则下列等式不成立的是( ) A.+ = B. ++=0 C. +=D. += 3.下列等式:①-(-a )=a ②o +a =a ③a +(-b )=a -b ④a -a =0 其中成立的等式为( )A.①③④B.①②④C.①②③D.②③④4.正方形ABCD 中,边长为1,则|++|为( ) A.0B.2C.22D.35.在□ABCD 中,设=a , =b , =c , =d ,则下列等式中不成立的是( )A.a +b =cB.a -b =dC.b -a =dD.c -a =b6.设O 为□ABCD 的中心,E 为任意一点,则AE +BE +CE +DE 为( ) A.B.2C.3D.47.下列各项正确的个数( ) ①|a +b |≤|a |+|b | ②|a +b |=|a |+|b | ③|a -b |≤|a +b | ④|a -b |<|a |+|b | A.0个 B.1个C.2个D.3个8.设点D 、E 、F 分别是△ABC 三边BC 、CA 、BA 的中点,又AB =a , BC =b , AC =c ,则AD +BE +CF 为( )A.0B.0C.a +b +cD.23(a +b +c ) 9.设G 为△ABC 的重心,则|++|为( )A.0B.0C.1D.2 10.若三非零向量a 、b 、c 满足a +b +c =0,则表示该三向量的三有向线段一定构成( ) A.一条直线 B.一条线段C.一个三角形D.以上都不正确二、填空题11.在□ABCD 中,已知AB =a , OB =b ,则AC = . 12.等式|a +b |=|a |+|b |成立的条件是 . 13.化简:-+ .14.若a +b 平分非零向量a 、b 之间的夹角,则a 、b 的关系是 . 15.在□ABCD 中,=a , =b ,已知|a +b |=|a -b |,则四边形ABCD 是 .三、解答题16.在正六边形ABCDEF 中,已知=a , =b ,用a 、b 表示,,,.17.已知|a |=8,|b |=12,求|a -b |的最大值和最小值.18.设点D 、E 、F 是△ABC 三边BC 、CA 、AB 上的中点,O 为任意点. 求证:(1) =21(+); (2) OA +OB +OC =OD +OE +OF .参考答案1.A2.C3.C4.A5.B6.D7.B8.B9.B 10.D11.2a -b 12.a 、b 方向相同 13.0 14.|a |=|b | 15.矩形16. BC=a+b, CD=b, DE=-a, EF=-a-b17.|a-b|max=|a|+|b|=20,|a-b|min=|b|-|a|=418.略。
【同步练习】2017-2018学年 高一数学 必修4 向量线性运算 向量减法运算 课后练习题(含答案详解)

2017-2018学年 高一数学 必修4 向量线性运算 向量减法运算课后练习题一、选择题:1.在四边形ABCD 中,设AB =a ,AD =b ,BC =c ,则DC =( ).A.a -b +cB.b -(a +c )C.a +b +cD.b -a +c2.已知向量a 、b 满足|a |=1,|b |=2,|a -b |=2,则|a +b |等于( ). A.1 B.2 C.5 D.63.当a ,b 满足下列何种条件时,等式|a +b |=|a |-|b |成立( ).A.a 与b 同向B.a 与b 反向C.a 与b 同向且|a |≤|b |D.a 与b 反向且|a |≥|b |4.下列四式中不能化简为PQ 的是( ). A.AB +(PA +BQ ) B.(AB +PC )+(BA -QC ) C.QC -QP +CQ D.PA +AB -BQ5.在边长为1的正三角形ABC 中,|AB -BC |的值为( ). A.1 B.2 C.23 D.3 二、填空题:6.化简下列各式:①AB -AC +BC ;②AB +CA +BD -CD ;③OA -OD -DA ;④NQ -PQ +MN -MP .结果为零向量的个数是________.7.如图,在梯形ABCD 中,AD ∥BC ,AC 与BD 交于O 点,则BA -BC -OA +OD +DA =________.8.设点O 是三角形ABC 所在平面上一点,若|OA |=|OB |=|OC |,则点O 是△ABC 的_____心.9.如图,已知O 为平行四边形ABCD 内一点,OA =a ,OB =b ,OC →=c ,则OD =________.三、解答题:10.如图,已知OA=a,OB=b,OC=c,OD=d,OE=e,OF=f,试用a,b,c,d,e,f表示以下向量:(1)AC;(2)AD;(3)DF+FE+11.如图所示,已知正方形ABCD的边长等于1,AB=a,BC=b,AC=c,试作出下列向量,并分别求出其长度:(1)a+b+c;(2)a-b+c.12.已知|a|=8,|b|=15.(1)求|a-b|的取值范围.(2)若|a-b|=17,则表示a,b的有向线段所在的直线所成的角是多少?参考答案1.答案为:A;解析:DC=DA+AB+BC=a-b+c.2.答案为:D;解析:设OA=a,OB=b,以OA、OB为邻边作▱ OACB,则a-b=BA.∵|a|=1,|b|=2,|a-b|=2,∴▱OACB中,OA=1,OB=2,BA=2,由平行四边形的对角线长的平方和等于四边的平方和可得|a+b|=|OC|=6.3.答案为:D;解析:当a与b反向且|a|≥|b|时,|a+b|=|a|-|b|.4.答案为:D;5.答案为:D;6.答案为:4;7.答案为:CA;8.答案为:外心;9.答案为:a-b+c;10.解:11.解:12.解:。
高一数学下学期向量加法减法习题精选 试题

智才艺州攀枝花市创界学校高一数学下学期向量加法减法习题精选一、选择题1.以下各式正确的选项是〔〕A.假设a、b同向,那么B.与表示的意义是一样的C.假设a、b不一共线,那么D.永远成立2.等于〔〕A.B.0 C.D.3.假设a、b、a+b均为非零向量,且a+b平分a与b的夹角,那么〔〕A.B.C.D.以上都不对①假设a与b的方向一样或者相反,那么的方向必与a、b之一的方向一样。
②△ABC中,必有0。
③假设0,那么A、B、C为一个三角形的三个顶点。
④假设a、b均为非零向量,那么与一定相等。
〕A.0B.1C.2D.35.一点O到平行四边形ABCD的三个顶点A、B、C的向量分别为a、b、c,那么向量等于〔〕A.B.C.D.6.如图,在四边形ABCD中,设,那么等于〔〕A.B.C.D.7.设b是a的相反向量,那么以下说法错误的选项是〔〕A.a与b的长度必相等B.C.a与b一定不相等D.a是b的相反向量8.可以写成:①;②;③;④,其中正确的选项是〔〕A.①②B.②③C.③④D.①④〕①是的必要不充分条件;②任一非零向量的方向都是惟一的;③;④假设,那么0;⑤A、B、C是平面上的任意三点,那么0。
A.1B.2C.3D.410.某人先位移向量a:“向东走3km〞,接着再位移向量b:“向北走3km〞,那么〔〕A.向东南走kmB.向东北走kmC.向东南走kmD.向东北走km11.假设,那么的取值范围是〔〕A.B.〔3,8〕C.D.〔3,13〕二、填空题12.假设三个向量a、b、c恰能首尾相接构成一个三角形,那么=。
13.设ABCDEF为一正六边形,,那么14.化简:15.如下列图,用两根绳子把重10kg的物体W吊在程度杆子AB上,,那么A和B处所受力的大小〔绳子的重量忽略不计〕分别是。
三、解答题16.如下列图,在ABCD中,,用a、b表示向量、。
17.如下列图,在矩形ABCD中,,设。
试求。
18.如下列图,在矩形ABCD中,O是对角线AC与BD的交点。
向量的加减基础练习题

向量的加减基础练习题向量的加减基础练习题在数学中,向量是一个有方向和大小的量。
它可以用箭头表示,箭头的方向表示向量的方向,箭头的长度表示向量的大小。
向量的加减是向量运算中的基础操作,它们在物理、工程、计算机科学等领域中都有广泛的应用。
首先,让我们来看一些向量的基本概念。
向量通常用小写字母加上箭头来表示,比如a→或b→。
一个向量有两个重要的属性:方向和大小。
方向可以用角度或者其他向量来表示,而大小则表示向量的长度或者大小。
现在,我们来练习一些向量的加法和减法。
假设有两个向量a→和b→,它们的分量分别为(a1, a2)和(b1, b2)。
向量的加法可以通过将相应的分量相加来实现,即(a1 + b1, a2 + b2)。
向量的减法可以通过将相应的分量相减来实现,即(a1 -b1, a2 - b2)。
让我们来看一个例子:假设有两个向量a→ = (3, 4)和b→ = (1, 2)。
我们可以通过将它们的分量相加来计算它们的和:a→ + b→ = (3 + 1, 4 + 2) = (4, 6)。
同样地,我们可以通过将它们的分量相减来计算它们的差:a→ - b→ = (3 - 1, 4 - 2) = (2, 2)。
现在,让我们来解决一些向量的加减练习题。
练习题1:计算向量c→ = (2, 3)和d→ = (4, 1)的和和差。
解答:c→ + d→ = (2 + 4, 3 + 1) = (6, 4);c→ - d→ = (2 - 4, 3 - 1) = (-2, 2)。
练习题2:计算向量e→ = (-1, 5)和f→ = (3, -2)的和和差。
解答:e→ + f→ = (-1 + 3, 5 - 2) = (2, 3);e→ - f→ = (-1 - 3, 5 + 2) = (-4, 7)。
练习题3:计算向量g→ = (0, 0)和h→ = (1, -1)的和和差。
解答:g→ + h→ = (0 + 1, 0 - 1) = (1, -1);g→ - h→ = (0 - 1, 0 + 1) = (-1, 1)。
向量加减法练习题(打印版)

向量加减法练习题(打印版)### 向量加减法练习题题目一:给定两个向量 A = (3, 2) 和 B = (-1, 4),计算以下向量加法和减法的结果。
1. A + B2. A - B3. B - A题目二:已知向量 C = (4, -1) 和向量 D = (-2, 3),计算以下向量运算。
1. C + D2. 2C - D3. D - 3C题目三:向量 E = (1, 0) 和向量 F = (0, 1),求以下结果。
1. E + F2. E - F3. -E + F题目四:向量 G = (-3, 5) 与向量 H = (2, -4),计算以下向量运算。
1. G + H2. G - 2H3. 3G - H题目五:向量 I = (5, 7) 和向量 J = (-6, 8),计算以下向量运算。
1. I + J2. I - 3J3. J - I题目六:向量 K = (1, 2, 3) 和向量 L = (4, -2, 1),计算以下三维向量的加法和减法。
1. K + L2. K - L3. 2K - L题目七:向量 M = (2, 3, 4) 和向量 N = (-1, -2, -3),计算以下三维向量运算。
1. M + N2. M - 2N3. N - M题目八:已知向量 O = (-1, 2, -3) 和向量 P = (3, -2, 1),求以下结果。
1. O + P2. O - P3. -O + P题目九:向量 Q = (4, 5, 6) 与向量 R = (-7, -8, -9),计算以下向量运算。
1. Q + R2. 2Q - R3. R - 3Q题目十:向量 S = (1, -1, 2) 和向量 T = (-2, 2, -3),求以下结果。
1. S + T2. S - 2T3. T - S答案提示:在进行向量加法时,对应分量相加;进行向量减法时,对应分量相减。
对于标量乘以向量,只需将标量与向量的每个分量相乘。
高一数学平面向量的几何运算试题答案及解析

高一数学平面向量的几何运算试题答案及解析1.已知为平行四边形,若向量,,则向量为()A.B.C.D.【答案】C【解析】【考点】向量的减法2.(1)化简(2)如图,平行四边形中,分别是的中点,为与的交点,若=,=,试以,为基底表示、、.【答案】(1);(2),,.【解析】(1)根据向量加法的三角形法则,可得到;在中,可得,在中,可得,在中,由条件可得为其重心,因此.(1) 3分;(2) 6分9分是的重心, 12分.【考点】1.向量加法的三角形法则;2.向量的减法运算.3.化简得()A.B.C.D.【答案】【解析】【考点】向量的三角形法则.4.如图BC是单位圆A的一条直径, F是线段AB上的点,且,若DE是圆A中绕圆心A运动的一条直径,则的值是()A.B.C.D.【答案】【解析】因为,同理可得所以,根提题意知,所以.【考点】三角形法则的应用.5.已知平行四边形,是的中点,若,则向量= (用向量表示).【答案】【解析】在三角形中,将所求向量表示成已知向量的和与差,利用平几性质将共线向量等价转化是解题关键.【考点】向量三角形法则,6.在平行四边形中,与交于点是线段的中点,的延长线与交于点,若,,则( )A.B.C.D.【答案】D【解析】由题意可知,与相似,且相似比为,所以,由向量加减法的平行四边形法则可知,,解得,,由向量加法的三角形法则可知,,故D正确。
【考点】平面向量的加减法7.已知向量,若,则( )A.B.C.D.【答案】C【解析】因为,所以,解得,即,所以,,所以【考点】向量共线数量积公式,向量加减法坐标公式8.化简下列式子:其结果为零向量的个数是()①;②;③;④A.1B.2C.3D.4【答案】D【解析】对于①成立,对于②,对于③=,对于成立,故答案为D.【考点】向量的加减法点评:主要是考查了向量的加减法法则运用,属于基础题。
9.已知向量表示“向东航行1km”,向量表示“向南航行1km”,则向量表示( )A.向东南航行km B.向东南航行2kmC.向东北航行km D.向东北航行2km【答案】A【解析】本题充分体现向量的大小和方向两个元素,根据实际意义知道两个向量的和向量方向是东南方向,大小可以用勾股定理做向量表示“向东航行1km”,向量表示“向南航行1km”,由向量加法的几何意义知两个向量的和是向东南航行km,故选A.【考点】向量的加法几何意义点评:本题考查向量的几何意义,大小和方向是向量的两个要素,分别是向量的代数特征和几何特征,借助于向量可以实现某些代数问题与几何问题的相互转化.10.如图.点M是的重心,则为()A.B.4C.4D.4【答案】D【解析】点M是的重心,所以有点是中点,【考点】向量的加减法点评:向量的加减法运算遵循平行四边形法则,三角形法则,加法:将两向量首尾相接由起点指向中点;减法:将两向量起点放在一起,连接终点,方向指向被减向量11.D、E、F分别是三边BC、CA、AB中点,则=()A. B.C. D.【答案】A【解析】∵D、F分别是三边BC、AB中点,∴,∴,故选A【考点】本题考查了向量的运算点评:熟练掌握向量的概念及运算是求解此类问题的关键,属基础题12.设不共线,则下列四组向量中不能作为基底的是()A.与B.与C.与D.和【答案】B【解析】∵=-2(),∴()∥(),故与不能作为基底,故选B【考点】本题考查了基底的概念点评:熟练掌握基底的概念及共线向量的判定是求解此类问题的关键,属基础题13.下列计算正确的有()个①②③A.0B.1C.2D.3【答案】C【解析】根据向量的运算法则可知:式子①,正确;②,正确,式子③,∴正确的由2个,故选C【考点】本题考查了向量的运算法则点评:熟练掌握数乘向量的概念及向量的运算是求解此类问题的关键,属基础题14.已知||=3,||=4,向量+与-的位置关系为()A.平行B.垂直C.夹角为D.不平行也不垂直【答案】B【解析】因为||=3,||=4,所以(+)·(-)==0,即向量+与-的位置关系为垂直,选B。
(完整版)高中数学向量的加减与数乘知识总结+题库
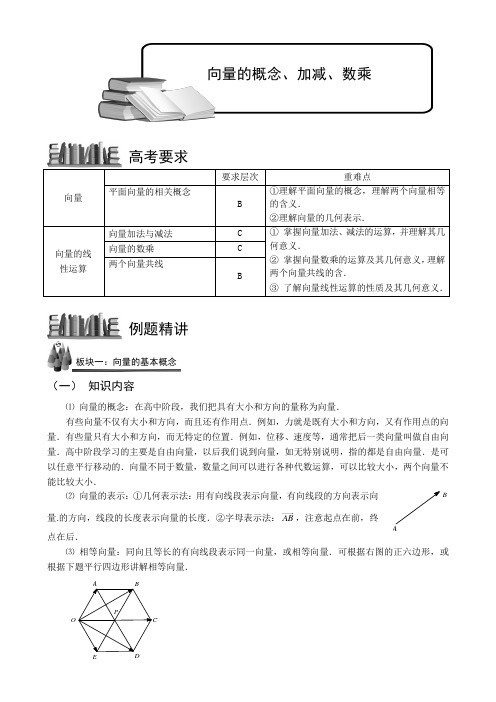
向量要求层次重难点平面向量的相关概念B①理解平面向量的概念,理解两个向量相等的含义.②理解向量的几何表示.向量的线 性运算向量加法与减法C ① 掌握向量加法、减法的运算,并理解其几何意义.② 掌握向量数乘的运算及其几何意义,理解两个向量共线的含.③ 了解向量线性运算的性质及其几何意义.向量的数乘 C 两个向量共线B(一) 知识内容⑴ 向量的概念:在高中阶段,我们把具有大小和方向的量称为向量.有些向量不仅有大小和方向,而且还有作用点.例如,力就是既有大小和方向,又有作用点的向量.有些量只有大小和方向,而无特定的位置.例如,位移、速度等,通常把后一类向量叫做自由向量.高中阶段学习的主要是自由向量,以后我们说到向量,如无特别说明,指的都是自由向量.是可以任意平行移动的.向量不同于数量,数量之间可以进行各种代数运算,可以比较大小,两个向量不能比较大小.⑵ 向量的表示:①几何表示法:用有向线段表示向量,有向线段的方向表示向量.的方向,线段的长度表示向量的长度.②字母表示法:AB ,注意起点在前,终点在后.⑶ 相等向量:同向且等长的有向线段表示同一向量,或相等向量.可根据右图的正六边形,或根据下题平行四边形讲解相等向量.POE DCBA例题精讲高考要求板块一:向量的基本概念向量的概念、加减、数乘B已知E、F、G、H分别是平行四边形ABCD边AB、DC、BC、AD的中点,O为对角线AC与BD的交点,分别写图中与DF,BH,AO相等的向量.解:DF FC GO OH AE EB========BH HC AG GD=AO OC⑷向量共线或平行:通过有向线段AB的直线,叫做向量AB的基线.如果向量的基线互相平行或重合,则称这些向量共线或平行.向量a平行于向量b,记作a∥b.说明:共线向量的方向相同或相反,注意:这里说向量平行,包含向量基线重合的情形,与两条直线平行的概念有点不同.事实上,在高等数学中,重合直线是平行直线的特殊情形.⑸零向量:长度等于零的向量,叫做零向量.记作:0.零向量的方向不确定,零向量与任意向量平行.⑹用向量表示点的位置:任给一定点O和向量a,过点O作有向线段OA a=,则点A相对于点O 位置被向量a所唯一确定,这时向量OA又常叫做点A相对于点O的位置向量.⋅=.AB AC3(二)典例分析:【例1】给出命题⑴零向量的长度为零,方向是任意的.⑵若a,b都是单位向量,则a=b.⑶向量AB与向量BA相等.⑷若非零向量AB与CD是共线向量,则A,B,C,D四点共线.以上命题中,正确命题序号是()A.⑴ B.⑵ C.⑴⑶ D.⑴⑷【例2】下列命题中正确的有:( )⑴四边形ABCD是平行四边形当且仅当AB DC=;⑵向量AB与BA是两平行向量;⑶向量AB与CD是共线向量,则A,B,C,D四点必在同一直线上;⑷单位向量不一定都相等;⑸a 与b 共线,b 与c 共线,则a 与c 也共线; ⑹平行向量的方向一定相同;【变式】 平面向量a ,b 共线的充要条件是( )A .a ,b 方向相同B .a ,b 两向量中至少有一个为零向量C .λ∃∈R ,b a λ=D .存在不全为零的实数1λ,2λ,120a b λλ+=【例3】 ⑴设0a 为单位向量,①若a 为平面内的某个向量,则0a a a =⋅;②若a 与0a 平行,则0a a a =⋅;③若a 与0a 平行且1a =,则0a a =.上述命题中,假命题个数是( ) A .0B .1C .2D .3⑵若非零向量a ,b 满足a b b -=,则( )A .22b a b >-B .22b a b <-C .22a a b >-D .22a a b <-【变式】 给出下列命题:①若a b =,则a b =;②若A B C D ,,,是不共线的四点,则AB DC =是四边形ABCD 为平行四边形的充要条件; ③若a b =,b c =,则a c =; ④a b =的充要条件是a b =且a b ∥; ⑤若a b ∥,b c ∥,则a c ∥;其中正确的序号是 .【例4】 如图所示,1A ,2A ,3A ,…,8A 是O 的8个等分点,以1A ,2A ,…,8A 及O 这9个点中任意两个为起始点和终点的向量中,模等于半倍的向量有多少个?【变式】 (海淀区2008-2009学年度第一学期期末试卷)如图,在正方形ABCD 中,下列描述中正确的是( )A .AB BC =B .AB CD =C .2AC AB = D.AB BC AB BC +=-A 35A D CBA(一) 知识内容1. 向量的加法:a+babbabb aba a+b CCOBa+b b+ccbaa+b+c⑴ 向量加法的三角形法则:已知向量,a b ,在平面上任取一点A ,作AB a =,BC b =,再作向量AC ,则向量AC 叫做a 和b 的和(或和向量),记作a b +,即a b AB BC AC +=+=. ⑵ 向量求和的平行四边形法则:① 已知两个不共线的向量a ,b ,作AB a =,AD b =,则A ,B ,D 三点不共线,以AB ,AD 为邻边作平行四边形ABCD ,则对角线上的向量AC a b =+,这个法则叫做向量求和的平行四边形法则. ② 向量的运算性质:向量加法的交换律:a b b a +=+ 向量加法的结合律:()()a b c a b c ++=++关于0:00a a a +=+= ⑶ 向量求和的多边形法则:已知n 个向量,依次把这n 个向量首尾相连,以第一个向量的始点为始点,第n 个向量的终点为终点的向量叫做这n 个向量的和向量.这个法则叫做向量求和的多边形法则.2. 向量的减法:dcbaa+b+c+dbacda-b baO⑴ 相反向量:与向量a 方向相反且等长的向量叫做a 的相反向量,记作a -. 零向量的相反向量仍是零向量.⑵ 差向量定义:如果把两个向量的始点放在一起,则这两个向量的差是以减向量的终点为始点,被减向量的终点为终点的向量.推论:一个向量BA 等于它的终点相对于点O 的位置向量OA 减去它的始点相对于点O 的位置向量OB ,或简记“终点向量减始点向量”.⑶ 一个向量减去另一个向量等于加上这个向量的相反向量板块二:向量的加减运算(三)典例分析:【例5】 设P 是ABC △所在平面内的一点,2BC BA BP +=,则( )A .0PA PB += B .0PC PA += C .0PB PC +=D .0PA PB PC ++=【变式】 如图,在平行四边形ABCD 中,下列结论中错误的是( )A .AB DC = B .AD AB AC += C .AB AD BD -= D .0AD CB +=【例6】 D 是ABC ∆的边AB 上的中点,则向量CD =( )A .12BC BA -B .12BC BA -- C .12BC BA -+D .12BC BA +.【例7】 设D ,E ,F ,分别是ABC ∆的三边BC 、CA 、AB 上的点,且2,DC BD =2,CE EA =2,AF FB =则AD BE CF ++与BC ( ) A.反向平行B.同向平行C.互相垂直D.既不平行也不垂直【例8】 根据图示填空:⑴ a b += ;⑵ e b d ++= .【例9】 化简下列各式:⑴ 7()8()a b a b +--; ⑵ 12(2)(432)6a b c a b c +---+【例10】 如图,D ,E ,F 分别是ABC ∆的边AB ,BC ,CA 的中点,则( )A .0AD BE CF ++=B .0BD CF DF -+=C .0AD CE CF +-= D .0BD BE FC --=DCBAFE DCBA【例11】 已知O A B ,,是平面上的三个点,直线AB 上有一点C ,满足20AC CB +=,则OC =( )A .2OA OB - B .2OA OB -+C .2133OA OB -D .1233OA OB -+【例12】 如图所示,E F 、是四边形ABCD 的对角线AC BD 、的中点,已知,AB a CD c ==,求向量EF .【例13】 已知O A B ,,是平面上的三个点,直线AB 上有一点C ,满足20AC CB +=,则OC =( )A .2OA OB - B .2OA OB -+C .2133OA OB -D .1233OA OB -+【例14】 已知任意四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:1()2EF AB DC =+.【例15】 ⑴ 已知ABCD □的两条对角线交于点O ,设AB a =,AD b =,用向量a 和b 表示向量BD ,AO .⑵ 已知ABCD □的两条对角线交于点O ,设对角线AC =a ,BD =b ,用a ,b 表示BC ,AB .CAAC【例16】 设P 是正六边形OABCDE 的中心,若OA a =,OE b =,试用向量a ,b 表示OB 、OC 、ODOE .【例17】 在ABC △中,AB c =,AC b =.若点D 满足2BD DC =,则AD =( )A .2133b c +B .5233c b -C .2133b c -D .1233b c +⑵在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点.若AC AE AF λμ=+,其中λ,μ∈R ,则λμ+= .【变式】 证明:若向量,,OA OB OC 的终点A B C 、、共线,当且仅当存在实数,λμ满足等式1λμ+=,使得OC OB OA λμ=+.OCA【变式】 如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =,则m n +的值为.ONM CBA【变式】 在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的点.且1BF a FC a =-,1DE bEC b=-, 若AC AE AF λμ=+,其中λ,μ∈R ,则λμ+= .FB【变式】 设正六边形ABCDEF 的对角线,AC CE 分别被内点,M N 分成为AM CNr AC CE==,如果,,B M N 共线,求r 的值.【变式】 证明:若向量,,OA OB OC 的终点A B C 、、共线,当且仅当存在实数,λμ满足等式1λμ+=,使得OC OB OA λμ=+.(一) 知识内容3. 数乘向量:定义:实数λ和向量a 的乘积是一个向量,记作a λ,且a λ的长a a λλ=<教师备案> 判断正误:已知λμ∈R ,.①()a b a b λλλ+=+;(√) ②()a a a λμλμ+=+;(√) ③()()a a λμλμ=;(√) ④()()a b a b λμλμ+=++.(×)4. 向量共线的条件⑴ 平行向量基本定理:如果a b λ=,则a ∥b ;反之,如果a ∥b ,且0b ≠,则一定存在唯一的一个实数λ,使a b λ=.⑵ 单位向量:给定一个非零向量a ,与a 同方向且长度等于1的向量,叫做向量a 的单位向量.如果a 的单位向量记作0a ,由数乘向量的定义可知0a a a =或0a a a=.(三)典例分析:【例18】 设12,e e 是不共线的向量,已知向量1212122,3,2AB e ke CB e e CD e e =+=+=-,若A B D 、、三点共线,求k 的值.OCBA板块三:向量的数乘与共线【变式】 设a ,b ,c 为非零向量,其中任意两个向量不共线,已知a b +与c 共线,且b c +与a 共线,则b a c ++= .【变式】 已知,a b 是不共线的向量,25AB a b =+,8BC a b =-+,3()CD a b =-,则A B D 、、C 、四点中共线的三点是___________【变式】 设,a b 是不共线的两个向量,已知22(2)AB ka k b =+-,BC a b =+,2CD a b =-,若A B D、、三点共线,求k 的值.【变式】 证明对角线互相平分的四边形是平行四边形.ODCBA【例19】 如图,平行四边形ABCD 中,E F 、分别是BC DC 、的中点,G 为DE BF 、的交点,若AB =a ,AD =b ,试以a ,b 为基底表示DE 、BF 、CG .F CBA【变式】 如图,在∆ABC 中,AD 、BE 、CF 分别是BC 、CA 、AB 上的中线,它们交于点G ,则下列各等式中不正确的是( ) A .23BG BE = B .2CG GF =C .12DG AG =D .121332DA FC BC +=【变式】 已知五边形ABCDE ,M 、N 、P 、Q 分别是边AB 、CD 、BC 、DE 的中点,K 、H 分别是MN 和PQ 的中点,求证:KH 平行且等于14AE .ED CBA MNP Q K HGFEDC BA【变式】 如图,E 、F 分别是平行四边形ABCD 的边AD 、CD 的中点,BE 、BF 与对角线AC 分别交于点R 和点T .求证AR RT TC ==.(向量法)TRF E D CB A【变式】 四边形ABCD 中,E ,F ,M ,N 分别为BC ,AD ,BD ,AC 的中点,O 为MN 的中点,试用向量的方法证明:O 也是EF 的中点.FEO MNDCB A【变式】 ⑴在平行四边形ABCD 中,AC 与BD 交于点O E ,是线段OD 的中点,AE 的延长线与CD 交于点F .若AC a =,BD b =,则AF =( )A .1142a b +B .2133a b +C .1124a b +D .1233a b +⑵如图,两块斜边长相等的直角三角板拼在一起.若AD xAB y AC =+, 则x = ,y = .OF E DCBA【变式】 若等边ABC ∆的边长为23,平面内一点M 满足1263CM CB CA =+,则MA = ,MB = .(用CB ,CA 向量表示) FECBA M三角形有五心:内心、外心、垂心、重心和旁心,这里我们用向量这个工具来研究三角形的前四心,有些地方涉及到数量积,老师可以根据情况先补充数量积的知识,或将这些地方跳过去以后再讲.板块四:三角形有五心相关证明60︒45︒EDBCA⑴内心:过点A ,方向平行于向量()(0)||||AB ACAB AC λλ+≠的直线过ABC ∆的内心(BAC ∠的角分线所在直线);||||||0AB PC BC PA CA PB P ++=⇔为ABC ∆的内心;⑵外心:PA PB PC ==⇔P 为ABC ∆的外心;⑶垂心:PA PB PB PC PC PA P ⋅=⋅=⋅⇔为ABC ∆的垂心(先补充数量积的相关知识) ⑷重心:0PA PB PC P ++=⇔为ABC ∆的重心.另外:在ABC ∆中,G 为平面上任意一点,有1()3GO GA GB GC =++⇔O 为ABC ∆的重心1()()()()03GO GA GB GC GA GO GB GO GC GO =++⇒-+-+-=,即0OA OB OC ++=,知O 为ABC ∆的重心;若O 为ABC ∆的重心,则11()(3)33GA GB GC GO OA OB OC ++=+++20OA OB OC OA OE ++=+=,故1()3GA GB GC GO ++=.【例20】 在OAB ∆中,M 为OB 的中点,N 为AB 的中点,P 为,ON AM 交点,利用向量证明23AP AM =,即重心为中线的一个三等分点.【变式】 ⑴已知3()2(2)4()0m a m a m a b -++-+-=,则m =⑵已知a ,b 方向相同,且3a =,7b =,则2a b -=【变式】 若O 是ABC ∆内一点,0OA OB OC ++=,则O 是ABC ∆的( )A.内心 B .外心 C .垂心 D .重心【变式】 (2003年天津)O 是平面内一定点,A ,B ,C 是平面上不共线的三个点,动点P 满足AB AC OP OA AB AC λ⎛⎫ ⎪=++ ⎪⎝⎭,[0,)λ∈+∞,则P 的轨迹一定通过ABC ∆的( ) A .外心 B .内心 C .重心 D .垂心【变式】 若点O 是ABC △的外心,且0OA OB CO ++=,则内角C 的大小为____OEDC BA【变式】 已知点G 是ABC ∆的重心,过G 作直线与AB 、AC 两边分别交于M 、N 两点,且设AM xAB =,AN y AC =,则113x y+=.NMGCBA【变式】 非正ABC △的外接圆的圆心为O ,两条边上的高的交点为H ,()OH m OA OB OC =++,求实数m 的值.【变式】 如图,设G 为OAB ∆的重心,过G 的直线与,OA OB 分别交于P 和Q ,已OP hOA =,OQ kOB =,OAB ∆与OPQ ∆的面积分别为S 和T .求证:⑴113h k+=;⑵4192S T S ≤≤.【例21】 已知任意四边形ABCD 中,,E F 分别是,AD BC 的中点,求证:1()2EF AB DC =+.E BBAMG QP O【例22】 如图所示,E F 、是四边形ABCD 的对角线AC BD 、的中 点,已知,AB a CD c ==,求向量EF .A【变式】 在平行四边形ABCD 中,AC 与BD 交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F .若AC a =,BD b =,则AF =( )A . 1142a b +B . 2133a b +C . 1124a b +D . 1233a b +【变式】 已知点M 是ABC ∆的重心,,MA a MB b ==,用,a b 表示,,AB AC BC .FEDCBAM【变式】 M 、N 分别是ABC ∆的边AB 、AC 的靠近A 的三等分点.求证:13MN BC =,且MN ∥BC .【变式】 已知矩形ABCD 中,宽为2,长为AB a =,BC b =,AC c =,试作出向量a b c ++,并求其长度.OFE DCBA【变式】 如图,在ABC △中,点O 是BC 的中点,过点O 的直线分别交直线AB ,AC 于不同的两点M N ,,若AB mAM =,AC nAN =,则m n +的值为 .ONMCBA。
高一数学向量同步练习向量加、减法二 试题

心尺引州丑巴孔市中潭学校高一数学向量同步练习向量加、减法二一、选择题 “假设a ∥b ,b ∥c ,那么a ∥c 〞 〔 〕 A.总成立 B.当a ≠0时成立 C.当b ≠0时成立 D.当c ≠0时成立 2、以下四式不能化简为AD 的是 〔 〕 A.〔AB +CD 〕+BC B.〔AD +MB 〕+〔BC +CM 〕 C. MB +-AD BM D. OC OA -+CD3、p :a 与b 方向相反; q :a 与b 互为相反向量; r :|a |=|b |. 那么 〔 〕A.p 是q 的必要条件,q 是r 的必要条件B.p 是q 的充分条件,q 是r 的充分条件C.p 是q 的必要条件,q 是r 的充分条件D.p 是q 的充分条件,q 是r 的必要条件4、M 是△ABC 的重心,那么以下各向量中与AB 共线的是 〔 〕 A.AM +MB +BC B.3AM +AC C. AB +BC +AC D.AM+ BM +CM 5、在平行四边形ABCD 中,BC +DC +BA 等于 〔 〕A.BCB.DAC.ABD.AC6、在△ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,那么AF —DB = 〔 〕A.FDB.FEC.FCD.BE二、填空题1、OA =a ,OB =b ,且|a |=|b |=4,∠AOB=600,那么|a +b |= ,|a b -|= ; a +b 与a 的夹角是 ;a b -与a 的夹角是 ;△AOB 的面积是 。
2、不共线向量a ,b 满足 时,使得a +b 平分a ,b 间的夹角。
3、向量|a |=2,|b |=8,那么|a +b |的最大值是 ,|ab -|的最小值是 。
4、如图5—5,在ABCD 中,a AB =,b DB =,那么=AD _______,=AC_______。
5、为与的和向量,且=,那么=______,=________。
6、a 、b 是非零向量,假设||||||b a b a +=-,那么a 、b 应满足条件________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题:
1、下列说法正确的有( )个.
①零向量是没有方向的向量,②零向量的方向是任意的,③零向量与任一向量共线,④零向
量只能与零向量共线.
A.1 B.2 C.3 D.以上都不对
2、下列物理量中,不能称为向量的有( )个.
①质量②速度③位移④力⑤加速度⑥路程
A.0 B.1 C.2 D.3
3、已知正方形ABCD的边长为1, = a , = b , = c,则| a+b+c|等于()
A.0 B.3 C.2 D.22
4、在平行四边形ABCD 中,设= a, = b,= c, = d,则下列不等式中不正确的是
()A.a+b=c B.a-b=d C.b-a=d D.c-d=b-d
5、△ABC中,D,E,F分别是AB、BC、CD的中点,则-等于()
A.B .C.D.
6、如图.点M是△ABC的重心,则MA+MB-MC为()
A.0 B.4
C .4 D.4
7、在正六边形ABCDEF中,不与向量相等的是()
A .+
B .-
C .+D.+
8、a=-b是|a| = |b|的()
A.充分非必要条件B.必要非充分条件
C.充要条件D.既非充分也非必要条件
二、填空题:
9、化简:+ + + + = ______.
10、若a =“向东走8公里”,b =“向北走8公里”,则| a + b |=___,a +b 的方向是_ ____. 11、已知D 、E 、F 分别是△ABC 中BC 、CA 、AB 上的点,且
=
3
1
, =
3
1 , =
3
1,设 = a , = b ,则 = __________.
12、向量a,b 满足:|a |=2,|a +b |=3,|a -b |=3,则|b |=_____. 三、解答题:
13、如图在正六边形ABCDEF 中,已知:= a ,
= b ,试用a 、b 表示向量
,
,
,
.
14、如图:若G 点是△ABC 的重心,求证: +
+
= 0 .
15、求证:|a +b | 2 +|a -b | 2 =2 (|a | 2+|b | 2).
16、如图 ABCD 是一个梯形,AB ∥CD 且AB=2CD,M,N 分别是DC 和AB 的中点,若
= a ,
= b ,试用a,b 表示
和
.
一、BCDBD DCA
E
二、(9)0 (10)28
千米、东偏北45° (11)b a 3
1
32+
- (12)5
三、(13)分析:连接AD 、BE 、FC ,由正六边形性质知它们交于点O ,再由正六边形性质知ABOF ,AOCB ,BODC 是全等的平行四边形.
F O C
A B
)(22,b a AO AO AO OD AO b AF BO CD b a AO BC +==+=+===+==∴
注:向量的加法依赖于图形,所以做加法时要尽量画出图形,以便更好的理解题意.另外也要注意三角形法则
和
平
行
四
边
形
的
运
用
.
即
“
首
尾
相
接
”
如
."".的平行四边形的对角线起点相同和AE DE CD BC AB =+++
(14)证明:延长GF 到H ,使GF=FH.连结HA 、HB ,则四边形AGBH 平行四边形,于是
,2,,2=+=++∴=∴∆==+ABC G 的重心为Θ(15)分a 、b 是否共线两种情况讨论.若a 、b 共线,则等式显然成立.若a 、b 不共线,则由向量的加、减法的几何意义可证.注:这是一个很有用的结论,请同学们记住.
(16)分析:解:连结CN ,将梯形ABCD 为平行四边形ANCD 和△BCN ,再进行向量运算.连结CN,N 是AB 的中点,
.
41
21,,0,,,//b a AN CN CM CN MN a b CN NB BC BC NB b ABCD DC AN DC AN -=+=-=∴-=--=∴=++
-=-=∴=ΘΘ又是平行四边形四边形且 注:只要向量a 、b 不共线,任何向量都可用a 、b 表示出来.在后面我们将证明这个定理。
