高一数学向量的加法一 人教版
向量的加法运算-高一数学教材配套教学课件(人教A版2019必修第二册)

新知探究
根据数的运算的学习经验,定义了一种运算,就要研究相应的运算律,
运算律可以有效地简化运算.
思考:数的加法满足交换律、结合律,向量的加法是否也满足交换律和结
合律呢? 非零向量,,研究
Ԧ
Ԧ + 与 + Ԧ .
作 = ,
Ԧ
= ,
以,为邻边作□,容易发现 = , = ,
Ԧ
故 = + = Ԧ + .
又 = + = + ,
Ԧ
所以Ԧ + = + .综上,向量的加法满足交换律.
Ԧ
+
新知探究
思考:你能否验证结合律,即(Ԧ + ) + Ԧ = Ԧ + ( + )呢?
Ԧ
如图,作 = ,
[3,13] .
牛刀小试:若|| = 8,|| = 5,则||的取值范围是__________
新知探究
思考:如图,在光滑的平面上,一个物体同时受到两个外力1 与2 的作用,
你能作出这个物体所受合力吗?
我们知道,合力在以,为邻边的平行四
2
边形的对角线上,并且大小等于这条对角线的长.
B.BE
C. AD
D. CF
)
E
F
A
D
思路:用相等向量代换,使首尾相接
C
B
习题演练
变2.如图所示,在∆中,为重心,,,分别是, , 的中
点,化简下列三式.
(1) + +
(2) + + .
向量的加法高一上学期数学人教B版(2019)必修第二册

首先在平面内任取一点 O,作向量=a,=b, =c,以 OA,OB 为邻边作
▱OADB,连接 OD,则 = + =a+b.再以 OD,OC 为邻边作▱ODEC,连接
OE,则 = + =a+b+c 即为所求.
变式探究1在例1(1)条件下,求 + .
1.对向量加法的两种法则的理解
(1)当两个向量不共线时,三角形法则和平行四边形法则的实质是一样的,
三角形法则作出的图形是平行四边形法则作出的图形的一半.但当两个向
量共线时,平行四边形法则便不再适用.
(2)向量加法的三角形法则和平行四边形法则就是向量加法的几何意义.
(3)向量a,b的模与a+b的模之间满足不等式||a|-|b||≤|a+b|≤|a|+|b|.
A.a∥b,且a与b方向相同
B.a,b是共线向量且方向相反
பைடு நூலகம்
C.a=b
D.a,b无论什么关系均可
解析 当两个非零向量a,b不共线时,a+b的方向与a,b的方向都不相同,且
|a+b|<|a|+|b|;当两个非零向量a,b同向时,a+b的方向与a,b的方向都相同,
且|a+b|=|a|+|b|;当两个非零向量a,b反向且|a|<|b|时,a+b的方向与b的方
向相同,且|a+b|=|b|-|a|,所以对于非零向量a,b,且|a+b|=|a|+|b|,有a∥b,且a
与b方向相同.故选A.
2.[北师大版教材习题]填空:(1) + =
(2) + + =
0
.
向量的加法运算(课件)高一数学(人教A版2019必修第二册)

经 典 例 题 题型一 向量加法的三角形法则和平行四边形法则
作法 1:如图 1 所示,首先在平面内任取一点 O,作向量O→A=a,接着作向量 A→B=b,则得向量O→B=a+b;然后作向量B→C=c,则向量O→C=(a+b)+c=a +b+c 即为所求.
经 典 例 题 题型一 向量加法的三角形法则和平行四边形法则
课堂小结
1.三角形法则和平行四边形法则都是求向量和的基本方法.当两个向 量首尾相连时常选用三角形法则,当两个向量共始点时,常选用平行四 边形法则. 2.向量的加法满足交换律,因此在进行多个向量的加法运算时,可以 按照任意的次序和任意的组合去进行. 3.向量加法的三角形法则可以推广为多个向量求和的多边形法则,即 把每个向量平移,使这些向量首尾相连,则由第一个向量的起点指向最 后一个向量终点的向量就是这些向量的和向量.
点拨:根据向量加法的三角形法则以及“三角形中两边之和大于第 三边,两边之差小于第三边”,可以得出上述结论.
三.向量加法的运算律 ①交换律:a+b=b+a; ②结合律:a+b+c=(a+b)+c=a+(b+c).
小试牛刀
思维辨析(对的打“√”,错的打“×”)
(1)任意两个向量的和仍然是一个向量.( √ ) (2)两个向量相加实际上就是两个向量的模相加.( × ) (3)对于任意两个向量,都可利用平行四边形法则求出它们的和向量.( × ) (4)若A→B+B→C+C→A=0,则 A,B,C 为一个三角形三个顶点.( × ) (5)对于任意的点 A,B,C,D,都有A→B+B→C+C→D+D→A=0.( √ ) (6)如果 a,b 是共线的非零向量,那么 a+b 的方向必与 a,b 之一的方向相同.( × )
当堂达标
5.已知非零向量 a,b,|a|=8,|b|=5,则|a+b|的最大值为__1_3___.
向量的加法运算课件高一下学期数学人教A版

求两个向量和的运算叫做向量的加法.
A
B
a
a
b
a+b
b
O
各向量“尾首相连”,和向量由第一个 向量的起点指向最后一个向量的终点.
根据向量加法的定义得出的求向量和的方法,
称为向量加法的三角形法则.
向量加法的拓展
各向量“尾首相连”,和向量由第一个 向量的起点指向最后一个向量的终点.
【1】在三角形ABC中,AB+BC+CA=0;AB+BC=AC
情景一:如图,某人从A点走到B.然后从B点走到C.这个人所走过的位移是多少?
C
分析 :由物理知识可以知道:
从A点到B点然后到C点的 合位移,就是从A点到C点 的位移.
A
AB + BC = AC
向量的加法的定义:求两个向量和
B
的运算叫做向量的加法
已知向量a和b,在平面内任取一点O,作OA=a, AB=b,则向量OB叫做a和b的和,记作a+b.即a+b= OA+AB=OB.
O·
F1 A·
从运算的角度看,F可以看作是 F1与 F2
的和,即力的合成可以看作向量的加法。
向量加法的平行四边形法则.
B
C
起点相同,
对角线为和
b
a
力的合成可以看作向量
加法的平行四边形法则
a +b
b
的物理模型
O
a
A
如图,以同一点O为起点的两个已知向量a和b为邻边作平
行四边形OACB,则以O为起点的对角线OC就是a与b的和,我
D
C
A
B
解:(1)如图所示,AD表示船速,AB表示水速,
向量的加法运算课件高一下学期数学人教A版(2019)2

a
O
A
b
| a | | b | | a b || a | | b |
ab
B
a
b
ab
ba
ab
| a b || a | | b |
| a b | | a | | b |
结论
一般地,对两个非零向量a,b, 有
| a | | b | | a b || a | | b |
当a,b同向时, 右边等号成立; a,b反向时,左边等号成立.
一是线性运算(加法,减法,数乘); 二是积运算(数量积,向量积). 本节我们就来研究平面向量的线性运算,并探究其性质,体 会向量运算的作用. 接下来我们首先学习向量的加法运算.
知识探究 (一)
思考1:物理中的位移、力都是向量,它们可以合成,这给 我们以向量加法的启示:从位移的合成、力的合成中引入向量的
B
F2
C
OC=F1+F2
O
F1 A
这种运算方法称为向量加法的平行四边形法则.
向量加法的平行四边形法则
先将相加的两个向量平移至起 点重合;
再以这两条线段为邻边作平行 四边形;
最后作出这两个向量所夹的对 角线 ,则这条对角线所对应的有 向线段就表示它们的和.
B b
O
a
A
起点重合,
夹出和.
C
返回
向量加法的运算法则
(1)试用向量表示江水速度、船速以及船实际航行的速度; (2)求船实际航行速度的大小(精确到0.1) 和方向(用与江水速度 间的夹角,精确到1°). (参考数据:261 16.2,tan 68 2.5)
解:(1)
CD
北
AB表示江水速度; AC表示船速;
船速 船的实 际速度
【课件】向量的加法运算 向量的减法运算课件高一下学期数学人教A版(2019)必修第二册

6.2.1 向量的加法运算 6.2.2 向量的减法运算
教学目标
借助实例和平面向量的几何意义,掌握平面向量
1
的加法、减法运算及其运算规律.
2 理解平面向量的加法、减法运算的几何意义.
(1)向量的加法:求两个向量和的运算, 叫做向量的加法.
对于零向量与任意向量a ,规定a+0 0 a a .
本节课学习了平面向量的加法、减 法运算.
解析:由题意和图形可知 BAC 90 ,因为| AB | 300 ,| BC | 300 2 ,
所以| AC | 300 ,因为 ABC 45 ,A 地在 B 地南偏东 30°的方向处. 所以 C 地在 B 地南偏东 75°的方向处. 故飞机从 B 地向 C 地飞行的方向为南偏东 75°.
9.化简下列各式: (1) ( AB MB) (OB MO) . (2) AB AD DC .
B a-b
b Oa A
例 1 长江两岸之间没有大桥的地方,常常通过轮渡进行运 输.如图,一艘船从长江南岸 A 地出发,垂直于对岸航行, 航行速度的大小为 15 km/h,同时江水的速度为向东 6 km/h. (1)用向量表示江水速度、船速以及船实际航行的速度; (2)求船实际航行的速度的大小(结果保留小数点后一位)与方向(用与江水速度 间的夹角表示,精确到 1°).
(2)向量加法的三角形法则:已知非零向量a,b ,在平面内
任取一点 A ,作 AB a , BC b ,则向量 AC 叫做a 与b 的和,
记作 a b ,即 a b AB BC AC .如图.
C
b a+b
Aa
B
(3)向量加法的平行四边形法则:已知两个不共线向量a,b , 作 AB a , AD b ,以 AB , AD 为邻边作 ABCD ,则对角线 上的向量 AC a b .如图.
高一数学人教A版平面向量的加法运算

AB
C a + b = AC
a
反向
b
a C A bB
AC = AB + BC
a + b = AC
对于零向量与任意向量a,我们规定 a+0=0+a=a
向量a , b的模与a + b的模的关系
问题2. a + b ,a ,b 之间有什么关系?
不共线向量
作 AB=a ,BC=b,则 AC=a + b.
所以 a + b a + b .
a+ b
b
A
a
B
不共线向量
作 AB=a ,BC=b,则 AC=a + b. 三角形三边关系:任意两边之差小于第三边,
C
a+ b
b
A
a
B
不共线向量
作 AB=a ,BC=b,则 AC=a + b.
三角形三边关系:任意两边之差小于第三边,
C 可得 | AB | | BC | | AC | ,
a
b
Aa
b B
向量加法的三角形法则
求两个向量和的运算,叫作向量的加法. 这种求向量和的方法,称为向量加法的三角形法则.
C
a
b
Aa
b B
向量加法的三角形法则
求两个向量和的运算,叫作向量的加法. 这种求向量和的方法,称为向量加法的三角形法则.
位移的合成可以看作向量加法三角形法则的物理模型.
C
a
b
Aa
平面向量的加法运算
高一年级 数学
引言
物理背景
向量的运算
启发 物理背景 引进
向量的运算
启发 物理背景 引进
高中数学 向量的加法教案 新人教A版必修1
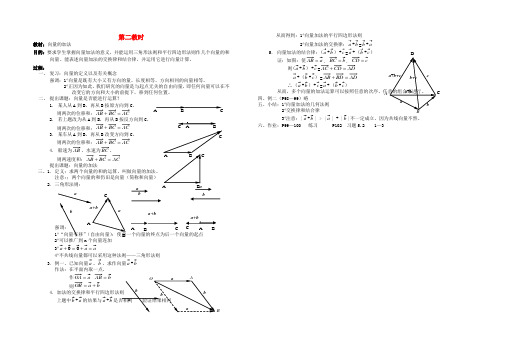
第二教时教材:向量的加法目的:要求学生掌握向量加法的意义,并能运用三角形法则和平行四边形法则作几个向量的和向量。
能表述向量加法的交换律和结合律,并运用它进行向量计算。
过程: 一、 复习:向量的定义以及有关概念强调:1︒向量是既有大小又有方向的量。
长度相等、方向相同的向量相等。
2︒正因为如此,我们研究的向量是与起点无关的自由向量,即任何向量可以在不改变它的方向和大小的前提下,移到任何位置。
二、 提出课题:向量是否能进行运算?1. 某人从A 到B ,再从B 按原方向到C ,则两次的位移和:=+2. 若上题改为从A 到B ,再从B 按反方向到C ,则两次的位移和:AC BC AB =+3. 某车从A 到B ,再从B 改变方向到C , 则两次的位移和:=+4. 船速为,水速为,则两速度和:=+ 提出课题:向量的加法三、1.定义:求两个向量的和的运算,叫做向量的加法。
注意:;两个向量的和仍旧是向量(简称和向量) 2.三角形法则:强调: 1︒“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点2︒可以推广到n 个向量连加3︒a a a =+=+004︒不共线向量都可以采用这种法则——三角形法则 3.例一、已知向量、,求作向量+ 作法:在平面内取一点, 作a OA = b AB = 则+=4.加法的交换律和平行四边形法则上题中+的结果与+是否相同验证结果相同 从而得到:1︒向量加法的平行四边形法则 2︒向量加法的交换律:+=+ 5. 向量加法的结合律:(+) +=+ (+)证:如图:使=, =, =则(+) +==+ a + (b +c ) =AD BD AB =+∴ (a +b ) +c =a + (b +c )从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行。
四、例二(P98—99)略五、小结:1︒向量加法的几何法则 2︒交换律和结合律 3︒注意:|a +b | > |a | + |b |不一定成立,因为共线向量不然。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学向量的加法一
一.课题:向量的加法
二.教学目标:1.理解向量加法的概念及向量加法的几何意义;
2.熟练掌握向量加法的平行四边形法则和三角形法则,会作已知两向量的和向量;
3.理解向量的加法交换律和结合律,并能熟练地运用它们进行向量计算。
三.教学重、难点:1.如何作两向量的和向量;
2.向量加法定义的理解。
四.教学过程:
(一)复习:
1.向量的概念、表示法。
2.平行向量、相等向量的概念。
3.已知O 点是正六边形ABCDEF 的中心,则下列向量组中含有相等向量的是( ) (A )OB uuu r 、CD uuu r 、FE u u u r 、CB u u u r (B )AB u u u r 、CD uuu r 、FA u u u r 、DE u u u r (C )FE u u u r 、AB u u u r 、CB u u u r 、OF u u u r (D )AF u u u r 、AB u u u r 、OC u u u r 、OD u u u r
(二)新课讲解: 1.向量的加法:求两个向量和的运算叫做向量的加法。
表示:AB BC AC +=u u u r u u u r u u u r . 规定:零向量与任一向量a r ,都有00a a a +=+=r r r r r . 说明:
①共线向量的加法: a r b r a b +r r
②不共线向量的加法:如图(1),已知向量a r ,b r ,求作向量a b +r r . 作法:在平面内任取一点O (如图(2)),作OA a =u u u r r ,AB b =r r ,则OB a b =+u u u r r r . (1) (2)
2.向量加法的法则:
(1)三角形法则:根据向量加法定义得到的求向量和的方法,称为向量加法的三角形法则。
表示:AB BC AC +=u u u r u u u r u u u r . (2)平行四边形法则:以同一点A 为起点的两个已知向量a r ,b r 为邻边作ABCD Y ,则 则以A 为起点的对角线AC u u u r 就是a r 与b r 的和,这种求向量和的方法称为向量加法的平行
四边形法则。
b r a r O B A b r a r b r a r A B C D
A B C
3.向量的运算律: 交换律:a b b a +=+r r r r . 结合律:()()a b c a b c ++=++r r r r r r .
说明:多个向量的加法运算可按照任意的次序与任意的组合进行:
例如:()()()()a b c d b d a c +++=+++r r r u r r u r r r ;[()]()a b c d e d a c b e ++++=++++r r r u r r u r r r r r . 4.例题分析:
例1.如图,一艘船从A
点出发以/km h 的速度向垂直于对岸的方向行驶,同时河水的流速为2/km h ,求船实际航行速度的大小与方向(用与流速间的夹角表示)。
解:设AD u u u r 表示船向垂直与对岸行驶的速度,AB u u u r 表示水流的 速度,以AD 、AB 为邻边作ABCD Y ,则AC u u u r 就是船实际 航行的速度, 在Rt △ABC 中,||AB uuu r 2=,||BC uuu
r =,
∴||AC =u u u r
4==,
∴tan 2
CAB
== ∴60CAB ∠=o . 答:船实际航行速度的大小为4/km h ,方向与流速间的夹角为60o . 例2.已知矩形ABCD 中,宽为2
,长为AB u u u r a =r ,BC b =u u u r r ,AC c =u u u r r ,试作出向量a b c ++r r r ,并求出其模的大小。
解:作CE AC =u u u r u u u r ,则如图a b c ++r r r AE =u u u r a b c ++r r r 22AB BC AC AC c =++==u u u r u u u r u u u r u u u r r ,
∴|||2|8a b c AC ++===r r r u u u r , 答:向量a b c ++r r r 就是向量AE ,其模为8
例3.一架飞机向北飞行200
五.课堂练习:(1)化简0AB BC CD DA +++=u u u r u u u r u u u r u u u r r ;(2)课本99P 练习:2,3,4题.
六.小结:1.理解向量加法的概念及向量加法的几何意义;
2.熟练掌握向量加法的平行四边形法则和三角形法则。
七.作业:1.书102P 习题5.2 第2,3题,6(2)
(3),7. 2.补充:已知两个力1F ,2F 的夹角是直角,且知它们的合力F 与1F 的夹角是60o
,||10F =牛,求1F 和2F 的大小。
B C A。
