数学竞赛辅导托勒密定理一
证明托勒密(ptolemy)定理

证明托勒密(ptolemy)定理
【提纲】
1.介绍托勒密定理
托勒密定理,又称托勒密-费马定理,是一个关于三角形内角和与边长之间关系的数学定理。
该定理的表述为:在同一个三角形中,任意两边之和大于第三边,任意两边之差小于第三边。
2.证明托勒密定理的步骤
证明托勒密定理的方法有多种,这里我们以几何证明法为例:
(1)假设三角形ABC的三边长分别为a、b、c,其中a+b>c、
a+c>b、b+c>a;
(2)作边BC的平行线,交边AC于点D,构造三角形ABD和DBC;
(3)根据平行线性质,可知∠ADB=∠C,∠BDA=∠BC;
(4)在三角形ABD和DBC中,根据三角形内角和为180°,可得
∠ABD+∠ADB+∠BDA=180°;
(5)将∠ADB和∠BDA替换为∠C和∠ABC,得到
∠ABC+∠ABD+∠C=180°;
(6)同理,可得∠ABC+∠ADB+∠BC=180°;
(7)将(4)和(6)两式相减,得到∠AB D-∠C=∠C-∠ABC;
(8)根据步骤1中的条件,可知a+b>c,故∠ABD>∠C,同理
∠C>∠ABC;
(9)结合(7)式,得到∠ABD>∠C>∠ABC,即证明了托勒密定理。
3.托勒密定理的应用
托勒密定理在几何学中具有广泛的应用,如在解决三角形的判定、性质、最值等问题时,都可以利用托勒密定理进行求解。
此外,托勒密定理还可以与其他定理相结合,如与勾股定理、相似三角形等定理相互验证。
4.结论
托勒密定理是一个重要的几何定理,通过几何证明法可以简洁明了地证明其正确性。
专题:三角之托勒密定理

专题:三角之托勒密定理知识梳理克罗狄斯·托勒密(Ptolemy)所著的《天文集》中讲述了制作弦表的原理,其中涉及如下定理:任意凸四边形中,两条对角线的乘积小于或等于两组对边乘积之和,当且仅当对角互补时取等号。
即圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.精选例题习题1.托勒密是古希腊天文学家、地理学家、数学家,托勒密定理就是由其名字命名,该定理原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.其意思为:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.已知四边形ABCD的四个顶点在同一个圆的圆周上,AC、BD是其两条对角线,BD=42,且△ACD为正三角形,则四边形ABCD的面积为()A.8B.16C.83D.1632.克罗狄斯·托勒密(Ptolemy)所著的《天文集》中讲述了制作弦表的原理,其中涉及如下定理:任意凸四边形中,两条对角线的乘积小于或等于两组对边乘积之和,当且仅当对角互补时取等号,根据以上材料,完成下题:如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上一点,以AB为一边作等边三角形ABC,则当线段OC的长取最大值时,∠AOC=()A.30°B.45°C.60°D.90°3.托勒密是古希腊天文学家、地理学家、数学家,托勒密定理就是由其名字命名,该定理指出:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.已知四边形ABCD的四个顶点在同一个圆的圆周上,AC,BD是其两条对角线,BD=8,且△ACD为正三角形,则四边形ABCD的面积为()A.83B.163C.243D.3234.数学家托勒密从公元127年到151年在亚历山大城从事天文观测,在编制三角函数表过程中发现了很多重要的定理和结论,如图便是托勒密推导倍角公式“cos2a=1-2sin2a”所用的几何图形,已知点B,C在以线段AC为直径的圆上,D为弧BC的中点,点E在线段AC上且AE=AB,点F为EC的中点.设AC=2r,∠DAC=a,那么下列结论:①DC=2r cos a,②AB=2r cos2a,③FC=r1-cos2a,④DC2=r2r-AB.其中正确的是()A.②③B.②④C.①③④D.②③④5.托勒密是古希腊天文学家、地理学家、数学家,托勒密定理就是以其名字命名的重要定理,该定理原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.其意思为:圆的内接凸四边形两组对边乘积的和等于两条对角线的乘积.从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.已知四边形ABCD的四个顶点在同一个圆的圆周上,AC、BD是其两条对角线,AC=2,△BCD为正三角形,则△ABD面积的最大值为;四边形ABCD的面积为.(注:圆内接凸四边形对角互补)6.托勒密是古希腊天文学家、地理学家、数学家,托勒密定理就是由其名字命名,该定理原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和.其意思为:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.已知四边形ABCD的四个顶点在同一个圆的圆周上,AC、BD是其两条对角线,BD=4,且△ACD为正三角形,则△ABC面积的最大值为,四边形ABCD的面积为.(注:圆内接凸四边形对角互补)7.托勒密定理指“圆内接凸四边形ABCD两组对边乘积的和等于两条对角线的积”.若直径AC=2,AB=2AD=1,则BD=,cos A=.8.托勒密是古希腊天文学家、地理学家、数学家.托勒密定理:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.已知四边形ABCD的四个顶点在同一圆的圆周上,AC,BD是其两条对角线,△BCD的三个内角所对的圆弧长均相等,且AC=4米,则四边形ABCD的面积为平方米.9.托勒密定理是数学奥赛中的常用定理,该定理指出:圆的内接四边形两对对边乘积的和等于两条对角线的乘积.如图,已知四边形ABCD的四个顶点在同一个圆的圆周上,AD=CD,cos∠ACD=35,BD=5,则四边形ABCD的面积为.10.托勒密(Ptolemy)是古希腊天文学家、地理学家、数学家,托勒密定理就是由其名字命名,该定理指出:圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积.已知凸四边形ABCD的四个顶点在同一个圆的圆周上,AC,BD是其两条对角线,AB=AD,∠BAD=120∘,AC=6,则四边形ABCD的面积为.。
赣县中学高中数学竞赛平面几何第9九讲托定理勒密
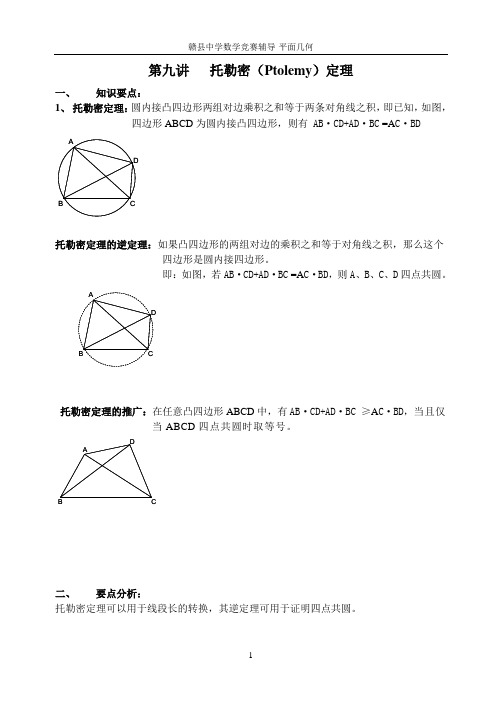
第九讲托勒密(Ptolemy)定理一、知识要点:1、托勒密定理:圆内接凸四边形两组对边乘积之和等于两条对角线之积,即已知,如图,四边形ABCD为圆内接凸四边形,则有 AB·CD+AD·BC =A C·BD ADB C托勒密定理的逆定理:如果凸四边形的两组对边的乘积之和等于对角线之积,那么这个四边形是圆内接四边形。
即:如图,若AB·CD+AD·BC =A C·BD,则A、B、C、D四点共圆。
ADB C托勒密定理的推广:在任意凸四边形ABCD中,有AB·CD+AD·BC ≥A C·BD,当且仅当ABCD四点共圆时取等号。
DAB C二、要点分析:托勒密定理可以用于线段长的转换,其逆定理可用于证明四点共圆。
三、 例题讲解:例1、设ABCD 为圆内接正方形,P 为弧DC 上的一点,求证:PA(PA+PC)=PB(PB+PD) PD CA B例2、如图,设P 、Q 为平行四边形ABCD 的边AB 、AD 上的两点,APQ ∆的外接圆交对角线AC 于R ,求证:A P ·AB+AQ ·AD=AR ·RCDA B CQP R例3、已知ABC ∆中,C B ∠=∠2,求证:AC 2=AB 2+AB ·BCAB C例4、如图所示,已知两同心圆O,四边形ABCD 内接于内圆,AB 、BC 、CD 、DA 的延长线交外圆于A 1、B 1、C 1、D 1,若外圆的半径是内圆的半径的2倍,求证:四边形A 1B 1C 1D 1的周长≥四边形ABCD 的周长的2倍,并确定等号成立的条件。
D 1例5、已知ABC ∆中,AB>AC,A ∠的一个外角平分线交ABC ∆的外接圆于点E,过E 作EF ⊥AB,垂足为F (如图),求证:2AF=AB-ACABC EF第九讲 托勒密(Ptolemy )定理练习1、 如图,已知圆内接正五边形ABCDE,若P 为弧AB 上一点,求证:PA+PD+PB=PE+PC AB C D EP2、 ABCD 为圆内接四边形,DC=BC ,对角线DB 与AC 交于E,若CE :EA=1:3,AB+AD=m,求BD 的长。
初二秋.第09讲.Ptolemy定理.联赛班

4
初二秋·第 09 讲·联赛班·教师版
BAD BCD 90 ,AB 2 , CD 1 ,对角线 AC 、 BD 【例7】 凸四边形 ABCD 中, ABC 60 , 交于点 O ,如图,求 sin AOB .
C D O A B P A D O B C
【解析】 因 BAD BCD 90° ,则 A 、 B 、 C 、 D 四点共圆,延长 BA , CD 交于 P , 则 ADP ABC 60°. 设 AD x ,有 AP 3x , DP 2 x . BP 4 3 . 由割线定理,有 (2 3x) 3x 2x(1 2x) ,求得 AD x 2 3 2 , BC 2 对四边形 ABCD 应用托勒密定理,有 BD AC (4 3)(2 3 2) 2 1 10 3 12 .
MH NH 3. OH
2 2 2 2 【拓2】 若 a 、 b 、 x 、 y 是正实数,且 a b 1,x y 1 . 求证: ax by ≤1 .
C a A y x D b B
【解析】 如图构造直径 AB 1 的圆,在 AB 两边任作 Rt△ACB 和 Rt△ADB , BC b , BD x ,AD y . 使 AC a , a 由勾股定理知 、 b 、 x 、 y 是满足题设条件的. 据托勒密定理,有 AC BD BC AD AB CD . ∵ CD ≤ AB 1 ,∴ ax by ≤1 .
证明托勒密(ptolemy)定理

证明托勒密(ptolemy)定理【最新版】目录1.托勒密定理的定义与概述2.托勒密定理的证明方法概述3.纯几何法证明托勒密定理4.托勒密定理的应用5.总结正文托勒密定理是数学中的一个重要定理,该定理描述了圆内接四边形对角线的乘积与两对对边乘积之间的关系。
具体来说,定理指出:圆内接四边形两条对角线的乘积等于两对对边乘积之和。
本文将介绍托勒密定理的证明方法,并简要讨论其应用。
一、托勒密定理的定义与概述托勒密定理最早由古希腊数学家托勒密提出,他在《几何原本》一书中详细阐述了该定理。
托勒密定理在数学中有着广泛的应用,尤其是在几何学、代数学以及数论等领域。
二、托勒密定理的证明方法概述托勒密定理的证明方法有很多,如三角法、复数法、纯几何法等。
下面我们将详细介绍纯几何法的证明过程。
三、纯几何法证明托勒密定理纯几何法是利用几何图形的性质来证明托勒密定理。
具体证明过程如下:1.在圆内接四边形 ABCD 中,作 AE 垂直于 BC,交 BC 于点 E。
2.根据垂直平分线定理,得到 AE 是 BC 的垂直平分线,即 AE=EC。
3.同理,作 AF 垂直于 CD,交 CD 于点 F,得到 AF=FD。
4.由于 AE=EC,AF=FD,所以四边形 AEFC 是矩形。
5.根据矩形的性质,得到 AC=EF,BD=AE。
6.因此,AC×BD=EF×AE,即 AC×BD=AB×CD。
四、托勒密定理的应用托勒密定理在数学中有广泛的应用,下面举一个简单的例子:已知一个圆内接四边形 ABCD,其中 AB=3,BC=4,CD=5,AD=6。
求 AC 的长度。
根据托勒密定理,有 AC×BD=AB×CD,代入已知数值,得到 AC×6=3×5,解得 AC=2.5。
五、总结托勒密定理是数学中的一个基本定理,它描述了圆内接四边形对角线的乘积与两对对边乘积之间的关系。
通过纯几何法的证明,我们可以更好地理解该定理的含义。
初中数学竞赛知识点归纳(定理)

1.中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2)初中竞赛需要,重要2.托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC初中竞赛需要,重要3.梅涅劳斯定理:设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有BPPC×CQQA×ARRB=1初中竞赛需要,重要4.梅涅劳斯定理的逆定理:(略)初中竞赛需要,重要5.梅涅劳斯定理的应用定理1:设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R,、∠B的平分线交边CA于Q,则P、Q、R 三点共线。
不用掌握6.梅涅劳斯定理的应用定理2:过任意△ABC的三个顶点A、B、C作它的外接圆的切线,分别和BC、CA、AB的延长线交于点P、Q、R,则P、Q、R三点共线不用掌握7.、塞瓦定理:设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线,分别与边BC、CA、AB或它们的延长线交于点P、Q、R,则BPPC×CQQA×ARRB()=1.初中竞赛需要,重要8.塞瓦定理的应用定理:设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E,又设BE和CD交于S,则AS一定过边BC的中心M不用掌握9.塞瓦定理的逆定理:(略)初中竞赛需要,重要10.塞瓦定理的逆定理的应用定理1:三角形的三条中线交于一点这个定理用塞瓦定理来证明将毫无几何美感,应该用中位线证明才漂亮11.塞瓦定理的逆定理的应用定理2:设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T,则AR、BS、CT交于一点。
不用掌握12.西摩松定理:从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线,设其垂足分别是D、E、R,则D、E、R共线,(这条直线叫西摩松线)初中竞赛的常用定理13.西摩松定理的逆定理:(略)初中竞赛的常用定理14.切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角15.圆的外切四边形的两组对边的和相等16.弦切角定理弦切角等于它所夹的弧对的圆周角 第一角元形式的梅涅劳斯定理 且因为AF=BF 所以AF/FB必等于1 所以AF=FB 所以三角形三条中线交于一点 此外,可用定比分点来定义塞瓦定理: 在△ABC的三边BC、CA、AB或其延长线上分别取L、M、N三点,又分比是λ=BL/LC、μ=CM/MA、ν=AN/NB。
数学奥赛-1(托勒密定理)

托勒密定理定理的提出一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。
定理的内容托勒密(Ptolemy)定理指出,圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ACD因为△ABE∽△ACD所以BE/CD=AB/AC,即BE·AC=AB·CD (1)又有比例式AB/AC=AE/AD而∠BAC=∠DAE所以△ABC∽△AED相似.BC/ED=AC/AD即ED·AC=BC·AD (2)(1)+(2),得AC(BE+ED)=AB·CD+AD·BC又因为BE+ED≥BD(仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”)所以命题得证复数证明用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、B C、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式:(a− b)(c− d) + (a− d)(b− c) = (a− c)(b− d) ,两边取模,运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
四点不限于同一平面。
平面上,托勒密不等式是三角不等式的反演形式。
二、设ABCD是圆内接四边形。
在弦BC上,圆周角∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。
在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK = ∠ABC = ∠CBD + ∠ABD,所以∠CBK = ∠ABD。
高中数学联赛常用定理

常用定理1、费马点(I)基本概念定义:在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
(II)证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠PA1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)PA+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结PD,则△PDB 为等边三角形,所以∠BPD=60度又∠BPA=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故PA+PB+PC=AA1。
(3)PA+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、CM,将△BMC以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1<A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
平面四边形费马点平面四边形中费马点证明相对于三角型中较为简易,也较容易研究。
(1)在凸四边形ABCD中,费马点为两对角线AC、BD交点P。
费马点(2)在凹四边形ABCD中,费马点为凹顶点D(P)。
经过上述的推导,我们即得出了三角形中费马点的找法:当三角形有一个内角大于或等于一百二十度的时候,费马点就是这个内角的顶点;如果三个内角都在120度以内,那么,费马点就是使得费马点与三角形三顶点的连线两两夹角为120度的点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
托
勒密定理 Ptolemy (约公元85年~165年),希腊数大天文学家,他的主要着作《天文集》被后人称为“伟大的数学书”。
托勒密定理 圆内接四边形中,两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和。
已知:四边形ABCD 内接于圆,如图,求证:AB·CD+BC·AD=AC·BD
证明:在∠BAD 内作∠BAE =∠CAD ,交BD 于E 。
因∠ABE=∠ACD ,所以△ABE ∽△ACD , 从而AB·CD =AC·BE ①;
易证△ADE ∽△ACB ,所以BC·AD=AC·DE ②;
①+②得AB·CD+BC·AD=AC·BD 。
托勒密定理的逆定理:如果凸四边形两组对边的积的和,等于两对角线的积,此四边形必内接于圆。
已知四边形ABCD 满足AB·CD+BC·AD=AC·BD , 求证:A 、B 、C 、D 四点共圆。
证明:构造相似三角形,即取点E ,使∠BCE =∠ACD ,且∠CBE =∠
CAD ,则△CBE ∽△CAD 。
所以BC·AD=AC·BE ①;
又CD CA CE CB =,∠BCA =∠ECD ,所以△BCA ∽△ECD 。
AB·CD =AC·DE ②;①+②得AB·CD+BC·AD=AC·(BE+DE )。
显然有BE+DE≥DB 。
于是AB·CD+BC·AD≥AC·DB 。
等号当且仅当E 在BD 上成立,结合已
知条件得到此时等号成立,这时∠CBD =∠CAD ,即A 、B 、C 、D 四点共圆。
托勒密定理的推广 托罗密不等式在四边形ABCD 中, 有AB·CD+AD·BC≥AC·BD. 并且当且仅当四边形内接于圆时,等式成立。
推论1(三弦定理) 如果A 是圆上任意一点,AB ,AC ,AD 是该圆上顺次的三条弦,则sin sin sin AC BAD AB CAD AD CAB ⋅∠=⋅∠+⋅∠
推论2(四角定理) 四边形ABCD 内接于O e ,则
直线上的托勒密定理(或欧拉定理) 若A ,B ,C ,D 为一直线上依次排序的四点,则AB CD BC AD AC BD ⋅+⋅=⋅
一、直接应用托勒密定理
例1如图,P 是正△ABC 外接圆的劣弧
上任一点(不与B 、C 重合),
求证:PA=PB +PC .
分析:此题证法甚多,一般是截长、补短,构造全等三角形,均为
繁冗.若借助托勒密定理论证,则有PA ·BC=PB ·AC +PC ·AB ,
∵AB=BC=AC . ∴PA=PB+PC .
二、完善图形借助托勒密定理
例2证明“勾股定理”:在Rt △ABC 中,∠B=90°,求证:AC 2=AB 2+BC 2 E B
D A A D C B E
证明:如图,作以Rt △ABC 的斜边AC 为一对角线的矩形ABCD ,显然ABCD 是圆内接四边形.
由托勒密定理,有 AC ·BD=AB ·CD +AD ·BC . ①
又∵ABCD 是矩形,∴AB=CD ,AD=BC ,AC=BD .②
把②代人①,得AC 2=AB 2+BC 2.
例3如图,在△ABC 中,∠A 的平分线交外接∠圆于D ,连结BD ,
求证:AD ·BC=BD(AB +AC).
证明:连结CD ,依托勒密定理,有AD ·BC =AB ·CD +AC ·BD .
∵∠1=∠2,∴ BD=CD .
故 AD ·BC=AB ·BD +AC ·BD=BD(AB +AC).
三、构造图形借助托勒密定理
例4若a 、b 、x 、y 是实数,且a 2+b 2=1,x 2+y 2=1.求证:ax +by ≤1.
证明:如图作直径AB=1的圆,在AB 两边任作Rt △ACB 和Rt △ADB ,
使AC =a ,BC=b ,BD =x ,AD =y .
由勾股定理知a 、b 、x 、y 是满足题设条件的.
据托勒密定理,有AC ·BD +BC ·AD=AB ·CD .
∵CD ≤AB =1,∴ax +by ≤1.
四、巧变原式妙构图形,借助托勒密定理
例5已知a 、b 、c 是△ABC 的三边,且a 2=b(b +c),求证:∠A=2∠B .
分析:将a 2=b(b +c)变形为a ·a=b ·b +bc ,从而联想到托勒密定理,进而构造一个等腰梯形,使两腰为b ,两对角线为a ,一底边为c .
证明:如图,作△ABC 的外接圆,以 A 为圆心,BC 为半径作弧交圆于D ,连结BD 、
DC 、DA .∵AD=BC ,¼
¼ACD BDC =∴∠ABD=∠BAC . 又∵∠BDA=∠ACB(对同弧),∴∠1=∠2.
依托勒密定理,有BC ·AD=AB ·CD +BD ·AC .①
而已知a 2=b(b +c),即a ·a=b ·c +b 2. ②
∴∠BAC=2∠ABC .
五、巧变形妙引线借肋托勒密定理
例6在△ABC 中,已知∠A ∶∠B ∶∠C=1∶2∶4,
分析:将结论变形为AC ·BC +AB ·BC=AB ·AC ,把三角形和圆联系起来,可联想到托勒密定理,进而构造圆内接四边形.
如图,作△ABC 的外接圆,作弦BD=BC ,边结AD 、CD .
在圆内接四边形ADBC 中,由托勒密定理,
有AC ·BD +BC ·AD=AB ·CD
易证AB=AD ,CD=AC ,∴AC ·BC +BC ·AB=AB ·AC ,
作业
1.已知△ABC 中,∠B=2∠C 。
求证:AC 2=AB 2+AB ·BC 。
2.证明:从圆周上一点到圆内接正方形的四个顶点的距离不可能都是有理数.
3.若a ≥b ≥c >0,且a <b +c ,解方程ax b x c c x b =-+-2222。
4.如图,圆O 外接于正方形ABCD ,P 为弧AD 上的任意一点,
求证PB PC PA +为定值。
O
C P。
