中考数学复习:旋转
初中数学专题复习:旋转(类型全面)

旋转旋转:在平面内,将一个图形绕一个定点沿某个方向转动一个角度成为与原来相等的图形,这样的图形运动叫做图形的旋转,这个定点叫做旋转中心,图形转动的角叫做旋转角.旋转特征:图形旋转时,图形中的每一点旋转的角都相等,都等于图形的旋转角。
(一)正三角形类型在正ΔABC中,P为ΔABC内一点,将ΔABP绕A点按逆时针方向旋转600,使得AB与AC重合。
经过这样旋转变化,将图(1-1-a)中的PA、PB、PC三条线段集中于图(1-1-b)中的一个ΔP'CP中,此时ΔP'AP也为正三角形。
例1. 如图:(1-1):设P是等边ΔABC内的一点,PA=3,PB=4,PC=5,∠APB的度数是________.(二)正方形类型在正方形ABCD中,P为正方形ABCD内一点,将ΔABP绕B点按顺时针方向旋转900,使得BA与BC重合。
经过旋转变化,将图(2-1-a)中的PA、PB、PC三条线段集中于图(2-1-b)中的ΔCPP'中,此时ΔBPP'为等腰直角三角形。
例2. 如图(2-1):P是正方形ABCD内一点,点P到正方形的三个顶点A、B、C的距离分别为PA=1,PB=2,PC=3。
求此正方形ABCD面积。
(三)等腰直角三角形类型在等腰直角三角形ΔABC中,∠C=90°, P为ΔABC内一点,将ΔAPC绕C点按逆时针方向旋转900,使得AC与BC重合。
经过这样旋转变化,在图(3-1-b)中的一个ΔP'CP为等腰直角三角形。
例3.如图,在ΔABC中,∠ACB =900,BC=AC,P为ΔABC内一点,且PA=3,PB=1,PC=2。
求∠BPC的度数。
旋转实际上是一种全等变换,由于具有可操作性,因而是考查同学们动手能力、观察能力的好素材,也就成了近几年中考试题中频繁出现的内容。
题型多以填空题、计算题呈现。
在解答此类问题时,我们通常将其转换成全等求解。
根据变换的特征,找到对应的全等形,通过线段、角的转换达到求解的目的。
中考数学复习:旋转之求线段最值
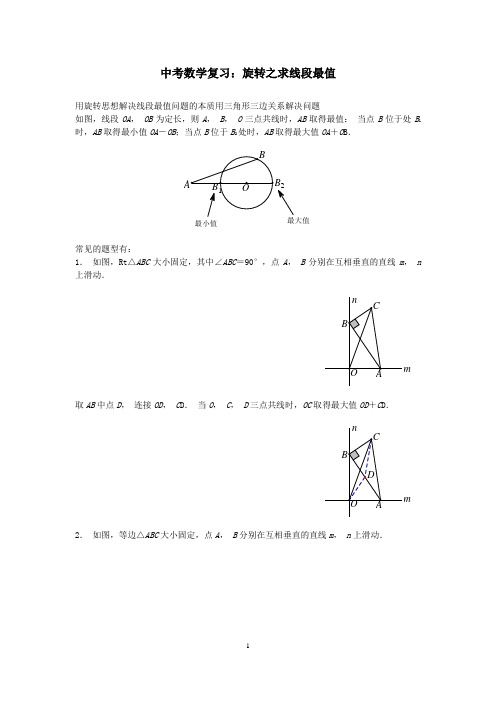
中考数学复习:旋转之求线段最值用旋转思想解决线段最值问题的本质用三角形三边关系解决问题如图,线段OA,OB为定长,则A,B,O三点共线时,AB取得最值:当点B位于处B1时,AB取得最小值OA-OB;当点B位于B2处时,AB取得最大值OA+O B.最小值常见的题型有:1.如图,Rt△ABC大小固定,其中∠ABC=90°,点A,B分别在互相垂直的直线m,n 上滑动.m取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最大值OD+C D.Arraym2.如图,等边△ABC大小固定,点A,B分别在互相垂直的直线m,n上滑动.m取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最大值OD+C D.m3.如图,Rt△ABC大小固定,其中∠ABC=90°,点A,B分别在互相垂直的直线m,n 上滑动.取AB中点D,连接OD,C D.当O,C,D三点共线时,OC取得最小值|CD –OD|.m例题讲解例1.已知Rt△ABC中,∠ACB=90°,tan∠BAC=12.若BC=6,点D在边AC的三等分点处,将线段AD绕A点旋转,E始终为BD的中点,求线段CE长度的最大值.解:在Rt△ABC中,AC=tan BCBAC=12,AB=①如图1,当AD=13AC时,取AB的中点F,连接EF和CF,则CF=12AB=,EF=12AD=2.所以当且仅当C,E,F三点共线且点F在线段CE上时,CE最大,此时CE=CF+EF=2+图1②如图2,当AD=23AC时,同理可得CE的最大值为4+.综上可得,当点D在靠近点C的三等分点处时,线段CE的长度的最大值为4+图2例2 以平面上一点O 为直角顶点,分别画出两个直角三角形,记作△AOB 和△COD ,其中∠ABO =30°.如图,若BO=N 在线段OD 上,且NO =2,P 是线段AB 上的一个动点,在将△AOB 绕点O 旋转的过程中,线段PN 长度的最小值为________,最大值为________.BCDPNO A-2;2. 过点O 作OE ⊥AB 于点E ,则OE =12OB.故当点P 在点E 处时,OP;当点P 在点B 处时,OP长度取最大值A O NPDBCE①当△AOB 绕点O 旋转到O ,E ,D 三点共线,且点E 在线段OD 上时,PN 取最小值,即OE -ON-2;D②当△AOB 绕点O 旋转到O ,B ,D 三点共线,且点B 在线段DO的延长线上时,PN 取最大值,OB +ON =2.所以线段PN 长度的最小值为-2,最大值为2.D进阶训练1. 已知△AOB 和△COD 是等腰三角形,其中BA =BO =2,CD =CO =3,∠ABO =∠DCO .连结AD ,BC ,M ,N 分别为OA ,BC 的中点.若固定△AOB ,将△COD 绕点O 旋转,求MN 的最大值.NMABCDO【答案】52. 【提示】如图,取OB 的中点E ,连结EM ,EN ,则EM ,EN 为定值,当点E 在线段MN 上时,MN 取最大值.EODCBAM N2. 已知:在Rt △ABC 中,∠BAC =90°,AC =AB =4,D ,E 分别是AB ,AC 的中点.若等腰Rt △ADE 绕点A 旋转,得到等腰Rt △AD 1E 1,记直线BD 1与CE 1的交点为P . (1)设BC 的中点为M ,求线段PM 的长; (2)求点P 到AB 所在直线的距离的最大值.E 1D 1A BC DEP【答案】(1)2)1【提示】(1)易证△E 1AC ≌△D 1AB ,所以∠E 1CA =∠D 1BA ,从而可得∠BPC =∠BAC =90°,所以PM =12BC=MPEDC BA D 1E 1(2)由题意知,点D1,E1在以A为圆心、AD为半径的圆上,而点P在直线BD1上,所以当直线BD1与⊙A相切时,点P到AB的距离最大.此时四边形AD1PE1是正方形,即PD1=AD1=2.如图,作PG⊥AB于点G,解Rt△PGB即可.B3.已知:正方形ABCD的边长为1,P为正方形内的一个动点,若点M在AB延长线上,且满足△PBC∽△PAM,延长BP交AD的延长线于点N,连结CM,是否存在满足条件的点P,使得PC=12?请说明理由.ACDPN【答案】不存在满足条件的点P,使得PC=12.【提示】因为△PBC∽△PAM,可得∠ABP+∠PAM=∠ABP+∠PBC=90°,所以AP⊥BN.以AB为直径,作半圆O,连结OC,OP,则OP+PC≥OC,从而PC件的点P,使得PC=12.ONPD CA。
2022年中考数学专题复习:旋转几何探究问题

2022年中考数学专题复习:旋转几何探究问题1.如图1,在平面直角坐标系中,点(),0A a 在x 轴负半轴上,点B 在y 轴正半轴上,设AB b =,且2240b a -=.(1)直接写出BAO ∠的度数.(2)如图2,点D 为AB 的中点,点P 为y 轴负半轴上一点,以AP 为边作等边三角形APQ ,连接DQ 并延长交x 轴于点M ,若6AB =,求点M 的坐标.(3)如图3,点C 与点A 关于y 轴对称,点E 为OC 的中点,连接BE ,过点B 作CBF AEB ∠=∠,且BF BE =,连接AF 交BC 于点P ,求BPCP的值.2.在△ABC 中,△BAC =90°,AB =AC .(1)如图1,过点C 作CD △BD 交AB 于M ,若BM =2,tan△DCB =13.求DM 的长;(2)如图2,若AD △AE ,且AD =AE ,延长AD 、CB 交于点F ,作EG △EA 交CB 于点G .猜想FD 、CE 、EG 之间有何数量关系?并证明你的结论.(3)如图3,若AB =D 为一动点且始终有BD △CD ,取CD 的中点M ,连接BM ,将MB 绕点B 逆时针旋转90°得到点E ,直接写出△ABE 面积的最大值.3.已知,在△ABC 中,AB=AC ,(1)如图1,2,,ABC BDA αα∠=∠=若30α=︒,且点D 在CA 的延长线上时,求证:222CD BD AD =+;(2)如图2,2,,ABC BDA αα∠=∠=若30α=︒,试判断AD ,BD ,CD 之间的等量关系,并说明理由(3)如图3,若45,BDA ABC AD ∠=∠=︒=BD =5,求CD 的长.4.在等腰ABC 中,AC BC =,P 为BC 边上一点(不与点B ,C 重合),连接P A ,以点P 为旋转中心顺时针旋转线段P A ,旋转角与C ∠相等,得到线段PD .连接DB . (1)当90C ∠=︒时,请你在图1中补全图形,并直接写出DBA ∠的度数; (2)如图2,若C α∠=,求DBA ∠的度数(用含α的代数式表示).5.(1)问题背景:如图1,正方形ABCD 中,F 在直线CD 上,E 在直线BC 上.若△EAF =45°,求证:BE +FD =EF ;(2)迁移应用:如图2,将正方形ABCD 的一部分沿GH 翻折,使A 点的对应点E 在BC上,且AD的对应边EM交CD于F点.若BE=3,EC=2,求EF的长;(3)联系拓展:如图3,正方形ABCD中,E、Q在CD上,F在BC上,若EF=EA,△FQA=△FEA.若△CFQ=34°,则△QAD=_______°.6.(1)问题引入:如图1,点F是正方形ABCD边CD上一点,连接AF,将ADF 绕点A顺时针旋转90°与ABG重合(D与B重合,F与G重合,此时点G,B,C在一条直线上),△GAF的平分线交BC于点E,连接EF,判断线段EF与GE之间有怎样的数量关系,并说明理由.(2)知识迁移:如图2,在四边形ABCD中,△ADC+△B=180°,AB=AD,E,F分别是边BC,CD延长线上的点,连接AE,AF,且△BAD=2△EAF,试写出线段BE,EF,DF之间的数量关系,并说明理由.(3)实践创新:如图3,在四边形ABCD中,△ABC=90°,AC平分△DAB,点E在AB上,连接DE,CE,且△DAB=△DCE=60°,若DE=a,AD=b,AE=c,求BE的长.(用含a,b,c的式子表示)7.如图,△OAB和△OCD中,OA=OB,OC=OD,△AOB=△COD= ,AC、BD交于M(1)如图1,当α=90°时,△AMD的度数为°;(2)如图2,当α=60°时,求△AMD的度数;(3)如图3,当△OCD绕O点任意旋转时,△AMD与α是否存在着确定的数量关系?如果存在,请你用α表示△AMD,不用证明;若不确定,说明理由.8.如图1,在四边形ABCD中,AB=AD,△B+△ADC=180°,点E,F分别在四边形ABCD的边BC,CD上,△EAF=1△BAD,连接EF,试猜想EF,BE,DF之间的数2量关系.(1)思路梳理将△ABE绕点A逆时针旋转至△ADG,使AB与AD重合,由△B+△ADC=180°,得△FDG=180°,即点F,D,G三点共线,易证△AFG△△AFE,故EF,BE,DF之间的数量关系为__;(2)类比引申如图2,在图1的条件下,若点E,F由原来的位置分别变到四边形ABCD的边CB,DC延长线上,△EAF=1△BAD,连接EF,试猜想EF,BE,DF之间的数量关系,并2给出证明.(3)联想拓展如图3,在△ABC中,△BAC=90°,AB=AC,点D,E均在边BC上,且△DAE=45°,若BD=1,EC=2,直接写出DE的长为________________.9.如图,在平面直角坐标系xOy中,A(a,0),B(0,b),C(-a,0)b2-4b+4=0.(1)求证:△ABC=90°;(2)△ABO的平分线交x轴于点D,求D点的坐标.(3)如图,在线段AB上有两动点M、N满足△MON=45°,求证:BM2+AN2=MN2.10.如图1,在Rt△ABC中,△ABC=90°,BA=BC,直线MN是过点A的直线CD△MN于点D,连接BD.(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE△BD,交MN于点E,进而得出:DC+AD=BD.(2)探究证明将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明(3)拓展延伸在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.11.如图,菱形ABCD中,E、F分别是边AD,CD上的两个动点(不与菱形的顶点重合),且满足CF=DE,△A=60°.(1)写出图中一对全等三角形:____________________.(2)求证:△BEF是等边三角形;(3)若菱形ABCD的边长为2,设△DEF的周长为m,则m的取值范围为(直接写出答案);(4)连接AC分别与边BE、BF交于点M、N,且△CBF=15º,试说明:222MN CN AM+=12.如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,BC =AD 可绕点A 旋转,AD(1)在旋转过程中,△当A 、D 、B 三点在同一直线上时,求BD 的长;△当A 、D 、B 三点为同一直角三角形的顶点时,求BD 的长.(2)若摆动臂AD 顺时针旋转90°,点D 的位置由△ABC 外的点D 1转到其内的点D 2处,如图2,此时△AD 2C =135°,CD 2=1,求BD 2的长;(3)如图3,若连接(2)中的D 1D 2,将(2)中△AD 1D 2的形状和大小保持不变,把△AD 1D 2绕点A 在平面内自由旋转,分别取D 1D 2、CD 2、BC 的中点M 、P 、N ,连接MP 、PN 、NM ,M 随着△AD 1D 2绕点A 在平面内自由旋转,△MPN 的面积是否发生变化,若不变,请直接写出△MPN 的面积;若变化,△MPN 的面积是否存在最大与最小?若存在,请直接写出△MPN 面积的最大值与最小值.13.已知正方形ABCD ,将线段BA 绕点B 旋转α(090α︒<<︒),得到线段BE ,连接EA ,EC .(1)如图1,当点E 在正方形ABCD 的内部时,若BE 平分△ABC ,AB =4,则△AEC =______°,四边形ABCE 的面积为______; (2)当点E 在正方形ABCD 的外部时,△在图2中依题意补全图形,并求△AEC 的度数;△作△EBC 的平分线BF 交EC 于点G ,交EA 的延长线于点F ,连接CF .用等式表示线段AE ,FB ,FC 之间的数量关系,并证明.14.在△ABC 中,AB AC =,BAC α∠=,点P 为线段CA 延长线上一动点,连接PB ,将线段PB 绕点P 逆时针旋转,旋转角为α,得到线段PD ,连接DB ,DC .(1)如图1,当60α=︒时,填空:△线段P A 与DC 的数量关系是______;△△DCP 的度数是______;(2)如图2,当120α=︒时,(1)中的结论还成立吗?若成立,请给出证明,不成立,说明理由.(3)当120α=︒时,若6AB =,BP =D 到CP 的距离.15.在△ABC 中,△BAC =90°,AB =AC ,点D 在边BC 上,13BD BC = 将线段DB 绕点D 顺时针旋转至DE ,记旋转角为α,连接BE ,CE ,以CE 为斜边在其一侧作等腰直角三角形CEF ,连接AF .(1)如图 1,当α=180°时,请直接写出线段AF 与线段BE 的数量关系; (2)当0°<α<180°时,△如图2,(1)中线段AF 与线段BE 的数量关系是否仍然成立?请说明理由; △如图3,当B ,E ,F 三点共线时,连接AE ,判断四边形AECF 的形状,并说明理由.16.问题探究:(1)如图1,△ABC、△ADE均为等边三角形,连接BD、CE,则线段BD与CE的数量关系是______.(2)如图2,在Rt△ABC和Rt△ADE中,△ACB=△AED=90°,△ABC=△ADE=30°,连接BD、CE,试确定BD与CE的数量关系,并说明理由.(3)如图3,在四边形ABCD中,AC△BC,且AC=BC,CD=4,若将线段DA绕点D 按逆时针方向旋转90°得到DA',连接BA',则线段BA'的长度是______.17.综合与实践如图1,在矩形ABCD中,对角线AC与BD交于点O,将△OBC绕点C顺时针旋转,点B对应点为点E,点O对应点为点F.(1)当点E落在CD的延长线上时,请解答以下两个问题△如图1,若AB=2a,BC=2,连接OE,则2OE ______(用含a的代数式表示);△如图2,延长BD交EF于点G,试猜想BG与EF的位置关系并加以证明;(2)如图3,在图1的基础上继续绕点C旋转△OBC,点B对应点为点E,点O对应点为点F,当点E落在BD的延长线上时,已知△ACE=90°,求证:四边形CDEF是菱形.18.如图,等边三角形ABC中,D为AB边上一点(点D不与点A、B重合),连接CD,将CD平移到BE(其中点B和C对应),连接AE.将△BCD绕着点B逆时针旋转至△BAF,延长AF交BE于点G.(1)连接DF,求证:△BDF是等边三角形;(2)求证:D、F、E三点共线;的值.(3)当BG=2EG时,求tan AEB19.如图1,在等边△ABC中,AB=2,过点C作CE△AB,垂足为E,P为CE上任意一点(点P与点C不重合),把AP绕点A顺时针旋转60°,点P的对应点为点D,分别连接BD、PD、ED.(1)求证:BD=CP;(2)当点P与点E重合时,请你按照题干要求,在图2中作出图形,并延长CE交BD 于点F,求出BF的长;(3)直接写出线段DE长度的最小值.20.已知正方形ABCD中,点E是边CD上一点(不与C、D重合),将△ADE绕点A 顺时针旋转90°得到△ABF,如图1,连接EF分别交AC、AB于点P、G.(1)请判断△AEF的形状;(2)求证:2PA PG PF=•(3)如图2,当点E是边CD的中点时,PE=1,求AG的长.。
中考数学压轴题之旋转(中考题型整理,突破提升)及详细答案

在△ DAG 与△ DCG 中, ∵ AD=CD,∠ ADG=∠ CDG,DG=DG, ∴ △ DAG≌ △ DCG. ∴ AG=CG. 在△ DMG 与△ FNG 中, ∵ ∠ DGM=∠ FGN,FG=DG,∠ MDG=∠ NFG, ∴ △ DMG≌ △ FNG. ∴ MG=NG 在矩形 AENM 中,AM=EN. 在 Rt△ AMG 与 Rt△ ENG 中, ∵ AM=EN, MG=NG, ∴ △ AMG≌ △ ENG. ∴ AG=EG ∴ EG=CG. (3)(1)中的结论仍然成立.
4.如图(1)所示,将一个腰长为 2 等腰直角△ BCD 和直角边长为 2、宽为 1 的直角△ CED 拼在一起.现将△ CED 绕点 C 顺时针旋转至△ CE’D’,旋转角为 a. (1)如图(2),旋转角 a=30°时,点 D′到 CD 边的距离 D’A=______.求证:四边形 ACED′ 为矩形; (2)如图(1),△ CED 绕点 C 顺时针旋转一周的过程中,在 BC 上如何取点 G,使得 GD’=E’D;并说明理由.
【答案】(1)详见解析;(2)FE·sin( -90°) 【解析】 【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE,所以∠ FAE=∠ BEA,由折叠的性质得 ∠ BAE=∠ FAE,∠ BEA=∠ FEA,所以∠ BAE=∠ FEA,故有 AB∥ FE,因此四边形 ABEF 是平行四 边形,又 BE=EF,因此可得结论; (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG=90°- ,利用菱形的性质得到
中考数学解答题压轴题突破 重难点突破八 几何综合题 类型六:旋转在几何综合题中的应用

(2)证明:BE=AH+DF.
(2)证明:将△ABH绕着点B顺时针旋转90° 得到△BCM,∵四边形ABCD是正方形, ∴AD=BC,∠ADC=∠C=90°,∴∠ADF=∠C, ∵AF∥BE,∴∠F=∠BEC,∴△ADF≌△BCE(AAS), ∴DF=CE.又由旋转可知AH=CM,∠AHB=∠M,∠BAH=∠BCM=90°, ∵∠BCD=90°,∴∠BCD+∠BCM=180°, ∴点E,C,M在同一直线.∴AH+DF=EC+CM=EM.
类型六:旋转在几何综合 题中的应用
模型一:旋转构造基本图形 【解题方法模型构建】 若题干中出现“共顶点、等线段(相邻等线段)”这一特征.常考虑构造 旋转,通过旋转可以将线段转移,将已知条件集中,从而解决问题.
1.遇60°旋转60°,构造等边三角形(等边三角形旋转模型).
通过旋转可将线段AP,BP,CP转移在同一个三角形中(△CPP′). 注:根据“旋转的相互性”也可绕A点旋转△APC,或绕B,C点旋转相应 三角形(还有5种构造方法).
模型二:旋转构造模型 【解题方法模型构建】 1.如图,在△OAB中,OA=OB,在△OCD中,OC=OD,∠AOB=∠COD=
α,将△OCD绕点O旋转一定角度后,连接AC,BD,相交于点E.简记 为:双等腰,共顶点,顶角相等,旋转得全等.
【结论】(1)△AOC≌△BOD(SAS); (2)AC=BD; (3)两条拉手线AC,BD所在直线的夹角与∠AOB相等或互补.
【结论】△ABD≌△AEC;△ABE∽△ADC.
2.请阅读下列材料: 问题:如图①,在等边三角形ABC内有一点P,且PA=2,PB= 3 ,PC= 1,求∠BPC度数的大小和等边三角形ABC的边长. 李明同学的思路:将△BPC绕点B逆时针旋转60°,画出旋转后的图形 (如图②),连接PP′,可得△P′PB是等边三角形,而△PP′A又是直角 三角形(由勾股定理的逆定理可证),∴∠AP′B=150°,而∠BPC=∠ AP′B=150°,进而求出等边角形ABC的边长为 7,问题得到解决.
2023年中考数学高频考点突破——旋转

2023年中考数学高频考点突破——旋转1.已知:∠AOB=60°.小新在学习了角平分线的知识后,做了一个夹角为120°(即∠DPE=120°)的角尺来作∠AOB的角平分线.(1)如图1,他先在边OA和OB上分别取OD=OE,再移动角尺使PD=PE,然后他就说射线OP是∠AOB的角平分线.试根据小新的做法证明射线OP是∠AOB的角平分线;(2)如图2,小新在确认射线OP是∠AOB的角平分线后,一时兴起,将角尺绕点P 旋转了一定的角度,他认为旋转后的线段PD和PE仍然相等.请问小新的观点是否正确,为什么?(3)如图3,在(2)的基础上,若角尺旋转后恰好使得DP∥OB,请判断线段OD与OE的数量关系,并说明理由.2.如图,在平面直角坐标系中,点O为坐标原点,点A(x,y)中的横坐标x与纵坐标y 满足+|y﹣8|=0,过点A作x轴的垂线,垂足为点D,点E在x轴的负半轴上,且满足AD﹣OD=OE,线段AE与y轴相交于点F,将线段AD向右平移8个单位长度,得到线段BC.(1)直接写出点A和点E的坐标;(2)在线段BC上有一点G,连接DF,FG,DG,若点G的纵坐标为m,三角形DFG 的面积为S,请用含m的式子表示S(不要求写m的取值范围);(3)在(2)的条件下,当S=26时,动点P从D出发,以每秒1个单位的速度沿着线段DA向终点A运动,动点Q从A出发,以每秒2个单位的速度沿着折线AB→BC向终点C运动,P,Q两点同时出发,当三角形FGP的面积是三角形AGQ面积的2倍时,求出P点坐标3.在△ABC中,点P为BC边中点,直线a绕顶点A旋转,BM⊥直线a于点M.CN⊥直线a于点N,连接PM,PN.(1)如图1,若点B,P在直线a的异侧,延长MP交CN于点E.求证:PM=PE;(2)若直线a绕点A旋转到图2的位置时,点B,P在直线a的同侧,其它条件不变,+S△CNP=7,BM=1,CN=3,求MN的长度.此时S△BMP(3)若过P点作PG⊥直线a于点G,试探究线段PG、BM和CN的数量关系.4.如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.(1)观察猜想:图1中,线段PM与PN的数量关系是,位置关系是;(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.5.如图,在△ABC中,AC=BC=2,∠C=90°,将一块三角板的直角顶点放在斜边AB 的中点P处,将三角板绕点P旋转,三角板的两直角边(或延长线)分别交射线AC、射线CB于D、E两点.(1)如图(a),当PD⊥AC,PE⊥BC时,线段PD与PE有何大小关系,并说明理由;(2)在旋转的过程中,当三角板处于图(b)和图(c)中的位置时,(1)中的结论是否仍然成立?请以图(b)为例说明理由;(3)在旋转的过程中,△PAD是否能构成等腰三角形?若能,直接写出CD的长;若不能,请说明理由.6.如图,在△ABC中,AB=AC,∠BAC=α,过A作AD⊥BC于点D,点E为直线AD 上一动点,把线段CE绕点E顺时针旋转α,得到线段EF,连接FC、FB,直线AD与BF相交于点G.(1)[发现]如图1,当α=60°时,填空:①的值为;②∠AGB的度数为;(2)[探究]如图2,当α=120°时,请写出的值及∠AGB的度数,并就图2的情形给出证明;(3)[应用]如图3,当α=90°时,若AB=2,∠ACE=15°,请直接写出△DFG 的面积.7.如图1,△ABC中,AB=AC,点D在BC上,点E在AC上,且AE=AD.(1)求证:∠BAD=2∠CDE;(2)如图2,过点D作DF⊥AC,垂足为F,若∠CAD=2∠B,求证:AC+AD=2CF;(3)如图3,在(2)的条件下,把△DCE沿DE翻折得到△DGE,若AG=8,CE=2,求BD的长.8.如图,△ABC为等边三角形,D为BC边上一点,连接AD.(1)如图1,将AD绕点A顺时针旋转60°得到AE.连接DE,BE,若,BC =6,求CD的长度;(2)如图2,将AD绕点A顺时针旋转120°得到AE,连接CE交AB于F,G为AC 边的中点,连接FG,猜想FG与AE存在的关系,并证明你的猜想;(3)如图3,以AC为斜边向AC边右侧作Rt△AEC,连接BE,F为BE上一点,且BF=BE,连接DF,若AB=4,CD=1,当DF取最小值时,请直接写出△BDF的面积.9.在△ABC和△ADE中,∠BAC=∠DAE=90°,且AB=AC,AD=AE.(1)如图1,如果点D在BC上,且BD=4,CD=3,求DE的长;(2)如图2,AD与BC相交于点N,点D在BC下方,连接BD,且AD⊥BD,连接CE并延长与BA的延长线交于点F,点M是CA延长线上一点,且CM=AF,求证:CF=AN+MN;(3)如图3,若AD=AB,△ADE绕着点A旋转,取DE中点M,连接BM,取BM中点N,连接AN,点F为BC中点,连接DN,若DN恰好经过点F,请直接写出DF:DN:AN的值.10.在△ABC和△CDE中,∠ACB=∠DCE=90°,AC=BC,CD=CE,点D在边AC上,点E在边BC上,如图1将△CDE绕点C按顺时针方向旋转,旋转角为α(0°<α≤90°).(1)连接AD,BE.求证:AD=BE.AD⊥BE;(2)当旋转至图2位置时,点A,D,E在一条直线上,连接BD,BE,若AD=2,CD=1,则BD=;(3)当α=90°时,如图3,连接AD,BE,延长AD交BE于点F,连接CF,若DF=1.EF=.则CF=.11.如图,直线MN∥PQ,将一副三角板中的两块直角三角板如图1放置,∠ACB=∠EDF=90°,∠ABC=∠BAC=45°,∠DFE=30°,∠DEF=60°,此时点A与点E 重合.(1)对于图1,固定△ABC的位置不变,将△DEF绕点E按顺时针方向进行旋转,旋转至DE与BC首次平行,如图2所示,求此时∠FAC的度数.(2)对于图1,固定△ABC的位置不变,将△DEF沿AC方向平移至点F正好落在直线MN上,再将△DEF绕点F按顺时针方向进行旋转,如图3所示.①若边EF与边BC交于点G,试判断∠BGF﹣∠EFN的值是否为定值,若是定值,则求出该定值,若不是定值,请说明理由;②对于图3,固定△ABC的位置不变,将△DEF绕点F顺时针方向以每秒10°的速度进行旋转,当EF与直线MN首次重合时停止运动当经过t秒时,线段DE与△ABC的一条边平行,求满足条件的t的值.12.已知△ABC,∠ACB=90°,AC=BC=4,D是AB的中点,P是平面上的一点,且DP=1,连接CP(1)如图,当点P在线段BD上时,求CP的长;(2)当△BPC是等腰三角形时,求CP的长;(3)将点B绕点P顺时针旋转90°得到点B′,连接AB′,求AB′的最大值.13.在△ABC中,∠ABC=90°,AB=BC,以点A为旋转中心,将边AC逆时针旋转一定角度,得到线段AD,使BD∥AC,AD交BC于点G,过点C作CE⊥AD交AD于点F.(1)若AB=3,求BD的长;(2)求证:AG=CF+DF;(3)点M是AC边上一动点,在线段BM上存在一点N,使NB+NA+NC的值最小时,NB的长为m,请直接用含m的式子表示NB+NA+NC的最小值.14.在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,过点D作DE⊥AB,交BC于点E,连接AE,取AE的中点P,连接DP,CP.(1)观察猜想如图(1),DP与CP之间的数量关系是,DP与CP之间的位置关系是.(2)类比探究将图(1)中的△BDE绕点B逆时针旋转45°,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明;若不成立,请说明理由.(3)问题解决若BC=3BD=3,将图(1)中的△BDE绕点B在平面内自由旋转,当BE⊥AB时,请直接写出线段CP的长.15.已知,在平面直角坐标系中,点A(0,2),B(﹣2,m),过B点作直线a与x轴互相垂直,C为x轴上的一个动点,且∠BAC=90°.(1)如图1,若点B是第二象限内的一个点,且m=4时,则点C的坐标为;AC =.(2)如图2,若点B是第三象限内的一个点,设C点的坐标(x,0),试判断m+x的值是否发生变化?若不变,请求出m+x的值;若发生变化,请说明理由.(3)如图3,连接BC,作∠ABC的平分线BD,点E、F分别是射线BD与边BC上的两个动点,连接CE、EF,当m=3.5时,试求CE+EF的最小值.16.△ABC为等边三角形,AB=4,AD⊥BC于点D,点E为AD的中点.(1)如图1,将AE绕点A顺时针旋转60°至AF,连接EF交AB于点G,求证:G为EF中点.(2)如图2,在(1)的条件下,将△AEF绕点A顺时针旋转,旋转角为α,连接BE,H为BE的中点,连接DH,GH.当30°<α<120°时,猜想∠DHG的大小是否为定值,并证明你的结论.(3)在△AEF绕点A顺时针旋转过程中,H为BE的中点,连接CH,问线段CH何时取得最大值,请说明理由,并直接写出此时△ADH的面积.17.在△ABC和△AEF中,∠AFE=∠ABC=90°,∠AEF=∠ACB=30°,AE=AC,连接EC,点G是EC中点,将△AEF绕点A顺时针旋转.(1)如图1,若E恰好在线段AC上,AB=2,连接FG,求FG的长度;(2)如图2,若点F恰好落在射线CE上,连接BG,证明:GB=AB+GC;(3)如图3,若AB=3,在△AEF旋转过程中,当GB﹣GC最大时,直接写出直线AB,AC,BG所围成三角形的面积.18.在平面直角坐标系中,A(a,0),B(0,b)分别是x轴负半轴和y轴正半轴上一点,点C与点A关于y轴对称,点P是x轴正半轴上C点右侧一动点.(1)当2a2+4ab+4b2+2a+1=0时,求A,B的坐标;(2)当a+b=0时,①如图1,若D与P关于y轴对称,PE⊥DB并交DB延长线于E,交AB的延长线于F,求证:PB=PF;②如图2,把射线BP绕点B顺时针旋转45o,交x轴于点Q,当CP=AQ时,求∠APB的大小.19.在△ABC中,AB=AC=6,∠BAC=90°,AD⊥BC于点D,E为线段AD上的一点,AE:DE=2:1,以AE为直角边在直线AD右侧构造等腰Rt△AEF,使∠EAF=90°,连接CE,G为CE的中点.(1)如图1,EF与AC交于点H,连接GH,求线段GH的长度.(2)如图2,将△AEF绕点A逆时针旋转,旋转角为α且45°<α<135°,H为线段EF的中点,连接DG,HG,猜想∠DGH的大小是否为定值,并证明你的结论;(3)如图3,连接BG,将△AEF绕点A逆时针旋转,在旋转过程中,请直接写出BG 长度的最大值.20.如图①,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,点D,E,N分别是△ABC 的AB,AC,BC边上的中点,连接AN,DE交于点M.(1)观察猜想:的值为;BD与CE的位置关系是.(2)探究与证明:将△ADE绕点A按顺时针方向旋转α角(0°<α<360°),且△ADE内部的线段AM 随之旋转,如图②所示,连接BD,CE,MN,试探究线段BD与MN之间分别有什么样的数量关系,以及BD与CE有什么样的位置关系,并证明;(3)拓展与延伸:△ADE在旋转的过程中,设直线CE与BD相交于点F,当∠CAE=90°时,请直接写出BF的值.参考答案:1.【解答】(1)证明:如图1中,在△OPD和△OPE中,,∴△OPD≌△OPE(SSS),∴∠POD=∠POE.(2)解:结论正确.理由:如图2中,过点P作PH⊥OA于H,PK⊥OB于K.∵∠PHO=∠PKO=90°,∠AOB=60°,∴∠HPK=120°,∵∠DPE=∠HPK=120°,∴∠DPH=∠EPK,∵OP平分∠AOB,PH⊥OA,PK⊥OB,∴∠POH=∠POK,∠PHO=∠PKO=90°,在△OPH和△OPK中,,∴△OPH≌△OPK(AAS),∴PH=PK,在△PHD和△PKE中,,∴△PHD≌△PKE(ASA),∴PD=PE.(3)解:结论:OE=2OD.理由:如图3中,在OB上取一点T,使得OT=OD,连接PT.∵OP平分∠AOB,∴∠POD=∠POT,在△POD和△POT中,,∴△POD≌△POT(SAS),∴∠ODP=∠OTP,∵PD∥OB,∴∠PDO+∠AOB=180°,∠DPE+∠PEO=180°,∵∠AOB=60°,∠DPE=120°,∴∠ODP=120°,∠PEO=60°,∴∠OTP=∠ODP=120°,∴∠PTE=60°,∴∠TPE=∠PET=60°,∴TP=TE,∵∠PTE=∠TOP+∠TPO,∠POT=30°,∴∠TOP=∠TPO=30°,∴OT=TP,∴OT=TE,∴OE=2OD.2.【解答】解:(1)∵+|y﹣8|=0,又∵≥0,|y﹣8|≥0,∴x=2,y=8,∴A(2,8),∵AD⊥x轴,∴OD=2,AD=8,∵AD﹣OD=OE,∴OE=6,∴E(﹣6,0).(2)如图1中,连接OG.由题意G(10,m).∵AD=DE=8,∠ADE=90°,∴∠AED=45°,∴∠OEF=∠OFE=45°,∴OE=OF=6,∴F(0,6),+S△OFG﹣S△OFD=×2×m+×6×10﹣×2×6=m+24(0≤m≤8).∴S=S△ODG(3)如图2中,设FG交AD于J,P(2,t),当点P在DJ上,点Q在AB上时,当S=26时,m=2,∴G(10,2),∵F(0,6),∴直线FG的解析式为y=﹣x+6,∴J(2,),由题意,•(﹣t)×10=2××2t×6,解得t=,∴P(2,),当点P在AJ上,点Q在BG上时,同法可得,•(t﹣)×10=2××(14﹣2t)×8,解得t=,∴P(2,).综上所述,满足条件的点P的坐标为(2,)或(2,).3.【解答】(1)证明:如图1中,∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMA=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P为BC边中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE(ASA),∴PM=PE(2)解:延长MP与NC的延长线相交于点E.∵BM⊥直线a于点M,CN⊥直线a于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,又∵P为BC中点,∴BP=CP,又∵∠BPM=∠CPE,∴△BPM≌△CPE(ASA),=S△PCE,∴PM=PE,S△PBM∴AE=CN+CE=4,+S△CNP=7,∵S△BMP=7,∴S△PNE=2S△PNE=14,∴S△MNE∴×MN×4=14,∴MN=7.(3)解:如图1﹣1中,当点B,P在直线a的异侧时,∵PG⊥a,CN⊥a,∴PG∥CN,∵PM=PE,∴MG=GN,∴PG=EN=(CN﹣EC),∵EC=BM,∴PG=(CN﹣BM).如图2﹣2中,当点B,P在直线a的同侧时,延长MP交NC的延长线于Q.∵PG⊥a,CN⊥a,∴PG∥CN,∵BM∥CQ,∴∠BMP=∠Q,∵∠BPM=∠CPQ,BP=CP,∴△PMB≌△PQC(AAS),∴PM=PQ,BM=CQ,∴MG=GN,∴PG=AQ=(CN+BM).综上所述,PG=(CN﹣BM)或PG=(CN+BM).4.【解答】解:(1)∵点P,N是BC,CD的中点,∴PN∥BD,PN=BD,∵点P,M是CD,DE的中点,∴PM∥CE,PM=CE,∵AB=AC,AD=AE,∴BD=CE,∴PM=PN,∵PN∥BD,∴∠DPN=∠ADC,∵PM∥CE,∴∠DPM=∠DCA,∵∠BAC=90°,∴∠ADC+∠ACD=90°,∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°,∴PM⊥PN,故答案为:PM=PN,PM⊥PN;(2)△PMN是等腰直角三角形.由旋转知,∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,BD=CE,利用三角形的中位线得,PN=BD,PM=CE,∴PM=PN,∴△PMN是等腰三角形,同(1)的方法得,PM∥CE,∴∠DPM=∠DCE,同(1)的方法得,PN∥BD,∴∠PNC=∠DBC,∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,∵∠BAC=90°,∴∠ACB+∠ABC=90°,∴∠MPN=90°,∴△PMN是等腰直角三角形;(3)方法1:如图2,同(2)的方法得,△PMN是等腰直角三角形,∴MN最大时,△PMN的面积最大,∴DE∥BC且DE在顶点A上面,∴MN最大=AM+AN,连接AM,AN,在△ADE中,AD=AE=4,∠DAE=90°,∴AM=2,在Rt△ABC中,AB=AC=10,AN=5,=2+5=7,∴MN最大=PM2=×MN2=×(7)2=.∴S△PMN最大方法2:由(2)知,△PMN是等腰直角三角形,PM=PN=BD,∴PM最大时,△PMN面积最大,∴点D在BA的延长线上,∴BD=AB+AD=14,∴PM=7,∴S=PM2=×72=.△PMN最大5.【解答】解:(1)PD=PE,理由如下:∵AC=BC,∠ACB=90°,∴∠A=∠B=45°,∵PD⊥AC,∴∠ADP=90°,∴∠APD=45°,在△ADP和△BEP中,,∴△ADP≌△BEP(AAS),∴OD=PE;(2)如图1,PD=PE仍然成立,理由如下:连接PC,∵AC=BC,AP=BP,∠ACB=90°∴CP⊥AB,∠ACP=∠BCP==45°,CP=BP=,∴∠BPC=90°,∠ACP=∠B,∴∠BPC=∠DPE=90°,∴∠BPC﹣∠CPE=∠DPE﹣∠CPE,即:∠BPE=∠CPD,在△BPE和△CPD中,,∴△BPE≌△CPD(ASA),∴PD=PE;(3)如图2,∵AC=BC=2,∠ACB=90°,∴AB=2,∵点P是AB的中点,∴AP=BP=,当AD=AP=时(图中D1和D2),∴CD1=AC﹣AD2=2﹣,CD2=AC+AD2=2+,当AP=PD时(图中D3),此时点D和C点重合,CD3=0,当AD=PD时(图中D4),CD4=AD4=1,综上所述:CD=2+或2﹣或0或1.6.【解答】解:(1)①∵α=60°,∴∠BAC=∠CEF=60°,∵AB=AC,线段CE绕点E顺时针旋转得到线段EF(CE=EF),∴△ABC和△EFC是等边三角形,∴BC=AC,FC=EC,∠BCA=∠FCE=∠ACB=60°,∴∠FCB=∠ECA,∴△FCB≌△ECA(SAS),∴BF=AE,∴=1;故答案为:1;②由①得△FCB≌△ECA,∴∠FBC=∠EAC,∵∠BDG=∠ADC,∴∠BGD=∠ACD=60°,即∠AGB=60°,故答案为:60°;(2)=,∠AGB=30°,证明如下:设CF与AD交于M,如图:∵α=120°,∴∠BAC=∠CEF=120°,∵AB=AC,线段CE绕点E顺时针旋转得到线段EF(CE=EF),∴∠BCA=∠FCE=30°,=,∴∠FCB=∠ECA,△ABC∽△EFC,∴=,∴△FCB∽△ECA,∴=,∠BFC=∠AEC,∵∠FMG=∠EMC,∴∠AGB=∠FCE=30°,在Rt △ACD 中,=cos30°,∴=,∴===;(3)①当E 在线段AD 上时,连接FD ,过F 作FK ⊥AG 于K ,如图:∵α=90°,AB =AC ,线段CE 绕点E 顺时针旋转α,得到线段EF ,∴△ABC 和△EFC 是等腰直角三角形,∴∠ACB =45°,∵∠ACE =15°,∴∠DCE =30°,∵AB =2,∴AC =2,,BC =2,∵AD ⊥BC ,∴BD =CD =,在Rt △ECD 中,cos30°=,∴CE =2=EF ,∵∠DEC =90°﹣∠DCE =60°,∴∠FEK=30°,∴FK=EF=,∵=,∠BCF=45°﹣∠BCE=∠ACE,∴△BCF∽△ACE,∴∠FBC=∠EAC=45°,∵AD⊥BC,∴△BDG时等腰直角三角形,∴DG=BD=,∴△DFG的面积为DG•FK=××=;②当E在DA延长线上时,连接FD,过F作FT⊥AD于T,如图:∵∠ACE=15°,∠ACD=45°,∴∠ECD=60°,∴∠DEC=30°,∠EFD=60°,∵CD=,∴CE=FE=2,在Rt△EFT中,FT=FE•sin60°=3,∵=,∠BCF=45°﹣∠ACF=∠ACE=15°,∴△BCF∽△ACE,∴∠BFC=∠AEC=30°,∴∠DGB=∠BFC+∠BCF=45°,∴△BDG是等腰直角三角形,∴DG=BG=BC=,∴△DFG的面积为DG•FT=××3=3;综上所述,△DFG的面积为或3.7.【解答】(1)证明:∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED,∵∠ADC=∠B+∠BAD=∠ADE+∠CDE,∠AED=∠C+∠CDE,∴∠B+∠BAD=∠C+∠CDE+∠CDE,∴∠BAD=2∠CDE.(2)证明:如图2中,在FC上截取FM,使得FM=AF,连接DM∵DF⊥AM,AF=FM,∴DA=DM,∴∠CAD=∠DMA,∵∠CAD=2∠B=2∠C,∠AMD=∠C+∠MDC,∴∠AMD=2∠C,∴∠C=∠MDC,∴MD=MC,∴AD+AF=DM+FM=CM+FM=CF,∴AC﹣CF=CF﹣CM,∴AC﹣CF=CF﹣AD,∴AC+AD=2CF.(3)解:如图3中,在FC上截取FM,使得FM=AF,连接DM,CG.设∠B=∠C=β,∠CDE=∠GDE=α,∵∠CAD=2β,∠ADE=∠AED=α+β,∴2β+2(α+β)=180°,∴2β=90°﹣α,∵∠AFD=90°,∴∠ADF=∠MDF=α,∴∠AEG=180°﹣α﹣β﹣(180°﹣2β)=2β,∵AE=CM,∴AM=CE=EG,∵AD=AE,∴△ADM≌△EAG(SAS),∴AG=DM=AD=AE=8,∵EC=2,∴AC=AE+CE=10=AB,AF=FM=1,∵DF2=AD2﹣AF2=CD2﹣CF2,∴CD=12,设BD=2m,则BC=2m+12,作AH⊥BC于H,则CH=BH=m+6,∴DH=6+m﹣2m=6﹣m,∵AH2=AD2﹣DH2=2﹣CH2,∴82﹣(6﹣m)2=102﹣(m+6)2,解得m=,∴BD=2m=3.8.【解答】解:(1)如图1,∵△ABC是等边三角形,∴AB=AC,∠BAC=60°,∵∠DAE =60°,∴∠BAC =∠DAE ,∴∠BAC ﹣∠BAD =∠DAE ﹣∠BAD ,∴∠BAE =∠CAD ,又∵AD =AE ,∴△ABE ≌△ACD (SAS ),∴CD =BE ,∵,∴=,∴CD =BC =;(2)如图2,延长EA 至H ,使AH =AE ,连接DH ,CH ,∵AD =AE ,∠EAD =120°,∴AH =AD ,∠DAH =60°,∴△ADH 是等边三角形,∴∠AHD =∠ADH =60°,∵△ABC是等边三角形,∴∠ACB=60°,∴∠ACB=∠AHD,∴点A、D、C、H共圆,∴∠ACH=∠ADH=60°,∴∠ACH=∠BAC=60°,∴AF∥CH,∴==1,∴EF=CF,又∵AG=GC,∴FG∥AE,FG=AE;(3)如图3,取AC的中点O,连接OE、OB,作FI∥OE交OB于I,∴△BIF∽△BOE,OE==2,∠OBC=30°,∴===,∴IF=,BI=,∴F点在以I为圆心,为半径的圆上运动,∴当D、F、I在同一条直线时,DF最小,作IK⊥BD于K,FG⊥BD于G,∴BK=BI•cos30°=×=,IK=BI=,∴DK=BD﹣BK=3﹣=,∴DI==,∴DF=DI﹣IF=﹣,由△DGF∽△DKI得,=,∴=,∴FG=,=BD•FG∴S△BDF==.9.【解答】解:(1)如图1,连接CE,∵∠BAC=∠DAE=90°,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,∴∠BAD=∠CAE,∵AB=AC,AD=AE,∴△ABD≌ACE(SAS),∴∠B=∠C=45°,∴CE=BD=4,∠ACE=∠B=45°,∴∠DCE=45°+45°=90°,在Rt△DCE中,CE=4,CD=3,∴DE==5;(2)如图2,延长AD至S,使AS=CF,连接CS,由(1)可得:△ABD≌ACE,∵AD⊥BD,∴∠AEC=∠ADB=90°,∵∠DAE+∠AEC=180°,∴AS∥CF,∴四边形ASCF是平行四边形,∠NCS=∠ABC=45°,∴CM=AF=CS,∵∠NCS=∠NCM=45°,NC=NC,∴△NCS≌NCM(SAS),∴SN=MN,∴CF=AS=AN+SN=AN+MN;(3)如图3,设BC,DE相交于点G,连接AG,CM,BE,AF,CD,作AH⊥DN交DN的延长线于点H,GI⊥FD于点I,∵AB=AD,∴AB=AC=AD=AE,BC=DE,∴∠ABE=∠AEB,∵∠ABG=∠AEG=45°,∴∠GBE=∠GEB,∴GB=GE,∴GC=GD,∵F为BC中点,M为DE中点,∴FC=MD,∴GF=GM,∵∠DGF=∠CGM,∴△GDF≌GCM(SAS),∴∠GDF=∠GCM,DF=CM,∵N为BM中点,∴NF是△BMC的中位线,∴NF∥CM,∴∠GDF=∠GCM=∠GFD,NF:DF=NF:CM=1:2,∴GF=GD=GC=GM,DF:DN=2:3,∴CF为⊙G直径,∴∠CDF=90°,∵AD=AC,∴AG垂直平分DC,∴AG∥FD,∴∠BFN=∠AGF,∵∠BFN+∠AFH=∠FAH+∠AFH=90°,∴∠FAH=∠BFN=∠AGF=∠GFI,设GF=GC=k,则AF=BC=FC=2k,NF=k,∴tan∠FAH=tan∠GFI=tan∠AGF==2,∴AH=k,FH=k,FI=k,GI=k,∴FD=2FI=k,DN=k,∴NF=FD=k,∴HN=FH﹣NF=k﹣k=k,在Rt△AHN中,AN==k,∴DF:DN:AN=k:k:k=2:3:.10.【解答】(1)证明:如图1中,延长AD交BE的延长线于T,设AT交BC于J.∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,在△ACD和△BCE中,,∴△ACD≌△BCE(SAS),∴AD=BE,∠CAD=∠CBE,∴∠BTJ=∠ACJ=90°,∴AD⊥BE.(2)解:如图2中,∵CD=CE=1,∠DCE=90°,∴DE===,∵AD=BE=2,∠AEB=90°,∴BD===.故答案为:.(3)如图3中,过点C作CP⊥BE于P,CQ⊥AF于Q.∵△ACD≌△BCE,CQ⊥AD,CP⊥BE,∴CQ=CP,∴CF平分∠AFE,∴∠CFP=∠CFQ=45°,∵∠CPF=∠CQF=90°,∴QC=QF=CP=PF,∴四边形QCPF是菱形,∵∠PFQ=90°,∴四边形QCPF是正方形,∵∠DCE=∠QCP=90°,∴∠QCD=∠PCE,在Rt△CQD和Rt△CPE中,,∴Rt△CQD≌Rt△CPE(HL),∴DQ=PE,∴DF+EF=FQ﹣DQ+PF+PE==1+,∴PF=,∴CF=PF=.故答案为:.11.【解答】解:(1)如图2中,∵DE∥BC,∴∠CED=∠BCA=90°,∴∠FAC=∠CED﹣∠FAD=90°﹣60°=30°.(2)①如图3中,过点G作直线HL∥MN.∵MN∥PQ,HL∥MN,∴MN∥HK∥PQ,∴∠HGF=∠EFN,∠BGH=∠ABC,∴∠BGF=∠HGF+∠BGH=∠EFN+∠ABC,∴∠BGF﹣∠EFN=∠ABC=45°.②如图4﹣1中,当DE∥BC时,t==3.如图4﹣2中,当DE∥AB时,当DE∥AB时,t=(90﹣15)÷10=7.5.同法,当DE∥AC时,t=(135﹣15)÷10=12.综上所述,满足条件的t的值为3或7.5或12.12.【解答】解:(1)如图1中,连接CD.在Rt△ABC中,∠ACB=90°,AC=BC=4,∴AB==4,∵AD=DB,∴CD=AB=2,CD⊥AB,在Rt△CDP中,PC==3.(2)如图2中,∵DP=1,∴点P在以点D为圆心的⊙D上.①当PB=PC时,∵CD=DB,∴P、D都在线段BC的垂直平分线上,设直线DP交BC于E.∴∠PEC=90°,BE=CE=2,∵∠CDB=90°,∴DE=BC=CE=2,在Rt△PCE中,PC=,当P在线段PD上时,PE=DE﹣DP=1,PC==,当P在线段ED的延长线上时,PE=ED+DP=3,PC==.②当PC=BC时,∵PC+1<BC,∴PC≠BC,此种情形不存在;③当PB=BC时,同理这种情形不存在;如图3中(3)如图4中,连接BB′.由旋转可知:PB=PB′,∠BPB′=90°,∴∠PBB′=45°,∴BB′=PB,∴=,∵AC=BC,∠ACB=90°,∴∠ABC=45°,∴∠ABC=∠PBB′,∴∠ABB′=∠CBP,∵==,∴=,∴=,∴△ABB′∽△CBP,∴==,∵PC≤CD+DP=2+1,∴点P落在CD的延长线与⊙D的交点处,PC的值最大,∴AB′≤(2+1)=4+.∴AB′的最大值为4+.13.【解答】(1)解:如图1中,过点B作BM⊥AC于M,过点D作DN⊥AC于N.∵AB=BC=3,∠ABC=90°,∴AC=AB=3,CM=AM,∴BM=AC=,∵BD∥AC,∴∠DBM=∠BMN=90°,∵∠DNM=90°,∴四边形BMND是矩形,∴BD=MN,DN=BM∵AD=AC,BM=AC,∴DN=AD,∴∠DAN=30°,∴AN=AD•cos30°=,∴MN=AN﹣AM=﹣,∴BD=MN=﹣.(2)证明:如图1中,延长CE交AB的延长线于T,连接TG,CD.∵CE⊥AD,∴∠CFG=∠ABG=90°,∵∠CGF=∠AGB,∴∠FCG=∠GAB,∵∠CBT=∠ABG=90°,CB=AB,∴△CBT≌△ABG(ASA),∴CT=AG,BT=BG,∠CTB=∠AGB,∴∠BTG=∠BGT=45°,∵∠AGB=∠CAG+∠ACG,由(1)可知,∠CAG=30°,∴∠AGB=75°,∴∠CTB=75°,∴∠FTG=30°,∴FT=FG,∵AD=AC,∠CAD=30°,∴∠ADC=∠ACD=75°,∵∠CGD=∠AGB=75°,∴∠CDG=∠CGD,∴CD=CG,∵CF⊥DG,∴DF=FG,∴FT=DF,∴AG=CT=CF+DF.(3)解:如图,将△CBN绕点B逆时针旋转60°得到△PBQ,连接QN,AP.则PQ=CN,△BQN是等边三角形,∴BN=NQ,∠BNQ=∠BQN=60°,∵CN+AN+BN=PQ+QN+NA≥AP,∴当P,Q,N,A共线时,NC+BN+AN的值最小,此时∠ANB=120°,∠BAN=15°,∴∠ABN=180°﹣120°﹣15°=45°,∵∠ABC=90°,∴∠ABN=∠CBN=45°,∵BA=BC,∴BM⊥AC,设MN=x,则AM=BM=x,∴m+x=x,∴x=m,∴AN=CN=2MN=(+1)m,∴NB+NA+NC的最小值=m+2(+1)m=(2+3)m.14.【解答】解:(1)如图1中,∵CA=CB,∠ACB=90°,∴∠CAB=∠B=45°,∵DE⊥AB,∴∠ADE=∠ACE=90°,∵AP=PE,∴PD=AE,PC=AE,∴PD=PC,∵PA=PD=PC,∴∠PAD=∠PDA,∠PAC=∠PCA,∵CPD=∠EPD+∠EPC=∠PAD+∠PDA+∠PAC+∠PCA=2(∠PAD+∠PAC)=90°,∴PC⊥PD,故答案为:PD=PC,PD⊥PC.(2)结论成立.理由如下:过点P作PT⊥AB交BC的延长线于T,交AC于点O.∵∠A=∠AOP=45°,∴PA=PO,∵∠COT=∠AOP=45°,∠OCT=90°,∴∠COT=∠T=45°,∴CO=CT,TO=CT,∵∠BPT=90°,∴∠PBT=∠T=45°,∴PB=PT,∴PE+BE=OP+OT,∵PA=PE=PO,∴BE=OT,∵BE=BD,OT=CT,∴BD=CT,∵∠DBP=∠T=45°,∴△DBP≌△CTP(SAS),∴PD=PC,∠BPD=∠CPT,∴∠DPC=∠BPT=90°,∴PD⊥PC.解法二:延长DE交AC于F,连接PF,证明△DPE≌△CPF.(3)如图3﹣1中,当点E在BC的上方时,过点P作PQ⊥BC于Q.∵BC=3BD=3,∴AC=BC=3,BD=DE=,∵DE∥PQ∥AC,PE=PA,∴DQ=QC,∴PQ=(DE+AC)=2,∵△PCD是等腰直角三角形,PQ⊥CD,∴DQ=CQ,∴CD=2PQ=4,∴PC=PD=4.如图3﹣2中,当点E在BC的下方时,同法可得PC=PD=2.综上所述,PC的长为4或2.15.【解答】解:(1)如图1,过B点作BH⊥y轴于点H,∴∠BHA=90°,∠ABH+∠BAH=90°,∴∠BHA=∠AOC=90°,∵∠BAC=90°,∴∠BAH+∠CAO=90°,∴∠ABH=∠CAO,∵点A(0,2),B(﹣2,4),∴AO=BH=2,OH=4,。
中考数学复习专项强化练习:旋转(人教版)

中考数学复习专项强化练习:旋转(人教版)一、选择题(本大题共10道小题)1. (2022·湖北黄石)如图,△OAB中,∠AOB=60°,OA=4,点B的坐标为(6,0),将△OAB绕点A逆时针旋转得到△CAD,当点O的对应点C落在OB上时,点D的坐标为( )。
A. (7,33)B. (7,5)C. (53,5)D. (53,33)2. (2022·湖北黄石)如图,Rt△OAB的斜边OA在y轴上,∠AOB=30°,OB将Rt△AOB绕原点顺时针旋转90°,则A的对应点A1的坐标为( )。
A. (1,3)B. (﹣1,3)C. (2,0)D. (﹣2,0)3. (2022·湖北黄石)如图,正方形OABC将正方形OABC绕原点O顺时针旋转45°,则点B的对应点B1的坐标为( )。
D. (0,2)4. (2022•青岛)如图,将△ABC先向上平移1个单位,再绕点P按逆时针方向旋转90°,得到△A′B′C′,则点A的对应点A′的坐标是()。
A. (0,4)B. (2,﹣2)C. (3,﹣2)D. (﹣1,4)5. (2022•天津)如图,在△ABC中,∠ACB=90°,将△ABC绕点C顺时针旋转得到△DEC,使点B的对应点E恰好落在边AC上,点A的对应点为D,延长DE交AB于点F,则下列结论一定正确的是()。
A. AC=DEB. BC=EFC. ∠AEF=∠DD. AB⊥DF6. (2021·湖北黄石)如图,△ABC的三个顶点都在方格纸的格点上,其中A点的坐标是(-1,0),现将△ABC绕A点按逆时针方向旋转90o,则旋转后点C的坐标是( )。
A. (2,-3)B. (-2,3)C. (-2,2)D. (-3,2)7. (2022•菏泽)如图,将△ABC绕点A顺时针旋转角α,得到△ADE,若点E恰好在CB的延长线上,则∠BED等于()。
2022年中考数学复习:旋转类综合体专项训练(含答案)

2022年中考数学复习:旋转综合体专项训练1.如图,在Rt ABC 中,90ABC ∠=︒,30ACB ∠=︒,将ABC 绕点C 顺时针旋转一定的角度α得到DEC ,点A ,B 的对应点分别是点D ,E .(1)如图①,当点E 恰好在AC 边上时,连接AD ,求①ADE 的度数;(2)如图①,当60α=时,若点F 为AC 边上的动点,当①FBC 为何值时,四边形BFDE 为平行四边形?请说出你的结论并加以证明2.综合与实践问题:如图1,已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,GF ⊥CD ,垂足为F .证明与推断(1)①四边形CEGF 的形状是 ;②AGBE的值为 ; 【探究与证明】(2)在图1的基础上,将正方形CEGF 绕点C 按顺时针方向旋转α角(0°<α<45°),如图2所示,并说明理由;【拓展与运用】(3)如图3,在(2)的条件下,正方形CEGF 在旋转过程中,AG 和GE 的位置关系是 .3.若①ABC ,①ADE 为等腰三角形,AC =BC ,AD =DE ,将①ADE 绕点A 旋转,连接BE ,F 为BE 中点,连接CF ,DF .(1)若①ACB =①ADE =90°,如图1,试探究DF 与CF 的关系并证明; (2)若①ACB =60°,①ADE =120°,如图2,请直接写出CF 与DF 的关系.4.在平面直角坐标系中,点(0,0)O ,点A ,点)(0),30B m m AOB >∠=︒.以点O 为中心,逆时针旋转OAB ,得到OCD ,点,A B 的对应点分别为,C D .记旋转角为α.(1)如图①,当点C 落在OB 上时,求点D 的坐标;(2)如图①,当45α=︒时,求点C 的坐标;(3)在(2)的条件下,求点D 的坐标(直接写出结果即可).5.如图,30HAB ∠=︒,点B 与点C 关于射线AH 对称,连接AC .D 点为射线AH 上任意一点,连接CD .将线段CD 绕点C 顺时针旋转60°,得到线段CE ,连接BE .(1)求证:直线EB 是线段AC 的垂直平分线;(2)点D 是射线AH 上一动点,请你直接写出ADC ∠与ECA ∠之间的数量关系.6.已知如图,等腰△ABC 中,AB=AC ,△BAC=α(α>90︒),F 为BC 中点,D 为BC 延长线上一点,以点A 为中心,将线段AD 逆时针旋转α得到线段AE ,连接CE ,DE .(1)补全图形并比较△BAD 和△CAE 的大小; (2)用等式表示CE ,CD ,BF 之间的关系,并证明;(3)过F 作AC 的垂线,并延长交DE 于点H ,求EH 和DH 之间的数量关系,并证明.7.一副三角尺(分别含30°,60°,90°和45°,45°,90°)按如图所示摆放,边OB ,OC 在直线l 上,将三角尺ABO 绕点O 以每秒10°的速度顺时针旋转,当边OA 落在直线l 上时停止运动,设三角尺ABO 的运动时间为t 秒.(1)如图,①AOD = °= ′; (2)当t =5时,①BOD = °; (3)当t = 时,边OD 平分①AOC ;(4)若在三角尺ABO 开始旋转的同时,三角尺DCO 也绕点O 以每秒4°的速度逆时针旋转,当三角尺ABO 停止旋转时,三角尺DCO 也停止旋转.在旋转过程中,是否存在某一时刻使①AOC =2①BOD ,若存在,请直接写出的值;若不存在,请说明理由.8.如图,正方形ABCO 的边OA 、OC 在坐标物上,点B 坐标为()3,3.将正方形ABCO 绕点A 顺时针旋转角度()090αα︒<<︒,得到正方形ADEF ,ED 交线段OC 于点G ,ED 的延长线交线段BC 于点P .连AP 、AG .(1)求证:AOG①ADG;∠的度数;并判断线段OG、PG、BP之间的数量关系,说明理由;(2)求PAG(3)当12∠=∠时,求直线PE的解析式(可能用到的数据:在Rt中,30°内角对应的直角边等于斜边的一半).(4)在(3)的条件下,直线PE上是否存在点M,使以M、A、G为顶点的三角形是等腰三角形?若存在,请直接写出M点坐标;若不存在,请说明理由.9.如图,等腰Rt①ABC中,AB=AC,D为线段BC上的一个动点,E为线段AB上的一个动点,使得CD=.连接DE,以D点为中心,将线段DE顺时针旋转90°得到线段DF,连接线段EF,过点D作射线DR①BC交射线BA于点R,连接DR,RF.(1)依题意补全图形;(2)求证:①BDE①①RDF;(3)若AB=AC=2,P为射线BA上一点,连接PF,请写出一个BP的值,使得对于任意的点D,总有①BPF为定值,并证明.10.在①ABC中,AB=AC,①BAC=90°,D为平面内的一点.(1)如图1,当点D在边BC上时,BD=2,且①BAD=30°,AD=;(2)如图2,当点D在①ABC的外部,且满足①BDC﹣①ADC=45°,求证:BD AD;(3)如图3,若AB =4,当D 、E 分别为AB 、AC 的中点,把①DAE 绕A 点顺时针旋转,设旋转角为α(0<α≤180°)直线BD 与CE 的交点为P ,连接P A ,直接出①P AB 面积的最大值 .11.已知:①ABC 为等边三角形,且AB =4,点D 在直线BC 上运动,线段DA 绕着点D 顺时针旋转60°得到线段DE ,连接AE 和BE ,直线AE 交直线BC 于点F . (1)如图,当点D 在点C 左侧时,求证:CD =BE ;(2)若①ABC 的面积等于①ABF 面积的4倍,直接写出线段CD 的长;(3)在(2)的条件下,若点E 关于直线AD 的对称点为点G ,连接DG 交线段AC 于点M ,DE 交线段AB 于点N ,连接MN ,直接写出线段MN 的长.12.已知在①ABC 中,90ACB ∠=︒,AC =BC =(1)如图1,以点A 为原点,AB 所在直线为x 轴建立平面直角坐标系,直接写出点B ,C 的坐标; (2)如图2,过点C 作①MCN =45°交AB 于点M ,N ,且AM =1,求MN 的长度;(3)如图3,过点C 作①MCN =45°,当点M ,N 分布在点B 异侧时,线段AM ,BN 和MN 满足怎样的数量关系?并给予证明.13.如图,在①ABC 中,AC = BC ,①ACB = 90°,D 是线段AC 延长线上一点,连接BD ,过点A 作AE ①BD 于E .(1)求证:①CAE =①CBD ;(2)将射线AE 绕点A 顺时针旋转45°后,所得的射线与线段BD 的延长线交于点F ,连接CE . ①依题意补全图形;①用等式表示线段EF ,CE ,BE 之间的数量关系,并证明.14.把两个等腰直角ABC 和ADE 按如图1所示的位置摆放,将ADE 绕点A 按逆时针方向旋转,如图2,连接BD ,EC ,设旋转角为α(0360α︒<<︒).(1)如图1,BD 与EC 的数量关系是___________,BD 与EC 的位置关系是___________;(2)如图2,(1)中BD 和EC 的数量关系和位置关系是否仍然成立,若成立,请证明;若不成立请说明理由.(3)如图3,当点D 在线段BE 上时,BEC ∠=___________. (4)当旋转角α=__________时,ABD △的面积最大.15.如图,在Rt ①ABC 中,BC =4,AC =2,①ACB =90°,矩形BDEF 的边BF =1,BD =2,矩形BDEF 可以绕点B 在平面内旋转,连接AE 、BE 、CD . (1)证明:①ABE ①①CBD ;(2)当A 、E 、F 三点共线时,求CD 的长;(3)设AE 的中点为M ,连接FM ,直接写出FM 的最大值.16.在平面直角坐标系中,四边形AOBC 是矩形,点A 的坐标为()5,0,点B 的坐标为()0,3,以点A 为中心,顺时针旋转矩形AOBC ,得到矩形ADEF ,点O ,B ,C 的对应点分别为D ,E ,F .(1)如图①,当点D 落在BC 边上时,求点D 的坐标;(2)如图①,当点D 落在线段BE 上时,连接AB ,AD 与BC 交于点H . ①求证:ADB AOB ≅△△; ①求点H 的坐标.(3)点K 为矩形AOBC 对角线的交点,S 为KDE 得面积,直接写出S 的取值范围.17.如图,P 是正三角形ABC 内的一点,且6,8,10PA PB PC ===,若将PAC △绕点A 顺时针旋转后得到P AB '△,(1)求旋转角的度数;(2)求点P 与点P '之间的距离; (3)求APB ∠的度数.18.如图在平面直角坐标系中,点O 为坐标原点,直线y 34=-x +b 分别交x 轴,y 轴于点A 、B ,OA =4,①OBA 的外角平分线交x 轴于点D .(1)求点D 的坐标;(2)点P 是线段BD 上一点(不与B 、D 重合),过点P 作PC ①BD 交x 轴于点C ,设点P 的横坐标为t ,△BCD 的面积为S ,求S 与t 之间的函数解析式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,PC 的延长线交y 轴于点E ,当PC =PB 时,将射线EP 绕点E 旋转45°交直线AB 于点F ,求F 点坐标.19.如图,在菱形ABCD 中,60ABC ∠=︒,E 为对角线AC 上一点,将线段DE 绕点D 逆时针旋转60︒,点E 的对应点为F ,连接BE ,AF ,CF .(1)求证:B ,C ,F 三点共线;(2)若点G 为BE 的中点,连接AG ,求证:2AF AG =.20.如图,在四边形ABCD中,BC=CD,△BCD=α°,△ABC+△ADC=180°,AC、BD交于点E.将△CBA 绕点C顺时针旋转α°得到△CDF(点B、A的对应点分别为点D、F).(1)画出旋转之后的图形(不要求写画法,保留画图痕迹);(2)求证:△CAB=△CAD;(3)若△ABD=90°,AB=3,BD=4,△BCE的面积为1S,△CDE的面积为2S,求1S:2S的值.参考答案:1.解:①将ABC绕点C顺时针旋转一定的角度α得到①DEC,E点在AC上,①CA=CD,①ECD=①BCA=30︒,(180︒−30︒)=75︒,①①CAD=①CDA=12又①①DEC=①ABC=90︒,①①ADE=90°-75︒=15︒;(2)①FBC=30︒时,四边形BFDE为平行四边形,①①FBC=①ACB=30︒,①①ABF=①A=60︒,①BF=CF=AF,①ABF是等边三角形,①BF=AB,①将ABC绕点C顺时针旋转60︒得到DEC,①DE=AB,BCE是等边三角形,①DEC=①ABC=90︒,①①CBE=①BEC=60︒,①①EBF=①EBC-①FBC=30︒,①①DEB+①EBF=180︒,①DE=BF,//DE BF,①四边形BFDE为平行四边形.2.①正方形;.理由:如图1中,∵四边形ABCD 是正方形,∴∠BCD =90°,∠BCA =45°,∵GE ⊥BC 、GF ⊥CD ,∴∠CEG =∠CFG =∠ECF =90°,∴四边形CEGF 是矩形,∠CGE =∠ECG =45°,∴EG =EC ,∴四边形CEGF 是正方形,∵AC BC ,,∴AG =AC ﹣CGBC ﹣EC ,∴AG BE(2)结论:AG ,理由:如图2中,连接CC ,∵四边形ABCD 是正方形,∴∠ABC =90°,AB =BC ,∴△ABC 为等腰直角三角形,∴AC BC由①得四边形GECF 是正方形,∴∠GEC =∠ECF =90°,GE =EC ,∴△EGC 为等腰直角三角形.∴CG CE∴AC CG BC EC=∴△ACG ∽△BCE ,∴AG CG BE EC∴线段AG 与BE 之间的数量关系为AG ;(3)如图3中,连接CG ,∵∠CEF =45°,点B 、E ,∴∠BEC =135°.∵△ACG ∽△BCE ,∴∠AGC =∠BEC =135°.∴∠AGF =∠AGC +∠CGF =135°+45°=180°,∴点A ,G ,F 三点共线,∴∠AGE =∠AGF ﹣∠EGF =180°﹣90°=90°,∴AG ⊥GE ,故答案为:AG ⊥GE .3.(1)DF =CF 且DF ①CF ;延长CF 至点M ,使CF =FM ,连接ME ,MD ,CD ,延长DE 交CB 延长线于点N ,如图1,①BF=EF,CF=FM,①BFC=①EFM,①①BFC①①EFM(SAS),①EM=BC=AC,①FME=①FCB,①BC①EM,①①N=①MEN,在四边形ACND中,①ACB=①ADE=90°,①①N+①CAD=360°-(①ACB+①ADE)=180°,又①①MEN+①MED=180°,①①MED=①CAD,又AD=DE,EM=AC,①①MED①①CAD(SAS),①DM=DC,①MDE=①CDA,①①MDC=①NDC+①MDE=①NDC+①CDA=①ADE=90°,①①DCM为等腰直角三角形,①点F是CM中点,CM=CF,DF①CF;①DF=12(2)DF①CF且CF;延长CF至点M,使CF=FM,连接ME,MD,CD,延长ED交BC延长线于点N,如图2,①BF=EF,CF=FM,①BFC=①EFM,①①BFC①①EFM(SAS),①EM =BC =AC ,①FME =①FCB ,①BC //EM ,①①N =①NER ,①①ACB =60°,①①ACN =120°,①①ADE =120°,①①ADN =60°,①①N +①CAD =360°-(①ACN +①ADN )=180°,①①DER +①DEM =180°,①①DEM =①CAD ,又 AD =DE ,EM =AC ,①①MED ①①CAD (SAS ),①DM =DC ,①MDE =①CDA ,①①DCM 为等腰三角形,①①CDM =①ADE =120°,①F 是CM 的中点,①DF ①CF①60CDF ∠=︒①30DCF ∠=︒①CD =2DE由勾股定理得,222CE DE CD +=①2224CE DE DE +=解得,CF (负值舍去)①DF ①CF 且CF .4.(1)如图,过点D 作DE OA ⊥,垂足为E .① 0A ,B m )0m (>),① AB OA ⊥,OA =AB m =.① 30AOB ∠=︒,① 22OB AB m ==.在Rt OAB 中,由222OA AB OB +=,得2234m m +=.解得1m =.① 1AB =,2OB =.① OCD 是由OAB 旋转得到的,① 2OD OB ==,30DOC AOB ∠=∠=︒.① 60DOE DOC BOA ∠=∠+∠=︒.① 9030ODE DOE ∠=︒-∠=︒.① 112OE OD ==. 在Rt OED 中,DE =① 点D 的坐标为(.(2)如图,过点C 作CT OA ⊥,垂足为T .由已知,得45COT ∠=︒.① 9045OCT COT ∠=︒-∠=︒.① OT CT=.① OCD是由OAB旋转得到的,① OC OA==在Rt OTC△中,由222T TO C OC+=,得OT CT=① 点C的坐标为.(3)如图①中,过点D作DJ①OA于点J,在DJ上取一点K,使得DK=OK,设OJ=m.①①DOC=30°,①COT=45°,①①DOJ=75°,①①ODJ=90°-75°=15°,①KD=KO,①①KDO=①KOD=15°,①①OKJ=①KDO+①KOD=30°,①OK=DK=2m,KJ,①OD2=OJ2+DJ2,①22=m2+(2m)2,解得m=,①OJ DJ①D⎫⎪⎪⎝⎭.5.(1)证明:连接AE,DB,CB①点B 与点C 关于射线AH 对称,30HAB ∠=︒ ①CD BD =,AC AB =①30HAB HAC ∠∠==︒①260CAB HAC ∠∠==︒①ABC 为等边三角形,60ACB ∠=︒ ①60DCE ∠=︒①DCE ACD ACB ACD ∠∠∠∠-=- ECA DCB ∠=∠①在ECA △和DCB 中,EC DC ECA DCB AC BC =⎧⎪∠=∠⎨⎪=⎩①()ECA DCB SAS ≅△△①BD EA =①DC BD EC ==,①AE EC =又AB BC =①EB 垂直平分AC(2)分两种情况来讨论:第一种情况,如图,当点D 在ABE △内部时:①点B 与点C 关于射线AH 对称,①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠+∠=︒+∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒+∠第二种情况,如图,当点D 在ABC 外部时: ①点B 与点C 关于射线AH 对称,①90CFA ∠=︒①90ADC CFA DCB DCB ∠=∠-∠=︒-∠ ①ECA DCB ∠=∠①90ADC ECA ∠=︒-∠6.如图,即为补全的图形,根据题意可知BAC DAE α∠=∠=,①BAC CAD DAE CAD ∠+∠=∠+∠,即BAD CAE ∠=∠.(2)由旋转可知AD AE =,①在BAD 和CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩,①()BAD CAE SAS ≅,①BD CE =.①BD BC CD =+,①CE BC CD =+.①点F 为BC 中点,①2BC BF =,①2CE BF CD =+,即2CE CD BF -=.(3)如图,连接AF ,作AN DE ⊥,①AB=AC ,F 为BC 中点,①90AFD ∠=︒,12FAB FAC α∠=∠=. 根据作图可知90AND ∠=︒,①180AFD AND ∠+∠=︒,①A 、F 、D 、N 四点共圆,①AFN ADN ∠=∠.①AD AE =,AN DE ⊥,①EN DN =,11(180)9022AFN ADN DAE α∠=∠=︒-∠=︒-. ①11909022AFN FAC αα∠+∠=︒-+=︒. ①90AFH FAC ∠+∠=︒,且点H 在线段DE 上,①点H 与点N 重合,①EH DH =.7.(1)①180AOD AOB COD ∠=︒-∠-∠,3045AOB COD ∠=︒∠=︒,,①10510560=6300AOD '∠=︒=⨯.故答案为:105,6300;(2)当5t =时,即三角尺ABO 绕点O 顺时针旋转了51050⨯︒=︒,如图,ABO 即为旋转后的图形.由旋转可知50BOM ∠=︒,①180180455085BOD COD BOM ∠=︒-∠-∠=︒-︒-︒=︒,故答案为85;(3)当三角尺绕点O 顺时针旋转到如图所示的ABO 的位置时,边OD 平分①AOC .①224590AOC COD ∠=∠=⨯︒=︒,①90AOM ∠=︒①90903060BOM AOB ∠=︒-∠=︒-︒=︒, ①60610t ==; 故答案为:6;(4)①当边OA 落在直线l 上时停止运动时, ①180150=1510t -≤. 当OA 和OC 重合时,即有10418030t t +=︒-︒, 解得:757t =. ①当757t ≤时,1801030415014AOC t t t ∠=︒--︒-=︒-, 当757t >时,1030418014150AOC t t t ∠=+︒+-︒=-︒. 当OB 和OD 重合时,即有10418045t t +=︒-︒, 解得:13514t =①当13514t ≤时,1801045413514BOD t t t ∠=︒--︒-=︒-, 当13514t >时,1045418014225BOD t t t ∠=+︒+-︒=-︒. ①可根据2AOC BOD ∠=∠分类讨论,①当13514t ≤时,有15014=2(13514)t t ︒-︒-, 解得:607t =,符合题意; ①当13575147t <≤时,即有150142(14225)t t ︒-=-︒ 解得:1007t =,符合题意; ①当757t >时,即有141502(14225)t t -︒=-︒解得:150157t =>,不符合题意舍; 综上,可知当607t =或1007t =时,2AOC BOD ∠=∠. 8.(1)证明:在Rt△AOG 和Rt△ADG 中,AO AD AG AG=⎧⎨=⎩ ①AOG ①ADG (HL ).(2)在Rt ①ADP 和Rt ①ABP 中,AD AB AP AP=⎧⎨=⎩ ΔΔADP ABP ∴≅(HL ), 则DAP BAP ∠=∠;ΔΔAOG ADG ≅,1DAG ∴∠=∠;又190DAG DAP BAP ∠+∠+∠+∠=︒,2290DAG DAP ∴∠+∠=︒,45DAG DAP ∴∠+∠=︒,PAG DAG DAP ∠=∠+∠,45∴∠=︒PAG ;ΔΔAOG ADG ≅,DG OG ∴=,ΔΔADP ABP ≅,DP BP ∴=,PG DG DP OG BP ∴=+=+.(3)解:ΔΔAOG ADG ≅,AGO AGD ∴∠=∠,又190AGO ∠+∠=︒,290PGC ∠+∠=︒,12∠=∠,AGO PGC ∴∠=∠,又AGO AGD ∠=∠,AGO AGD PGC ∴∠=∠=∠,又180AGO AGD PGC ∠+∠+∠=︒,180360AGO AGD PGC ∴∠=∠=∠=︒÷=︒,12906030∴∠=∠=︒-︒=︒;∴在Rt ΔAOG 中,2,3AG OG OA ==,222AG OG OA =+∴222(2)3OG OG =+ 解得OGG ∴点坐标为0),3CG =在Rt ΔPCG 中,2PG CG =,222PG CG PC =+∴222(2)CG CG PC =+, ∴3PC =,P ∴点坐标为:(3,3),设直线PE 的解析式为:y kx b =+,则033b k b +=+=⎪⎩,解得3k b ⎧=⎪⎨=-⎪⎩∴直线PE 的解析式为3y =-.(4)①如图1,当点M 在x 轴的负半轴上时,AG MG =,点A 坐标为(0,3),∴点M 坐标为(0,3)-.①如图2,当点M 在EP 的延长线上时,由(3),可得60AGO PGC ∠=∠=︒,EP ∴与AB 的交点M ,满足AG MG =,A 点的横坐标是0,GM ∴的横坐标是3,∴点M 坐标为3).综上,可得点M 坐标为(0,3)-或3).9.(1)如图,(2)DR ①BC90RDB ∴∠=︒将线段DE 顺时针旋转90°得到线段DF ,90,EDF ED FD ∴∠=︒=BDR EDF ∴∠=∠即BDE EDR EDR RDF ∠+∠=∠+∠BDE RDF ∴∠=∠ ABC 是等腰直角三角形90BDR ∠=︒45BRD ∴∠=︒BRD ∴是等腰直角三角形BD DR ∴=∴①BDE ①①RDF ;(2)如图,当24PB AB ==时,使得对于任意的点D ,总有①BPF 为定值,证明如下,ABC 是等腰直角三角形,2AB AC ==BC ∴=DC =设DE a =,则CD =,①BDE ①①RDF ,DR BD ∴==,FR BR a == ABC 是等腰直角三角形,45EBD ∴∠=︒DR BC ⊥45BRD ∴∠=︒BDR ∴是等腰直角三角形,42BR a ∴==-()4422PR BP BR a a ∴=-=--=①BDE ①①RDF ,45FRD EBD ∴∠=∠=︒90BRF BRD DRF ∴∠=∠+∠=︒1tan 22RF a BPF RP a ∴∠=== BPF ∴∠为定值10.证明:(1)如图1,将①ABD 沿AB 折叠,得到①ABE ,连接DE ,①AB =AC ,①BAC =90°,①①ABC =45°,①将①ABD 沿AB 折叠,得到①ABE ,①①ABD ①①ABE ,①AE =AD ,BE =BD ,①ABE =①ABD =45°,①BAD =①BAE =30°,①①DBE =90°,①DAE =60°,且AD =AE ,BE =BD ,①①ADE 是等边三角形,DE =,①AD =DE =故答案为:(2)如图2,过点A 作AE ①AD ,且AE =AD ,连接DE ,①AE ①AD ,①①DAE =①BAC =90°,①①BAE =①DAC ,且AD =AE ,AB =AC ,①①BAE ①①CAD (SAS )①①ACD=①ABE,①①ACD+①DCB+①ABC=90°,①①DCB+①ABC+①ABE=90°,①①BOC=90°,①AE=AD,AE①AD,①DE=,①ADE=45°,①①BDC﹣①ADC=45°,①①BDC=①ADC+45°=①EDC,且DO=DO,①DOB=①DOE=90°,①①DOB①①DOE(ASA)①BD=DE,①BD=;(3)如图3,连接PC交AB于G点①①DAE绕A点旋转①AD=AE,AB=AC,①①DAE=①BAC=90°①①DAB=①EAC①①DAB①①EAC①①DBA=①ECA①①PGB=①AGC①①BPC=①GAC=90°①①BPC为直角三角形①点P在以BC中点M为圆心,BM为半径的圆上,连接PM交AB所在直线于点N,当PM①AB时,点P到直线AB的距离最大,①①BAC=90°①A 、P 、B 、C 四点共圆①PM ①AB ,①N 是AB 的中点①M 是BC 的中点①MN =122AC = ①AB =AC =4,①CB =22442,①BM =PM =12BC =,①PN =2 ,①点P 到AB 所在直线的距离的最大值为:PN =2 . ①①P AB的面积最大值为12AB ×PN =4. 11.(1)证明:ABC 是等边三角形60,BAC AB AC ∴∠=︒=线段DA 绕着点D 顺时针旋转60°得到线段DE , 60,DAE DA DE ∴∠=︒=ADE ∴是等边三角形DAC DAE CAE BAC CAE EAB ∴∠=∠-∠=∠-∠=∠ 即DAC EAB ∠=∠∴ADC AEB △≌△∴CD BE =(2)ABC 是等边三角形,AB =4,则60BAC ∠=︒过点A 作AM BC ⊥,则1302BAH BAC ∠=∠=︒ Rt ABH 中,122BH AB ==AH ∴=142ABC S ∴=⨯⨯△①ABC 的面积等于①ABF 面积的4倍ABF S ∴=△11sin 60422ABF S BF AB =⋅⨯︒=⨯=△ 1BF ∴= ①当F 点在B 点的左侧时,如图,60ACB ABC ∠=∠=︒120ACD ∴∠=︒ADC AEB △≌△ADC AEB ∴∠=∠,BE DC =60ABC ∠=︒60EBF ABE ABC ∴∠=∠-∠=︒60FBE FCA ∴∠=∠=︒又AFC EFB ∠=∠AFC EFB ∴∽FB BE FC AC∴= 4,1AC BC AB BF ====413FC ∴=-=14433FB AC BE FC ⋅⨯∴=== 43CD EB ∴==①当F 点在B 点的右侧时,如图,ADC AEB △≌△60ACD EBA ∴∠=∠=︒60ABC ∠=︒18060EBF ABC ABE ∴∠=︒-∠-∠=︒BE AC ∴∥FEB FAC ∴∽FB BE FC AC∴= 1,4,145FB AC FC BC BF ===+=+=45FB AC BE FC ⨯∴== 45CD EB ∴==综上所述CD 的长为43或45(3)如图,点E 关于直线AD 的对称点为点G ,ADE 是等边三角形60ADE ADG ∴∠=∠=︒,AE AD =AEN ADM ∴∠=∠60=︒60,60MAD DAB CAB EAB DAB DAE ∠+∠=∠=︒∠+∠=∠=︒MAD NAE ∴∠=∠MAD NAE ∴=AM AN ∴=60MAN ∠=︒AMN ∴是等边三角形MN AN ∴=由(2)可得45BE =,FEB FAC ∽ 445525EF BF BF AF FC BC BF ∴====+过点A 作AH BC ⊥,则AH =,2CH HB ==,3HF HB BF =+=AF ∴=425EF AF ∴==AE AF EF ∴=-==60,ABE AEN EAB NAE ∠=∠=︒∠=∠∴BEA ENA ∽BE BA EN EA∴= 则BE EA EN BA ⨯=60,ADN ABE AND ENB ∠=∠=︒∠=∠ADN EBN ∴∽AD AN EB EN∴= 即AN EB EN AD ⨯= BE EA AN EB BA AD ⨯⨯∴= EA AD AN AB⨯∴=AE AD =,4AB =2926142500AN ⎝⎭∴== 即92612500MN =12. 解:(1)如图1,过点C 作CD ①x 轴于D ,①在①ABC 中,90ACB ∠=︒,AC =BC=①4AB = ,①点B (4,0),①CD ①AB ,①AD =CD =12AB =12×4=2,①点C 的坐标为(2,2);(2)如图,把①ACM 绕点C 逆时针旋转90°得到①BCM ′,连接M ′N ,①90ACB ∠=︒,AC =BC ,①①ABC 是等腰直角三角形,①①CAB =①CBA =45°,由旋转的性质得,45AM BM CM CM CAM CBM ACM BCM '''==∠=∠=︒∠=∠'、、,,①454590M BN ABC CBN ∠'=∠+∠'=︒+︒=︒ ,①①MCN =45°,①90904545M CN BCN BCM BCN ACM MCN ∠'=∠+∠'=∠+∠=︒-∠=︒-︒=︒ , ①MCN M CN ∠=∠' ,在①MCN 和①M ′CN 中,①CM CM MCN M CN CN CN ''=⎧⎪∠=∠⎨⎪=⎩,①MCN M CN SAS '≌(), ①MN M N =' ,在Rt M NB ' 中,222BM BN M N +='' ,①222AM BN MN += ,1AM =,①3MN BN AB AM +=-=,1BM '= ,设MN x =,则BN =3x -,()22213-x x ∴+=,解得:53x =, 53MN ∴=; (3)AM 2+BN 2=MN 2,证明如下:如图3,把①BCN 绕点C 顺时针旋转90°得到ACN ' ,①90ACB ∠=︒,AC =BC ,①①ABC 是等腰直角三角形,①①CAB =①CBA =45°,由旋转的性质得,135AN BN CN CN CAN CBN '='=∠'=∠=︒,, , ①1354590MAN ∠'=︒-︒=︒,①点N '在y 轴上,①①MCN =45°,①904545MCN ∠'=︒-︒=︒,①MCN MCN ∠=∠' ,在①MCN 和①MCN ′中,①CN CN MCN MCN CM CM =''⎧⎪∠=∠⎨⎪=⎩,①()MCN MCN SAS ≅' ,①MN MN =' ,在Rt AMN ' 中,222AM AN MN +''= ,①222AM BN MN += .13.(1)如图1,①90ACB ∠=︒,AE BD ⊥,①90ACB AEB ∠=∠=︒,又①12∠=∠,①CAE CBD ∠=∠;(2)①补全图形如图2;①EF BE =.理由如下:在AE 上截取AM ,使AM BE =.又①AC CB =,CAE CBD ∠=∠,①ΔΔACM BCE ≌,①CM CE =,ACM BCE ∠=∠,又①90ACB ACM MCB ∠=∠+∠=︒,①90MCE BCE MCB ∠=∠+∠=︒,①ME =,又①射线AE 绕点A 顺时针旋转45︒,后得到AF ,且90AEF ∠=︒,①EF AE AM ME BE ==+=.14.解:(1)如图:BD 与EC 的数量关系是相等,理由如下:,AB AC AD AE ==,AB AD AC AE ∴-=-,BD EC ∴=;BD 与EC 的位置关系是垂直,理由如下:AB AC ⊥, 又点,D E 分别在,AB AC 上,BD EC ⊥;(2)成立:理由分别如下:如图:根据旋转的性质可得:,,AD AE AB AC BAD CAE ==∠=∠, ()ABD ACE SAS ∴≌,BD EC ∴=,作BD 的延长线交EC 于点F ,交AC 于点G ,如下图:由ABD ACE SAS △≌△()可知,ABD ACE ∠=∠,AGB FGC ∠=∠,AGB FGC ∴∽,90GAB GFC ∴∠=∠=︒,GF CF ∴⊥,即BD EC ⊥;(3)当点D 在线段BE 上时,90BAD BAC DAC DAC ∠=∠-∠=︒-∠,90CAE DAE DAC DAC ∠=∠-∠=︒-∠,BAD CAE ∴∠=∠,又AB AC =,AD AE =,()BAD CAE SAS ∴∆≅∆,180135ADB AEC ADE ∴∠=∠=︒-∠=︒,451354590BEC AEC ∴∠=∠-︒=︒-︒=︒;(4)由题意知,点D 的轨迹在以A 为圆心,AD 为半径的圆, 在ABD ∆中,当AB 为底时,点D 到AB 的距离最大时,ABD ∆的面积最大, 故如图所示,当AD AB ⊥时,ABD ∆的面积最大,∴旋转角为90︒或270︒,故答案为:90︒或270︒.15.解:(1)在Rt ①ABC 中,BC =4,AC =2,①ACB =90°,AB ∴=在Rt ①BDE 中,BF =1,BD =2,BE ∴=121tan ,tan 242ED AC EBD ABC BD BC ∴∠==∠=== EBD ABC ∴∠=∠EBD ABD ABC ABD ∴∠-∠=∠-∠ABE CBD ∴∠=∠24AB BE BC BD ===∴①ABE ①①CBD ;(2)当A 、E 、F 三点共线时,分两种情况讨论: ①90AED ∠=︒,如图,在Rt ①AFB 中,222AB BF AF =+21(2)20AE ∴++=2(2)19AE ∴+=2AE ∴=①ABE ①①CBDAE CD ∴=CD ∴= ①如图,90AFB ∠=︒在Rt ①AFB 中,22220119AF AB BF =-=-=AF ∴=2AE AF EF ∴=+=EBD ABC ∠=∠90EBF ABC ∴∠+∠=︒EBF ABC FBC DBF FBC ∴∠+∠+∠=∠++∠24AB BE BC BD ===∴①ABE ①①CBDAE CD ∴=CD ∴=综上所述,CD =CD =(3)如图,延长EF 至点G ,使得EF =FG ,连接BG ,此时①BEG 是等腰三角形, 当G B A 、、三点共线,此时FM 最大//BD GEG DBA ∴∠=∠9090180DBA FBD GBF G FBD GBF ∴∠+∠+∠=∠+∠+∠=︒+︒=︒, 此时,G B A 、、三点共线,F M 、分别是BE 、AE 的中点,FM ∴是①EGA 的中位线,111==()222FM AG AB BG ∴+==16.解:(1)如图①中,(5,0)A ,(0,3)B ,5OA ∴=,3OB =,四边形AOBC 是矩形,3AC OB ∴==,5OA BC ==,90OBC C ∠=∠=︒,矩形ADEF 是由矩形AOBC 旋转得到,5AD AO ∴==,在Rt ADC 中,4CD ,1BD BC CD ∴=-=,(1,3)D ∴.(2)①如图①中,由四边形ADEF 是矩形,得到90ADE ∠=︒,点D 在线段BE 上,90ADB ∴∠=︒,由(①)可知,AD AO =,又AB AB =,90AOB ∠=︒,()Rt ADB Rt AOB HL ∴≌.①如图①中,由ADB AOB ∆≅∆,得到BAD BAO ∠=∠,又在矩形AOBC 中,//OA BC ,CBA OAB ∴∠=∠,BAD CBA ∴∠=∠,BH AH ∴=,设AH BH m ==,则5HC BC BH m =-=-,在Rt AHC 中,222AH HC AC =+,2223(5)m m ∴=+-,175m ∴=, 175BH ∴=, 17(5H ∴,3). (3)如图①中,当点D 在线段BK 上时,DEK ∆的面积最小,最小值113(522DE DK ==⨯⨯=当点D 在BA 的延长线上时,①D E K ''的面积最大,最大面积113(522D E KD =⨯''⨯'=⨯⨯=. 17.解:(1)∵P AB ∆'由PAC ∆绕点A 旋转得到,∴P AB PAC ∆≅∆',∴P AB PAC ∠=∠',P A PA '=,∵60BAC PAC PAB ∠=∠+∠=︒,∴60P AB PAB ∠+∠='︒,即:60P AP ∠='︒,∴旋转角度数为60︒;(2)如图所示,连接P P ',∵60P AP ∠='︒,P A PA '=,∴P AP ∆'为等边三角形,∴6P P PA '==,即点P 与点P '之间的距离为6;(3)在P PB ∆'中,由(1)得:10P B PC ='=,6P P '=,8PB =,∴222P B P P PB ''=+,∴P PB ∆'为直角三角形,∴90P PB ∠='︒,由(1)得60APP ∠='︒,∴150APB P PB APP ∠=∠+='∠'︒,∴APB ∠的度数为150︒.18.( 1 )①OA =4,①A (4,0),把A (4,0)代入34y x b =-+, 得:b =3,过点D 作DH ①AB 于点H ,则DH =DO ,BH =BO ,①当x =0时,y =3,①B (0,3),①OA =4,BO =BH =3,在Rt OAB 中,①5AB ,AD =DO +OA =DH +4, ①1122ABD S AD OB AB DH =⋅⋅=⋅⋅, ①()1143522DH DH ⨯+⨯=⨯⋅, 解得:DH =6,①OD =6,①点D 的坐标为(﹣6,0),(2)过点P 作PE ①OD 于点E ,则△DPE ①①DBO ,①点P 在直线BD 上,且点P 的横坐标为t ,①DE =t +6,①OD =6,OB =3,在Rt OBD △中,BD ==①①DPE ①①DBO , ①DP DE DB DO =,66t +,解得:)6DP t =+, ①PC ①BD , ①①PDC ①①ODB , ①PC DP OB OD=,①)6236t PC +=,①)6PC t =+,①)()1115154566=22884BCD S BD PC t t t =⋅⋅=⨯+=++; (3)作PH 垂直于x 轴于点H ,设射线EP 绕点E 逆时针旋转45°交x 轴于点K ,顺时针旋转45°交x 轴于点G .①①BPC =90°,①BOC =90°①B ,P ,C ,O 四点共圆,①PC PB =,①45PCB PBC ∠=∠=︒,①①POC =①PBC =45°,①90PHO ∠=︒,①45HPO POC ∠=∠=︒,①PH =HO ,①DH =6﹣HO =6﹣PH ,①DHP DOB ∽, ①663PH DO PH BO -==, 得PH =2,①HC =CO =1,①OE =2,①点(0,2)E -,①①KEP =①DBC ,①PEB =①BDC ,①①KEP +①PEB =①DBC +①BDC ,即①KEO =①BCO ,①OE :GK =CO :BO =1:3,①GK =6,①K (﹣6,0),设直线KE 的解析式为:y kx b =+,则62y k b b =-+⎧⎨-=⎩,解得:132k b ⎧=-⎪⎨⎪=-⎩,, ①直线KE 为:y 13=-x ﹣2, 联立方程组:123334y x y x ⎧=--⎪⎪⎨⎪=-+⎪⎩解得x =12,y =﹣6,①F 1(12,﹣6),①①KEP +①PEG =90°,①①DEG =90°,①①OEG =①ODE ,①OG :OE =OE :OD =1:3,①OG 23=; ①G (23,0), 设直线EG 的解析式为:y mx n =+, 则20=32m n n⎧+⎪⎨⎪-=⎩,解得:32m n =⎧⎨=-⎩, ①直线EG 的解析式为:y =3x ﹣2, 联立方程组:32334y x y x =-⎧⎪⎨=-+⎪⎩, 解得x 43=,y =2, ①F 2(43,2), 综上所述:F 的坐标为(12,﹣6)或(43,2). 19.证明:(1)①四边形ABCD 是菱形,①ABC =60°, ①AB =BC =AD =CD ,①ADC =①ABC =60°,①①ADC 是等边三角形,①AD =AC =AB =BC ,①①ACB 是等边三角形,①①ACB =①ACD =60°,①①ADC =①EDF =60°,①①ADE =①CDF ,①将线段DE 绕点D 逆时针旋转60︒,点E 的对应点为F , ①DE DF =,在①ADE 和①CDF 中,DA DC ADE CDF DE DF =⎧⎪∠=∠⎨⎪=⎩①①ADE ①①CDF (AAS ),①60DCF DAE ∠=∠=︒,①180DCF BCD ∠+∠=︒,①B ,C ,F 三点共线;(2)如图,过点B 作BH ①AC ,交AG 的延长线于点H ,①BH ①AC ,①①H =①GAE ,①ABH +①BAC =180°,①①ABH =120°=①ACF ,①点G 为BE 的中点,①BG =GE ,在①AGE 和①HGB 中,H GAE AGE BGH BG GE ∠=∠⎧⎪∠=∠⎨⎪=⎩,①①AGE ①①HGB (AAS ),由(1)得AE CF =,①AE =BH =CF ,AG =GH =12AH ,在①ABH 和①ACF 中,AB AC ABH ACF BH CF =⎧⎪∠=∠⎨⎪=⎩,①①ABH ①①ACF (SAS ),①AF =AH ,①AF =2AG .20.(1)如图①CDF 即为旋转之后的图形;(2)证明:由旋转旋转可知:①CAB ①①CFD ,①①CDF =①CBA ,①F =①CAB ,CA =CF ,①①CBA +①CDA =180°,①①CDF +①CDA =180°,①A 、D 、F 三点共线,①AC =CF ,①①F =①CAD ,①①CAB =①CAD ;(3)过点E 作EM ①AF 于点M ,过点C 作CN ①BD 于点N , ①①ABE =①AME =90°,在①ABE 和①AME 中,EAB EAM ABE AME AE AE ∠=∠⎧⎪∠=∠⎨⎪=⎩, ①①ABE ①①AME (AAS ),①AM =AB =3,BE =ME ,①①ABD =90°,AB =3,BD =4,①5AD ==,①DM =2,设BE EM x ==,则4DN x =-,①()222x 24x +=-,解得 1.5x =,①BE =1.5,DE =2.5, ①12113::225S S BE CN DE CN =⋅⋅=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
B
O
DGEF NhomakorabeaC
2.( 1)△ AEF是等边三角形;( 2) CG= 8 . 3
【提示】( 1)证△ ABE≌△ ACF( ASA)即可;
(2)易证△ CAE∽△ CFG,从而 CG CF ,即可求得 CG的长. CE CA
4
中考数学复习:旋转
经过旋转, 对应线段相等, 对应角相等; 任意两条对应线段所在直线的夹角都等于旋转 角;旋转前后的图形全等. l .旋转的基本图形有: (1)如图,将∠ AOB旋转至∠ A ' OB' ,则∠ AOA' =∠ BOB' . (2)如图,将△ AOB旋转至△ A' OB' ,连结 AA' , BB' ,则△ AOA' ∽△ BOB'
解 ( 1)由旋转的性质可得 AB= AD, AE= DE,∠ BAD= a= 60°. 所以△ ABD为等边三角形,所以 AB= DB. 从而得到 BE为 AD的垂直平分线,所以 BF⊥ AD, AF= DF.
1
(2)如图,按照题意画出图形,令 CE与 AB的交点为 H. 由旋转的性质可得 CA= CB= EA= ED,∠ CAB=∠ CBA =∠ EAD=∠ EDA. 因为∠ DAG+∠ DAE+∠ EAB=∠ ACB+∠CAB+∠CBA=180°,且已知∠ DAG=∠ ACB, 所以∠ CAB=∠ EAB. 所以 AB, CE互相垂直平分,则 AC= CB= BE= EA.
2.利用旋转性质解题的步骤为: (1)找旋转点,得等边、等角; (2)证全等或相似; (3)利用全等或者相似得到边、角关系. 例题讲解 例 1 已知: 在△ ABC中,AB= 6,AC= BC= 5,将△ ABC绕点 A 按顺时针方向旋转, 得到△ ADE, 旋转角为 a(0°< a< 180°),点 B 的对应点为点 D,点 C的对应点为点 E,连结 BD, BE. (1)如图,当 a=60°时,延长 BE交 AD于点 F,求证: BF⊥ AD, AF= DF. (2)在旋转的过程中,过点 D作 DG⊥ AB于点 G,连结 CE. 当∠ DAG=∠ ACB,且线段 DG与 线段 AE无公共点时,求 BE+CE.
G,则△ EBG为等边三角形.
E
A
F
BD
CG 图3
进阶训练 1.如图,将正五边形 ABCDE绕点 A 顺时针旋转 60°后,旋转前后两图形有另一交点 O,连
结 AO;再将 AO所在的直线绕点 A 逆时针旋转 60°后,交旋转前的图形于点 P,连结 PO, 判断△ AOP的形状,并说明理由.
P E
D
C E'
所以 BE+ CE= 5+ 2 52 33 13.
例 2 已知:如图,△ ABC是等边三角形,点 E 在线段 AB上,点 D在直线 BC上,且 ED= EC, 将△ BCE绕点 C顺时针旋转 60°至△ ACF,连结 EF. (1)求证: AB= DB+ AF; (2)若点 E在线段 AB的延长线上,其他条件不变,线段 AB, DB, AF之间有怎样的数量关 系?请说三明理由; (3)若点 E在线段 BA的延长线上,其他条件不变,线段 AB, DB, AF之间有怎样的数量关 系?请说明理由. 证明 ( 1)如图 1,过点 E作 EG∥ AC交 BC干表 G,则△ EBG为等边三角形. 易证△ EBD≌△ EGC,所以 DB= CG= AE.由旋转的性质可得 AF= BE,所以 AB= BE+ AE=AF+ DB.
(2) AB= DB- AF.理由如下: 如图 2,过点 E 作 EG∥ AC,交 CD于点 G,则△ EBG为等边三角形. 易证△ EGD≌△ EBC,所以 DG=BC= AB. 由旋转的性质可得 AF= BE= BG. 所以 AB= DG= DB- AF.
2
FA
GB
D
C
E
图2
(3) AB= AF- DB.理由如下: 如图 3,过点 E 作 EG∥ AC,交 BC的延长线于点 易证△ EBD≌△ EGC, 所以 DB= CG= AE. 由旋转的性质可得 AF= BE, 所以 AB= BE- AE= AF- DB.
O
B D' A
C' B'
1.△ AOP为等边三角形. 【提示】由旋转的性质得∠ EAE' =∠ PAO= 60°,从而∠ EAP=∠ E' AB,又∠ E=∠ E' ,AE=
AE' ,从而△ PEA≌△ OE' A,则 AP= AO,即得证.
3
2.如图,在菱形 ABCD中, AC= 2,BD= 2 3 , AC, BD相交于点 O,将一个足够大的直角三
