六年级上册分类复习：圆的知识点总结练习提升
六年级数学上册圆知识点总结及练习题
六年级数学上册圆知识点总结及练习题《圆》知识点一、圆的特征1、圆是平面内封闭曲线围成的平面图形。
2、圆的特征：外形美观，易滚动。
3、圆心O：圆中心的点叫做圆心．圆心一般用字母O表示。
圆多次对折之后，折痕的相交于圆的中心即圆心。
圆心确定圆的位置。
半径r：连接圆心到圆上任意一点的线段叫做半径。
在同一个圆里，有无数条半径，且所有的半径都相等。
半径确定圆的大小。
直径d:通过圆心且两端都在圆上的线段叫做直径。
在同一个圆里，有无数条直径，且所有的直径都相等。
直径是圆内最长的线段。
同圆或等圆内直径是半径的2倍：d=2r 或r=d÷24、等圆：半径相等的圆叫做同心圆，等圆通过平移可以完全重合。
同心圆：圆心重合、半径不等的两个圆叫做同心圆。
5、圆是轴对称图形：如果一个图形沿着一条直线对折，两侧的图形能够完全重合，这个图形是轴对称图形。
折痕所在的直线叫做对称轴。
有一条对称轴的图形：半圆、扇形、等腰梯形、等腰三角形、角。
有二条对称轴的图形：长方形有三条对称轴的图形：等边三角形有四条对称轴的图形：正方形有无条对称轴的图形：圆，圆环6、画圆（1）圆规两脚间的距离是圆的半径。
（2）画圆步骤：定半径、定圆心、旋转一周。
二、圆的周长：围成圆的曲线的长度叫做圆的周长，周长用字母C 表示。
1、圆的周长总是直径的三倍多一些。
2、圆周率：圆的周长与直径的比值是一个固定值，叫做圆周率，用字母π表示。
即：圆周率π = 周长÷直径≈3.14所以,圆的周长(c)=直径(d)×圆周率(π)—周长公式：c=πd, c=2πr圆周率π是一个无限不循环小数，3.14是近似值。
3、周长的变化的规律：半径扩大多少倍直径也扩大多少倍，周长扩大的倍数与半径、直径扩大的倍数相同。
4、半圆周长=圆周长一半+直径= πr+d三、圆的面积s1、圆面积公式的推导如图把一个圆沿直径等分成若干份，剪开拼成长方形，份数越多拼成的图像越接近长方形。
人教版六年级数学上册圆的知识点寒假复习提升卷
人教版六年级数学上册比的知识点寒假复习提升卷思维导图+知识梳理+例题精讲+易错专练一、思维导图二、知识点梳理知识点一：圆的认识1.圆心、半径、直径用圆规画圆时，针尖所在的点叫做圆心，一般用字母O表示，连接圆心和圆上任意一点的线段叫做半径，一般用字母r表示，通过圆心并且两端都在圆上的线段叫做直径，一般用字母d表示。
在任意一个圆中都可以画出无数条半径和无数条直径。
2.同圆或等圆中半径、之间的关系在同圆或等圆中，所有的半径都相等，所有的直径也都相等，直径是半径的2倍；圆心相同，半径不同的圆叫做同心圆；圆是轴对称图形，它有无数条对称轴。
3.用圆规画圆用圆规画圆的方法：先定好两脚之间的距离，再把带有针尖的脚固定在一点上，最后把装有铅笔的脚旋转一周，就画出了一个圆。
知识点二：圆的周长1.意义：围成圆的曲线的长叫做圆的周长，周长一般用字母C来表示。
2.测量方法：滚动法、绕绳法、直接测量法。
3.圆周率：圆的周长总是它的直径的3倍多一些，这个固定的比值叫做圆周率，用字母π来表示，π是一个无线不循环小数。
C＝πd或2πr。
已知圆的半径，求周长时，用C＝2πr进行计算；已知圆的直径，求周长时，用C＝πd进行计算。
知识点三：圆的面积1.意义：圆所占平面的大小叫做圆的面积，圆的面积一般用S表示。
2.已知圆的半径为r，S＝πr2已知直径或周长求面积时，都要先求出半径，再求出面积。
3.圆环：两个半径不相等的同心圆之间的部分叫做圆环，也叫做环形。
S＝πR2－πr23.圆与正方形组合的面积问题的应用（1）“外方内圆” 图形中，圆的直径等于正方形的边长。
如果圆的半径为r，那么正方形和圆之间部分的面积为0.86r2。
（2）“外圆内方”图形中，这个正方形的对角线等于圆的直径。
如果圆的半径为r，那么圆和正方形之间部分的面积为1.14r2。
知识点四：扇形1.意义：圆上两点之间的部分叫做弧；一条弧和经过这条弧两端的两条半径所围成的图形叫做扇形。
六年级圆的知识点总结
六年级圆的知识点总结
一、圆的定义
圆是平面上离定点距离等于定长的点的集合。
这个定点叫做圆心，这个定长叫做半径。
以
O为圆心，以r为半径做出的圆记为Γ。
二、圆的性质
1. 圆的直径：圆的直径是过圆心，并且两端点在圆上的线段。
圆的直径恰好是其半径的两倍。
2. 圆周长：圆的周长等于圆的直径和π的乘积。
即C=2πr。
3. 圆的面积：圆的面积等于半径的平方乘π。
即A=πr²。
4. 弧长和扇形面积：圆的弧长和扇形的面积与圆的周长和面积有很密切的关系。
三、圆的相关定理
1. 钝角圆周定理：在同一个圆中，对于一个圆周上的三个点A、B、C，如果角ABC是钝角，那么对应于这个圆面积内的两条弧AB和AC所对的圆心角分别是直角和钝角。
2. 相交圆周定理：当两个不同圆的圆心不在一直线上，但它们却有一个公共点，则这两个
圆相交。
此时，两个不在一条直线上的圆的交点在圆周上形成四个交点。
两个圆的圆周在
它们两个交点之间有两个弧。
对应于任意这样的一个圆周上的交点P，到P的两条圆周所
对的圆心角是互补的。
3. 切线定理：切线是与圆的圆周相切的直线。
圆周上任意一点到相切点的切线所构成的角
恰好是直角。
切线与半径的关系紧密，在圆心的两边与切点相连的线段构成直角三角形。
以上是关于圆的一些基本知识点和相关定理，通过学习这些知识，我们可以更好地理解和
应用圆的几何特性。
希望同学们在学习中能够加深对圆的理解，更好地掌握圆的相关知识。
六年级上册数学《圆》知识点整理
六年级上册数学《圆》知识点整理
圆是数学中的一个重要概念，是指平面上所有到固定点的距离都相等的点的集合。
六年级上册数学《圆》主要包括以下几个知识点：
1. 圆的基本概念：圆由圆心和半径确定。
圆心是圆上任何一点到圆心的距离都相等的点，半径是圆心到圆上任意一点的距离。
2. 圆的性质：
- 所有点到圆心的距离都相等。
- 圆上任意两点间的距离最短。
- 圆与直线的关系：直线与圆相交于两点、一点或者无交点。
3. 圆的要素之间的关系：
- 半径的两端是圆上的两个点。
- 直径是连接圆上任意两点的线段，且通过圆心，其长度等于两个半径的和。
- 弦是连接圆上任意两点的线段，且不通过圆心。
- 弧是圆上的一段弯曲的部分，两端是圆上的两点，弧比弦长。
4. 圆的部分：
- 扇形：是由圆心、圆上一点和圆上两点所确定的部分。
- 弓形：是由圆心和圆上一点所确定的部分。
- 圆心角：是由圆心和圆上两点所确定的角，度数等于所对弧的角度。
5. 圆的计算：
- 圆的面积：面积公式为πr²，其中π≈3.14，r为圆的半径。
- 圆的周长：周长公式为2πr，其中π≈3.14，r为圆的半径。
以上是六年级上册数学《圆》的知识点整理，希望对你有帮助！。
六年级圆的知识点复习汇总
圆是初中数学中的一个重要知识点，学好圆的知识对于提高数学水平具有重要意义。
下面是六年级圆的知识点复习汇总。
1.圆的定义：圆是由平面上的一点到另一点距离相等的所有点的集合。
其中，距离相等的两个点叫做圆的直径的两个端点，直径的长度叫做圆的直径。
以圆心为中心，直径为半径的线段叫做圆的半径，圆心到圆上任意一点的线段叫做圆的半径。
2.圆的表示方法：圆可以用一个字母表示，通常用大写字母O表示圆心，小写字母r表示半径，用圆心和半径共同表示一个圆。
3.圆的位置关系：两个圆的位置关系可以分为以下几种情况：外离、外切、相交、内切、内含。
4.直径和周长：圆的周长是由圆心到圆上任意一点的线段长度乘以2π得到的，即：C=πd，其中C表示圆的周长，d表示圆的直径。
5.半径和面积：圆的面积可以通过半径的平方乘以π得到，即：S=πr²，其中S表示圆的面积，r表示圆的半径。
6.弧长和扇形面积：弧长是圆上两点之间的弧所对应的圆心角的弧长，圆心角是以圆心为顶点的角。
弧长可以通过圆心角的度数除以360度，然后乘以圆的周长得到。
扇形面积是由圆心、弧和两条半径形成的扇形所覆盖的面积，扇形面积可以通过圆心角的度数除以360度，然后乘以圆的面积得到。
7.弦和切线：弦是连接圆上两点的线段，切线是与圆只有一个交点的直线。
切线与半径的关系是相互垂直。
8.弦和切线的性质：在一个圆中，两条相等的弦的弦长相等；相等的弦所对应的弧长也相等；相等的切线所对应的切点在同一直径上。
9.弧和弦的关系：在一个圆中，如果两个圆心角相等，则它们所对应的弧长也相等；如果两个弧的弧长相等，则它们所对应的圆心角也相等。
10.圆内接四边形：一个四边形的四个顶点都位于同一个圆上，该四边形叫做圆内接四边形。
在一个圆内接四边形中，相对的两条边之和相等。
以上就是六年级圆的知识点复习的汇总，希望能帮助你更好地复习圆的知识。
祝你学习进步！。
小学六年级人教版数学上册第四单元《圆》知识点汇总
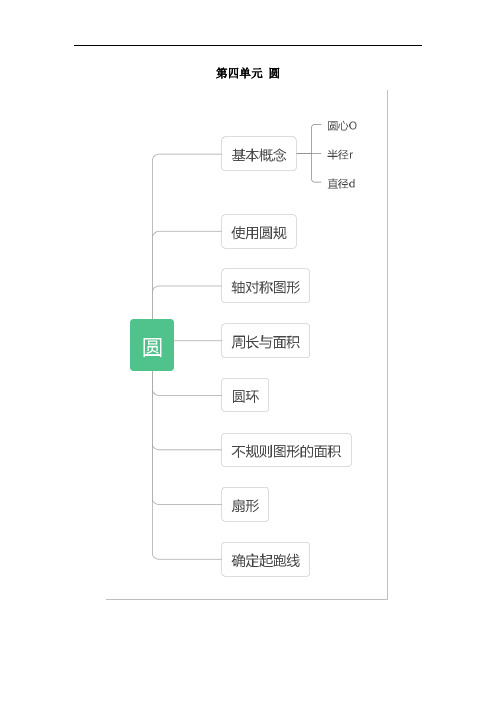
第四单元圆一、基本概念1、圆心一个圆最中心的那一点，用大写字母O 表示(1) 圆心决定圆的位置。
(2) 圆心到圆上任意一点的距离都相等。
(3) 一张圆形纸片至少对折两次，就能找到圆心。
2、半径圆心到圆上任意一点的线段，用小写字母r 表示(1) 半径决定圆的大小。
(2) 在同一个圆里面，半径都相等。
(3) 在同一个圆里面，半径有无数条。
(4) 半径是直径的一半，即d 21r =3、直径通过圆心并且两端都在圆上的线段，用小写字母d 表示(1) 在同一个圆里面，直径都相等。
(2) 在同一个圆里面，直径有无数条。
(3) 直径是半径的两倍，即r 2d =(4) 在一个正方形内画最大的圆，圆的直径等于正方形的边长(5) 在一个长方形内画最大的圆，圆的直径等于长方形的宽二、使用圆规的步骤1、先确定圆心的位置和半径。
(1) 轴对称图形中，两条对称轴的交点就是中心点(2) 如果知道直径，那么直径的一半就是半径2、用直尺量出两脚之间的距离为半径。
(1) 量好后不能再改变两脚之间的距离3、把针尖放在圆心位置，保持针尖不动，旋转另一只脚一周，即可画出指定的圆。
(1)如果旋转圆规一周不顺手，可以保持圆规不动，旋转纸一周。
(2)如果旋转一周画出来的线条不清晰，可以多旋转几周加深线条。
三、轴对称图形1、轴对称图形沿对称轴对折之后，两边可以完全重合。
2、常见的轴对称图形以及它们的对称轴条数：(1)只有一条对称轴的图形：角、等腰三角形、等腰梯形、扇形、半圆(2)有2条对称轴的图形：长方形(3)有3条对称轴的图形：等边三角形(4)有4条对称轴的图形：正方形(5)有无数条对称轴的图形：圆、圆环【圆的对称轴就是直径】四、周长与面积1、圆周率ππ是一个无限不循环小数，一般取 3.14π≈。
我国数学家祖冲之是第一个把圆周率算出来的人。
2、圆的周长(1)圆的周长用大写字母C 表示，计算公式是πd πr 2C ==即圆的周长等于两倍的π乘以半径，也等于π乘以直径(2) 半圆的周长半圆的周长等于半个圆的周长加上直径，即r 2πr +3、圆的面积圆的面积用大写字母S 表示，计算公式是2πr S =4、周长与面积的关系(1) 在同一个圆中，半径扩大或缩小几倍，直径和周长就扩大或缩小几倍，而面积扩大或者缩小这个倍数的平方倍，例如：在同一个圆内，如果半径扩大3倍，那么直径和周长就扩大3倍，面积扩大9倍。
人教版六年级数学上册第五单元圆(知识梳理+课本例题+练习)
人教版六年级数学上册第五单元圆(知识梳理+课本例题+练习)一、知识梳理1、圆心：圆中心一点叫做圆心。
用字母“O ”来表示。
半径：连接圆心和圆上任意一点的线段叫做半径,用字母“r ”来表示。
直径：通过圆心并且两端都在圆上的线段叫做直径,用字母“d ”表示。
2、圆心确定圆的位置,半径确定圆的大小。
3、在同一个圆内,所有的半径都相等,所有的直径都相等。
在同一个圆内,有无数条半径,有无数条直径。
在同一个圆内,直径的长度是半径的2倍,半径的长度是直径的一半。
用字母表示为：r d 2= d r 21= 4、圆的周长：围成圆的曲线的长度叫做圆的周长。
5、圆的周长总是直径的3倍多一些,这个比值是一个固定的数。
我们把圆的周长和直径的比值叫做圆周率,用字母π表示。
圆周率是一个无限不循环小数。
在计算时,取14.3π≈。
世界上第一个把圆周率算出来的人是我国的数学家祖冲之。
6、圆的周长公式：πd C = 或πr 2C =7、圆的面积：圆所占平面的大小叫圆的面积。
8、把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,宽相当于圆的半径,因为长方形面积=长×宽,所以圆的面积2πr r ×r ×π==9、圆的面积公式：22)÷π(d S = 或者2πr S = 或者22)÷π÷π(C S =10、在一个正方形里画一个最大的圆,圆的直径等于正方形的边长。
圆的面积和正方形面积的比是π：4。
在一个圆里画一个最大正方形的,圆的直径的长度等于正方形的对角线的长度,正方形的面积=对角线×对角线÷2=直径×直径÷2 。
11、在一个长方形里画一个最大的圆,圆的直径等于长方形的短边。
12、一个环形,外圆的半径是R,内圆的半径是r,它的面积是22πr πR S -=或 )r π(R S 22-=（其中R ＝r ＋环的宽度．）13、环形的周长＝外圆周长＋内圆周长14、半圆的周长等于圆的周长的一半加直径。
人教版六年级数学上册《第五单元圆的知识点+练习题》(实用)
圆知识点总结一、圆的意义1、圆是由一条曲线围成的平面图形。
（以前所学的图形如长方形、梯形等都是由几条线段围成的平面图形）2、画圆时，针尖固定的一点是圆心，通常用字母O表示；连接圆心和圆上任意一点的线段是半径，通常用字母r表示；通过圆心并且两端都在圆上的线段是直径，通常用字母d表示。
在同一个圆里，有无数条半径和直径。
在同一个圆里，所有半径的长度都相等，所有直径的长度都相等。
3、用圆规画圆的过程：先两脚叉开，再固定针尖，最后旋转成圆。
画圆时要注意：针尖必须固定在一点，不可移动；两脚间的距离必须保持不变；要旋转一周。
4、在同一个圆里，半径是直径的一半，直径是半径的2倍。
（d=2r, r =d÷2）5、圆是轴对称图形，有无数条对称轴，对称轴就是直径所在的直线。
6、圆心决定圆的位置，半径决定圆的大小。
要比较两圆的大小，就是比较两个圆的直径或半径。
7、正方形里最大的圆。
两者联系：边长＝直径；圆的面积=78.5%正方形的面积画法：（1）画出正方形的两条对角线；（2）以对角线交点为圆心，以边长为直径画圆。
8、长方形里最大的圆。
两者联系：宽＝直径画法：（1）画出长方形的两条对角线；（2）以对角线交点为圆心，以宽为直径画圆。
9、同一个圆内的所有线段中，圆的直径是最长的。
10、车轮滚动一周前进的路程就是车轮的周长。
每分前进米数（速度）＝车轮的周长×转数11、任何一个圆的周长除以它直径的商都是一个固定的数，我们把它叫做圆周率。
用字母π表示。
π是一个无限不循环小数。
π＝3.141592653……我们在计算时，一般保留两位小数，取它的近似值3.14。
π>3.14二、圆的基本公式12、如果用C表示圆的周长，那么C＝πd或C = 2πr13、求圆的半径或直径的方法：d = C÷π r = C÷π÷2= C÷2π14、半圆的周长等于圆周长的一半加一条直径。
C半圆= πr＋2r=5.14r C半圆= πd÷2＋d=2.57d15、常用的3.14的倍数：3.14×2＝6.28 3.14×3＝9.42 3.14×4＝12.563.14×5＝15.7 3.14×6＝18.84 3.14×7＝21.983.14×8＝25.12 3.14×9＝28.26 3.14×12＝37.68 3.14×14＝43.963.14×16＝50.24 3.14×18＝56.52 3.14×24＝75.36 3.14×25＝78.53.14×36＝113.04 3.14×49＝153.86 3.14×64＝200.96 3.14×81=254.3416、圆的面积公式：S=πr2。
北师大版六年级数学上册必背知识总结及知识点练习卷
北师大版六年级数学上册必背知识总结及知识点练习卷一、圆的知识1、圆是由曲线围成的平面封闭图形。
圆中心的一点叫圆心，用字母0表示。
以某一点为圆心，可以画无数个圆。
连接圆心和圆上任意一点的线段叫半径，用字母r表示。
连接圆心并且两端都在圆上的线段叫直径，用字母d表示。
2、圆有无数条半径，有无数条直径。
圆心决定圆的位置，半径决定圆的大小。
3、在同一个圆中，所有的半径都相等，所有的直径都相等。
在同一个圆中，直径是半径的2倍，半径是直径的1/2。
4、车轮为什么是圆的？答：因为圆心到圆上各点的距离相等，所以圆在滚动时，圆心在一条直线上运动，这样的车轮运行才稳定。
5、圆内最长的线段是直径，圆规两脚之间的距离是半径。
6、在一个正方形里画一个最大的圆，圆的直径就是正方形的边长。
在一个长方形里画一个最大的圆，圆的直径就是长方形的宽7、把圆对折，再对折（对折2次）就能找到圆心。
因此，圆是轴对称图形，直径所在的直线是圆的对称轴，圆有无数条对称轴。
半圆只有1条对称轴。
&如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也说这个图形关于这条直线的轴对称。
对称轴是一条直线。
9、常见的轴对称图形：等腰三角形（1条）、等边三角形（3条）、等腰梯形（1条）、长方形（2条）、正方形（4条）、圆（无数条）、半圆（1条）。
10、圆一周的长度就是圆的周长。
圆的周长总是直径的3倍多一些，圆的周长除以直径的商（圆的周长与直径的比值）是一个固定的数，我们把它叫做圆周率，用字母n表示，n是一个无限不循环小数，为了计算简便，通常取近似值 3.14。
11、圆的周长=圆周率X直径即C圆=n d =2 nr12、圆所占平面的大小叫圆的面积。
把圆等分的份数越多，拼成的图形就越接近平行四边形或长方形。
拼成的平行四边形的底相当于圆周长的一半，高相当于圆的半径；S 圆=n r2。
长方形的长相当于圆周长的一半，宽相当于圆的半径。
六年级上册圆的知识点总结
六年级上册圆的知识点总结
六年级上册圆的知识点总结如下：
1. 圆的基本性质：
圆的定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。
固定的端点O叫做圆心，线段OA叫做半径。
直径与半径：连接圆上任意两点的线段叫做弦，经过圆心的弦叫做直径。
半径是连接圆上一点和圆心的线段。
圆心角与圆周角：顶点在圆心的角叫做圆心角，顶点在圆上，两边与圆相交的角叫做圆周角。
垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。
2. 圆的计算：
圆的周长公式：C = 2πr，其中r是圆的半径。
圆的面积公式：S = πr^2，其中r是圆的半径。
扇形面积公式：扇形面积= (n/360)πr^2，其中n是扇形的圆心角（单位是度）。
3. 圆与圆的位置关系：
圆与圆的位置关系有五种：相离、相切（内切和外切）、相交、内含和重合。
4. 圆与直线的位置关系：
圆与直线有三种位置关系：相离、相切（直线与圆相切）和相交。
5. 圆的综合应用：
在解决实际问题时，常常需要综合运用圆的性质和定理，如计算圆的周长、面积、扇形面积等。
希望以上内容对你有帮助，如需更多信息，可以查阅教育部门发布的课程大纲或相关教辅资料。
六年级圆的知识点总结
六年级圆的知识点总结一、圆的基本概念1. 圆的定义：平面上所有与给定点（圆心）距离相等的点的集合。
2. 圆心（Center）：圆心是圆的中心点，所有圆上的点到圆心的距离都等于半径。
3. 半径（Radius）：圆心到圆上任意一点的距离称为半径。
4. 直径（Diameter）：通过圆心的任意两点之间的线段称为直径，其长度是半径的两倍。
5. 弦（Chord）：圆上任意两点间的线段。
6. 弧（Arc）：圆上两点之间的曲线部分。
7. 优弧（Major Arc）：大于半圆的弧。
8. 劣弧（Minor Arc）：小于半圆的弧。
9. 半圆（Semicircle）：圆的一半，即180度的弧。
10. 切线（Tangent）：与圆只有一个交点的直线。
二、圆的基本性质1. 半径性质：圆上任意两点间的所有线段中，直径是最长的。
2. 圆周角定理：圆周上一条弧所对的圆周角等于该弧的度数的一半。
3. 圆周角的补角性质：圆周角的补角等于它的余弧所对的圆周角。
4. 内接四边形性质：圆内接于四边形，则对边之和相等。
5. 外切四边形性质：四边形的四个顶点都在同一个圆上，则对边之和相等。
6. 切线性质：圆的切线垂直于过切点的半径。
三、圆的计算公式1. 圆的周长（Circumference）：C = 2πr 或C = πd，其中r是半径，d是直径。
2. 圆的面积（Area）：A = πr²。
3. 扇形面积：S = (θ/360)πr²，其中θ是扇形的中心角度数。
4. 弓形面积：S = (θ/360)πr² - (θ/360)πR²，其中θ是弓形的中心角度数，r是小圆半径，R是大圆半径。
5. 切线长度：L = √(r² - (d/2)²)，其中d是切线到圆心的距离。
四、圆的应用题解法1. 求解圆的半径或直径：利用周长或面积公式，通过已知的周长或面积来计算。
2. 求解扇形的弧长和面积：利用扇形面积公式和圆的周长公式。
六年级上册圆的知识点归纳总结
圆的知识点归纳总结1. 圆的基本概念圆是平面上到一个定点距离等于定长的点的全体构成的图形。
定点叫圆心，定长叫半径。
2. 圆的性质- 圆上任意一点到圆心的距离都是半径；- 圆心到圆上任意一点的距离都是半径；- 直径是通过圆心的两个互为相反的弧的长度。
直径是圆的最大的弦； - 圆的周长是圆周的长度，用C表示；- 圆的面积用S表示。
3. 圆的周长和面积计算公式- 圆的周长C=2πr，其中r为半径；- 圆的面积S=πr²。
4. 圆的相关定理- 弧长定理：圆的周长是2πr，那么一个圆的弧对应的圆心角是θ(弧度制)的弧长为πrθ，其中θ/2π=弧/周；- 圆内接四边形的性质：把一个四边形内接在一个圆上，然后四边形的两个对角线相互垂直，且相互平分；- 切线定理：相切的线与圆心连线是垂直的，且切点处的切线与半径的夹角是90°；- 切线定理的逆定理：若一条直线与圆上的一点相交，且与通过该点的切线垂线相交，那它就是切线。
5. 圆的相关应用- 圆的问题在生活中随处可见，例如轮胎、盘子、饼干等的形状都是圆形的，因此对圆的理解和应用非常重要；- 圆的相关计算也应用在工程学、建筑学、物理等领域中。
总结：通过对圆的基本概念、性质、周长和面积计算公式、相关定理以及应用的学习和理解，我们可以更好地应用圆的知识解决实际问题，培养自身数学素养。
圆是几何中的重要概念，对于进一步学习几何和数学都具有重要意义。
希望同学们能够认真学习圆的知识，提高自身的数学素养和解决实际问题的能力。
圆是几何中非常重要的一个概念，它的性质和定理在数学的学习中具有重要意义。
我们需要了解圆的基本概念和性质，这对于理解圆的相关定理和应用是非常重要的。
在圆的基本概念中，我们知道圆是平面上到一个定点距离等于定长的点的全体构成的图形，其中定点叫圆心，定长叫半径。
这个概念简单明了，但是我们需要深入理解其中的含义。
圆的性质包括了任意一点到圆心的距离都是半径，以及圆心到圆上任意一点的距离都是半径。
六上圆的知识点归纳总结
六上圆的知识点归纳总结圆是我们生活中常见的几何形状之一，它具有许多特性和属性。
在六年级上册数学课本中，我们学习了与圆相关的知识点，下面将对这些知识点进行归纳总结。
一、圆的定义和基本概念圆是由平面上到一个点的距离都相等的所有点组成的集合。
圆上的每个点到圆心的距离都相等，这个距离叫做半径。
圆的直径是通过圆心的一条线段，它的两个端点都在圆上。
圆的周长是圆上所有点到圆心的距离之和，用符号C表示。
二、圆的相关计算公式1. 圆的周长公式：C = 2πr，其中π取近似值3.14，r为圆的半径。
2. 圆的面积公式：S = πr²，其中π取近似值3.14，r为圆的半径。
三、圆的性质1. 圆的对称性：圆具有中心对称性，即圆上的任意一点关于圆心对称的点仍然在圆上。
2. 圆的切线性质：切线与半径垂直。
3. 圆的弦性质：圆的直径是最长的弦，且平分圆。
4. 圆的相交性质：两个圆最多只有两个交点。
5. 圆的切与交性质：若两个圆相切，切点与连接两圆心的直线垂直。
6. 圆的内接与外接：内接圆是一个圆，它的圆心在另一个图形的内部，且与这个图形的每一边相切；外接圆是一个圆，它的圆心在另一个图形的外部，且与这个图形的每一边相切。
四、圆的应用圆在我们的生活中有广泛的应用，下面介绍几个常见的应用场景：1. 轮胎：汽车、自行车等交通工具的轮胎大多为圆形，圆形的结构使得车辆行驶更加平稳。
2. 餐盘：餐桌上的盘子多为圆形，圆形的设计便于食物的摆放和取用。
3. 时钟：时钟的表盘为圆形，采用圆形的设计可以更清晰地显示时间。
4. 灯罩：很多灯具的灯罩采用圆形设计，圆形的光线散射效果较好。
5. 球类运动：篮球、足球、网球等球类运动中使用的球都是圆形，圆形的设计使得球的滚动和运动更加稳定。
圆是一种常见的几何形状，具有许多特性和应用。
通过学习六上圆的知识点，我们对圆的定义、性质和应用有了更深入的了解，也能更好地应用圆的知识解决实际问题。
希望大家通过对圆的学习，能够培养出准确观察、分析问题的能力，提高数学思维和解决问题的能力。
六年级上圆知识点
六年级上圆知识点圆是数学中非常基础且重要的一个几何形状，我们在六年级上学期学习的圆知识点，主要包括圆的定义、圆的性质、圆的元素以及圆的应用等内容。
以下将对这些知识点进行详细的介绍。
一、圆的定义圆是由平面上与一个确定点的距离相等的所有点组成的图形。
这个确定点被称为圆心，而距离被称为半径。
圆可以用一个符号“⊙”来表示。
二、圆的性质1. 圆的内部和圆的外部圆的内部指的是位于圆内部的点，而圆的外部指的是位于圆外部的点。
2. 圆的直径圆的直径是通过圆心，并且两端点都在圆上的一条线段，它的长度是圆周长的两倍。
3. 圆的弦圆上的任意两个点所确定的线段叫做圆的弦。
4. 圆的弧圆上两个点之间的一段曲线叫做圆的弧。
5. 圆心角圆心角是由圆心和圆上的两个点所形成的角。
当圆心角的两个端点在圆上的正向划分的弧长等于反向划分的弧长时，该角被称为圆心角。
6. 圆的面积圆的面积是指圆所包围的区域的大小，它由半径决定，计算公式是：面积= π × 半径²，其中π 的取值约为3.14159。
7. 圆的周长圆的周长是指圆所围成的一条闭合曲线的长度，它也由半径决定，计算公式是：周长= 2 × π × 半径。
三、圆的元素圆主要由以下几个要素组成：1. 圆心：圆心是圆的中心点，用字母O表示。
2. 半径：半径是从圆心到圆的任意一点的距离，用字母r表示。
3. 直径：直径是通过圆心，且两端点都在圆上的线段，用字母d表示。
直径的长度是半径的两倍，即d = 2r。
4. 弦：弦是圆上的任意两个点所确定的线段，用字母AB表示。
5. 弧：弧是圆上两个点之间的一段曲线，用字母AB表示。
弧可以被弦所截，被截下的弧叫做弦所对应的弧。
6. 切点：切点是直线与圆相切时，直线上所与圆相接触的点。
四、圆的应用圆在我们日常生活中有着广泛的应用，以下是几个常见的应用场景：1. 车轮是圆的，它们能够顺利地滚动。
2. 圆形的盖子能够完全覆盖圆形容器的口。
六年级上册圆知识点复习
六年级上册圆知识点复习圆是我们数学学习中非常重要的一个概念，它在几何形状中起着至关重要的作用。
在六年级上册，我们已经学习了很多关于圆的知识点，下面我们来进行复习。
1. 圆的定义圆是平面上所有到圆心的距离都相等的点的集合。
在图形上，我们可以用一个闭合曲线来表示圆，这个曲线称为圆周。
2. 圆的要素圆主要由两个要素来定义：圆心和半径。
- 圆心：圆心是圆周的中心点，通常用字母O表示。
- 半径：半径是从圆心到圆周上的任意一点的距离，通常用字母r表示。
3. 圆的性质- 圆的半径相等：圆心到圆周上的任意一点的距离都相等，所以圆的半径都相等。
- 圆的直径：直径是通过圆心、并且两端点在圆周上的线段。
直径的长度等于半径的两倍，即直径=2r。
- 圆的周长：周长是指围绕圆一圈的长度，也叫做圆的周长或者圆周长。
圆的周长计算公式为C=2πr，其中π是一个常数，约等于3.14159。
- 圆的面积：面积是指圆所占据的平面的大小，也叫做圆的面积。
圆的面积计算公式为A=πr^2。
4. 相关公式- 圆的周长公式：C=2πr- 圆的面积公式：A=πr^2- 相关单位换算：当给定直径d时，可以通过d=2r来求得半径r；当给定周长C时，可以通过C=πd或C=2πr来求得半径r。
5. 圆的图形判断当给定一个图形时，我们可以通过以下条件判断它是不是圆：- 图形是一个闭合曲线。
- 曲线上的所有点到同一个点的距离都相等。
- 图形的形状和半径符合圆的定义。
通过对六年级上册圆知识点的复习，我们再次强化了对圆的认识。
圆是几何形状中的重要一员，在数学中起着重要的作用。
我们不仅学习了圆的定义、要素和性质，还学会了计算圆的周长和面积。
掌握了这些知识，我们可以更好地理解和应用圆形相关的数学问题。
在以后的学习和生活中，我们将会经常遇到和使用圆的知识，因此加深对圆的理解非常重要。
希望同学们能够牢固掌握圆的相关知识，为数学学习打下坚实的基础。
六年级上册数学圆知识点总结
六年级上册数学圆知识点总结
六年级上册数学圆的知识点主要包括以下内容：
1. 圆的概念：圆是由平面上距离一个定点（圆心）相等的所有点组成的集合。
2. 圆的要素：圆心、半径、直径。
圆心是圆上的任意一点，半径是圆心到圆上任何一
点的距离，直径是通过圆心的一条线段，并且其长度等于两个相对点到圆心的距离之和。
3. 圆的表示方式：可以用圆心的坐标和半径的长度来表示一个圆。
4. 圆的性质：圆的任意一条弦等分其所夹的圆心角，圆的直径是其所在原圆周上最长
的弦，圆的内接四边形的对角线互相垂直且互相平分。
5. 圆的周长和面积：圆的周长是圆周上的一段弧长，可以使用圆的半径或直径来计算。
圆的面积是圆内所有点的集合，可以使用圆的半径来计算。
6. 圆的判定：两个圆相等，当且仅当它们的半径相等；两个圆相切，当且仅当它们只
有一个公共点；两个圆相离，当且仅当它们没有公共点。
7. 圆的应用：圆常常应用于建筑、工程、艺术等领域。
例如，圆形的台阶、圆形的广场、圆形的雕塑等。
以上是六年级上册数学圆的主要知识点总结，希望对你有帮助！。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆的知识
班级______ 姓名______
一、圆各部分的名称.
1、圆心：圆心确定圆的位置。
把圆形纸片对折再对折（对折两次），折痕的交点就是圆心。
2、半径：连接圆心到圆上任意一点的线段叫半径。
有无数条半径。
半径决定圆的大小。
3、直径：通过圆心，两端都在圆上的线段叫直径。
直径所在的直线就是圆的对称轴，圆有无数条对称轴。
同一个圆内的所有线段中，圆的直径是最长的
二、圆的周长
1、圆周率表示圆的周长和直径的比值，是一个固定的数。
（它不因圆的大小而改变）
它是一个无限不循环小数，用字母∏表示，约等于。
2、圆的周长计算公式
顺用：C=πd c=2πr（求周长要知道半径或者直径）反用：d=c÷πr= c÷π÷2 3、C半圆= πr＋2r= → r=C半圆÷（π＋2）=C半圆÷
C半圆= πd÷2＋d= →d=C半圆÷（π÷2＋1）=C半圆÷
4、正方形里最大的圆（内切圆正方形的面积与圆的面积比=4：π）。
正方形的边长＝圆的直径；圆的面积=%正方形的面积
5、圆里面最大的正方形（外切圆内切圆正方形的面积与圆的面积比=2：π）。
圆的直径=正方形的对角线。
正方形的面积=对角线×对角线÷2
6、两个圆的半径比＝直径比＝周长比，面积比＝半径的平方比（即r扩大n倍，直径扩大n倍，周长扩大n倍，面积扩大n2倍）
7、求周长增加的数量就是用:增加的半径×2π或者用增加的直径×π
8、车轮滚动一周前进的路程就是车轮的周长。
每分前进米数（速度）＝车轮的周长×转数
9、钟表的分针时针的长度是圆的半径，牛吃草的绳子是圆的半径，喷水的距离是圆的半径。
三、圆的面积
1、圆面积公式的推导过程
注意：切拼后的长方形的周长比圆的周长多了两条半径。
C长方形＝2πr＋2r =C圆＋d 2、求面积的4种基本情况
（1）已知半径求面积直接用公式。
s=πr2
（2）已知直径求面积先求半径，再用公式。
r =d÷2 s=πr2
（3）已知周长求面积先求半径，再用公式。
r= c÷π÷2 s=πr2
（4）已知r2求面积把r2看作一个整体直接用公式。
在图中一般用r2正方形的面积
4、S圆环=S外圆—S内圆=πR2-πr2= π（R2－r2）环宽=R-r R=r+环宽圆环的直径等于r+两个环宽
5、半圆的周长等于同圆周长的一半加直径半圆的面积是圆面积的一半。
求半圆环的周长等于两个圆周长的一半加两个环宽。
半圆环的面积就是圆环面积
的一半。
四、几个常用结论
1. 几个直径和为n的圆的周长=直径为n的圆的周长（如图）
几个直径和为n的圆的面积<直径为n的圆的面积。
2.周长相等的长方形、正方形和圆，圆的面积最大，长方形的面积最
小。
3.面积相等的长方形、正方形和圆，长方形的周长最大，圆的周长最小。
4.求阴影部分的周长一般就是求围成阴影部分所有的曲线和线段之和：求阴影部分的面积一般用总面积减去空白部分的面积。
有时会用到割补法。
（根据题意灵活运用）五、圆章节的解题步骤：
1、确定问题：(1)求圆的周长还是半圆的周长或者是求圆周长的一半(2)求圆的面积还是求半圆的面积
(3)求圆环的面积还是半圆环的面积(4)求圆环的周长还是半圆环的周长2、写公式：C=πd=2πr C半圆= πr＋2r或πd÷2＋d C一半=πd÷2=πr
s=πr2 s半圆=πr2÷2 s=π（R2－r2）S半圆环= π（R2－r2）÷2
C=2πR+2πr C半圆环=πR+πr+两个环宽
3、代入数字：一个字母对应一个数字
4、计算，检查单位
5、答题、验算
4、常用的倍数。
×2＝×3＝×4＝×5＝×6＝
×7＝×8＝×9＝×12＝×14＝
×16＝×18＝×24＝×25＝
×36＝×49＝×64＝×81=
5、常用的平方数：112＝121 122＝144 132＝169 142＝196 152＝225
162＝256 172＝289 182＝324 192＝361 202＝400
练习
一、考点1：圆、周长、圆周率等的基本概念。
判断： 1、通过圆心的线段是半径。
（ ） 2、 所有的直径都相等 （ ）
3、半径的长度是直径的 21 （ ）
4、半径是2厘米的圆，其周长和面积相等 （ ） 填空： 1.正方形有（ ）条对称轴；等腰三角形有（ ）条对称轴；半圆有（ 1 ）条对称轴。
圆有（ ）条对称轴。
2、圆的周长总是半径的（ ）倍，。
3、一圆的半径增加1厘米，周长就增加（ ）厘米。
4、圆周率表示同一个圆内（ ）和（ ）的倍数关系。
二、考点2：正方形、长方形与圆的关系。
1、在边长为6cm 的正方形中画一个最大的圆，这个圆的半径是（ ）。
2、在长28cm ，宽26cm 的长方形纸板上剪出一个最大的圆，这个圆的半径是（ ）。
3、在一张长50厘米，宽6厘米的长方形纸片
中剪最大的圆，这样的圆最多可剪（ ）个。
三、考点3：圆的周长公式及其应用。
1.、一种压路机的前轮直径是米，每分钟转10圈，
压路机每分钟前进多少米？
2、一种钟表时针长5厘米，走一昼夜走了多少厘
米？
3、用一个硬纸板做成的圆在直尺上滚动一周，经过
的距离是 ，这个圆的直径是多少？
4、杂技演员表演独轮车走钢丝，车轮直径80厘米。
要骑过米长的钢丝，车轮要滚动多少周？
四、考点4：圆的面积公式及其应用。
1、一个钟表的分针长5cm ，从1时到2时，分针针尖扫过的面积是多少？ 2、用26米长的篱笆围成一个圆形苗圃，篱笆接头处用去米。
苗圃的面积多少？ 3、
五、考点5：半圆的性质、周长和面积。
1、把周长为厘米的圆平均分成两个半圆，每个半圆
的周长是多少？
面积是多少？
六、考点6：圆环和阴影部分的面积。
1：求阴影部分的面积。
（单位：厘米）
2、阴影部分的面积。
（单位：厘米）
3、求阴影部分的面积。
（单位：厘米）
4、一个直径为8米的圆形花坛，要在花坛外围修一
条1米宽的石头小路。
（1）石头小路的面积是多少？
（2）如果每平方米需要花费100元，修这条石头
小路总共要花费多少钱？。