哈夫曼树
哈夫曼树定义

哈夫曼树定义
哈夫曼树是一种二叉树,它用来表示一组符号权值的最优编码。
它应用于编码论,通常用来代表数据权值的树。
哈夫曼树是指一种最短带宽传输时能够有效工作的最优编码树。
哈夫曼树是每个节点都包含一个权值的二叉树。
它的定义如下:每一个权值所构成的数据集合,其最优树形式是每一个数据项的权值都比它的子节点的权值大,最终形成一个哈夫曼树。
哈夫曼树的构建一般是以权值的大小为基础进行的,权值越大,在哈夫曼树上就越靠近根节点,在结点之间的路径越短,这样便可以减少树的总长度,可以加快数据的传输速度。
此外,哈夫曼树还可以用于实现多种额外的功能。
哈夫曼树的构建有一种特别的方法,叫做“哈夫曼编码”,它采用“编码”和“解码”的方法来把一个数据集分成不同的组,这些组就是哈夫曼树的节点。
每组的数据都含有一个权值,当这些组被组合到一起时,它们就构成了一棵哈夫曼树。
哈夫曼树的建立是低耗时的,最优建立方式是将权值数组排序,然后依次添加,添加过程为:先将最小的两个数字添加到根节点,再将它们的和也添加到根节点,重复此过程,直到所有数字都被添加完为止。
哈夫曼树在编码的时候,如果一个字符出现的次数越多,它的权值就越大,它就越接近根节点。
数据结构哈夫曼树和哈夫曼编码权值

数据结构哈夫曼树和哈夫曼编码权值一、引言在计算机领域,数据结构是非常重要的一部分,而哈夫曼树和哈夫曼编码是数据结构中非常经典的部分之一。
本文将对哈夫曼树和哈夫曼编码的权值进行全面评估,并探讨其深度和广度。
通过逐步分析和讨论,以期让读者更深入地理解哈夫曼树和哈夫曼编码的权值。
二、哈夫曼树和哈夫曼编码的基本概念1. 哈夫曼树哈夫曼树,又称最优二叉树,是一种带权路径长度最短的二叉树。
它的概念来源于一种数据压缩算法,可以有效地减少数据的存储空间和传输时间。
哈夫曼树的构建过程是基于给定的权值序列,通过反复选择两个最小权值的节点构建出来。
在构建过程中,需要不断地重排权值序列,直到构建出一个满足条件的哈夫曼树。
2. 哈夫曼编码哈夫曼编码是一种变长编码方式,它利用了哈夫曼树的特点,对不同的字符赋予不同长度的编码。
通过构建哈夫曼树,可以得到一套满足最优存储空间的编码规则。
在实际应用中,哈夫曼编码经常用于数据压缩和加密传输,能够有效地提高数据的传输效率和安全性。
三、哈夫曼树和哈夫曼编码的权值评估1. 深度评估哈夫曼树和哈夫曼编码的权值深度值得我们深入探究。
从构建哈夫曼树的角度来看,权值决定了节点在树中的位置和层次。
权值越大的节点往往位于树的底层,而权值较小的节点则位于树的高层。
这种特性使得哈夫曼树在数据搜索和遍历过程中能够更快地找到目标节点,提高了数据的处理效率。
而从哈夫曼编码的角度来看,权值的大小直接决定了编码的长度。
权值越大的字符被赋予的编码越短,可以有效地减少数据传输的长度,提高了数据的压缩率。
2. 广度评估另哈夫曼树和哈夫曼编码的权值也需要进行广度评估。
在构建哈夫曼树的过程中,权值的大小直接影响了树的结构和形状。
当权值序列较为分散时,哈夫曼树的结构会更加平衡,节点的深度差异较小。
然而,当权值序列的差异较大时,哈夫曼树的结构也会更不平衡,而且可能出现退化现象。
这会导致数据的处理效率降低,需要进行额外的平衡调整。
6-10+哈夫曼树

哈夫曼--编码
按A B C D E F G H 这八个字母出现的频率构造哈夫曼树。
A:0110,B:10,C:1110,D:1111, E:110,F:00,G:0111,H:010
树的带权路径长度的含义是各个字符的编码长与 其出现次数的乘积之和,也就是电文的代码总长, 所以采用哈夫曼树构造的编码是一种能使电文代码 总长最短的不等长编码。
对于同一组给定叶结点所构造的哈夫曼树,树的形状可 能不同,但带权路径长度值是相同的,一定是最小的
哈夫曼树—示例 叶结点权值集合为W = W = {7,5,3,1}构造哈夫曼树三种形态:
给定n个权值,需经过n-1次合并最终能得到一棵哈夫曼树。 经过n-1次合并得到n-1个新结点,这n-1个新结点都是具有两个孩子结点的分支 结点。也就是说哈夫曼树中没有度为1的结点。 构造的哈夫曼树共有2n-1个结点。
这样的编码不能保证译码的唯一性,我们称之为具有二义性的译码。
哈夫曼--编码
哈夫曼树可用于构造使电文的编码总长最短的编码方案,且不会产生二义性。
设需要编码的字符集合为{d1,d2,…,dn}, 它们在电文中出现的次数或频率集合为{w1,w2,…,wn}, 以d1,d2,…,dn作为叶结点,w1,w2,…,wn作为它们的权值, 构造一棵哈夫曼树,然后,规定哈夫曼树中的左分支代表0,右分支代表1, 则从根结点到每个叶结点所经过的路径分支组成的0和1的序列便为该结点对应 字符的编码,我们称之为哈夫曼编码。
哈夫曼树--基本概念
给定一组权值,用以作为叶结点可以构造出不同形状的二叉树。 例如,设有4个权值分别为1,3,5,7,作为4个叶结点,构造二叉树。
(a)
(b)
(c)
(d)
(e)
简述哈夫曼树的定义

简述哈夫曼树的定义哈夫曼树是一种重要的二叉树,它有着广泛的应用,是许多计算机系统中常用的数据结构。
哈夫曼树是一种完全二叉树,其中任意一个结点都有左右子树,叶子结点只有左子树或者右子树。
它是根据“最优化原则”建立的,目的是使总代价最低。
它是一种最高效率、最具有利用价值的数据结构,因此深受广大科学家和技术工作者的喜爱。
简而言之,哈夫曼树是一种带权路径长度最小的二叉树,即它的任一非叶子结点的权值之和等于所有叶子结点的权值之和。
它的定义如下:将n个权值不同的叶子结点组成的n棵二叉树,它们的带权路径长度之和最小称为哈夫曼树。
哈夫曼树的带权路径长度指的是从根节点到叶子节点的路径上结点权值的乘积之和,它是求解最优二叉树的重要参数。
哈夫曼树可分为正哈夫曼树和负哈夫曼树,它们的不同之处在于哈夫曼树的根节点权值是正数或者负数,而负哈夫曼树的根节点权值总是负数。
哈夫曼树的构造方法是从叶子结点开始,依次将权值较小的两棵二叉树合并,然后将这两棵子树的权值之和作为新的父母亲结点,新的子树的根节点的权值就是这两个结点的权值之和。
构造方法至将所有的n个结点合并为一棵树,最后得到的哈夫曼树即为最优二叉树。
哈夫曼树是最优二叉树,在许多需要使用最优二叉树的算法中均可运用,如字符编码算法、矩阵乘法算法、最短路径算法等,它的应用非常广泛。
哈夫曼树的设计既可以给出解决问题的最佳答案,又能将数据结构设计得非常有效。
哈夫曼树可以帮助计算机系统显著提高性能,在网络通信、数据压缩、资源分配等方面均有用处。
总而言之,哈夫曼树是一种完全二叉树,其中每一个结点都有左右子树,根据“最优化原则”建立,其带权路径长度最小,广泛应用于计算机系统中。
它可以有效地解决许多计算机系统中的性能瓶颈问题,无论是在数据组织方面还是在计算机系统性能提升方面都有重要的意义。
8哈夫曼树

b d e c
2 3 4 5 6 7 b c d e
d
e f g f g h
f
g
h
8
h
25
3、用孩子兄弟表示法来存储
思路:用二叉链表来表示树,但链表中的两个 指针域含义不同。 左指针指向该结点的第一个孩子; 右指针指向该结点的下一个兄弟结点。
firstchild data nextsibling
100
40
21 32 g e 17 7 a
60
28 11 10 h 6 d 2 c 5 3 f
10
对应的哈夫曼编码(左0右1):
符 编码 频率 符 编码 频率
100
a
b
1100
00
0.07
0.19
a
b
000
001
0.07
0.19 0.06
0 b
0 40
1
1
0 60 1 28 1 0 6 d 0 2 c 11 1d Path Length
树的带权路径长度如何计算? WPL = 哈夫曼树则是:WPL 最小的树。
w kl k
k=1
n
经典之例:
4 d
2 c 7 a (b) 5 b
Huffman树
7 a
7 a
5
2 b c
4 d
5 b
2 c (c)
4 d
(a)
WPL=36
WPL=46
WPL= 35
3
构造霍夫曼树的基本思想: 权值大的结点用短路径,权值小的结点用长路径。 构造Huffman树的步骤(即Huffman算法):
(1) 由给定的 n 个权值{w0, w1, w2, …, wn-1},构造具有 n 棵扩充 二叉树的森林F = { T0, T1, T2, …, Tn-1 },其中每一棵扩充二叉树 Ti 只有一个带有权值 wi 的根结点,其左、右子树均为空。 (2) 重复以下步骤, 直到 F 中仅剩下一棵树为止: ① 在 F 中选取两棵根结点的权值最小的扩充二叉树, 做为左、 右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为 其左、右子树上根结点的权值之和。 ② 在 F 中删去这两棵二叉树。 ③ 把新的二叉树加入 F。
哈夫曼树

哈夫曼树及其应用一、基本术语1.路径和路径长度在一棵树中,从一个结点往下可以达到的孩子或子孙结点之间的通路,称为路径。
通路中分支的数目称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2.结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3.树的带权路径长度树的带权路径长度(Weighted Path Length of Tree):也称为树的代价,定义为树中所有叶结点的带权路径长度之和,通常记为:其中:n表示叶子结点的数目wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。
二、哈夫曼树构造1.哈夫曼树的定义在权为w l,w2,…,w n的n个叶子所构成的所有二叉树中,带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。
【例】给定4个叶子结点a,b,c和d,分别带权7,5,2和4。
构造如下图所示的三棵二叉树(还有许多棵),它们的带权路径长度分别为:(a)WPL=7*2+5*2+2*2+4*2=36(b)WPL=7*3+5*3+2*1+4*2=46(c)WPL=7*1+5*2+2*3+4*3=35其中(c)树的WPL最小,可以验证,它就是哈夫曼树。
2.哈夫曼树的构造假设有n个权值,则构造出的哈夫曼树有n个叶子结点。
n 个权值分别设为w1,w2,…,wn,则哈夫曼树的构造规则为:(1) 将w1,w2,…,wn看成是有n 棵树的森林(每棵树仅有一个结点);(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加入森林;(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为我们所求得的哈夫曼树。
下面给出哈夫曼树的构造过程,假设给定的叶子结点的权分别为1,5,7,3,则构造哈夫曼树过程如下图所示。
数据结构第六章 哈夫曼树
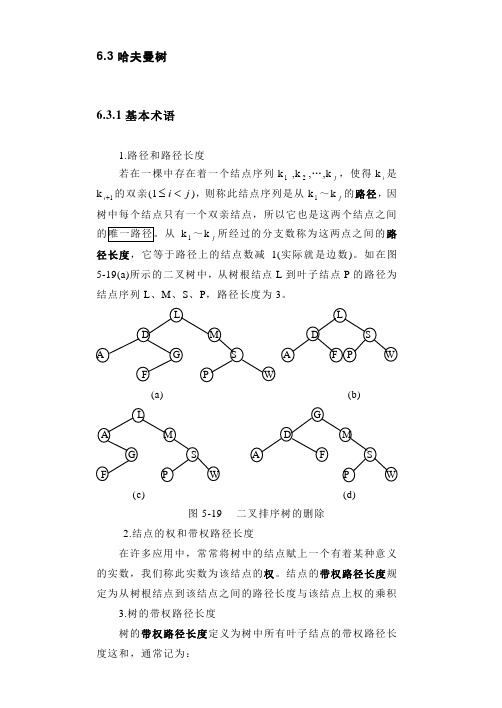
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
哈夫曼树的定义

哈夫曼树的定义
哈夫曼树的定义:给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树。
扩展资料:
哈夫曼树也可以是k叉的,只是在构造k叉哈夫曼树时需要先进行一些调整。
构造哈夫曼树的思想是每次选k个权重最小的元素来合成一个新的元素,该元素权重为k个元素权重之和。
但是当k大于2时,按照这个步骤做下去可能到最后剩下的元素少于k个。
解决这个问题的办法是假设已经有了一棵哈夫曼树(且为一棵满k叉树),则可以计算出其叶节点数目为(k-1)nk+1,式子中的nk表示子节点数目为k的节点数目。
于是对给定的n个权值构造k叉哈夫曼树时,可以先考虑增加一些权值为0的叶子节点,使得叶子节点总数为(k-1)nk+1这种形式,然后再按照哈夫曼树的方法进行构造即可。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
承诺书郑重声明:本人所呈交的课程设计是本人在导师指导下独立撰写并完成的,课程设计没有剽窃、抄袭、造假等违反学术道德、学术规范和侵权行为。
本课程设计不包含任何其他个人或集体已经发表或撰写过的研究成果,如果引用则标识出了出处。
对本课程设计的研究做出贡献的个人和集体,均已在文中以明确方式标明。
课程设计与资料若有不实之处,本人承担一切相关责任。
特此声明。
签名:年月日目录一.需求分析 (3)1.问题描述 (3)2.功能要求 (3)二.系统总框图和功能模块说明.41.系统总框图 (4)2.功能模块说明 (4)2.功能模块说明 (4)3.系统设计 (4)3.1主要链表 (4)3.2主要功能函数 (6)3.3关键函数的流程图 (6)4.系统调试: (9)5.总结 (13)6.源程序: (13)一.需求分析哈夫曼编/译码器1.问题描述利用哈夫曼编码进行信息通信可以大大提高信道利用率,缩短信息传输时间,降低传输成本。
但是,这要求在发送端通过一个编码系统对待传数据预先编码,在接收端将传来的数据进行译码(复原)。
对于双工信道(即可以双向传输信息的信道),每端都需要一个完整的编/译码系统。
试为这样的信息收发站写一个哈夫曼编/译码系统。
2.功能要求I:初始化(Initialization)。
从终端读入字符集大小n,以及n个字符和n个权值,建立哈夫曼树,并将它存于文件hfmTree中。
E:编码(Encoding)。
利用已建好的哈夫曼树(如不在内存,则从文件htmTree中读入),对文件ToBeTran中的正文进行编码,然后将结果存入文件CodeFile中。
D:译码(Decoding)。
利用已建好的哈夫曼树将文件CodeFile中的代码进行译码,结果存入文件TextFile中。
P:印代码文件(Print)。
将文件CodeFile以紧凑格式显示在终端上,每行50个代码。
同时将此字符形式的编码写入文件CodePrint中。
T:印哈夫曼树(Tree Printing)。
将已在内存中的哈夫曼树以直观的方式(树或凹入表形式)显示在终端上,同时将此字符形式的哈夫曼树写入文件TreePrint中。
二.系统总框图和功能模块说明图1. 系统总框图2.功能模块说明(1).初始化; Initialization(LiHTNode *&ht);(2).编码; Encoding(LiHTNode *&ht,LeafCode *&lc);(3).译码; Decoding(LeafCode *&lc);(4).印代码模块; Print();(5).印哈夫曼树。
Tree_Printing(LiHTNode *&ht);3.系统设计3.1主要链表struct LiHTNode //用于建立哈夫曼树{char data; //节点double weight; //权值char code; //编码LiHTNode *parent; //双亲LiHTNode *lchild; //左孩子LiHTNode *rchild; //右孩子};存储结构如图所示图2. 哈夫曼树节点存储结构struct LeafCode //用于存储叶子节点和哈夫曼编码{char leaf; //叶子char code[N]; //叶子到根节点的编码串int top; //栈顶指针LeafCode *next;};存储结构如图所示图3. 叶子哈夫曼编码存储结构3.2主要功能函数Initialization(LiHTNode *&ht) //初始化Encoding(LiHTNode *&ht,LeafCode *&lc) //编码 Decoding(LeafCode *&lc) //译码Print() //印代码模块Tree_Printing(LiHTNode *&ht) //印哈夫曼树3.3关键函数的流程图(1). Initialization(LiHTNode *&ht) //初始化图4. 初始化(2). Encoding(LiHTNode *&ht,LeafCode *&lc) //编码图5. 编码(3). Decoding(LeafCode *&lc) //译码图6. 译码(4). Print() //印代码模块图7. 印代码模块(5). Tree_Printing(LiHTNode *&ht) //印哈夫曼树图8. 印哈夫曼树4.系统调试:(1).调试结果如下:图9. 调试结果(2).终端显示如下:图10. 终端显示图11. 终端显示图12. 终端显示(3).各文件如下:1).文件hfmTree.txt2).文件ToBeTran.txt3).文件CodeFile.txt图15. 文件CodeFile.txt4).文件TextFile.txt图16. 文件TextFile.txt 5).文件Codeprint.txt图17. 文件Codeprint.txt6).文件TreePrint.txt图18. 文件TreePrint.txt5.总结本程序为哈夫曼编/译器的制作,主要是对文件的操作,在创建哈夫曼树的过程中有点难度,创建哈夫曼编码时也有一定难度,译码时不难;但是在用凹入表形式打印哈夫曼树时,有点难度。
通过本程序,我对二叉树的递归操作更加熟练了,对了解并掌握了树和二叉树这一章节的内容,尤其是二叉树。
6.源程序:#include<iostream.h>#include<fstream.h>#define N 150 //存放哈夫曼编码的最大长度#define M 200 //存放字符的最大长度#define Max 1000 //存放原文的哈夫曼编码的最大长度struct LiHTNode{char data; //节点double weight; //权值char code; //编码LiHTNode *parent; //双亲LiHTNode *lchild; //左孩子LiHTNode *rchild; //右孩子};struct LeafCode{char leaf; //叶子char code[N]; //叶子到根节点的编码串int top; //栈顶指针LeafCode *next;};void DisplayHT(LiHTNode *&ht) //哈夫曼树的输出{LiHTNode *p=ht;ofstream out("F:\\hfmTree.txt",ios::out|ios::app);if(p!=NULL){out<<p->data<<" "<<p->weight<<" ";if(p->parent!=NULL){out<<p->parent->weight<<" ";}else{out<<"NULL"<<" ";}if(p->lchild!=NULL){out<<p->lchild->weight<<" ";}else{out<<"NULL"<<" ";}if(p->rchild!=NULL){out<<p->rchild->weight<<"\n";}else{out<<"NULL"<<"\n";}DisplayHT(p->lchild);DisplayHT(p->rchild);}out.close();}void Initialization(LiHTNode *&ht) //初始化{LiHTNode *p,*q,*g;int temp;char ch;ht=new LiHTNode;ht->parent=NULL;ht->lchild=NULL;ht->rchild=NULL;ht->data=0;ht->weight=0;p=ht;for(int i=1;i<=128;i++) //存储ASCLL码字符作为哈夫曼树的叶子,权值设为对应ASCLL码{p->parent=new LiHTNode;p=p->parent;p->data=i;p->weight=i;p->lchild=NULL;p->rchild=NULL;p->parent=NULL;}p=ht;q=p->parent;while(p->parent!=NULL) //对权值大小进行排序{while(q!=NULL){if(p->weight>q->weight){temp=p->weight;ch=p->data;p->weight=q->weight;p->data=q->data;q->weight=temp;q->data=ch;q=q->parent;}p=p->parent;q=p->parent;}p=ht;q=p->parent;while(p->parent!=NULL) //哈夫曼树的构造{g=new LiHTNode;g->lchild=p;g->rchild=q;g->parent=q->parent;p->parent=g;q->parent=g;g->weight=p->weight+q->weight;p=g;q=p->parent;while(q!=NULL){if(g->weight<q->weight){ht=g->parent;g->parent=q;p->parent=g;g=ht;break;}if(q->parent==NULL&&g->weight>q->weight)ht=g->parent;g->parent=q->parent;q->parent=g;g=ht;break;}p=q;q=q->parent;}p=g;q=p->parent;}ht=g;ofstream out("F:\\hfmTree.txt",ios::out);out<<"节点\t权重\t双亲权重\t左孩子权重\t右孩子权重\n";out.close();DisplayHT(ht); //输出哈夫曼树各个节点以及权重}void CreateHCode(LiHTNode *&ht) //哈夫曼编码的创建{LiHTNode *p=ht;if(p!=NULL){if(p->lchild!=NULL){p->lchild->code='0';}if(p->rchild!=NULL){p->rchild->code='1';}CreateHCode(p->lchild);CreateHCode(p->rchild);}}void FindLeaf(LiHTNode *&ht,LeafCode *&lc) //查找叶子节点{LiHTNode *p=ht,*g;LeafCode *q=lc;while(q->next!=NULL)q=q->next;if(p!=NULL){if(p->lchild==NULL&&p->rchild==NULL){q->next=new LeafCode;q=q->next;q->next=NULL;q->leaf=p->data;g=p;q->top=-1;while(g->parent!=NULL){q->top++;q->code[q->top]=g->code;g=g->parent;}cout<<p->data<<":"<<p->weight<<"\t";}FindLeaf(p->lchild,q);FindLeaf(p->rchild,q);}}void Encoding(LiHTNode *&ht,LeafCode *&lc) //编码{LiHTNode *p=ht;int temp,i=0,k;char str[M],ch;CreateHCode(p);cout<<"叶子以及权重的形式为(叶子:权重):"<<endl;FindLeaf(ht,lc);LeafCode *q=lc->next;ifstream in("F:\\ToBeTran.txt",ios::in);while(in.get(ch)){str[i]=ch;i++;}k=i;in.close();cout<<endl;ofstream out("F:\\CodeFile.txt",ios::out);for(i=0;i<k;i++){q=lc->next;while(q!=NULL){if(str[i]==q->leaf){temp=q->top;while(temp!=-1){out<<q->code[temp];temp--;}}q=q->next;}}out.close();cout<<endl;}void Decoding(LeafCode *&lc) //译码{char ch;int i=0,k,temp,g;char str1[Max];LeafCode *q=lc->next;cout<<endl;ifstream in("F:\\CodeFile.txt",ios::in);while(in.get(ch)){str1[i]=ch;i++;}k=i;in.close();ofstream out("F:\\TextFile.txt",ios::out);for(i=0;i<k;i++){q=lc->next;while(q!=NULL){if(str1[i]==q->code[q->top]){g=i;temp=q->top;while(temp!=-1){if(str1[i]==q->code[temp]){temp--;i++;}else{i=g;break;}}if(temp==-1){cout<<q->leaf;out<<q->leaf;i--;break;}}q=q->next;}}out.close();cout<<endl;}void Print() //印代码文件{char str2[Max],ch;int i=0,k;ifstream in("F:CodeFile.txt",ios::in);while(in.get(ch)){str2[i]=ch;i++;}k=i;in.close();cout<<endl;for(i=0;i<k;i++){cout<<str2[i];if((i+1)%50==0)cout<<endl;}cout<<endl<<endl<<endl;ofstream out("F:CodePrint.txt",ios::out);for(i=0;i<k;i++){out<<str2[i];if((i+1)%50==0)out<<"\n";}out.close();}void Printing(LiHTNode *&ht) //印哈夫曼树中的一个递归函数{LiHTNode *p=ht,*q;char str3[20];int i=0,j,k=20;q=p;ofstream out("F:\\TreePrint.txt",ios::out|ios::app);if(p!=NULL){while(q->parent!=NULL){cout<<" ";out<<" ";q=q->parent;i++;}cout<<p->weight;out<<p->weight;for(j=0;j<k-i;j++){cout<<"▅";out<<"▅";}cout<<endl;out<<"\n";Printing(p->lchild);Printing(p->rchild);}out.close();}void Tree_Printing(LiHTNode *&ht) //印哈夫曼树{cout<<"用凹入表示法显示哈夫曼树:"<<endl<<endl;ofstream out("F:\\TreePrint.txt",ios::out);out<<"用凹入表示法显示哈夫曼树:"<<"\n";out.close();Printing(ht);}void main(){LiHTNode *ht;LeafCode *lc;lc=new LeafCode; //创建叶子的头结点lc->next=NULL;Initialization(ht); //初始化Encoding(ht,lc); //编码Decoding(lc); //译码Print(); //印代码文件Tree_Printing(ht); //印哈夫曼树}。
