数电第1章 习题作业
数电习题解(1-2章)

数电习题解答(1,2章)第一章数制与码制(教材p17)题1.2 将下列二进制整数转换为等值的十进制数。
(3)(10010111)2=1×27+1×24+1×22+1×21+1×20=151题1.4 将下列二进制数转换为等值的十进制数。
(2)(110.101)2=1×22+1×21+1×2-1+1×2-3=6.625题1.4 将下列二进制数转换为等值的八进制数和十六进制数。
(3)(101100.110011)2=(54.63)8, (101100.110011)2=()16题1.6 将下列十六进制数转换为等值的二进制数。
(2)(3D.BE)16=(111101.10111110)2题1.8将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后8位有效数字。
(2) (0.251)10≈(0.01000000)2=(0.40)16题1.9将下列十进制数转换为等值的二进制数和十六进制数。
要求二进制数保留小数点以后4位有效数字。
(1) (25.7)10≈(11001.1011)2=(19.B)16题1.10 写出下列二进制数的原码、反码和补码。
(2) (+00110)2(+00110)原=000110, (+00110)反=000110, (+00110)补=000110.(3) (-1101)2(-1101)原=11101, (-1101)反=10010, (-1101)补=10011.题1.11 写出下列带符号位二进制数(最高位为符号位)的反码和补码。
(2) (001010)2(3) (111011)2(001010)2反码: 001010 , (001010)2补码: 001010(111011)2反码:100100, (111011)2补码:100101题1.12 用8位的二进制数补码表示下列十进制数。
数电第1章 习题作业

1 1
1 1 1
1 1
1 1 1
(5) Y(A,B,C)=∑m(1,4,7) Y=A'B'C+AB'C'+ABC
BC 00 A 0
1 1
01 1
11
10
1
(6) Y(A,B,C,D)=∑m(0,1,2,5,8,9,10,12,14)
CD 00 AB 00 01 11 10 1 1
01 1
11
10 1
0 1 0 0
0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0
1
0 0 1 1 0 0 1 0 1 1
1 1 1 1
Y= A'B'C'D+A'B'CD'+A'BC'D'+A'BCD+ AB'C'D'+AB'CD+ABC'D+ABCD'
ABC
0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1
Y1
0 0 0 1 0 1 1 1
Y2
0 1 1 1 1 1 1 0
1 1 1
1
1
题1.9 在举重比赛中,有甲、乙、丙三名裁判,其中甲为主裁 判,乙、丙为副裁判,当主裁判和一名以上(包括一名) 副裁判认为运动员上举合格后,才可发出合格信号。列出 该函数的真值表。
数字电子技术基础第一章练习题及参考答案

第一章数字电路基础第一部分基础知识一、选择题1.以下代码中为无权码的为。
A. 8421BCD码B. 5421BCD码C.余三码D.格雷码2.以下代码中为恒权码的为。
A .8421BCD码B. 5421BCD码C.余三码D.格雷码3. 一位十六进制数可以用位二进制数来表示。
A. 1B.2C. 4D.164.十进制数25用8421BCD码表示为。
A .10 101B .0010 0101 C. 100101 D .101015.在一个8位的存储单元中,能够存储的最大无符号整数是。
A. (256) 10B. (127) 10C. (FF) 16D. (255) 106.与十进制数(53.5) 10等值的数或代码为。
A.(0101 0011. 0101)8421BCDB.(35. 8)16C.(110101. 1)2D.(65. 4)87.矩形脉冲信号的参数有。
A.周期B.占空比C.脉宽D.扫描期8.与八进制数(47. 3) 8等值的数为:A. (100111 . 011 )2B. (27. 6)16C. (27. 3 )16D. (1 00111 . 11 )29. 常用的BCD码有。
A.奇偶校验码B.格雷码C. 8421码D.余三码10 .与模拟电路相比,数字电路主要的优点有。
A.容易设计B.通用性强C.保密性好D.抗干扰能力强二、判断题(正确打,,错误的打X)1.方波的占空比为0. 5。
()2. 8421 码1001 比0001 大。
( )3.数字电路中用“ 1”和“ 0”分别表示两种状态,二者无大小之分。
()4.格雷码具有任何相邻码只有一位码元不同的特性。
()5.八进制数(18) 8比十进制数(18) 10小。
()6.当传送十进制数5时,在8421奇校验码的校验位上值应为1。
( )7.在时间和幅度上都断续变化的信号是数字信号,语音信号不是数字信号。
()8.占空比的公式为:q = t w / T,则周期T越大占空比q越小。
数电习题及解答

图 P2.7
题 2.7 解:
2.9 试写出图 P2.9 所示 CMOS 电路的输出逻辑表达式。
(a) 图 P2.9
(b)
题 2.9 解:
F1 A B A B ; F2 A B A B
2.11 试写出图 P2.11 中各 NMOS 门电路的输出逻辑表达式。
图 P2.11
0 1 1 1
0 1 1 1
证明 A B C AB AC
A
B
C
A B C
0 0 0 0 0 1 1 0
AB AC
0 0 0 0 0 1 1 0
0 0 0 0 1 1 1 1
(3)
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
证明 A B C A B C
(3) F ABC BC D A BD (4) F ( A, B, C , D) 题 1.15 解: (1) F A BC BC
m0,2,3,8,9,10,11,13
F B C A C B C
或
F B C B C A B
A
B
C
AB C
A BC
1 0 1
0 0 0
0 0 1
0 1 0
1 0 1
0 1 1 1 1
(4)
1 0 0 1 1
1 0 1 0 1
0 0 0 1 0
0 0 0 1 0
证明 AB AC A B AC
A
B
C
AB AC
A B AC
1 0 1 0 1 1 0 0
数字电子技术练习题第1、2章 习题

第1、2章 习题一、填空题1.由二值变量所构成的因果关系称为 关系。
能够反映和处理 关系的数学工具称为逻辑代数。
2.在正逻辑的约定下,“1”表示 电平,“0”表示 电平。
3.数字电路中,输入信号和输出信号之间的关系是 关系,所以数字电路也称为 电路。
在 关系中,最基本的关系是 、 和 。
4.计数制中的数码个数称为 ,计数制中的每一位数都对应该位上的数码乘以一个固定的数,这个固定的数称作 。
5. 十进制整数转换成二进制整数时需采用 法;十进制小数转换成二进制小数时需采用 法。
十进制数转换为八进制和十六进制时,应先转换成 制,然后再根据转换的 数,按照 一组转换成八进制;按 一组转换成十六进制。
6. 将八进制数(47.5)8转换为十六进制数的结果是 ;将十六进制数(FD )16转换为二进制数的结果是 。
7. 1+1=2是在 数制中成立的,1+1=1是在 代数中成立的。
8. 逻辑代数的基本定律有 律、 律、 律、 律和 律。
9. 在化简的过程中,约束项可以根据需要看作 或 。
最简与或表达式是指在表达式中 最少,且 也最少。
10. 卡诺图是将代表 的小方格按 原则排列而构成的方块图。
卡诺图的画图规则:任意两个几何位置相邻的 之间,只允许 的取值不同。
二、判断正误题1.奇偶校验码是最基本的检错码,用来使用PCM 方法传送讯号时避免出错。
( )2.异或函数与同或函数在逻辑上互为反函数。
( )3.8421BCD 码、2421BCD 码和余3码都属于有权码。
( )4.逻辑函数有多种描述形式,惟独真值表是惟一的。
( )5.每个最小项都是各变量相“与”构成的,即n 个变量的最小项含有n 个因子。
( )6.因为逻辑表达式A+B+AB=A+B 成立,所以AB=0成立。
( )7.逻辑函数F =A B +A B+B C+B C 已是最简与或表达式。
( )8.利用约束项化简时,将全部约束项都画入卡诺图,可得到函数的最简形式。
数电第一章题
√
C 0, A
×
D 1, A
×
分析提示
双输入端 A、B 的或非门的逻辑表达式 YAB 当 B = 0 时, YA0A 当 B = 1 时, YA110
第 10 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
10、一个有双输入变量 A、B 的异或门,当B分别为0、1时,输出 Y
分别为
最小项表达式共含有 3 个最小项。
第 14 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
14、当变量 A、B、C 取值为101 时,下列三变量函数最小项中等于
1 的是
( )。
A m1
×
B m3
×
C m5
√
D m7
×
分析提示
将 ABC = 101 代入各最小项: m 1AB C1010 m3ABC 1010 m5ABC1011 m 7AB 1C 010
第 17 页
数字电子技术
第 1 章 逻辑代数基础
单项选择题
17、函数 F = A+ B+C 的对偶函数 F' =
A A(BC)
×
B
A(B C)
( )。
√
C A BC
×
D ABC
×
分析提示
求对偶函数,需将给定的函数作如下变换: 常量 0 ↔ 常量 1
运算符号 ∙ ↔ 运算符号+ 并保持原来运算顺序不变。
3
9
1
第3页
数字电子技术
第 1 章 逻辑代数基础
3、 ( 1000 0110 1001 ) 余3 BCD 转换成十进制数是
A 536
数电 第一章 逻辑代数习题

1-13(1) 用卡诺图简化下面逻辑函数
Y BC AC AB
1
1
1
1
五邑大学
第一章 逻辑代数基础 习题
数 字 Y ( A, B, C, D) m(0,1,2,3,4,6,7,8,9,10,11,14) 电 表2.4.16 Y的卡诺图 路 CD 与 解: AB 00 01 11 10 逻 00 1 1 1 1 辑 01 1 Y CD AD B AC 1 1 设 11 1 计
10
1-14(4)简化下列逻辑函数,写最简成与或式
01
11
10
× × 1
1
×
1
1
五邑大学
字 电 路 Y ABC ABC ABC 与 ABC ABC 逻 辑 AB C 设 计
数
A B C 0 0 0 0 0 0 1 1 0 1 1 0 0 1 0 1 0 1 Y 0 1 0 1 0 1
1 1
1 1
0 1
1 1
五邑大学
第一章 逻辑代数基础 习题
• 题1-2已知真值表如表所示,试写出输出的逻辑函 数
第一章 逻辑代数 习题
数 字 电 路 与 逻 辑 设 计
题1-1、题1-7(2) 、题1-8(5) 题1-9(2) 题1-2、题1-3、题1-4(a) 题1-10(3)(8) 题1-11(1) 、题1-12(1) 题1-13(1)(5)、题1-14(1)(4)
五邑大学
第一章 逻辑代数基础 习题
• 题1-1 如图,列出真值表,试写出输出的逻辑函 数
3.
将这些变量相加即得 Y。
五邑大学
第一章 逻辑代数基础 习题
• 题1-2已知真值表如表所示,试写出输出的逻辑函 数
《数电》教材习题答案 第1章习题答案
思考题与习题1-1 将下列二进制数转化为十进制数。
(1)(100101100)2=(300)10 (2)(101011)2=(43)10(3)(1111111)2=(127)10 (4)(1011110)2=(94)101-2 将下列十进制数转化为二进制数。
(1)(28)10=(11100)2 (2) (100)10=(1100100)2(3)(210)10=(11010010)2 (4)(321)10=(101000001)2 1-3 将八进制数34、567、4633转化为二进制数。
(34)8=(11100)2 (567)8=(101110111)2(4633)8=(100110011011)21-4 将二进制数转化为八进制数。
(1011010)2=(132)8 (11010011)2=(323)8 1-5 将二进制数转化为十六进制数。
(100100110101)2=(935)16 (1010110011)2=(2B3)16 1-6 将十六进制数转化为二进制数。
(7AF4)16=( 111101*********)2 (F9DE )16=(1111100111011110)2 1-7 将十进制数691用8421BCD 码表示。
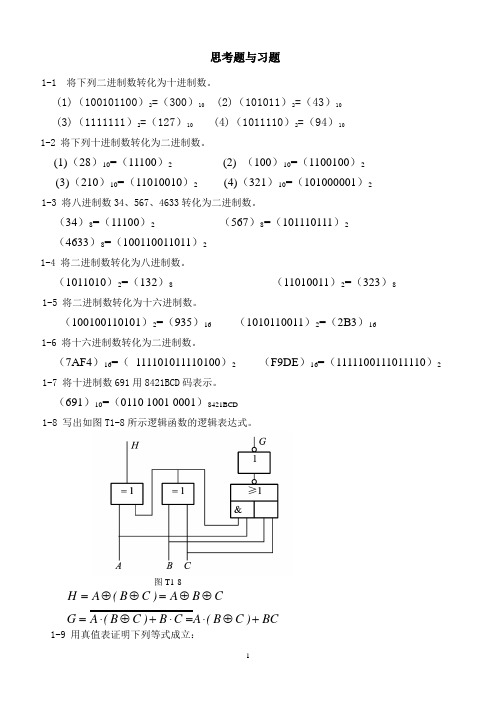
(691)10=(0110 1001 0001)8421BCD1-8 写出如图T1-8所示逻辑函数的逻辑表达式。
图T1-8BC)C B (A C B )C B (A G CB A )C B (A H +⊕⋅=⋅+⊕⋅=⊕⊕=⊕⊕= 1-9 用真值表证明下列等式成立:(1)A B + A B = (A +B )(A+B)可见,左式=右式,得证。
(2)A ⊕B =A ⊕B可见,左=右,得证。
(3)A ⊕0 = A可见,左式=右式,得证。
(4)A ⊕1 = A可见,左式=右式,得证。
1-10 利用公式和运算规则证明下列等式:(1)ABC + A BC + A B C = BC + AC证明:左=(ABC + A BC ) +( A B C +ABC )= BC + AC =右(2)C AB = AB + C证明:左=C AB C AB +=+=右(3)(A +B)(A + C)(B + C + D) = (A + B)(A + C)证明:将以上等式两边作对偶变换,可得到以下公式:AB +A C +BCD =AB +A C由常用公式四可知该式是成立的,则由对偶定理可知,对偶等式成立,则原等式也成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 1 1 0 0 1 1 0 0 1 1 0 0 1 1 0
CD 00 AB 00 01 11 10
01
11
10
5位格雷码可按P26图1-13卡 诺图,按此方法书写。
题1.6 用基本定律和定理证明以下等式。 (1) A+BC+D=(A'B'D'+A'C'D')' 利用反演定理: (Y左式)'=A'(B'+C')D'=A'B'D'+A'C'D' Y左式=(A'B'D'+A'C'D')'=Y右式 (2) A+A'(B+C)'=A+B'C' 利用分配律第二个公式 : 左式= (A+A')(A+(B+C)')= A+(B+C)'= A+B'C'=右式 (3) A'B'+A'B+AB'+AB =1 利用结合律、分配律 : 左式= (A'B'+A'B)+(AB'+AB) = A'(B'+B)+A(B'+B)= A'+A =1
题1.7 在下列各个逻辑函数中,当变量A,B,C为哪些取值组合时, 函数Y的值为1。 (1) Y=AB+BC+A'C Y= AB(C+C')+BC (A+A')+A'C(B+B') =m7+m6+m1+m3 使以上四个最小项为1时,Y为1。 即:111;110;011;001
同理: (2)000,001,011,100 (3)100,101,000,011,010,111 (4)110,111,010
题1.15 利用公式法将下列各函数化为最简与或式。 (1)Y=AB'C+A'+B+C' 或=AB'C+(AB'C)'=1 =B'C+A'+B+C' = C+A'+B+C' =1 (2)Y=(A'BC)'+(AB')' =(A'BCAB')' =1 或=A+B'+C'+A'+B =1
(3)Y=AB'CD+ABD+AC'D =AD(B'C+B+C') =AD
(4)Y=AB' (A'CD+(AD+B'C')') (A'+B) = AB' (A'CD+(AD+B'C')') (AB')' =0
(5)Y=AC (C'D+A'B) +BC((B'+AD)'+CE)' = BC(B'+AD) (CE)' =ABCDE' (6)Y=AC +AC'D+AB'E'F’+B(D⊕E)+BC'DE'+BC'D'E+ABE'F = AC+AD+AB'E'F'+B(D⊕E)+BC'(D⊕E)+ABE'F
0100 1000 0111 0101 0110 0001 0110 1110 0110 0111 0110 0001 0110 1110 0111
练习题
题1.2 写出4位自然二进制码和格雷码。
格雷码 ABCD 二进制码 ABCD
0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1
0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1
第1章 数字逻辑基础习题
作业 实验
0011 0110 0100 1000 0111 0101 0110 0001 0110 1110 0110 0111 0110 0001 0110 1110
0111 0010 0110 0001 0110 1110 0011 0010 0011 0000 0011 0000 0011 0110 0011 0100 0011 0001 0011 0110 0100 1000 0111 0101 0110 0001 0110 1110 0110 0111 0110 0001
1
1
1
1
1
1
1
1 1
1 1
1
10
1
1
CD 00 (3) Y=A' (B'C+B(CD'+D))+ABC'D AB Y=A' (B'C+BC+BD)+ABC'D 00 = A'B'C+A'BC+A'BD+ABC'D Y= A'C+BC'D 01 11
01
11 1
10 1
1 1
1
1
10 (4)Y=ABC+ABD+C'D'+AB'C +A'CD'+AC'D
保留 大非号
Y'=((A'+B)C'+D')E'+C'
(4)Y=(A+B+C)A'B'C'
题1.5 证明下面的恒等式相等。 (1) (AB+C)B=ABC'+A'BC+ABC 左式=AB+BC=AB(C+C')+ (A+A')BC =ABC+ABC'+ABC+ A'BC=右 (2) AB'+B+A'B=A+B 左式=A+B+A'B =A+B (3) BC+AD=(A+B)(B+D)(A+C)(C+D) Y左D= (B+C)(A+D)=AB+AC+BD+CD Y右D=AB+AC+BD+CD 对偶式相等,推得左=右。 (4) (A+C')(B+D)(B+D')=AB+BC' 左式= (A+C')(B+BD+BD') = (A+C')B=AB+BC'=右
1 1 1 1
0
题1.16 写出下图中各逻辑图的逻辑函数式,并化简为最简与或式。
(a)Y=((AB'C)'(BC')') '
=AB'C+BC'
(b)Y=((A'+C)' +(A+B')' +(B+C')')' = (A'+C)(A+B')(B+C') =(AC+A'B'+B'C) (B+C') =(AC+A'B') (B+C') =ABC + A'B'C'
题1.18 检查图1-30中各卡诺图的圈法是否正确。
作业题
题1.4 直接写出下面函数的对偶函数和反函数。 应用对偶定理,应注意保持运算的优先级别不变。 应用反演定理应注意1.保持运算的优先级别:2.大非号。
(1)Y=((AB'+C)D+E)C YD=((A+B')C+D)E+C
(2)Y=AB+(A'+C)(C+D'E) YD=(A+B)(A'C+C(D'+E)) Y'=(A'+B')(AC'+C'(D+E')) (3)Y=A+(B+C'+(D+E)')' YD=A(BC'(DE)')' YD=ABC+A'+B'+C' Y'=A' (B'C(D'E')')' Y'=A'B'C'+A+B+C
0 1 1
1 1 1 1 1 1
1 1
0 1 1 0 0 1 1 1 1 0 0 0
11
10
1 0 0 1
1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1
0
0 1 0 1 1 0
Y=A'B'C'D+A'B'CD'+A'BC'D'+A'BCD +AB'C'D’+AB'CD+ABC'D+ABCD'
