大学物理第三章课件
合集下载
大学物理第三章刚体和流体运动
2
返回
退出
对刚体内各个质点的相应式子，相加得：
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力，对同一转轴的力矩之和为零，则：
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑： 联立方程，可解得 T1 ，T2，a， 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R，质量为m匀质圆盘，平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ，令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转，问它 经过多少时间才停止转动？ 解： 把圆盘分成许多环形 质元，每个质元的质量 dm=rddre ， e 是 盘 的 厚 度，质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为：
刚体定轴转动的动能定理：总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点，刚体和地 球系统的重力势能：
z
i
O
返回
退出
例3-5 一质量为m ，长为 l 的均质细杆，转轴在O点， 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动，求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
返回
退出
对刚体内各个质点的相应式子，相加得：
F r sin f
i i i i i
i i
r sin i ( mi ri )
2 i
对于成对的内力，对同一转轴的力矩之和为零，则：
f
i
i
ri sin i 0
2 i i i
F r sin ( m r
r
问题中包括平动和转动。
T1 m1 g m1a m2 g T2 m2a T2 r T1r M r J
轮不打滑： 联立方程，可解得 T1 ，T2，a， 。
此装置称阿特伍德机——可用于测量重力加速度 g
返回
退出
例3-4 一半径为R，质量为m匀质圆盘，平放在粗糙的 水平桌面上。设盘与桌面间摩擦系数为 ，令圆盘最 初以角速度0 绕通过中心且垂直盘面的轴旋转，问它 经过多少时间才停止转动？ 解： 把圆盘分成许多环形 质元，每个质元的质量 dm=rddre ， e 是 盘 的 厚 度，质元所受到的阻力矩 为 rdmg 。 圆盘所受阻力矩为：
刚体定轴转动的动能定理：总外力矩对刚体所做的功 等于刚体转动动能的增量。
返回
退出
四、刚体的重力势能 以地面为势能零点，刚体和地 球系统的重力势能：
z
i
O
返回
退出
例3-5 一质量为m ，长为 l 的均质细杆，转轴在O点， 距A端 l/3 。今使棒从静止开始由水平位置绕O点转 动，求(1)水平位置的角速度和角加速度。(2)垂直位 置时的角速度和角加速度。
第三章 刚体和流体的运动
§3-1 刚体模型及其运动 §3-2 力矩 转动惯量 定轴转动定律 §3-3 定轴转动中的功能关系
大学物理静电场3(电势)ppt课件
最新课件
9
单个点电荷的场的电势 U q
2）电势叠加原理（标量叠加）
q
Up Edl
Eidl
1
4
0r r1 r2
p
p
P Ei dl
qi
q2
4 0ri
或对连续分布带电体
U p
dq
4 0r
q
最新课件
dq
r
p
r3
ri
q3
qi
p
Up=?
10
Ua
i
qi
40ri
一个点电荷系的电场中,任一点的电势等于每一个点电 荷单独存在时在该点所产生电势的代数和。——电势 叠加原理
电势叠加原理 习题最指新课导件 P65 16
34
形状如图所示的绝缘细线，其上均匀分布着
正电荷。已知电荷线密度为λ，两段直线长 均为a，半圆环的半径为a。求环心O点的电 势？
电势叠加原理
求电势能和电力
习题指导P65 17
最新课件
35
３．有一边长为a的正方形平面，在其中垂线上距 中心O点a/2处，有一电量为q的正点电荷，如图所 示，则通过该平面的电场强度通量为：
b
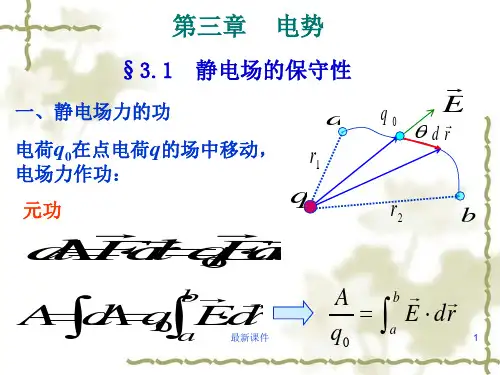
W a W bA a bq 0 aE d r
二、电势差：
移动单位正电荷从电场中a 点到b点，静电力所做 的功，为静电场中两点的电势差:
U abU aU ba bEdr最 新W 课q 件aW qb 描只述与电电场场的有性关质6
➢某点 (a点) 的电势：
首先设定电势0点（b点）：
Ua
b
Edr
积分与路径无关
最新课件
4
对任何静电场，电场强度的线积分都只取决于起 点和终点的位置而与积分路径无关－－静电场的
大学物理学3ppt课件
0 . 15 10 sin( 30 60 ) F 0 . 15 9 . 8 175 N 0 . 01 sin 60
小球对地面的平均冲力是的反作用力，其大小为175N， 方向与相反，沿法线方向竖直向下。
3.1.2 质点系的动量定理
在研究多个有相互作用的物体的运动情况时，可以把这些 物体作为整体系统来研究，称为物体系。若其中的每一个物体 都能抽象为质点，则该物体系就可以抽象为质点系。在一个由 质点系构成的力学系统中，我们把系统外的物体对系统内各质 点的作用力称为外力；把系统内各质点间的相互作用力称为内 力。 如右图所示，两质点的质量分别为m1和 m2，在t1到t2时间内，除有相互作用的内力 为f12和f21外，它们还分别受到外力F1和F2的 作用，其速度分别从v10和v20变为v1和v2。分 别对两质点应用动量定理，有：
上式为矢量式，它在直角坐标系中的分量式为：
I x Fx dt mv 2 x mv1x
t1 t2
I y Fy dt mv 2 y mv1 y
t1
t2
I z Fz dt mv 2 z mv1z
t1
t2
【例3-1】如下图所示，质量m＝0.15kg的小球以v0＝ 10m/s的速度射向光滑地面，入射角θ1＝30°，然后沿θ2＝ 60°的反射角方向弹出。设碰撞时间Δt＝0.01s，计算小球对 地面的平均冲力。 【解】选小球为研究对象。因地面光 滑，碰撞时小球在水平方向上不受作用力 ，地面对小球的作用力沿法线方向竖直向 上。设地面对小球的平均冲力为 F ，碰后 小球速度为v。建立坐标系如右图所示， 根据质点的动量定理有：
I 0 mv sin mv sin x 2 0 1
I ( F mg ) Δ t mv cos ( mv cos ) y 2 0 1
小球对地面的平均冲力是的反作用力，其大小为175N， 方向与相反，沿法线方向竖直向下。
3.1.2 质点系的动量定理
在研究多个有相互作用的物体的运动情况时，可以把这些 物体作为整体系统来研究，称为物体系。若其中的每一个物体 都能抽象为质点，则该物体系就可以抽象为质点系。在一个由 质点系构成的力学系统中，我们把系统外的物体对系统内各质 点的作用力称为外力；把系统内各质点间的相互作用力称为内 力。 如右图所示，两质点的质量分别为m1和 m2，在t1到t2时间内，除有相互作用的内力 为f12和f21外，它们还分别受到外力F1和F2的 作用，其速度分别从v10和v20变为v1和v2。分 别对两质点应用动量定理，有：
上式为矢量式，它在直角坐标系中的分量式为：
I x Fx dt mv 2 x mv1x
t1 t2
I y Fy dt mv 2 y mv1 y
t1
t2
I z Fz dt mv 2 z mv1z
t1
t2
【例3-1】如下图所示，质量m＝0.15kg的小球以v0＝ 10m/s的速度射向光滑地面，入射角θ1＝30°，然后沿θ2＝ 60°的反射角方向弹出。设碰撞时间Δt＝0.01s，计算小球对 地面的平均冲力。 【解】选小球为研究对象。因地面光 滑，碰撞时小球在水平方向上不受作用力 ，地面对小球的作用力沿法线方向竖直向 上。设地面对小球的平均冲力为 F ，碰后 小球速度为v。建立坐标系如右图所示， 根据质点的动量定理有：
I 0 mv sin mv sin x 2 0 1
I ( F mg ) Δ t mv cos ( mv cos ) y 2 0 1
大学物理课件 第3章 动量 角动量
例 如图所示,一个有四分之一圆弧光滑槽的大物体,质量为 M, 置于 光滑的水平面上。另一质量为m的小物体从圆弧顶点由静止开始下滑。 求当小物体m滑到底时，M滑槽在水平上移动的距离。
解 以 M和 m 为研究对象，其在水平方向不受外力（所受外力都 在竖直方向），故水平方向动量守恒。
设在下滑过程中，m相对于M的滑动速度为m ， M 对地速 度为 M ，并以水平方向右为正，则有
t
问题 结果与m与槽M间是否存在摩擦有关系吗？
3. 质心运动定理
C
mii mc m i 1 质点系的动量 p mc
i 1
m
n
rC
mi ri
n i 1
m
n
i i
质点系的动量等于质点系的质量乘以质心的速度。 注 质点系的动量的两种表达式
n p mii , p mc
pA m j ,
pB mi
y
B
I AB pB pA m (i j )
C
pC m j
o
A
x
I AC pC pA 2m j
质点的动量定理
例 一质量为10kg的物体沿x轴无摩擦地运动，设t=0时，物体 位于原点，速度为零。设物体在力(F=3+4t)N作用下运动了3秒， 求此时它的速度和加速度。 解
3.2
角动量定理 角动量守恒定律
3.2.1 质点的角动量定理及守恒定律
1. 力矩
讨论
力F 对定点O 的力矩 Mo F r F
单位：牛 米（N m）
(1)力矩的大小和方向
所组成的平面，指向是由 180 的角转到 F 时的右手螺旋前进的方向
①方向垂直于 r 和 F o
r 经小于
x 方向： m sin m0 sin 0 y 方向： ( f mg )t m cos m0 cos sin 由第一式 0 sin
大学物理 第3章 刚体力学基础
2 1
Jd
1 2
J22
1 2
J12
2 Md (1 J2 )
1
2
力矩对刚体所做的功，等于刚体转动动能的增量。
例 如图所示，一根质量为m，长为l的均匀细棒OA，可绕固定点O在竖直平 面内转动.今使棒从水平位置开始自由下摆，求棒摆到与水平位置成30°角 时中心点C和端点A的速度.
F
·
F
式中为力F到轴的距离
F
若力的作用线不在转动在平面内，
则只需将力分解为与轴垂直、平行
r
的两个分力即可。
力对固定点的力矩为零的情况：
1、力F等于零， 2、力F的作用线与矢径r共线
（有心力对力心的力矩恒为零）。
力对固定轴的力矩为零的情况：
若力的作用线与轴平行 若力的作用线与轴相交
则力对该轴无力矩作用。
dJ R2dm
考虑到所有质元到转轴的距离均为R，所以细圆环对中心轴的转动惯量为
J dJ R2dm R2 dm mR2
m
m
(2)求质量为m，半径为R的圆盘对中心轴的转动惯量.整个圆盘可以看成许
多半径不同的同心圆环构成.为此，在离转轴的距离为r处取一小圆环，如
图2.36(b)所示，其面积为dS＝2πrdr，设圆盘的面密度(单位面积上的质量)
力矩在x,y,z轴的分量式，称力对轴的矩。例如上面所列
Ｍx , My , Mz , 即为力对Ｘ轴、Ｙ轴、Ｚ轴的矩。 设力Ｆ 的作用线就在Z轴
的转动平面内，作用点到Ｚ
轴的位矢为r，则力对Ｚ轴
的力矩为
M z rF sin
r sin F F rF sin rF
大学物理课课件第3章_刚体的定轴转动
G2 G1
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
（支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统，忽略轴摩擦，脱离驱动力矩后，系 统受合外力矩为零，角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间，系统在
铅直位置，受合外力矩为零，角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体（上某点）的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
(m1-m2)g R(m1+ m2+ m 2) (m1-m2)g R(m1+ m2+ m 2)
a
gt 2
(rad)
两匀直细杆
两者瞬时角加速度之比 转动定律例题五
θ
θ
根据
1 2 1 2
θ θ
1 3 1 3
地面 从等倾角 处静止释放
短杆的角加速度大 且与匀质直杆的质量无关
第3节 机械能守恒定律
用两个对 转的顶浆
（支奴干 CH47)
A、B两轮共轴 A以ωΑ作惯性转动
守恒例题一
两轮啮合后 一起作惯性转动的角速度
ωΑΒ
以A、B为系统，忽略轴摩擦，脱离驱动力矩后，系 统受合外力矩为零，角动量守恒。
初态角动量 末态角动量
得
守恒例题二
木棒 弹
以弹、棒为系统 击入阶段 子弹击入木棒瞬间，系统在
铅直位置，受合外力矩为零，角动量守恒。 该瞬间之始 该瞬间之末 棒 弹 棒
对 质点运动和刚体转动定律
m 1 m 2 和 m 分别应用
及
β
R
T2 T2
m
T1 T1 m1
m1 g – T1 = m1a T2 – m2 g = m2a ( T1 – T2 ) R = Iβ
得 故
a = Rβ
1 I = 2 mR2 常量
β
(m1-m2)g = R(m1+ m2+ m 2) 由
m2
a
定轴转动物理量
1. 角位置
描述刚体（上某点）的位置 刚体定轴转动 的运动方程 刚体
刚体中任 一点
(t+△t) (t) 参考 方向
2. 角位移
大学物理第三章刚体力学PPT课件
精选
7
F is iin fis iin m ir i
两边同乘ri，得
F ir i siin fir i siin m ir i2
上式左边第一项为外力Fi对转轴的力矩，而第二项是 内力fi 对转轴的力矩。对刚体的所有质点都可写出类 似上式的方程，求和得
F ir is ii n fir is ii n ( m ir i 2 )
密度为，则dm=dx，有：
Ox
dx
l
J0r2dm ll2 2x2dx1l32 1 1m 22 l
（2）当转轴通过棒的一端A并与棒垂直时：
JAr2dm0 lx2dx3 l31 3m2l
精选
12
例2 求质量为m、半径为R、厚 为h的均质圆盘对通过盘心并与 盘面垂直的轴的转动惯量。
解：如图所示，将圆盘看成许多薄圆环组成。取任一 半径为r，宽度为dr的薄圆环，它的转动惯量为：
转动惯量与刚体的大小形状、质量分布以及转
轴的位置等有关。
精选
9
一般的情况下刚体质量是连 续分布的，把它分割成无限多个 微小部分，其中质量为dm的小块 到转轴的垂直距离为r，则它对该 转轴的转动惯量为
dJr2dm
r dm
积分得到整个刚体对相应转轴的转动惯量为
J r2dm
精选
10
常见刚体的转动惯量
MF 2dF 2rsin
精选
5
若F位于转动平面内，则上式简化为
MFd Fsri n
力矩是矢量，在定轴转动中， 力矩的方向沿着转轴，其指向 可按右手螺旋法则确定：右手 四指由矢径r的方向经小于的 角度转向力F方向时，大拇指的 指向就是力矩的方向。根据矢 量的矢积定义，力矩可表示为：
M rF
大学物理：第三章 理想光学系统
2. 像的大小；
3. 物右移200mm，像移动多大距离？
例：有一光组将物放大3倍，成像在影屏上，当透镜向物 体方向移动18mm时，物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式：
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 （主面间隔）
相应于牛顿公式：
l HA,l H A
由图，有： x l f , x l f
代入牛顿公式，得： lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为：
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 （光学间隔）
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为： yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距（后焦距或第二焦距）
f h tgU
说明：
1）对于理想光学系统，不管其结构（r,d,n）如何，只 要知道其焦距值和焦点或主点的位置，其光学性质就确 定了。
2） f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3－2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点：对应像点在像方光轴上无限远处
焦点 像方焦点：对应物点在物方光轴上无限远处
3. 物右移200mm，像移动多大距离？
例：有一光组将物放大3倍，成像在影屏上，当透镜向物 体方向移动18mm时，物象放大率为4倍。求光组焦距。
三、由多个光组组成的理想光学系统
相应于高斯公式：
l2 l1 d1
………
d1 H1H 2
lk …lk1 d k1 （主面间隔）
相应于牛顿公式：
l HA,l H A
由图，有： x l f , x l f
代入牛顿公式，得： lf lf ll
f f 1 l l
n n n n l l f f
放大率公式为：
f f f f l nl
x f x f l n l
x f f f f f x f
x2 x1 1
………
1 F1F2
xk … xk 1 k1 （光学间隔）
光学间隔Δ和主面间隔d 的关系为:
1 d1 f1 f 2
………
k 1 …d k 1 f k1 f k 1
垂轴放大率为： yk y1 y2 yk
y1 y1 y2
yk
1 2 k
四、光学系统的光焦度
f h tgU
象方主点H′到象方焦点F′的距离称为象方 焦距（后焦距或第二焦距）
f h tgU
说明：
1）对于理想光学系统，不管其结构（r,d,n）如何，只 要知道其焦距值和焦点或主点的位置，其光学性质就确 定了。
2） f n n =n′ f f
fn
h ltgU ltgU
x f tgU x f tgU
§ 3－2 理想光学系统的基点、基面
1. 焦点、焦平面 物方焦点：对应像点在像方光轴上无限远处
焦点 像方焦点：对应物点在物方光轴上无限远处
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
dt dt
M d L －角动量定理微分形式 dt
设 t1 t2时间内，刚体角速度由 1 2
t2 M dt L2 d L I 2 I1
t1
L1
－定轴转动的角动量定理积分形式
t2 M dt L2 d L I 2 I1
t1
L1
定轴转动的刚体对轴的角动量的增量等于对同一
转轴合力矩的角冲量（冲量矩）
2
2
A力矩
1 2
I2
1 2
I02
可得
3g L
I 1 mL2 3
例2，劲度系数为k的轻弹簧，一端固定另一端通
过一定滑轮系一质量为m的物体，滑轮半径为R，
转动惯量为I，绳与滑轮无相对滑动，求物体从弹
簧原长时开始(静止)下落到h距离时的速度？
k I,R
解 机械能守恒
m mgh 1 kh2 1 mv 2 1 I 2
度。因为： M一定时I I
如一个外径和质量相同的实心圆柱与 空心圆筒，若 受力和力矩一样，谁转 动得快些呢？
M
I
M
M
刚体定轴转动的转动定律与牛顿定律的对比
转动定律
M
r
F
I M
r 2dm
I
L
M
I
dL
dt
牛顿定律 F
m
F
ma
P
F
mv
dP
dt
例2 一轻绳绕在半径 r =20 cm 的飞轮边缘，在绳端施以F=98 N 的拉力，飞轮的转动惯量 I=0.5 kg·m2，飞轮与转轴间的摩擦
二 转动惯量的计算 1 计算公式
I miri2
i
r 2dm
－质量不连续分布 －质量连续分布
线分布
dl －线分布λ＝m/l dm ds －面分布σ＝m/S
dV －体分布ρ＝m/V
面分布
2 决定 I 的三要素:
体分布
(1)总质量 (2)质量分布 (3)转轴的位置
例1 一质量为 m 、长为 l 的均匀细长棒，求
0
3
例2 圆环绕中心轴旋转的转动惯量
I L R2dm 2πR R2dl
0
0
R2
2πR
dl
2πR3
m
mR 2
0
2πR
例3 圆盘绕中心轴旋转的转动惯量
ds 2π rdr
dm
ds
π
m R2
2π
rdr
2mr R2
dr
I
m r 2dm
0
R 0
2m R2
r 3dr
m 2
R2
dl m
R O
定轴转动定律：绕某定轴转动的刚体，所受
合外力矩在该轴上的分量等于刚体对该轴的
转动惯量与角加速度的乘积。
M I
或
M
I
说明：1）定律是瞬时对应关系；
2）M , I , 应是对同
一轴而言的
Z
F
F
如何求力对轴的力矩呢？ 如图可将力分解为两个
M
Z
r
F
力，只求那个垂直于轴
的力的力矩就可以了。
3）转动定律说明了I是物体转动惯性大小的量
0
O
x
图
解：（1）
m l
,
df gdm gdx
M
dM
xdf
l
0 x gdx
r 900
ds rd
A Fds sin Frd sin
Fr sin d Md
A Md －力矩的功 dA Md
说明
(1) 合力矩的功
A
2 1 i
Mid
i
2 1
M
i
d
i
Ai
(2) 力矩的功就是力的功
(3) 内力矩作功之和为零
力矩的功率： N dA M d M
注意：该定理也适应于刚体的一般运动中转轴通过
质心的运动。
m、I
C
C1
t2 t1
M Cdt
IC2
IC1
m、I
C
vCC2
例：一长为l、质量为m的均匀细杆，可绕轴O轴转 动。桌面与细杆间的滑动摩擦系数为，杆初始转 速为0 ，求：
（1）细杆受的摩擦力矩； （2）从0到停止转动共经历的时间； （3）从0到停止转动共转了多少圈（如图）。
通过棒中心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ，取一距离转轴OO´为
处的质量元 dm dr dI r 2dm r 2dr
I 2 l /2 r 2dr 1 l 3 1 m l2
0
12
12
如转轴过端点垂直于棒 I l r 2dr 1 ml2
刚体的动能：
r i vi mi
M
Ek
n i 1
1 2mi
ri2
2
1 2
(
n i 1
mi ri2
)
2
质量连续分布 mi 0
Ek
lim
mi 0 n
n i 1
12miri2 2
r i vi mi
M
1 ( r 2dm) 2 1 I 2
2
2
Ek
1 I 2
2
令I r 2dm
I－转动惯量（rotational inertia）
解：I A I杆 I球
ω
I杆
1 3
ml
2
A m, ι
m,R
由平行轴定理：
I球A I球O m( R l )2
I 球O
2 mR 2 5
IA
1 3
ml
2
2 5
mR 2
m( R
l )2
§3-3 力矩 转动定律
一、力矩
F
φ
rp
力矩： M rF sin
矢量式：
M
r
F
单位：米.牛顿
说明： 1）力
受力：mg，N（不产生 对轴的力矩）
建立OXYZ坐标系 A
建立OXYZ坐标系（并以Z轴为转动量的正方向）
N
Y
M
Z
L
M mg L sin
XO
r
2
I
1
mL2
(1)
3
mg M mg sin 3g sin
I
1 mL2 2L
3
r F沿Z轴正向，
0则 0 / 2则 3g / 2L
三、刚体转动动能定理
力矩的功定义 dA Md Id
I d d Id
dt
A 2 Md 2 Id
1
1
2
1
Md
1 2
I
2 2
1 2
I12
此称刚体转动 的动能定理
定轴转动刚体的动能定理：合外力矩对绕定轴 转动的刚体所作的功等于刚体转动动能的增量 .
四、刚体转动时的机械能守恒定律
机械能：
E机械
第一定律：一个定轴转动的刚体，当它所受的 合外力矩（对该转轴而言）等于零时，它将保 持原有的转动状态不变即原来静止的仍然静止， 原来转动的则仍保持原来的角速度转动。
第二定律：一个定轴转动的刚体，当它所受的 合外力矩（对该转轴而言）不等于零时，它将 获得角加速度，角加速度的方向与合外力矩的 方向相同；角加速度α的量值与合外力矩M的 量值成正比，并与转动惯量I成反比 .
2
2
2
h
v R
解之，可得
2mgh kh2
v
m I R2
3－5 角动量守恒定律
力的时间累积效应
冲量、动量、动量定理.
力矩的时间累积效应 冲量矩、角动量、角动量定理.
一、角动量
L
r
P
r mv rmr r 2m I
二、定轴转动的角动量定理积分形式
Z
MZ
F
M I I d d(I)
不计， (见图) 求 (1) 飞轮的角加速度
(2) 如以重量P =98 N的物体挂在绳端， 试计算飞轮的角加速
rO T
解 (1) Fr I Fr 98 0.2 39.2 rad/s 2
(2) mg T ma
Tr I
I 0.5
I
mgr mr 2
两者区别
F mg
a r
98 0.2 0.5 10 0.22
mghC
1 2
mvC2
1 2
Ic 2
若刚体系统 A外＋ A非保守＝0 ，则刚体的机械
能守恒E1＝E2。
例1 设一细杆的质量为m，长为L，一端支以枢 轴而能自由旋转，设此杆自水平静止释放。求：
当杆过铅直位置时的角加速度、角速度以及 此时A和C点的线速度量值。
N YZ
L
解(一)
XO
C
mg
1）以杆为研究对象
例1: 一均匀细杆，在平面内以角速度ω转动，
求M摩擦力。 ω
解 力是连续的
dm
r F dr
所以
M合 rdF
r 其中：
dF gdm g m dr
l
M合
rdF l mg 1rdr 1 mgl
0
l
2
二、转动定律
要揭示转动惯量的物理意义，实际上是要找到一个 类似于牛顿定律的规律——转动定律。
dt dt
当输出功率一定时,力矩与角速度成反比。
二、转动动能
Ek
n i 1
1 2
Δmiri
2ω2
1 2
(
n i 1
Δmiri
2
)ω2
1 2
Iω2
刚体绕定轴转动时转动动能等于刚体的转动惯量与角 速度平方乘积的一半。