佳鑫诺专接本数学教案资料规范标准答案
2022佳鑫诺专升本专业课模拟卷答案

2022佳鑫诺专升本专业课模拟卷答案1、下列对有关名著的说明,不正确的一项是( ) [单选题] *A.宝玉神志不清,贾府决定给宝玉娶亲冲喜。
袭人得知是宝钗要做宝二奶奶,怕宝玉承受不了,便把宝玉和黛玉交往的情形告诉了王夫人。
贾府感到为难,王熙凤献了个掉包儿计,在贾府公开宣扬宝玉要娶黛玉。
洞房之夜宝玉虽然不太高兴,但婚后身体还是逐渐恢复过来。
(正确答案)B.《红楼梦》是一部百科全书式的长篇小说,它以一个贵族家庭为中心展开了一幅广阔的社会历史图景,社会的各阶级和阶层都得到了生动的描写。
C.《红楼梦》中别号“蕉下客”的贾探春是个大气、具有男子性格的女性,她发起组织了大观园里的诗社活动,但是“才自精明志自高,生于末世运偏消”,她想用“兴利除弊”的微小改革来挽回这个封建大家庭的颓势,却注定无济于事。
D.“花谢花飞花满天,红消香断有谁怜?一朝春尽红颜老,花落人亡两不知”这首诗出自《红楼梦》中林黛玉的《葬花词》。
2、1四大文学体裁是指小说、诗歌、散文、戏剧。
[判断题] *对(正确答案)错3、36. 对下列病句的病因解说,不正确的一项是()[单选题] *A.能否激发同学们的学习兴趣是提高同学们成绩的有效途径。
(两面对一面,搭配不当)B.经过全校师生共同努力,使我校环境卫生状况有了很大改变。
(成分残缺,缺少主语)C.每年全国青少年科技创新大赛有超过1000万名左右的青少年参加。
(句式杂糅)(正确答案)D.春节回到家乡,我又看到了母亲那亲切的笑容和久违的乡音。
(动宾搭配不当)4、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、稀疏(shū) 旋律(lǜ)羞涩(sè)B、酣睡(hāng)波痕(héng)宛然(wǎng)(正确答案)C、明珠(zhū) 薄雾(wù)蝉鸣(míng)D、脉脉(mò)牵涉(shè) 逾越(yuè)5、下列词语中,加着重号字的注音正确的一项是()[单选题] *A、细腻(nì)硝烟(xiāo)凫水(niǎo)B、撅着嘴(juē)打点(dian)脱缰(jiāng)(正确答案)C、菱角(líng)虾篓(lǒu)苇眉(wéi)D、吮指头(sǔn)嘱咐(zhǔ)白洋淀(diàn)6、下列选项中加着重号字读音与其它三项不相同的一项是()[单选题] *A、嗜好(正确答案)B、麻痹C、刚愎自用D、包庇7、下列词语中,加着重号字的注音不正确的一项是()[单选题] *A、爱而不见(xiàn)B、搔首踟蹰(zhī)(正确答案)C、静女其娈(luán)D、彤管有炜(wěi)8、1《致橡树》的作者是舒婷,中国当代朦胧诗派的代表诗人之一。
(完整word版)年佳鑫诺专接本点睛班数学精选100题

2013年专接本点睛班数学精选100题一、选择题1.某公交车站每个整点的的第10分钟、30分钟、50分钟有公交车通过,一乘客在早八点的第x 分钟到达该公交车站,则他的等待时间T 是x 的( )。
A. 连续函数B. 非连续函数C. 单增函数D. 单减函数 2.设函数()f x 在(,)-∞+∞内有定义,下列函数必为偶函数的是( ) A .()y f x = B. ()y f x =- C. ()y f x =-- D. 2()y f x = 3. 下列各函数是同一函数的是( )A .2B .x 与sin(arcsin )x ;C .2ln x 与2ln x ; D .1ln 2x e -4.设10()10u u f u u u +<⎧=⎨-≥⎩,()lg u x x ϕ==,则()10f ϕ=⎡⎤⎣⎦( ) A .1- B. 0 C. 1 D. 2 5.下列函数在0x =处有极限的是( )A.00()10x f x x =⎧=⎨≠⎩B. 110()01x x f x x x --<≤⎧=⎨<<⎩C.1()f x x =D. 10()0x x f x xx ->⎧=⎨≤⎩ 6.函数()y f x =在点0x 处左、右极限都存在是它在该点有极限的( ) A.充分条件 B.必要条件 C.充要条件 D.无关条件 7. 下列等式正确的是( ).A.01lim 1xx e x →⎛⎫+= ⎪⎝⎭; B.10lim2x x →=∞; C. sin lim1x x x →∞=; D. 1sin(1)lim 11x x x →-=-.8. 当0x →时,2sin x x -是x 的( ).A.高阶无穷小;B. 低阶无穷小;C.同阶非等价无穷小;D.等价无穷小9.设001()01ln(1)1xx e x f x x x e x x <⎧⎪--⎪=<≤⎨⎪+->⎪⎩,则()f x 的间断点的个数为( ) A. 0 B. 1 C. 2 D. 3 10.设()f x 在(,)-∞+∞内有定义,且lim ()x f x a →∞=,1()0()00f x g x x x ⎧≠⎪=⎨⎪=⎩则( )A.0x =必是()g x 的第一类间断点B. 0x =必是()g x 的第二类间断点C.0x =必是()g x 的连续点D.()g x 在0x =处的连续性与a 的值有关 11.设()f x 是不恒等于0的奇函数,且(0)f '存在,则0x =是()()f x g x x=的( ). A.跳跃间断点; B.可去间断点; C.第二类间断点; D.连续点.12.设函数0()sin 0ax e x f x b x x ⎧<=⎨+≥⎩在0x =处可导,则( )A. 1,0a b ==B. 2,2a b ==C. 1,1a b ==D. 1,2a b == 13.设()f x y e =,()f x 二阶可导,则y ''=( ) A. ()f x e B. ()()f x e f x '' C. []()()()f x e f x f x '''+ D. []{}2()()()f x e f x f x '''+14.设函数()y f x =在1x =点可导,1(1)2f '=,则当0x ∆→时 A.1x dy=是比x ∆低阶的无穷小 B. 1x dy =是比x ∆高阶的无穷小 C. 1x dy=与x ∆是等价无穷小 D. 1x dy=与x ∆是同阶非等价无穷小15. 曲线()21()12x f x x -=-- ( )A.既没有水平渐近线也没有垂直渐近线;B. 有水平渐近线没有垂直渐近线; B.没有水平渐近线有垂直渐近线; D. 既有水平渐近线也有垂直渐近线 16.设()f x 为可导的奇函数,则()f x '( )A.是奇函数B.是偶函数C.是非奇非偶函数D.既是奇函数又是偶函数17.点0x =是11,01()0,01sin ,0x x e f x x x x x ⎧<⎪⎪+⎪==⎨⎪⎪>⎪⎩的( ).A.跳跃间断点;B.可去间断点;C.第二类间断点;D.连续点. 18.下列函数在区间[]1,1-上满足罗尔定理条件的是( ) A. ()x f x e = B. 21()1f x x =-C. ()ln f x x= D. 2()1f x x =-19.设函数()(1)(2)(3)f x x x x x =---,则方程()0f x '=( ) A.无实根 B.有一个实根 C. 有两个实根 D. 有三个实根 20. 3()2f x x x =+在[0,1]上满足Lagrange 定理的条件,则定理中的ξ=( ) AB.D.21. 设函数321sin ,0()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩,则()f x 在0x =处的性质是( ). A.连续且可导; B.连续但不可导; C.既不连续也不可导; D.可导但不连续.22.设函数42()25f x x x =-+,则(0)f 是()f x 在[2,2]-上的( ).A . 极大值B .极小值C .最大值D .最小值23.设()()f x dx F x C =+⎰,则2(cot )sin f x dx x=⎰( ). A. (cot )F x C + B. (cot )F x C -+C. (sin )F x C +D. (sin )F x C -+ 24.下列广义积分收敛的是( )A .0x e dx +∞⎰; B .1ln edx x x +∞⎰; C.1+∞⎰ ; D .321x dx +∞-⎰25. 直线34273x y z++==--与平面4223x y z --=的关系是( ). A. 垂直 B. 相交但不垂直 C. 直线在平面上 D. 平行26.对于正项级数1n n b ∞=∑,其部分和数列{}n s 有界是其收敛的 .A. 必要条件;B. 充分条件;C. 充分必要条件;D. 既非充分又非必要条件。
2012佳鑫诺数学教材习题参考答案

专接本答案i第一章练习题1.1.11.(1)[-3,3]; (2)[1,3]; (3)(),a a εε-+; (4)()(),55,-∞+∞ ; (5)),2()4,(+∞--∞2.(1)33x <-<; (2)40x <<且2x ≠3. ()()(),02,33,-∞+∞练习题1.1.21.(1)不是;提示:定义域不同。
(2)不是;提示:定义域不同。
(3)不是;提示:对应规则不同。
(4)是.2. 2, 0,232x x ++,2x x -. 3. 0, 1, 1,0,0,21)(<≥⎩⎨⎧-=--a a a a f a4.(1)],0()0,2(+∞- ;提示:解不等式组⎩⎨⎧≠>+002x x .(2)]1,1(-;提示:解不等式组101xx -≥+,即1010x x -≥⎧⎨+>⎩或1010x x -≤⎧⎨+<⎩. (3)]2,1[-;(4)(1,(5)[-(6)[-5.(1)[-(2)41[6. (1f x -7.(1)y (2)y (3)y 8.(1) y = (2) y =定义域为[]1,1-.练习题1.1.31.(1)非奇非偶函数; (2)偶函数; (3)奇函数; (4)奇函数; (5)非奇非偶函数; (6)偶函数.2. 证明略。
提示:(1)令()F x =)(x f +()f x -;(2)令()F x =)(x f -()f x -3.0)1(=f .提示:令1x =-,代入)()2(x f x f =+.练习题1.1.41.(1)是由u e y =,15+=x u 复合而成; (2)是由2u y =,23-=x u 复合而成; (3)是由2u y =,x u tan =复合而成; (4)是由u y = x y ln 21=复合而成; (5)是由331u y =,v u ln =,)1(2-=x v 复合而成; (6)是由u y arcsin =,vu 1=21-=v,12+=x v 复合而成.2.(1)(x x f 2)(+=3. ()x ϕarcsin(1=练习题1.1.51. 222VS r rπ=+2. Q C 150)(+=3.R =2122P P -.一、单项选择题1.B ;2.C ;6.D ; 7.C ;二、填空题1.(0,1]; 4. 3log (1)y x =+三、计算题1. -3;4. 1,1010⎡⎤⎢⎥⎣⎦; 5. ; 6. 020001(2000)2000250020125(2500)25004000103175(4000)40007000201625(7000)70005x x x y x x x x x x ⎧⎪≤⎪⎪-<≤⎪⎪⎪=+-<≤⎨⎪⎪+-<≤⎪⎪⎪+->⎪⎩习题1.21.(1)收敛, 极限值为1; (2)收敛, 极限值为0; (3) 收敛极限值为0; (4)不收敛; (5)不收敛。
(完整版)高职专升本第一章函数极限与连续习题及答案

(完整版)高职专升本第一章函数极限与连续习题及答案高等数学习题集第一章函数极限与连续一.选择题1.若函数)(x f 的定义域为[0,1],则函数)(ln x f 的定义域是( B )。
A [0,1]B [1,e]C [0,e]D (1,e)2.设xx f 11)(+=,则)]([x f f =( A )。
(2002-03电大试题) A.x x ++11 B.x x +1 C.x ++111 D.x+11。
3.设)(x f =e 2x ,则函数)()()(x f x f x F -+=是( B )。
A 奇函数;B 偶函数;C 既是奇函数又是偶函数;D 非奇非偶函数。
4.下列说法错误的是( D )。
A y=2x 与y=|x|表示同一函数;B x x f 3sin 21)(=是有界函数; C x x x f +=cos )(不是周期函数; D 12+=x y 在(-∞,+∞)内是单调函数。
5.下列函数中非奇非偶的函数是( D )。
A ||lg )(x x f =;B 2)(xx e e x f --=; C x x x f sin )(+=; D ||)(x x x f -=。
6.下列函数中( A )是基本初等函数。
A x x f 2=)(;B x x f 2=)(;C 2)(+=x x f ;D x x x f +=2)(。
7.函数( A )是初等函数: A x x y arccos 12-=;B =≠--=.1,0,1,112x x x x y C xx y ln )ln(-=;D ΛΛ+++++=+12421n y 8.“数列{x n }的极限存在”是“数列{x n }有界”的( A )。
A 充分但非必要条件;B 必要但非充分条件;C 充分必要条件;D 既非充分亦非必要条件。
9.∞→x lim 5x 的值是( D )。
A +∞; B -∞; C 0; D 不存在。
10.+∞→x lim e -x 的值是( A )。
专升本高等数学的教材答案

专升本高等数学的教材答案本文为《专升本高等数学的教材答案》。
第一章:导数与微分1. 计算下列函数的导数:a) f(x) = 3x^2 + 2x - 1b) g(x) = sin(x) + cos(x)c) h(x) = ln(x^2 + 1)2. 求下列函数在给定点处的导数:a) f(x) = x^3 - 2x^2 + x, 求 f'(2) 的值b) g(x) = e^x + 2x, 求 g'(0) 的值c) h(x) = tan(x) - 2sin(x), 求h'(π/4) 的值3. 证明下列函数具有一阶导数:a) f(x) = x^2 - 2x + 1b) g(x) = √(x + 1)第二章:积分与不定积分1. 计算下列函数的不定积分:a) ∫(3x^2 + 2x - 1) dxb) ∫(sin(x) + cos(x)) dxc) ∫(ln(x^2 + 1)) dx2. 求下列函数在给定区间上的定积分:a) ∫[0, 2] (x^3 - 2x^2 + x) dxb) ∫[0, π] (e^x + 2x) dxc) ∫[0, π/2] (tan(x) - 2sin(x)) dx3. 利用定积分计算下列求和:a) ∑[k=1, 5] (2k + 1)b) ∑[k=1, 6] (k^2 + 3k)c) ∑[k=1, 10] (√k)第三章:微分方程1. 解下列微分方程:a) dy/dx = 2xb) dy/dx + y = e^xc) d^2y/dx^2 + 4y = 02. 求解给定初值条件的初值问题:a) dy/dx = x^2, y(0) = 1b) dy/dx = e^x - y, y(0) = 0c) d^2y/dx^2 + 4y = 0, y(0) = 1, y'(0) = 23. 求解下列二阶齐次常系数线性微分方程:a) d^2y/dx^2 + 4dy/dx + 4y = 0b) d^2y/dx^2 - dy/dx - 2y = 0c) d^2y/dx^2 + 9y = 0第四章:级数1. 判断下列级数的敛散性:a) ∑(1/n^2), n从1到∞b) ∑(n/2^n), n从1到∞c) ∑(1/n!), n从1到∞2. 计算下列级数的和:a) ∑(1/2^n), n从1到∞b) ∑(n/(n^2 + 1)), n从1到∞c) ∑(1/(3^n + 2)), n从1到∞3. 判断下列幂级数的收敛半径:a) ∑(x^n/n), n从1到∞b) ∑((x-1)^n/n), n从1到∞c) ∑(n!(x-2)^n), n从1到∞第五章:多元函数与偏导数1. 计算下列函数的偏导数:a) f(x, y) = x^2y - xy^2b) g(x, y) = sin(x)cos(y)c) h(x, y) = ln(x^2 + y^2)2. 求下列函数在给定点处的偏导数:a) f(x, y) = 3x^2y - 2xy^2, 求∂f/∂x (1, 2) 的值b) g(x, y) = e^xsin(y), 求∂g/∂y (0, π/4) 的值c) h(x, y) = x^2 + y^2 + 2xy, 求∂h/∂y (2, 3) 的值3. 计算下列函数的二阶偏导数:a) f(x, y) = x^3y - 2x^2y^2 + xy^3b) g(x, y) = cos(xy) + sin(x^2)c) h(x, y) = ln(x^2 + y^2)最后总结:通过本套教材答案,你可以系统地学习和掌握专升本高等数学的重要知识点,包括导数与微分、积分与不定积分、微分方程、级数以及多元函数与偏导数。
佳鑫诺专接本会计全真模拟试卷会计答案

佳鑫诺专接本会计全真模拟试卷会计答案一、单项选择题1.下列项目中,应计入企业存货成本的是( )。
A.非正常消耗的轻易材料、轻易人工和制造费用B.为建造固定资产而储备的各种材料C.拒绝接受来料加工的原材料D.经过加工已经完工入库的来料加工代制品2.以下项目中,不应当所列在企业资产负债表“存货”项目的就是( )。
A.房地产开发企业购入的用于建造商品房的土地使用权B.企业订货用作广告营销活动的特定商品C.已经取得商品所有权,但尚未验收入库的在途物资D.已经发货但存货的风险和报酬未迁移给购货方的收到商品3.永华公司属于工业企业,为增值税一般纳税人,适用的增值税税率为17%。
年9月2日,购入D材料一批,取得的增值税专用发票上注明价款600万元,增值税税额102万元。
另支付运输费用32.26万元,取得运输单位开具的运输发票(运费的7%可作为增值税的进项税额抵扣)。
9月20日,E产品生产过程中领用了全部的D材料,另发生加工费100万元,其他为生产产品而发生的费用30万元,其中,发生超定额废品损失4万元。
E产品当月加工完毕,并验收入库。
则E产品的入账价值为( )万元。
A.756B.762C.760D.7644.甲公司为增值税一般纳税人,适用的增值税税率为17%。
年12月20日,发出D产品一批,委托长城公司以收取手续费方式代销,该批产品的成本为万元。
长城公司按照D产品销售价格的5%收取手续费,并在应付甲公司的款项中扣除。
12月31日,甲公司收到长城公司的代销清单,代销清单载明长城公司已销售D产品的40%,销售价格为500万元。
甲公司尚未收到上述款项,年12月31日甲公司应收长城公司账款的账面价值为( )万元。
A.475B.560C.190D.2245.某企业属于工业企业,为增值税一般纳税人,适用的增值税税率为17%。
年9月8日,购入A工程物资一批,支付价款万元(含增值税),另支付运杂费40万元。
A工程物资专门用于本企业厂房的建设。
专科大学高等数学教材答案

专科大学高等数学教材答案在这里,我将为您呈现专科大学高等数学教材的答案。
根据您的要求,我将以文章的形式为您提供答案,并尽力确保语句通顺,整洁美观,以方便您的阅读。
答案如下:1. 1. 题目: 数列的概念和性质数列是由一系列按照一定规律排列的数所组成的序列。
数列常常出现在数学问题中,在解决数学难题时,往往需要对数列的性质进行研究和分析。
接下来,我们将分章节介绍数列的基本概念和性质。
1.1 答案:数列的定义数列是由一系列按照一定规律排列的数所组成的有序集合。
数列通常用a₁, a₂, a₃, ...来表示,其中a₁、a₂、a₃代表数列中的第一项、第二项、第三项等。
例如,1, 2, 3, 4就是一个简单的数列。
1.2 答案:数列的数学符号数列可以用数学符号来表示。
常见的表示方法有:- 通项公式:用f(n)表示数列的第n个项。
例如,f(n) = 2n表示数列的第n个项是2n。
- 递推公式:用f(n+1)表示数列的第n+1个项,以及前一项f(n)。
例如,f(n+1) = f(n) + 2表示数列的第n+1个项是前一项加2。
1.3 答案:数列的分类数列可分为等差数列、等比数列和其他特殊数列等。
- 等差数列:数列中相邻两项之差相等。
例如,1, 3, 5, 7就是一个等差数列,公差为2。
- 等比数列:数列中相邻两项之比相等。
例如,1, 2, 4, 8就是一个等比数列,公比为2。
1.4 答案:数列的性质数列有许多重要的性质,如有界性、单调性、极限等。
这些性质在数学中具有广泛的应用。
- 有界性:如果一个数列存在上界或下界,那么我们说这个数列是有界的。
- 单调性:如果一个数列中的项随着n的增加而单调递增或递减,那么我们说这个数列是单调的。
- 极限:数列的极限是指随着项数的增加,数列逐渐趋于某个常数。
极限在微积分中有着重要的地位。
......2. 2. 题目: 函数的图像与性质2.1 答案:函数的定义函数是一种数学映射关系,它将一个集合的每一个元素映射为另一个集合的一个元素。
数值计算课后规范标准答案2
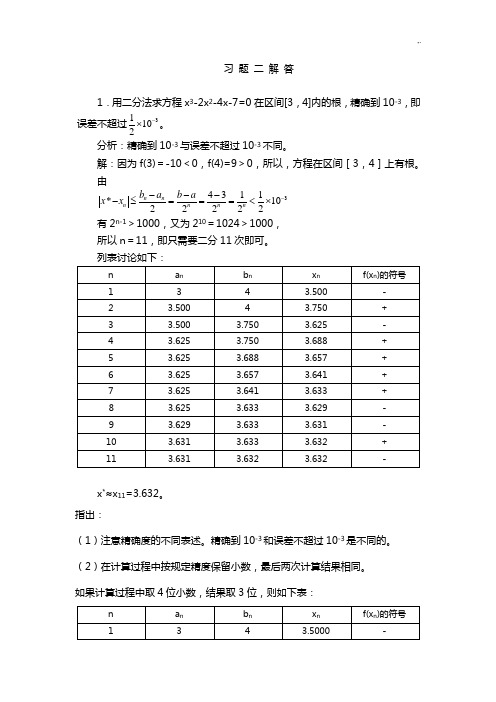
习 题 二 解 答1.用二分法求方程x 3-2x 2-4x-7=0在区间[3,4]内的根,精确到10-3,即误差不超过31102-⨯。
分析:精确到10-3与误差不超过10-3不同。
解:因为f(3)=-10<0,f(4)=9>0,所以,方程在区间[3,4]上有根。
由34311*1022222n n n n n n b a b a x x -----≤===<⨯ 有2n-1>1000,又为210=1024>1000, 所以n =11,即只需要二分11次即可。
x *≈x 11=3.632。
指出:(1)注意精确度的不同表述。
精确到10-3和误差不超过10-3是不同的。
(2)在计算过程中按规定精度保留小数,最后两次计算结果相同。
如果计算过程中取4位小数,结果取3位,则如下表:(3)用秦九韶算法计算f(x n )比较简单。
1*.求方程x 3-2x 2-4x-7=0的隔根区间。
解:令32247y x x x =---, 则2344322()()y x x x x '=--=+-当23443220()()y x x x x '=--=+-=时,有12223,x x =-=。
函数单调区间列表分析如下:因为214902150327(),()y y -=-<=-<,所以方程在区间223(,)-上无根; 因为21490327()y -=-<,而函数在23(,)-∞-上单调增,函数值不可能变号,所以方程在该区间上无根;因为2150()y =-<,函数在(2,+∞)上单调增,所以方程在该区间上最多有一个根,而(3)=-10<0,y(4)=9>0,所以方程在区间(3,4)有一个根。
所以,该方程有一个根,隔根区间是(3.4)。
2.证明1sin 0x x --=在[0,1]内有一个根,使用二分法求误差不大于41102-⨯的根,需要迭代多少次?分析:证明方程在指定区间内有一个根,就是证明相应的函数在指定区间有至少一个零点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题1.11. (2)定义域不同,{X ≠-1};R (3)X =且定义域也不同,{X ≠0};R (4)值域不同[-1,1];[0,1] (5)定义域不同,{X>0};R 2. (4)()()ln lnf x x x -=-=()(()1ln ln lnf x x x x ---=--+=+=故()()f x f x -=-,()f x 为奇函数.(6)()()()()()()f x g x g x g x g x f x -=--=----⎡⎤⎣⎦,奇函数。
3. (1)y=sinx 与y=cosx 的周期都是2π,故y=sinx+cosx 的周期为2π(2)设周期为T,则1+sin2x=1+sin2(x+T) ⇒ sin2x=sin(2x+2T) ⇒2T=2TV ⇒T=TV5.010X X X ≥⎧⎪⇒≥⎨≥⎪⎩6. 2222(sin cos )sin cos 2sin cos 1sin 2y x x x x x x x =+=++=+ 又[]0,2x π∈,故[]1sin 20,2x π+∈,故y的值域为⎡⎣7.令u x =-则x u =-故()()22sin()sin ,0,0()1,01,0u uu u f u f u u uu u u u -⎧⎧-<>⎪⎪-=⇒-=-⎨⎨⎪⎪-+-≥+≤⎩⎩ 故()f x -2sin ,01,0xx x x x ⎧>⎪=⎨⎪+≤⎩8. ()1f x =-是偶函数()()1f x f x -==Q()0f x =是奇函数()()0f x f x ∴-==-9.定义域为0220x x x ≠⎧⇒>⎨->⎩10.(1)22290933101x x x x x ⎧⎧-≥≤⇒⇒-≤≤⎨⎨-≠≠±⎩⎩且1x ≠±(2) .0. 1 (2)x k k ππ≠+=±(3) 111021*******10x x xx x x x x ≤-≤⎧≤≤⎧⎪-⎪⎪<⇒-<<⇒≤<⎨⎨+⎪⎪≠-⎩+≠⎪⎩(4) R12. ()f x Q 的定义域为[-2,2]则21213x x -≤-≤⇒-≤≤故()1y f x =-的定义域为[-1,3] 13.设它的一个边为x =故面积()S x = 0<x<2习题1.2-1.31. 否,例如数列()1nn x =- 2. 否,同上3. 否,例如数列()1nnx n-=5.不一定,例:()1nn x =-,()11n n y +=-,n=1.2.3.4.5……则0n n x y +=6.是7.否,()1nn x =-,lim 1n x x →∞=则lim n x x →∞是不存在的8.否12.cos cos lim lim 1sin sin x x xx x x x xx x x x→∞→∞++==++14.01sinsin lim lim 01x u u x u x→→∞== 15.因为222113lim lim 1112x x a x a x x x x x →→--⎛⎫+== ⎪---⎝⎭,故21lim 02x a x x a →--=⇒= 17. 1lim xx e →不存在110lim 0,lim xxx x e e -+→→==+∞ 18. 2200limlim 0sin 22x x x x x x →→== 222200limlim 1x x x x arctg x x→→== 22200limlim 21cos 2x x x x xx →→==- ()220lim 0ln 2x x x →=+ 20.()()()()()222221111sin 1sin 1sin 1limlim1limlim 12111x x x x x x x x x x x x →→→→---=+=+=---21.(1)123233lim lim 323213nn n n n n n n +→∞→∞⎛⎫+ ⎪+⎝⎭==+⎛⎫+ ⎪⎝⎭(2)1111211111...282222lim lim lim 1151151 (155)445545n nn n n n nn n-→∞→∞→∞-⎛⎫- ⎪⎝⎭+++-===⎛⎫+++-- ⎪⋅⎝⎭(3)原式= 111111111lim1 (2335577)2121n n n →∞⎛⎫-+-+-++- ⎪-+⎝⎭ =()111111lim1lim 221222212n n n n →∞→∞⎛⎫⎛⎫-=-= ⎪ ⎪ ⎪--⎝⎭⎝⎭ (4)原式=()22212122limlim 1122n n n n n n n →∞→∞+-==++ (5) 原式=2224221111lim lim 1111nnn n n e n n e e n n --→∞→∞⎛⎫⎛⎫-- ⎪ ⎪⎝⎭=== ⎪⎛⎫ ⎪++ ⎪⎝⎭⎝⎭(6) 原式= lim 33nn n nx →∞⋅= (7) 原式= 111112224lim 22 (2)lim 22nnn n -→∞→∞⋅==(8) 原式=2252n n n ⎡⎤-⎢⎥==22.(1)原式= 24223342232sin 1sin lim lim sin lim 1001111x x x x x x x x x x x x x-→∞→∞→∞=⋅=⋅=⋅=+++ (2)原式= 088lim 55x x x →= (3)1x →故10x -→又0x →时()11nx +-~ nx即 原式=()11lim1x n x n x →-=-(4)()()()()sin sin limlim 1x x x x x x πππππππ→→-+--==----(5)原式= 121211lim 112xx e x e e x →∞⎛⎫+ ⎪== ⎪ ⎪+⎝⎭ (6)原式= 221x x x ===(7)原式= ()()211220lim 12lim 12xx x x x x e ---→→⎛⎫-=-= ⎪⎝⎭(8)原式= ()001sin 1ln cos cos 1ln cos lim lim 00lim cos lim 1x x xx x x xxxxx x x eeee →→-⋅→→=====23.(1)()1lim lim 211xx x f x --→→=-=- ()0lim lim 1x x xf x tgx++→→== ()()00lim lim x x f x f x -+→→≠故()0lim x f x →不存在. (2)①2200limlim 0x x tgx x xx →→== ②200cos 12lim lim 0x x x x xx →→-==③()00ln 122limlim 2x x x xxx →→+==④2001sin1limlim sin 0x x x x x x x→→==(3) 22lim 01x x ax b x →∞⎛⎫---= ⎪-⎝⎭Q 故()()212lim 01x a x a b x b x →∞⎛⎫-+-+-= ⎪-⎝⎭则10,0a a b -=-=则1a b ==习题1.42.否,例:()()()11,1f x x xg x x =+=+ ()()f x g x x =在01x =-处不间断. 3.否,例:()131f x x x =++ ()11g x x =-+ ()()3g x f x x +=在01x =-处不间断 4.否,例:()x f x x ⎧⎨-⎩ 00x x ≥< 5.否,例:()0f x x ⎧⎨-⎩0112x x ≤<≤≤ 6.否,例:()x f x e = x -∞<<+∞ 7.否,例:()11f x -⎧=⎨⎩ 0112x x ≤≤<≤ 12. ()()()111lim 1lim 10xxx x x x e f k -+-→→-=-=== 13. ()f x 在0x 点连续,则()()()00lim lim x x x x f x f x e f x -→→===14.定义域229032,2340x x x x ⎧-≥⇒-≤<-<≤⎨->⎩故连续区间()()3,22,3-⎡⎤⎣⎦U 15. 1x =-和2x =为间断点,2x =为第二类间断点. 17. 0lim 1x y -→=- 0lim 1x y +→=-故在x=0处不连续. 18. 220001cos 1cos 11lim lim lim sin 1cos 1cos 2x x x x x x x x ---→→→--===-+ 2011lim 22x x +→+= 故001lim lim 2x x y y +-→→== 故在R 上连续 19. 00lim lim 110x x tgx xa a x x--→→===-⇒=01lim sin 11x x b b a b x+→+==-⇒= 20. 定义域为x ≠1,故间断点为x=111lim 12x xarctg x π-→=-- 11lim 12x xarctg x π+→=-21. 证明:令()51xf x x =⋅-,考虑闭区间10,2⎡⎤⎢⎥⎣⎦,()f x 在10,2⎡⎤⎢⎥⎣⎦是连续的。
且()010f =-<,1102f ⎛⎫=-> ⎪⎝⎭由零点存在定理,在10,2⎛⎫ ⎪⎝⎭内至少存在一点ξ使得,()0fξ=即510ξ-=22. 证:令()()F x x f x =-则()F x 在[]0,1上是连续的,且()()()00000F f f =-=-≤ ()()1110F f =-≥由零点存在定理,在()1,0上至少存在一点ξ使得,()0f ξξ-=即得证习题2.11. ()()()()()0000002021limlim 2h h f x h f x f x h f x f x h h ∆→-→+∆---'===∆∆ 2. ()0sin00f -'=-= ()00f a +'==∵可导故在x=0处连续,则()()0lim lim cos 1lim x x x f x x ax b b --+→→→===+=故a=0,b=1. 5.由题意得:()()0003lim0x f x x f x xx∆→+∆--∆=∆()()()()000000limlim 30303x x f x x f x x f x f x x∆→∆→+∆-''⇒-∆=⇒-=⇒=∆ 6. ()211lim lim 12x x f x x --→→=+=()11lim lim 22x x f x x ++→→==故连续 ()0022f x x -'== ()02f x +'=故可导习题2.21. ()()()1ln ln ln y f t t f t t''''==⋅()()()()()()()22111111ln ln ln ln ln ln y f t f t f t f t f t f t t t t t t t'⎛⎫⎛⎫''''''''''=+⋅=⋅+⋅-=-⎡⎤ ⎪ ⎪⎣⎦⎝⎭⎝⎭ 2. 1e y x '=-故切线的斜率为1e x -,又t 与x 轴平行,则100ex x -=⇒=代入11ey x y =-⇒=-则切点为(0,-1)5. 22cos1111112sec cos 1222sin sin cos 2sin cos 2222xx y x x x x x x tg x '=⋅⋅=⋅⋅=== 6.(1)()()()ln ln ln ln ln xxx x x x y x ee===故()()()()ln ln 111ln ln ln ln ln ln ln x x x y ex x x x x x x x ⎛⎫⎡⎤'=⋅+⋅⋅=+ ⎪⎢⎥⎝⎭⎣⎦ (2)()()2sin sin ln121xx x y x e+=+=故()()()()2sin sin ln 12222212cos ln 1sin 21cos ln 1sin 11x x x x y ex x x x x x x x xx +⎛⎫⎡⎤'=⋅⋅++⋅⋅=+⋅++ ⎪⎢⎥++⎝⎭⎣⎦7. (1)()22121211y x arctgx xxarctgx x'=⋅++⋅=++ 21221y arxtgx x x''=+⋅+ (2)212x y e-=⋅ 2122x y e -''=⋅⋅()104y e -''=8.(1)()()()2sec 1y tg x y y x y y ''=+⇒=+⋅+()()()()22222sec 11cos 1sec cos 1sin ()x y y x y x y x y x y +'⇒====-+-++--+(2)1yyyy xe y e xe y ''=+⇒=+⋅1yye y xe '⇒=-9.(1)11dxdx dt dy dy t tdt-===-22231111d x t dx dy t t t dt-⎛⎫=-=⋅= ⎪⎝⎭ (2)32439t ttdx dx e dt e dy dy e dt-===- 22232214143339t t ttd xe e e dx dy e dt-'⎛⎫=-⋅=-⋅= ⎪-⎝⎭10.(1)ln y x x =1ln ln 1y x x x x '=+⋅=+11y x x-''== 2y x -'''=- 32y x -'''=故()()()112!n n n n d y n x dx--=-- (n ≥2) (2) xy xe =x x y e xe '=+ x x x y e e xe ''=++()n x x x nd yne xe e x n dx=+=+ 11. ()22y f xx ''=⋅()()()()2222222242y f x x x f x x f x f x ''''''''=⋅⋅+=+习题2.32. ()()()()2221sin cos 212cos x y x x y x y y x x y ''+=⇒+⋅+=⇒=-+ 故()()()22212cos 12cos cos x x y dy x dx dx x y x y ⎡⎤-+⎢⎥=-=++⎢⎥⎣⎦习题2.42. ()14f -= ()316f = ()41f x x '=-则()()()()()31124411f f f b a ξξξ''--=-⇒=-⇒= 3. ()00f = ()14f = ()212f x x '= 则2214123ξξ=⇒=又[]0,1ξ∈故ξ=习题2.51. ()1111211ln 1ln 1lim lim lim lim 1111ln 1ln 2ln (1)x x x x xx x x x xx x x x x x x x x→→→→-+⎛⎫-====⎪--⎝⎭+-+2. 123000021ln lim lim lim lim 20112x x x x x x x x x++++→→→→-===-=- 3. 1001sin sin lim ln lim ln 00sin lim 1xx x x x xx x x x e ee x ++→→+⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭→⎛⎫==== ⎪⎝⎭习题2.61. 定义域 101x x +>⇒>- 又111y x'=-+ 令00y x '=⇒= 当0x <时0y '<;当0x >时0y '>故在[-1,0]上单调减少,在[0,+∞]上单调增加.2. 22002lim lim 1sin cos 2x x x xx x e e e e x x x--→→+--==⋅ 3. 212ln 2ln y x x x x x xπ'=⋅+⋅=⋅+令00y x '=⇒=或12x e -=又定义域为x ≠0故在12x e-=处有极值当12x e-<时,0y '<. 当12x e ->时,0y '>故为极小值.4. 232y ax bx '=+ 62y ax b ''=+令06206203b y ax b ax b x a''=⇒+=⇒+=⇒=- ∵(1,3)为拐点 ∴13b a -=又293,32a b a b =+⇒=-= 5. (1)定义域为[0,+∞)又110y '=+=+> 故[0,+∞)为单调增区间. (2)2ln 1(ln )x y x -'=令0y x e '=⇒=定义域()()0,11,+∞U 当()0,1x ∈时0y '<;当()0,x e ∈时0y '<,当[,)x e ∈+∞时,0y '>故单调减区间()0,1和()0,e ,单调增区间[,)e +∞6. 344y x x '=-+ 令00y x '=⇒=或1x =± 则当0x =时,0y =为极小值, 当1x =±时,y=1为极大值 7. 11ln x xx y x e==,()11ln 222111ln 1ln x xx y ex x x x x x ⎛⎫⎛⎫=⋅+-=⋅- ⎪ ⎪⎝⎭⎝⎭令0y x e '=⇒=当x<e 时0y '>,当x>e 时0y '< 故x=e 的极大值,为1ee 8. 22ex y xex e --'=-令()0200xy xex x -'=⇒-=⇒=或2x =极小值()00y =,极大值()224y e -= 9. 3416y x x '=-解:0y '=得y 在[-1,3]上的驻点为,10,2x x ==,由于()()()()15,02,214,311y y y y -=-=-= 故最大值()311y =,最小值()214y -. 10. 设矩形的边a.b ,周长为c ,面积为S 则()2,c a b s ab =+= 则2c s a a ⎛⎫=-⎪⎝⎭ 02c a ⎛⎫<< ⎪⎝⎭又22c s a '=- 令0s '=得驻点,4c a =,又S 为可导函数,且最大值一定存在,故当4c a =时S 最大,此时216c s =,此时4ca b ==即为正方形的面积最大11. 设扇形面积为S ,弧长为L ,周长为C则2L rS ⋅=,2C r L =+ 则25022S C r r r r =+=+ (0<r<+∞)又21250C r'=-,令05C r '=⇒=由于C 为可导函数,且只有一个驻点a 和b ,且最小值一定存在,故5r =时,C 取最小值. 12. 设小屋的长和宽分别为a 和b ,面积为S ,则20220,2aa b S ab S a -+==⇒= 又0S '=得a=10故a=10时S 最大,此时b=5. 13. (1)定义域为R.e x y e xe --'=-()2e x x x y e xe e e x ----''=-+-=-令0y ''=得x=2故拐点22,2e -,在(),2-∞凸,在()2,+∞凹(2)定义域R 2121y x x '=⋅+ ()()()22222221222211x x x x y x x +-⋅-''==++ 令0y ''=则1x =±15.(1)定义域为(-∞, +∞)2321y x x '=-- 262y x =-(2)0y '=的根为1x =或者13x =-,0y ''=的根为13x =则与划分为几个区间:1111(,],[,],(,1),[1,)3333-∞--+∞(3)(4)该曲线无水平渐近线与垂直渐近线(5)由127332y ⎛⎫-=⎪⎝⎭,116327y ⎛⎫= ⎪⎝⎭,()10y = (6)故可做出图形(略) 16. 令()2(1)ln 1x f x x x -=-+ ()2212(1)2(1)(1)01(1)x x x f x x x x x +---'=-=>++ (x>0) 故在x>1上,()f x 为单调增,则()()10f x f >=则2(1)ln 01x x x -->+ 习题2.7 1. ()C Q CC aQ b Q Q==++2CC a Q '=-令 0C Q '=⇒=2. ()343151535dQ P P P P dP Q Q P η---=-⋅=--⋅== 3. ()90020C x C x x x==++ 29001C x -'=-+令030C x '=⇒=31800C x -''=则2(30)03C ''=>故30x =时平均成本最小(30)80C =(万元) 4. 设总利润为S则()21610001000499616S y x x x x x x ⎛⎫=-⋅=---⋅=-- ⎪⎝⎭9962S x =-令0498S x '=⇒=,且S '处处存在又20S ''=-<,故498x =时,S 最大习题3.1(一)2.(A )()21cos 2112sin 2(1cos 2)22sin 2222x xdx dx x d x x x c -=⋅=-=-+⎰⎰⎰()11cos 2cos 22sin 222xdx xd x x c ==+⎰⎰ (C )()21cos 22sin 21cos 22x xdx dx x dx -=⋅=-⎰⎰⎰(二)3. 2sec xdx tgx c =+⎰过,24π⎛⎫⎪⎝⎭则 214tg c c π=+⇒=(三)6.()()2221122112122ln x x xdx dx x x dx x x x c x x----+-==+-=--+⎰⎰⎰ 7. 21cos 11sinsin 2222x x dx dx x x c -==-+⎰⎰ 9. ()()222222221221111111x x dx dx arctgx C x x x x x x x ++⎛⎫==-=-++ ⎪+++⎝⎭⎰⎰⎰ 10. ()()()323211111132x x x x x dx dx x x dx x x C x x +--==-=-+++⎰⎰⎰11.(22212x x dx x C ==-=+⎰12. 222222221122222111x x x dx dx dx x arctgx C x x x +++-⎛⎫==-=-+ ⎪+++⎝⎭⎰⎰⎰ 13. 3222222cos cos 1sin 11sin sin 1sin sin sin sin sin sin sin x x x dx d x d x d x x C x x x x x -⎛⎫===-=--+ ⎪⎝⎭⎰⎰⎰⎰ 14.2222cos 24cos 222sin 2sin cos sin 2sin 2sin 2x x dx dx d x C x x x x x===-+⎰⎰⎰ 15. 2222221cos 1cos 1cos sin 1cos 21cos sin 2s x x x dx dx d x x x x co x +++==++-⎰⎰⎰ 22111111sec 2cos 22222dx x dx tgx C x ⎛⎫⎛⎫=+=+=++ ⎪ ⎪⎝⎭⎝⎭⎰⎰ 16. 2135225235333ln 2ln33xx xx dx dx x C +⎛⎫-⋅⎛⎫⎛⎫=-⋅=-⋅+ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎰⎰ 17.4444x x x edx e dx e C ---=-=+⎰⎰(一)1. ()()()2222211d x x d x x d x +=++=+2. 211darctgx dx x =+ 211darcctgx dx darctgx darcctgx x=-⇒=-+(二)3. 10210111sec 11tg x xdx tg xdtgx tg x C ==+⎰⎰4.11ln ln ln ln ln ln ln ln ln ln dx d x x C x x x x x ==+⎰⎰5. 221111x x x xx x x e dx dx de arctge c e e e e -===++++⎰⎰⎰ 6.()22444sin cos sin 111sin sin sin 1sin 1sin 21sin 2x x x dx d x d x arctg x C x x x ==⋅=++++⎰⎰⎰ 7. ()()233sin cos sin cos2d x x x x C =-=-+ 8. ()()32222222222211991ln 9929292229x x x x dx dx dx dx x C x x x x ⎛⎫==⋅=-=-++ ⎪++++⎝⎭⎰⎰⎰⎰ 9.22212ln 4242dx dx x C x x x -=-=-+--+⎰⎰10. ()()()()()()332226626322111ln ln 4362444344dx dx dx dt t t C x x x x x x x t t====-++++⋅⋅++⋅⎰⎰⎰⎰ 则()6661ln 2444dx x C x x x =+++⎰ 11. 2222cos cos cos sin cos 2cos sin sin 2222222x x x x x x x x dx dx d ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰ 224212sin sin 2sin sin 22232x x x xd C ⎛⎫=-=-+ ⎪⎝⎭⎰ 12. ()22322232sin 111sec sec 11cos cos 3x tg x xdx tg xd x d t dt t dt t t C x x t ⎛⎫⎛⎫===-=-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰⎰ 则 331sec sec sec 3tg x xdx x x C =-+⎰13.()22arctan 122arctan arctan 2arctan 12t dt td t t C t ===⋅++⎰⎰则(2C =+14.()()()()()()2221ln 1ln 11ln ln ln ln 1ln ln ln xxdx d x x d x x C x xx x x x x x x ++===-++⎰⎰⎰16.()112211C x ===+⎰⎰17.()2212ln 1C ⎛====+ ⎝⎰18.22222=-=-+2arcsin x a C a ⎛⎫=-+ ⎪⎝⎭⎰22arcsin x a C a ⎛⎫=-++ ⎪⎝⎭则22arcsin 2a x C a ⎛⎫= ⎪⎝⎭19.sec tan sec tan d d C θθθθθθθ===+⎰⎰又1arccos xθ=故1arccos C x =+20.23sec cos sin sec d d C θθθθθθ===+⎰⎰ 又tan x θ=则 2222222111sin 1cos 111sec tan 111x x x θθθθ=-=-=-=-=+++ 则sin θ=则C =21. 令 2sin x t = 则cos2x=1-2t 2tan 1t x t =- 则 ()121tf t t t'=-+- 则()121tf t t t'=-+- 1.sin cos cos cos cos sin x xdx xd x x x xdx x x x C =-=-+=-++⎰⎰⎰2. sin arcsin arcsin arcsin arcsin arc xdx x x xd x x x x x C =⋅-=⋅-=+⎰⎰3.xx x x x x xedx xde x e e dx x e e C ------=-=-⋅+=-⋅-+⎰⎰⎰4. 3333321ln ln ln ln ln 33333x x x x x x xdx xd x d x x dx x ==⋅-=-⋅⎰⎰⎰⎰3333111ln ln 33339x x x x C x x C =-⋅+=-+ 5.cos cos cos cos cos sin x x x x x xe xdx xde e x e d x e x e xdx ------=-=-⋅+=-⋅-⋅⎰⎰⎰⎰()cos sin sin sin cos x x x x x e x xde e x e x e xdx C -----=-⋅--=-⋅+⋅-⋅+⎰⎰()1cos sin cos 2x x e xdx e x x C --⇒⋅=-+⎰6.()()222tan sec 1sec x xdx x dx x x x dx ⋅=⋅-=-⎰⎰⎰2tan tan tan 2x xd x xdx x x xdx C =-=⋅--+⎰⎰⎰2tan ln cos 2x x x x C =⋅+-+7.()()()()22221ln ln ln ln 2ln x dx x x xd x x x x x dx x=⋅-=⋅-⋅⋅⎰⎰⎰()()22ln 2ln ln 2ln 2ln x x xdx x x x x xd x =⋅-=⋅-⋅+⎰⎰()()221ln 2ln 2ln 2ln 2x x x x x dx x x x x x C x=⋅-⋅+⋅=⋅-⋅++⎰8. 1111sin cos sin 2cos 2cos 2cos 22444x x xdx x xdx xd x x x xdx ==-=-⋅+⎰⎰⎰⎰1111cos 2cos 22cos 2sin 24848x x xd x x x x C =-⋅+=-⋅++⎰9. ()()()()()()3333322ln ln ln 1111ln ln 3ln x x x dx x d d x x dx x x x x xx x =-=---=-+⋅⋅⎰⎰⎰⎰()()()()33222ln ln 113ln 3ln x x x dx x d xx x x=-+⋅=-+-⎰⎰ ()()()()()333222ln ln ln 3ln 12ln 3ln 3x x x x x d x dx xx x x x x ⎛⎫=-+-+=--+ ⎪ ⎪⎝⎭⎰⎰ ()()()()3232ln 3ln ln 3ln 1ln 116ln 66x x x x x xd dx x x x x x x x x =--+-=---+⋅⎰⎰ ()()32ln 3ln ln 166x x x C xx x x=----+10.()()()()()1cos ln cos ln sin ln cos ln sin ln x dx x x x x dx x x x dx x=⋅+⋅⋅=⋅+⎰⎰⎰ ()()()1cos ln sin ln cos ln x x x x x x x dx x=⋅+⋅-⋅⋅⎰故 ()()()1cos ln cos ln sin ln 2x dx x x x C =++⎡⎤⎣⎦⎰ 11.()()()()ln ln ln ln ln ln ln ln ln ln ln x dx x d x x x xd x x ==-⎰⎰⎰()()()111ln ln ln ln ln ln ln ln ln ln ln ln x x x dx x x dx x x x C x x x=-⋅⋅=-=-+⎰⎰12.222xd x =-=-⎰⎰2424x x =-=-⎰2x C =-13.()()2221ln 1ln 121x dx x x x xdx x +=+-⋅⋅+⎰⎰ ()()222222222ln 1ln 1211x x x dx x x dx x x +-⎛⎫=+-=+-- ⎪++⎝⎭⎰⎰ ()2ln 122arctan x x x x C =+-++14. 2233sin tan sec tan sec tan sec sec cos x dx x xdx xd x x x xdx x===-⎰⎰⎰⎰ 32sec tan sec sec tan tan sec x x xdx x x x xdx ==⋅-⎰⎰⎰()2sec tan sec 1sec x x x xdx =⋅--⎰3sec tan sec sec x x xdx xdx =⋅-+⎰⎰31111sec sec tan sec sec tan ln sec tan 2222xdx x x xdx x x x x C ∴=+=+++⎰⎰23sin 11sec tan ln sec tan cos 22x dx x x x x C x ∴=-++⎰15.11x x x =⋅+⎰⎰()11211x dx xx x⎛⎫==-⎪++⎝⎭⎰⎰x C=()1x C=+1. ()()22311ln2ln5325xdx dx x x Cx x x x+⎛⎫=+=-+++⎪+-+⎝⎭⎰⎰2. ()()()222222222212111111ln221211211x xdx dx dx dx Cx x x x x x x x x⎛⎫===-=+⎪+++++⎝⎭⎰⎰⎰⎰3.()2222222122213sin62sin61cos27cos117cos7221wdx dx dx du dwduwx x x u w wuw+=====++++--⎛⎫+---⎪+⎝⎭⎰⎰⎰⎰⎰⎰22222221211134444dw dw dw dwC Cww w w======+ ++++⎝⎭⎝⎭⎝⎭⎰⎰⎰⎰5.cos1cot11sin sin sin sin1sin1sin1sin sin1sinxx x xdx dx d x d xx x x x x⎛⎫===-⎪++++⎝⎭⎰⎰⎰⎰1sinln sin ln1sin ln ln csc1sinxx x C C x Cx+=-++=-+=-++6. 22222tan11113cos231xudx du du C Cux uu+===+=+-++++⎰⎰⎰8. dxx令2211tt xt-=⇒=+则()241tdx dtt-=+则()()()22222221441111dx t t tt dt dtx t t tt+--=⋅⋅=-+-+⎰⎰()()22111122arctan2ln2111tdt t Ctt t⎛⎫-⎪=+=+⋅+⎪++-⎝⎭⎰ln C=+7.()3224144111t t dt dt t dt t t t t ⎡⎤===--⎢⎥+++⎣⎦⎰⎰⎰ 24ln 12t t t C ⎛⎫=+-++ ⎪⎝⎭(4ln 1C =+-习题3.22.(1)在[1,4]上,m=2,M=17,b -a=3,则()4216151xdx ≤+≤⎰(2)在[2,0]上,14m e-=,2M e =, b -a=2,则21024222x xe edx e ---≤≤-⎰3. (2)在[1,2]上32x x >,则331x dx ⎰大(3)在[0,1]上ln(1)x x >+,则1xdx ⎰大5.220sin sin 2td u dudx t t dtdt==⋅⎰220cos cos 2td u dudy t t dtdt==⋅⎰222cos 2cot sin 2dy dt dy t t t dt dx dx t t⋅⋅===⋅ 6.()2x dI x xe dx -= 令 ()0dI x dx= 则x=0 故x=0时()I x 有极值. 7.(1) 22220200cos cos 2limlim lim cos 12x x x x t dt x xx x x →→→⋅===⎰ (2)()()()()22222arctan arctan arctan limlimlim arctan 24xx x x x t dtx x x xxπ→∞→∞→∞==== (3)210lim 1n x dx x→∞+⎰ []0,1x ∈Q 故 原式=0 8. (1)()()()12F x f x a f x a a'=+--⎡⎤⎣⎦ (2)()()()()()()()001limlim 222x a x a a a f x a f x a f x f x f t dt f x a +-→→----+===⎰ 9.(1)()()()12F x f x f x '=+≥1.()()332201sin sin sin cos 1cos cos d d d d d πππππθθθθθπθθπθθ-=-=+=+-⎰⎰⎰⎰⎰314cos cos 033ππθθπ=+-=-2.())222212111ln 12ln 1211e e e d x e x +===+=⎰⎰⎰3. ()()()()00022222201arctan 122221111d x dx dx x x x x x π---+===+=-++++++⎰⎰⎰ 4.222x dx xdx xdx πππ--===+⎰⎰2224cos cos 333x x π-=+=+=⎰5.2202xdx xdx x x πππππππ==-==⎰⎰⎰6.1002244sin sin tan cos t tdt tdt t ππ---=-⋅=⎰⎰ ()()24sec1tan 144t dt t t πππ-=-=-=--⎰7.3332221444sec cos 113sin tan sin sin sin 4t t dt dt d t t t tt ππππππππ====-=⎰⎰⎰8.22111335514286t t t dt dt t---⎛⎫=⋅-== ⎪⎝⎭⎰⎰⎰9.()()111111011120x x xx xe dx xde xe e d x e e e -------=-=---=----=-⎰⎰⎰() 4ln4ln4ln4ln4222222000002ln4ln42244ln444ln41002t t t t t ttt te dt te dt tde t e e d ee=⋅==⋅=⋅-=-=-⎰⎰⎰⎰⎰11. ()111001sin ln sin sin cose t t tx dx t e dt t e e tdt=⋅=⋅-⎰⎰⎰11001cos cos sint t te tdt e t e tdt=+⎰⎰()()1100sin sin1cos11sint tt e dt e e tdt∴-=⋅---⎰⎰()11sin sin1cos112tt e dt e e∴⋅=⋅-+⎰12. 0001111lne t t tex dx t e dt t e dt t e dt---=⋅=-⋅+⋅⎰⎰⎰⎰0110t tt e dt tde-=-⋅+⎰⎰()()01110012210t t t tte e d t te e d t e--=---+-=--⎰⎰13.(1)()4sinf x x x=为奇函数,则()0f x dxππ-=⎰(2)()2242220021cos24cos2421cos22d d dππππθθθθθθ-+⎛⎫=⋅=+⎪⎝⎭⎰⎰⎰()22222001cos421cos22cos2212cos22d dππθθθθθθ+⎛⎫=++=++⎪⎝⎭⎰⎰311132sin42sin2222422πθθθπ⎛⎫=+⋅+⋅=⎪⎝⎭(3)221122600arcsin arcsin22coscosx x ttdttπ==⋅⎰⎰⎰3262324t dtππ==⎰(4)()f x为奇函数,则()55f x dx-=⎰14.()()()()222aad x dxa a a daϕϕϕϕ-=+=⎰()()22022ad x dxa daϕϕ=⎰()()220aax dx x dx ϕϕ=⎰⎰习题3.3 1.(1)431111133dx x x +∞+∞=-=⎰(2)11+∞=⎰ 发散 (3)()()()00110k p tk p t ktpte e e dt e d k p t k p k p k p -+∞+∞--+∞⋅=-==---⎰⎰ (4)11011sin sin sin cos 0ptpt pt pt ewtdt wtde wte e w wtdt p p+∞+∞+∞----+∞=-=--⋅⋅⎰⎰⎰ 2200cos cos sin 0pt pt ptww wtde wt e e w wtdt p p +∞+∞---⎛+∞⎫=-=-⋅+⋅ ⎪⎝⎭⎰⎰ 22222sin sin pt pt w w we wtdt e wtdt p pp w +∞+∞--=+-⇒=+⎰⎰(5)()()()2221arctan 10221111dx dx dx x x x x x π+∞+∞+∞-∞-∞-∞+∞+===+=++++++⎰⎰⎰ 2.10x x xx xxe dx xde xe e dx e +∞+∞+∞-----+∞+∞=-=-+=-=⎰⎰⎰2220220xxxx x e dx x dex exe dx +∞+∞+∞----+∞=-=-+=⎰⎰⎰33300330x x xx x e dx x de x e xe dx +∞+∞+∞----+∞=-=-+=⎰⎰⎰!n xn x x e dx x de n +∞+∞--=-=⎰⎰3. 21lim lim 1xx cc c x x c x c e x e c x c e x -→∞→∞⎛⎫+ ⎪+⎛⎫=== ⎪ ⎪-⎝⎭ ⎪-⎝⎭ 222222211111122222224cc c t tt t c t c c c c c te dt tde te e dt e e e -∞-∞-∞⎛⎫==-=-⋅=- ⎪-∞-∞⎝⎭⎰⎰⎰ 2215242c c c e e c ⎛⎫∴=-⇒= ⎪⎝⎭习题3.4 1.(1)221213ln ln 2122x A x dx x x ⎛⎫⎛⎫=-=-=- ⎪ ⎪⎝⎭⎝⎭⎰(2)()110120xxxxA eedx eee e ---=-=-=+-⎰2. 24y x '=-+ 则在()0,3-与()3,0处的切线的斜率为4和-2则这两切线分别为43x y -=,26x y -+=,两直线焦点为3,32⎛⎫⎪⎝⎭则()()3322230243432643A x xx dx x x x dx =-+-++-++-+⎰⎰()33222302934x dx x dx =+-=⎰⎰ 3. 22y px =在点,2p p ⎛⎫⎪⎝⎭处的切线斜率为1y '==则法线斜率为-1,则发现方程为32x p y -+=2322x p y y px⎧-+=⎪⇒⇒⎨⎪=⎩发现与抛物线的交点为,2p p ⎛⎫ ⎪⎝⎭9,32p p ⎛⎫- ⎪⎝⎭则92220231623pp p A x p dx p ⎛=+-+= ⎝⎰⎰4. ()()22222212244a a A ae d e d e e ππθθππππθθ---===-⎰⎰5.(1)例题3.486.当焦点为通径时,面积最小,通径为x=a 习题4.21. a r垂直于b r ,230a b ⋅=r r ,()()2sin ,2a b a b a b a b ⋅-=⋅⋅=⋅r r r r r r r ra r ∥b r ,()236sin 0a b a b ab ⨯==r r r r r r2. 不存在5. ()()32339632a b a b a a b a a a b b -⋅+=⋅-⋅+⋅-⋅=-r r r r r r r r r r r r6. 设i i k c x y z =++r u r u u r u u r 且2221x y z ++=则220c a x y z ⋅=++=r r5063b c x y z x y z ⋅=-++=⇒===-r r或 63x y z ==-= 7.(1)28100a b ⋅=--+=r r垂直(2)517010214333ij kc d ⋅=-=-r r r r u r平行8. cos ,0a b <>==r r则夹角为2π9. cos ,a b <>==r r则a r 在b r 上的投影为cos ,5a a b ⋅<>=r r r10. ()()2220a kb a kb a k b +⋅-=-=r r r r r r 则 293255k k =⇒=±习题4.31. ()12,3,4n =u r ()22,3,4n =-u u r1π与2π的夹角为θ111111cos 29n n n n θ⋅==u r u ru r u r 故补充和也不垂直但相交 3. 设平面方程为3x+2y+3z+d=0 则61206d d -++=⇒=-4. 设平面方程为ax+by+cz+d=0 则2022040b c d a b c d a b c d ++=⎧⎪-+++=⎨⎪-++=⎩5. 垂直于x 轴,则平面方程为x=k ,又过(1,-2,4)则 x=16. 设平面法向量为()12,3,4n =u r。
