苏教版高中数学必修二第15课时——圆与圆的位置关系(配套练习)
高中数学圆与圆的位置关系总结练习含答案解析S
2.2.3 圆与圆的位置关系圆与圆的位置关系及判定1.圆与圆的位置关系圆与圆的位置关系外离外切相交内切内含公共点个数0 ①② 1 02.设两圆半径分别为r1,r2,圆心距为d,则两圆相交时,r1,r2,d的关系为③.两圆外切时,r1,r2,d的关系为④.3.设两圆方程分别为x2+y2+D1x+E1y+F1=0,x2+y2+D2x+E2y+F2=0,联立得{x2+y2+D1x+E1y+F1=0,x2+y2+D2x+E2y+F2=0,方程组有两组不同实数解⇔两圆⑤,有⑥实数解⇔两圆相切,无实数解⇔两圆外离.圆系方程的应用1.(2014湖北黄冈期中,★☆☆)圆C1:x2+y2+4x-4y+4=0与圆C2:(x-2)2+(y-5)2=9的公切线有条.思路点拨求出圆心距,即可得出结论.2.(2013江苏白蒲模拟,★★☆)求圆心在直线x-y-4=0上,且经过两圆x2+y2-4x-6=0和x2+y2-4y-6=0交点的圆的方程.思路点拨本题解法较多,可考虑利用公共弦求解,也可以利用圆系方程求解.3.(2014江苏建湖中学训练,★★☆)已知圆M:x2+y2-2mx-2ny+m2-1=0与圆N:x2+y2+2x+2y-2=0交于A,B两点,且这两点平分圆N的圆周,求圆心M的轨迹方程,并求圆M的半径最小时的方程.思路点拨从几何性质入手分析,抓住圆心和半径分析圆的方程.4.(2013苏南四校月考,★★★)已知☉O:x2+y2=1和点M(4,2).(1)过点M向☉O引切线l,求直线l的方程;(2)求以点M为圆心,且被直线y=2x-1截得的弦长为4的☉M的方程;(3)设P为(2)中☉M上任一点,过点P向☉O引切线,切点为Q.试探究:平面内是否存在一定点R,使得PQPR为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.一、填空题1.已知圆O1:x2+y2-2x-4y+4=0与圆O2:x2+y2-8x-12y+36=0,两圆的位置关系为.2.圆C1:(x+2)2+(y-m)2=9与圆C2:(x-m)2+(y+1)2=4外切,则m的值为.3.若a2+b2=4,则圆(x-a)2+y2=1与圆x2+(y-b)2=1的位置关系是.4.半径为6的圆与x轴相切,且与圆x2+(y-3)2=1内切,则此圆的方程是.5.已知半径为1的动圆与圆(x-5)2+(y+7)2=16相切,则动圆圆心的轨迹方程是.6.点P在圆x2+y2-8x-4y+11=0上,点Q在圆x2+y2+4x+2y+1=0上,则|PQ|的最小值是.7.集合M={(x,y)|x2+y2≤4},N={(x,y)|(x-1)2+(y-1)2≤r2},且M∩N=N,则r的取值范围是.8.设A={(x,y)|y=√2a2-x2,a>0},B={(x,y)|(x-1)2+(y-√3)2=a2,a>0},若A∩B≠⌀,则a的最大值为.9.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为.10.圆C1:x2+y2=1与圆C2:x2+y2-2x-2y+1=0的公共弦所在直线被圆C3:(x-1)2+(y-1)2=254截得的弦长是.二、解答题11.试分别确定圆C1:x2+y2+4x-6y+12=0与C2:x2+y2-2x-14y+k=0(k<50)外切、内切、相交、内含、外离时,k的取值范围.12.已知圆x2+y2-4ax+2ay+20(a-1)=0(a≠2).(1)求证:对于任意实数a(a≠2),该圆过定点;(2)若该圆与圆x2+y2=4相切,求实数a的值.知识清单①1 ②2 ③|r 1-r 2|<d<r 1+r 2 ④d=r 1+r 2 ⑤相交 ⑥两组相同链接高考1.答案 3解析 C 1(-2,2),r 1=2,C 2(2,5),r 2=3,|C 1C 2|=√(-2-2)2+(2-5)2=5,∵|C 1C 2|=r 1+r 2,∴圆C 1与圆C 2外切.所以圆C 1与圆C 2有3条公切线.2.解析 解法一:由{x 2+y 2-4x -6=0,x 2+y 2-4y -6=0,得到两圆公共弦所在直线方程为y=x, 由{y =x ,x 2+y 2-4y -6=0, 解得{x 1=-1,y 1=-1或{x 2=3,y 2=3.∴圆x 2+y 2-4x-6=0和x 2+y 2-4y-6=0的交点分别为A(-1,-1)、B(3,3), 线段AB 的垂直平分线方程为y-1=-(x-1). 由{y -1=-(x -1),x -y -4=0,得{x =3,y =-1. ∴所求圆的圆心为(3,-1), 半径为√(3-3)2+[3-(-1)]2=4. ∴所求圆的方程为(x-3)2+(y+1)2=16. 解法二:由解法一,求得A(-1,-1)、B(3,3). 设所求圆的方程为(x-a)2+(y-b)2=r 2,由{a -b -4=0,(-1-a )2+(-1-b )2=r 2,(3-a )2+(3-b )2=r 2,得{a =3,b =-1,r 2=16. ∴所求圆的方程为(x-3)2+(y+1)2=16. 解法三:设经过两圆交点的圆系方程为 x 2+y 2-4x-6+λ(x 2+y 2-4y-6)=0(λ≠-1), 即x 2+y 2-41+λx-4λ1+λy-6=0. ∴圆心坐标为(21+λ,2λ1+λ),又∵圆心在直线x-y-4=0上, ∴21+λ-2λ1+λ-4=0,即λ=-13,∴所求圆的方程为x 2+y 2-6x+2y-6=0.3.解析 两圆方程相减,得公共弦AB 所在的直线方程为2(m+1)x+2(n+1)y-m 2-1=0, 由于A,B 两点平分圆N 的圆周,所以A,B 为圆N 直径的两个端点, 即直线AB 过圆N 的圆心N,而N(-1,-1),所以-2(m+1)-2(n+1)-m 2-1=0, 即m 2+2m+2n+5=0,即(m+1)2=-2(n+2)(n≤-2), 又圆M 的圆心M(m,n),所以圆心M 的轨迹方程为(x+1)2=-2·(y+2)(y≤-2), 又圆M 的半径r=2+1≥√5(n≤-2), 当且仅当n=-2,m=-1时半径取得最小值,∴当圆M 的半径最小时,圆M 的方程为x 2+y 2+2x+4y=0.4.解析 (1)显然,直线l 的斜率存在.设切线l 的方程为y-2=k(x-4),易得√k 2+1=1,解得k=8±√1915. ∴切线l 的方程为y-2=8±√1915(x-4). (2)圆心到直线y=2x-1的距离为√5,设圆M 的半径为r,则r 2=22+(√5)2=9,∴☉M 的方程为(x-4)2+(y-2)2=9.(3)假设存在这样的点R(a,b),设点P 的坐标为(x,y),相应的定值为λ(λ>0), 根据题意及勾股定理可得PQ=√x 2+y 2-1, ∴√x 2+y 2√(x -a )+(y -b )=λ,即x 2+y 2-1=λ2(x 2+y 2-2ax-2by+a 2+b 2),(*) 又点P 在☉M 上, ∴(x -4)2+(y-2)2=9,即x 2+y 2=8x+4y-11,代入(*)式得,8x+4y-12=λ2[(8-2a)x+(4-2b)y+(a 2+b 2-11)].若系数对应相等,则等式恒成立,∴{λ2(8-2a )=8,λ2(4-2b )=4,λ2(a 2+b 2-11)=-12,解得a=2,b=1,λ=√2或a=25,b=15,λ=√103, ∴可以找到这样的定点R,使得PQPR 为定值.当点R 的坐标为(2,1)时,比值为√2; 当点R 的坐标为(25,15)时,比值为√103.基础过关一、填空题 1.答案 外切解析 由题意得圆的半径分别为1,4,圆心距为√(4-1)2+(6-2)2=5=4+1,故两圆外切. 2.答案 2或-5解析 圆C 1:(x+2)2+(y-m)2=9的圆心为(-2,m),半径为3;圆C 2:(x-m)2+(y+1)2=4的圆心为(m,-1),半径为2.依题意有√(-2-m )2+(m +1)2=3+2, 即m 2+3m-10=0, 解得m=2或m=-5. 3.答案 外切解析 ∵两圆的圆心分别为O 1(a,0),O 2(0,b),半径r 1=r 2=1,∴O 1O 2=√a 2+b 2=2=r 1+r 2,则两圆外切. 4.答案 (x±4)2+(y-6)2=36解析 设所求圆的圆心为(a,6),由两圆内切,得√a 2+(6-3)2=6-1,解得a=±4,则此圆的方程是(x±4)2+(y-6)2=36.5.答案 (x-5)2+(y+7)2=25或(x-5)2+(y+7)2=9解析 动圆圆心的轨迹是以已知圆的圆心(5,-7)为圆心,以3或5为半径的圆. 6.答案 3√5-5解析 (x-4)2+(y-2)2=9的圆心为C 1(4,2),半径为r 1=3;(x+2)2+(y+1)2=4的圆心为C 2(-2,-1),半径为r 2=2.又|C 1C 2|=3√5,显然两圆外离,所以|PQ|的最小值是3√5-5. 7.答案 (0,2-√2]解析 由于M∩N=N,故圆(x-1)2+(y-1)2=r 2在圆x 2+y 2=4内部,当两圆内切时,√2=2-r,则r=2-√2,因此r 的取值范围是(0,2-√2].8.答案2(√2+1)解析A表示以O(0,0)为圆心,√2a为半径的半圆,B表示以O'(1,√3)为圆心,a为半径的圆.∵A∩B≠⌀,即半圆O与圆O'有公共点,则当两圆内切时,a最大,即√2a-a=OO'=2,∴a的最大值为2(√2+1).9.答案√7解析记直线y=x+1上任意一点与圆心的距离为h,记切线长为l,则始终有等量关系h2=l2+1.故当h取得最小值时,切线长取最小值,易知h的最小值即为圆心到直线y=x+1的距离,故hmin=2√2,此时l=√7.10.答案√23解析圆C1与圆C2的公共弦所在直线的方程为x2+y2-1-(x2+y2-2x-2y+1)=0,即x+y-1=0.圆心C3到直线x+y-1=0的距离d=√2=√22,所以所求弦长为2√r2-d2=2√254-12=√23.二、解答题11.解析将两圆的一般方程化为标准方程,C1:(x+2)2+(y-3)2=1,C2:(x-1)2+(y-7)2=50-k.圆C1的圆心为C 1(-2,3),半径r1=1;圆C2的圆心为C2(1,7),半径r2=√50-k(k<50).从而圆心距d=√(-2-1)2+(3-7)2=5.当两圆外切时,d=r1+r2,即1+√50-k=5,解得k=34;当两圆内切时,d=|r1-r2|,即|1-√50-k|=5,解得k=14;当两圆相交时,|r1-r2|<d<r1+r2,即|1-√50-k|<5<1+√50-k,解得14<k<34;当两圆内含时,d<|r1-r2|,即|1-√50-k|>5,解得k<14;当两圆外离时,d>r1+r2,即1+√50-k<5,解得34<k<50.12.解析(1)证明:将圆的方程整理得(x2+y2-20)+a(-4x+2y+20)=0,此方程表示过圆x2+y2=20与直线-4x+2y+20=0的交点的圆系.解方程组{x2+y2=20,-4x+2y+20=0得{x=4,y=-2,所以该圆恒过定点(4,-2).(2)圆的方程可化为(x-2a)2+(y+a)2=5(a-2)2(a≠2).若两圆外切,则2+√5(a -2)2=√(2a -0)2+(-a -0)2,解得a=1+√55. 若两圆内切,则|2-√5(a -2)2|=√(2a -0)2+(-a -0)2,解得a=1-√55或a=1+√55(舍去). 综上所述,a=1±√55.。
苏教版学案必修2高中数学 2.2.3圆与圆的位置关系课时作业
2．2．3 圆与圆的位置关系【课时目标】 1．掌握圆与圆的位置关系及判定方法．2．会利用圆与圆位置关系的判断方法进行圆与圆位置关系的判断．3．能综合应用圆与圆的位置关系解决其他问题．圆与圆位置关系的判定有两种方法：1．几何法：若两圆的半径分别为r 1、r 2，两圆的圆心距为d ，则两圆的位置关系的判断方法如下：⎭⎪⎬⎪⎫圆C 1方程圆C 2方程――→消元一元二次方程⎩⎪⎨⎪⎧Δ>0⇒ Δ＝0⇒ Δ<0⇒一、填空题1．两圆(x ＋3)2＋(y －2)2＝4和(x －3)2＋(y ＋6)2＝64的位置关系是________． 2．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公切线有________条． 3．圆x 2＋y 2－4x ＋6y ＝0和圆x 2＋y 2－6x ＝0交于A 、B 两点，则AB 的垂直平分线的方程是__________．4．圆C1：(x－m)2＋(y＋2)2＝9与圆C2：(x＋1)2＋(y－m)2＝4外切，则m的值为__________．5．已知半径为1的动圆与圆(x－5)2＋(y＋7)2＝16相切，则动圆圆心的轨迹方程是________________________________________________________________________．6．集合M＝{(x，y)|x2＋y2≤4}，N＝{(x，y)|(x－1)2＋(y－1)2≤r2，r>0}，且M∩N ＝N，则r的取值范围是__________．7．两圆x2＋y2＝1和(x＋4)2＋(y－a)2＝25相切，则实数a的值为________．8．两圆交于A(1,3)及B(m，－1)，两圆的圆心均在直线x－y＋n＝0上，则m＋n的值为________．9．两圆x2＋y2－x＋y－2＝0和x2＋y2＝5的公共弦长为____________．二、解答题10．求过点A(0,6)且与圆C：x2＋y2＋10x＋10y＝0切于原点的圆的方程．11．点M在圆心为C1的方程x2＋y2＋6x－2y＋1＝0上，点N在圆心为C2的方程x2＋y2＋2x＋4y＋1＝0上，求MN的最大值．能力提升12．若⊙O：x2＋y2＝5与⊙O1：(x－m)2＋y2＝20(m∈R)相交于A、B两点，且两圆在点A 处的切线互相垂直，则线段AB的长度为________．13．已知点P(－2，－3)和以点Q为圆心的圆(x－4)2＋(y－2)2＝9．(1)画出以PQ为直径，Q′为圆心的圆，再求出它的方程；(2)作出以Q为圆心的圆和以Q′为圆心的圆的两个交点A，B．直线PA，PB是以Q为圆心的圆的切线吗？为什么？(3)求直线AB的方程．1．判定两圆位置关系时，结合图形易于判断分析，而从两圆方程出发往往比较繁琐且不准确，可充分利用两圆圆心距与两圆半径的和差的比较进行判断．2．两圆的位置关系决定了两圆公切线的条数．3．两圆相交求其公共弦所在直线方程，可利用两圆方程作差，但应注意当两圆不相交时，作差得出的直线方程并非两圆公共弦所在直线方程．2．2．3 圆与圆的位置关系答案知识梳理1．2．相交内切或外切外离或内含作业设计1．外切解析圆心距d＝10＝R＋r，∴外切．2．3解析∵两圆标准方程为(x－2)2＋(y＋1)2＝4，(x＋2)2＋(y－2)2＝9，∴圆心距d＝＋2＋－1－2＝5，r1＝2，r2＝3，∴d＝r1＋r2，∴两圆外切，∴公切线有3条．3．3x－y－9＝0解析两圆圆心所在直线即为所求．4．2或－5解析外切时满足r1＋r2＝d，即m＋2＋－2－m2＝5，解得m＝2或－5．5．(x－5)2＋(y＋7)2＝25或(x－5)2＋(y＋7)2＝9解析设动圆圆心为P，已知圆的圆心为A(5，－7)，则外切时PA＝5，内切时PA＝3，所以P 的轨迹为以A 为圆心，3或5为半径的圆．6．(0,2－2]解析 由已知M ∩N ＝N 知N ⊆M ，∴圆x 2＋y 2＝4与圆(x －1)2＋(y －1)2＝r 2内切或内含，∴2－r ≥2，∴0<r ≤2－2． 7．±25或0解析 ∵圆心分别为(0,0)和(－4，a )，半径分别为1和5，两圆外切时有－4－2＋a －2＝1＋5，∴a ＝±25，两圆内切时有－4－2＋a －2＝5－1，∴a ＝0．综上，a ＝±25或a ＝0． 8．3解析 A 、B 两点关于直线x －y ＋n ＝0对称， 即AB 中点(m ＋12，1)在直线x －y ＋n ＝0上，则有m ＋12－1＋n ＝0， ①且AB 斜率41－m＝－1 ②由①②解得：m ＝5，n ＝－2，m ＋n ＝3． 9． 2解析 由⎩⎪⎨⎪⎧x 2＋y 2－x ＋y －2＝0 ①x 2＋y 2＝5 ②②－①得两圆的公共弦所在的直线方程为x －y －3＝0， ∴圆x 2＋y 2＝5的圆心到该直线的距离为d ＝|－3|1＋－2＝32，设公共弦长为l ，∴l ＝25－⎝ ⎛⎭⎪⎫322＝2．10．解 设所求圆的方程为 (x －a )2＋(y －b )2＝r 2， 则⎩⎨⎧a＝b ①b ＝3 ②a 2＋b 2＝r ③由①②③得⎩⎨⎧a ＝b ＝3r ＝32．∴(x －3)2＋(y －3)2＝18．11．解 把圆的方程都化成标准形式，得(x ＋3)2＋(y －1)2＝9，(x ＋1)2＋(y ＋2)2＝4．如图，C 1的坐标是(－3,1)，半径长是3；C 2的坐标是(－1，－2)，半径长是2．所以，C 1C 2＝－3＋2＋＋2＝13．因此，MN 的最大值是13＋5． 12．4解析 如图所示，在Rt △OO 1A 中，OA ＝5，O 1A ＝25， ∴OO 1＝5， ∴AC ＝5×255＝2， ∴AB ＝4． 13．解(1)∵已知圆的方程为 (x －4)2＋(y －2)2＝32， ∴Q (4,2)．PQ 中点为Q ′⎝⎛⎭⎪⎫1，－12，半径为r ＝PQ 2＝612，故以Q ′为圆心的圆的方程为(x －1)2＋⎝ ⎛⎭⎪⎫y ＋122＝614．(2)∵PQ 是圆Q ′的直径，∴PA ⊥AQ (如图所示) ∴PA 是⊙Q 的切线，同理PB 也是⊙Q 的切线． (3)将⊙Q 与⊙Q ′方程相减，得6x ＋5y －25＝0． 此即为直线AB 的方程．。
高中数学第二章第15课时圆与圆的位置关系学案苏教版必修2
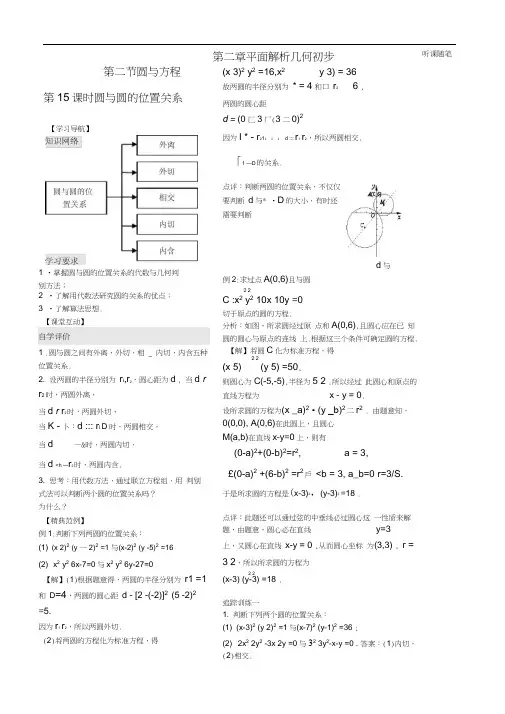
第二节圆与方程第15课时圆与圆的位置关系1 •掌握圆与圆的位置关系的代数与几何判别方法；2 •了解用代数法研究圆的关系的优点；3 •了解算法思想.自学评价1 .圆与圆之间有外离，外切，相 _ 内切，内含五种位置关系.2. 设两圆的半径分别为r i,r2，圆心距为d , 当d r r2时，两圆外离，当d r r2时，两圆外切，当K - 卜：d ::: r i D时，两圆相交，当d —&时，两圆内切，当d <h —r2时，两圆内含.3. 思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？【精典范例】例1:判断下列两圆的位置关系：(1) (x 2)2(y 一2)2=1 与(x-2)2(y -5)2=16(2) x2 y2 6x-7=0与x2 y2 6y-27=0【解】(1)根据题意得，两圆的半径分别为r1 =1和D=4，两圆的圆心距d - [2 -(-2)]2(5 -2)2=5.因为r1r2，所以两圆外切.(2)将两圆的方程化为标准方程，得(x 3)2 y2 =16,x2y 3) = 36故两圆的半径分别为* = 4和口r2 6 ,两圆的圆心距d = (0 匚3厂(3二0)2因为I * - r21：：： d ::: r1r2，所以两圆相交.点评：判断两圆的位置关系，不仅仅要判断d与* •D的大小，有时还需要判断d与例2:求过点A(0,6)且与圆2 2C :x2 y2 10x 10y =0切于原点的圆的方程.分析：如图，所求圆经过原点和A(0,6),且圆心应在已知圆的圆心与原点的连线上.根据这三个条件可确定圆的方程.【解】将圆C化为标准方程，得2 2(x 5) (y 5) =50,则圆心为C(-5,-5),半径为5 2 .所以经过此圆心和原点的直线方程为x - y = 0.设所求圆的方程为(x _a)2• (y _b)2二r2. 由题意知，0(0,0), A(0,6)在此圆上，且圆心M(a,b)在直线x-y=0上，则有(0-a)2+(0-b)2=r2, a = 3,£(0-a)2 +(6-b)2 =r2戶<b = 3, a_b=0 r=3/S.于是所求圆的方程是(x-3)2，(y-3)2=18 .点评：此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线y=3上，又圆心在直线x-y = 0 ,从而圆心坐标为(3,3) , r =3 2，所以所求圆的方程为2 2(x-3) (y-3) =18 .追踪训练一1. 判断下列两个圆的位置关系：(1) (x-3)2 (y 2)2 =1与(x-7)2 (y-1)2 =36 ;(2) 2x2 2y2 -3x 2y =0与32 3y2-x-y =0 . 答案：(1)内切，(2)相交.第二章平面解析几何初步听课随笔「1 —D的关系.【学习导航】2. 若圆x2• y2= m 与圆x2■ y2，6x-8yT1=0相交，求实数m的取值范围. 答案：1 ：：：m <121 .例 3: 已 知 圆 2 2G : x y 2x _6y 1=0 , 圆2 2C 2: x y -4x • 2y -1仁0 ,求两圆的公共弦所在的直线方程及公共弦长.分析：因两圆的交点坐标同时满足两个圆方 程，联立方程组，消去 x 2项、y 2项，即得 两圆的两个交点所在的直线方程， 利用勾股 定理可求出两圆公共弦长.【解】设两圆交点为Ad ,,%)、B(x 2,y 2), 则A B两点坐标满足方程组-2 2 x y 2x -6y 1 =0, (1)2 2， x y -4x 2y -11 =0, (2)(1)一(2)得 3x —4y 6 =0 .因为，A B 两点坐标都满足此方程，所以，3x - 4y • 6 =0即为两圆公共弦所在所以，所求圆方程为(x —1)2・(y ・7)2 =89 , 2 2 2 2 2 即 x y —x 7y 一32 = 0 (法二)设所求圆的方程为 2 2 2 2 x y 6 x4 . - ( x y 6 y2即8 ) 2 2 6 6■ 4 28■ x y x y 0 . 1 + & 1 + 扎 1 + k 故此圆的圆心为(一丄，二竺),它在直线 1+扎1+扎 x-y-4=0 上，所以 一 3—-4 = 0, 1 +人1 +九 所以，--7 . 所以所求圆方程为 x 2 • y 2 _x • 7y-32 = 0 点评：“解法二”中设出的经过两已知圆交点的 圆方程叫做经过两已知圆的圆系方程.的直线方程.易知圆G 的圆心(-1,3)，半径r =3 . 又G 到直线的距离为99 .所以,524点评：本题较为复杂，要讨论的情况比较多, 解题过程中要注重分析.思维点拔： 解题时要充分利用两圆位置关系的几何性质. 追踪训练二 1 .一个圆经过圆 G :x 2 • y 2-8x-9 = 0和圆 C 2 ：x 2 • y 2 -8y • 15 = 0的两个交点，且圆心 在直线2x-y-1=0上，求该圆的方程. 2 2 10 14 答案：x y x y-12 = 0. 3 3 2 .已知一个圆经过直线2x y ^0与圆 x 2 y 2 2x -4y • 1 = 0的两个交点，并且有 最小面积，求此圆的方程.例5 :求过两圆x 2 • y 2 • 6x - 4 = 0和 x 2 y 2 6y -28 =0的交点，且圆心在直 线x - y -4 =0上的圆的方程.分析：所求圆圆心是两已知圆连心线和已知 直线的交点，再利用弦心距、弦长、半径之 间的关系求圆半径【解】(法一)可求得两圆连心线所在直线 的方程为x y 3 0.1x —y —4=0, 1 7由 得圆心(丄，-上).x y 3 = 0, 2 2 利用弦心距、弦长、半径之间的关系可求得 公共弦长d 二・.50 , 所以，圆半径 听课随笔 | -1 3 -4 3 6| .32 (4)2 两圆的公共弦长为答案：(x 1■一)2 . (y _6)5 5。
苏教版高中数学高一必修二 圆与圆的位置关系
① ②
由①－②，得(D1－D2)x0＋(E1－E2)y0＋F1－F2＝0， 这个方程说明了 M(x0，y0)在直线(D1－D2)x＋(E1－E2)y＋F1 －F2＝0 上．
研一研·问题探究、课堂更高效
问题 2 若两圆 C1：x2＋y2＋D1x＋E1y＋F1＝0 和 C2：x2＋y2
＋D2x＋E2y＋F2＝0 相交，它们的交点弦所在的直线方程
目 开
(4)当 d＝|r1－r2|时，圆 C1 与圆 C2内切 ；
关 (5)当 d<|r1－r2|时，圆 C1 与圆 C2 内含 ．
2．代数法判断圆与圆的位置关系：将两个圆方程联立，消去其
中的一个未知数 y 或 x，得关于 x 或 y 的一元二次方程. 若
方程中Δ>0 ，则两圆相交；若方程中Δ＝0，则两圆相切；
本 答 (1)将两圆的方程化为标准方程；
课 时
(2)求两圆的圆心坐标和半径 R、r；
栏 目
(3)求两圆的圆心距 d;
开 关
(4)比较 d 与|R－r|，R＋r 的大小关系得出结论.
研一研·问题探究、课堂更高效
例 1 判断下列两圆的位置关系：
(1)(x＋2)2＋(y－2)2＝1 与(x－2)2＋(y－5)2＝16；
.
所以所求圆的圆心坐标是12，－72.
研一研·问题探究、课堂更高效
设所求圆的方程是 x2＋y2－x＋7y＋m＝0.
由三个圆有同一条公共弦，
x2＋y2＋6x－4－(x2＋y2＋6y－28)＝0，
本 得 x－y＋4＝0，
课
时 x2＋y2＋6x－4－(x2＋y2－x＋7y＋m)＝0，
栏
目 开 关
得 x－y－4＋7 m＝0，
2019—2020年最新苏教版高中数学必修二同步课堂精练-2.2.3圆与圆的位置关系课堂同步练习题.docx
（新课标）2019—2020学年苏教版高中数学必修二圆与圆的位置关系1．两圆x2＋y2－2ax＋4y＋a2－5＝0和x2＋y2＋2x－2ay＋a2－3＝0.(1)当a＝__________时，两圆外切；(2)当a＝__________时，两圆相内切．2．(1)圆x2＋y2－2x－5＝0和圆x2＋y2＋2x－4y－4＝0的交点为A，B，则线段AB的垂直平分线方程为__________．(2)已知两圆x2＋y2＝10和(x－1)2＋(y－3)2＝20相交于A，B两点，则直线AB的方程是__________．3．已知点P在圆x2＋y2－8x－4y＋11＝0上，点Q在圆x2＋y2＋4x＋2y＋1＝0上，则PQ 的最小值是__________．4．若圆x2＋y2＝4与圆x2＋y2＋2ay－6＝0(a＞0)的公共弦的长为23，则a＝__________.5．过原点的直线与圆x2＋y2－2x－4y＋4＝0相交所得弦的长为2，则该直线的方程为__________．6．圆x2＋y2＝1和圆(x－1)2＋(y－1)2＝1的公共弦所在直线被圆4x2＋4y2＝25所截，则截得的弦长为__________．7．求以圆C1：x2＋y2－12x－2y－13＝0和圆C2：x2＋y2＋12x＋16y－25＝0的公共弦为直径的圆的方程．8．已知圆x2＋y2－4ax＋2ay＋20(a－1)＝0.(1)求证：对任意实数a，该圆恒过一定点；(2)若该圆与圆x2＋y2＝4相切，求a的值．9.已知圆C1：x2＋y2＋2x＋2y－2＝0，圆C2：x2＋y2－2ax－2by＋a2－1＝0.当a，b变化时，圆C2始终平分圆C1的周长，求圆C2的面积最小时圆的方程．参考答案1．(1)－5或2 (2)－2或－1 ∵圆C 1：(x －a )2＋(y ＋2)2＝9，圆心C 1(a ，－2)，r 1＝3，圆C 2：(x ＋1)2＋(y －a )2＝4，圆心C 2(－1，a )，半径r 2＝2.当221212125C C a a r r =(--)+(+)=＋＝时，两圆外切，此时可解得a ＝－5或2；当221212121C C a a r r =(+)+(+)=－＝时，两圆内切，此时可解得a ＝－1或－2.2．(1)x ＋y －1＝0 (2)x ＋3y ＝0 (1)由题意知，两圆的连心线即为AB 的垂直平分线．由已知得两圆圆心分别为(1,0)，(－1,2)，∴由两点式方程得012011y x --=---，即x ＋y －1＝0. (2)两圆方程联立消去二次项得到的x 、y 的二元一次方程即为直线AB 的方程．设点P (x ，y )为交点弦上任意一点，则2222101320x y x y ⎧+=⎨(-)+(-)=⎩相减得2x －1＋6y －9＝10－20，即x ＋3y ＝0.3．355- 由x 2＋y 2－8x －4y ＋11＝0得(x －4)2＋(y －2)2＝9.∴圆心C 1为(4,2)，半径r 1＝3；由x 2＋y 2＋4x ＋2y ＋1＝0得(x ＋2)2＋(y ＋1)2＝4， ∴圆心C 2为(－2，－1)，半径r 2＝2. ∴22min 12124221323532355PQ C C r r (+)+(+)＝－－＝－－＝－－＝－4．1依题意，画出两圆的位置如图，公共弦为AB ，交y 轴于点C ，连结OA ，则OA ＝2. 两圆方程相减，得2ay ＝2，解得1y a =，∴1OC a=. 又公共弦长为23， ∴3AC =.于是，由Rt △AOC 可得OC 2＝AO 2－AC 2，即22212(3)a=－， 整理得a 2＝1.又a ＞0，∴a ＝1.5．2x －y ＝0 圆的方程可化为(x －1)2＋(y －2)2＝1，可知圆心为(1,2)，半径为1. 设直线方程为y ＝kx ，则圆心到直线的距离为2|2|1k d k -=+，故有：2|2|01k k -=+，解得k ＝2.故直线方程为y ＝2x ，即2x －y ＝0. 6.23 由两圆方程可得其公共弦方程为x ＋y －1＝0，原点O 到该直线的距离22d =，而半径52r =，故弦长22251222342r d -=-=＝. 7．解法一：联立两圆方程22221221301216250.x y x y x y x y ⎧+---=⎨+++-=⎩ 相减得公共弦所在直线方程为4x ＋3y －2＝0.再由224320122130x y x y x y +-=⎧⎨+---=⎩ 联立得两交点坐标A (－1,2)、B (5，－6)．∵所求圆以AB 为直径，∴圆心是AB 的中心点M (2，－2)，圆的半径为152r AB =＝.于是圆的方程为(x －2)2＋(y ＋2)2＝25.解法二：设所求圆的方程为x 2＋y 2－12x －2y －13＋λ(x 2＋y 2＋12x ＋16y －25)＝0(λ为参数)，得圆心C 1212162,.2121λλλλ⎛⎫---- ⎪(+)(+)⎝⎭. ∵圆心C 应在公共弦AB 所在直线上， ∴121216243202121λλλλ-(-)(--)⨯+⨯-=(+)(+). 解得12λ= ∴所求圆的方程为x 2＋y 2－4x ＋4y －17＝0.8．(1)证明：将圆的方程整理，得(x 2＋y 2－20)＋a (－4x ＋2y ＋20)＝0， 此方程表示过圆x 2＋y 2＝20与直线－4x ＋2y ＋20＝0的交点的圆系．解方程组222042200x y x y ⎧+=⎨--=⎩得42.x y =⎧⎨=-⎩所以该圆恒过定点(4，－2)．(2)解：圆的方程可化为(x －2a )2＋(y ＋a )2＝5a 2－20a ＋20＝5(a －2)2. 若两圆外切，则r 1＋r 2＝O 1O 2， 即222525a a (-)=＋，整理，得252560a a (-)=－＞， 所以65a ＞，解得515a ＝＋. 若两圆内切，则|r 1－r 2|＝O 1O 2， 即225225a a (-)-=，整理，得252650a a (-)=－＞，所以65a ＜. 解得515a ＝－或515a ＝＋ (舍去)． 综上所述，515a ±＝. 9.解：将两圆方程相减，得到两圆相交弦所在直线方程为2(1＋a )x ＋2(1＋b )y －a 2－1＝0. 由于圆C 2始终平分圆C 1的周长，因此C 1(－1，－1)必在相交弦所在直线上，∴2(1＋a )×(－1)＋2(1＋b )×(－1)－a 2－1＝0， 即2252a ab ++=-. 由圆C 2方程，得21r b +＝，∴S ＝πr 2＝π(1＋b 2)2222254[(1)4]4a a a ππππ(++)⨯=+＝＋＋＋. ∴当a ＝－1时，S 取最小值5π，此时b ＝－2，∴圆C 2的方程为x 2＋y 2＋2x ＋4y ＝0.。
苏教版数学高一必修2试题 圆与圆的位置关系
2．2.3圆与圆的位置关系基础巩固知识点一圆与圆的位置关系1．两圆x2＋y2＋6x＋4y＋9＝0和x2＋y2－6x－12y－19＝0的位置关系是________．解析：圆心分别为O1(－3，－2)，O2(3,6)，半径满足r21＝4，r22＝64，∴r1＝2，r2＝8.又O1O2＝3＋32＋6＋22＝10＝r1＋r2，∴两圆相外切．答案：外切2．已知0＜r＜22，则两圆x2＋y2＝r2与(x－1)2＋(y＋1)2＝2的位置关系是________．解析：∵两圆的圆心距为O1O2＝2，又R＝2，0＜r＜22，∴|R－r|＜O1O2＜|R＋r|，故两圆相交．答案：相交3．若圆C1：x2＋y2＋m＝0与圆C2：x2＋y2－6x＋8y＝0没有公共点，则实数m的取值范围是________．解析：因为圆C1以原点为圆心，而圆C2过原点，所以两圆无公共点必有圆C2内含于圆C1，从而－m>100，即m<－100.答案：(－∞，－100)4．已知两圆x2＋y2＝10和(x－1)2＋(y－3)2＝20相交于A，B两点，则直线AB的方程是________．解析：两圆相交其交点所在的直线方程为：(x－1)2＋(y－3)2－20－x2－y2＋10＝0，即：x＋3y＝0.答案：x＋3y＝0知识点二 利用圆与圆的关系确定圆的方程5．圆x 2＋y 2－2x －1＝0关于直线x －y ＋3＝0对称的圆的方程是________．解析：已知圆方程为(x －1)2＋y 2＝2，则该圆圆心关于直线x －y ＋3＝0的对称点为(－3,4)，半径也是 2.答案：(x ＋3)2＋ (y －4)2＝26．半径为6的圆与x 轴相切，且与圆x 2＋(y －3)2＝1内切，则此圆的方程是________．解析：半径为1的圆内切于半径为6的圆．答案：(x±4)2＋(y －6)2＝367．过两圆x 2＋y 2－x －y －2＝0与x 2＋y 2＋4x －4y －8＝0的交点和点(3,1)的圆的方程是________．解析：求出两圆的交点后用待定系数法；或利用圆系方程：设所求圆方程为(x 2＋y 2－x－y －2)＋λ(x 2＋y 2＋4x －4y －8)＝0，又过点(3,1)代入求出λ＝－25. 答案：x 2＋y 2－133x ＋y ＋2＝0 知识点三 两圆的公切线与公共弦8．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公切线有________条．解析：易判知两圆相外切，故有3条公切线．答案：39．已知圆C 1：x 2＋y 2＋4x －4y －1＝0与圆C 2：x 2＋y 2－2x ＋2y －7＝0相交于A 、B 两点，求公共弦AB 的长．解析：由方程⎩⎪⎨⎪⎧x 2＋y 2＋4x －4y －1＝0，x 2＋y 2－2x ＋2y －7＝0，消去二次项得6x －6y ＋6＝0，即x －y ＋1＝0为所求的公共弦AB 所在的直线的方程．圆C 1即：(x ＋2)2＋(y －2)2＝9，∴C 1(－2,2)到直线AB 的距离d ＝|－2－2＋1|2＝32， 又圆C 1半径r ＝3，故弦长AB ＝232－322＝3 2.能力升级综合点一 与圆有关的最值问题10．若直线mx ＋2ny －4＝0始终平分圆x 2＋y 2－4x －2y ＋4＝0的周长，则mn 的最大值是________．解析：由直线mx ＋2ny －4＝0始终平分圆x 2＋y 2－4x －2y ＋4＝0的周长，知直线过圆的圆心(2,1)，∴2m ＋2n －4＝0，m ＋n ＝2.∴mn ＝m(2－m)＝－(m －1)2＋1≤1.答案：111．一束光线从点A(－1,1)出发经x 轴反射，到达圆C ：(x －2)2＋(y －3)2＝1上一点的最短路程是________．解析：圆C ：(x －2)2＋(y －3)2＝1关于x 轴的对称圆C′：(x －2)2＋(y ＋3)2＝1.∴A(－1,1)到C′的圆心C′(2，－3)的距离AC′＝5.∴从A 发出的光线经x 轴反射到圆C 上一点的最短距离等于A 到圆C′的圆心C′的距离减去半径长1.即d min ＝5－1＝4.答案：412．过直线x ＝2上一点M 向以C 为圆心的圆(x ＋5)2＋(y －1)2＝1作切线，切点分别为A ，B ，则四边形MACB 的面积的最小值为________．解析：易知S MACB ＝2S △MAC ＝MA·AC ＝MC 2－1显然MC 的最小值为7，故四边形MACB 的面积的最小值为49－1＝4 3.答案：4 3综合点二 圆的位置关系及其应用13．求圆C 1：x 2＋y 2＋2kx ＋k 2－1＝0与圆C 2：x 2＋y 2＋2(k ＋1)y ＋k 2＋2k ＝0的圆心距的最小值及相应的k 值，并指出此时两圆的位置关系．[]解析：两圆的圆心C 1(－k,0)，C 2(0，－k －1)，∴圆心距C 1C 2＝k 2＋k ＋12＝2k 2＋2k ＋1，当k ＝－12时，C 1C 2有最小值22. 此时，两圆的方程为C 1：⎝⎛⎭⎫x －122＋y 2＝1， C 2：x 2＋⎝⎛⎭⎫y ＋122＝1，由|r 1－r 2|＜d ＜r 1＋r 2，可知两圆相交．14．已知集合A ＝{(x ，y)|x 2＋y 2＝4}，集合B ＝{(x ，y)|(x －3)2＋(y －4)2＝r 2，r ＞0}．若A∩B 中有且仅有一个元素，求r 的值．解析：∵A∩B 中有且仅有一个元素，∴圆C 1：x 2＋y 2＝4与圆C 2∶(x －3)2＋(y －4)2＝r 2外切或内切．又∵圆心距C 1C 2＝5.∴r ＝3或7.综合点三 轨迹与证明问题15．已知两定圆O 1：(x －1)2＋(y －1)2＝1，圆O 2：(x ＋5)2＋(y ＋3)2＝4，动圆P 恒将两定圆的周长平分．试求动圆圆心P 的轨迹方程．解析：设动圆P 的方程为(x －a)2＋(y －b)2＝r 2，即：x 2＋y 2－2ax －2by ＋a 2＋b 2－r 2＝0. 将此方程分别与圆O 1，圆O 2的方程相减得公共弦所在的直线方程为：(2－2a)x ＋(2－2b)y ＋a 2＋b 2－r 2－1＝0.(10＋2a)x ＋(6＋2b)y ＋30－a 2－b 2＋r 2＝0.由于圆P 平分两定圆的周长，所以公共弦分别过两圆圆心，从而有：⎩⎪⎨⎪⎧－2a －2b ＋3＋a 2＋b 2＝r 2，10a ＋6b ＋a 2＋b 2＋38＝r 2. 消去r 2得：12a ＋8b ＋35＝0.用(x ，y)替换(a ，b)得：点P 的轨迹方程为：12x ＋8y ＋35＝0.。
苏教版数学高一必修2试题 圆与圆的位置关系
2.2.3 圆与圆的位置关系双基达标 限时15分钟1．圆O 1：x 2＋y 2－2x ＝0与圆O 2：x 2＋y 2－4y ＝0的位置关系是________．解析 化为标准方程：O 1：(x －1)2＋y 2＝1，O 2：x 2＋(y －2)2＝4，则圆心为O 1(1,0)，O 2(0,2)；∴O 1O 2＝1－02＋0－22＝5＜3＝R ＋r ，O 1O 2＝1－02＋0－22＝5＞1＝R －r ；∴两圆相交．答案 相交2．圆C 1：(x －m )2＋(y ＋2)2＝9与圆C 2：(x ＋1)2＋(y －m )2＝4外切，则m 的值为________． 解析 外切得圆心距等于半径之和，即m ＋12＋－2－m 2＝3＋2，解得m 的值为2或－5.答案 2或－53．两圆x 2＋y 2－4x ＋6y ＝0和x 2＋y 2－6x ＝0的连心线方程为________．解析 将两圆的一般方程配方整理得标准方程分别为(x －2)2＋(y ＋3)2＝13和(x －3)2＋y 2＝9，故它们的圆心为(2，－3)与 (3,0)；所以它们的连心线方程为y －0－3－0＝x －32－3，即为3x －y －9＝0.答案 3x －y －9＝04．若两圆x 2＋y 2－10x －10y ＝0与x 2＋y 2－6x ＋2y －40＝0相交于两点，则它们的公共弦所在直线的方程是________．解析 两圆方程相减即得公共弦所在直线的方程为4x ＋12y －40＝0，即为x ＋3y －10＝0.答案 x ＋3y －10＝05．两圆C 1：x 2＋y 2＋4x －4y ＋7＝0，C 2：x 2＋y 2－4x －10y ＋13＝0的公切线有________条解析 先确定两圆的位置关系：圆C 1即为(x ＋2)2＋(y －2)2＝1，故圆心为(－2,2)，半径为r ＝1；同理得圆C 2的圆心为(2,5)，半径为R ＝4；∵C 1C 2＝42＋32＝5＝R ＋r ，故两圆外切，有3条公切线．答案 36．已知圆x 2＋y 2－4ax －2ay ＋20(a －1)＝0，其中常数a ＜2；若该圆与圆x 2＋y 2＝4相切，求常数a 的值．解 圆的方程可化为(x －2a )2＋(y －a )2＝5a 2－20a ＋20＝5(a －2)2，所以圆心为(2a ，a )，半径为5(2－a )． 若两圆外切，则2a －02＋a －02＝2＋5(2－a )，即5|a |＝2＋5(2－a )，由此解得a ＝1＋55. 若两圆内切，则2a 2＋a 2＝|2－5(2－a )|，即5|a |＝|2－5(2－a )|，由此解得a ＝1－55或a ＝1＋55(舍去)． 综上所述，两圆相切时，a ＝1－55或a ＝1＋55. 综合提高 限时30分钟7．圆x 2＋y 2＋8x －4y ＝0与圆x 2＋y 2＝20关于直线y ＝kx ＋b 对称，则k 的值为________，b 的值为________．解析 因两圆相交，且两圆的半径相等，故相交弦所在的直线方程即为对称轴，由⎩⎪⎨⎪⎧x 2＋y 2＋8x －4y ＝0x 2＋y 2＝20⇒8x －4y ＋20＝0即2x －y ＋5＝0为对称轴方程，∴k ＝2，b ＝5. 答案 2 58．若圆x 2＋y 2＝4与圆x 2＋y 2＋2ay －6＝0(a ＞0)的公共弦的长为23，则a ＝________.解析 x 2＋y 2＋2ay ＝6，x 2＋y 2＝4两式相减得y ＝1a. 联立⎩⎪⎨⎪⎧ y ＝1a ，x 2＋y 2＝4.消去y 得x 2＝4a 2－1a 2(a ＞0)． ∴2×4a 2－1a＝23，解得a ＝1. 答案 19．若圆(x －a )2＋(y －b )2＝b 2＋1始终平分圆(x ＋1)2＋(y ＋1)2＝4的圆周，则a ，b 应满足的关系式为________．解析 因为圆(x －a )2＋(y －b )2＝b 2＋1始终平分圆(x ＋1)2＋(y ＋1)2＝4的圆周，所以两圆的公共弦为圆(x ＋1)2＋(y ＋1)2＝4的一条直径；而两圆方程相减即得公共弦所在直线方程，为－＝b 2＋1－4，即为(2a ＋2)x ＋(2b ＋2)y －a 2－1＝0；所以圆(x ＋1)2＋(y ＋1)2＝4的圆心(－1，－1)在公共弦所在直线(2a ＋2)x ＋(2b ＋2)y －a 2－1＝0上，即a 2＋2a ＋2b ＋5＝0.答案 a 2＋2a ＋2b ＋5＝010．已知半径为1的动圆与圆(x －5)2＋(y ＋7)2＝16相切，则动圆圆心的轨迹方程(即动圆圆心坐标所满足的关系式)为________．解析 设动圆圆心的坐标为(x ，y )，若两圆外切，则x －52＋y ＋72＝4＋1，即(x －5)2＋(y ＋7)2＝25；若两圆内切，则x －52＋y ＋72＝4－1，即(x －5)2＋(y ＋7)2＝9；综上，所求的动圆圆心的轨迹方程为(x －5)2＋(y ＋7)2＝25或(x －5)2＋(y ＋7)2＝9. 答案 (x －5)2＋(y ＋7)2＝25或(x －5)2＋(y ＋7)2＝911．求圆C 1：x 2＋y 2＝1与圆C 2：x 2＋y 2－2x －2y ＋1＝0的公共弦所在直线被圆C 3：(x－1)2＋(y －1)2＝254所截得的弦长． 解 圆C 1与圆C 2的公共弦所在直线方程为：x 2＋y 2－1－(x 2＋y 2－2x －2y ＋1)＝0即x＋y －1＝0；圆心C 3到直线x ＋y －1＝0的距离d ＝|1－1－1|2＝22. 所以所求弦长为2r 2－d 2＝2 254－12＝23. 12．已知两个圆C 1：x 2＋y 2＝4，C 2：x 2＋y 2－2x －4y ＋4＝0，直线l ：x ＋2y ＝0，求经过C 1和C 2的交点且和l 相切的圆的方程．解 法一 由⎩⎪⎨⎪⎧x 2＋y 2＝4，x 2＋y 2－2x －4y ＋4＝0，解得圆C 1和C 2的交点为(0,2)与⎝⎛⎭⎫85，65；设经过C 1和C 2的交点且和l 相切的圆的圆心为(a ，b )，半径为r ，则⎩⎪⎨⎪⎧ a 2＋b －22＝r ，⎝⎛⎭⎫a －852＋⎝⎛⎭⎫b －652＝r ，|a ＋2b |12＋22＝r ， 解得⎩⎨⎧ a ＝12，b ＝1，r ＝52，∴所求圆的方程为⎝⎛⎭⎫x －122＋(y －1)2＝54. 法二 设所求圆的方程为x 2＋y 2－2x －4y ＋4＋λ(x 2＋y 2－4)＝0，即(1＋λ)x 2＋(1＋λ)y 2－2x －4y ＋4－4λ＝0；∴圆心为⎝⎛⎭⎫11＋λ，21＋λ，半径为 12 ⎝ ⎛⎭⎪⎫－21＋λ2＋⎝ ⎛⎭⎪⎫－41＋λ2－16⎝ ⎛⎭⎪⎫1－λ1＋λ； 依题意有⎪⎪⎪⎪11＋λ＋41＋λ5＝4＋16－161－λ21＋λ2， 解之得λ＝1，∴所求圆的方程为x 2＋y 2－x －2y ＝0.13．(创新拓展)已知圆O ：x 2＋y 2＝1，圆C ：(x －2)2＋(y －4)2＝1，由两圆外一点P (a ，b )引两圆的切线PA 、PB ，切点分别为A 、B ，满足PA ＝PB .(1)求实数a ，b 间满足的等量关系；(2)求切线长PA 的最小值；(3)是否存在以P为圆心的圆，使它与圆O相内切并且与圆C相外切？若存在，求出圆P的方程；若不存在，说明理由．解(1)连接PO、PC，∵PA＝PB，OA＝CB＝1；∴PO2＝PC2，从而a2＋b2＝(a－2)2＋(b－4)2，化简得实数a，b间满足的等量关系为：a＋2b－5＝0.(2)由a＋2b－5＝0，得a＝－2b＋5；∵PA＝PO2－OA2＝a2＋b2－1＝－2b＋52＋b2－1＝5b2－20b＋24＝5b－22＋4，∴当b＝2时，PA min＝2.(3)∵圆O和圆C的半径均为1，若存在半径为R圆P，与圆O相内切并且与圆C相外切，则有PO＝R－1且PC＝R＋1；于是有：PC－PO＝2，即PC＝PO＋2，从而得a－22＋b－42＝a2＋b2＋2，整理得a2＋b2＝4－(a＋2b)；将a＋2b＝5代入上式，得a2＋b2＝－1＜0；故满足条件的实数a、b不存在．∴不存在符合题设条件的圆P.。
高中数学第2章平面解析几何初步 2.2.2.3 圆与圆的位置关系练习苏教版必修
2.2.3 圆与圆的位置关系A级基础巩固1．两圆x2＋y2＝9和x2＋y2－8x＋6y＋9＝0的位置关系是( )A．相离B．相交C．内切D．外切解析：圆C1：x2＋y2＝9的圆心为C1(0，0)，半径长为r1＝3；圆C2：x2＋y2－8x＋6y＋9＝0化为(x－4)2＋(y＋3)2＝16，圆心为C2(4，－3)，半径长为r2＝4，圆心距|C1C2|＝42＋（－3）2＝5.因为|r1－r2|<|C1C2|<r1＋r2＝3＋4，所以两圆相交．答案：B2．已知0<r<2＋1，则两圆x2＋y2＝r2与(x－1)2＋(y＋1)2＝2的位置关系是( ) A．外切 B．相交 C．外离 D．内含解析：设圆(x－1)2＋(y＋1)2＝2的圆心为O′，则O′(1，－1)．圆x2＋y2＝r2的圆心O(0，0)，两圆的圆心距离d OO′＝12＋（－1）2＝ 2.显然有|r－2|<2<2＋r.所以两圆相交．答案：B3．两圆x2＋y2－6x＋16y－48＝0与x2＋y2＋4x－8y－44＝0的公切线条数为( ) A．4 B．3 C．2 D．1解析：⊙O1为(x－3)2＋(y＋8)2＝121，O1(3，－8)，r＝11，⊙O2为(x＋2)2＋(y－4)2＝64，O2(－2，4)，R＝8，所以|O1O2|＝（3＋2）2＋（－8－4）2＝13.所以r－R<|O1O2|<R＋r.所以两圆相交．所以公切线有2条．答案：C4．(2014·湖南卷)若圆C1：x2＋y2＝1与圆C2：x2＋y2－6x－8y＋m＝0外切，则m＝( ) A．21 B．19 C．9 D．－11解析：将圆C2的方程化为标准方程，利用圆心距等于两圆半径之和求解．圆C2的标准方程为(x－3)2＋(y－4)2＝25－m.又圆C1：x2＋y2＝1，所以|C1C2|＝5.又因为两圆外切，所以5＝1＋25－m，解得m＝9.答案：C5．半径长为6的圆与x 轴相切，且与圆x 2＋(y －3)2＝1内切，则此圆的方程为( )A ．(x －4)2＋(y －6)2＝6B ．(x ±4)2＋(y －6)2＝6C ．(x －4)2＋(y －6)2＝36D ．(x ±4)2＋(y －6)2＝36解析：因为半径长为6的圆与x 轴相切，设圆心坐标为(a ，b )，则b ＝6. 再由a 2＋32＝5，可以解得a ＝±4，故所求圆的方程为(x ±4)2＋(y －6)2＝36.答案：D6．圆x 2＋y 2＝50与圆x 2＋y 2－12x －6y ＋40＝0公共弦长为( ) A. 5 B. 6 C ．2 5 D ．2 6解析：x 2＋y 2＝50与x 2＋y 2－12x －6y ＋40＝0作差，得两圆公共弦所在的直线方程为2x ＋y －15＝0，圆x 2＋y 2＝50的圆心(0，0)到2x ＋y －15＝0的距离d ＝35，因此，公共弦长为2（52）2－（35）2＝2 5.答案：C7．若圆C 1：x 2＋y 2＋m ＝0与圆C 2：x 2＋y 2－6x ＋8y ＝0没有公共点，则实数m 的取值范围是________．解析：因为圆C 1以原点为圆心，而圆C 2过原点，所以两圆无公共点必有圆C 2内含于圆C 1，从而－m >100，即m <－100.答案：(－∞，－100)8．圆x 2＋y 2－2x －1＝0关于直线x －y ＋3＝0对称的圆的方程是________．解析：已知圆方程为(x －1)2＋y 2＝2，则该圆圆心关于直线x －y ＋3＝0的对称点为(－3，4)，半径也是 2.答案：(x ＋3)2＋(y －4)2＝29．过两圆x 2＋y 2－x －y －2＝0与x 2＋y 2＋4x －4y －8＝0的交点和点(3，1)的圆的方程是________．解析：设所求圆方程为(x 2＋y 2－x －y －2)＋λ(x 2＋y 2＋4x －4y －8)＝0，又过点(3，1)代入求出λ＝－25. 答案：x 2＋y 2－133x ＋y ＋2＝0 10．两圆x 2＋y 2－4x ＋2y ＋1＝0与x 2＋y 2＋4x －4y －1＝0的公切线有________条．解析：易判知两圆相外切，故有3条公切线．答案：311．已知圆C 1：x 2＋y 2＋4x －4y －1＝0与圆C 2：x 2＋y 2－2x ＋2y －7＝0相交于A ，B 两点，求公共弦AB 的长．解：由方程⎩⎪⎨⎪⎧x 2＋y 2＋4x －4y －1＝0，x 2＋y 2－2x ＋2y －7＝0，消去二次项得6x －6y ＋6＝0，即x －y ＋1＝0为所求的公共弦AB 所在的直线的方程．圆C 1即：(x ＋2)2＋(y －2)2＝9，所以C 1(－2，2)到直线AB 的距离d ＝|－2－2＋1|2＝32. 又圆C 1半径r ＝3，故弦长|AB |＝2 32－322＝3 2. B 级 能力提升12．点P 在圆C 1：x 2＋y 2－8x －4y ＋11＝0上，点Q 在圆C 2：x 2＋y 2＋4x ＋2y ＋1＝0上，则|PQ |的最小值是( )A ．5B ．1C ．35－5D ．35＋5 解析：圆C 1：x 2＋y 2－8x －4y ＋11＝0，即(x －4)2＋(y －2)2＝9，圆心为C 1(4，2)；圆C 2：x 2＋y 2＋4x ＋2y ＋1＝0，即(x ＋2)2＋(y ＋1)2＝4，圆心为C 2(－2，－1)，两圆相离，|PQ |的最小值为|C 1C 2|－(r 1＋r 2)＝35－5.答案：C13．若直线mx ＋2ny －4＝0始终平分圆x 2＋y 2－4x －2y ＋4＝0的周长，则mn 的最大值是________．解析：由直线mx ＋2ny －4＝0始终平分圆x 2＋y 2－4x －2y ＋4＝0的周长，知直线过圆的圆心(2，1)，所以2m ＋2n －4＝0，m ＋n ＝2.所以mn ＝m (2－m )＝－(m －1)2＋1≤1.答案：114．一束光线从点A (－1，1)出发经x 轴反射，到达圆C ：(x －2)2＋(y －3)2＝1上一点的最短路程是________．解析：圆C ：(x －2)2＋(y －3)2＝1.关于x 轴的对称圆C ′：(x －2)2＋(y ＋3)2＝1.所以A (－1，1)到C ′的圆心C ′(2，－3)的距离|AC ′|＝5.所以从A 发出的光线经x 轴反射到圆C 上一点的最短距离等于A 到圆C ′的圆心C ′的距离减去半径长1.即d min ＝5－1＝4.答案：415．求圆C 1：x 2＋y 2＋2kx ＋k 2－1＝0与圆C 2：x 2＋y 2＋2(k ＋1)y ＋k 2＋2k ＝0的圆心距的最小值及相应的k 值，并指出此时两圆的位置关系．解：两圆的圆心C 1(－k ，0)，C 2(0，－k －1)，所以圆心距|C 1C 2|＝k 2＋（k ＋1）2＝2k 2＋2k ＋1，当k ＝－12时，C 1C 2有最小值22. 此时，两圆的方程为C 1：⎝ ⎛⎭⎪⎫x －122＋y 2＝1， C 2：x 2＋⎝ ⎛⎭⎪⎫y ＋122＝1，由|r 1－r 2|＜d ＜r 1＋r 2，可知两圆相交． 16．已知两定圆O 1：(x －1)2＋(y －1)2＝1，圆O 2：(x ＋5)2＋(y ＋3)2＝4，动圆P 恒将两定圆的周长平分．试求动圆圆心P 的轨迹方程．解：设动圆P 的方程为(x －a )2＋(y －b )2＝r 2，即x 2＋y 2－2ax －2by ＋a 2＋b 2－r 2＝0. 将此方程分别与圆O 1，圆O 2的方程相减得公共弦所在的直线方程为：(2－2a )x ＋(2－2b )y ＋a 2＋b 2－r 2－1＝0.(10＋2a )x ＋(6＋2b )y ＋30－a 2－b 2＋r 2＝0.由于圆P 平分两定圆的周长，所以公共弦分别过两圆圆心，从而有：⎩⎪⎨⎪⎧－2a －2b ＋3＋a 2＋b 2＝r 2，10a ＋6b ＋a 2＋b 2＋38＝r 2. 消去r 2得：12a ＋8b ＋35＝0.用(x ，y )替换(a ，b )，得点P 的轨迹方程为：12x ＋8y ＋35＝0.。
高中数学苏教版必修2第二章第15课时圆与圆的位置关系配套练习
第15课 圆与圆的位置关系分层训练1． 圆222220x y x y +-+-=与圆22x y + 68240x y ---=的位置关系是 （ ）()A 相离 ()B 相交 ()C 外切 ()D 内切2． 两圆1C ：224470x y x y ++-+=，2C ：22410130x y x y +--+=的公切线有（ ）()A 2条 ()B 3条 ()C 4条 ()D 0条3．已知半径为1的动圆与圆22(5)(7)16x y -++=相切，则动圆圆心的轨迹方程(动圆圆心坐标所满足的关系式)为（ ）()A 22(5)(7)25x y -++=()B 22(5)(7)17x y -++=或22(5)(7)15x y -++=()C 22(5)(7)9x y -++=()D 22(5)(7)25x y -++=或22(5)(7)9x y -++=4．若圆222()()1x a y b b -+-=+始终平分圆22(1)(1)4x y +++=的圆周，则,a b 应满足的关系式为 （ ）()A 22250a a b +++=()B 22230a a b ---=()C 222210a b a +++=()D 22322210a b a b ++++=5．若圆224x y +=和圆22(2)(2)4x y ++-=关于直线l 对称，则l 的方程为 ．6．圆224410x y x y ++--=与圆222130x y x ++-=相交于,P Q 两点，则直线PQ 的方程为 ，公共弦PQ 的长为 ．7．已知动圆0264222=-+--+m my mx y x 恒过一个定点,这个定点的坐标是______ ．8．求经过点(4,1)A -，且与圆22:2650C x y x y ++-+=相切于点(1,2)B 的圆的方程．9．求与两条平行直线210x y +-=和2x y + 50-=相切，且圆心在直线310x y ++=上的圆的方程．拓展研究10．已知圆221:2280C x y x y +++-=与圆222:210240C x y x y +-+-=相交于,A B 两点．（1）求直线AB 的方程；（2）求经过,A B 两点且面积最小的圆的方程；（3）求圆心在直线y x =-上，且经过,A B 两点的圆的方程．11．若两圆2216x y +=及222(4)(3)x y r -++=在交点处的切线互相垂直，求实数r 的值．本节学习疑点：第15课时 圆与圆的位置关系⒈B ⒉B 3．D 4．A5．20x y -+= 6．260x y -+= ，67．(1,1) 8．22(3)(1)5x y -+-= 9．224(1)(2)5x y ++-= 10．（1）240x y -+=； （2）22(2)(1)5x y ++-=； （3）22(3)(3)10x y ++-=．11． 3r =±．学生质疑 教师释疑。
高二数学圆与圆的位置关系试题答案及解析
高二数学圆与圆的位置关系试题答案及解析1.已知动圆与圆和圆都外切,则动圆圆心的轨迹是（）A．圆B．椭圆C．双曲线D．双曲线的一支【答案】D【解析】设动圆的圆心坐标为（x，y），半径为，由于动圆与圆和圆都外切，所以，所以，根据双曲线的定义可知动圆的轨迹为双曲线的一支.【考点】1.圆与圆的位置关系；2.双曲线的定义.2.已知动圆C与圆及圆都内切，则动圆圆心C的轨迹方程为．【答案】.【解析】记两已知圆圆心为A（-1,0），B（1,0），设动圆半径为r，由动圆和两已知圆都内切得：BC+r=5，AC+1=r，两式相加得BC+AC=4＞AB=2，所以C的轨迹是椭圆，即可得其轨迹方程.【考点】（1）两圆相切的性质；（2）椭圆的定义.3.与圆都相切的直线有（）A．1条B．2条C．3条D．4条【答案】A【解析】两圆方程配方得：，，∴圆心距= ,∴圆和圆相内切，所以与两圆都相切的直线有1条.【考点】平面内两个圆的位置关系.4.在平面直角坐标系xOy中，已知圆C1：(x＋3)2＋(y－1)2＝4和圆C2：(x－4)2＋(y－5)2＝9.(1)判断两圆的位置关系;(2)求直线m的方程，使直线m被圆C1截得的弦长为4，与圆C截得的弦长是6.【答案】(1) 两圆相离 (2) 4x－7y＋19＝0【解析】(1)先由圆方程确定圆心坐标和半径，然后根据两圆心之间的距离与两圆半径和差的关系，判断两圆的位置关系；(2)由条件可知两弦长分别是两圆的直径，故所求直线过两圆圆心，故求连心线的直线方程即可.试题解析：(1)圆C1的圆心C1(－3,1)，半径r1＝2；圆C2的圆心C2(4,5)，半径r2＝2.∴C1C2＝＝>r1＋r2，∴两圆相离.（2）由题意得，所求的直线过两圆的圆心，即为连心线所在直线，易得连心线所在直线方程为：4x－7y＋19＝0.【考点】1.两圆位置关系的判断；2.直线方程.5.已知一个动圆与圆C：相内切，且过点A（4，0），则这个动圆圆心的轨迹方程是_______________.【答案】【解析】设动圆的圆心为P（x,y）,半径为r，由题意，,∴,∴动圆圆心P的轨迹是以A、C为焦点的椭圆，所以a=5,c=4,∴,∴动圆圆心的轨迹方程是【考点】本题考查了轨迹方程的求法点评：熟练掌握椭圆的定义是解决此类问题的关键，属基础题6.圆和圆的位置关系是( )A．外切B．内切C．外离D．内含【答案】A【解析】因为圆和圆的圆心坐标分别是（0，0）和（0，3），而半径内分别是1，和2，那么可知圆心距离，利用两点的距离公式可知为3，半径1+2=3，可知满足两圆相互外切的情况，故选A.【考点】本题主要是考查圆与圆的位置关系的判定问题。
2021年高中苏教版数学必修二名师导学：第2章 第15课时 直线和圆的位置关系
第15课时直线和圆的位置关系教学过程一、问题情境在课桌中心放置一张白纸,用圆规在白纸上画一个圆,将一把直尺从桌子的一边平行于课桌边缘平移到桌子的另一边.假如将直尺一条边看成一条直线,在这条直线移动过程中你看到了什么现象?(这是一个开放问题,没有精确答案,同学回答时可能都是“白话”,同学可能会回答“直线先靠近圆,再远离圆”、“直线先相离,再相切,然后相交,再相切,最终又远离”等.只要意思对,就应当赐予确定.让同学充分表达,为后面一系列问题做预备)二、数学建构问题1学校学过的平面几何中,直线和圆有哪几种位置关系?(该问题可能同学一开头已经回答了,在这里再次毁灭的目的是明确在数学中直线和圆位置关系的精确表述,只能是“相离”、“相切”、“相交”,不能用其他意思相近的词语代替)问题2在刚才的操作中,你能用数学符号来表示直线靠近(远离)圆吗?你会推断直线和圆的位置关系吗?(这实际上是直线和圆的位置关系的判定,同学在学校已经有确定的基础.在本节课中,再次毁灭这个判定,目的在于说明这个判定揭示的是直线和圆位置关系的几何特征)设圆心到直线的距离为d,圆的半径为r,则d>r时,直线和圆相离;d=r时,直线和圆相切;d<r时,直线和圆相交.问题3当直线和圆分别“相离”、“相切”、“相交”时所表现出来的几何特征分别是什么?(启发同学由图形猎取推断直线与圆的位置关系的直观认知,即他们看到的直线和圆相离时没有公共点,相切时只有一个公共点,相交时有两个公共点)问题4你能用数学语言来解释直线和圆没有公共点、只有一个公共点、有两个公共点的含义吗?(引导同学用直线与圆的方程推断它们之间的位置关系,即图象交点个数就是它们所构成方程组的解的个数)设直线l和圆C的方程分别为:Ax+By+C=0 (A,B不全为0),x2+y2+Dx+Ey+F=0 (D2+E2-4F>0).由直线l和圆C的方程联立方程组则方程组无解时,直线和圆相离;方程组仅有一组解时,直线和圆相切;方程组有两组不同的解时,直线和圆相交.问题5请总结一下到目前为止,推断直线和圆的位置关系有哪几种方法?它们有什么不同?(引导对学过的内容总结,由学校学过的平面几何过渡到解析几何,从“形”过渡到“数”,了解学问之间的联系和进展)几何法是平面几何的方法,是直线和圆的几何特征;而利用联立方程组的方法是解析法,是直线和圆的代数特征.利用代数的方法解决几何问题就是解析的思想.三、数学应用【例1】(教材P113例1)求直线4x+3y=40和圆x2+y2=100的公共点的坐标,并推断它们的位置关系.[3] [处理建议]直线和圆的交点坐标就是它们联立的方程组的解,本题让同学板演.[规范板书]解直线4x+3y=40和圆x2+y2=100的公共点的坐标就是方程组的解.解这个方程组,得所以公共点坐标为(10, 0),.直线4x+3y=40和圆x2+y2=100有两个公共点,所以直线和圆相交.[题后反思]求两曲线的交点坐标或交点的个数可以用联立方程组的方法,用方程组的解反映图形的状况,这是一般的方法,是通解.变式已知直线y=3x+m和圆x2+y2=2相交于点(1, 1),求直线和圆的另一个交点的坐标.[处理建议]让同学比较和例1的区分,直线的方程未知,先依据条件求出直线的方程,再联立方程组求解.在解方程时,实际上已经知道方程的一个根了,可以利用根与系数关系来解决,在上课时要引导同学留意这一点,这也是近几年高考中有所体现的题型.解由于线y=3x+m过点(1, 1),所以1=3+m,所以m=-2,将直线和圆的方程联立方程组消去y,得10x2-12x+2=0,由题意方程一个根为1,设另一个根为x2,则1×x2=,得x2=.将x2=代入直线的方程得y2=-,所以直线和圆的另一个交点的坐标为.【例2】(教材P113例2)自点A(-1, 4)作圆(x-2)2+(y-3)2=1的切线l,求切线l的方程.[4][处理建议]要求直线的方程还需要知道什么?先引导同学找准解决问题的方向,即还需要知道直线的斜率.再依据直线和圆相切的条件,列出关于斜率的方程,求出斜率.让同学在下面书写,老师可以找出用不同方式解题的同学上黑板板演.[规范板书]解方法一:当直线l垂直于x轴时,直线l:x=-1与圆相离,不满足条件.当直线l不垂直于x轴时,可设直线l的方程为y-4=k(x+1),即kx-y+(k+4)=0,由于直线和圆相切,所以圆心(2, 3)到直线l的距离等于圆的半径,故=1.解得k=0或k=-,因此,所求直线l的方程为y=4或3x+4y-13=0方法二:当直线l垂直于x轴时,直线l:x=-1与圆相离,不满足条件.当直线l不垂直于x轴时,可设直线l的方程为y-4=k(x+1),由于直线和圆相切,所以方程组仅有一解.由方程组消去y,得关于x的一元二次方程(1+k2)x2+(2k2+2k-4)x+k2+2k+4=0.依题意,这个一元二次方程有两个相等实根,所以判别式Δ=(2k2+2k-4)2-4(1+k2)(k2+2k+4)=0.解得k=0或k=-.因此,所求直线l的方程为y=4或3x+4y-13=0.[题后反思]处理直线和圆相切时,一般有两种方法,一是用几何法,即d=r;另一个是代数法,即通过方程组的解来分析.特殊要留意在设直线方程时,要关注直线方程适用的条件,往往要分状况争辩,这一点格外简洁遗漏.变式(2010年山东枣庄模拟改编)将圆x2+y2=1沿x轴正方向平移1个单位后得圆C,若过点(3, 0)的直线l 和圆C相切,求直线l的方程.[处理建议]本题照旧强调在设直线方程时,要分状况争辩.解将圆x2+y2=1向右平移1个单位后得圆的方程为(x-1)2+y2=1.过点(3, 0)的直线l方程分为两种状况:当斜率不存在时x=3,与圆不相切;当斜率存在时,设直线方程为y=k(x-3),即kx-y-3k=0,由于直线和圆相切,所以圆心(1, 0)到直线l的距离等于圆的半径,故=1.解得k=±.因此,所求直线l的方程为y=±(x-3).【例3】(教材P114例3)求直线x-y+2=0被圆x2+y2=4截得的弦长.[5][处理建议]本题同样有两种方法,让同学先思考,再找用不同方式解题的同学上黑板板演.假犹如学不能用两种方法解决,老师可以引导,如用“弦长就是一条线段长,即两点之间的距离.”引导同学用代数法;用“在我们学校平面几何中还学过关于弦长的问题吗?”引导同学用几何法,即用垂径定理来解决.[规范板书]解法一直线x-y+2=0和圆x2+y2=4的公共点坐标就是方程组的解.解这个方程组,得所以公共点坐标为(, 1),(0, 2),直线x-y+2=0被圆x2+y2=4截得的弦长为=2.(图2)解法二如图2,设直线x-y+2=0和圆x2+y2=4交于A,B两点,弦AB的中点为M,则OM⊥AB(O为坐标原点),所以AB=2AM=2=2=2.[题后反思]弦的相关问题不外乎用代数法或几何法解决,几何法侧重于图形特征,代数法侧重于运算,当条件具备几何图形的某些特征时,用几何法解答会更便利快捷.圆的弦长的求法:①几何法:设圆的半径为r,弦心距为d,弦长为L,则=r2-d2;②代数法:设直线与圆相交于A(x1,y1),B(x2,y2)两点,解方程组由方程组消去y,得关于x的一元二次方程,求出A,B的坐标,再用两点之间的距离公式求出弦长AB.变式1已知点A(1, 1),求过点A的圆x2+y2-4y=0的最长与最短的弦长.[处理建议]结合图象分析,找出过圆内一点作最长弦和最短弦的条件.[规范板书]解圆x2+y2-4y=0圆心为C(0, 2),r=2,由于点A(1, 1)在该圆内,所以过A最长的弦就是过A及圆心的直径,长为4;最短的弦就是与AC垂直的弦,由于AC==,所以弦长为2=2.变式2已知过点M(-3,-3)的直线l被圆x2+y2+4y-21=0所截得的弦长为8,求直线l的方程.[处理建议]把圆的方程化为标准式,求出圆心坐标和半径,求出弦心距的值.设出直线l的方程,由弦心距的值求出直线的斜率,即得直线l的方程.[规范板书]解圆x2+y2+4y-21=0的圆心坐标为(0,-2),半径r=5.由于直线l被圆所截得的弦长是8,所以弦心距为=3.由于直线l过点M(-3,-3),所以,当斜率不存在时,直线方程为x=-3,满足题意;当斜率存在时,可设所求直线l的方程为y+3=k(x+3),即kx-y+3k-3=0.则由圆心到直线的距离等于弦心距,得=3,解得k=-,此时直线方程为4x+3y+21=0.故所求直线有两条,它们分别为x=-3, 4x+3y+21=0.*【例4】已知点P(0, 5)及圆:C:x2+y2+4x-12y+24=0.(1)若直线l过点P且被圆C截得的线段长为4,求l的方程;(2)求圆C内过点P的弦的中点的轨迹方程.[6][处理建议]对于(1),要求直线的方程只需要求出直线的斜率,利用垂径定理求出圆心到直线的距离,从而得出关于斜率的等量关系,求出斜率;对于(2)只需要列出关于弦中点D(x,y)的等式即可.解(1)如图,AB=4,D是AB的中点,则AD=2,AC=4,(图3)在Rt△ADC中,可得CD=2.设所求直线的斜率为k,则直线的方程为y-5=kx,即kx-y+5=0.由点C 到直线的距离公式=2,得k=,此时直线l的方程为3x-4y+20=0.又直线l的斜率不存在时,也满足题意,此时的方程为x=0.所以所求直线为x=0或3x-4y+20=0.(2)方法一:设圆C上过点P的弦的中点为D(x,y),由于CD⊥PD,所以·=0,即(x+2,y-6)·(x,y-5)=0,化简得轨迹方程x2+y2+2x-11y+30=0.方法二:设弦的两个端点分别为A(x1,y1),B(x2,y2),弦的中点为D(x,y),则x1+x2=2x,y1+y2=2y.将A(x1,y1),B(x2,y2)代入圆的方程得①-②得(x1-x2)(x1+x2)+(y1-y2)(y1+y2)+4(x1-x2)-12(y1-y2)=0,同除以(x1-x2),得x+k AB y+2-6k AB=0,由于k AB=k PD =,所以x++2-=0,整理得轨迹方程x2+y2+2x-11y+30=0.[题后反思]在争辩与弦的中点有关问题时,留意运用“平方差法”,即设弦AB两端点的坐标分别为A(x1,y1), B(x2,y2),中点为(x0,y0),由得k==-=-.该法常用来解决与弦的中点、直线的斜率有关的问题.四、课堂练习1.对任意实数k,圆C:x2+y2-6x-8y+12=0与直线l:kx-y-4k+3=0的位置关系是相交.提示由于动直线kx-y-4k+3=0过定点(4, 3),而该点恰好在圆内部.所以直线和圆相交.2.若直线ax+by=1与圆x2+y2=1相交,则点P(a,b)与圆的位置关系是在圆外.解由于直线ax+by=1与圆x2+y2=1相交,所以圆心到直线的距离小于半径,则<1,即>1,所以点在圆外.3.(1)求过圆x2+y2=4上一点的圆的切线方程.(2)求过原点且与圆(x-3)2+(y-1)2=1相切的直线方程.答案(1)-x+y-4=0.(2)y=x和y=0.4.求过原点且倾斜角为60°的直线被圆x2+y2-4y=0所截得的弦长.提示本题有多种方法,用几何法,代数法都可以,都比较简洁.答案2.五、课堂小结1.在直线与圆的位置关系中,“直线与圆相切时求切线”和“相交时争辩与弦长有关的问题”是两个重点内容;求切线时,若知道切点,可直接利用公式;若过圆外一点求切线,一般运用圆心到直线的距离等于半径来求,但留意有两条.2.解决与弦长有关的问题时,留意运用由半径、弦心距、弦长的一半构成的直角三角形,也可以运用弦长公式,就是通常所说的“几何法”和“代数法”.3.解决直线与圆的位置关系问题,一般有两种方法,即几何法或代数法,从运算的合理、简明的要求选择,通常接受几何法,但代数法具有一般性.4.数形结合法(如几何法)是解决直线与圆的位置关系的重要方法.。
苏教版高中数学必修二第15课时——圆与圆的位置关系(配套练习).docx
桑水第15课 圆与圆的位置关系分层训练1． 圆222220x y x y +-+-=与圆22x y +68240x y ---=的位置关系是 （ ）()A 相离 ()B 相交 ()C 外切 ()D 内切2． 两圆1C ：224470x y x y ++-+=，2C ：22410130x y x y +--+=的公切线有（ ）()A 2条 ()B 3条 ()C 4条 ()D 0条3．已知半径为1的动圆与圆22(5)(7)16x y -++=相切，则动圆圆心的轨迹方程(动圆圆心坐标所满足的关系式)为（ ）()A 22(5)(7)25x y -++= ()B 22(5)(7)17x y -++=或22(5)(7)15x y -++= ()C 22(5)(7)9x y -++= ()D 22(5)(7)25x y -++=或22(5)(7)9x y -++= 4．若圆222()()1x a y b b -+-=+始终平分圆22(1)(1)4x y +++=的圆周，则,a b 应满足的关系式为 （ ）()A 22250a a b +++=()B 22230a a b ---= ()C 222210a b a +++=()D 22322210a b a b ++++=5．若圆224x y +=和圆22(2)(2)4x y ++-=关于直线l 对称，则l 的方程为 ．6．圆224410x y x y ++--=与圆222130x y x ++-=相交于,P Q 两点，则直线PQ 的方程为 ，公共弦PQ 的长为 ．7．已知动圆0264222=-+--+m my mx y x 恒过一个定点,这个定点的坐标是______ ． 8．求经过点(4,1)A -，且与圆22:2650C x y x y ++-+=相切于点(1,2)B 的圆的方程．9．求与两条平行直线210x y +-=和2x y +50-=相切，且圆心在直线310x y ++=上的圆的方程．拓展研究10．已知圆221:2280C x y x y +++-=与圆222:210240C x y x y +-+-=相交于,A B两点．（1）求直线AB 的方程； （2）求经过,A B 两点且面积最小的圆的方程； （3）求圆心在直线y x =-上，且经过,A B 两点的圆的方程．桑水11．若两圆2216x y +=及222(4)(3)x y r -++=在交点处的切线互相垂直，求实数r 的值．本节学习疑点：学生质疑教师释疑。
高中数学 第二章 第15课时 圆与圆的位置关系学案 苏教版必修2-苏教版高一必修2数学学案
第二章 平面解析几何初步 第二节 圆与方程第15课时 圆与圆的位置关系【学习导航】 知识网络 学习要求 1．掌握圆与圆的位置关系的代数与几何判别方法； 2．了解用代数法研究圆的关系的优点； 3．了解算法思想． 【课堂互动】自学评价1．圆与圆之间有外离，外切，相交， 内切，内含五种位置关系．2.设两圆的半径分别为12,r r ，圆心距为d ，当12d r r >+时，两圆外离， 当12d r r =+时，两圆外切， 当1212||r r d r r -<<+时，两圆相交， 当12d r r =-时，两圆内切， 当12d r r <-时，两圆内含．3.思考：用代数方法，通过联立方程组，用判别式法可以判断两个圆的位置关系吗？为什么？ 【精典范例】 例1：判断下列两圆的位置关系： 2222(1)(2)(2)1(2)(5)16x y x y ++-=-+-=与 222226706270x y x x y y ++-=++-=（）与 【解】（1）根据题意得，两圆的半径分别为1214r r ==和，两圆的圆心距 22[2(2)](52) 5.d =--+-= 因为 12d r r =+，所以两圆外切． （2）将两圆的方程化为标准方程，得2222(3)16,(3)36x y x y ++=++=． 故两圆的半径分别为1246r r ==和， 两圆的圆心距 22(03)(30)32d =-+-= ． 因为1212||r r d r r -<<+，所以两圆相交． 点评：判断两圆的位置关系，不仅仅要判断 d 与12r r +的大小，有时还需要判断d 与12r r -的关系． 例2：求过点(0,6)A 且与圆 22:10100C x y x y +++= 切于原点的圆的方程． 分析：如图，所求圆经过原点和(0,6)A ，且圆心应在已知圆的圆心与原点的连线上．根据这三个条件可确定圆的方程． 【解】将圆C 化为标准方程，得 22(5)(5)50x y +++=， 则圆心为(5,5)C --，半径为52．所以经过听课随笔圆与圆的位外切 相交 内切 外离 内含此圆心和原点的直线方程为0x y -=． 设所求圆的方程为222()()x a y b r -+-=．由题意知，(0,0),(0,6)O A 在此圆上，且圆心(,)M a b 在直线0x y -=上，则有222222(0)(0),3,(0)(6),3,0a b r a a b r b a b r ⎧-+-=⎧=⎪⎪-+-=⇒=⎨⎨⎪⎪-==⎩⎩ 于是所求圆的方程是22(3)(3)18x y -+-=．点评：此题还可以通过弦的中垂线必过圆心这一性质来解题，由题意，圆心必在直线3y =上，又圆心在直线0x y -=，从而圆心坐标为(3,3)，r =，所以所求圆的方程为22(3)(3)18x y -+-=．追踪训练一1.判断下列两个圆的位置关系：2222(1)(3)(2)1(7)(1)36x y x y -++=-+-=与；2222(2)2232030x y x y x y x y +-+=+--=与3．答案：（1）内切，（2）相交．2. 若圆22x y m +=与圆2268x y x y ++- 110-=相交，求实数m 的取值范围． 答案：1121m <<．【选修延伸】一、两圆公共弦长及公共弦所在直线方程 例3: 已知圆221:2610C x y x y ++-+=，圆222:42110C x y x y +-+-=，求两圆的公共弦所在的直线方程及公共弦长． 分析：因两圆的交点坐标同时满足两个圆方程，联立方程组，消去2x 项、2y 项，即得两圆的两个交点所在的直线方程，利用勾股定理可求出两圆公共弦长． 【解】设两圆交点为11(,)A x y 、22(,)B x y ，则A B 、两点坐标满足方程组 22222610,(1)42110,(2)x y x y x y x y ⎧++-+=⎪⎨+-+-=⎪⎩，(1)(2)-得3460x y -+=． 因为，A B 、两点坐标都满足此方程， 所以，3460x y -+=即为两圆公共弦所在的直线方程． 易知圆1C 的圆心(1,3)-，半径3r =． 又1C 到直线的距离为95d ==．所以，245AB ===．即两圆的公共弦长为245． 点评:本题较为复杂，要讨论的情况比较多，解题过程中要 注重分析． 例5：求过两圆22640x y x ++-=和 226280x y y ++-=的交点，且圆心在直线40x y --=上的圆的方程．分析：所求圆圆心是两已知圆连心线和已知直线的交点，再利用弦心距、弦长、半径之间的关系求圆半径【解】（法一）可求得两圆连心线所在直线的方程为30x y ++=．由40,30,x y x y --=⎧⎨++=⎩得圆心17(,)22-．利用弦心距、弦长、半径之间的关系可求得公共弦长d = 所以，圆半径22217|()4|89()22d r ⎛⎫--+ ⎪=+=． 所以，所求圆方程为221789()()222x y -++=， 即227320x y x y +-+-=（法二）设所求圆的方程为222264(628)0x y x x y y λ++-+++-=即22664280111x y x y λλλλλ++++-=+++． 故此圆的圆心为33(,)11λλλ--++，它在直线40x y --=上， 所以334011λλλ--+-=++，所以7λ=-．所以所求圆方程为227320x y x y +-+-=点评:“解法二”中设出的经过两已知圆交点的圆方程叫做经过两已知圆的圆系方程．思维点拔：解题时要充分利用两圆位置关系的几何性质． 追踪训练二 1．一个圆经过圆221:890C x y x +--=和圆222:8150C x y y +-+=的两个交点，且圆心在直线210x y --=上，求该圆的方程． 答案：22101412033x y x y +---=． 2．已知一个圆经过直线240x y ++=与圆222410x y x y ++-+=的两个交点，并且有最小面积，求此圆的方程． 答案：221364()()x y ++-=．。
圆和圆的位置关系经典例题+练习
例1. 已知⊙O 1、⊙O 2半径分别为15cm 和13cm ，它们相交于A 、B 两点，且AB 长24cm ，求O 1O 2长。
分析：该题没有给出图形，两圆相交有两种可能性： 1. 两圆心在公共弦的两侧； 2. 两圆心在公共弦的同侧；因此，我们必须分两种情况来解。
解：（1）连结O 1O 2交AB 于C （2）连结O 1O 2并延长交AB 于C ∵⊙O 1 ⊙O 2交于A 、B 两点 ∴⊥，且O O AB AC AB cm 121212== 在Rt △AO 1C 中，由勾股定理： O C O A AC cm 11222215129=-=-=() 在Rt △AO 2C 中，由勾股定理： O C O A AC cm 22222213125=-=-=∴如图（1） O 1O 2=O 1C+O 2C=14cm如图（2） O 1O 2=O 1C －O 2C=4cm例1是两圆相交时的一题两解问题，希望引起同学们的重视。
例2. 如图，⊙O 1与⊙O 2外切于点P ，AC 切⊙O 2于C 交⊙O 1于B ，AP 交⊙O 2于D ，求证：（1）PC 平分∠BPD（2）若两圆内切，结论还成立吗？证明你的结论。
证明：（1）过P 点作公切线PM 交AC 于M 点 ∵AC 切⊙O 2于C∴MP=MC ∴∠MCP=∠MPC在⊙O1中，由弦切角定理：∠BPM=∠A∵∠CPD为△APC的外角∴∠CPD=∠A+∠MCP=∠BPM+∠MPC=∠BPC∴PC平分∠BPD。
（2）两圆内切时仍有这样的结论。
证明：过P点作公切线PM交AB延长线于M∵AM切⊙O2于C，∴MC=MP∴∠MPC=∠MCP∴∠MPB=∠A∵∠MCP为△CPA的外角∠MCP=∠CPA+∠A又∠MPC=∠MPB+∠BPC∴∠BPC=∠CPA即PC平分∠BPD。
在解决有关两圆相切的问题时，过切点作两圆的公切线是常见的一条辅助线，利用弦切角及圆周角的性质或切线长定理，可使问题迎刃而解。
苏教版学高中数学必修二平面解析几何初步圆与圆的位置关系讲义
学习目标核心素养１．能根据两个圆的方程，判断两圆的位置关系．（重点）２．当两个圆有公共点时能求出它们的公共点，能运用两圆的位置关系解决有关问题．（易错点）３．了解两圆相交时公共弦所在直线的求法；了解两圆公切线的概念，会判断所给直线是不是两圆的公切线．（难点）通过学习本节内容提升学生的逻辑推理和数学运算核心素养.圆与圆的位置关系１．几何法：若两圆的半径分别为r１，r２，两圆的圆心距为d，则两圆的位置关系的判断方法如下：位置关系外离外切相交内切内含图示d与r１，r２的关系d>r１＋r２d＝r１＋r２|r１—r２|<d<r１＋r２d＝|r１—r２|d<|r１—r２|错误!错误!错误!错误!１．思考辨析（１）两圆方程联立，若方程组有两个解，则两圆相交．（）（２）若两个圆没有公共点，则两圆一定外离．（）（３）若两圆外切，则两圆有且只有一个公共点，反之也成立．（）（４）若两圆有公共点，则|r１—r２|≤d≤r１＋r２. （）[答案] （１）√（２）×（３）×（４）√２．两圆x２＋y２＋6x＋４y＝0及x２＋y２＋４x＋２y—４＝0的公共弦所在的直线方程为______________．x＋y＋２＝0 [联立错误!１—２得：x＋y＋２＝0．]３．圆x２＋y２＝１与圆x２＋y２＋２x＋２y＋１＝0的交点坐标为________．（—１，0）和（0，—１）[由错误!解得错误!或错误!]４．圆C１：x２＋y２＋４x—４y＋7＝0和圆C２：x２＋y２—４x—１0y＋１３＝0的公切线有________条．３[圆C１的圆心坐标为C１（—２，２），半径r１＝１．∵圆C２的圆心坐标为C２（２，５），半径r２＝４．∴|C１C２|＝错误!＝５，r１＋r２＝５，∴两圆外切．故公切线有３条．]两圆位置关系的判定１２２２２２２（１）m＝１时，圆C１与圆C２有什么位置关系？（２）是否存在m使得圆C１与圆C２内含？思路探究：（１）参数m的值已知，求解时可先找出圆心及半径，然后比较两圆的圆心距d与r１＋r和|r１—r２|的大小关系．（２）假设存在m使得圆C１与圆C２内含，则圆心距d<|r１—r２|.２[解] （１）∵m＝１，∴两圆的方程分别可化为：C１：（x—１）２＋（y＋２）２＝9．C２：（x＋１）２＋y２＝１．两圆的圆心距d＝错误!＝２错误!，又∵r１＋r２＝３＋１＝４，r１—r２＝３—１＝２，∴r１—r２<d<r１＋r２，所以圆C１与圆C２相交．（２）假设存在m使得圆C１与圆C２内含，则错误!<３—１，即（m＋１）２<0，显然不等式无解．故不存在m使得圆C１与圆C２内含．判断圆与圆的位置关系时，通常用几何法，即转化为判断圆心距与两圆半径的和与差之间的大小关系．１．已知圆C１：x２＋y２—２ax—２y＋a２—１５＝0，C２：x２＋y２—４ax—２y＋４a２＝0（a>0）．试求a为何值时两圆C１，C２（１）相切；（２）相交；（３）相离；（４）内含．[解] 对圆C１，C２的方程，经配方后可得：C１：（x—a）２＋（y—１）２＝１6，C２：（x—２a）２＋（y—１）２＝１，∴圆心C１（a，１），r１＝４，C２（２a，１），r２＝１，∴|C１C２|＝错误!＝a，（１）当|C１C２|＝r１＋r２＝５，即a＝５时，两圆外切，当|C１C２|＝r１—r２＝３，即a＝３时，两圆内切．（２）当３<|C１C２|<５，即３<a<５，时，两圆相交．（３）当|C１C２|>５，即a>５时，两圆外离．（４）当|C１C２|<３，即0<a<３时，两圆内含．两圆相交的问题１２２２２２（１）求公共弦所在直线的方程；（２）求公共弦的长．思路探究：错误!→错误!→错误!→错误![解] （１）设两圆的交点分别为A（x１，y１），B（x２，y２）．将点A的坐标代入两圆方程，得错误!１—２，得x１—２y１＋４＝0，故点A在直线x—２y＋４＝0上．同理，点B也在直线x—２y＋４＝0上，即点A，B均在直线x—２y＋４＝0上．因为经过两点有且只有一条直线，所以直线AB的方程为x—２y＋４＝0，即公共弦所在直线的方程为x—２y＋４＝0．（２）圆C１的方程可化为（x—１）２＋（y＋５）２＝５0，所以C１（１，—５），半径r１＝５错误!.C１（１，—５）到公共弦的距离d＝错误!＝３错误!.设公共弦的长为l，则l＝２错误!＝２错误!＝２错误!.１．利用两圆的方程相减求两圆公共弦所在直线的方程时，必须注意只有当两圆方程中二次项的系数相同时，才能如此求解，若二次项的系数不同，需先调整方程中各项的系数．２．求两圆的公共弦长有两种方法：一是先求出两圆公共弦所在直线的方程；再利用圆的半径、弦心距、弦长的一半构成的直角三角形求解；二是联立两圆的方程求出交点坐标，再利用两点间的距离公式求弦长．２．求圆心在直线x—y—４＝0上，且经过两圆x２＋y２—４x—6＝0和x２＋y２—４y—6＝0的交点的圆的方程．[解] 由错误!得错误!或错误!即两圆的交点坐标为A（—１，—１），B（３，３）．设所求圆的圆心坐标C为（a，a—４），由题意可知CA＝CB，即错误!＝错误!，解得a＝３，∴C（３，—１）．∴CA＝错误!＝４，所以，所求圆的方程为（x—３）２＋（y＋１）２＝１6．两圆相切的问题１．若已知圆C１：x２＋y２＝a２（a>0）和C２：（x—２）２＋y２＝１，那么a取何值时C１与C２相外切？[提示] 由|C１C２|＝a＋１，得a＋１＝２，∴a＝１．２．若将探究１中，C２的方程改为（x—２）２＋y２＝r２（r>0），那么a与r满足什么条件时两圆相切？[提示] 若两圆外切，则a＋r＝|C１C２|＝２，即a＋r＝２时外切．若两圆内切，则|r—a|＝|C１C２|＝２．∴r—a＝２或a—r＝２．【例３】已知圆C１：x２＋y２＋４x—４y—５＝0与圆C２：x２＋y２—8x＋４y＋7＝0．（１）证明：圆C１与圆C２相切，并求过切点的公切线的方程；（２）求过点（２，３）且与两圆相切于（１）中切点的圆的方程．思路探究：（１）证明|C１C２|＝r１＋r２，两圆方程相减得公切线方程．（２）由圆系方程设圆的方程，将已知点代入．[解] （１）把圆C１与圆C２都化为标准方程形式，得（x＋２）２＋（y—２）２＝１３，（x—４）２＋（y＋２）２＝１３；圆心与半径长分别为C１（—２，２），r１＝错误!；C２（４，—２），r２＝错误!，因为|C１C２|＝错误!＝２错误!＝r１＋r２，所以圆C１与圆C２相切．由错误!得１２x—8y—１２＝0，即３x—２y—３＝0，这就是过切点的两圆公切线的方程．（２）由圆系方程，可设所求圆的方程为x２＋y２＋４x—４y—５＋λ（３x—２y—３）＝0．点（２，３）在此圆上，将点坐标代入方程解得λ＝错误!.所以所求圆的方程为x２＋y２＋４x—４y—５＋错误!（３x—２y—３）＝0，即x２＋y２＋8x—错误!y—9＝0．两圆相切有如下性质（１）设两圆的圆心分别为O１，O２，半径分别为r１，r２，则两圆相切错误!（２）两圆相切时，两圆圆心的连线过切点（两圆若相交时，两圆圆心的连线垂直平分公共弦）．在解题过程中应用这些性质，有时能大大简化运算．３．求与圆C：x２＋y２—２x＝0外切且与直线l：x＋错误!y＝0相切于点M（３，—错误!）的圆的方程．[解] 圆C的方程可化为（x—１）２＋y２＝１，圆心C（１，0），半径为１．设所求圆的方程为（x—a）２＋（y—b）２＝r２（r>0），由题意可知错误!解得错误!或错误!所以所求圆的方程为（x—４）２＋y２＝４或x２＋（y＋４错误!）２＝３6．１．本节课的重点是理解并掌握圆与圆的位置关系，会利用方程判断圆与圆的位置关系，以及解决有关问题，能利用直线与圆的方程解决平面几何问题．难点是利用方程判断圆与圆的位置关系．２．本节课要重点掌握的规律方法（１）判断两圆位置关系的方法及应用．（２）求两圆公共弦长的方法．３．本节课的易错点是判断两圆位置关系时易忽略相切的两种情况而丢解．１．圆（x＋２）２＋y２＝４与圆（x—２）２＋（y—１）２＝9的位置关系为（）Ａ．相离Ｂ．相切Ｃ．相交Ｄ．内含C[两圆圆心分别为（—２，0），（２，１），半径分别为２和３，圆心距d＝错误!＝错误!.∵３—２<d<３＋２，∴两圆相交．]２．已知圆C１：x２＋y２—２mx＋m２＝１与圆C２：x２＋y２＋２y＝8外离，则实数m的取值范围是________．（—∞，—错误!）∪（错误!，＋∞）[圆C１可化为（x—m）２＋y２＝１，圆C２可化为x２＋（y ＋１）２＝9，所以圆心C１（m，0），C２（0，—１），半径r１＝１，r２＝３，因为两圆外离，所以应有C１C２>r１＋r２＝１＋３＝４，即错误!>４，解得m>错误!或m<—错误!.]３．半径长为6的圆与x轴相切，且与圆x２＋（y—３）２＝１内切，则此圆的方程为________．（x±４）２＋（y—6）２＝３6 [设圆心坐标为（a，b），由题意知b＝6，错误!＝５，可以解得a ＝±４，故所求圆的方程为（x±４）２＋（y—6）２＝３6．]４．已知圆C１：x２＋y２—２mx＋４y＋m２—５＝0，圆C２：x２＋y２＋２x—２my＋m２—３＝0，m为何值时，（１）圆C１与圆C２外切；（２）圆C１与圆C２内含．[解] 将圆C１，圆C２化为标准形式得C１：（x—m）２＋（y＋２）２＝9，C２：（x＋１）２＋（y—m）２＝４．则C１（m，—２），C２（—１，m），r１＝３，r２＝２，C１C２＝错误!＝错误!.（１）当圆C１与圆C２外切时，有r１＋r２＝C１C２，则错误!＝５，解得m＝—５或２，即当m＝—５或２时，两圆外切．（２）当圆C１与圆C２内含时，C１C２<r１—r２，∴错误!<１，即m２＋３m＋２<0．∵f（m）＝m２＋３m＋２的图象与横坐标轴的交点是（—２，0），（—１，0），∴由m２＋３m＋２<0，可得—２<m<—１，即当—２<m<—１时，两圆内含．。
2.2.3圆与圆的位置关系作业 高中数学 必修二 苏教版 含答案
2.2.3 圆与圆的位置关系5分钟训练(预习类训练,可用于课前)1.类比直线和圆的位置关系,说明如何判断圆与圆的位置关系.思路解析：通常可以利用圆心到直线的距离与圆的半径的大小关系来判断直线和圆的位置关系,对于两圆来说,可以利用两个圆心间距离与两圆半径的和或差之间的大小关系来判断两圆的位置关系.答案：利用两圆圆心之间距离与两圆半径的和或差的大小关系判定.2.设两圆的半径分别为R 、r,圆心距为d,当d>R+r 时,两圆_________;当d=R+r 时,两圆_________;当R-r<d<R+r(R≥r)时,两圆_________;当d=R-r(R>r)时,两圆_________;当d<R-r(R>r)时,两圆_________.思路解析：可以作图利用平面几何知识分析得到结果.答案：外离 外切 相交 内切 内含3.已知两圆的半径分别为方程x 2-7x+12=0的两个根,如果O 1O 2=8,两圆的位置关系是( )A.外离B.外切C.内切D.相交思路解析：由方程x 2-7x+12=0得两个根分别为3或4，故两圆半径之和为7，而两圆心之间的距离为8，根据两圆的位置关系知这两圆外离.答案：A10分钟训练(强化类训练，可用于课中)1.两圆x 2+y 2=4和x 2+y 2-2x+4y+1=0关于直线l 对称，则l 的方程为( )A.2x-4y-5=0B.2x-3y+1=0C.2x-y+1=0D.x+3y-1=0 思路解析：考查两圆轴对称的概念,即两圆的圆心关于直线对称.由题意知两圆的圆心分别为C 1(0,0),C 2(1,-2).若要两圆关于直线l 对称,则C 1、C 2关于l 对称.因为 C 1C 2的中点为(21,-1),k C1C2=-2.所以l 的方程为y+1=21(x-21)，即2x-4y-5=0. 答案：2x-4y-5=02.已知0＜r ＜12+,则两圆x 2+y 2=r 2与(x-1)2+(y+1)2=2的位置关系是( )A.外切B.相交C.外离D.内含思路解析：设圆(x-1)2+(y+1)2=2的圆心为O′，则O′(1,-1).两圆的圆心距离|OO′|=2)1(122=-+.显然有r r +<<-22|2|，所以两圆相交.答案：B3.已知圆C 1:x 2+y 2-4x+6y=0和圆C 2:x 2+y 2-6x=0交于A 、B 两点,则AB 的垂直平分线方程为( )A.x+y+3=0B.2x-y-5=0C.3x-y-9=0D.4x-3y+7=0 思路解析：由平面几何知识，知AB 的垂直平分线即为两圆心的连线,把两圆分别化为标准式可得两圆心分别为C 1(2,-3),C 2(3,0),因为C 1C 2斜率为3,所以直线方程为y-0=3(x-3),化为一般式可得3x-y-9=0.答案：C4.若圆x 2+y 2=4与x 2+y 2-2ax+a 2-1=0相内切,则a=_____________.思路解析：两圆的圆心和半径分别为O 1(0,0),r 1=2,O 2(a,0),r 2=1,由两圆内切可得|O 1O 2|=r 1-r 2,即|a|=1,所以a=±1.答案：±15.已知动圆M 与y 轴相切且与定圆A ：(x-3)2+y 2=9外切，求动圆的圆心M 的轨迹方程.思路解析：可用直接法求点的轨迹，即(1)建系；(2)设点；(3)列式；(4)化简；(5)检验.解：如下图，设点M(x,y),动圆的半径为r ，由题意|MA|=r+3且r=|x|，∴22)3(y x +-=|x|+3.当x>0时，两边平方化简得y 2=12x(x>0)；当x<0时，两边平方化简得y=0(x<0).30分钟训练(巩固类训练，可用于课后)1.圆x 2+y 2-2x=0和x 2+y 2+4y=0的位置关系是( )A.外离B.外切C.相交D.内切思路解析：两圆的圆心和半径分别为O 1(1,0),r 1=1;O 2(0,-2),r 2=2,因为|O 1O 2|=5,又2-1<5<2+1,所以两圆相交.答案：C2.内切两圆的半径长是方程x 2+px+q=0的两根,已知两圆的圆心距为1,其中一圆的半径为3,则p+q=( )A.1B.5C.1或5D.以上都不对 思路解析： 由x 2+px+q=0得⎩⎨⎧=-=+,9,2121x x p x x ①因为有一圆半径为3,不妨设x 2=3,因为两圆内切,所以|x 1-3|=1,所以x 1=4或2.当x 1=4时,p=-7,q=12,p+q=5;当x 1=2时,p=-5,q=6,p+q=1. 答案：C3.圆C 1:x 2+y 2+4x-4y+7=0和圆C 2:x 2+y 2-4x-10y+13=0的公切线有( )A.2条B.3条C.4条D.0条思路解析：由x 2+y 2+4x-4y+7=0得圆心和半径分别为O 1(-2,2),r 1=1；由x 2+y 2-4x-10y+13=0得圆心和半径分别为O 2(2,5),r 2=4.因为|O 1O 2|=5,r 1+r 2=5,即r 1+r 2=|O 1O 2|,所以两圆外切,由平面几何知识得两圆有3条公切线.答案：B4.若圆(x-a)2+(y-b)2=b 2+1始终平分圆(x+1)2+(y+1)2=4的周长,则a 、b 应满足的关系式是( )A.a 2-2a-2b-3=0B.a 2+2a+2b+5=0C.a 2+2b 2+2a+2b+1=0D.3a 2+2b 2+2a+2b+1=0思路解析：利用两圆的公共弦始终经过圆(x+1)2+(y+1)2=4的圆心即可求得.把两圆分别化成一般式方程,作差可得公共弦方程为(2a+2)x+(2b+2)y-a 2-1=0,它经过圆心(-1,-1),代入后有a 2+2a+2b+5=0.答案：B5.两圆相交于两点(1,3),(m,-1)，两圆圆心都在直线x-y+c=0上,则m+c 的值为___________. 思路解析：由两圆的公共弦的垂直平分线为两圆心的连线，可得1131=---m ,所以m=-3,又两公共点(1,3)和(-3,-1)的中点(-1,1)在直线x-y+c=0上,所以c=2,所以m+c=-1.答案：-16.已知两个圆x 2+y 2=1①与x 2+(y-3)2=1②，则由①式减去②式可得上述两圆的对称轴方程，将上述命题在曲线仍为圆的情况下加以推广，即要求得到一个更一般的命题，而已知命题应成为推广命题的一个特例，推广的命题为____________。
高中数学必修二 圆与圆的位置关系 附答案解析版
4.2.2圆与圆的位置关系基础巩固1.圆C 1:(x+2)2+(y-2)2=1与圆C 2:(x-2)2+(y-5)2=16的位置关系是（）A.外离B.相交C.内切D.外切2.圆C 1:x 2+y 2+4x+8y-5=0与圆C 2:x 2+y 2+4x+4y-1=0的位置关系为（）A.相交B.外切C.内切D.外离3.已知圆A 与圆B 相切,圆心距为10cm,其中圆A 的半径为4cm,则圆B 的半径为（）A .6cm 或14cmB .10cmC .14cmD .无解4.已知圆O 1的方程为x 2+y 2=4,圆O 2的方程为(x-a )2+y 2=1,如果这两个圆有且只有一个公共点,那么a 的所有取值构成的集合是（）A.{1,-1}B.{3,-3}C.{1,-1,3,-3}D.{5,-5,3,-3}5.圆x 2+y 2+4x-4y+7=0与圆x 2+y 2-4x+10y+13=0的公切线的条数是（）A.1B.2C.3D.46.已知以C (4,-3)为圆心的圆与圆O :x 2+y 2=1相切,则圆C 的方程为（）A .(x-4)2+(y+3)2=16B .(x+4)2+(y-3)2=36C .(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36D .(x+4)2+(y-3)2=16或(x+4)2+(y-3)2=367.圆C 1:x 2+y 2-12x-2y-13=0和圆C 2:x 2+y 2+12x+16y-25=0的公共弦所在的直线方程是.8.若圆C 1:(x-3)2+(y-4)2=16与圆C 2:x 2+y 2=m (m>0)内切,则实数m=.9.已知圆O :x 2+y 2=25和圆C :x 2+y 2-4x-2y-20=0相交于A ,B 两点,则公共弦AB 的长为.10.求与圆O :x 2+y 2=1外切,切点为1,22P ⎛-- ⎝⎭,半径为2的圆的方程.能力提升1.圆C 1:(x+1)2+(y+2)2=4与圆C 2:(x+2)2+(y+3)2=1的位置关系是（）A.外离B.外切C.相交D.内切2.若圆x 2+y 2=4与圆x 2+y 2+ay-2=0的公共弦的长度为,则常数a 的值为（）A .2±B .2C .-2D .4±3.已知圆C :(x-3)2+(y-4)2=1和两点A (-m ,0),B (m ,0)(m>0).若圆C 上存在点P ,使得90APB ∠=︒,则m的最大值为（）A .7B .6C .5D .4★4.若圆(x-a )2+(y-a )2=4上,总存在不同的两点到原点的距离等于1,则实数a 的取值范围是（）A.22⎛ ⎝⎭B.22⎛-- ⎝⎭C.,2222⎛⎛-- ⎝⎭⎝⎭D.22⎛⎫⎪ ⎪⎝⎭5.若点A (a ,b )在圆x 2+y 2=4上,则圆(x-a )2+y 2=1与圆x 2+(y-b )2=1的位置关系是.6.求和圆(x-2)2+(y+1)2=4相切于点(4,-1)且半径为1的圆的方程.7.一动圆与圆C 1:x 2+y 2+6x+8=0外切,与圆C 2:x 2+y 2-6x+8=0内切,求动圆圆心的轨迹方程.★8.圆O 1的方程为x 2+(y+1)2=4,圆O 2的圆心O 2(2,1).(1)若圆O 2与圆O 1外切,求圆O 2的方程;(2)若圆O 2与圆O 1交于A ,B 两点,且AB =求圆O 2的方程.参考答案基础巩固1.【解析】圆C 1的圆心是C 1(-2,2),半径r 1=1,圆C 2的圆心是C 2(2,5),半径r 2=4,则圆心距|C 1C 2|=5.因为|C 1C 2|=r 1+r 2,所以两圆外切.【答案】D2.【解析】由已知,得C 1(-2,-4),r 1=5,C 2(-2,-2),r 2=3,则d=|C 1C 2|=2,所以d=|r 1-r 2|.故两圆内切.【答案】C3.【解析】令圆A 、圆B 的半径分别为r 1,r 2,当两圆外切时,r 1+r 2=10,所以r 2=10-r 1=10-4=6;当两圆内切时,|r 1-r 2|=10,即|4-r 2|=10,r 2=14或r 2=-6(舍),即圆B 的半径为6cm 或14cm .【答案】A4.【解析】因为两个圆有且只有一个公共点,所以两个圆内切或外切.当两圆内切时,|a|=1;当两圆外切时,|a|=3,即实数a 的取值集合是{1,-1,3,-3}.故选C .【答案】C5.【解析】两圆的圆心分别为C 1(-2,2),C 2(2,-5),则两圆的圆心距d =又半径分别为r 1=1,r 2=4,则d>r 1+r 2,即两圆外离,因此它们有4条公切线.【答案】D6.【解析】设所求圆的方程为(x-4)2+(y+3)2=r 2(r>0).因为圆C 与圆O 相切,所以|r-1|=5或r+1=5,解得r=6或r=4(负值舍去).故所求圆的方程为(x-4)2+(y+3)2=16或(x-4)2+(y+3)2=36.【答案】C7.【解析】两圆的方程相减得公共弦所在的直线方程为4x+3y-2=0.【答案】4x+3y-2=08.【解析】圆心距5d =,由题意得两圆半径差的绝对值45-=,解得m=81.【答案】819.【解析】两圆方程相减得弦AB 所在的直线方程为4x+2y-5=0.圆x 2+y 2=25的圆心到直线AB 的距离d ==故公共弦AB 的长为AB =10.【解析】设所求圆的圆心为C (a ,b ),则所求圆的方程为(x-a )2+(y-b )2=4.因为两圆外切,切点为1,22P ⎛-- ⎝⎭,所以|OC|=r 1+r 2=1+2=3,|CP|=2.所以2222913422a b a b ⎧+=⎪⎪⎛⎨⎛⎫+++= ⎪ ⎪ ⎝⎭⎪⎝⎭⎩,解得322a b ⎧=-⎪⎪⎨⎪=-⎪⎩.所以圆心C 的坐标为333,22⎛-- ⎝⎭,所求圆的方程为223422x y ⎛⎫⎛⎫+++= ⎪ ⎪ ⎪⎝⎭⎝⎭.能力提升1.【解析】圆心距d =,两圆半径的和为2+1=3,两圆半径之差的绝对值为1,1212r r d r r -<<+,所以两圆的位置关系是相交.【答案】C2.【解析】两圆方程左右两边分别相减得公共弦所在直线的方程为ay+2=0.由题意知0a ≠.圆x 2+y 2=4的圆心到直线ay+2=0的距离为2a,又公共弦长为,所以=解得2a =±.【答案】A3.【解析】因为A (-m ,0),B (m ,0)(m>0),所以使90APB ∠=︒的点P 在以线段AB 为直径的圆上,该圆的圆心为O (0,0),半径为m.而圆C 的圆心为C (3,4),半径为1.由题意知点P 在圆C 上,故两圆有公共点.所以两圆的位置关系为外切、相交或内切,故11m CO m -≤≤+,即151m m -≤≤+,解得46m ≤≤.所以m 的最大值为6.故选B .【答案】B4.【解析】圆(x-a )2+(y-a )2=4的圆心C (a ,a ),半径r=2,到原点的距离等于1的点的集合构成一个圆,这个圆的圆心是原点O ,半径R=1,则这两个圆相交,圆心距d =,则|r-R|<d<r+R ,则13<<,所以22a<<,所以22a-<<或22a <<.【答案】C5.【解析】因为点A (a ,b )在圆x 2+y 2=4上,所以a 2+b 2=4.又圆x 2+(y-b )2=1的圆心C 1(0,b ),半径r 1=1,圆(x-a )2+y 2=1的圆心C 2(a ,0),半径r 2=1,则122d C C ===,所以d=r 1+r 2.所以两圆外切.【答案】外切6.【解析】设所求圆的圆心为(a ,b ),1=.①若两圆外切,则有123+=.②由①②,解得5,1a b ==-,所以所求圆的方程为(x-5)2+(y+1)2=1.若两圆内切,则有211-=.③由①③,解得3,1a b ==-,所以所求圆的方程为(x-3)2+(y+1)2=1.综上,可知所求圆的方程为(x-5)2+(y+1)2=1或(x-3)2+(y+1)2=1.7.【解析】圆C 1:(x+3)2+y 2=1,所以圆心为(-3,0),半径r 1=1;圆C 2:(x-3)2+y 2=1,所以圆心为(3,0),半径r 2=1.设动圆圆心为(x ,y ),半径为r ,由题意得1r =+1r =-,2,化简并整理,得8x 2-y 2=8(1x ≥).所以动圆圆心的轨迹方程是8x 2-y 2=8(1x ≥).8.【解析】(1)设圆O 1的半径为r 1,圆O 2的半径为r 2.因为两圆外切,所以|O 1O 2|=r 1+r 2,r 2=|O 1O 2|-r 1=1-),故圆O 2的方程是(x-2)2+(y-1)2=1-)2.(2)设圆O 2的方程为(x-2)2+(y-1)2=22r .因为圆O 1的方程为x 2+(y+1)2=4,将两圆的方程相减,即得两圆公共弦AB 所在直线的方程224480x y r ++-=,①作O 1H ⊥AB ,则|AH|=12,O 1,由圆心O 1(0,-1)到直线①的距离得=,得224r =或2220r =,故圆O 2的方程为(x-2)2+(y-1)2=4或(x-2)2+(y-1)2=20.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高中数学学习材料
金戈铁骑整理制作
第15课 圆与圆的位置关系
分层训练
1． 圆222220x y x y +-+-=与圆22x y +
68240x y ---=的位置关系是 （ ）
()A 相离 ()B 相交 ()C 外切 ()D 内切
2． 两圆1C ：22
4470x y x y ++-+=，2C ： 22410130x y x y +--+=的公切线有（ ）
()A 2条 ()B 3条 ()C 4条 ()D 0条
3．已知半径为1的动圆与圆
22(5)(7)16x y -++=相切，则动圆圆心的轨
迹方程(动圆圆心坐标所满足的关系式)为（ ） ()A 22(5)(7)25x y -++= ()B 22
(5)(7)17x y -++=或22(5)(7)15x y -++= ()C 22(5)(7)9x y -++= ()D 22(5)(7)25x y -++=或22(5)(7)9x y -++= 4．若圆222
()()1x a y b b -+-=+始终平分圆
22(1)(1)4x y +++=的圆周，则,a b 应满足的
关系式为 （ ）
()A 22250a a b +++= ()B 22230a a b ---= ()C 222210a b a +++=
()D 22322210a b a b ++++=
5．若圆224x y +=和圆22
(2)(2)4x y ++-=关于直线l 对称，则l 的方程为 ．
6．圆22
4410x y x y ++--=与圆222130x y x ++-=相交于,P Q 两点，则直线PQ 的方程为 ，公共弦PQ 的长为 ．
7．已知动圆0264222=-+--+m my mx y x 恒过一个定点,这个定点的坐标是______ ． 8．求经过点(4,1)A -，且与圆
22:2650C x y x y ++-+=相切于点(1,2)
B 的圆的方程．
9．求与两条平行直线210x y +-=和2x y +
50-=相切，且圆心在直线310x y ++=上的
圆的方程．
拓展研究
10．已知圆221:2280C x y x y +++-=与圆222:210240C x y x y +-+-=相交于,A B 两点．
（1）求直线AB 的方程； （2）求经过,A B 两点且面积最小的圆的方程； （3）求圆心在直线y x =-上，且经过,A B 两点的圆的方程．
11．若两圆22
16x y +=及222(4)(3)x y r -++=在交点处的切线互相垂直，求实数r 的值．
本节学习疑点：学生质疑
教师释疑。