2019-2020年中考政治考点整理:关键词、句及常用答案方式
专题12 关注安徽发展,建设“三个”强省-2020年中考道德与法治二轮复习热点专题

-24-
8.我省取得一系列科技成就的原因有哪些? (1)坚持中国共产党的正确领导。 (2)坚持实施科教兴国与人才强国战略、创新驱动发展战略。 (3)我省综合实力显著增强,为科技发展提供了坚实的物质基础。 (4)我省推进以科技创新为核心的全面创新,鼓励大众创业,万众创新。 (5)广大科技工作者顽强拼搏,发扬实干、勇于创新的精神。
-8-
6.我省公安机关开展“净网 2019”专项行动体现了教材中的哪些观 点?
(1)我省坚持全面依法治国(省)基本方略。 (2)我省坚持以人民为中心的发展思想。 (3)中国共产党始终代表最广大人民的根本利益。 (4)法不可违,违法行为都会受到法律的制裁等。
-9-
7.我省 2019 年上半年经济运行取得显著成就表明了什么? (1)我省坚持以经济建设为中心,大力发展生产力。 (2)我省坚持以人民为中心的发展思想,不断保障和改善民生。 (3)我省广大人民群众勤劳勇敢,努力为美好生活不懈奋斗。
(1)创新是引领发展的第一动力。 (2)创新带来财富,推动社会长足进步。 (3)实施科教兴国与人才强国战略、创新驱动发展战略是正确的选择。 (4)在激烈的国际竞争中,唯创新者进,唯创新者强,唯创新者胜。
-23-
7.世界制造业大会招募志愿者。你认为应该具备哪些方面的素质? (1)强烈的社会责任感、无私奉献精神。 (2)良好的团队协作意识。 (3)较好的语言表达能力、人际交往能力等。
-2-
材料二:宪法宣誓仪式 2019 年 9 月 30 日上午,安徽省凤阳县检察院 举行向宪法宣誓仪式,新任的 1 名检察委员会委员和 3 名检察员参加宣誓。 4 名检察人员整齐排列,面朝国徽,右手握拳,神情严肃,齐诵誓词,宣告 对宪法的忠诚,对职业的敬畏。
材料三:安徽省“净网 2019”专项行动 2019 年 8 月 28 日,安徽省公 安厅通报了我省公安机关开展“净网 2019”专项行动相关情况。专项行动 开展以来,全省警方严厉打击网上源头性犯罪和利用网络实施的突出犯罪, 共侦破网络犯罪案件 6528 起,其中公安部挂牌督办案件 9 起,省公安厅挂 牌督办案件 43 起,抓获犯罪嫌疑人 6037 名。
2020年山东省青岛市中考化学试卷和答案解析

2020年山东省青岛市中考化学试卷和答案解析一、选择题(本题共16小题,每小题1分,共16分)在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(1分)下列物质属于纯净物的是()A.不锈钢B.碘酒C.氢气D.粗盐解析:物质分为混合物和纯净物,混合物是由两种或两种以上的物质组成,不锈钢、碘酒、粗盐都属于混合物;纯净物是由一种物质组成。
纯净物又分为单质和化合物。
由同种元素组成的纯净物叫单质;由两种或两种以上的元素组成的纯净物叫化合物。
参考答案:解:A、不锈钢是铁的合金,属于混合物;故选项错误;B、碘酒中有碘和酒精,属于混合物;故选项错误;C、氢气是一种物质,属于纯净物;故选项正确;D、粗盐中有氯化钠和杂质,属于混合物;故选项错误;故选:C。
点拨:本考点考查了物质的分类,要加强记忆混合物、纯净物、单质、化合物等基本概念,并能够区分应用。
本考点的基础性比较强,主要出现在选择题和填空题中。
2.(1分)适当增加蛋白质的摄入量,有助于提高人体免疫力。
下列食物富含蛋白质的是()A.菠菜B.鸡蛋C.香蕉D.馒头解析:根据人体所需六大营养素的种类、食物来源,结合题中所给的食物判断所含的营养素,进行分析判断。
参考答案:解:A、菠菜中富含维生素,故选项错误。
B、鸡蛋中富含蛋白质,故选项正确。
C、香蕉中富含维生素,故选项错误。
D、馒头中富含淀粉,淀粉属于糖类,故选项错误。
故选:B。
点拨:本题难度不大,掌握各种营养素的生理功能、食物来源等是正确解答此类题的关键。
3.(1分)下列液体去除油污效果最好的是()A.洗洁精B.食盐水C.白醋D.自来水解析:根据常见的洗涤原理有三种,一是利用乳化作用,二是利用溶解原理,三是利用物质与油污等发生化学反应,进行分析判断。
参考答案:解:A、洗洁精具有乳化作用,能将大的油滴分散成细小的油滴随水冲走,去除油污效果较好。
B、油污不能与食盐水反应,不能用于去除油污。
C、白醋不能与油污反应,不能用于去除油污。
中考数学5年真题(2019-2023)专题汇总解析—二次根式

中考数学5年真题(2019-2023)专题汇总解析—二次根式考点1二次根式一、单选题1.(2023)A.25与30之间B.30与35之间C.35与40之间D.40与45之间【答案】D【详解】解∶∵160020232025<<.即4045<,40与45之间.故选D.【点睛】本题主要考查了估算无理数的大小,正确估算无理数的取值范围是解题关键.2.(2023年江苏省无锡市中考数学真题)实数9的算术平方根是()A.3B.3±C.19D.9-【答案】A【分析】根据算术平方根的定义即可求出结果.3=,故选:A.【点睛】本题考查了平方根和算术平方根的定义.注意一个正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.3.(2023年重庆市中考数学真题(A卷)的值应在()A .7和8之间B .8和9之间C .9和10之间D .10和11之间【答案】B【分析】先计算二次根式的混合运算,再估算结果的大小即可判断.=4=+∵2 2.5<<,∴45<<,∴849<+<,故选:B .【点睛】此题考查了二次根式的混合运算,无理数的估算,正确掌握二次根式的混合运算法则是解题的关键.4.(2019·广东·的结果是()A .4-B .4C .4±D .2【答案】B【分析】根据算术平方根的定义进行求解即可.,故选B.【点睛】本题考查了算术平方根,熟练掌握算术平方根的定义是解题的关键.5.(2020·广西贵港·在实数范围内有意义,则实数x 的取值范围是()A .1x <-B .1x ≥-C .0x ≥D .1x ≥【答案】B【分析】根据二次根式的被开方数为非负数即可得出的取值范围.∴x+1≥0∴x≥﹣1故选:B【点睛】本题考查了二次根式有意义的条件,解答本题的关键是掌握二次根式有意义:被开方数为非负数.6.(2020·山东聊城·÷).A.1B.53C.5D.9【答案】A【分析】利用二次根式的乘除法则计算即可得到结果.÷==1=,故选:A.【点睛】本题主要考查了二次根式的乘除法,熟练掌握运算法则是解题的关键.7.(2023年辽宁省大连市中考数学真题)下列计算正确的是()A.0=B.+=C=D)26=-【答案】D【分析】根据零指数幂,二次根式的加法以及二次根式的性质,二次根式的混合运算进行计算即可求解.【详解】解:A.)1=,故该选项不正确,不符合题意;B.=C.=D.)26=-,故该选项正确,符合题意;故选:D .【点睛】本题考查了零指数幂,二次根式的加法以及二次根式的性质,二次根式的混合运算,熟练掌握二次根式的运算法则是解题的关键.8.(2021·广东·统考中考真题)若0a =,则ab =()AB .92C .D .9【答案】B【分析】根据一个实数的绝对值非负,一个非负实数的算术平方根非负,且其和为零,则它们都为零,从而可求得a 、b 的值,从而可求得ab 的值.【详解】∵0a ≥0≥,且0a =∴0a =0==即0a =,且320a b -=∴a =b∴92ab ==故选:B .【点睛】本题考查了绝对值和算术平方根的非负性,一般地,几个非负数的和为零,则这几个非负数都为零.9.(2022·河北·统考中考真题)下列正确的是()A23=+B 23=⨯CD 0.7=【答案】B【分析】根据二次根式的性质判断即可.【详解】解:23=≠+,故错误;=⨯,故正确;23=≠≠,故错误;0.7故选:B.【点睛】本题主要考查二次根式的性质,掌握二次根式的性质是解题的关键.10.(2023()A.点P B.点Q C.点R D.点S【答案】B<<【详解】解:∵479<<,<<23Q,故选:B.11.(2023年河北省中考数学真题)若a b===()A.2B.4C D【答案】A【分析】把a b【详解】解:∵a b==2==,故选:A.【点睛】本题考查了求二次根式的值,掌握二次根式的乘方和乘除运算是解题的关键.12.(2019·四川资阳·统考中考真题)设x=x的取值范围是()A.23x<<B.34x<<C.45x<<D.无法确定【答案】B【分析】根据无理数的估计解答即可.【详解】解:∵91516<<,∴34<<,故选B.【点睛】此题考查估算无理数的大小,关键是根据无理数的估计解答.13.(2021·广东·统考中考真题)设6a,小数部分为b,则(2a b+的值是()A.6B.C.12D.【答案】A的整数部分可确定a的值,进而确定b的值,然后将a与b的值代入计算即可得到所求代数式的值.【详解】∵34<<,∴263<<,∴62a=,∴小数部分624b==∴(((22244416106a b+=⨯+-=+-=-=.故选:A.【点睛】本题考查了二次根式的运算,正确确定6a与小数部分b的值是解题关键.二、填空题14.(2019·江苏苏州·x的取值范围为.【答案】6x≥【分析】根据根式有意义的条件,得到不等式,解出不等式即可.-60x≥,解出得到6x≥.【点睛】本题考查根式有意义的条件,能够得到不等式是解题关键.15.(2020·广西·=.【分析】利用二次根式的性质化简,再相减.==【点睛】本题考查了二次根式的减法,解题的关键是掌握二次根式的化简及性质.16.(2021·天津·统考中考真题)计算1)的结果等于.【答案】9【分析】根据二次根式的混合运算法则结合平方差公式计算即可.【详解】21)19=-=.故答案为9.【点睛】本题考查二次根式的混合运算.掌握二次根式的混合运算法则是解答本题的关键.17.(2023年湖北省武汉市数学真题)写出一个小于4的正无理数是.【分析】根据无理数估算的方法求解即可.<4<..【点睛】本题主要考查了无理数的估算,准确计算是解题的关键.18.(2023x 的取值范围是.【答案】13x ≥-【分析】根据二次根式有意义的条件得到130x +≥,解不等式即可得到答案.∴130x +≥,解得13x ≥-,故答案为:13x ≥-【点睛】此题考查了二次根式有意义的条件,熟知被开方式为非负数是解题的关键.19.(2019·河南·12--==.【答案】112【分析】本题涉及二次根式化简、负整数指数幂两个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.12--122=-112=.故答案为11 2.【点睛】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握负整数指数幂、二次根式等考点的运算.20.(2021·安徽·统考中考真题)埃及胡夫金字塔是古代世界建筑奇迹之一,其底面是正方形,侧面是全等的等腰三角形,1-,它介于整数n和1n+之间,则n的值是.【答案】11即可完成求解.2.236≈;1 1.236≈;因为1.236介于整数1和2之间,所以1n=;故答案为:1.分即可;该题题干前半部分涉及到数学文化,后半部分为解题的要点,考查了学生的读题、审题等能力.21.(20231+=.【答案】3【分析】根据求一个数的立方根,有理数的加法即可求解.1+=213+=,故答案为:3.【点睛】本题考查了求一个数的立方根,熟练掌握立方根的定义是解题的关键.22.(2023年上海市中考数学真题)已知关于x2=,则x=【答案】18【分析】根据二次根式的性质,等式两边平方,解方程即可.【详解】解:根据题意得,140x -≥,即14x ≥,2=,等式两边分别平方,144x -=移项,18x =,符合题意,故答案为:18.【点睛】本题主要考查二次根式与方程的综合,掌握含二次根式的方程的解法是解题的关键.23.(2023年黑龙江省绥化市中考数学真题)若式子x有意义,则x 的取值范围是.【答案】5x ≥-且0x ≠/0x ≠且5x ≥-【分析】根据分母不为零,二次根式的被开方数是非负数,列出不等式计算即可.【详解】∵式子∴50x +≥且0x ≠,∴5x ≥-且0x ≠,故答案为:5x ≥-且0x ≠.【点睛】本题考查了分母不为零,二次根式的被开方数是非负数,熟练掌握二次根式和分式有意义的条件是解题的关键.24.(2023年黑龙江省齐齐哈尔市中考数学真题)在函数12y x +-中,自变量x 的取值范围是.【答案】1x >且2x ≠【分析】根据分式有意义的条件,二次根式有意义的条件得出10,20x x ->-≠,即可求解.【详解】解:依题意,10,20x x ->-≠∴1x >且2x ≠,故答案为:1x >且2x ≠.【点睛】本题考查了求函数自变量的取值范围,熟练掌握分式有意义的条件,二次根式有意义的条件是解题的关键.三、解答题25.(2019·福建·统考中考真题)先化简,再求值:(x -1)÷(x -21xx-),其中x【答案】1x x -,1+2【分析】先化简分式,然后将x 的值代入计算即可.【详解】解:原式=(x−1)÷221x x x-+()()211xx x =-⋅-1x x =-当x +1时,12=+【点睛】本题考查了分式的化简求值,熟练掌握分式混合运算法则是解题的关键.26.(2022·福建·统考中考真题)先化简,再求值:2111aa a -⎛⎫+÷ ⎪⎝⎭,其中1a =.【答案】11a -.【分析】根据分式的混合运算法则化简,再将a 的值代入化简之后的式子即可求出答案.【详解】解:原式()()111a a a a a+-+=÷()()111a a a a a +=⋅+-11a =-.当1a =时,原式2=.【点睛】本题考查了分式的化简求值,熟练掌握运算法则是解题的关键.27.(2023年安徽中考数学真题)先化简,再求值:2211x x x +++,其中1x =.【答案】1x +【分析】先根据分式的性质化简,最后将字母的值代入求解.【详解】解:2211x x x +++()211x x +=+1x =+,当1x =-时,∴原式11+=.【点睛】本题考查了分式化简求值,解题关键是熟练运用分式运算法则进行求解.28.(20232133-⎛⎫- ⎪⎝⎭【答案】6-【分析】根据立方根、负整数指数幂及二次根式的运算可进行求解.【详解】解:原式2293=-+6=-.【点睛】本题主要考查立方根、负整数指数幂及二次根式的运算,熟练掌握立方根、负整数指数幂及二次根式的运算是解题的关键.29.(2023年吉林省长春市中考数学真题)先化简.再求值:2(1)(1)a a a ++-,其中3a =.【答案】31a +1+【分析】根据完全平方公式以及单项式乘以单项式进行化简,然后将字母的值代入进行计算即可求解.【详解】解:2(1)(1)a a a ++-2221a a a a =+++-31a =+当a =311==【点睛】本题考查了整式乘法的化简求值,实数的混合运算,熟练掌握完全平方公式以及单项式乘以单项式的运算法则是解题的关键.30.(2023年内蒙古通辽市中考数学真题)计算:21tan 453-⎛⎫+︒-⎪⎝⎭【答案】0【分析】根据负整数次幂、特殊角的三角函数值、算术平方根化简,然后在计算即可.【详解】解:21tan 453-⎛⎫+︒-⎪⎝⎭9110=+-,0=.【点睛】本题主要考查了负整数次幂、特殊角的三角函数值、算术平方根等知识点,掌握基本的运算法则是解答本题的关键.31.(2019·河南·统考中考真题)先化简,再求值:22121244x x x x x x +-⎛⎫-÷ ⎪--+⎝⎭,其中x =【答案】3x【分析】先根据分式的混合运算顺序和运算法则化简原式,再将x 的值代入计算可得.【详解】解:原式212(2)22(2)x x x x x x x +--⎛⎫=-÷ ⎪---⎝⎭322x x x-=⋅-3x=,当x ===.【点睛】本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则.32.(2023年辽宁省营口市中考数学真题)先化简,再求值:524223m m m m-⎛⎫++⋅⎪--⎝⎭,其中tan 45m =︒.【答案】26--m ,原式16=-【分析】先根据分式的混合计算法则化简,然后根据特殊角三角函数值和二次根式的性质求出m 的值,最后代值计算即可.【详解】解:524223m m m m-⎛⎫++⋅⎪--⎝⎭()22245223m m m m m-⎛⎫-=-⋅⎪---⎝⎭()222923m m m m--=⋅--()()()332223m m m m m+--=⋅--()23m =-+26m =--,∵tan 45m =︒,∴415m =+=,∴原式25610616=-⨯-=--=-.【点睛】本题主要考查了分式的化简求值,求特殊角三角函数值,化简二次根式等等,正确计算是解题的关键.33.(2023·重庆九龙坡·的值应在()A .2和3之间B .3和4之间C .4和5之间D .5和6之间【答案】A【分析】根据二次根式的乘法进行计算,以及估算无理数的大小的方法解答即可.=6=∵91416<<,∴34<,∴43-<<-,∴263<<,故选:A .【点睛】本题考查了估算无理数的大小和二次根式的运算.解题的关键是掌握二次根式的运算方法,以及估算无理数的大小的方法.34.(2023·辽宁丹东·统考二模)在函数y =x 的取值范围是()A .12x -<≤B .21x -<≤C .12x ≤≤D .12x <≤【答案】D【分析】根据函数有意义的条件得到2010x x -≥⎧⎨->⎩,解不等式组即可得到自变量x 的取值范围.【详解】解:由题意得2010x x -≥⎧⎨->⎩,解不等式组得12x <≤,故选:D .【点睛】此题考查了自变量的取值范围,熟练掌握二次根式和分式有意义的条件是解题的关键.35.(2023·安徽蚌埠·统考三模)下列运算正确的是()A 3=B .()3328a a -=-C =D .112235+=【答案】B【分析】根据二次根式的性质,积的乘方法则,二次根式的加法运算法则,有理数的加法运算法则依次判断即可得出答案.【详解】解:A 333==B .()3328a a -=-,故此选项符合题意;CD .11522365+=≠,故此选项不符合题意.故选:B .【点睛】本题考查二次根式的性质,积的乘方法则,二次根式的加法运算法则,有理数的加法运算法则.掌握相应的运算法则和性质是解题的关键.36.(2023·河北沧州·校考模拟预测)下列运算中,正确的是().A3=±B 2=C 2=D 8=-【答案】C【分析】利用二次根式的化简的法则对各项进行运算即可.【详解】解答:解:A 3=,故A 不符合题意;B 2=-,故B 不符合题意;C 2=,故C 符合题意;D 8=,故D 不符合题意;故选:C .【点睛】本题主要考查二次根式的化简,解答的关键是对相应的运算法则的掌握.37.(2023·四川泸州·四川省泸县第一中学校考三模)实数2的平方根为()A .2B .2±C D .【答案】D【分析】利用平方根的定义求解即可.【详解】∵2的平方根是.故选D .【点睛】此题主要考查了平方根的定义,注意一个正数的平方根有2个,它们互为相反数.38.(2023·西南大学附中校考三模)估计(3-)A .0和1之间B .2和3之间C .3和4之间D .4和5之间【答案】A【分析】由题意知(34-,由1.4 1.5=<<=,可得4.2 4.5<<,0.240.5<<,然后判断作答即可.【详解】解:(34-⨯,∵1.4 1.5=<<=,∴4.2 4.5<<,∴0.240.5<<,∴估算(3-0和1之间,故选:A .39.(2023·河北石家庄·校联考一模)下列计算正确的是()A =B1=-C =D 23=【答案】C【分析】根据二次根式加法、二次根式减法、二次根式乘法、二次根式除法分别进行判断即可.【详解】解:AB 0-=,故选项错误,不符合题意;C =D 1=,故选项错误,不符合题意.故选:C .【点睛】此题考查了二次根式的加法、减法、乘法、除法,熟练掌握运算法则是解题的关键.40.(2023·江苏无锡·校考二模)函数y x的取值范围是()A .5x ≥-B .5x ≤-C .5x ≥D .5x ≤【答案】C【详解】试题分析:求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数x 50x 5-≥⇒≥.故选C.考点:1.函数自变量的取值范围;2.二次根式有意义的条件.41.(2023·湖南长沙·校联考二模)4的算术平方根是()A .2B .2±C .8D .16【答案】A【分析】如果一个数x 的平方等于(0)a a ≥,那么这个数x 叫做a 的平方根,可以表示为平方根叫做a 的算术平方根.正数的算术平方根是正数,0的算术平方根是0,负数没有算术平方根.【详解】解:42=,故选:A .【点睛】本题考查算术平方根的定义,明确平方根与算术平方根的区别与联系是本题的关键.42.(2023·重庆九龙坡·重庆市育才中学校考一模)x)A .0B .2C .3D .5【答案】D【分析】根据二次根式有意义的条件进行求解即可.∴40x -≥,即4x ≥,∴四个选项中只有D 选项中的5符合题意,故选:D .【点睛】本题主要考查了二次根式有意义的条件,熟知二次根式有意义的条件是被开方数大于等于零是解题的关键.43.(2023·甘肃平凉·的结果是.【答案】2【分析】根据二次根式的性质进行化简即可.2=.故答案为:2.()()(0000a a a a a a ⎧⎪===⎨⎪-⎩>)<.44.(2021·黑龙江大庆·=【答案】4【分析】先算4(2)-,再开根即可.==4=故答案是:4.【点睛】本题考查了求一个数的4次方和对一个实数开根号,解题的关键是:掌握相关的运算法则.45.(2023·广东茂名·校考一模)已知实数x,y |4|0y -=,则1x y -=⎛⎫⎪⎝⎭.【答案】2【分析】根据算术平方根的非负性,绝对值的非负性得出24x y ==,,进而根据负整数指数幂进行计算即可求解.40y -=0≥,40y -≥,∴20x -=,40y -=,∴24x y ==,,∴11112422x y ---⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭===.故答案为:2.【点睛】本题主要考查了算术平方根和绝对值的非负性、负整数次幂等知识点,根据非负性正确求得x 、y 的值是解答本题的关键.46.(2023·福建福州·校考二模)已知2a =2b =22a b ab -的值等于.【答案】【分析】先求出a b -=1ab =,再由()22a b ab ab a b -=-进行求解即可.【详解】解:∵2a =2b =∴22a b -=++=((22431ab =+⨯-=-=,∴22a b ab -()ab a b =-1=⨯=故答案为:【点睛】本题主要考查了二次根式的混合运算、求代数式的值,正确得到a b -=1ab =是解题的关键47.(2023·山东聊城·x 的取值范围是.【答案】12x ≥【分析】根据二次根式有意义的条件可得210x -≥,即可.【详解】解:由题意得:210x -≥,解得:12x ≥,故答案为:12x ≥.【点睛】此题主要考查了二次根式有意义的条件,关键是掌握二次根式中的被开方数是非负数.48.(2023·安徽滁州·校考模拟预测)计算)11-的结果等于.【答案】22【分析】直接利用平方差公式进行简便运算即可.【详解】解:)2211123122=-=-=,故答案为:22【点睛】本题考查的是二次根式的乘法运算,熟练的利用平方差公式进行简便运算是解本题的关键.49.(2023·陕西西安·校考模拟预测)-64的立方根是.【答案】-4【分析】直接利用立方根的意义,一个数的立方等于a ,则a 的立方根是这个数进行求解.【详解】解:根据立方根的意义,一个数的立方等于a ,则a 的立方根是这个数,可知-64的立方根为-4.故答案为:-4.【点睛】本题考查了立方根,解题的关键是掌握一个数的立方等于a ,则a 的立方根是这个数.50.(2023·云南昭通·x 的取值范围是.【答案】x>8【分析】由分式的分母不等于零和二次根式的被开方数是非负数得到x﹣8>0.【详解】解:由题意,得x﹣8>0,解得x>8.故答案是:x>8.【点睛】考查了分式有意义的条件和二次根式有意义的条件,注意,二次根式在分母上,所以不能取到0.51.(2023·四川泸州·四川省泸县第一中学校考三模)函数y=x的取值范围是.【答案】x>3【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件.x30x3x>3x30x3-≥≥⎧⎧⇒⇒⎨⎨-≠≠⎩⎩.52.(2023·河南洛阳·统考一模)计算:22-=.【答案】74-【分析】先计算22-,再算减法.【详解】解:原式17244=-=-.故答案为:74-.【点睛】本题考查了实数的计算,掌握负整数指数幂、二次根式的化简是解决本题的关键.53.(2023·安徽蚌埠·统考三模)计算:212022--=.【答案】2023【分析】根据有理数的乘方,二次根根式的性质,化简绝对值进行计算即可求解.【详解】解:212022--=122022-++2023=,故答案为:2023.【点睛】本题考查了有理数的乘方,二次根根式的性质,化简绝对值,正确的计算是解题的关键.54.(2022·新疆·x的取值范围是.【答案】x≥3【分析】直接利用二次根式有意义的条件得到关于x的不等式,解不等式即可得答案.【详解】由题意可得:x—3≥0,解得:x≥3,故答案为:x≥3【点睛】本题考查了二次根式有意义的条件,熟练掌握二次根式的被开方数是非负数是解题的关键.55.(2023·黑龙江哈尔滨·统考三模)计算=.【答案】【分析】先根据二次根式的性质化简,然后根据二次根式的加减法则求解即可.【详解】解:=-2=-=故答案为:【点睛】本题主要考查了二次根式的性质、二次根式的加减运算等知识点,灵活运用二次根式的的性质化简是解题的关键.x的取值范围是.56.(2023·云南昆明·一模)要使式子3有意义,x≥【答案】5【分析】二次根式中的被开方数是非负数,依此即可求解.x-≥,【详解】解:依题意有:50x≥.解得5x≥.故答案为:5【点睛】本题考查了二次根式有意义的条件,关键是熟悉二次根式中的被开方数是非负数的知识点.57.(云南省丽江市华坪县2020-2021=.【答案】6【分析】利用二次根式的乘法法则进行求解即可.==.6故答案为:6.【点睛】本题考查了二次根式的乘法,熟练掌握二次根式的乘法法则和二次根式的性质是解题的关键.58.(2023·山西·模拟预测)计算:=.【答案】【分析】先化简二次根式,再根据二次根式的加减计算法则求解即可.【详解】解:3=⨯=+=故答案为:【点睛】本题主要考查了二次根式的加减计算,二次根式的化简,正确计算是解题的关键.59.(2023·重庆沙坪坝·重庆八中校考模拟预测)如果2y=+,那么yx的值是.【答案】225【分析】根据二次根式有意义的条件,求出,x y的值,进而求出y x的值即可.【详解】解:∵2y=,∴150,150x x -≥-≥,∴15150x x -=-=,∴15,2x y ==,∴215225y x ==;故答案为:225.【点睛】本题考查二次根式有意义的条件,代数式求值.熟练掌握二次根式的被开方数是非负数,是解题的关键.60.(江西省崇仁县第二中学2016-2017学年八年级上学期第二次月考数学试题)计算:=【答案】61.(2015年初中毕业升学考试(山东滨州卷)数学(带解析))计算的结果为.【答案】﹣1【分析】此题用平方差公式计算即可.【详解】22=-23=-1=-62.(2023·黑龙江哈尔滨·=.【答案】3【分析】根据二次根式的化简方法和运算法则进行计算.【详解】解:原式33==【点睛】本题考查二次根式的计算,在化简二次根式的基础上再把同类二次根式合并.63.(福建省永春县第一中学2017【分析】根据二次根式乘法,加减法运算法则计算即可.【详解】解:原式=【点睛】本题考查了二次根式的混合运算,熟练掌握二次根式的化简方法是解题的关键.64.(2023·广东茂名·校考一模)先化简,再求值:2121211x x x x +⎛⎫÷+ ⎪-+-⎝⎭其中1x +.【答案】11x -;2【分析】先通分算括号内的,把除化为乘,再约分,化简后将x 的值代入计算.【详解】解:212(1)211x x x x +÷+-+-211(1)1x x x x ++=÷--211(1)1x x x x +-=⋅-+11x =-,当1x =+时,原式=2=.【点睛】本题考查了分式化简求值,掌握分式的基本性质,将分式通分和约分进行化简是关键.65.(2023·四川泸州·011+()3-23-【答案】【分析】根据实数的混合运算法则即可求解.011+()3-23-=(1+32-=1+32-+【点睛】此题主要考查实数的运算,解题的关键是熟知实数的性质及运算法则.66.(2023·安徽六安·1+【分析】先计算算术平方根.化简绝对值,求解立方根,再合并即可.1+=+-413=【点睛】本题考查是算术平方根的含义,化简绝对值,求解立方根,实数的混合运算,掌握“算术平方根与立方根的含义”是解本题的关键.67.(2022·新疆·统考中考真题)计算:20-+(2)|(3【分析】分别计算有理数的乘方、绝对值、二次根式及零指数幂,再进行加减即可.【详解】解:原式451=++=【点睛】本题考查有理数的乘方,绝对值和二次根式的化简及零指数幂的性质,属于基础题,正确运算是=.解题的关键.要熟练掌握:任何一个不等于零的数的零次幂都等于1a。
2019年广东省中考语文试卷及答案解析

2019年广东省中考语文试卷一、基础运用(24分)1.根据课文默写古诗文。
(1)关关雎鸠,在河之洲。
窈窕淑女,________。
(诗经·关雎)(2)臣本布衣,躬耕于南阳,________,________。
(诸葛亮《出师表》)(3)唐代李商隐《夜雨寄北》中“________,________”的诗句,表现了诗人在羁旅中无奈、孤独的心情。
(4)________?曹刘,生子当如孙仲谋,(辛弃疾《南乡子·登京口北固亭有怀》)(5)请把文天祥的《过零丁洋》默写完整。
辛苦遭逢起一经,干戈寥落四周星。
________,________。
惶恐滩头说惶恐,零丁洋里叹零丁。
________,________。
2.根拼音写出相应的词语。
①在夏天,因为棚顶是玻璃的,横屋里面zào rè________得像温室。
②月还没有落,……而一离赵庄,月光又显得格外的jiǎo jié________。
③我páo gēn wèn dǐ________才从他嘴里知道了一些事。
④十年之久,于勒叔叔没再来信。
可是父亲的希望却yǔ rì jù zēng________。
3.下列句子划线词语使用不恰当的一项是()A. 公园里,老人悠闲地聊着天,孩子在尽情嬉戏,空气中洋溢着祥和的气氛。
B. 在《我和橘皮的往事》中,作者用大量的笔墨饱含深情地缅怀自己的小学班主任。
C. 电视剧《破冰行动》主要讲述了警察剿灭“第一毒村”这样一个惊心动魄的故事。
D. 一年一度的四川甘孜山地旅游节拉开了帷幕。
远远望去,大渡河畔人声鼎沸。
4.下列句子修改个正硝的一项是()A. 香港学员与广州优秀大学生一起来到社区家庭服务中心,探望外来工子女和他们的生活状况。
(将“探望”改为“探访”)B. 目前,我国发现的时间最早的青铜制品,是在甘肃东乡林家1977年出土的青铜。
(将“1997年”移至“是”和“在”之间)C. 爱国是检验一个人品格高尚与否的试金石,也是评价一个人道德感情操的重要标准。
2020年中考科目表,以及2020年中考各科备考策略!

2020年中考科目表,以及2020年中考各科备考策略!我国每一年的中考科目一般都是各省自己进行中考命题和考试的,所以每年中考政策和科目都或许会有一些小调整,而且同一省不同的市县区,也有自己的政策。
小编在这里为您整理了2020年中考科目表,以及各科备考策略!供您参考!一、2020年中考科目表一般来说必考的科目有:语文,数学,英语,物理,化学,历史,政治,体育。
不过从现在的教育新闻中我们可以看到2019年中考,好多省市都增加了地理,生物二个科目。
所以2020年中考科目,大家最好亲自或让家人朋友到当地教委咨询,也可以登录当地教委的官网,在局长信箱中查询或通过网站上的热线客服询问。
二、2020年中考各科备考策略A、2020年中考语文备考策略:加强识记注重作文1、充分梳理资料书上各个知识点,包括考点、方法技巧和答题模式,使重点内容处于待提取的激活状态。
2、停止大量试题练习,多看错题集和已做试卷失分题,总结归纳运用的知识点,适当做一点热身题。
3、加强记忆方面的知识,注重基础题和默写题,回归课本。
4、注重考前作文材料的整理和复习。
B、2020年中考数学备考策略:巩固基础,用好错题1、巩固基础制作“失分分析表”,分析失分情况,针对薄弱环节重点改进。
别一味冲刺难题。
做题是对理论知识的进一步巩固与实检,我们要在理解的基础上加强练习,以达到巩固的目的,但不能一味追求难题偏题。
在基础掌握后,有条件的同学可再进行一些难题怪题的攻关,这样的策略才更能保证效率。
2、反思错题,不要盲目找题做,陷入题海中,不要试图“做过”中考题(基础题除外),不要“就题论题”停留在“这题我会了”的低水平上。
解题能力是在反思中提升的。
3、关注几个问题1).新定义题型、非常规题型、存在性问题。
2).分析法—执果索因,逆向思维,倒过来想,假设存在;不完全归纳法—根据例子,大胆猜想、努力验证。
反例排除法、特殊图形(特殊位置、极端值)探究法等。
C、2020年中考英语备考策略:坚持每天练习,朗读范文最后阶段,对日常交际用语、词汇表、语法表、话题表,哪些内容要求“掌握”,哪些内容要求“理解”,要做到心中有数。
2019中考语文基础训练-第五节-仿写句子、压缩语段

寒来暑往,秋收冬藏,一年四季景象不同,所代表的生
命状态也不相同:春天(1)
,
,
;夏天骄阳似火,蛙鸣虫唱,是生命的张扬;秋天
(2)
,
,
;冬天落雪无声,
闲云舒卷,是生命的恬静。
返回
语文
【答案】 (1)惠风和畅,莺飞草长,(1分)是生命的萌发;(1分) (2)明月朗照,五谷飘香,(1分)是生命的纯熟;(1分)
返回
语文 答题步骤:第一步:确定小概念、大概念;第二步:筛选本 质特征,删除无用信息;第三步:按照格式,将重要信息连 词成句,调整字数。
返回
语文 【拟写新闻标题】 题例:请给下面的新闻材料拟写标题,并简述理由。
2018年10月23日10∶05 新华社 港珠澳大桥开通仪式23 日上午在广东珠海举行。习近平主席出席仪式并宣布大桥正 式开通。港珠澳大桥跨越伶仃洋,东接香港,西接广东珠海 和澳门,总长约55公里,是粤港澳三地首次合作共建的超大 型跨海交通工程。(记者:霍小光、张晓松)
头脑,拓展你的思维,沉淀你的智慧,丰盈你的精神;阅读
是一种照亮心路的对话,广泛的阅读能够
,
,
,
。
返回
语文
【答案】 示例:丰富你的知识,开阔你的眼界,陶冶你的性情,净化 你的灵魂。(每空1分) 探究 续写式仿写;构成排比句;要扣紧“广泛的阅读”这个主 题,仿照例句,以动宾结构的短语写出其作用,并写出内在 逻辑关系,组成排比;搭配得当,句式整齐。
返回
语文
探究分析: 1.2018年本题的考查围绕新考纲要求及新增考点进行了新 的设计。新题型由材料和两个问题组成,要求阅读完材料 后,按要求作答。第(1)小题考查的是“压缩语段”,第(2)小 题考查的是“修辞表达”。
2024年中考第一轮复习直角三角形 课件

[解析] 设AB=x,则AC=x-2.由勾股定理,
.
得x2-(x-2)2=82.解得x=17.
■ 知识梳理
勾股定理
直角三角形两条直角边的平方和等于⑥ 斜边的平方
勾股定理
如果三角形中两边的平方和等于第三边的⑦ 平方 ,那么这个三角形
的逆定理 是直角三角形
勾股数
能够成为直角三角形三条边长的三个正整数,称为勾股数
∴AD=BC,∠A=∠B=∠CFE=90°,AB∥CD,∴∠AED=∠CDF,∠A=∠CFD=90°,
AD=CF,∴△ADE≌△FCD,∴ED=CD=x,∴FD=x-1,
在Rt△CFD中,FD2+CF2=CD2,∴(x-1)2+32=x2,解得x=5,∴CD=5.故选B.
考向三
勾股定理与拼图
例 3 [2020·孝感]如图 19-11①,四个全等的直角三角形围成一个大正方形,中间是个
图19-6
∴∠BEC=90°,∠BFC=90°,
1
2
∵G 是 BC 的中点,∴EG=FG= BC=5,
∵D 是
1
EF 的中点,∴ED= EF=3,GD⊥EF,
2
∴∠EDG=90°.在 Rt△ EDG 中,
由勾股定理得,DG= 2 - 2 =4,故答案为 4.
考向二
利用勾股定理进行计算
例2 [2020·宜宾]如图19-7,在Rt△ABC中,∠ACB=90°,D是AB的中点,BE平分
∠ABC交AC于点E,连结CD交BE于点O.若AC=8,BC=6,则OE的长是
.
图19-7
【方法点析】勾股定理是求线段长的重要工具,主要应用:(1)已知直角三角形的
两边长求第三边长;(2)已知直角三角形的一边长求另两边的关系;(3)用于证明平
决胜2020年中考数学压轴题专题15 动点综合问题(含答案)
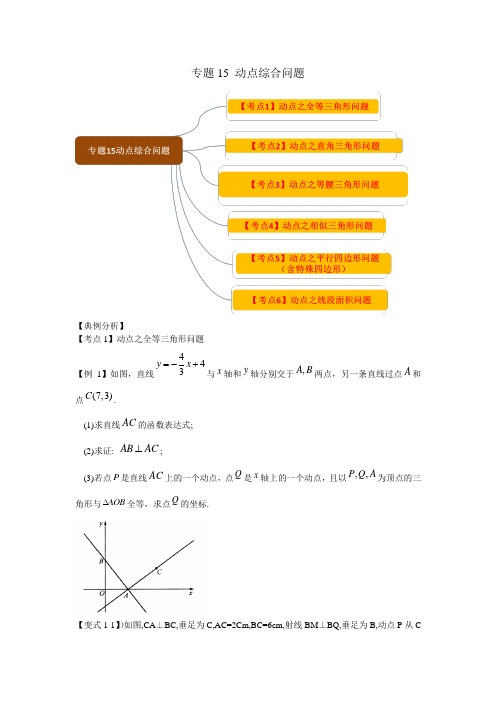
专题15 动点综合问题【典例分析】【考点1】动点之全等三角形问题【例1】如图,直线443y x=-+与x轴和y轴分别交于,A B两点,另一条直线过点A和点(7,3) C.(1)求直线AC的函数表达式;(2)求证: AB AC⊥;(3)若点P是直线AC上的一个动点,点Q是x轴上的一个动点,且以,,P Q A为顶点的三角形与AOB∆全等,求点Q的坐标.【变式1-1】)如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ 运动,点N 为射线BM 上一动点,满足PN=AB,随着P 点运动而运动,当点P 运动_______秒时,△BCA 与点P 、N 、B 为顶点的三角形全等.(2个全等三角形不重合)【考点2】动点之直角三角形问题 【例2】(模型建立)(1)如图1,等腰直角三角形ABC 中,90ACB ∠=o,CB CA =,直线ED 经过点C ,过A 作AD ED ⊥于点D ,过B 作BE ED ⊥于点E .求证:BEC CDA ∆≅∆; (模型应用)(2)已知直线1l:443y x =+与坐标轴交于点A 、B ,将直线1l 绕点A 逆时针旋转45o 至直线2l,如图2,求直线2l的函数表达式;(3)如图3,长方形ABCO ,O 为坐标原点,点B 的坐标为()8,6-,点A 、C 分别在坐标轴上,点P 是线段BC 上的动点,点D 是直线26y x =-+上的动点且在第四象限.若APD ∆是以点D 为直角顶点的等腰直角三角形,请直接写出点D 的坐标.【变式2-1】(2019·辽宁中考模拟)如图,已知二次函数y =ax2+bx+4的图象与x 轴交于点A(4,0)和点D(﹣1,0),与y 轴交于点C ,过点C 作BC 平行于x 轴交抛物线于点B ,连接AC(1)求这个二次函数的表达式;(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动;点N 从点B 同时出发,以每秒1个单位长度的速度向点C 运动,其中一个动点到达终点时,另一个动点也随之停动,过点N 作NQ 垂直于BC 交AC 于点Q ,连结MQ.①求△AQM的面积S与运动时间t之间的函数关系式,写出自变量的取值范围;当t为何值时,S有最大值,并求出S的最大值;②是否存在点M,使得△AQM为直角三角形?若存在,求出点M的坐标;若不存在,说明理由.【变式2-2】如图,四边形ABCD是正方形,以DC为边向外作等边△DCE,连接AE交BD 于点F,交CD于点G,点P是线段AE上一动点,连接DP、BP.(1)求∠AFB的度数;(2)在点P从A到E的运动过程中,若DP平分∠CDE,求证:AG•DP=DG•BD;(3)已知AD=6,在点P从A到E的运动过程中,若△DBP是直角三角形,请求DP的长.【考点3】动点之等腰三角形问题【例3】(2019·湖南中考真题)如图一,在射线DE的一侧以AD为一条边作矩形ABCD,53AD=5CD=,点M是线段AC上一动点(不与点A重合),连结BM,过点M作BM的垂线交射线DE于点N,连接BN.(1)求CAD ∠的大小;(2)问题探究:动点M 在运动的过程中,①是否能使AMN ∆为等腰三角形,如果能,求出线段MC 的长度;如果不能,请说明理由. ②MBN ∠的大小是否改变?若不改变,请求出MBN ∠的大小;若改变,请说明理由. (3)问题解决:如图二,当动点M 运动到AC 的中点时,AM 与BN 的交点为F ,MN 的中点为H ,求线段FH 的长度.【变式3-1】如图①,已知正方形ABCD 边长为2,点P 是AD 边上的一个动点,点A 关于直线BP 的对称点是点Q ,连结PQ 、DQ 、CQ 、BQ .设AP=x.(1)当1x =时,求BP 长;(2)如图②,若PQ 的延长线交CD 边于E ,并且90CQD ∠=o,求证:CEQ ∆为等腰三角形;(3)若点P 是射线AD 上的一个动点,则当CDQ ∆为等腰三角形时,求x 的值.【变式3-2】(2019·河南中考模拟)如图,抛物线y=ax2+bx+3交y 轴于点A ,交x 轴于点B (-3,0)和点C (1,0),顶点为点M . (1)求抛物线的解析式;(2)如图,点E 为x 轴上一动点,若△AME 的周长最小,请求出点E 的坐标;(3)点F 为直线AB 上一个动点,点P 为抛物线上一个动点,若△BFP 为等腰直角三角形,请直接写出点P 的坐标.【变式3-3】(2019·广西中考真题)已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -,点O 为坐标原点,点P 为抛物线上的动点,直线y x b =-+与x 轴、y 轴分别交于AB 、两点. (1)求m b 、的值;(2)当PAM ∆是以AM 为底边的等腰三角形时,求点P 的坐标; (3)满足(2)的条件时,求sin BOP ∠的值. 【考点4】动点之相似三角形问题【例4】在边长为4的正方形ABCD 中,动点E 以每秒1个单位长度的速度从点A 开始沿边AB 向点B 运动,动点F 以每秒2个单位长度的速度从点B 开始沿边BC 向点C 运动,动点E 比动点F 先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动,设点F 的运动时间为t 秒.()1如图1,连接DE ,AF ,若DE AF ⊥,求t 的值 ()2如图2,连接,EF DF ,当t 为何值时,?EBF DCF V :V【变式4-1】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=34AC(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D 的坐标;(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.【变式4-2】如图,已知抛物线2y ax bx c =++经过A(-3,0)、B(8,0)、C(0,4)三点,点D是抛物线上的动点,连结AD与y轴相交于点E,连结AC,CD.(1)求抛物线所对应的函数表达式;(2)当AD平分∠CAB时.①求直线AD所对应的函数表达式;②设P是x轴上的一个动点,若△PAD与△CAD相似,求点P的坐标.【考点5】动点之平行四边形问题(含特殊四边形)【例5】(2019·广东中考模拟)如图,点O是平面直角坐标系的原点,点A33),AC⊥OA 与x轴的交点为C.动点M3A向点O运动.同时,动点N以每秒3个单位长度由点O向点C运动,当一动点先到终点时,另一动点立即停止运动.(1)写出∠AOC的值;(2)用t表示出四边形AMNC的面积;(3)求点P的坐标,使得以O、N、M、P为顶点的四边形是特殊的平行四边形?【变式5-1】(2019·江西中考真题)在图1,2,3中,已知,,点为线段上的动点,连接,以为边向上作菱形,且.(1)如图1,当点与点重合时,________°;(2)如图2,连接.①填空:_________(填“>”,“<”,“=”);②求证:点在的平分线上;(3)如图3,连接,,并延长交的延长线于点,当四边形是平行四边形时,求的值.【变式5-2】(2019·湖南中考真题)如图,二次函数213y x bx c=-++的图象过原点,与x轴的另一个交点为() 8,0【变式5-3】.如图,在平面直角坐标系中,AOB ∆的顶点O 是坐标原点,点A 坐标为()1,3,A 、B 两点关于直线y x =对称,反比例函数()0ky x x =>图象经过点A ,点P 是直线y x=上一动点.(1)B 点的坐标为______;(2)若点C 是反比例函数图象上一点,是否存在这样的点C ,使得以A 、B 、C 、P 四点为顶点的四边形是平行四边形?若存在,求出点C 坐标;若不存在,请说明理由; (3)若点Q 是线段OP 上一点(O 不与O 、P 重合),当四边形AOBP 为菱形时,过点Q 分别作直线OA 和直线AP 的垂线,垂足分别为E 、F ,当QE QF QB ++的值最小时,求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图已知平面内有一动点A ,x 轴上有一定点B (4,0),连接AB ,且将线段AB 绕B 点逆时针旋转90°得到线段BC .①当A 点坐标为(1,1)时,求C 点坐标;②当A 点在直线x=1上滑动时,求在此运动过程中△BOC 的面积是否发生变化,若不变,请求出面积,若变化,请说明理由;③若总条件中的动点A 改为直线y=x 上的动点A ,其余条件都不变,请直接写出当A 点在直线y=x 上滑动时,点D (0,-2)到C 点的最短距离.【变式6-1】(2019·山东中考模拟)如图,抛物线2y x bx c =-++交x 轴于点()30A -,和点B ,交y 轴于点()0,3C .(1)求抛物线的函数表达式; (2)若点P 在抛物线上,且4AOP BOCS S ∆∆=,求点P 的坐标;(3)如图,设点Q 是线段AC 上的一动点,作DQ x ⊥轴,交抛物线于点D ,求线段DQ 长度的最大值,并求出DAC ∆面积的最大值.【变式6-2】如图,矩形ABCD 中,3,4AD AB ==,点P 是对角线AC 上一动点(不与A C 、重合),连接PB ,过点P 作PE PB ⊥,交射线DC 于点E ,以线段,PE PB 为邻边作矩形BPEF ,过点P 作GH CD ⊥。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
……是具有社会责任感的表现,奉献精神,不言代价与回报。
青奥会志愿者等公益活动/ 参加环保活动
答应别人的事努力做好/答 应的事逃避
做错事时主动认错/做错事 时隐瞒
主动报名参加公益活动等
……是能够正确对待父母的关爱与教育的表现。(不是盲目的顺从)
不听父母话、 赌气不理父母, 和父母吵架
……这是一种逆反心理的表现,我们要正确认识逆反心理,克服消 极的逆反心理;没有正确对待父母的关爱与教育,不尊重父母,不 孝敬父母的表现。
与老 师交 往
正确与老师 交往
正确对待教 师的表扬与 批评
老师上课讲错一道题,下课 告诉老师
◎认真学习完成学习任务/逃课、 上课不认真听讲
◎沉迷游戏、看“鬼故事”、暴力 等不良书籍 ◎课间哄闹、说脏话等认为是小事
◎看到不法行为,及时举报、报警 或提醒他人、协助他人抓获违法犯 罪分子
◎强烈谴责打砸抢的暴力行为…… ◎帮助少数民族同学
答案
……符合依法治国基本方略的要求, ◎有法可依是依法治国的前提, ◎体现有法必依、执法必严、违法必究, ◎依法行政是依法治国的重要环节,
如果不维权:……是缺乏法制观念的表现,没有依法维权意 识、纵容违法犯罪行为,没有履行同违法犯罪行为作斗争的 义务。 如果以牙还牙:……是法制观念淡薄的表现,是违法行为、 侵犯了××权利,没有依法维护自身合法权益,将受到法律 制裁。
如果用合法方式维权:……表明有较强的法制观念;有防范 侵害、保护自己的意识,依法维护了自身合法权益;履行同 违法犯罪行为作斗争的义务。 ……是法制观念淡薄的表现; ……(侵犯了××权),是违法行为,会受到法律的制裁。 ……没有正确认识权利和义务的关系,权利和义务具有一致 性,必须在法律允许的范围内,正确行使权利,自觉履行义 务。
看到别人难过或困难 等能安慰、同情别人/和父 母、老师、同学吵架等
……是(没有)正确对待竞争与合作的表现,竞争与合作是相互依 存的,我们应学会在竞争中合作,在合作中竞争。
……是(没有)换位思考、与人为善的表现。
尊重他人、 平等待人
待人彬彬有礼、谦和/看不 起其他不如自己的人
……是(没有)尊重他人、平等待人的表现。
在学习或活动后能思考得与 失
……是(不)负责任的表现。慎重许诺、坚决履行诺言是负责任的 表现。 ……是(不)负责任的表现,勇于承认错误、并承担错误所造成的 后果也是负责任的表现。 ……是自觉承担责任的表现,享受承担责任的快乐。
……说明学会反思自己的责任,在承担责任中不断成长。
(二)法律
分类 考点关键词
2019-2020 年中考政治考点整理:关键词、句及常用答案方式
(一)心理、道德
分类 考点关键词
材料类型
答案
珍爱生命
自己 身上 的一 些表 现
正确认识自 己
情绪
患病后积极面对,创造生命 奇迹
出院后成了“爱心大使”
认为自己一无是处/根据自 己的优劣势、制订复习计划
心情不好、闷闷不乐,一气 之下,导致问题与矛盾
法制观念;
民
违法行为
: 违 正确行使权
树
立
法
利,自觉履 行义务
法
制 观
和 守
受教育权利
念 防范侵害、
法 提高自我保
类 护意识;防
微杜渐、远
离违法犯罪
履行同违法
犯罪行为作 护 斗争的义务 法 类 维护国家安
全、民族团
结的义务
◎闯红灯、敲诈、食品非法添加和 滥用添加剂、让孩子辍学、退学 ◎学习、娱乐是我的自由,别人无 权干涉 ◎捏造事实发布错误言论
……是(不)诚信的表现,对人守信,对事负责是诚信的基本要求; 也是(不)负责任的表现。
与他 人集 体社 会交 往
个人与集体 责任
学业紧张仍为班级出黑板报 等/不出黑板报、值日逃跑
在家做有孝心的子女/在学 校做好学生、在社会做好公 民
抗震救灾、捐款捐物、参加
……能(不能)正确处理个人利益与集体利益的关系,我们应关爱 集体,自觉维护集体的荣誉和利益。
交往 品德 与 艺术
宽容
诚信
原谅别人无意的过错/对别 人的过错斤斤计较
他闯红灯 (或作弊或违法等) 是有原因的、算了,原谅别 人所有错误
履行承诺/不守时、迟到、 抄作业、考试作弊、卖假货 (地沟油、毒胶囊、瘦肉精 等)
……是(没有)宽容的表现,宽容是一种美德,我们应学会相互宽 容。
……是没有正确认识宽容的表现,宽容是有原则的,不能盲目的宽 容。
……说明每个人生命都是有价值的,珍爱自己的生命,同时善待他 人生命。
……说明我们要珍爱生命,不断延伸生命的价值,为社会做出贡献。
……是(没有)正确认识自己的表现。我们要学会用全面、发展的 眼光看待自己,客观地认识、评价自己的优缺点。
……说明情绪是双刃剑,积极情绪可能产生积极影响,消极情绪可 能产生消极影响,我们要学会调控情绪,保持乐观心态。
Hale Waihona Puke 自强不息困难面前不低头,通过自己 的努力奋斗度过难关
……是自强不息精神的体现,自强不息是我们的民族精神,我们要 弘扬自强不息的民族精神。
孝敬父母
认真学习、做家务
……是孝敬父母的表现,从小事做起,尽到作为子女的责任。
与父 母交 往
正确对待父 母的关爱与 教育
正确认识逆 反心理
认真听取父母的建议/没有 听从父母错误的意见
国家 依法治国
材料类型
◎制定《刑法修正案》或条例、醉 驾人刑等 ◎公安人员严格执法、警察抓酒后 驾车等违法犯罪、开展专项整治行 动 ◎政务公开、听证会
法制观念; 依法维权意 维 识;生命健 权 康权;消费 者合 法权 益;受教育 类 权利;建议 权、监督权
◎瘦肉精、三聚氰胺等 ◎消费者买到假货 ◎东西被偷 ◎被敲诈、被抢钱 ◎被勒令退学 ……
教师教育学生,接受老师批 评/不以为然
……是正确与老师交往的表现,掌握了与老师沟通的方法,能恰当 指出老师的错误。
……是(没有)正确对待教师的表扬与批评的表现;受到表扬要再 接再厉;受到批评有则改之,无则加勉。
竞争与合作
交往 品德 与 艺术
换位思考、 与人为善
主动与竞争对手分享学习资 料/不和比自己成绩差的同 学来往
……是(没有)珍惜受教育权利,自觉履行受教育义务的表 现,是对自己和他人(不)负责任的表现。
……是不对的,要防范侵害,提高自我保护意识和能力。 ……许多违法犯罪行为都是从沾染不良习气开始的,我们要 防微杜渐、远离违法犯罪。
