高中物理 匀速圆周运动例题
高一物理匀速圆周运动试题答案及解析

高一物理匀速圆周运动试题答案及解析1.如图所示,把一个小球放在玻璃漏斗中,晃动漏斗,可以使小球沿光滑的漏斗壁在某一水平面内做匀速圆周运动。
小球的向心力由以下哪个力提供A.重力B.支持力C.重力和支持力的合力D.重力、支持力和摩擦力的合力【答案】C【解析】小球受到重力和支持力,由于小球在水平面内做匀速圆周运动,所以小球的向心力由重力和支持力的合力提供,故C正确.【考点】考查了向心力2.图中所示为一皮带传动装置,右轮的半径为r,a是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r,b点在小轮上,到小轮中心的距离为r,c点和d点分别位于小轮和大轮的边缘上,若在传动过程中,皮带不打滑,则()A.ab两点的线速度大小相等B.ab两点的角速度大小相等C.ac两点的线速度大小相等D.ad两点的向心加速度大小相等【答案】CD【解析】由图可看出,a点的线速度等于c点的线速度,而c点的线速度大于b点的线速度,故a点的线速度大于b点的线速度,选项A错误,C正确;设c点的线速度为v,则a点的角速度为,b点的角速度,选项B错误;a点的向心加速度,d点的向心加速度,选项D正确。
【考点】线速度、角速度及向心加速度。
3.如图所示,A、B是两个摩擦传动轮(不打滑),两轮半径大小关系为RA =2RB,则两轮边缘上的( )A.角速度之比ωA :ωB=2:1B.周期之比TA :TB=2:1C.转速之比nA :nB=2:1D.向心加速度之比aA :aB=2:1【答案】B【解析】A、B两轮边缘线速度相同,由公式ɷ=得ωA :ωB=rB:rA=1:2,故选项A错误;由公式T=得,TA :TB=ωB:ωA=2:1,故B正确;由公式n=知,nA:nB=TB:TA=1:2,故选项C错误;由加速度公式a==知aA :aB=rB:rA=1:2,故选项D错误。
【考点】匀速圆周运动的公式4.如图所示,一个圆盘绕轴心O在水平面内匀速转动,圆盘半径R= 0.4m,转动角速度=15rad/s。
高中物理必修二圆周运动经典大题例题

(每日一练)高中物理必修二圆周运动经典大题例题单选题1、以A、B为轴的圆盘,A以线速度v转动,并带动B转动,A、B之间没有相对滑动则()A.A、B转动方向相同,周期不同B.A、B转动方向不同,周期不同C.A、B转动方向相同,周期相同D.A、B转动方向不同,周期相同答案:A解析:两轮接触位置没有相对滑动,所以两轮边缘线速度相同,根据题意可知,转动方向相同,均为逆时针;根据周期公式T=2πr v可知,线速度大小相同,而半径不同,所以周期不同,BCD错误,A正确。
故选A。
2、如图所示为大小不同的两个转轮,两转轮边缘接触,且接触点无打滑现象。
A点位于大转轮内,B点位于小转轮边缘,两点到各自圆心的距离相等。
当两轮转动时,关于A、B两点周期、线速度及角速度等物理量的关系正确的是()A.T A>T B,v A<v BB.T A=T B,v A<v BC.ωA>ωB,v A<v BD.ωA<ωB,v A=v B答案:A解析:因为轮边缘无打滑,则两轮边缘的线速度相同,设大轮边缘有一点C,则有v B=v C由v=ωR而R C>R B所以ωC<ωB又由ω=2πT则T C>T B点A与点C同轴,则有ωA=ωC,T A=T C所以T A>T B,ωA<ωB又由R A<R C,ωA=ωC由v=ωR则v A<v C所以v A<v B故A正确,BCD错误;故选A。
3、2022年的北京冬奥会,任子威获得短道速滑1000米项目的金牌,如图是他比赛中正沿圆弧形弯道匀速率滑行,则他()A.所受的合力为零,做匀速运动B.所受的合力恒定,做匀加速运动C.所受的合力变化,做变加速运动D.所受的合力恒定,做变加速运动答案:C解析:根据题意可知,运动员做匀速圆周运动。
合力大小不变,但方向改变,合力变化,做变加速运动。
故选项C正确。
4、如图将红、绿两种颜色石子放在水平圆盘上,围绕圆盘中心摆成半径不同的两个同心圆圈。
高一物理匀速圆周运动试题

高一物理匀速圆周运动试题1.如图所示,光滑水平面上,小球m在拉力F作用下作匀速圆周运动。
若小球运动到P点时,拉力F发生变化,关于小球运动情况的说法正确的是A.若拉力突然消失,小球将沿轨迹Pa作离心运动B.若拉力突然变小,小球将沿轨迹Pa作离心运动C.若拉力突然变大,小球将沿轨迹Pb作离心运动D.若拉力突然变小,小球将沿轨迹Pc作离心运动【答案】A【解析】在水平面上,细绳的拉力提供m所需的向心力,当拉力消失,物体受力合为零,将沿切线方向做匀速直线运动,故A正确.当拉力减小时,将沿pb轨道做离心运动,故BD错误;当拉力增大时,将沿pc轨道做近心运动,故C错误.【考点】考查了离心现象2.如图所示,两轮用皮带传动,皮带不打滑,图中有A、B、C三点,这三点所在处半径rA>r B =rC,则这三点的向心加速度aA、aB、aC的关系是A.aA =aB=aCB.aC>aA>aBC.aC<aA<aBD.aC=aB>aA【答案】C【解析】由皮带传动规律知,A、B两点的线速度相同,A、C两点的角速度相同,由得:aA <aB,aC<aA,则aC<aA<aB,C正确。
【考点】本题考查皮带传动规律。
3.物体在做匀速圆周运动的过程中,保持不变的物理量为()A.线速度B.角速度C.向心力D.向心加速度【答案】 B【解析】物体在做匀速圆周运动时,速度方向改变,线速度变,向心力和向心加速度指向圆心,方向时刻改变,所以本题选择B。
【考点】匀速圆周运动4.如图所示,物体A、B随水平圆盘绕轴匀速转动,物体B在水平方向所受的作用力有( ) A.圆盘对B及A对B的摩擦力,两力都指向圆心B.圆盘对B的摩擦力指向圆心,A对B的摩擦力背离圆心C.圆盘对B及A对B的摩擦力和向心力D.圆盘对B的摩擦力和向心力【答案】B【解析】据题意,A、B两个物体均做匀速转动,对A物体,其转动的向心力由B对A的静摩擦力提供,据相互作用力关系,B物体一定受到A物体给的静摩擦力,其方向向外,在水平方向B 物体还受到圆盘给的指向圆心的摩擦力,故选项B正确。
匀速圆周运动实例分析

18
第19页/共31页
【例题1】如图所示,一质量为m=2kg的小球,在半径大小
为R=1.6m的轻绳子作用下在竖直平面内做圆周运动。
(1)小球恰好经过最高点的速度V2=?此时最低点要给 多大的初速度V1=?(2)若在最低点的速度V1=10m/s, 则在最高点绳的拉力为多大?
T
解:(1)依题意得,物体恰好经过最高点,mg提供做
3、汽车过凹形桥时,车对桥的压力大于 自身重力。此时汽车处于超重状态。
3
第4页/共31页
例一 、当汽车通过桥面粗糙的拱形桥顶时拱形桥顶的速度为10m/s
时,车对桥顶的压力为车重的3/4,如果汽车行驶至该桥顶时刚好不
受摩擦力作用,则汽车通过桥顶时速度应为 ( B )
A、25m/s
B、20m/s
C、15m/s
离心运动本质: (1)离心现象的本质是物体惯性的表现。 (2)离心运动是物体逐渐远离圆心的一 种物理现象。
15
第16页/共31页
离心运动的应用:
1、洗衣机脱水桶
原理:利用离心运动把附 着在衣物上的水分甩掉。
解释当:脱水桶快速转动时,
衣物对水的附着力F不足以
ν
提供水随衣服转动所需的向 心力 F,于是水滴做离心运 动,穿过网孔,飞到脱水桶
一、汽车过拱形桥
在各种公路上拱形桥是常 见的,质量为m的汽车在 拱桥上以速度v前进,桥 面的圆弧半径为R,分析 汽车通过桥的最高点时对 桥面的压力。
问题:汽车通过桥顶时重力G和支持 力N相等吗,为什么?
1
第2页/共31页
分析:
1、当汽车在桥面上运动到最高点时,重力G和桥的支持 力N在一条直线上,它们的合力是使汽车做圆周运动的向 心力F向。
(完整版)匀速圆周运动练习题含答案

匀速圆周运动——练习题一、选择题1、关于角速度和线速度,下列说法正确的是(B)A.半径一定,角速度与线速度成反比B.半径一定,角速度与线速度成正比C.线速度一定,角速度与半径成正比D.角速度一定,线速度与半径成反比2、下列关于甲乙两个做圆周运动的物体的有关说法正确的是( C)A.它们线速度相等,角速度一定相等B.它们角速度相等,线速度一定也相等C.它们周期相等,角速度一定也相等D.它们周期相等,线速度一定也相等3、时针、分针和秒针转动时,下列正确说法是(A)A.秒针的角速度是分针的60倍B.分针的角速度是时针的60倍C.秒针的角速度是时针的360倍D.秒针的角速度是时针的86400倍4、关于物体做匀速圆周运动的正确说法是(D)A.速度大小和方向都改变B.速度的大小和方向都不变C.速度的大小改变,方向不变D.速度的大小不变,方向改变5、物体做匀速圆周运动的条件是(D)A.物体有一定的初速度,且受到一个始终和初速度垂直的恒力作用B.物体有一定的初速度,且受到一个大小不变,方向变化的力的作用C.物体有一定的初速度,且受到一个方向始终指向圆心的力的作用D.物体有一定的初速度,且受到一个大小不变方向始终跟速度垂直的力的作用6、甲、乙两物体都做匀速圆周运动,其质量之比为1:2,转动半径之比为1:2,在相等时间里甲转过60°,乙转过45°,则它们所受外力的合力之比为(C)A. 1:4B.2:3C.4:9D.9:167、如图1所示,用细线吊着一个质量为m的小球,使小球在水平面内做圆锥摆运动,关于小球受力,正确的是(B)A.受重力、拉力、向心力B.受重力、拉力C.受重力D.以上说法都不正确8、冰面对溜冰运动员的最大摩擦力为运动员重力的k倍,在水平冰面上沿半径为R的圆周滑行的运动员,若依靠摩擦力充当向心力,其安全速度为(B)9、火车转弯做圆周运动,如果外轨和内轨一样高,火车能匀速通过弯道做圆周运动,下列说法中正确的是(A)A.火车通过弯道向心力的来源是外轨的水平弹力,所以外轨容易磨损B.火车通过弯道向心力的来源是内轨的水平弹力,所以内轨容易磨损C.火车通过弯道向心力的来源是火车的重力,所以内外轨道均不磨损D.以上三种说法都是错误的10、一圆筒绕其中心轴OO1匀速转动,筒内壁上紧挨着一个物体与筒一起运动相对筒无滑动,如图2所示,物体所受向心力是(C)A.物体的重力B.筒壁对物体的静摩擦力C.筒壁对物体的弹力D.物体所受重力与弹力的合力11、一圆盘可以绕其竖直轴在水平面内转动,圆盘半径为R,甲、乙两物体的质量分别为M 与m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用一根长为l(l <R)的轻绳连在一起,如图3所示,若将甲物体放在转轴的位置上,甲、乙之间接线刚好沿半径方向拉直,要使两物体与转盘之间不发生相对滑动,则转盘旋转的角速度最大值不得超过(C)二、填空题12、做匀速圆周运动的物体,当质量增大到2倍,周期减小到一半时,其向心力大小是原来的___8__倍,当质量不变,线速度大小不变,角速度大小增大到2倍时,其向心力大小是原来的__2____倍。
(完整版)圆周运动典型例题及答案详解
vA∶vB∶vC=2∶1∶1.
根据向心加速度公式a=ω2R,所以A、B、C三轮边缘向心加速度之比
=8∶4∶2=4∶2∶1.
【例2】【分析】由于木块随圆盘一起作匀速圆周运动,时刻存在着一个沿半径指向圆心的向心加速度,因此,它必然会受到一个沿半径指向中心、产生向心加速度的力——向心力.
【例8】用长L1=4m和长为L2=3m的两根细线,拴一质量m=2kg的小球A,L1和L2的另两端点分别系在一竖直杆的O1,O2处,已知O1O2=5m如下图(g=10m·s-2)
(1)当竖直杆以的角速度ω匀速转动时,O2A线刚好伸直且不受拉力.求此时角速度ω1.
(2)当O1A线所受力为100N时,求此时的角速度ω2.
D.当转台转速继续增加时,A比B先滑动
【例4】如图,光滑的水平桌面上钉有两枚铁钉A、B,相距L,另一端拴住一个质量为500g的小球.小球的初始位置在AB连线上A的一侧.把细线拉直,给小球以2m/s的垂直细线方向的水平速度,使它做圆周运动.由于钉子B的存在,使细线逐步缠在A、B上.
“匀速圆周运动”的典型例题
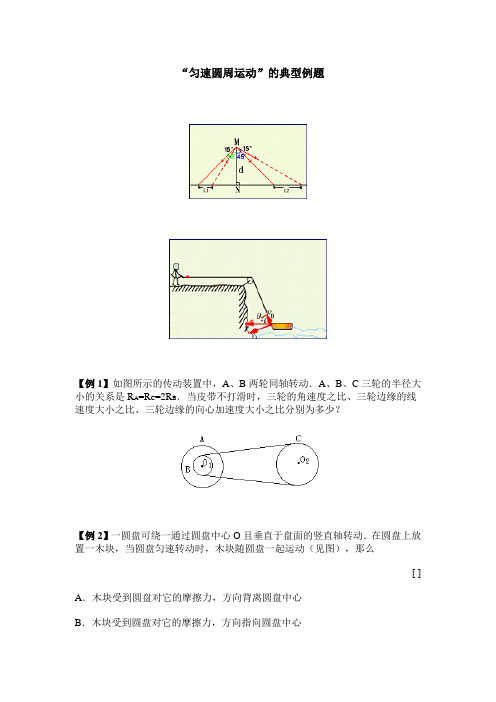
【例1】如图所示的传动装置中,A、B两轮同轴转动.A、B、C三轮的半径大小的关系是RA=RC=2RB.当皮带不打滑时,三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少?
【例2】一圆盘可绕一通过圆盘中心O且垂直于盘面的竖直轴转动.在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动(见图),那么
【例6】杂技节目中的“水流星”表演,用一根绳子两端各拴一个盛水的杯子,演员抡起杯子在竖直面上做圆周运动,在最高点杯口朝下,但水不会流下,如下图所示,这是为什么?
【例7】如下图所示,自行车和人的总质量为M,在一水平地面运动.若自行车以速度v转过半径为R的弯道.(1)求自行车的倾角应多大?(2)自行车所受的地面的摩擦力多大?
匀速圆周运动 典型例题

匀速圆周运动 典型例题【例1】如图所示的传动装置中,A 、B 两轮同轴转动.A 、B 、C 三轮的半径大小的关系是RA=RC=2RB.当皮带不打滑时,三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少?【例2】一圆盘可绕一通过圆盘中心O 且垂直于盘面的竖直轴转动.在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动(见图),那么()A.木块受到圆盘对它的摩擦力,方向背离圆盘中心B.木块受到圆盘对它的摩擦力,方向指向圆盘中心C.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同D.因为摩擦力总是阻碍物体运动,所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反【例3】在一个水平转台上放有A 、B 、C 三个物体,它们跟台面间的摩擦因数相同.A 的质量为2m ,B 、C 各为m.A 、B 离转轴均为r,C 为2r.则()A.若A 、B 、C 三物体随转台一起转动未发生滑动,A 、C 的向心加速度比B 大B.若A 、B 、C 三物体随转台一起转动未发生滑动,B 所受的静摩擦力最小C.当转台转速增加时,C 最先发生滑动D.当转台转速继续增加时,A 比B 先滑动【例4】如图,光滑的水平桌面上钉有两枚铁钉A 、B ,相距L0=0.1m.长L=1m 的柔软细线一端拴在A 上,另一端拴住一个质量为500g 的小球.小球的初始位置在AB 连线上A 的一侧.把细线拉直,给小球以2m/s的垂直细线方向的水平速度,使它做圆周运动.由于钉子B的存在,使细线逐步缠在A、B上.若细线能承受的最大张力Tm=7N,则从开始运动到细线断裂历时多长?【例5】如图(a)所示,在光滑的圆锥顶用长为L的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和球一起以角速度ω匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少?【例6】杂技节目中的“水流星”表演,用一根绳子两端各拴一个盛水的杯子,演员抡起杯子在竖直面上做圆周运动,在最高点杯口朝下,但水不会流下,如下图所示,这是为什么?【例7】用长L1=4m和长为L2=3m的两根细线,拴一质量m=2kg的小球A,L1和L2的另两端点分别系在一竖直杆的O1,O2处,已知O1O2=5m如下图(g=10m⋯−2)(1)当竖直杆以的角速度ω匀速转动时,O2A线刚好伸直且不受拉力.求此时角速度ω1.(2)当O1A线所受力为100N时,求此时的角速度ω2.。
人教版高中物理必修2匀速圆周运动”的典型例题

“匀速圆周运动”的典型例题【例1】如图所示的传动装置中,a、b两轮同轴转动.a、b、c三轮的半径大小的关系是r a =r c=2r b.当皮带不打滑时,三轮的角速度之比、三轮边缘的线速度大小之比、三轮边缘的向心加速度大小之比分别为多少?【分析】皮带不打滑,表示轮子边缘在某段时间内转过的弧长总是跟皮带移动的距离相等,也就是说,用皮带直接相连的两轮边缘各处的线速度大小相等.根据这个特点,结合线速度、角速度、向心加速度的公式即可得解.【解】由于皮带不打滑,因此,b、c两轮边缘线速度大小相等,设v b=v c=v.由v=ωr得两轮角速度大小的关系ωb∶ωc=r c∶r b=2∶1.因a、b两轮同轴转动,角速度相等,即ωa=ωb,所以a、b、c三轮角速度之比ωa∶ωb∶ωc=2∶2∶1.因a轮边缘的线速度v a=ωa r a=2ωb r b=2v b,所以a、b、c三轮边缘线速度之比v a∶v b∶v c=2∶1∶1.根据向心加速度公式a=ω2r,所以a、b、c三轮边缘向心加速度之比=8∶4∶2=4∶2∶1.【例2】一圆盘可绕一通过圆盘中心o且垂直于盘面的竖直轴转动.在圆盘上放置一木块,当圆盘匀速转动时,木块随圆盘一起运动(见图),那么[ ]a.木块受到圆盘对它的摩擦力,方向背离圆盘中心b.木块受到圆盘对它的摩擦力,方向指向圆盘中心c.因为木块随圆盘一起运动,所以木块受到圆盘对它的摩擦力,方向与木块的运动方向相同d.因为摩擦力总是阻碍物体运动,所以木块所受圆盘对它的摩擦力的方向与木块的运动方向相反e.因为二者是相对静止的,圆盘与木块之间无摩擦力【分析】由于木块随圆盘一起作匀速圆周运动,时刻存在着一个沿半径指向圆心的向心加速度,因此,它必然会受到一个沿半径指向中心、产生向心加速度的力——向心力.以木块为研究对象进行受力分析:在竖直方向受到重力和盘面的支持力,它处于力平衡状态.在盘面方向,可能受到的力只有来自盘面的摩擦力(静摩擦力),木块正是依靠盘面的摩擦力作为向心力使它随圆盘一起匀速转动.所以,这个摩擦力的方向必沿半径指向中心【答】b.【说明】常有些同学认为,静摩擦力的方向与物体间相对滑动的趋势方向相反,木块随圆盘一起匀速转动时,时时有沿切线方向飞出的趋势,因此静摩擦力的方向应与木块的这种运动趋势方向相反,似乎应该选d.这是一种极普遍的错误认识,其原因是忘记了研究运动时所相对的参照系.通常说做圆运动的物体有沿线速度方向飞出的趋势,是指以地球为参照系而言的.而静摩擦力的方向总是跟相对运动趋势的方向相反,应该是指相互接触的两个相关物体来说的,即是对盘面参照系.也就是说,对站在盘上跟盘一起转动的观察者,木块时刻有沿半径向外滑出的趋势,所以,木块受到盘面的摩擦力方向应该沿半径指向中心【例3】在一个水平转台上放有a、b、c三个物体,它们跟台面间的摩擦因数相同.a的质量为2m,b、c各为m.a、b离转轴均为r,c为2r.则[ ]a.若a、b、c三物体随转台一起转动未发生滑动,a、c的向心加速度比b大b.若a、b、c三物体随转台一起转动未发生滑动,b所受的静摩擦力最小c.当转台转速增加时,c最先发生滑动d.当转台转速继续增加时,a比b先滑动【分析】a、b、c三物体随转台一起转动时,它们的角速度都等于转台的角速度,设为ω.根据向心加速度的公式a n=ω2r,已知r a=r b<r c,所以三物体向心加速度的大小关系为a a=a b<a c.a错.三物体随转台一起转动时,由转台的静摩擦力提供向心力,即f =f n=mω2r,所以三物体受到的静摩擦力的大小分别为f a=m aω2r a=2mω2r,f b=m bω2r b=mω2r,f c=m cω2rc =mω2·2r=2mω2r.即物体b所受静摩擦力最小.b正确.由于转台对物体的静摩擦力有一个最大值,设相互间摩擦因数为μ,静摩擦力的最大值可认为是f m=μmg.由f m=f n,即得不发生滑动的最大角速度为即离转台中心越远的物体,使它不发生滑动时转台的最大角速度越小.由于r c>r a=r b,所以当转台的转速逐渐增加时,物体c最先发生滑动.转速继续增加时,物体a、b将同时发生滑动.c正确,d错.【答】b、c.【例4】如图,光滑的水平桌面上钉有两枚铁钉a、b,相距l0=0.1m.长l=1m的柔软细线一端拴在a上,另一端拴住一个质量为500g的小球.小球的初始位置在ab连线上a的一侧.把细线拉直,给小球以2m/s的垂直细线方向的水平速度,使它做圆周运动.由于钉子b的存在,使细线逐步缠在a、b上.若细线能承受的最大张力t m=7n,则从开始运动到细线断裂历时多长?【分析】小球转动时,由于细线逐步绕在a、b两钉上,小球的转动半径会逐渐变小,但小球转动的线速度大小保持不变.【解】小球交替地绕a、b作匀速圆周运动,因线速度不变,随着转动半径的减小,线中张力t不断增大,每转半圈的时间t不断减小.令t n=t m=7n,得n=8,所以经历的时间为【说明】圆周运动的显著特点是它的周期性.通过对运动规律的研究,用递推法则写出解答结果的通式(一般表达式)有很重要的意义.对本题,还应该熟练掌握数列求和方法.如果题中的细线始终不会断裂,有兴趣的同学还可计算一下,从小球开始运动到细线完全绕在a、b两钉子上,共需多少时间?【例5】如图(a)所示,在光滑的圆锥顶用长为l的细线悬挂一质量为m的小球,圆锥顶角为2θ,当圆锥和球一起以角速度ω匀速转动时,球压紧锥面.此时绳的张力是多少?若要小球离开锥面,则小球的角速度至少为多少?【分析】小球在水平面内做匀速圆周运动,由绳子的张力和锥面的支持力两者的合力提供向心力,在竖直方向则合外力为零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B.做圆周运动的物体除受其他力外,还要受一个 向心力作用
C.向心力不改变圆周运动物体速度的大小
D.做匀速圆周运动的物体其向心力是不变的
能力· 思维· 方法
【例1】汽车以一定的速度在宽阔的马路上匀速行 驶,司机突然发现正前方有一墙,把马路全部堵死, 为了避免与墙相碰,司机是急刹车好,还是马上转 弯好?试定量分析说明道理。
延伸· 拓展
【解题回顾】近年高考压轴题中经常会遇到类 似的题型(如1995年高考最后一题的扔沙袋问 题)这类问题要先由前次的过程找规律,得出 n次时的通式,而后求解.
能力· 思维· 方法
绳断裂后小球沿圆周的切线方向做平抛运动,设小 球从抛出至落地的水平射程为x,如图4-3-4所示
x=v1t,h1=1/2gt2,
R= r 2 x 2
解得R=3L.
图4-3-4
能力· 思维· 方法
【解题回顾】由于速度是缓慢增长,所以在 绳断裂前,小球在任何一点的运动均可看做 是匀速圆周运动(大家可类比力的平衡那一章 中动态平衡问题)
延伸· 拓展
(1)小球从开始运动到细线完全缠到A、B上的时间 t=t1+t2+…+t0=[1+2+3+ … +(10-1)LAB] /v
[10L0-10×(10-1)/2×0.1]/v≈8.6s
(2)设在第x个半周期时,T=7N,
由Tx=m· v2/[L0-(x-1)LAB],代入数据得x=8. 所经历的时间t= [8L0-8×(8-1)LAB/2]/v = [8×1-8(8-1)/2×0.1]/2=8.2s
图4-3-3
能力· 思维· 方法
(2)小球从抛出到落地,根据机械能守恒定律 1/2mv21+mgh1=1/2mv22,式中h1为绳断裂时小球距地 面的高度,由上式解得
h1=(v22-v21)/(2g)=11L/4, 设绳断裂时小球距天花板的高度为h2,则 h2=Lcos60°=L/2,
故房屋的高度H=h1+h2=13L/4.
课 前 热 身
3.下列关于甲、乙两个做匀速圆周运动的物 体的有关说法正确的是(C) A.它们的线速度相等,角速度一定相等
B.它们的角速度相等,线速度一定相等
C.它们的周期相等,角速度一定相等 D.它们的周期相等,线速度一定相等
课 前 热 身
4.关于向心力的说法正确的是(C) A.物体由于做圆周运动而产生了一个向心力
匀速圆周运动
要点· 疑点· 考点 课 前 热 身 能力· 思维· 方法
延伸· 拓展
课 前 热 身
1.做匀速圆周运动的物体,下列哪个来自理量是不 变的(C) A.运动速度
B.运动的加速度
C.运动的角速度 D.相同时间内的位移
课 前 热 身
2.匀速圆周运动特点是(D) A.速度不变,加速度不变 B.速度不变,加速度变化 C.速度变化,加速度不变 D.速度和加速度的大小不变,方向时刻在变
图4-3-2
能力· 思维· 方法
【解析】绳断裂前小球做圆锥摆运 动,绳断裂后小球沿切线方向做平 抛运动,直到落地,小球做平抛运 动的过程满足机械能守恒定律
(1)绳断前瞬间小球受力如图4-3-3 所示,由于
Tm=2mg,cos=mg/Tm=1/2,=60°
F合=mgtan60°=mv21/r,r=L· sin , 3 gL 解得v1= 2
图4-3-5
延伸· 拓展
(1)如果细线不会断裂,从小球开始运动 到细线完全缠在A、B上需要多长时间? (2)如果细线的抗断拉力为7N,从开始运 动到细线断裂需经历多少时间?
延伸· 拓展
【解析】小球交替地绕A、B做匀速圆周运动,因线速 度不变,随着半径的减小,线中张力T不断增大,半 周期t不断减小推算出每个半周期的时间及半周期 数就可求出总时间,根据绳子能承受的最大拉力, 可求出细绳断裂所经历的时间.
能力· 思维· 方法
【解析】如果急刹车,则汽车做加速度a=g的匀 减速运动,设初速度为v0,则位移s=v20/(2g)式 中,表示汽车与水平面之间的动摩擦因数,g为 重力加速度. 如果是以v0的速率做匀速圆周运动转弯,则 摩擦力来提供物体做圆周运动所需的向心力,则 有: mg=mv20/R,R=v20/g,由于R>s,故司 机应紧急刹车好.
【解析】剪断绳子前,A球做匀速圆周运动的向心力 由B、C的重力提供,
(mB+mC)g=mAv2/r.
当剪断细绳的瞬间,v不变,所需的向心力不变, 但绳的拉力F=mAg<mv2/r,则A球将做离心运动,半 径增大,物体B将上升,其势能增大,而A球的动能 减小,速率也减小.当mBg=mAv′2/r′时,重新做匀 速圆周运动这时的角速度=v′/r′<v/r,即减小, 因而T=2/,T增大.故此题的答案为A、D
延伸· 拓展
【例4】如图4-3-5所示,光滑的水平面上钉有两枚铁 钉A和B相距0.1m,长1m的柔软细绳拴在A上,另一端 系一质量为0.5kg的小球,小球的初始位置在AB连线 上A的一侧,把细线拉紧,给小球以2m/s的垂直细线 方向的水平速度使它做圆周运动,由于钉子B的存在, 使线慢慢地绕在A、B上。
能力· 思维· 方法
【例2】如图4-3-1所示,小球用轻绳通过桌面上一光 滑小孔与物体B和C相连,小球能在光滑的水平桌面上 做匀速圆周运动,若剪断B、C之间的细绳,当A球重新 达到稳定状态后,则A球的( ) A.运动半径变大
B.速率变大 C.角速度变大 D.周期变大 图4-3-1
能力· 思维· 方法
能力· 思维· 方法
【解题回顾】大家容易人注意用圆周运动知道 论问题,不易想起用机械来讨论A动能变化,望 大家以后要扩展思维.
能力· 思维· 方法
【例3】如图4-3-2所示,在圆柱形 房屋天花板中心O点悬挂一根长为L 的细绳,绳的下端挂一个质量为m 的小球,已知绳能承受的最大拉力 为2mg,小球在水平面内做圆周运 动,当速度逐渐增大到绳断裂后, 小球恰好以速度v2= 7 gL 落到墙角 边,求(1)绳断裂瞬间小球的速度v1; (2)圆柱形房屋的高度H和半径R.
在第一半周期内:T1=mv2/L0,t1=L0/v; 在第二个半周期内:T2=mv2/(L0-LAB), t2=[L0-LAB]/v;
延伸· 拓展
在第三个半周期内:T3=mv2/(L0-2LAB),
t3=(L0-2LAB)/;…; 在第n个半周期内:Tn=mv2/[L0-(n-1)LAB], tn=[L0-(n-1)LAB]/v. 由于L0/LAB=1/0.1=10,∴n≤10.
