2012版步步高高考数学考前三个月抢分训练13:圆锥曲线
2012年高考试题汇编——圆锥曲线

2012年高考数学真题分类汇编:圆锥曲线一、选择题1.【2012高考真题浙江理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心率是B【答案】B【解析】由题意知直线B F 1的方程为:b x c b y +=,联立方程组⎪⎪⎩⎪⎪⎨⎧=-+=0,b y a x b x cb y 得点Q ),(a c bc a c ac --,联立方程组⎪⎪⎩⎪⎪⎨⎧=++=0,b y a x b x cb y 得点P ),(ac bc a c ac ++-,所以PQ 的中点坐标为),(222b c b c a ,所以PQ 的垂直平分线方程为:)(222b ca xbc b c y --=-,令0=y ,得)1(22b ac x +=,所以c ba c 3)1(22=+,所以2222222a cb a -==,即2223c a =,所以26=e 。
故选B 2.【2012高考真题新课标理8】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B两点,AB =;则C 的实轴长为( )()A ()B()C 4 ()D 8【答案】C【解析】设等轴双曲线方程为)0(22>=-m m y x ,抛物线的准线为4-=x ,由34=AB ,则32=A y ,把坐标)32,4(-代入双曲线方程得4121622=-=-=y x m ,所以双曲线方程为422=-y x ,即14422=-y x ,所以2,42==a a ,所以实轴长42=a ,选C.3.【2012高考真题新课标理4】设12F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P为直线32ax =上一点,12PF F ∆是底角为30的等腰三角形,则E 的离心率为( )()A 12 ()B 23 ()C 34 ()D 45【答案】C【解析】因为12PF F ∆是底角为30的等腰三角形,则有P F F F 212=,,因为02130=∠F PF ,所以0260=∠D PF ,0230=∠DPF ,所以21222121F F PF D F ==,即c c c a =⨯=-22123,所以c a 223=,即43=a c ,所以椭圆的离心率为43=e ,选C. 4.【2012高考真题四川理8】已知抛物线关于x 轴对称,它的顶点在坐标原点O ,并且经过点0(2,)M y 。
【步步高】2012高考数学 考前三个月抢分训练11 立体几何

训练11 立体几何1.(2011·浙江改编)若直线l 不平行于平面α,且l ⊄α,则下列结论判断正确的为________.(填序号)①α内的所有直线与l 异面;②α内不存在与l 平行的直线;③α内存在唯一的直线与l 平行;④α内的直线与l 都相交.2.以下命题中,正确的命题为________.(填序号)①已知A 、B 、C 、D 是空间任意四点,则AB →+BC →+CD →+DA →=0;②若{a ,b ,c }为空间一个基底,则{a +b ,b +c ,c +a }构成空间的另一个基底;③对空间任意一点O 和不共线三点A 、B 、C ,若OP →=xOA →+yOB →+zOC →(其中x ,y ,z ∈R ),则P 、A 、B 、C 四点共面.3.过三棱柱ABC —A 1B 1C 1的任意两条棱的中点作直线,其中与平面ABB 1A 1平行的直线共有________条.4.如图,AB 为圆O 的直径,点C 在圆周上(异于点A ,B ),直线PA 垂直于圆O 所在的平面,点M 为线段PB 的中点.有以下四个命题:①PA ∥平面MOB ;②MO ∥平面PAC ;③OC ⊥平面PAC ;④平面PAC ⊥平面PBC .其中正确的命题是________(填上所有正确命题的序号).5.平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是m ′和n ′,给出下列四个命题:①m ′⊥n ′⇒m ⊥n ;②m ⊥n ⇒m ′⊥n ′;③m ′与n ′相交⇒m 与n 相交或重合;④m ′与n ′平行⇒m 与n 平行或重合.其中不正确的命题个数为________.6.过正方形ABCD 的顶点A ,引PA ⊥平面ABCD .若PA =BA ,则平面ABP 和平面CDP 所成的二面角的大小为________.7.如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B 与AC所成角的余弦值是________.8.在正三棱锥S—ABC中,M、N分别是棱BC、SC的中点,且MN⊥AN,若侧棱SA=23,则正三棱锥S—ABC外接球的表面积是________.9.如图是一个由三根细铁杆组成的支架,三根细铁杆的两夹角都是60°,一个半径为1的球放在该支架上,则球心到P的距离为________.10.设α,β是空间两个不同的平面,m,n是平面α及平面β外的两条不同直线.从“①m⊥n;②α⊥β;③n⊥β;④m⊥α”中选取三个作为条件,余下一个作为结论,写出你认为正确的一个命题:________(填序号).11.(2011·福建)如图,正方体ABCD—A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上.若EF∥平面AB1C,则线段EF的长度为________.12.如图,在正三棱柱ABC-A1B1C1中,D为棱AA1的中点,若截面△BC1D是面积为6的直角三角形,则此三棱柱的体积为______.13.已知四棱锥P—ABCD的底面ABCD是矩形,PA⊥底面ABCD,点E、F分别是棱PC、PD 的中点,则①棱AB与PD所在直线垂直;②平面PBC 与平面ABCD 垂直;③△PCD 的面积大于△PAB 的面积;④直线AE 与直线BF 是异面直线.以上结论正确的是________.(写出所有正确结论的序号)14.三棱锥S -ABC 中,∠SBA =∠SCA =90°,△ABC 是斜边AB =a 的等腰直角三角形,则以下结论中:①异面直线SB 与AC 所成的角为90°;②直线SB ⊥平面ABC ;③平面SBC ⊥平面SAC ;④点C 到平面SAB 的距离是12a .其中正确结论的序号是________.答案1.② 2.①② 3.6 4.②④ 5.4 6.45° 7.66 8.36π 9. 3 10.①③④⇒②(或②③④⇒①) 11. 2 12.8 3 13.①③14.①②③④。
【步步高】(浙江专用)高考数学 考前三个月 压轴大题突破练 直线与圆锥曲线(二)

压轴大题突破练——直线与圆锥曲线(二)1. 已知直线x +ky -3=0所经过的定点F 恰好是椭圆C 的一个焦点,且椭圆C 上的点到点F 的最大距离为8.(1)求椭圆C 的标准方程;(2)已知圆O :x 2+y 2=1,直线l :mx +ny =1,试证:当点P (m ,n )在椭圆C 上运动时,直线l 与圆O 恒相交,并求直线l 被圆O 所截得的弦长L 的取值范围. 解 (1)直线x +ky -3=0经过定点F (3,0),即点F (3,0)是椭圆C 的一个焦点.设椭圆C 的方程为x 2a 2+y 2b2=1(a >b >0),因为椭圆C 上的点到点F 的最大距离为8, 所以a +3=8,即a =5. 所以b 2=a 2-32=16.所以椭圆C 的方程为x 225+y 216=1.(2)因为点P (m ,n )在椭圆C 上,所以m 225+n 216=1,即n 2=16-16m 225(-5≤m ≤5).所以原点到直线l :mx +ny =1的距离d =1m 2+n2=1925m 2+16<1.所以直线l :mx +ny =1与圆O :x 2+y 2=1恒相交,L 2=4(r 2-d 2)=4⎝⎛⎭⎪⎪⎫1-1925m 2+16. 因为-5≤m ≤5,所以152≤L ≤465. 2. 已知点A 是圆F 1:(x +3)2+y 2=16上任意一点,点F 2与点F 1关于原点对称.线段AF 2的中垂线m 分别与AF 1、AF 2交于M 、N 两点.(1)求点M 的轨迹方程;(2)设不过原点O 的直线l 与该椭圆交于P 、Q 两点,满足直线OP ,PQ ,OQ 的斜率依次成等比数列,求△OPQ 面积的取值范围.解 (1)由题意得,F1(-3,0),F 2(3,0),圆F 1的半径为4, 且|MF 2|=|MA |.从而|MF 1|+|MF 2|=|MF 1|+|MA |=|AF 1|=4>|F 1F 2|.∴点M 的轨迹是以F 1,F 2为焦点的椭圆,其中长轴2a =4,得a =2,焦距2c =23,则短半轴b =1,∴点M 的轨迹方程为x 24+y 2=1.(2)由题意可知,直线l 的斜率存在且不为0,故可设直线l 的方程为y =kx +m (m ≠0),P (x 1,y 1),Q (x 2,y 2), 由⎩⎪⎨⎪⎧y =kx +m ,x 2+4y 2-4=0消去y 得(1+4k 2)x 2+8kmx +4(m 2-1)=0,则Δ=64k 2m 2-16(1+4k 2)(m 2-1)=16(4k 2-m 2+1)>0,且x 1+x 2=-8km 1+4k 2,x 1x 2=m 2-1+4k 2. 故y 1y 2=(kx 1+m )(kx 2+m )=k 2x 1x 2+km (x 1+x 2)+m 2. 因为直线OP ,PQ ,OQ 的斜率依次成等比数列, 所以y 1x 1·y 2x 2=k 2x 1x 2+km x 1+x 2+m 2x 1x 2=k 2,即-8k 2m 21+4k2+m 2=0, 又m ≠0,所以k 2=14,即k =±12.由于直线OP ,OQ 的斜率存在,且Δ>0,得0<m 2<2且m 2≠1.S △OPQ =12|x 1-x 2||m |=m 2-m 2,所以S △OPQ 的取值范围为(0,1).3. 如图,已知点A (1,2)是离心率为22的椭圆C :x 2b 2+y2a2=1(a >b >0)上的一点,斜率为2的直线BD 交椭圆C 于B 、D 两点,且A 、B 、D 三点互不重合.(1)求椭圆C 的方程;(2)△ABD 的面积是否存在最大值?若存在,求出这个最大值;若不存 在,请说明理由.(3)求证:直线AB 、AD 的斜率之和为定值.(1)解 由题意,可得e =c a =22,1b 2+2a 2=1,a 2=b 2+c 2,解得a =2,b =2,c =2, 所以椭圆C 的方程x 22+y 24=1.(2)解 设直线BD 的方程为y =2x +m ,D (x 1,y 1),B (x 2,y 2),由⎩⎨⎧y =2x +m ,2x 2+y 2=4,得4x 2+22mx +m 2-4=0,所以Δ=-8m 2+64>0⇒-22<m <22,x 1+x 2=-22m ,x 1x 2=m 2-44.所以|BD |=1+22|x 1-x 2|=62·8-m 2. 设d 为点A 到直线BD :y =2x +m 的距离,所以d =|m |3.所以S △ABD =12|BD |·d =24·-m2m 2≤2,当且仅当8-m 2=m 2,即m =±2时取等号.因为±2∈(-22,22),所以当m =±2时,△ABD 的面积最大,最大值为 2. (3)证明 设直线AB 、AD 的斜率分别为k AB 、k AD ,则k AD +k AB =y 1-2x 1-1+y 2-2x 2-1=2x 1+m -2x 1-1+2x 2+m -2x 2-1=22+m ·x 1+x 2-2x 1x 2-x 1+x 2+1,(*) 将(2)中①、②式代入(*)式,整理得22+m ⎣⎢⎡⎦⎥⎤x 1+x 2-2x 1x 2-x 1+x 2+1=0,即k AB +k AD =0.4. 已知椭圆E :x 2a 2+y 2b2=1(a >b >0)的右焦点F ,过原点和x 轴不重合的直线与椭圆E 相交于A ,B 两点,且|AF |+|BF |=22,|AB |的最小值为2.(1)求椭圆E 的方程;(2)若圆:x 2+y 2=23的切线l 与椭圆E 相交于P ,Q 两点,当P ,Q 两点横坐标不相等时,问OP →与OQ →是否垂直?若垂直,请给出证明,若不垂直,请说明理由. 解 (1)设A (x 0,y 0),B (-x 0,-y 0),F (c,0)(c 2=a 2+b 2), 则|AF |+|BF |=2a =22,∴a = 2. |AB |=x 02+y 02=2x 20+⎝ ⎛⎭⎪⎫1-x 20a 2b 2 =2b 2+c 2x 20a2,∵0≤x 20≤a 2,∴|AB |min =2b =2,∴b =1. 所以椭圆E 的方程为x 22+y 2=1.(2)由题设条件可知直线的斜率存在,设直线l 的方程为y =kx +m .l 与圆x 2+y 2=23相切,∴|m |1+k2=63,∴m 2=23(k 2+1).把l 的方程y =kx +m 代入x 22+y 2=1中得:(1+2k 2)x 2+4kmx +2m 2-2=0,Δ=8(2k 2+1-m 2)>0,令P (x 1,y 1),Q (x 2,y 2),x 1+x 2=-4km1+2k 2① x 1x 2=2m 2-21+2k2② y 1y 2=k 2x 1x 2+km (x 1+x 2)+m 2=m 2-2k 21+2k 2③OP →·OQ →=x 1x 2+y 1y 2=2m 2-21+2k 2+m 2-2k 21+2k 2=3m 2-2k 2-21+2k2=0, ∴OP →⊥OQ →.。
2012年高考圆锥曲线

2012年高考真题数学圆锥曲线一、选择题1.【2012高考浙江理8】如图,F 1,F 2分别是双曲线C :22221x y a b-=(a,b >0)的左、右焦点,B 是虚轴的端点,直线F 1B 与C 的两条渐近线分别交于P,Q 两点,线段PQ 的垂直平分线与x 轴交与点M ,若|MF 2|=|F 1F 2|,则C 的离心率是A.BD. 2.【2012高考新课标8】等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线x y 162=的准线交于,A B 两点,AB =C 的实轴长为( )()A ()B C/4 ()D 83.【2012高考新课标4】设12F F 是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点,P 为直线32a x =上一点,12PF F ∆是底角为30的等腰三角形,则E 的离心率为( )()A 12 ()B 23 C 34 ()D 454.【2012高考山东理10】已知椭圆2222:1(0)x y C a b a b +=>>的离心学率为.双曲线221x y -=的渐近线与椭圆C 有四个交点,以这四个焦点为顶点的四边形的面积为16,则椭圆C 的方程为(A )22182x y += (B )221126x y += (C )221164x y += (D )221205x y += 6.【2012高考湖南5】已知双曲线C :22x a -22y b=1的焦距为10 ,点P (2,1)在C 的渐近线上,则C 的方程为A .220x -25y =1 B.25x -220y =1 C.280x -220y =1 D.220x -280y =17.【2012高考福建8】已知双曲线22214x y b-=的右焦点与抛物线y 2=12x 的焦点重合,则该双曲线的焦点到其渐近线的距离等于A.B. C.3 D.58.【2012高考安徽9】过抛物线24y x =的焦点F 的直线交抛物线于,A B 两点,点O 是原点,若3AF =,则AOB ∆的面积为( )()A 2()B C2()D 9.【2012高考全国卷3】 椭圆的中心在原点,焦距为4 一条准线为x=-4 ,则该椭圆的方程为A 216x +212y =1B 212x +28y =1C 28x +24y =1D 212x +24y =1 10.【2012高考全国卷理8】已知F 1、F 2为双曲线C :x ²-y ²=2的左、右焦点,点P 在C 上,|PF 1|=|2PF 2|,则cos ∠F 1PF 2= (A)14 (B )35 (C)34 (D)45二、填空题13.【2012高考四川15】椭圆22143x y +=的左焦点为F ,直线x m =与椭圆相交于点A 、B ,当FAB ∆的周长最大时,FAB ∆的面积是____________。
【步步高】2012高考数学 考前三个月抢分训练21 综合(五)

训练21 综合(五)1.复数z =11-i的共轭复数是________. 2.函数f (x )=⎩⎪⎨⎪⎧ x +2,x ≤0-x +2, x >0,则不等式f (x )≥x 2的解集是________. 3.已知函数f (x )=x 2-2ax +a 2-1的定义域为A,2∉A ,则a 的取值范围是________.4.f (n )=cos ⎝⎛⎭⎪⎫n π2+π4,则f (1)+f (2)+f (3)+…+f (2 011)=________. 5.若圆x 2+y 2-2mx +m 2-4=0与圆x 2+y 2+2x -4my +4m 2-8=0相切,则实数m 的取值集合是________.6.已知数列{a n }的前n 项和为S n ,且S n =n 2+n ,数列{b n }满足b n =1a n a n +1(n ∈N *),T n 是数列{b n }的前n 项和,则T 9=________.7.一个正方体的外接球的表面积是它内切球的表面积的________倍.8.执行下面的流程图,若p =0.8,则输出的n =______.9.设等差数列{a n }的各项均为整数,其公差d ≠0,a 5=6,若a 3,a 5,a m (m >5)是公比为q (q >0)的等比数列,则m 的值为________.10.若二项式⎝ ⎛⎭⎪⎫3x 2-1x n 的展开式中各项系数的和是512,则展开式中的常数项为________. 11.如果实数x 、y 满足(x -2)2+y 2=3,那么y x的最大值是________.12.已知抛物线y 2=4x 上两个动点B 、C 和点A (1,2),且∠BAC =90°,则动直线BC 必过的定点的坐标为________.13.2009年在山东第十一届全国运动会射击比赛的预赛场上,专家们预测某射手在一次射击中命中9环的概率是0.48,命中8环的概率是0.19,不够8环的概率是0.08.则这个射手在一次射击中命中9环或10环的概率为________.14.甲、乙、丙、丁四人独立破解一类数据,甲、乙二人能独立破解成功的概率都是12,丙、丁二人能独立破解成功的概率都是23,今由4人同时破解这类数据,则数据不能被破解的概率是________.答案1.12-12I 2.[-1,1] 3.(1,3) 4.22 5.{-125,-52,0,2} 6.9407.3 8.4 9.11 10.2 268 11. 3 12.(5,-2) 13.0.73 14.136。
【步步高】2012高考数学 考前三个月抢分训练16 算法初步、复数
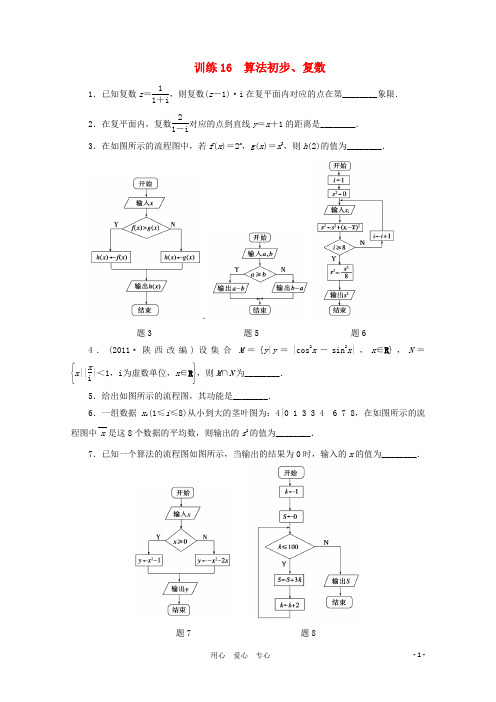
训练16 算法初步、复数1.已知复数z =11+i ,则复数(z -1)·i 在复平面内对应的点在第________象限.2.在复平面内,复数21-i 对应的点到直线y =x +1的距离是________.3.在如图所示的流程图中,若f (x )=2x,g (x )=x 3,则h (2)的值为________..题3 题5 题64.(2011·陕西改编)设集合M ={y |y =|cos 2x -sin 2x |,x ∈R },N =⎩⎨⎧⎭⎬⎫x ||xi |<1,i 为虚数单位,x ∈R ,则M ∩N 为________.5.给出如图所示的流程图,其功能是________.6.一组数据x i (1≤i ≤8)从小到大的茎叶图为:4|0 1 3 3 4 6 7 8,在如图所示的流程图中x 是这8个数据的平均数,则输出的s 2的值为________.7.已知一个算法的流程图如图所示,当输出的结果为0时,输入的x 的值为________.题7 题88.执行如图所示的流程图,则输出的S =________.9.若复数z 1=4+29i ,z 2=6+9i ,其中i 是虚数单位,则复数(z 1-z 2)i 的实部为________.10.已知集合A =⎩⎨⎧⎭⎬⎫12i,i 2,|5i 2|,+2i,-i 22,则集合A ∩R +的子集个数为________.11.(2010·北京)在复平面内,复数2i1-i 对应的点的坐标为______.12.阅读如图所示的流程图,运行相应的程序,输出的结果是________.题12 题13 题1413.某地区为了解70岁~80岁的老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查,下表是这50位老人睡眠时间的频率分布表:14.若如图所示的算法流程图中输出y 的值为0,则输入x 的值可能是________(写出所有可能的值). 答案1.四 2.223.8 4.[)0,1 5.求|a-b|的值 6.7 7.-2或18.7 500 9.-20 10.8 11.(-1,1) 12.8 13.6.42 14.0,-3,1。
2012版步步高高考数学考前三个月专题复习课件6(2汇总

§ 2椭圆.双曲线、抛物线真题热身1. (2011-安徽改编)双曲线2X2-/=8的实轴长是_12解析•/ 2x2 - y2 = 8,・••才 $:.a = 2, 2a = 4.・•・/ +,= 9.由①②得«2= 5, Z?2 = 4.2 2・・・双曲线的标准方程为1.2. (2011-广东改编)设,+(y —3尸=1外切,与直线y=0相切,则C 的 E I 心轨迹为抛物线・解析 设圆C 的半各为厂,则圆心C 到直线y = O 的距离 为厂.由两圆外切可得,圆心C 到点(0,3)的距离为厂+1,也 就是说,圆心C 到点(0,3)的距离比到直线y = ()的距离大 1,故点C 到点(0,3)的距离和它到直线- 1的距离相等, 符合抛物线的特征,故点C 的轨迹为抛物线.3. (2011-山东改编 线均和圆X 2 v 2£、2下1(4>0, 〃>0)的两条渐近,且双曲线的右焦点为圆C 的圆心,则该双曲线的方程为5一 4 = 192解析 ・・•双曲线1的渐近线方程为厂 b ±-X,a 圆C 的标准方程为(x - 3)2+ y 2= 4,・・・圆心为C(3,0).又渐近线方程与圆C 相切, 即直线bx - ay =()与圆C 相切,又:•缶-話=1的右焦点尸2(#2 +①b\ 0)为圆心 C(3,0),4. (2011-iI宁)已知点(2,3)在双曲线C:》一器=1(4>0, 〃>0)上,C的焦距为4,则它的离心率为___________ •4 9解析由题意知7 一戸=1'疋=/ + /?2= 4得a = 1,/? =羽,C.e = 2.锥曲线的又 F X F 2 = 2^/3, 由余弦定理可知COS ZF I PF 2 = -壬.范围 丄皿QO几 何 性质(0,0)顶 "7±a,0)(0, ±b)(±a,0) 对称性 关于X 轴,丿轴和原点对称关于x 轴对称焦点 (±c,0)§ o )轴长轴长2a 9 短轴长2b实轴长2a f 虚轴长”离心率C e=~FA /1-? (0<e<l)c e=~=A /1+?(e>l)e=l准线x=~2渐近线by =±a x锥曲鋸亘义及几何性质 °例1 (1)已知P 为椭圆亍+b=l 和双曲线X 2-^=1的一个交 点尺、F2为椭圆的两个焦点,那么ZF.PF2的余弦值为 _____ ・ (2)已知直线y=k(x+2)(k>0)与抛物线G ?=8r 相交于A 、〃两点,F 为C 的焦点.若FA = 2FB 9则比= ______________ ・(1) 由椭圆和双曲线的方程可知,Fp 尸2为它们的公共 PF { + PF? = 4PF\_ PF? = 2所以解析不妨设\PFi = 3回2 = 1又F X F2 = 2^/3, 由余弦定理可知COS ZF I PF2 = -壬.(2)方+ 2)(* > 0)恒过定点 P( - 2,0). 如图,过A 、B 分别作AM 丄Z 于点M, BN 丄I 于点N ・ 由皿=2FB 9则AM = 2BN,点B 为AP 的中点. 连结OB,则OB = R F ,・・・OB = BF,点B 的横坐标为1, 故点B 的坐标为(1,2^2). . 2岛0 _2\耳 ・・ 1_(_2)一 3 ••匹 BB‘ 1 9AC~AA f"2J即B 是AC 的中点. .2x 〃 ■必 _ 2,* * [2yn = y AJ42= 8X4,yin =张〃,联立可得4(4,4迈),〃(1,2迈). . 4迈 一 2^2 2^2• ^AB = 川―- =2一•答案⑴一扌(2)2屮方法二如F, AA f-AF,归纳拓展1 •圆锥曲线的定义是根本,它是标准方程和几何性质的“源”,“回归定义”是一种重要的解题策略.对于圆锥曲线的定义不仅要熟记,还要深入理解细节部分:比如椭圆的定义中要■求PF. + PF2 > F X F2,双曲线的定义中要求IPFj - PF2\ < FX F2,抛物线上的点到焦点的距离与到准线的距离相等的转化.2.注意数形结合,提倡画出合理草图.变式训练1卫欖交点,F1、尸2分别是它们的左、右焦点,设椭圆离心率为"双曲线离心率为巾,若两•航=0,则A+A = ______________ ・(2)如图,过抛物线j2=2px(p>0)的焦点的直线Z依次交抛物线及其准线与点A、B、C,若BC=2BF,且AF=3,则抛物线的方程是_____________________ ・=i ・(2)作 丄 垂足分别娇 则由抛物线定义得, Ag = AF-3, BF = BM.— 2BF,所以 BC = 2BM.解析(1兄 轴长为0,双曲线实半轴长为",由题意,得PFi + PFi = 2a,①由BM//二、圆锥曲线的方程及应用= l(a>b>0)的离心率e=例2 (2010-天津)已知椭圆弓,连结椭圆的四个顶点得到的菱形的面积为4・(1)求椭圆的方程;(2)设直线/与椭圆相交于不同的两点A, B,已知点A的坐标为(一0,0),点0(0,为)在线段的垂直平分线上,且QA QIi =4,求旳的值.=i ・由方程组消今三严―F(1 + 4k 2)x 2 + 16k 2x + (16k 2- 4) = 0.16, - 4 由根与系数的关系,得-加L〒W , 所以从而J, =1^4p*设线段4B 的中点为M, 则M 的坐标为(一岸気, 以下分两种情况讨论:①当Ar = 0时,点B 的坐标是(2,0),线段AB 的垂直平分线为y 轴,于是鬲=(-2, -jo),筋=(2, -jo). 由芮L •函=4,得为=±2\「2・②当直平分线的方程为 2k y T^P =-*"1 + 40・ 令x = 0,解得旳=-务.由QA = (~2f -jo), QB = (xi ,yi -j 0),一 2(2 一 蛇) 6k z 4k ~ +1+ 4*^1 + 4*2 + 4(16^4 +丄5宀卫+ 4J12)2QA-QB = ~ 2xi-jo(yi- jo)整理得7k27・综上,jo = ±2-\/2或为=归纳拓展1 •求圆锥曲线的标准方程的基本步骤: ⑴定型(确定圆锥曲线类型).(2) 定位(判断它的中心在原点,焦点在哪条坐标轴上). (3) 定量(建立关于基本量的方程或方程组,解得基本量a, b 的值).2.椭圆、双曲线.抛物线是常见的曲线,利用它们的方程及 几何性质,可以解决一些简单的实际问题;利用方程可以研究 它们与直线的交点、相交弦等有关问题.的点M 与椭圆右焦点F 、的连线MF X 与 x 轴垂直,且OM (O 是坐标原点)与椭圆 长轴和短轴端点的连线AB 平行. (1)求椭圆的离心率;⑵巧是椭圆的左焦点,C 是椭圆上的任一点, 证明:ZF X CF 2^⑶过F I 且与4〃垂直的直线交椭圆于P 、Q,若△PAO 的 面积是2叭5,求此时椭圆的方程.=1±变式训练y B M:.—=~=^b = c=>a = y<2c ac a v⑵证明 由椭圆定义得:FiC +尺< =加,COSZF1CF2 =4a 1 2-4c 2- 2F& F2C即 j = - \[2(x - c).代入椭圆方程消去工得:^(c~^y)2+^= 1, 整理得:5y 2- 2yj2cy - 2<?2 = 0,. 2\l2c 2c 2・・ Jl +J2= 5 ' ^1J2= 一亏一・ m 警沪誓:礬S&F Q |-2<-lyi -j 2l == 2叭/§, c 2= 25,因此a 2= 50,沪= 25,所以椭圆方程为备+幺".2F I CF 2C一 FiC + F 2C 2F]C ・F2CW(」2 )=2b 22c 2•••COSZF1CF2 工 72■- 1 =茲2 -1 = 0, ・・・ZF1CF2W 务则M(c,-2F X CF 2C 2b 2F I CF 2C 2 0),b "a (1)解设你,k OM = k设冼=(七兀3 =加1 +例 3 (2011 •江西)P(x 0, ,o)(xoH±a)是双曲线 E :》一点2= 1(°>0, 〃>0)上一点,M, N 分别是双曲线E 的左,右顶点,直线 PM, PV 的斜率之积为占⑴求双曲线的离心率;(2)过双曲线E 的右焦点且斜率为1的直线交双曲线于A, B 两点,O 为坐标原点,C 为双曲线上一点,且满足荒=2芮 +OB 9求久的值.解(1)由点竺由题意有—.Jo Jo5’⑵联立设 A (x 5c +(加1 + X 2)2丹卅-50 + (xl - 5yl ) + 2>.(X J X 2 - 5丿也)=5b 2.又A(x n J O ,B(X 29力)在双曲线上, 所以 xj - 5yi = 5b 2, xj - 5yl= 5b 2.由①式又有- 5JIJ 2 =小*2 - 5(*1 - c)(x 2 - c)=一 4XJ X 2 + 5c(*i + x 2) 一 5c 2= 10b 2, ②式可化为A 2 + 4x = 0,解得久=0或2二-4.归纳拓展 本题考查了双曲线方程和它的几何性质,同时 还考查了直线与双曲线的位置关系,圆锥曲线与直线的综合类题目中数形结合法是解题首选,根与系数的关系是解 题利器,方程思想是解题的切入点.变式训练3 (20U ・江西)已知过抛物线y 2=2px(p>0)的焦点, 斜率为2边的直线交抛物线于A (X|, yi)9 B(X 2,歹2)仗心2)两 点,且AB=9. (1)求该抛物线的方程,(2)0为坐标原点,C 为抛物线上一点,若OC=OA+;VB,求 2的值.又C 为双b\有⑴直线^牡鱼科2 ,2(x-伶),与y2 = 2px联立,从而有4x2 - 5px + p2 = 0, 所以Xi+X2*由抛物线定义得AB +x2 + p - 9,所以p = 4,从而抛物线方程是y2 = Sx・(2)由” _ 4 知4x2— 5px + _ o 可化为x2— 5x + 4 — 0,从而Xi = 1, x2 = 4, Ji = - 2^/2, y2 = 4^/2, 从而4(1, -2迈),3(4,4迈)・设OC = (x3, J3)= (b - 2迈)+ 2(4,4迈)= (4z+l, 4血-2^2), 又J3 = 8x3,所以[2^(22-1)]2 = 8(42+1),即(22-1)2 = 42+1,解得;>0或・一、填空题1. AB是某平面上一定线段,点P是该半面内的一动点,满足质I一I两1 = 2, I芮一苛1 = 2诟,则点P的轨迹是双曲线的一支.解析由I芮-丙1 = 2击得I芮l = 2\S. 又I芮I - I萌=2 <2审,由双曲线定义可得轨迹为双曲线的一支线y 2=2px (p>0)^J 焦点的距离为4,且双曲线的一条渐近线 与抛物线的准线的交点坐标为(一2, -1),则双曲线的焦距 为 _______ ・解析双曲线左顶点为人(-Q,0), 渐近线为y = 土务,抛物线y 2= 2px (p>0)焦点为F 時、0), 准线为直线%= - 2- 由题意知-纟=-2,•*.p = 4,由题意知 2 + a = 4, /.a = l.-1)的渐近线为歹=尹, - 1 pX (- 2),/.c 2 = a 2 + Z>2 = 5, ・・・c = \M,・・.2c = 2迟 答案2^52. (2011 天津雷毬fjg^=lS>0, b>0)的左顶点与抛物・•・双曲线渐近线y = 中与准线x = -纟交于(- 2,2,焦点与椭圆£+£ =1的焦点相同,那么双曲线的焦点坐标为_1±红QL;渐近线方程为心/±)=°.解析・••双曲线的焦点与椭圆的焦点相同,・= 4.Ve = - =2,・\a = 2,・\b2 = 12,・\b = 2^/3.a v・・•焦点在x轴上,・・・焦点坐标为(±4,0),渐近线方程为y= 土务,即y = ±^/3x, 化为一般式为帝兀土y = 0.4. (2010-陕西)已知抛物线y2=2px(p>0)的准线与圆x2+y2—6x 一7=0相切,则D的值为 2 .解析抛物线y2 = 2px(p>0)准线为x=圆x2 + y2 - 6x - 7 = 0 即(x - 3)2 + y2 = 16,则圆心为(3,0),半径为4;又因为抛物线b = 2px(p>0)的准线与圆x2 + y2 - 6x - 7 = 0 相切,所以3+号=4,解得p = 2.=0的距离的最小值为&)・解析 设P (x (),为),则点P 到直线x + 2y + 8 = 0的距离 ,+ 2y ()+ 81 d =―疋—■ 又点P 在抛物线y =上,所以y ()= 2x <),所以 d=+x ()+ 81,所以当Xo = 一+时,46.设抛物线_/=2p.心>0)的焦点为F,点4(0,2).若线段皿 的中点B 在抛物线上,则B 到该抛物线准线的距离为卫_・ 解析抛物线的焦点F 的坐标为(£ 0),线段朋的中点B 的坐标为(? 1),代入抛物线方程得1 =2pX^,解得p = d 故点B 的坐标为序,1,故点B 到该抛物线 准线的距5.已知抛八、、127审则点P 到127审80 -〃min离为普+警普.7.已知点F为抛物线y =—8x的焦点,O为原点,点尸是抛物线准线上一动点,点4在抛物线上,且AF=4,则必+ PO的毘小値为2屈.解析抛物线的准线方程为x = 2,因为AF = 4,由抛物线定义可得,点A的横坐标为-2,取点A( - 2,4)・因为原点O关于准线的对称点为3(4,0),贝y M + PO = M + PBMAB = 2(13.8.已知A(—刃0),3是・・・B4 + PF=2,即P 到两定点A 、F 距离之和为定值2且大于两定点A 、F 之间的距离1, 故3-4 - 2 b 1一29右焦点为(2迈,0).斜率为1的直线/与椭圆G 交于A 、B 两点,以4〃为底边作等腰三角形,顶点为尸(一3,2)・ (1)求椭(2)求的面积. ft? (1)由已知得c = 2翻,'=半,解得■。
【步步高】2012高考数学 考前三个月抢分训练4 不等式

训练4 不等式1.“a >0且b >0”是“a +b2≥ab ”成立的________条件.2.(2010·江西改编)对于实数a ,b ,c ,“a >b ”是“ac 2>bc 2”的________条件. 3.若实数x ,y 满足1x 2+1y2=1,则x 2+2y 2的最小值为________.4.不等式x 2-4>3|x |的解集是________.5.(2011·天津)已知集合A ={x ∈R ||x +3|+|x -4|≤9},B ={x ∈R |x =4t +1t-6,t ∈(0,+∞)},则集合A ∩B =________.6.已知p :关于x 的不等式|x -2|+|x +2|>m 的解集为R ;q :关于x 的不等式x 2+mx +4>0的解集为R .则p 成立是q 成立的________条件.7.设a >b >0,则a 2+1ab +1a a -b的最小值是________.8.(2011·大纲全国)若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤6,x -3y ≤-2,x ≥1,则z =2x +3y 的最小值为________.9.已知关于x 的不等式组⎩⎪⎨⎪⎧x 2-x -2>0,2x 2+k +x +5k <0的解集是M ,若M ∩Z =∅,则常数k的取值范围是________.10.若关于x 的不等式(a +b )x +2a -3b <0的解集是⎩⎨⎧⎭⎬⎫x |x <-13,则(a -3b )x +b -2a >0的解集是________.11.(2010·江苏)已知函数f (x )=⎩⎪⎨⎪⎧x 2+1,x ≥0,1,x <0,则满足不等式f (1-x 2)>f (2x )的x的取值范围是________.12.若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围为________. 13.若关于x 的不等式(2x -1)2<ax 2的解集中整数恰好有3个,则实数a 的取值范围是__________.14.(2011·四川改编)某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需送往A 地至少72吨的货物,派用的每辆车需满载且只运送一次,派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润为________.答案1.充分不必要 2.必要不充分 3.3+2 2 4.(-∞,-4)∪(4,+∞) 5.{x |-2≤x ≤5} 6.必要不充分 7.4 8.5 9.2≤k ≤310.{x |x <-3} 11.(-1,2-1) 12.5<b <7 13.⎝ ⎛⎦⎥⎤259,4916 14.4 900元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
训练13 圆锥曲线
1.已知椭圆x 2a 2+y 2
b 2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若AP →=2PB →,则椭圆的离心率是________.
2.若抛物线y 2
=2px 的焦点与椭圆x 26+y 22=1的右焦点重合,则p 的值为________. 3.已知椭圆x 210-m +y 2
m -2
=1,长轴在y 轴上.若焦距为4,则m =________. 4.若直线y =x +t 与椭圆x 24
+y 2=1相交于A ,B 两点,当t 变化时,AB 的最大值是________. 5.已知点M (3,0),椭圆x 24
+y 2=1与直线y =k (x +3)交于点A 、B ,则△ABM 的周长为________.
6.(2011·福建)设圆锥曲线Γ的两个焦点分别为F 1,F 2,若曲线Γ上存在点P 满足PF 1∶F 1F 2∶PF 2=4∶3∶2,则曲线Γ的离心率为________.
7.若双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一个焦点到一条渐近线的距离等于焦距的14
,则该双曲线的离心率是________.
8.如图所示,F 为双曲线C :x 29-y 216
=1的左焦点,双曲线C 上的点P i 与P 7-i (i =1,2,3)关于y 轴对称,则P 1F +P 2F +P 3F -P 4F -P 5F -P 6F 的值是________. ]
9.对于抛物线y 2=4x 上任意一点Q ,点P (a,0)都满足PQ ≥|a |,则a 的取值范围是________.
10.设双曲线x 2a 2-y 2
b 2=1的一条渐近线与抛物线y =x 2+1只有一个公共点,则双曲线的离心率为________.
11.(2010·浙江改编)设F 1、F 2分别为双曲线 x 2a 2-y 2
b 2=1(a >0,b >0)的左、右焦点,若在双曲线右支上存在点P ,满足PF 2=F 1F 2,且F 2到直线PF 1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为________.
12.经过点(3,0)的直线l 与抛物线y =x 22
相交,两个交点处的抛物线的切线相互垂直,则直线l 的斜率k =________.
13.从双曲线x 2a 2-y 2
b 2=1(a >0,b >0)的左焦点F 引圆x 2+y 2=a 2的切线l ,切点为T ,且l
交双曲线的右支于点P.若点M是线段FP的中点,O为坐标原点,则OM-TM=________.
14.(2011·课标全国)在平面直角坐标系xOy中,椭圆C的中心为原点,焦点F1,F2在x
轴上,离心率为
2
2.过F1的直线l交C于A,B两点,且△ABF2的周长为16,那么椭圆C的
方程为__________.答案
1.1
22.4 3.8 4.
410
55.8 6.
1
2或
3
27.
23
38.18 9.(-∞,2]
10. 5 11.4x±3y=0 12.-1
613.b-a14.
x2
16+
y2
8=1。
