概率论与数理统计
概率论与数理统计目录

概率论与数理统计目录一、随机事件及其概率1.1 随机事件的基本概念定义与分类事件的运算1.2 概率的定义与性质概率的公理化定义概率的基本性质1.3 古典概型与几何概型古典概型的计算几何概型的计算1.4 条件概率与独立性条件概率事件的独立性1.5 全概率公式与贝叶斯公式全概率公式贝叶斯公式及其应用二、随机变量及其分布2.1 随机变量的概念随机变量的定义随机变量的分类2.2 离散型随机变量及其分布常见的离散型分布分布律与分布函数2.3 连续型随机变量及其分布常见的连续型分布概率密度函数与分布函数2.4 随机变量函数的分布离散型随机变量函数的分布连续型随机变量函数的分布三、多维随机变量及其分布3.1 多维随机变量的概念联合分布函数边缘分布3.2 多维离散型随机变量联合分布律边缘分布律3.3 多维连续型随机变量联合概率密度函数边缘概率密度函数3.4 条件分布离散型条件分布连续型条件分布3.5 随机变量的独立性独立性的定义独立性的判定与性质四、数字特征4.1 数学期望数学期望的定义与性质数学期望的计算4.2 方差方差的定义与性质方差的计算4.3 协方差与相关系数协方差的定义与性质相关系数的定义与性质4.4 矩与协矩阵矩的定义与计算协矩阵的定义与计算五、大数定律与中心极限定理5.1 大数定律切比雪夫大数定律伯努利大数定律5.2 中心极限定理林德贝格-莱维中心极限定理德莫佛尔-拉普拉斯中心极限定理六、数理统计的基本概念6.1 总体与样本总体的定义与性质样本的定义与性质6.2 统计量与抽样分布统计量的定义与性质常见的抽样分布七、参数估计与假设检验7.1 参数估计点估计区间估计7.2 假设检验假设检验的基本概念单侧检验与双侧检验正态总体的假设检验八、回归分析与方差分析8.1 回归分析一元线性回归多元线性回归回归模型的检验与预测8.2 方差分析单因素方差分析双因素方差分析方差分析的应用。
概率论与数理统计

概率论与数理统计概率论与数理统计是现代数学中非常重要的分支之一,它们在自然科学、社会科学,以及工程技术等领域都有广泛的应用。
在生物学,物理学,化学等领域,常常需要采用概率论和数理统计的方法,来研究和分析现象。
这篇文章将要探讨概率论和数理统计的一些基本概念和方法,并介绍它们在现实生活中的应用。
一、概率论概率论是一门研究随机现象及其规律的数学学科。
它的基本思想是通过建立数学模型,来描述随机事件的概率分布及其规律。
随机事件指某一次试验中可能发生或不发生的事情,例如掷骰子、抛硬币、抽扑克牌等,这些事件的结果是随机的,因此需要采用概率论的方法来研究。
1.概率和概率分布概率是指某一事件发生的可能性,用一个数值来表示。
在概率论中,对于某一特定随机事件,概率的大小常常用P(A)来表示,其中A是这个事件。
例如,抛一枚硬币,正面朝上的概率是0.5,用数学语言可以表示为P(正面)=0.5,反面朝上的概率也是0.5,即P(反面)=0.5。
概率分布是指某个随机事件的各种结果的概率分布情况。
在一次试验中,随机事件可能会有多个结果,即样本空间。
概率分布用来描述每个结果的概率大小。
例如,抛一枚硬币的样本空间是{正面,反面},正面和反面各占1/2的概率。
2.条件概率和独立事件条件概率是指在已知某个事件发生的情况下,某个随机事件会发生的概率。
条件概率的计算方法一般采用贝叶斯公式,例如给定事件A,以及事件B,P(A|B)表示在B发生的情况下,A 发生的概率,则条件概率可以表示为:P(A|B) = P(AB)/P(B)其中AB表示事件A和事件B同时发生的概率,P(B)表示事件B发生的概率。
独立事件是指某个随机事件的发生不会对另一个随机事件的发生产生影响。
如果事件A、B是独立事件,则可以表示为P(A|B) = P(A),P(B|A) = P(B),即A和B的概率相互独立,并不受对方的影响。
3.期望值和方差期望值是统计学中一个非常重要的概念,用来描述一个随机变量的总体平均数。
概率论与数理统计

一、事件的频率与概率
次数, µ n ( A ) : 事件 A 在 n 次可重复试验中出现的 次数,
称为 A 在 n 次试验中出现的频数
频率—— f n ( A) = 频率
µ n ( A)
n
.
频率有如下性质: 频率有如下性质:
1. 非负性:对任何事件 A,有 0 ≤ f n ( A) ≤ 1 非负性:
掷一骰子, 如: A =“掷一骰子,点数小于 4”, B =“掷一骰子,点数小于 5”, 掷一骰子, 则A ⊂ B.
显然对任何事件 A,有 Φ ⊂ A ⊂ Ω⊂ A,则称事件 A与事件 B相等,记作 A = B .
2.事件的和(并) 事件的和(
两个事件 A, B 中至少有一个发生 (属于A或属于 B的样本点 构成的集合 ),称为事件 A 与 B 的和(并 ), 记作 A + B 或 A ∪ B .
显然, 显然,事件 A 与 A 可以构成一个完备事件 组
类似地,称可列个事件 A1 , A2 , L , An, 构成一个 L 类似地, 完备事件组, 完备事件组,如果满足 :
(1)
( 2)
Ai A j = Φ
(i ≠ j )
∑A
i
i
=Ω
律 事件运算满足下列运算 :
(1) 交换律 A + B = B + A AB = BA
设袋中有红, 黄各一球, 例: 设袋中有红,白,黄各一球,有放回抽取三 取出球后仍把球放回原袋中),每次取一球, ),每次取一球 次(取出球后仍把球放回原袋中),每次取一球,试 说明下列各组事件是否相容?若不相容, 说明下列各组事件是否相容?若不相容,说明是否 对立? 对立? 三次抽取, 三次抽取, (1) A=“三次抽取,颜色全不同”,B=“三次抽取, = 三次抽取 颜色全不同” = 三次抽取 相容 颜色不全同” 颜色不全同” (2) A=“三次抽取,颜色全同”,B=“三次抽取, 三次抽取, 三次抽取, = 三次抽取 颜色全同” = 三次抽取 颜色不全同” 颜色不全同” 不相容, 不相容,对立 三次抽取, 三次抽取, (3) A=“三次抽取,无红色球”,B=“三次抽取, = 三次抽取 无红色球” = 三次抽取 无黄色球” 无黄色球” 相容 三次抽取, (4) A=“三次抽取,无红色球也无黄色”, = 三次抽取 无红色球也无黄色” B=“三次抽取, 无白色球” 不相容,不对立 三次抽取, = 三次抽取 无白色球” 不相容,
概率论与数理统计公式整理(超全免费版)

「 ef(x) w0,其中 0,则称随机变量X 服从参数为X 的分布函数为1xe, xF(x)'0,x<0。
记住积分公式:x ne xdx n!指数分布的指数分布如果二维随机向量(X, Y)的所有可能取值为至多可列个有序对(x,y),则称为离散型随机(1)联合分离散型布设=(X,Y)的所有可能取值为(X i,y j)(i,j 1,2,),且事件{ =(X i,y j)}的概率为P ij,,称P{(X,Y) (X i,y j)} P j(i,j 1,2,)为=(X,Y)的分布律或称为X和Y的联合分布律。
联合分布有时也用下面的概率分布表来表示:这里P ij具有下面两个性质(1)P ij>0 (i,j=1,2,…);(2)P j 1.i j(1)大数定律X 切比雪夫大数定律设随机变量冶,X2,…相互独立,均具有有限方差,且被同一常数C所界:D (X i) <C(i=1,2,…),则对于任意的正数£,有limnPLx,丄n i 1 n° E(X i)i 11特殊情形: 若X1,X2,…具有相同的数学期望 E (X)=「则上式成为lim Pn1n X i大数定辛钦大数定律1.设卩是n次独立试验中事件A发生的次数,p是事件A在每次试验中发生的概率,则对于任意的正数£,有limn伯努利大数定律说明,当试验次数小,即limn这就以严格的数学形式描述了频率的稳定性。
很大时,事件1.A发生的频率与概率有较大判别的可能性很0.设X1, X2,…,Xi,…是相互独立同分布的随机变量序列,且 E ( X n) =g,则对于任意的正数£有lim Pn1 nX in i 11.(2)中心极限定理2X N(,)n 格定理设随机变量X1,X2,…相互独立,服从同一分布,且具有相同的数学期望和方差:E(X k) ,D(X k) 0(k 1,2, ),则随机变量的分布函数F n(x)对任意的实数X,Y nnX k nk 1X k nlim F n(x) limn n此定理也称为独立同分布的中心极限定理。
概率论与数理统计完整ppt课件

在化学领域,概率论与数理统计被用于研究化学反应的速率和化 学物质的分布,如化学反应动力学、量子化学计算等。
生物
在生物学中,概率论与数理统计用于研究生物现象的变异和分布, 如遗传学、生态学、流行病学等。
在工程中的应用
通信工程
01
概率论与数理统计在通信工程中用于信道容量、误码率、调制
解调等方面的研究。
边缘分布
对于n维随机变量(X_1,...,X_n),在概 率论中,分别定义了X_1的边缘分布 、...、X_n的边缘分布。
04
数理统计基础
样本与抽样分布
01
02
03
总体与样本
总体是包含所有可能数据 的数据集合,样本是总体 的一个随机子集。
抽样方法
包括简单随机抽样、分层 抽样、系统抽样等。
样本分布
描述样本数据的分布情况 ,如均值、中位数、标准 差等。
参数估计与置信区间
参数估计
利用样本数据估计总体的 未知参数,如均值、方差 等。
点估计
用样本统计量作为总体参 数的估计值。
置信区间
给出总体参数的一个估计 区间,表示对总体的参数 有一个可信的估计范围。
假设检验与方差分析
假设检验
通过样本数据对总体参数提出 假设,然后根据假设进行检验
01
定义
设E是一个随机试验,X,Y是定义在E上,取值分别为实数的随机变量
。称有序实数对(X,Y)为一个二维随机变量。
02
分布函数
设(X,Y)是一个二维随机变量,对于任意实数x,y,二元函数
F(x,y)=P({X<=x,Y<=y})称为二维随机变量(X,Y)的分布函数。
03
边缘分布
对于二维随机变量(X,Y),在概率论中,分别定义了X的边缘分布和Y的
概率论与数理统计公式整理(超全版)
设 ABC 是三个事件,如果满足两两独立的条件,
P(AB)=P(A)P(B);P(BC)=P(B)P(C);P(CA)=P(C)P(A)
(15)全概公式 (16)贝叶斯公式 (17)伯努利概型
并且同时满足 P(ABC)=P(A)P(B)P(C)
那么 A、B、C 相互独立。
泊松分布为二项分布的极限分布(np=λ ,n→∞)。
P( X
k)
CMk
C nk N M
CNn
k 0,1,2,l , l min(M , n)
随机变量 X 服从参数为 n,N,M 的超几何分布,记为 H(n,N,M)。
P( X k ) q k1 p, k 1,2,3, ,其中 p≥0,q=1-p。
对于 n 个事件类似。
设事件 B1, B2,, Bn 满足
1° B1, B2,, Bn 两两互不相容, P(Bi) 0(i 1,2,, n) ,
n
A Bi
2°
i1 , 则有
P(A) P(B1)P(A | B1) P(B2)P(A | B2) P(Bn)P(A | Bn) 。
第 1 章 随机事件及其概率
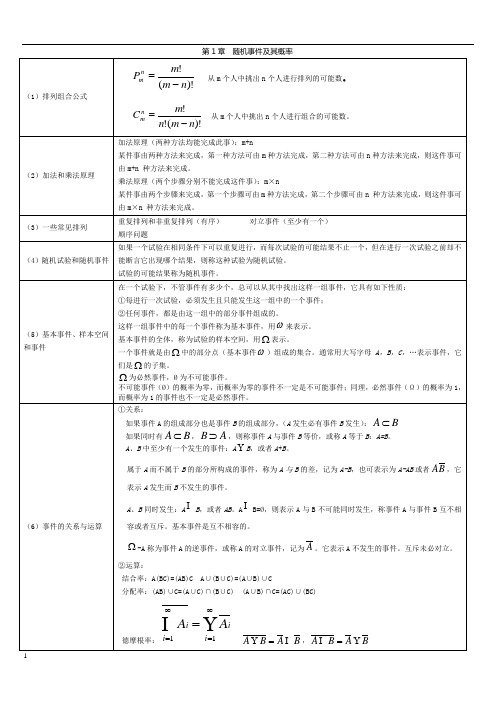
(1)排列组合公式
Pmn
m! (m n)!
从 m 个人中挑出 n 个人进行排列的可能数。
Cmn
m! n!(m
n)!
从 m 个人中挑出 n 个人进行组合的可能数。
加法原理(两种方法均能完成此事):m+n
某件事由两种方法来完成,第一种方法可由 m 种方法完成,第二种方法可由 n 种方法来完成,则这件事可
。
概率论与数理统计电子版教材

概率论与数理统计电子版教材概率论与数理统计是一门重要的数学学科,它旨在研究随机现象和数据的统计规律,是自然科学、社会科学和工程技术等领域中不可或缺的基础学科。
本文将简要介绍概率论与数理统计的基本概念、分布、随机变量、随机过程和大数定律等内容。
一、概率论的基本概念概率是指一个事件在所有可能性中出现的可能性大小,它是一个0和1之间的实数。
概率论是一个基于集合论的数学理论,它研究随机事件,即不确定性事件的概率规律。
基本的概念包括样本空间、样本点、基本事件、和事件、差事件、交事件等。
样本空间是指所有可能的结果的集合,样本点是指样本空间中的一个元素,基本事件是指随机事件中最简单的一种,和事件是指随机事件中两个或多个事件发生的交集,差事件是指B事件不包含A事件的部分,交事件是指随机事件中两个或多个事件发生的并集。
二、分布概率论中的分布是指随机变量的概率分布模型,通常用于描述随机变量的概率密度函数或累积分布函数。
常见的分布包括离散分布和连续分布。
离散分布适用于描述一些离散的取值,像二项分布和泊松分布,而连续分布适用于描述取值连续的情况,像正态分布和t分布。
三、随机变量随机变量是指一个随机事件对应于一个实数或者一组实数的函数。
随机变量可以是离散的或连续的,离散的随机变量通常用概率质量函数描述,而连续的随机变量则用概率密度函数描述。
随机变量的期望和方差是随机变量的两个重要指标,它们可以用来描述随机变量的总体性质。
四、随机过程随机过程是指随机事件随时间变化的过程,它尤其适用于描述在不断变化的状态下的随机事件。
随机过程主要包括马尔科夫链、布朗运动和泊松过程等。
其中,马尔科夫链是指每一个状态都只依赖于前一步的状态,布朗运动是指在固定时间段内任意时刻的随机步长相加所得的路径,而泊松过程则是以随机变量为时间间隔的增量为标记的过程。
五、大数定律大数定律是概率论中的重要结果之一,它意味着随着试验次数的增加,随机事件的频率将趋近于其真实概率。
概率论与数理统计知识点总结(超详细版)

概率论与数理统计知识点总结(超详细版)eik则有P(A)=k/n,其中n为样本空间中元素的个数。
在概率论中,样本空间和随机事件是基本概念。
如果事件A发生必然导致事件B发生,则称事件B包含事件A,记作A⊂B。
当A和B中至少有一个发生时,称A∪B为事件A和事件B的和事件。
当A和B同时发生时,称A∩B为事件A和事件B的积事件。
当A发生、B不发生时,称A-B为事件A和事件B的差事件。
如果A和B互不相容,即A∩B=∅,则称A和B是互不相容的,或互斥的,基本事件是两两互不相容的。
如果A∪B=S且A∩B=∅,则称事件A和事件B互为逆事件,又称事件A和事件B互为对立事件。
在概率论中,还有一些运算规则。
交换律指A∪B=B∪A,A∩B=B∩A;结合律指(A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C);分配律指A∪(B∩C)=(A∪B)∩(A∪C),A∩(B∪C)=(A∩B)∪(A∩C);德摩根律指A∪B=A∩B,A∩B=A∪B。
频率与概率是概率论的重要概念。
在相同的条件下,进行了n次试验,在这n次试验中,事件A发生的次数n A称为事件A发生的频数,比值nAn称为事件A发生的频率。
概率指对于随机试验E的每一事件A赋予一个实数P(A),称为事件的概率。
概率P(A)满足非负性,即对于每一个事件A,0≤P(A)≤1;规范性,即对于必然事件S,P(S)=1;可列可加性,即设A1,A2,…,An是两两互不相容的事件,则有P(∪Ai)=∑P(Ai)(n可以取∞)。
概率还有一些重要性质,包括P(∅)=0,P(∪Ai)=∑P(Ai)(n可以取∞),如果A⊂B,则P(B-A)=P(B)-P(A),P(A)≤1,P(A)=1-P(A'),以及P(A∪B)=P(A)+P(B)-P(A∩B)。
等可能概型又称为古典概型,是指试验的样本空间只包含有限个元素,试验中每个事件发生的可能性相同。
如果事件A 包含k个基本事件,即A={e1}∪{e2}∪…∪{ek},则有P(A)=k/n,其中n为样本空间中元素的个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⋅
1 非负性 2 规范性
P(A) ≥ 0 P(S)= 1
3 可列可加性 若事件 A1 , A2 ,… 两两互不相容,则有 两两互不相容,
P(A U A UL = P(A ) + P(A ) +L ) 1 2 1 2
三、概率的性质
质 性 1 P(∅) =0
质 , 性 2 若 1 , A2 ,L An 是 两 不 容 件 两 互 相 事 ,则 A
40 频率的稳定性 抛硬币试验, 抛硬币试验,n=500时 时 nH 251 249 256 253
nA f n ( A) = n
251 246 244 0.488
fn(H) 0.502 0.498 0.512 0.506 0.502 0.492
实验者 德•摩根 摩根 蒲 丰
n 2048 4040
注:相同试验由于试验目的不同,其样本空间可能 相同试验由于试验目的不同, 不同. 不同.
E2:将一枚硬币抛掷三次,观察每次正、反面出现 将一枚硬币抛掷三次,观察每次正、
的情况. 的情况. S={ HHH ,HHT ,HTH ,THH, HTT , THT ,TTH ,TTT }
E3:将一枚硬币抛掷三次,观察正面出现的次数. 将一枚硬币抛掷三次,观察正面出现的次数. S={ 0, 1, 2, 3 }
请回答: 请回答: 2. 随机现象有没有规律可言? 随机现象有没有规律可言? 有!
例如: 例如: 1.抛硬币,一次试验不知道正面和反面,
抛很多次,正面和反面一样多。 2.学习好和学习差的学生的考试成绩。
在一定条件下对随机现象进行大量 在一定条件下对随机现象进行大量 观测会发现某种规律性. 观测会发现某种规律性
二、概率的定义
是随机试验, 是它的样本空间 对于S中 是它的样本空间, 设E是随机试验,S是它的样本空间,对于 中 是随机试验 的每一个事件A,赋予一个实数,记为P(A) ,称为 的每一个事件 ,赋予一个实数,记为 事件A的概率 的概率, 事件 的概率,如果集合函数 P( ) 满足下述三条公 理:
第一章 随机事件的概率
§1 随机事件 一、随机现象 二、随机试验 三、样本空间 四、随机事件 五、事件的关系与运算
一、随机现象
现实生活中存在两种现象: 现实生活中存在两种现象:
1.确定性现象 1.确定性现象 确定性
举例
向上抛出物体, 落到地面 烧水,标准大气压100度, 水沸腾 磁铁的N、S极 抛硬币 买彩票 吸引 H or T朝上 中奖 or not
掌握随机现象的规律很重要! 掌握随机现象的规律很重要! 例如: 例如: 经营一家商店, 经营一家商店,某种产品的月销售额 为多少是随机现象,应该掌握其规律, 为多少是随机现象,应该掌握其规律, 用以确定进货量。 用以确定进货量。
概率论与数理统计的研究内容
随机现象的统计规律性
二、随机试验
在概率论中, 把具有以下三个特征的试验称 定义 在概率论中, 把具有以下三个特征的试验称 三个特征 随机试验 为随机试验. 1. 可以在相同的条件下重复地进行; . 可以在相同的条件下重复地进行; 2. 每次试验的可能结果不止一个, 并且能 . 每次试验的可能结果不止一个 不止一个, 事先明确试验的所有可能结果; 事先明确试验的所有可能结果 不能确定哪一个结果 3. 进行一次试验之前不能确定哪一个结果 . 进行一次试验之前不能确定 会出现. 会出现 随机试验通常用E 来表示. 随机试验通常用 来表示
必然事件: 必然事件: 样本空间 S 本身 不可能事件: 不可能事件: 空集∅ 空集∅
五、事件间的关系与运算
10 包含关系
A⊂ B
A
B S
事件B发生 事件 发生
事件A发生 事件 发生
实例 掷骰子试验中 “出现偶数点” 包含“出现 点”. 出现偶数点”包含“出现2点 出现偶数点
10* 相等关系 若A ⊂ B且B ⊂ A,
40 差事件
A − B = {x x ∈ A且x ∉ B}
A− B
A
B
A− B
A B
A发生且 发生且B不发生 A − B 发生 ⇔ 发生且 不发生 “长度合格但直径不合格” 是 “长度合格”与 长度合格但直径不合格” 长度合格” 长度合格但直径不合格 直径合格” “直径合格” 的差 直径合格 的差.
P( A U A ULU A ) 1 2 n
= P( A ) + P( A ) +L+ P( A ) 1 2 n
有限可加性
性质3 对任一事件 ,有 对任一事件A 性质 P(A) =1− P(A) 证明 因为 AU A = S A与 互不 容 A 相
(4)
P(S) =P(A) + P(A)=1
(3)分配律 分配律
(4)德.摩根律 德
A U B = A I B;
AI B = A U B.
第一章§2 随机事件的概 率
一、频率 二、概率的定义 三、概率的性质
一、频率
在相同的条件下,进行了n 次试验, 定义 在相同的条件下,进行了 次试验, 在这 n 次试验中,事件 A 发生的次数 nA 称为 次试验中, 事件 A 发生的频数。比值 n A / n 称为事件 发生的频数。 A 发生的频率,并记成 fn(A) 。 发生的频率, 即
请回答: 请回答: 3. "天有不测风云"和"天气可以预报"有 天有不测风云" 天气可以预报" . "天有不测风云 矛盾吗? 矛盾吗? 无! “天有不测风云”指的是对随机现象 天有不测风云” 一次观察. 的一次观察. “天气可以预报”指的是研究者从大 天气可以预报” 量的气象资料来探索随机现象的规律性 随机现象的规律性. 量的气象资料来探索随机现象的规律性.
E4:掷一颗骰子,观察出现的点数。 掷一颗骰子, 掷一颗骰子 观察出现的点数。
, , , , , 样本空间 S = {1,2,3,4,5,6}
E5: 测试某灯泡的寿命: 测试某灯泡的寿命: 样本空间
} S = {t :t ≥0}
课堂练习
写出下列随机试验的样本空间. 写出下列随机试验的样本空间. 1. 同时掷三颗骰子,记录三颗骰子之和. . 同时掷三颗骰子,记录三颗骰子之和. 2. 生产产品直到得到 件正品,记录生产产品的 . 生产产品直到得到10件正品 件正品, 总件数. 总件数
nH 1061 2048 6019
fn(H) 0.5181 0.5096 0.5016 0.5005
K •皮尔逊 12000 皮尔逊
K •皮尔逊 24000 12012 皮尔逊
这n次试验中 次试验中 事件发生的频 事件发生的频 繁程度 频 率 频率的性质
定量地刻画了一次 定量地刻画了一次 试验中事件发生的 试验中事件发生的 可能性 稳 定值 概率 概率的公理化定义
B ={1,3,5} 是随机事件。 } 是随机事件。
B={掷出奇数点 掷出奇数点} 掷出奇数点 我们称一个随机事件发生当且仅当它所包含 我们称一个随机事件发生当且仅当它所包含 随机事件发生当且仅当它所 的某一个样本点在试验中出现 在试验中出现. 的某一个样本点在试验中出现
三个特殊的事件
基本事件: 基本事件 由一个样本点组成的单点集
“出现花面” 与 “出现字面”是对立的两 出现花面” 出现字面” 对立的两 出现花面 个事件. 个事件
事件间的运算规律 设 A, B , C 为事件, 则有 (1)交换律 交换律 (2)结合律 结合律
A U B = B U A; A I B = B I A.
A U ( B U C ) = ( A U B) U C; A I ( B I C ) = ( A I B) I C . A U ( B I C ) = ( A U B ) I ( A U C ); A I ( B U C ) = ( A I B ) U ( A I C ).
nA f n ( A) = n
频率的性质: 频率的性质
nA f n ( A) = n
1o 0 ≤ f n( A) ≤ 1
2o
f n(S) =1
o 若 , A2 ,L Ak 是 两 不 容 件 , 两 互 相 事 ,则 3 A 1
U k f n ( A U A UL A ) 1 2 = f n( A ) + f n( A ) +L+ f n( A ) 1 2 k
在一定条件下必然发生。 在一定条件下必然发生。
2.随机现象 2.随机现象
举例
在一定条件下, 在一定条件下,出现的 可能结果不止一个,事先不能够知道确切的结果。 可能结果不止一个,事先不能够知道确切的结果。
请回答: 请回答: 1.下面的现象哪些是随机现象? 下面的现象哪些是随机现象? 下面的现象哪些是随机现象 A. 太阳从东方升起; 太阳从东方升起; B. 明天的最高温度; 明天的最高温度; C. 上抛物体一定下落; 上抛物体一定下落; D. 新生婴儿的体重 新生婴儿的体重.
例 某种产品的合格与否是由该产品的长度与直 产品不合格” 径是否合格所决定, 径是否合格所决定 因此 “产品不合格”是“长 度 不合格” 径不合格” 和事件. 不合格”与“直径不合格”的并或和事件 某种产品的合格与否是由该产品的长度与直径 是否合格所决定, 因此“产品合格” 长度合格” 是否合格所决定 因此“产品合格”是“长度合格” 直径合格” 积事件. 与“直径合格”的交或积事件
四、随机事件
定义 称样本空间S的子集为随机事件. 称样本空间S的子集为随机事件 随机事件 常用大写字母A,B,C表示。 常用大写字母A,B,C表示。 A,B,C表示 例如,掷一颗骰子,观察出现的点数. 例如,掷一颗骰子,观察出现的点数 样本空间: S = { 1,2,3,4,5,6} 样本空间: }
50 互不相容
60 对立事件
