2014安徽省数据结构与算法一点通科目一
数据结构与算法试卷A答案

滁州学院2013/2014学年度第一学期期末考试试卷参考答案地理信息系统专业(本)12级《数据结构与算法》A 卷(时间120分钟)一、 选择题(每题1分,共20分)1-5 DCDDA 6-10 CDDAB 11-15 DADDC 16-20 CACCA二、 判读正误题(每题1分,共10分)1-5 √√×√√ 6-10√××××三、算法阅读填空题(每题5分,共20分)1、写出算法划线语句的执行次数和x 的结果。
(答对执行次数55或者结果55给2分) 执行次数55次 x 的结果552、在划线处填空,完成循环队列入队(答错任何一个字符给0分) cq->rear=(cq->rear+1)%MAXCSIZE;3、在划线处填空,完成单链表的查找(答对一空给2分) while( p!=NULL && p->data!=x )4、在划线处填空,完成顺序栈弹栈(栈使用base 数组存储数据) *e = s->base[--s->top]; (答案使用先对top 减;再把结果赋给e 两条语句也正确)四、计算操作题(每题10分,共40分)1、给定如图所示,画出该图的邻接表存储结构; 画出该图的邻接矩阵;分别给出从顶点1开始的按照所画的邻接矩阵写出深度优先遍历和广度优先遍历顺序。
邻接矩阵0101000101001001010101010100000100101100010000110(3分) 邻接表(3分)广度优先:1243657;(2分) 深度优先:1234576(2分)2、设权值集合W={5、29、7、8、14、23、3、11},以W 为基础,建立一颗霍夫曼树,并求出其WPL 的值。
答:(6分,不同形态也对)专业: 年级/班级: 姓名: 学号:装 订 线 内 不 要 答 题WPL=29*2+12*3+3*4+8*4+3*4+5*4+11*3+23*2=271 (4分,缺少中间这一步扣2分)3、已知一颗二叉树的中序遍历序列和后序遍历序列分别为:中序:CBEDAFIGH,后序:CEDBIFHGA。
安徽大学-834-2014-真题

安徽大学2014年硕士研究生入学考试试题计算机专业基础(数据结构、操作系统)——手打版,绝对真实哦操作系统(75分)一、单选题(每题2分,共20分)1、___不是基本的操作系统。
A.批处理操作系统B.分时操作系统C.实时操作系统D.网络操作系统2、在计算机系统中,通常把财务管理程序看作是____。
A.系统软件B.支援软件C.借口软件D.应用软件3、进程所请求的一次打印输出结束后,将使进程状态从___。
A.运行态变为就绪态B.运行态变为阻塞态C.就绪态变为运行态D.阻碍态变为就绪态4、进程在执行中状态会发生变化,不可能出现的状态变化情况是____。
A.运行变为就绪B.运行变为阻塞C.阻塞变为就绪D.阻塞变为运行5、若在一个单处理器的计算机系统中同时存在5个并发进程,则任何时刻允许占用处理器的进程数为____。
A.至少1个B.最多1个C.至少5个D.最多5个6、等待当前磁道上的某指定扇区旋转到磁头下所需时间为___。
A.寻道时间B.启动时间C.延迟时间D.传送时间7、作业调度选中一个作业并把它装入主存,就为该作业创建一个进程,这个进程的初始状态为_____。
A.收容状态B.就绪状态C.执行状态D.阻塞状态8、对记录式文件,操作系统为用户存取文件信息的最小单位是____。
A.字符B.数据项C.记录D.文件9、为了提高设备分配的灵活性,用户申请设备时应指定______号。
A、逻辑设备B、物理设备C、相对D、绝对10、虚拟存储管理策略可以______。
A、扩大逻辑内存容量B、扩大物理内存容量C、扩大逻辑外存容量D、扩大物理外存容量二、填空题(7*2=14分)1、UNIX系统中,文件贮存器的管理采用的是_________。
2、一个文件系统的组织方式与MS-DOS相似,在FA T中可有32K个指针,磁盘的盘块大小为1K,则其能指引的最大逻辑磁盘容量为_____________M bytes。
3、某操作系统的磁盘文件空间共有2000块,若字长为64位的位示图管理磁盘空间,位示图需要____________字。
(双面)2014年安徽大学计算机考研初试真题-精选

安徽大学2014年硕士研究生入学考试试题计算机专业基础(数据结构、操作系统)——手打版,绝对真实哦操作系统(75分)一、单选题(每题2分,共20分)1、___不是基本的操作系统。
A.批处理操作系统B.分时操作系统C.实时操作系统D.网络操作系统2、在计算机系统中,通常把财务管理程序看作是____。
A.系统软件B.支援软件C.借口软件D.应用软件3、进程所请求的一次打印输出结束后,将使进程状态从___。
A.运行态变为就绪态B.运行态变为阻塞态C.就绪态变为运行态D.阻碍态变为就绪态4、进程在执行中状态会发生变化,不可能出现的状态变化情况是____。
A.运行变为就绪B.运行变为阻塞C.阻塞变为就绪D.阻塞变为运行5、若在一个单处理器的计算机系统中同时存在5个并发进程,则任何时刻允许占用处理器的进程数为____。
A.至少1个B.最多1个C.至少5个D.最多5个6、等待当前磁道上的某指定扇区旋转到磁头下所需时间为___。
A.寻道时间B.启动时间C.延迟时间D.传送时间7、作业调度选中一个作业并把它装入主存,就为该作业创建一个进程,这个进程的初始状态为_____。
A.收容状态B.就绪状态C.执行状态D.阻塞状态8、对记录式文件,操作系统为用户存取文件信息的最小单位是____。
A.字符B.数据项C.记录D.文件9、为了提高设备分配的灵活性,用户申请设备时应指定______号。
A、逻辑设备B、物理设备C、相对D、绝对10、虚拟存储管理策略可以______。
A、扩大逻辑内存容量B、扩大物理内存容量C、扩大逻辑外存容量D、扩大物理外存容量二、填空题(7*2=14分)1、UNIX系统中,文件贮存器的管理采用的是_________。
2、一个文件系统的组织方式与MS-DOS相似,在FAT中可有32K个指针,磁盘的盘块大小为1K,则其能指引的最大逻辑磁盘容量为_____________M bytes。
3、某操作系统的磁盘文件空间共有2000块,若字长为64位的位示图管理磁盘空间,位示图需要____________字。
2014年普通高等学校招生全国统一考试(安徽卷)

2014年普通高等学校招生全国统一考试(安徽卷)数学(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分. 参考公式:如果事件A 与B 互斥,那么P (A +B )=P (A )+P (B ) 如果事件A 与B 相互独立,那么P (AB )=P (A )P (B )第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设i 是虚数单位,z 表示复数z 的共轭复数.若z =1+i ,则zi +i·z =( )A .-2B .-2iC .2D .2i2.“x <0”是“ln(x +1)<0”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件D .既不充分也不必要条件3.如图所示,程序框图(算法流程图)的输出结果是( )A .34B .55C .78D .894.以平面直角坐标系的原点为极点,x 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位.已知直线l 的参数方程是⎩⎪⎨⎪⎧x =t +1,y =t -3(t 为参数),圆C 的极坐标方程是ρ=4cos θ,则直线l 被圆C 截得的弦长为( )A.14 B .214 C. 2 D .2 25.x ,y 满足约束条件⎩⎪⎨⎪⎧x +y -2≤0,x -2y -2≤0,2x -y +2≥0.若z =y -ax 取得最大值的最优解不唯一,则实数a 的值为( )A.12或-1 B .2或12 C .2或1 D .2或-16.设函数f (x )(x ∈R )满足f (x +π)=f (x )+sin x .当0≤x <π时,f (x )=0,则f ⎝⎛⎭⎫23π6=( ) A.12 B.32 C .0 D .-127.一个多面体的三视图如图所示,则该多面体的表面积为( )A .21+ 3B .18+ 3C .21D .188.从正方体六个面的对角线中任取两条作为一对,其中所成的角为60°的共有( ) A .24对 B .30对 C .48对 D .60对9.若函数f (x )=|x +1|+|2x +a |的最小值为3,则实数a 的值为( ) A .5或8 B .-1或5 C .-1或-4 D .-4或810.在平面直角坐标系xOy 中,已知向量a ,b ,|a |=|b |=1,a ·b =0,点Q 满足=2(a +b ).曲线C ={P |=a cos θ+b sin θ,0≤θ<2π},区域Ω={P |0<r ≤||≤R ,r <R }.若C ∩Ω为两段分离的曲线,则( )A .1<r <R <3B .1<r <3≤RC .r ≤1<R <3D .1<r <3<R第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上.11.若将函数f (x )=sin ⎝⎛⎭⎫2x +π4的图象向右平移φ个单位,所得图象关于y 轴对称,则φ的最小正值是________.12.数列{a n }是等差数列,若a 1+1,a 3+3,a 5+5构成公比为q 的等比数列,则q =________.13.设a ≠0,n 是大于1的自然数,⎝⎛⎭⎫1+xa n 的展开式为a 0+a 1x +a 2x 2+…+a n x n .若点A i (i ,a i )(i =0,1,2)的位置如图所示,则a =________.14.若F 1,F 2分别是椭圆E :x 2+y 2b2=1(0<b <1)的左、右焦点,过点F 1的直线交椭圆E于A ,B 两点.若|AF 1|=3|F 1B |,AF 2⊥x 轴,则椭圆E 的方程为________.15.已知两个不相等的非零向量a ,b ,两组向量x 1,x 2,x 3,x 4,x 5和y 1,y 2,y 3,y 4,y 5均由2个a 和3个b 排列而成.记S =x 1·y 1+x 2·y 2+x 3·y 3+x 4·y 4+x 5·y 5,S min 表示S 所有可能取值中的最小值.则下列命题正确的是________(写出所有正确命题的编号).①S 有5个不同的值 ②若a ⊥b ,则S min 与|a |无关 ③若a ∥b ,则S min 与|b |无关 ④若|b |>4|a |,则S min >0⑤若|b |=2a ,S min =8|a |2,则a 与b 的夹角为π4三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(本小题满分12分)设△ABC 的内角A ,B ,C 所对边的长分别是a ,b ,c ,且b =3,c =1,A =2B . (Ⅰ)求a 的值; (Ⅱ)求sin ⎝⎛⎭⎫A +π4的值.17.(本小题满分12分)甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完 5局仍未出现连胜,则判定获胜局数多者赢得比赛.假设每局甲获胜的概率为23,乙获胜的概率为13,各局比赛结果相互独立.(Ⅰ)求甲在4局以内(含4局)赢得比赛的概率;(Ⅱ)记X 为比赛决出胜负时的总局数,求X 的分布列和均值(数学期望).18.(本小题满分12分)设函数f (x )=1+(1+a )x -x 2-x 3,其中a >0. (Ⅰ)讨论f (x )在其定义域上的单调性;(Ⅱ)当x ∈[0,1]时,求f (x )取得最大值和最小值时的x 的值.19.(本小题满分13分)如图,已知两条抛物线E 1:y 2=2p 1x (p 1>0)和E 2:y 2=2p 2x (p 2>0),过原点O 的两条直线l 1和l 2,l 1与E 1,E 2分别交于A 1,A 2两点,l 2与E 1, E 2分别交于B 1, B 2两点.(Ⅰ)证明:A 1B 1∥A 2B 2;(Ⅱ)过O 作直线l (异于l 1,l 2)与E 1,E 2分别交于C 1,C 2两点.记△A 1B 1C 1与△A 2B 2C 2的面积分别为S 1与S 2,求S 1S 2的值.20.(本小题满分13分)如图,四棱柱ABCD -A 1B 1C 1D 1中,A 1A ⊥底面ABCD .四边形ABCD 为梯形,AD ∥BC ,且AD =2BC .过A 1,C ,D 三点的平面记为α,BB 1与α的交点为Q .(Ⅰ)证明:Q 为BB 1的中点;(Ⅱ)求此四棱柱被平面α所分成上下两部分的体积之比;(Ⅲ)若AA 1=4,CD =2,梯形ABCD 的面积为6,求平面α与底面ABCD 所成二面角的大小.21.(本小题满分13分) 设实数c >0,整数p >1,n ∈N *.(Ⅰ)证明:当x >-1且x ≠0时,(1+x )p >1+px ; (Ⅱ)数列{a n }满足a 1>c 1p ,a n +1=p -1p a n +c p a 1-p n.答案第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.解析:选C 因为z =1+i ,所以zi+i·z =(-i +1)+i +1=2.2.解析:选B ln(x +1)<0⇔0<x +1<1⇔-1<x <0,而(-1,0)是(-∞,0)的真子集,所以“x <0”是“ln(x +1)<0”的必要不充分条件.3.解析:选B 由题中程序框图知:x =1,y =1,z =2;x =1,y =2,z =3;x =2,y =3,z =5;x =3,y =5,z =8;x =5,y =8,z =13;x =8,y =13,z =21;x =13,y =21,z =34;x =21,y =34,z =55,跳出循环.故输出结果是55.4.解析:选D 由题意得,直线l 的普通方程为y =x -4,圆C 的直角坐标方程为(x -2)2+y 2=4,圆心到直线l 的距离d =|2-0-4|2=2,直线l 被圆C 截得的弦长为222-(2)2=2 2.5.解析:选D 法一:由题中条件画出可行域,可知A (0,2),B (2,0),C (-2,-2),则z A =2,z B =-2a ,z C =2a -2,要使目标函数取得最大值的最优解不唯一,只要z A =z B >z C 或z A =z C >z B 或z B =z C >z A ,解得a =-1或a =2.法二:目标函数z =y -ax 可化为y =ax +z ,令l 0:y =ax ,平移l 0,则当l 0∥AB 或l 0∥AC 时符合题意,故a =-1或a =2.6.解析:选A f ⎝⎛⎭⎫23π6=f ⎝⎛⎭⎫17π6+sin 17π6=f ⎝⎛⎭⎫11π6+sin 17π6+sin 11π6=f ⎝⎛⎭⎫5π6+sin 17π6+sin 11π6+sin 5π6=2sin 5π6+sin ⎝⎛⎭⎫-π6=12. 7.解析:选A 由三视图可知该几何体是棱长为2的正方体从后面右上角和前面左下角分别截去一个小三棱锥后剩余的部分,其表面积为S =6×4-12×6+2×34×(2)2=21+ 3.8.解析:选C 法一:直接法:如图,在上底面中选B 1D 1,四个侧面中的面对角线都与它成60°,共8对,同样A 1C 1对应的也有8对,下底面也有16对,这共有32对;左右侧面与前后侧面中共有16对.所以全部共有48对.法二:间接法:正方体的12条面对角线中,任意两条垂直、平行或成角为60°,所以成角为60°的共有C 212-12-6=48.9.解析:选D 当a ≥2时,f (x )=⎩⎪⎨⎪⎧3x +a +1,x >-1,x +a -1,-a 2≤x ≤-1,-3x -a -1,x <-a 2,如图1可知,当x =-a2时,f (x )min =f ⎝⎛⎭⎫-a 2=a 2-1=3,可得a =8;当a <2时,f (x )=⎩⎪⎨⎪⎧3x +a +1,x >-a2,-x -a +1,-1≤x ≤-a 2,-3x -a -1,x <-1,如图2可知,当x =-a 2时,f (x )min =f ⎝⎛⎭⎫-a 2=-a2+1=3,可得a =-4.综上可知,答案为D.10.解析:选A 由已知可设=a =(1,0),=b =(0,1),P (x ,y ),则=(2,2),曲线C ={P |=(cos θ,sin θ),0≤θ<2π},即C :x 2+y 2=1,区域Ω={P |0<r ≤||≤R ,r <R }表示圆P 1:(x -2)2+(y -2)2=r 2与圆P 2:(x -2)2+(y -2)2=R 2所形成的圆环,如图所示,要使C ∩Ω为两段分离的曲线,只有1<r <R<3.第Ⅱ卷(非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分.把答案填在题中的横线上. 11.解析:法一:f (x )=sin ⎝⎛⎭⎫2x +π4的图象向右平移φ个单位得函数y =sin ⎝⎛⎭⎫2x +π4-2φ的图象,由函数y =sin ⎝⎛⎭⎫2x +π4-2φ的图象关于y 轴对称可知sin π4-2φ=±1,即sin ⎝⎛⎭⎫2φ-π4=±1,故2φ-π4=k π+π2,k ∈Z ,即φ=k π2+3π8,k ∈Z ,又φ>0,所以φmin =3π8.法二:由f (x )=sin ⎝⎛⎭⎫2x +π4=cos ⎝⎛⎭⎫2x -π4的图象向右平移φ个单位所得图象关于y 轴对称可知2φ+π4=k π,k ∈Z ,故φ=k π2-π8,又φ>0,故φmin =3π8.答案:3π812.解析:法一:因为数列{a n }是等差数列,所以a 1+1,a 3+3,a 5+5也成等差数列,又a 1+1,a 3+3,a 5+5构成公比为q 的等比数列,所以a 1+1,a 3+3,a 5+5是常数列,故q =1.法二:因为数列{a n }是等差数列,所以可设a 1=t -d ,a 3=t ,a 5=t +d ,故由已知得(t +3)2=(t -d +1)(t +d +5),得d 2+4d +4=0,即d =-2,所以a 3+3=a 1+1,即q =1.答案:113.解析:由题图可知a 0=1,a 1=3,a 2=4,由题意知⎩⎨⎧C 1n ·1a=a 1=3,C 2n·1a 2=a 2=4,故⎩⎨⎧na =3,n (n -1)a 2=8,可得⎩⎪⎨⎪⎧n =9,a =3.答案:314.解析:设点A 在点B 上方,F 1(-c,0),F 2(c,0),其中c =1-b 2,则可设A (c ,b 2),B (x 0,y 0),由|AF 1|=3|F 1B |,可得=3,故⎩⎪⎨⎪⎧-2c =3(x 0+c ),-b 2=3y 0,即⎩⎨⎧x 0=-53c ,y 0=-13b 2,代入椭圆方程可得25(1-b 2)9+19b 2=1,得b 2=23,故椭圆方程为x 2+3y 22=1.答案:x 2+3y 22=115.解析:对于①,若a ,b 有0组对应乘积,则S 1=2a 2+3b 2,若a ,b 有2组对应乘积,则S 2=a 2+2b 2+2a ·b ,若a ,b 有4组对应乘积,则S 3=b 2+4a ·b ,所以S 最多有3个不同的值,①错误;因为a ,b 是不等向量,所以S 1-S 3=2a 2+2b 2-4a ·b =2(a -b )2>0,S 1-S 2=a 2+b 2-2a ·b =(a -b )2>0,S 2-S 3=(a -b )2>0,所以S 3<S 2<S 1,故S min =S 3=b 2+4a ·b ,对于②,当a ⊥b 时,S min =b 2与|a |无关,②正确;对于③,显然S min 与|b |有关,③错误;对于④,设a ,b 的夹角为θ,则S min =b 2+4a ·b >16|a |2+16|a |2cos θ=16|a |2(1+cos θ)≥0,故S min >0,④正确;对于⑤,|b |=2|a |,S min =4|a |2+8|a |2cos θ=8|a |2,所以cos θ=12,又θ∈[0,π],所以θ=π3,⑤错误. 答案:②④三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.解析:(Ⅰ)因为A =2B ,所以sin A =sin 2B =2sin B cos B . 由正、余弦定理得a =2b ·a 2+c 2-b 22ac .因为b =3,c =1,所以a 2=12,a =2 3.(Ⅱ)由余弦定理得cos A =b 2+c 2-a 22bc =9+1-126=-13.由于0<A <π,所以sin A =1-cos 2A =1-19=223.故sin ⎝⎛⎭⎫A +π4=sin A cos π4+cos A sin π4=223×22+⎝⎛⎭⎫-13×22=4-26. 17.解析:用A 表示“甲在4局以内(含4局)赢得比赛”,A k 表示“第k 局甲获胜”,B k 表示“第k 局乙获胜”,则P (A k )=23,P (B k )=13,k =1,2,3,4,5.(Ⅰ)P (A )=P (A 1A 2)+P (B 1A 2A 3)+P (A 1B 2A 3A 4)=P (A 1)P (A 2)+P (B 1)P (A 2)P (A 3)+P (A 1)P (B 2)·P (A 3)P (A 4) =⎝⎛⎭⎫232+13×⎝⎛⎭⎫232+23×13×⎝⎛⎭⎫232=5681. (Ⅱ)X 的可能取值为2,3,4,5.P (X =2)=P (A 1A 2)+P (B 1B 2)=P (A 1)P (A 2)+P (B 1)P (B 2)=59,P (X =3)=P (B 1A 2A 3)+P (A 1B 2B 3) =P (B 1)P (A 2)P (A 3)+P (A 1)P (B 2)P (B 3) =29, P (X =4)=P (A 1B 2A 3A 4)+P (B 1A 2B 3B 4)=P (A 1)P (B 2)P (A 3)P (A 4)+P (B 1)P (A 2)P (B 3)·P (B 4) =1081, P (X =5)=1-P (X =2)-P (X =3)-P (X =4)=881.故X 的分布列为EX =2×59+3×29+4×1081+5×881=22481.18.解析:(Ⅰ)f (x )的定义域为(-∞,+∞),f ′(x )=1+a -2x -3x 2. 令f ′(x )=0,得x 1=-1-4+3a 3,x 2=-1+4+3a3,x 1<x 2.所以f ′(x )=-3(x -x 1)(x -x 2).当x <x 1或x >x 2时,f ′(x )<0;当x 1<x <x 2时,f ′(x )>0.故f (x )在(-∞,x 1)和(x 2,+∞)内单调递减,在(x 1,x 2)内单调递增. (Ⅱ)因为a >0,所以x 1<0,x 2>0. ①当a ≥4时,x 2≥1.由(Ⅰ)知,f (x )在[0,1]上单调递增.所以f (x )在x =0和x =1处分别取得最小值和最大值.②当0<a <4时,x 2<1.由(Ⅰ)知,f (x )在[0,x 2]上单调递增,在[x 2,1]上单调递减. 所以f (x )在x =x 2=-1+4+3a3处取得最大值.又f (0)=1,f (1)=a ,所以当0<a <1时,f (x )在x =1处取得最小值; 当a =1时,f (x )在x =0处和x =1处同时取得最小值; 当1<a <4时,f (x )在x =0处取得最小值.19.解析:(Ⅰ)设直线l 1,l 2的方程分别为y =k 1x ,y =k 2x (k 1,k 2≠0),则由⎩⎪⎨⎪⎧y =k 1x ,y 2=2p 1x ,得A 1⎝⎛⎭⎫2p 1k 21,2p 1k 1,由⎩⎪⎨⎪⎧y =k 1x ,y 2=2p 2x ,得A 2⎝⎛⎭⎫2p 2k 21,2p 2k 1. 同理可得B 1⎝⎛⎭⎫2p 1k 22,2p 1k 2,B 2⎝⎛⎭⎫2p 2k 22,2p 2k 2.所以=⎝⎛⎭⎫2p 1k 22-2p 1k 21,2p 1k 2-2p 1k 1=2p 11k 22-1k 21,1k 2-1k 1,=⎝⎛⎭⎫2p 2k 22-2p 2k 21,2p 2k 2-2p 2k 1=2p 21k 22-1k 21,1k 2-1k 1.故=p 1p 2,所以A 1B 1∥A 2B 2.(Ⅱ)由(Ⅰ)知A 1B 1∥A 2B 2,同理可得B 1C 1∥B 2C 2,C 1A 1∥C 2A 2. 所以△A 1B 1C 1∽△A 2B 2C 2.因此S 1S 2=.又由(Ⅰ)中的=p 1p 2知=p 1p 2. 故S 1S 2=p 21p 22.20.解析:(Ⅰ)因为BQ ∥AA 1,BC ∥AD ,BC ∩BQ =B ,AD ∩AA 1=A . 所以平面QBC ∥平面A 1AD .从而平面A 1CD 与这两个平面的交线相互平行,即QC ∥A 1D . 故△QBC 与△A 1AD 的对应边相互平行,于是△QBC ∽△A 1AD . 所以BQ BB 1=BQ AA 1=BC AD =12,即Q 为BB 1的中点.(Ⅱ)如图1,连接QA ,QD .设AA 1=h ,梯形ABCD 的高为d ,四棱柱被平面α所分成上下两部分的体积分别为V 上和V 下,BC =a ,则AD =2a .VQ -A 1AD =13·12·2a ·h ·d =13ahd ,V Q -ABCD =13·a +2a 2·d ·⎝⎛⎭⎫12h =14ahd , 所以V 下=VQ -A 1AD +V Q -ABCD =712ahd , 又VA 1B 1C 1D 1-ABCD =32ahd ,所以V 上=VA 1B 1C 1D 1-ABCD -V 下 =32ahd -712ahd =1112ahd , 故V 上V 下=117. (Ⅲ)法一:如图1,在△ADC 中,作AE ⊥DC ,垂足为E ,连接A 1E . 又DE ⊥AA 1,且AA 1∩AE =A , 所以DE ⊥平面AEA 1,于是DE ⊥A 1E .所以∠AEA 1为平面α与底面ABCD 所成二面角的平面角. 因为BC ∥AD ,AD =2BC ,所以S △ADC =2S △BCA .又因为梯形ABCD 的面积为6,DC =2,所以S △ADC =4,AE =4. 于是tan ∠AEA 1=AA 1AE =1,∠AEA 1=π4.故平面α与底面ABCD 所成二面角的大小为π4.法二:如图2,以D 为原点,分别为x 轴和z 轴正方向建立空间直角坐标系.图2设∠CDA =θ.因为S ABCD =a +2a 2·2sin θ=6. 所以a =2sin θ. 从而C (2cos θ,2sin θ,0),A 1⎝⎛⎭⎫4sin θ,0,4,y =cos θ,所以n =(-sin θ,cos θ,1).又因为平面ABCD 的法向量m =(0,0,1),所以cos 〈n ,m 〉=n ·m |n ||m |=22, 故平面α与底面ABCD 所成二面角的大小为π4. 21.解析:(Ⅰ)用数学归纳法证明:①当p =2时,(1+x )2=1+2x +x 2>1+2x ,原不等式成立.②假设p =k (k ≥2,k ∈N *)时,不等式(1+x )k >1+kx 成立.当p =k +1时,(1+x )k +1=(1+x )(1+x )k >(1+x )·(1+kx )=1+(k +1)x +kx 2>1+(k +1)x . 所以p =k +1时,原不等式也成立.综合①②可得,当x >-1,x ≠0时,对一切整数p >1,不等式(1+x )p >1+px 均成立.(Ⅱ)法一:先用数学归纳法证明a n >c 1p. ①当n =1时,由题设a 1>c 1p 知a n >c 1p成立. ②假设n =k (k ≥1,k ∈N *)时,不等式a k >c 1p成立. 由a n +1=p -1p a n +c pa 1-p n 易知a n >0,n ∈N *. 当n =k +1时,a k +1a k =p -1p +c p a -p k =1+1p ⎝⎛⎭⎫c a p k-1. 由a k >c 1p >0得-1<-1p <1p ⎝⎛⎭⎫c a p k-1<0. 由(Ⅰ)中的结论得⎝⎛⎭⎫a k +1a k p =⎣⎡⎦⎤1+1p ⎝⎛⎭⎫c a p k-1p >1+p ·1p ⎝⎛⎭⎫c a p k -1=c a p k . 因此a p k +1>c ,即a k +1>c 1p. 所以n =k +1时,不等式a n >c 1p也成立.综合①②可得,对一切正整数n ,不等式a n >c 1p均成立. 再由a n +1a n =1+1p ⎝⎛⎭⎫c a p n -1可得a n +1a n<1,即a n +1<a n . 综上所述,a n >a n +1>c 1p,n ∈N *. 法二:设f (x )=p -1p x +c p x 1-p ,x ≥c 1p ,则x p ≥c ,并且f ′(x )=p -1p +c p (1-p )x -p =p -1p⎝⎛⎭⎫1-c x p >0,x >c 1p. 由此可得,f (x )在[c 1p ,+∞)上单调递增,因而,当x >c 1p 时,f (x )>f (c 1p )=c 1p. ①当n =1时,由a 1>c 1p>0,即a p 1>c 可知 a 2=p -1p a 1+c p a 1-p 1=a 1⎣⎡⎦⎤1+1p ⎝⎛⎭⎫c a p 1-1<a 1,并且a 2=f (a 1)>c 1p, 从而a 1>a 2>c 1p. 故当n =1时,不等式a n >a n +1>c 1p成立. ②假设n =k (k ≥1,k ∈N *)时,不等式a k >a k +1>c 1p成立,则 当n =k +1时,f (a k )>f (a k +1)>f (c 1p ),即有a k +1>a k +2>c 1p. 所以n =k +1时,原不等式也成立.综合①②可得,对一切正整数n ,不等式a n >a n +1>c 1p均成立.。
2014年安徽大学图情挡专业真题

爱考机构中国高端(保过保录限)考研第一品牌一
1信息论2自信息量3信息组织4信息饽论5关键词法6信息检索7IRM8信息需求9信息政策
二
1控制信息采集质量的措施一般有哪些
2简述信息技术的特性
3OSI参考模型的层次结构
4什么是超文本信息组织法?与传统信息组织法有何区别
三
1试述信息生命周期的几个发展阶段
2试述信息技术的正效应
3试述信息人力资源管理中人员管理系统的职能
四分析题
∙造成英龙乡采石场生产经营不景气的原因是什么?
∙试从企业信息管理系统开发思路的角度解释这一现象
这是信息资源管理
第二大题还有一题是关于概念组配词的拆分问题。
数据结构与算法习题与答案

A .大于 1
B.等于 1
C. 小于 1 D.不能确定
( 8)将两个各有 n 个元素的有序表归并成一个有序表,其最少的比较次数是(
)。
A.n
B .2n-1
C. 2n
D .n-1
( 9)在一个长度为 n 的顺序表中,在第 i 个元素( 1≤ i≤ n+1 )之前插入一个新元素时
须向后移动( )个元素。
(15) 在双向循环链表中,在 p 指针所指的结点后插入 q 所指向的新结点,其修改指针 的操作是( )。
A . p->next=q; q->prior=p; p->next->prior=q; q->next=q; B. p->next=q; p->next->prior=q; q->prior=p; q->next=p->next; C. q->prior=p; q->next=p->next; p->next->prior=q; p->next=q; D. q->prior=p; q->next=p->next; p->next=q; p->next->prior=q;
第 1 章 绪论
习题
1.简述下列概念:数据、数据元素、数据项、数据对象、数据结构、逻辑结构、存储 结构、抽象数据类型。
2.试举一个数据结构的例子,叙述其逻辑结构和存储结构两方面的含义和相互关系。 3.简述逻辑结构的四种基本关系并画出它们的关系图。
4.存储结构由哪两种基本的存储方法实现?
5.选择题
( 1)在数据结构中,从逻辑上可以把数据结构分成(
( 5)以下与数据的存储结构无关的术语是(
2013-2014第二学期数据结构期末试卷A卷答案
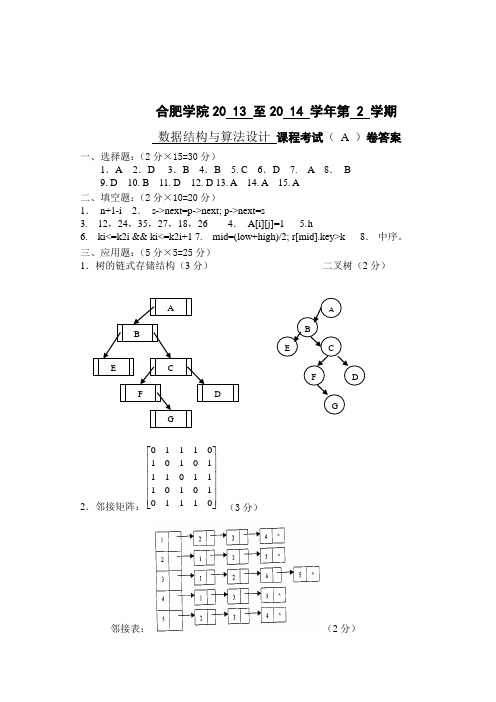
合肥学院20 13 至20 14 学年第 2 学期数据结构与算法设计 课程考试( A )卷答案一、选择题:(2分×15=30分)1.A 2.D 3.B 4.B 5. C 6.D 7. A 8. B 9. D 10. B 11. D 12. D 13. A 14. A 15. A二、填空题:(2分×10=20分)1. n+1-i 2. s->next=p->next; p->next=s3. 12,24,35,27,18,26 4. A[i][j]=1 5. h6. ki<=k2i && ki<=k2i+17. mid=(low+high)/2; r[mid].key>k 8. 中序。
三、应用题:(5分×5=25分)1.树的链式存储结构(3分) 二叉树(2分)2.邻接矩阵:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡011110101110111010101110(3分)邻接表:(2分)3.(3分)(2分)4.(4分)E={(1,3),(1,2),(3,5),(5,6),(6,4)} (1分) 5、(5分)四、算法阅读题:(7分+5分=12分) 1、(1)查询链表的尾结点 (3分) (2)将第一个结点链接到链表的尾部,作为新的尾结点 (3分) (3)返回的线性表为(a2,a3,…,an,a1)。
(1) 2.递归地后序遍历链式存储的二叉树 (5分) 五、算法设计题:(7分+6分=13分) 1.void mergelklist(lklist *ha,lklist *hb,lklist *&hc)AB GC EH JF D Ilklist *s=hc=0; (2分)while(ha!=0 && hb!=0)if(ha->data<hb->data){if(s==0) hc=s=ha; else {s->next=ha; s=ha;};ha=ha->next;} else {if(s==0) hc=s=hb; else {s->next=hb; s=hb;};hb=hb->next;} (3分)if(ha==0) s->next=hb; else s->next=ha; (2分)}2.typedef struct node {int data; struct node *lchild,*rchild;} bitree; (2分)void swapbitree(bitree *bt){bitree *p;if(bt==0) return;swapbitree(bt->lchild); swapbitree(bt->rchild); (2分)p=bt->lchild; bt->lchild=bt->rchild; bt->rchild=p; (2分)}。
全国2014年10月自学考试《数据结构》试题和标准答案【在最后】

大题共4小题,每小题5分。
共20分)
请在答题卡上作答。
26.设Q是有N个存储空间的循环队列,初始状态front=rear=0,约定指针rear指向的单元始终为空,回答下列问题。
请根据最优二叉树的基本原理,采用类C语言,描述你所设计的成绩判定过程。
29.给定有向无环图G如题29图所示,写出G的5种不同的拓扑排序序列。
的单链表定义如下,其中freq域记录本结点被访问的次数,初值为0,单链表始终以freq 序。
函数f3l完成的功能是:查找给定关键字所在结点,若查找成功,则该结点的freq域加值调整结r旨位置。
请将空白处(1)~(3)补充完整。
在答题卡上作答。
回答下列问题。
五、算法设计题(本大题共l小题,共“l0分) 请在答题卡上作答。
34.已知带头结点的单链表类型定义如下:
- 10 -。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、若采用邻接矩阵法存储一个n个顶点的无向图,则该邻接矩阵是一个( D )。
A)上三角矩阵 B) 稀疏矩阵
C) 对角矩阵 D) 对称矩阵
2、二叉树第i(i≥1)层上至多有( C )结点。
A)2i B)2i C)2i-1 D)2i-1
3、线性表的链接实现有利于( A )运算。
A)插入 B)读元素
C)查找 D)定位
4、n个顶点的强连通图至少有( A )条边。
A)n B)n+1 C)n-1 D)n(n-1)
5、设单链表中指针p指向结点m,若要删除m之后的结点(若存在),则需修改指针的操作为( A )。
A)p->next=p->next->next; B) p=p->next;
C)p=p->next->next; D) p->next=p;
6、队列的操作的原则是( A )。
A)先进先出 B) 后进先出
C) 只能进行插入 D) 只能进行删除
7、倘若在对串的插入、删除运算中,期望运算速度最快,则应采用( C )。
A)顺序表示法 B)单字符为结点的单链表表示法
C)等量分块表示法 D)不等量分块表示法
8、若某线性表最常用的操作是存取任一指定序号的元素和在最后进行插入和删除运算,则利用( D )存储方式最节省时间。
A)顺序表B)双链表C)带头结点的双循环链表D)单循环链表
9、线性表的链接实现有利于( A )运算。
A)插入 B)读元素
C)查找 D)定位
10、设单链表中指针p指着结点A,若要删除A之后的结点(若存在),则需要修改指针的操作为( A )。
A)p->next=p->next->next B)p=p->next
C)p=p->nexe->next D)p->next=p
11、n个顶点的图的最小生成树必定( D ),是不正确的描述。
A)不唯一 B)权的总和唯一
C)不含回路 D)有n条边。
