高中数学——空间图形基本关系的认识
4.1空间图形基本关系的认识

4.1空间图形基本关系的认识班级:姓名:编号:04设计:史旭龙审核:审批:教学目标:(1)学会观察长方体模型中点线面关系,并能结合长方体模型掌握五类位置关系的分类及有关概念(2)能用图形语言和符号语言表示五类位置关系(3)给定的空间图形能指出有关点线面的位置关系教学重点:点线面的位置关系分类及有关概念教学难点:“异面直线”的理解一、自主学习:1.点、线、面的图形画法和符号表示(1)符号表示:(2)点、线、面的画法:点:A,B,C,D,…线:面:α,β,γ…2. 空间点与直线的关系(1)关系及符号表达:① A∈a (2)图形画法:②点在直线外3. 空间点与平面的关系(1)关系及符号表达:①点在平面内(2)图形画法:② A ∉α4. 空间直线与平面的关系(1)关系及符号表达:(2)图形画法:①直线在平面内:, a ⊂α②直线与平面相交:直线与平面只有一个公共点, b ⋂β=B③直线与平面平行:直线与平面没有公共点,5. 空间直线与直线的关系(1)关系及符号表达:(2)图形画法:①平行:,a⋂b=A②相交:只有一个公共点的两条直线,③异面:同在任何一个平面内的两条直线,a和b异面6.空间平面与平面的关系:(1)关系及符号表达:(2)图形画法:①平行:没有公共点的两个平面,α//β②相交:有公共点且不重合的两个平面,二、自主检测1、观察下图中A,B和a,b,c并用数学符号表达它们的关系。
2、观察上图中A ,B 和α,β并用数学符号表达它们的关系。
三、合作探究1、在上图中找出两对对异面直线.2、两个平面可以将正方体分为几份?三个平面呢?并且画出各种可能.3、在长方体ABCD —1111D C B A 找出今天所学的各种关系.☺今天学到了什么?。
4.1空间图形基本关系的认识
c
b
B
记作: P
β
3. 空间两条直线的位置关系有三种:A
①平行直线—— 在同一个平面内,没有公 共点的两条直线。 ②相交直线—— 在同一个平面内,有且只有 一个公共点的两条直线。
α α
a
c
b
B
b 记作:a//b
a
β
a O b
记作: b O a
③异面直线— 不在任何一个平面内,没有公共点的两条直线。 —
b
α
b
a
a β b
α
γ
a
A (1)直线在平面内— 直线与平面有无数个 — 公共点。 (2)直线与平面相交— 直线与平面只 α 有一个公共点。 —
4. 空间直线与平面的位置关系有三种:
b
a
β
F
E
(3)直线与平面平行—— 直线与平面没有公共点。
5. 空间平面与平面的位置关系有两种:
(1)平行平面—— 没有公共点的两个平面。 (2)相交平面—— 两个平面不重合, 并且有公共点。 α
E
β
F
练习
1.思考题:
(1)没有公共点的两条直线叫做平行直线,对吗? (2)空间两条没有公共点的直线叫做异面直线,对吗?
(3)分别在两个平面内的两条直线一定是异面直线吗?
(4)平面内一直线与这个平面外的一条直线一定是异面直线吗?
2.说出正方体中各对线段、线段与平面的位置关系: (1)AB和CC1; D1 (2)A1 C和BD1 ; B1 A1 (3)A1 A和CB1; (4)AC和A1 C1; (5)BC与平面A1 C1; (6)B1 C与平面AC; D (7)AB与平面AC。 A B
§4
实例分析
高中数学第六章立体几何初步6.3.1空间图形基本位置关系的认识6.3.刻画空间点线面位置关系的公理一

课时分层作业(四十二) 空间图形基本位置关系的认识刻画空间点、线、面位置关系的公理(一)(建议用时:40分钟)一、选择题1.下列图形表示两个相交平面,其中,画法正确的是()A BC DD[A中没有画出平面α与平面β的交线,也没有完全按照实、虚线的画法作图,故A不正确;B,C中交线的画法不对,且实、虚线的画法也不对,故B,C都不正确.]2.如图所示,用符号语言可表示为()A.α∩β=m,n⊂α,m∩n=AB.α∩β=m,n∈α,m∩n=AC.α∩β=m,n⊂α,A⊂m,A⊂nD.α∩β=m,n∈α,A∈m,A∈nA[α与β交于m,n在α内,m与n交于点A,注意符号语言的正确运用,故选A.]3.给出以下四个命题:①不共面的四点中,其中任意三点不共线;②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;③若直线a,b共面,直线a,c共面,则直线b,c共面;④依次首尾相接的四条线段必共面.其中正确命题的个数是()A.0B.1C.2 D.3B[①假设其中有三点共线,则该直线和直线外的另一点确定一个平面,这与四点不共面矛盾,故其中任意三点不共线,所以①正确;②如图,两个相交平面有三个公共点A,B,C,但A,B,C,D,E不共面;③显然不正确;④不正确,因为此时所得的四边形的四条边可以不在一个平面上,如空间四边形.]4.下列图形中不一定是平面图形的是()A.三角形B.菱形C.梯形D.四边相等的四边形D[四边相等的四边形可能四边不共面.]5.下列各图均是正六棱柱,P,Q,R,S分别是所在棱的中点,这四个点不共面的图形是()A B C DD[在选项A、B、C中,由棱柱、正六边形、中位线的性质,知均有PS∥QR,即在此三个图形中P,Q,R,S共面,故选D.]二、填空题6.已知空间四点中无任何三点共线,那么这四点可以确定平面的个数是________.1或4[其中三个点可确定唯一的平面,当第四个点在此平面内时,可确定1个平面,当第四个点不在此平面内时,则可确定4个平面.]7. 如果在两个平面内分别有一条直线,且这两条直线互相平行,那么两个平面的位置关系是________.平行或相交[如图,在正方体ABCD-A1B1C1D1中,AB⊂平面ABCD,C1D1⊂平面A1B1C1D1,C1D1⊂平面CDD1C1,AB∥C1D1,但平面ABCD∥平面A1B1C1D1,平面ABCD与平面CDD1C1相交.]8。
高中数学第一章立体几何初步1.4空间图形的基本关系与公理1.4.1空间图形的基本关系与公理1公理3课

问题导学
当堂检测
1.公理 1 的应用 活动与探究 例 1 已知 a∥b,a∩c=A,b∩c=B,求证:a,b,c 三条直线在同一 平面内. 思路分析:依题意,可先证 a 与 b 确定一个平面,再证明 c 在这个平 面内,从而可证 a,b,c 在同一平面内. 证明:∵ a ∥b , ∴ a 与 b 确定一个平面 α, ∵ a∩c=A,∴ A∈a,从而 A∈α; ∵ b∩c=B,∴ B∈b,从而 B∈α. 于是 AB⫋α,即 c⫋α,故 a,b,c 三条直线在同一平面内.
若 A∈α,A∈β,且 α,β 不重 合,则 α∩β=l,且 A∈l
目标导航
预习引导
预习交流 3
公理 1 的三个推论是什么? 提示:推论 1:一条直线和直线外一点确定一个平面. 推论 2:两条相交直线确定一个平面. 推论 3:两条平行直线确定一个平面.
预习交流 4
公理 1 中的“有且只有一个”的含义是什么? 提示:“有”是说图形存在,“只有一个”是说图形唯一.“有且只有”强 调的是存在性和唯一性两个方面,确定一个平面中的“确定”是“有且只 有”的同义词,也是指存在性和唯一性这两个方面.
【数学】1.4.1 空间图形基本关系的认识 课件 (北师大版必修2)

4.1 空间图形基本关系的认识
构成空间图形的基本元素
• 点是构成空间图形的最基本的元素
• 线可看作是具有某一特点的点的集合, 也是构成空间图形的元素 • 面也可视为无数点的集合,同时也是构 成空间图形的元素 • 它们之间有什么关系呢?
阅读课本实验分析
• • • • • 试思考以下问题 1、点和直线有什么关系? 2、点和平面有什么关系? 3、直线与直线有哪些关系? 4、平面与平面有什么关系?
异面直线:不在任何一个平面内的两条直线, 作图时为了表示异面直线不共面的特点通 常用一个或两个平面来衬托
例 如图是一个正方体的展开图,如果将它还 原为正方体,那么AB、CD、EF、GH这四条 线段所在的直线是异面直线的有 __________对,分别是______________?
解:3对,分别是AB、GH;AB、CD;GH、EF。
空间直线与平面的位置关 系
空间平面与平面的位置关 系
• 空间平面与平面的位置关系:平行;相 交
ห้องสมุดไป่ตู้
空间点与线的关系
• 空间点与直线的位置关系有两种:
点 P 在直线 上:
点 P 在直线 外: ;
空间点与平面的关系
• 空间点与平面的位置关系有两种:
空间直线与直线的位置关 系
平行直线:在同一平面内但没有公共点的两条直线, 记作:a∥b 相交直线:在同一平面内有且只有一个公共点的两 条直线,记作a∩b=P
高中数学第一章立体几何初步4空间图形的基本关系与公理4.1空间图形基本关系的认识4.2空间图形的公理

[小组合作型]
空间点、线、面的位置(wèi zhi)关系
(1)如果 a α,b α,l∩a=A,l∩b=B,l β,那么 α 与 β 的位置关系是________.
(2)如图 1-4-1,在正方体 ABCD-A′B′C′D′中, 哪几条棱所在的直线与直线 BC′是异面直线?
图 1-4-1
第十页,共42页。
两个平面若有三个公共点,则这两个平面( )
A.相交
B.重合
C.相交或重合
D.以上都不对
【解析】 若三个点在同一条直线上,则两平面可能相交;若这三个点不 在同一直线上,则这两个平面重合.
【答案】 C
第十一页,共42页。
[质疑·手记] 预习完成后,请将你的疑问记录,并与“小伙伴们”探讨交流: 疑问 1: _____________________________________________________ 解惑: _______________________________________________________ 疑问 2: _____________________________________________________ 解惑: _______________________________________________________ 疑问 3: ______________________________________________________ 解惑: _______________________________________________________
平面与平面 的位置关系
面面平行 面面相交
α∥β α∩β=a
第五页,共42页。
空间图形的基本关系与公理(1)

分析 可先转换成符号语言,再作图.
解 (1)A∈α,B∈α,A∈l,B∈l
(2)l α,P∈l,P∈α.
(3)α∩β=l,m α,m∥l.
变式训练
将下面用符号语言表示的关系改用文
字语言予以叙述,并且用图形语言予以表示.
解 文字语言叙述为: 点 A 在平面 α 与平面 β 的交线 l 上,AB、AC 分 别在 α、β 内. 图形语言表示为如图所示.
B α
A
(2)点在平面外
记作:
B
空间两条直线的位置关系有三种:
①平行直线——
在同一个平面内,没有公共点的两条直线.
②相交直线—— 在同一个平面内,有且只有一个公共点的两
条直线.
记作:a//b a b α
b
记作: β
ab O
a O b b
③异面直线——不同在任何一个平面内
α a
a
β b
④若直线 a∥直线 b,b α,那么直线 a 平行于平面α内的
变式训练
下面命题中正确的个数是
( C )
①如果 a、b 是两条直线,a∥b,那么 a 平行于经过 b 的任何一个平面; ②如果直线 a 满足 a∥α,那么 a 与平面α内的任何 一条直线平行; ③如果直线 a、b 满足 a∥α,b∥α,则 a∥b; ④如果直线 a、 和平面α满足 a∥b, α, α, b a∥ b 那么 b∥α; ⑤如果 a 与平面α上的无数条直线平行,那么直线 a 必平行于平面α. A.0 B.2 C.1 D.3
解析
A、B 都不能保证 α、β 无公共点,如图 1
所示;C 中当 a∥α,a∥β 时 α 与 β 可能相交,如 图 2 所示;只有 D 说明 α、β 一定无公共点.
高中数学-4.1空间图形基本关系的认识

l
∥
l
5.空间两条直线的位置关系
Ab
a
相交
a
b
Ab
平行
异面 a
课堂探究
空间图形的公理 思考1:如果直线 l 与平面α有一个公共点P,直线 l 是否在平面α内?
思考2:如果直线l与平面α有两个公共点,直线l是否在平面α内?
实际生活中,我们有这样的经验:把一根直尺边缘上的任意两点放到 桌面上,可以看到,直尺的整个边缘就落在了桌面上.
4.1空间图形基本关系的认识
学习目标
1. 通过长方体这一常见的空间图形,了解空间图形的基 本构成----点、线、面的基本位置关系; 2. 理解异面直线的概念,掌握空间图形的三个基本公理; 3. 培养和发展自己的空间想象能力、运用图形语言进行 交流的能力、几何直观能力,通过典型例子的学习和自 主探索活动,理解数学概念和结论,体会蕴涵在其中的 数学思想方法.
错误
C1 D1
B1 A1
②设正方形ABCD与 A1B1C1D的1 中心分别为O,O1 ,则平面 AA1C1C与平面BB1D1D的交线为OO1 ;
C
B
正确
D
OA
C1
B1
D1
O1
A1
③由点A,O,C可以确定一个平面;
C
B
D
OA
错误
C1 D1
B1 A1
④由 A, C1, B确1定的平面是ADC1B1;
(7)AB与平面AC。
D1 A1
D A
C1 B1
C B
归纳总结 提高认识
1.空间点与直线的位置关系
(1)点在直线上;(2)点在直线外.
2.空间点与平面的位置关系 (1)点在平面内;(2)点在平面外. 3.空间直线与平面的位置关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
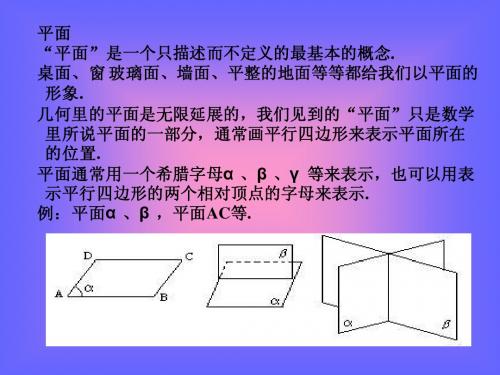
D平面β,平面ABCD,平面
AC,平面BD等.
问题讨论
三、用数学符号来表示点、线、面之间的位置关系:
(1)空间点与直线的位置关系:
点A在直线a上: 记为:A∈a
a
点B不在直线a上: 记为:B∈a
A
B
(2)空间点与平面的位置关系:
点A在平面α上: 记为:A∈α
B
点B不在平面α上:记为:B∈ α
空间两直线的位置关系及判断
问题2:没有公共点的直线 一定平行吗?
问题3:没有公共点的两直 线一定在同一平面内吗?
引入新知
定义 不同在任何一个平面内的两 条直线叫作异面直线.
位置关系 公共点个数 是否共面
相交
平行
异面
只有一个 没有 没有
共面 共面 不共面
异面直线 ⒈ 异面直线: 不同在任何一个平面内的两条直线.
空间两直线的位置关系:
(1)从公共点的数目来看可分为: ①有且只有一个公共点则两直线相交 两直线平行
②没有公共点则 两直线为异面直线
(2)从平面的性质来讲,可分为: 两直线相交
①在同一平面内 两直线平行
②不在同一平面内则两直线为异面直线.
结论:不同在任何一个平面内的两条直线 为异面直线
复习巩固 空间两条直线的位置关系:
问题讨论
(4)空间平面与平面的位置关系:
当平面α上的所有点都在平面β上时,称平面α与 平面β重合.
当两个不同平面α与平面β有公共点时,它们的公
共点组成集合a,称平面α与平面β相交.
记做:
α∩ β=a.
当平面α与平面β没有公共点时,称平面α与平面β 平行.记做: α∩ β= 或α ∥β.
β
a
α
α
α
β
相交、平行、异面 ⑴空间两条直线的位置关系归纳为:
位置关系 是否共面 公共点情况 记 法
相交直线 平行直线 异面直线
在同一个平 有且只有一
面内
个公共点
没有公共点
不同在任何 一个平面内
a∩b=A a∥b
例题解析
例1.把下列语句用集合符号表示,并画出直观图.
(1)点A在平面α内,点B不在平面α内,点A,B
都在直线 a上;
(2)平面α与平面β相交于直线 m,直线 a 在平
面α内且平行于直线 m.
B A α
a
α
a
m β
例题解析
例2.把下列图形中的点、线、面关系用 集合符号表示出来.
l
αa
A
a
a
α A
α A
l
l
B β
B β
谢谢
知识回顾 Knowledge Review
祝您成功!
A
α
问题讨论
(3)空间直线与平面的位置关系:
直线a上的所有点都在平面α上,称直线a在平
面α内,或称平面α通过直线a.记为: a
直线a与平面α只有一个公共点A时,称直线a 与平面α相交. 记为:a∩α=A
直线a与平面α没有公共点时,称直线a与平面
α平行. 记为:a∩α= 或 a∥α.
a
a
a
A
α
α
α
m
l
复习巩固
巩固:①画两个相交平面,在这两个平面内 各画一条直线,使它们成为:⑴平行直线 ;⑵相 交直线; ⑶异面直线.
β
β
b
α a
β
b
a
α
b
α a
复习巩固
两条异面直线指:
A.空间中不相交的两条直线; B.某平面内的一条直线和这平面外的直线; C.分别在不同平面内的两条直线; D.不在同一平面内的两条直线; E.不同在任一平面内的两条直线; F.分别在两个不同平面内的两条直线; G.某一平面内的一条直线和这个平面外的一条 直线; H.空间没有公共点的两条直线; I.既不相交,又不平行的两条直线.
β
问题讨论
用数学符号来表示点、线、面之间的位置关系:
a B
B
b
a
A
α
A
aA
α
α
A∈a B∈a
α
β
与β重合
A∈α B∈α
β a
α
α∩β =a
a a∩α=
b∩α=A 或 a∥α
α β
α∩ β= 或α ∥ β
问题讨论
(5)空间直线与直线的位置关系: 问题1: 在平面几何中, 两直线的位置关系如何?
空间图形基本 关系的认识
引入新知
一、平面的画法: (1)水平放置的平面:(2)垂直放置的平面:
ß
通常把表示平面的平行四边形的锐角画 成450.
引入新知
(3)在画图时,如果图形的一部分被 另一部分遮住,可以把遮住部分画成虚线, 也可以不画.
问题讨论
二、平面的表示方法:
平面可以用希腊字母表示,也可以用代 表表示平面的平行四边形的四个顶点或相对 的两个顶点字母表示.
b βb
b
α
a
α
a α
a
异面直线
A
lB
议一议
如图所示:正方体的棱所在的直线 中,与直线A1B异面的有哪些?
D1 A1
D
答案:
C1
D1C1、 C1C、 CD
B1
D1D、 AD、 B1C1
C
A
B
引入新知
异面直线直观图的画法 两条直线异m面:
l
引入新知
异面直线直观图的画法
分别在两个相交平面内的两条异面直线:
