控制工程基础(王积伟、吴振顺)课后答案资料
控制工程基础(王积伟、吴振顺)课后答案

x(t) = e t et 2sint cos2t, t 0
3)s2X(s)2sX(s)5X(s) = 3
s
1
31
X(s) = s2 2s5
s
= 0.6 s
0.6(ss1)224
1
s1
= 0.6 s
0.6 (s1)2 4
0.3
2 (s1)2
4
19
121班 刘辉 整理
第二章 习题解答
2-6 证明图示两系统具有相同形式的传递函数。
当水箱液位处于给定高度时,水箱流入水量与流 出水量相等,液位处于平衡状态。一旦流入水量 或流出水量发生变化,导致液位升高(或降 低),浮球位置也相应升高(或降低),并通过 杠杆作用于进水阀门,减小(或增大)阀门开 度,使流入水量减少(或增加),液位下降(或 升高),浮球位置相应改变,通过杠杆调节进水 阀门开度,直至液位恢复给定高度,重新达到平衡 状态。
第一章 习题解答
给定 液位
给定 液位
7
121班 刘辉 整理
杠杆
阀门
浮子
a)
开关 电磁阀
浮子
b)
水箱
实际 液位
水箱
实际 液位
第二章 习题解答
2-1 试建立图示各系统的动态微分方程,并说明 这些动态方程之间有什么特点。
C ui
xi
xo
Hale Waihona Puke R uoBK
a)
b)
8
121班 刘辉 整理
第二章 习题解答
R1
xi
5
121班 刘辉 整理
第一章 习题解答
对b)图所示液位控制系统: 当水箱液位处于给定高度时,电源开关断开,进 水电磁阀关闭,液位维持期望高度。若一旦打开 出水阀门放水,导致液位下降,则由于浮球位置 降低,电源开关接通,电磁阀打开,水流入水 箱,直至液位恢复给定高度,重新达到平衡状态。
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c?(idt2?i1)dt得到:cr2du2?(1?r2r1)u2?cr2du1dt?r2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1c?idt消去i得到:(r1?r2)一阶微分方程du2dt?u2c?r2du1dt?u1c第二章2-2解:1)确定输入、输出变量f(t)、x2f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f?f?m2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44?(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33?(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22?(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?1?1s?22e?t?e?2t (4)199s?4e?4t?19119s?1?t?1123(s?1)?t?e?13te1(s?1)2(5)?2(s?2)?2(s?1)??2e?2t?2e?t?te?t (6)?0.25?2ss?42?0.5?2?2s?42?2s?1?2.5s?t?0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,?1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程??mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图??mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x??2x?2x (2) ???2x??2tx?2x xxxoooioooi??2x?2x(4) ???2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
机械控制工程基础第二版课后答案

机械控制工程基础第二版课后答案机械控制工程基础第二版课后答案【篇一:《控制工程基础》王积伟_第二版_课后习题解答(完整)】解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△u=u1-u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2=u 上:如合上开门开关,u1=u上,△u=0,大门不动作;如合上关门开关,u1=u下,△u0,大门逐渐关闭,直至完全关闭,使△u=0。
当大门在关闭位置,u2=u下:如合上开门开关,u1=u上,△u0,大门执行开门指令,直至完全打开,使△u=0;如合上关门开关,u1=u下,△u=0,大门不动作。
2)控制系统方框图4解:1)控制系统方框图2)工作原理:a)水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球顶杆的长度给定,杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制系统。
b) 水箱是控制对象,水箱的水位是被控量,水位的给定值h’由浮球拉杆的长度给定。
杠杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后,在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离散控制系统。
2-1解:(c)确定输入输出变量(u1,u2)u1?i1r1?i2r2u2?i2r2u1?u2?1c(idt2i1)dt得到:cr2du2(1?r2r1)u2?cr2du1dtr2r1u1一阶微分方程(e)确定输入输出变量(u1,u2)u1?ir1?ir2? i? u1?u2r1cidt消去i得到:(r1?r2)一阶微分方程du2dtu2cr2du1dtu1c第二章2-2解:1)确定输入、输出变量f(t)、x2 f(t)?fk1(t)?fb1(t)?fb3(t)?m1fb3?f fm2dx2(t)dtdx1dt22dx1(t)dt222)对各元件列微分方程:k2b2fk1?k1x1;fb1?b1fb3?b3d(x1?x2)dt;fk2?k2x223)拉氏变换:f(s)?k1x1(s)?b1sx1(s)?b3s[x1(s)?x2(s)]?m1sx1(s)b3s[x1(s)?x2( s)]?k2x2(s)?b2sx2(s)?m2sx2(s)24)消去中间变量:f(s)?b3sx2(s)?(b1s?k1?b3s?m1s)2b3s?k2?b3s?m2sb3s2x2(s)5)拉氏反变换:m1m2dx2dt44(b1m2?b2m1?bsm2?b3m1)dx2dtdx2dt33(b1b3?b1b2?bsb2?k1m2?m1k2)dfdtdx2dt22(k1b2?k1b3?k2b1?k2b3)?k1k2x2?b32-3 解:(2)2s?11s?22e?t?e?2t (4)199s?4e4t19119s?1t1123(s?1)te?13te1(s?1)2(5)?2(s?2)2(s?1)2e?2t?2e?t?te?t (6)0.25?2ss?420.5?2?2s?422s?12.5st0.5cos2t?sin2t?2e?2.52-5解:1)d(s)=0,得到极点:0,0,-2,-5m(s)=0,得到零点:-1,??,??,?? 2) d(s)=0,得到极点:-2,-1,-2 m(s)=0,得到零点:0,0,-1 3) d(s)=0,得到极点:0, ?1?j3,1?j32m(s)=0,得到零点:-2,??,??4) d(s)=0,得到极点:-1,-2,?? m(s)=0,得到零点:??2-8解:1)a)建立微分方程mx(t)?f(t)?fk1(t)?fk2(t)f(t)?abfi(t)fk1(t)?k1x0(t)fk2(t)?k2(x0(t)?x(t))fk2(t)?fb(t)?bdx(t)dtb)拉氏变换msx0(s)?f(s)?ff(s)?abfi(s)2k1(s)?fk2(s)fk1(s)?k1x0(s)fk2(s)?k2(x0(s)?x(s))fk2(s)?bsx(s)c)画单元框图(略)d)画系统框图mx0(t)?fk(t)?fb1(t)?fb2(t)fk(t)?k(xi(t)?x0(t))2)a)建立微分方程:fb1(t)?b1fb2(t)?b2d(xi(t)?xo(t))dtdxo(t)dtmsxo(s)?fk(s)?fb1(s)?fb2(s)2b)拉氏变换:fk(s)?k(xi(s)?xo(s))fb1(s)?b1s(xi(s)?xo(s))fb2(s)?b2sx0(s)c)绘制单元方框图(略)4)绘制系统框图【篇二:机械工程控制基础第二版答案】p> 234【篇三:2机械控制工程基础第二章答案】是线性系统?其最重要的特性是什么?下列用微分方程表示的系统中,xo表示系统输出,xi表示系统输入,哪些是线性系统? (1) ??o?2x (3) ??o?2x2x?2x (2) 2x??2tx?2x xxxoooioooi2x?2x(4) 2xx??2tx?2x xxooiooooi解: 凡是能用线性微分方程描述的系统就是线性系统。
《控制工程基础》(王积伟 吴振顺)课后习题答案 高等教育出版社
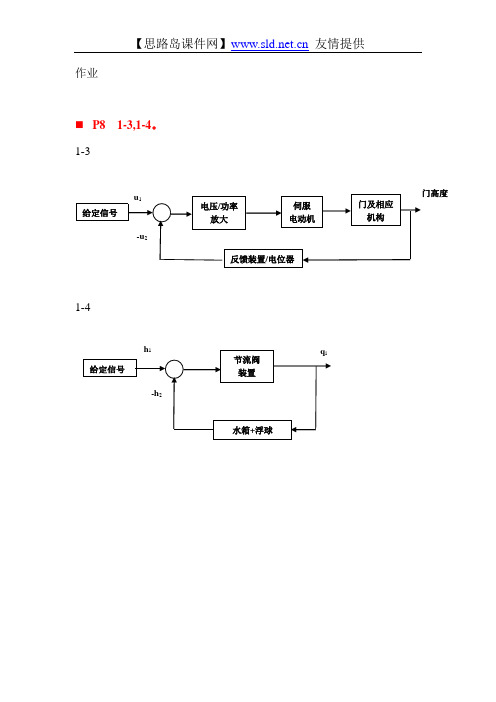
作业P81-3,1-4。
1-31-4(P72)2-1,2-2。
2-1-a22,u u u u u u i c i c -==+dt du dt du c RC RC R i u i22-==dt du dt du i RC u RC =+222-1-b221Kx B B dt dx dt dx =-dt dx dt dx B Kx B 122=+2-1-c2u u u i c -=2212()(1212R C C R i i u R u R u dt du dt du R c i i -+-=+=i dt du dt du u R C R R u R R C R R i 22121221)(2+=++2-1-d22211121x K x K x K B B dt dx dt dx =-+-1122112)(x K B x K K B dt dx dt dx +=++2-1-e1211R u R u R ii -=⎰⎰⎰-+-=+=dt u dt u u u dt i R i u C R i C R R R i R R R CR 211211212111212i dt du dt du u C R u C R R i +=++22212)(⏹ (P72)2-1,2-2 2-1-fdt dy B y K X K y K x K x K x K =--=-2222222111,122121)1(x x y K K K K -+= dt dx K BK dt dx K K B x K x K K x K 121221)1()(1122122-+=-+- 111212112)(x K BK x K K K B dt dx dtdx +=++ 2-22222212121212222311311)(,)()(dt x d dtdx dtdx dtdx dt x d dtdx dtdx dtdx mBx K B mBB x K t f =---=----22322322221)(x K B B m Bdt dx dtx d dtdx +++=313222212113311)()(dt x d dt x d dt x d dtdx dtt df m B B B K=++--22222223233312222313232222322)(])([])([dt x d dtdx dt x d dt x d B B B dtdx dt x d B K dtt df B KB B m x K B B m ++++-+++-+2223213233321424321)(dt x d B K m dt x d B B B m dt x d B m m ++=+222323424][)(12323121213212312121dt x d dt x d dt x d K m B B B B B B K m B m B m B m B m m m +++++++++dt t df dtdx B x K K B B K B B K )(32213213122)]()([=+++++⏹ (P72)2-3:-2)、-4)、-6);2-4:-2)。
《控制工程基础》王积伟第二_课后习题解答完整
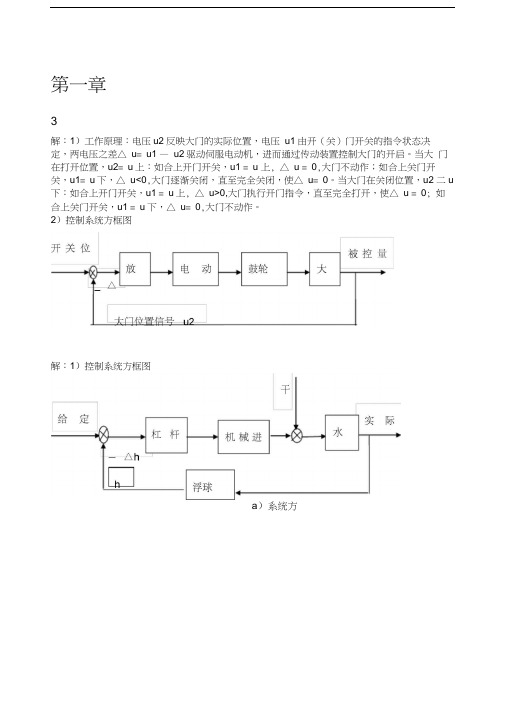
第一章3解:1)工作原理:电压u2反映大门的实际位置,电压u1由开(关)门开关的指令状态决定,两电压之差△ u= u1 —u2驱动伺服电动机,进而通过传动装置控制大门的开启。
当大门在打开位置,u2= u上:如合上开门开关,u1 = u 上, △ u = 0,大门不动作;如合上关门开关,u1= u下,△ u<0,大门逐渐关闭,直至完全关闭,使△ u= 0。
当大门在关闭位置,u2 二u 下:如合上开门开关,u1 = u上, △ u>0,大门执行开门指令,直至完全打开,使△ u = 0; 如合上关门开关,u1 = u下,△ u= 0,大门不动作。
2)控制系统方框图解:1)控制系统方框图a)系统方a )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球顶杆的长度给定,杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),通过杠杆机构是 进水阀的开度增大(减小),进入水箱的水流量增加(减小),水位升高(降低),浮球也随 之升高(降低),进水阀开度增大(减小)量减小,直至达到新的水位平衡。
此为连续控制 系统。
b )水箱是控制对象,水箱的水位是被控量,水位的给定值 h '由浮球拉杆的长度给定。
杠 杆平衡时,进水阀位于某一开度,水位保持在给定值。
当有扰动(水的使用流出量和给水 压力的波动)时,水位发生降低(升高),浮球位置也随着降低(升高),到一定程度后, 在浮球拉杆的带动下,电磁阀开关被闭合(断开),进水阀门完全打开(关闭),开始进水(断水),水位升高(降低),浮球也随之升高(降低),直至达到给定的水位高度。
随后水 位进一步发生升高(降低),到一定程度后,电磁阀又发生一次打开(闭合)。
此系统是离 散控制系统。
2-1 解:(c )确定输入输出变量(u1,u2)得到:CR 2dU 1(1 匹)u 2 =CR 2dU 1-R2u 1 dt R 1 dt R一阶微分方程(e )确定输入输出变量(u1,u2)消去i 得到:(& R 埒汁2牛亡 一阶微分方程第二章2- 2解:1)确定输入、输出变量f (t ) 、X 2□2)工作原理:b )系统方框图干f(t)-fK1⑴-fB 1⑴-fBMF^d^- - 1 -(s 2) (s 1) (s 1)2M(s)=0, 4) D(s)=0,得到极点:一1, M(s)=0, 得到零点:2) 对各元件列微分方程:2f f f _ d X 2(t)fB3 ~'T K2-'T B 2= m 2K1B3 dt 2=K 1X 1; f B1 = B 1 -- -dt B d (x 1 - x2) =B 3 甬;fK2 = K 2X23)4) 5) 拉氏变换.F(s)—KX(s)—B 1SX1G)—B3$(X 1(s) —X 2(s)] = gs 2X 1(s) 叉'B 3S[X 1(s) -X 2(s)] -K 2X2G)-B 2SX2G ) = m 2S 2X 2(s) 消去中间变量: 拉氏反变换:mi|m 2 d 4X d 3X d 2X$ (B 1m 2 七2口1 B s mh B s mJ $(B 1B 3 B 1B 2 B s B ?心口2 ^心)/dt dt dt 2_3(K 1B 2 K 1B 3 K 2B 1 K 2B 3)等 K 1g 弋詈解:(2) (4)1 1 11 1 1 — 29 s 49 s 13 (s 1)(5)(6)-0.25 2s 0.5 2 22 2.5 s2- 5解:1)D(s)=0, M(s)=0,2) D(s)=0, M(s)=0,得到极点:0,0,-2,-5得到零点:一 1 , ' 得到极点:一 2, — 1, —2 得到零点:0 , 0 , — 1+ □0 +oci3) D(s)=O, 得到极点:0,得到零点:一2,2- 8解:1) a )建立微分方程b) 拉氏变换 c) 画单元框图(略) d) 画系统框图mx o (t) = f k (t) f Bl (t) - f B2(t) f k (t)二 k(X i (t) —x °(t))ms 2X o (s) = F k (s) F BI (S ) -F B 2(S )b) 拉氏变换:F k (s )=k (X i (s )-X o (s))F Bi (s)=B i S (X j (s)—X o (s))F B 2(S )工 B 2S X O (S )c) 绘制单元方框图(略)4)绘制系统框图Fi ( s )2)a)建立微分方程:f B1(t) B id (N (t)-")) dtf B2 (t)=B 2 dX o (t) dt由于扰动产生的输出为:要消除扰动对输出的影响,必须使 X o2(S )=0 得到:QK 2K 3G o (s) -K 3K 4S =0第三章3- 1解:1)法一:一阶惯性环节的调整时间为 4T ,输出达稳态值的98%故: 4T = 1min ,得到:T = 15s法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
《控制工程基础》王积伟_第二版_课后习题解答

d)画系统框图
2)a)建立微分方程:
b)拉氏变换:
c)绘制单元方框图(略)
4)绘制系统框图
2-11
解:a)
b)
2-14
解:(1)
(2)由于扰动产生的输出为:
要消除扰动对输出的影响,必须使
得到:
得到:
第三章
3-1
解:1)法一:一阶惯性环节的调整时间为4T,输出达稳态值的98%,故:
3-8
解:闭环传递函数
1)K=200:
最大超调量
峰值时间
调整时间
上升时间
振动次数
2)K=150,得到:
依次得到的动态性能指标:0、54,0037s,0、175s,0、02s,2、34。
3)K=13、5,得到:
此时,系统为过阻尼系统,为两个惯性环节串联。
4)对于二阶系统传递函数化为标准形式后,只要 不变,系统调整时间ts不变;随着 增大,过渡过程在缩短(tp,tr),但总过渡时间(调整时间ts)不变;而随着 的减小,振动幅度在加剧,振动次数N、超调量Mp都在加大。
3)单位加速度输入稳态误差;
法二:
3-11
解:开环传递函数 ,此系统为 型系统。
1)稳态误差系数
2)输入信号为阶跃信号、速度信号与加速度信号的组合,它们的系数分别为:
根据信号线性叠加的原理,系统的稳定误差为:
a)当 时,
b)当 时,
c)当 时,
3-12
解:
1)仅有输入信号作用下的稳态误差
偏差传递函数
4T=1min,得到:T=15s
法二:求出一阶惯性环节的单位阶跃时间响应,代入,求出。
2)法一:输入信号 ,就是速度信号;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 习题解答
对b)图所示液位控制系统: 当水箱液位处于给定高度时,电源开关断开,进 水电磁阀关闭,液位维持期望高度。若一旦打开 出水阀门放水,导致液位下降,则由于浮球位置 降低,电源开关接通,电磁阀打开,水流入水 箱,直至液位恢复给定高度,重新达到平衡状态。
=1 2 1 s s2
s
s1 2s4
=1 s
1 2
s2
s1 (s1)2 3
22
2
g(t) = L 1[G(s)]=1 2e 2t e t cos 3t, t 0
13)
G(s)
=s(s
2
1
2)
=
1
2
1 s
1
s
s
2
1
2
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
s3 5s2 9s7
= s2 s3 (s1)(s2)
uo uo(t) =i(t)R
RC
d dt
uo(t)uo(t)
=
RC
d dt ui(t)
fB(t)
=
d B
[xi(t)
xo(t)]
dt
f ( t ) = f ( t ) = Kx ( t )
B
b)
xo
北京工商大学 机械121班 刘辉 整理
xi(t)
第二章 习题解答
1
i u o = iR 2 C idt
R1
ui
i
R2 uo
e)
C
1 u2=iCR iR 1 idt
d
d
(R1 R2)C dt uo(t)uo(t) = R2C dt ui(t)ui(t)
xi
xo
K1 K2 B f)
dx K1(xi xo) = K2(xo x) = B dt
d
d
(K1 K2)B dt xo(t) K1K2xo(t) = K1B dt xi(t) K1K2xi(t)
第一章 习题解答
1-3 仓库大门自动控制系统原理如图所示,试说 明其工作原理并绘制系统框图。
放大器
电动机 绞盘
门
u2
反馈
u1开
关
北京工商大学 机械121班 刘辉 整理
第一章 习题解答
解: 当合上开门开关时, u1>u2,电位器桥式测 量电路产生偏差电压,经放大器放大后,驱动电
机带动绞盘转动,使大门向上提起。与此同时, 与大门连在一起的电位器滑动触头上移,直至桥 路达到平衡( u1=u2),电机停止转动,大门开 启。反之,合上关门开关时,电机反向转动,带
c b)
2
c a
b b
t e bt ,
t 0
7)
G(s)
s2 =s(s1)2(s3)
= 21 1 1 3 s 12 s3
11 2 (s1)2
31 4 s1
(s)]= 2 1 3 12
北京工商大学 机械121班 刘辉 整理
3 1 4 2
第二章 习题解答
3s2 2s8
8)G(s) = s(s2)(s2 2s4)
dt2
2
2
dt
dt
22
2
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
d4x2
d3x2
m1m2 dt4 (m1B2 m1B3 m2B1 m2B3) dt3
d2x2 (m1K2 m2K1 B1B2 B1B3 B2B3) dt2
(K1B2
K1B3
K2B1
K2B3)
dx2 dt
K1K2x2
动绞盘使大门关闭;
开、关 门位置
电位器
放大器
电动机
绞盘
大门
Hale Waihona Puke 实际 位置北京工商大学 机械121班 刘辉 整理
第一章 习题解答
1-4 分析图示两个液位自动控制系统工作原理并 绘制系统功能框图
qi
h
qo a)
北京工商大学 机械121班 刘辉 整理
第一章 习题解答
qi
h
北京工商大学 机械121班 刘辉 整理
= s22 1
1
s1 s2
g(t) = L 1[G(s)]= d (t)2(t)2e t e 2t, t 0
dt
北京工商大学 机械121班 刘辉 整理
X(s) = 1 1 s1 s 1
22 2
1
s
s 1 s 4
x(t) = e t et 2sint cos2t, t 0
3)s2X(s)2sX(s)5X(s) = 3
北京工商大学 机械121班 刘辉 整理
第一章 习题解答
给定 液位
杠杆
给定 液位
开关
北京工商大学 机械121班 刘辉 整理
阀门
浮子
a)
电磁阀
浮子
b)
水箱
实际 液位
水箱
实际 液位
第二章 习题解答
2-1 试建立图示各系统的动态微分方程,并说明 这些动态方程之间有什么特点。
C ui
xi
xo
R uo
B
K
a)
b)
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
R1
xi
xo
K1
ui
C
R2 uo
K2
B
c)
d)
xi
xo
R1 ui
R2 uo
C
K1
K2 B
e)
f)
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
解:
C
ui
iR
a)
xi fB(t)
xo fK(t)
1
ui(t) =
i(t)dt i(t)R C
s
1
31
X(s) = s2 2s5
s
= 0.6 s
G(s)
s3 =
5s2
9s7
(s1)(s2)
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
解:
3)G(s)
sc =(sa)(sb)2
= c a 1 c b 1 (a b) 2 sa a b (sb)
2
a (a
c b)2
1 sb
g(t) =
L
1[G(s)]=
c (a
a b)
2
e
at
a (a
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
2-2 试建立图示系统的运动微分方程。图中外加 力f(t)为输入,位移x2(t)为输出。
x1
x2
f(t)
m1
m2
K1
B3
K2
B1
B2
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
解:
x1
x2
f(t)
m1
m2
K1
B3
K2
B1
B2
dt
dt dt
df (t) = B3 dt
北京工商大学 机械121班 刘辉 整理
第二章 习题解答
2-3 试用部分分式法求下列函数的拉氏反变换。
3)
G(s)
sc =(sa)(sb)2
7)
G(s)
s2 =s(s1)2(s3)
3s2 2s8
8)G(s) = s(s2)(s2 2s4)
13)
G(s)
=s(s2
1
2)
17)
b)
~220V
浮球
qo
第一章 习题解答
解: 对a)图所示液位控制系统: 当水箱液位处于给定高度时,水箱流入水量与流 出水量相等,液位处于平衡状态。一旦流入水量 或流出水量发生变化,导致液位升高(或降 低),浮球位置也相应升高(或降低),并通过 杠杆作用于进水阀门,减小(或增大)阀门开 度,使流入水量减少(或增加),液位下降(或 升高),浮球位置相应改变,通过杠杆调节进水 阀门开度,直至液位恢复给定高度,重新达到平衡 状态。
