不等式与不等式组测试题
《不等式与不等式组》基础测试题及参考答案

《不等式与不等式组》基础测试题一、选择题1.下列各式中,是一元一次不等式的是( )A .5+2>3B .7x+2=5C .2x-1≤5D .1x≥0 2.如图在数轴上表示是哪一个不等式的解( )A .3x-5>1B .-2x+4>0C .-3x ≥-6D .-2+x ≥0 3.不等式x-1≥2的解集在数轴上表示为( )A .B .C .D .4.如果a >b ,那么下列结论错误的是( )A .a +1>b +1B .33a b ->-C .2a >2bD .a ﹣1>b ﹣15.不等式2x-1<5中,则x 的最大整数是( )A .0B .1C .2D .36.已知关于x 的不等式2x+m ≤1与-2x ≥2的解集相同,则m 的值为( )A .4B .3C .2D .17.不等式组121452(1)x x x x +≥-⎧⎨+>+⎩的整数解是( ) A .0,1 B .0,1,2 C .-1,0,1,2 D .以上都不对8.小倩用30元购买铅笔和钢笔,已知铅笔和钢笔的单价分别是2元和5元,她买了2支铅笔后,最多还能买几支钢笔?设小倩明还能买x 支钢笔,则下列正确的是( )A .5×2+2x≥30B .5×2+2x≤30C .2×2+2x≥30D .2×2+5x≤309.若a,b 是有理数,则下列说法中正确的是( )A .若a b >则22a b >B .若22a b >则a b >C .若||||a b >则22a b >D .若a b 则22a b ≠10.对非负整数x 四舍五入到个位的值记为(x),即当a 为非负整数时,若a-0.5≤x <a+0.5,则 (x)=a .如(1.28)=1,(4.67)=5.若 (0.5x-1)=3,则整数x 的值是( )A .6,7B .7,8C .7,8,9D .6,7,811.若关于x 的不等式组23120x x a +>⎧⎨-≤⎩恰有2个整数解,则实数a 的取值范围是( ) A .6<a<7 B .6<a ≤7 C .6≤a<7 D .6≤a ≤712.若关于x 的不等式组1122x n x x ->⎧⎨->-⎩无解,则n 的取值范围是( ) A .n >0B .n ≥0C .n <0D .n ≤0 二、填空题13.不等式3122x -≤-的解集是______. 14.当m________时,代数式213132m m +--的值是非负数. 15.已知关于x 的不等式(1+a )x >3的解集为x <31a +,则a 的取值范围是_______. 16.不等式组6156x x -≤-⎧⎨-<⎩的解集是____________. 17.点P(x -1,-x-2)在第四象限,则整数x 的值是___.18.如果不等式组324x m x m +⎧⎨-⎩<<的解集是x <m ﹣4,则m 的取值范围是_______. 19.某种商品的进价为800元,出售时标价为1200元,后来由于该商品积压,商店准备打折销售,但要保证利润率不低于5%,则最多打____ 折.三、解答题20.解不等式或不等式组,并把解集表示在数轴上.21311322x x +--≥ 123164x x --<-21372x x x ≥-⎧⎨-+-⎩ ()()27311542x x x x ⎧-<-⎪⎨-+≥⎪⎩21.解不等式31-23x x-≥,并把它的解集在数轴上表示出来,再写出最大正整数解.22.关于x的方程5315626x n n-=+的解是非负数, 求负整数n的值.23.解不等式组131722324334x xx x x⎧+<-⎪⎪⎨--⎪≥+⎪⎩,并写出它的所有整数解.24.若关于x,y的二元一次方程组2355433x y ax y a-=-⎧⎨+=+⎩中,x<0,y>0,求a的取值范围.25.某市争为创卫生城市,对广大市民发出号召,某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.(1)求提示牌和垃圾箱的单价各是多少元?(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.26.某工厂现需购买一批材料,用于生产A、B两种型号的风衣,已知生产B型风衣所需的材料费比生产A型风衣所需的材料费每件多100元,且生产A型风衣40件和生产B型风衣30件需购买材料的费用相同.(1)求生产A、B两种型号风衣所需的材料费每件各多少元?(2)若工厂购买这批材料的资金不超过135000元,且需生产两种风衣共400件,求至少能生产A种风衣多少件?参考答案一、选择题CBABC BCDCB CB二、填空题13.x≤-114.m≤115.a<-116.-1≤x<517.-1,018.m≥-319.720. x ≤52;x >194;-1≤x ≤3;-4<a ≤221.x ≤3,最大正整数是3.22.-123.5-34x ≤<,整数解是-1,0,1,2. 24.1312a -<< 25.(1)提示牌单价50元,垃圾箱单价150元.(2) 50≤x ≤52,有三种购买方案.26.(1)A 为300元,B 为400元.(2)250件。
(完整版)不等式与不等式组练习题答案

(完整版)不等式与不等式组练习题答案第九章不等式与不等式组测试1 不等式及其解集学习要求:知道不等式的意义;知道不等式的解集的含义;会在数轴上表⽰解集.(⼀)课堂学习检测⼀、填空题:1.⽤“<”或“>”填空:⑴4______-6; (2)-3______0;(3)-5______-1; (4)6+2______5+2;(5)6+(-2)______5+(-2); (6)6×(-2)______5×(-2). 2.⽤不等式表⽰:(1)m -3是正数______; (2)y +5是负数______; (3)x 不⼤于2______; (4)a 是⾮负数______;(5)a 的2倍⽐10⼤______; (6)y 的⼀半与6的和是负数______;(7)x 的3倍与5的和⼤于x 的31______;(8)m 的相反数是⾮正数______.3.画出数轴,在数轴上表⽰出下列不等式的解集: (1)?>213x(2)x ≥-4.(3)?≤51x(4)?-<312x⼆、选择题:4.下列不等式中,正确的是( ).(A)4385-<-(B)5172< (C)(-6.4)2<(-6.4)3 (D)-|-27|<-(-3)3 5.“a 的2倍减去b 的差不⼤于-3”⽤不等式可表⽰为( ). (A)2a -b <-3 (B)2(a -b )<-3 (C)2a -b ≤-3 (D)2(a -b )≤-3三、解答题:6.利⽤数轴求出不等式-2<x ≤4的整数解.(⼆)综合运⽤诊断⼀、填空题:7.⽤“<”或“>”填空:⑴-2.5______-5.2; (2);125______114--(3)|-3|______-(-2.3); (4)a 2+1______0; (5)0______|x |+4; (6)a +2______a .8.“x 的23与5的差不⼩于-4的相反数”,⽤不等式表⽰为______.⼆、选择题:9.如果a 、b 表⽰两个负数,且a <b ,则( ).(A)1>b a(B)1a 11< (D)ab <110.如图在数轴上表⽰的解集对应的是( ).(A)-2<x <4 (B)-2<x ≤4 (C)-2≤x <4 (D)-2≤x ≤4 11.a 、b 是有理数,下列各式中成⽴的是( ).(A)若a >b ,则a 2>b 2 (B)若a 2>b 2,则a >b (C)若a ≠b ,则|a |≠|b | (D)若|a |≠|b |,则a ≠b 12.|a |+a 的值⼀定是( ).(A)⼤于零 (B)⼩于零 (C)不⼤于零 (D)不⼩于零三、判断题:13.不等式5-x >2的解集有⽆数多个. ( ). 14.不等式x >-1的整数解有⽆数多个. ( ).15.不等式32421<<-x 的整数解有0、1、2、3、4. ( ). 16.若a >b >0>c ,则.0>cab( ).四、解答题:17.若a 是有理数,⽐较2a 和3a 的⼤⼩.(三)拓⼴、探究、思考18.若不等式3x -a ≤0只有三个正整数解,求a 的取值范围.19.对于整数a 、b 、c 、d ,定义db a -=,已知3411<<db ,则b +d 的值为______.测试2 不等式的性质学习要求:知道不等式的三条基本性质,并会⽤它们解简单的⼀元⼀次不等式.(⼀)课堂学习检测⼀、填空题:1.已知a <b ,⽤“<”或“>”填空:⑴a +3______b +3; (2)a -3______b -3; (3)3a ______3b ;(4);2______2b a (5);7______7ba -- (6)5a +2______5b +2; (7)-2a -1______-2b -1; (8)4-3b ______6-3a . 2.⽤“<”或“>”填空: (1)若a -2>b -2,则a______b ; (2)若,33ba <则a ______b ; (3)若-4a >-4b ,则a ______b ;(4),22ba -<-则a ______b . 3.不等式3x <2x -3变形成3x -2x <-3,是根据______. 4.如果a 2x >a 2y (a ≠0).那么x______y .⼆、选择题:5.若a >2,则下列各式中错误的是( ). (A)a -2>0 (B)a +5>7 (C)-a >-2 (D)a -2>-4 6.已知a >b ,则下列结论中错误的是( ). (A)a -5>b -5 (B)2a >2b (C)ac >bc (D)a -b >0 7.若a >b ,且c 为有理数,则( ). (A)ac >bc (B)ac <bc (C)ac 2>bc 2 (D)ac 2≥bc 2 8.若由x <y 可得到ax >ay ,应满⾜的条件是( ). (A)a ≥0 (B)a ≤0 (C)a >0 (D)a <0三、解答题:9.根据不等式的基本性质解下列不等式,并将解集表⽰在数轴上.(1)x -10<0.(2).621(3)2x ≥5.(4).131-≥-x10.⽤不等式表⽰下列语句并写出解集:⑴8与y 的2倍的和是正数;(2)a 的3倍与7的差是负数.(⼆)综合运⽤诊断⼀、填空题:11.(1)若x <a <0,则把x 2;a 2,ax 从⼩到⼤排列是______.(2)关于x 的不等式mx -n >0,当m ______时,解集是;mnx <当m ______时,解集是?>mn x 12.已知b <a <2,⽤“<”或“>”填空:(1)(a -2)(b -2)______0; (2)(2-a )(2-b )______0; (3)(a -2)(a -b )______0.13.不等式4x -3<4的解集中,最⼤的整数x =______. 14.如果ax >b 的解集为,abx >则a ______0.⼆、选择题:15.已知⽅程7x -2m +1=3x -4的根是负数,则m 的取值范围是( ).(A)25=m (B)25>m (C)25≤m 16.已知⼆元⼀次⽅程2x +y =8,当y <0时,x 的取值范围是( ).(A)x >4 (B)x <4 (C)x >-4 (D)x <-4 17.已知(x -2)2+|2x -3y -a |=0,y 是正数,则a 的取值范围是( ).(A)a <2 (B)a <3 (C)a <4 (D)a <5三、解答题:18.当x 取什么值时,式⼦563-x 的值为(1)零;(2)正数;(3)⼩于1的数.(三)拓⼴、探究、思考19.若m 、n 为有理数,解关于x 的不等式(-m 2-1)x >n .20.解关于x 的不等式ax >b (a ≠0).测试3 解⼀元⼀次不等式会解⼀元⼀次不等式.(⼀)课堂学习检测⼀、填空题:1.⽤“>”或“<”填空:(1)若x ______0,y <0,则xy >0;(2)若ab >0,则b a ______0;若ab <0,则ab______0; (3)若a -b <0,则a ______b ;(4)当x >x +y ,则y ______0.2.当a ______时,式⼦152-a 的值不⼤于-3.3.不等式2x -3≤4x +5的负整数解为______.⼆、选择题:4.下列各式中,是⼀元⼀次不等式的是( ).(A)x 2+3x >1(B)03<-yx (C)5511≤-x(D)31312->+x x 5.关于x 的不等式2x -a ≤-1的解集如图所⽰,则a 的取值是( ).(A)0 (B)-3 (C)-2 (D)-1三、解下列不等式,并把解集在数轴上表⽰出来:6.2(2x -3)<5(x -1). 7.10-3(x +6)≤1.8.?-->+22531x x 9.-≥--+612131y y y10.求不等式361633->---x x 的⾮负整数解.11.求不等式6)125(53)34(2+<-x x 的所有负整数解.(⼆)综合运⽤诊断⼀、填空题:12.已知a <b <0,⽤“>”或“<”填空:⑴2a ______2b ;(2)a 2______b 2;(3)a 3______b 3;(4)a 2______b 3;(5)|a |______|b |(6)m 2a ______m 2b (m ≠0). 13.⑴已知x <a 的解集中的最⼤整数为3,则a 的取值范围是______;(2)已知x >a 的解集中最⼩整数为-2,则a 的取值范围是______.⼆、选择题:14.下列各对不等式中,解集不相同的⼀对是( ).(A)72423xx +<-与-7(x -3)<2(4+2x ) (B)3921+<-x x 与3(x -1)<-2(x +9) (C)31222-≥+x x 与3(2⼗x )≥2(2x -1) (D)x x ->+414321与3x >-1 15.如果关于x 的⽅程5432bx a x +=+的解不是负值,那么a 与b 的关系是( ) (A)b a 53>(B)a b 53≥(C)5a =3b(D)5a ≥3b三、解下列不等式:16.(1)3[x -2(x -7)]≤4x . (2).17)10(2383+-≤--y y y(3).151)13(21+<--y y y (4)-+≤--+15)2(22537313x x x(5)).1(32)]1(21[21-<---x x x x (6)->+-+2503.002.003.05.09.04.0x x x四、解答题:17.已知⽅程组?-=++=+②①m y x m y x 12,312的解满⾜x +y <0.求m 的取值范围.18.x 取什么值时,代数式413--x 的值不⼩于8)1(32++x 的值.19.已知关于x 的⽅程3232xm x x -=--的解是⾮负数,m 是正整数,求m 的值.*20.当310)3(2k k -<-时,求关于x 的不等式k x x k ->-4 )5(的解集.(三)拓⼴、探究、思考21.适当选择a 的取值范围,使1.7<x <a 的整数解:(1)x 只有⼀个整数解; (2)x ⼀个整数解也没有.22.解关于x 的不等式2x +1≥m (x -1).(m ≠2)23.已知A =2x 2+3x +2,B =2x 2-4x -5,试⽐较A 与B 的⼤⼩.测试4 实际问题与⼀元⼀次不等式学习要求:会从实际问题中抽象出不等的数量关系,会⽤⼀元⼀次不等式解决实际问题.(⼀)课堂学习检测⼀、填空题:1.若x 是⾮负数,则5231x-≤-的解集是______. 2.使不等式x -2≤3x +5成⽴的负整数有______. 3.代数式231x-与代数式x -2的差是负数,则x 的取值范围为______ 4.6⽉1⽇起,某超市开始有偿..提供可重复使⽤的三种环保购物袋,每只售价分别为1元、2元和3元,这三种环保购物袋每只最多分别能装⼤⽶3公⽄、5公⽄和8公⽄.6⽉7⽇,⼩星和爸爸在该超市选购了3只环保购物袋⽤来装刚买的20公⽄散装⼤⽶,他们选购的3只环保购物袋⾄少..应付给超市______元.⼆、选择题:5.三⾓形的两边长分别为4cm 和9cm ,则下列长度的四条线段中能作为第三边的是( ). (A)13cm (B)6cm (C)5cm (D)4cm6.⼀商场进了⼀批商品,进价为每件800元,如果要保持销售利润不低于15%,则售价应不低于( ). (A)900元 (B)920元 (C)960元 (D)980元三、解答题:7.某种商品进价为150元,出售时标价为225元,由于销售情况不好,商品准备降价出售,但要保证利润不低于10%,那么商店最多降价多少元出售商品?8.某次数学竞赛活动,共有16道选择题,评分办法是:答对⼀题给6分,答错⼀题倒扣2分,不答题不得分也不扣分.某同学有⼀道题未答,那么这个学⽣⾄少答对多少题,成绩才能在60分以上?(⼆)综合运⽤诊断⼀、填空题:9.直接写出解集:(1)4x -3<6x +4的解集是______; (2)(2x -1)+x >2x 的解集是______;(3)5231052--≤-x x x 的解集是______. 10.若m >5,试⽤m 表⽰出不等式(5-m )x >1-m 的解集______.⼆、选择题:11.初三⑴班的⼏个同学,毕业前合影留念,每⼈交0.70元,⼀张彩⾊底⽚0.68元,扩印⼀张相⽚0.50元,每⼈分⼀张,将收来的钱尽量⽤掉的前提下,这张相⽚上的同学最少有( ). (A)2⼈ (B)3⼈ (C)4⼈(D)5⼈12.某出租车的收费标准是:起步价7元,超过3km 时,每增加1km 加收2.4元(不⾜1km 按1km 计).某⼈乘这种出租车从甲地到⼄地共⽀付车费19元,设此⼈从甲地到⼄地经过的路程是x km ,那么x 的最⼤值是( ). (A)11 (B)8 (C)7 (D)5三、解答题:13.已知:关于x 、y 的⽅程组?-=++=+134,123p y x p y x 的解满⾜x >y ,求p 的取值范围.14.某⼯⼈加⼯300个零件,若每⼩时加⼯50个可按时完成;但他加⼯2⼩时后,因事停⼯40分钟.那么这个⼯⼈为了按时或提前完成任务,后⾯的时间每⼩时他⾄少要加⼯多少个零件?(三)拓⼴、探究、思考15.某商场出售A 型冰箱,每台售价2290元,每⽇耗电1度;⽽B 型节能冰箱,每台售价⽐A ⾼出10%,但每⽇耗电0.55度.现将A 型冰箱打折出售(打九折后的售价为原价的⼗分之九),问商场最多打⼏折时,消费者购买A 型冰箱才⽐购买B 型冰箱更合算?(按使⽤期10年,每年365天,每度电0.4元计算)16.某零件制造车间有20名⼯⼈,已知每名⼯⼈每天可制造甲种零件6个或⼄种零件5个,且每制造⼀个甲种零件可获利150元,每制造⼀个⼄种零件可获利260元,在这20名⼯⼈中,车间每天安排x 名⼯⼈制造甲零件,其余⼯⼈制造⼄种零件.⑴若此车间每天所获利润为y (元),⽤x 的代数式表⽰y ;(2)若要使每天所获利润不低于24000元,⾄少要派多少名⼯⼈去制造⼄种零件?测试5 ⼀元⼀次不等式组(⼀)学习要求:会解⼀元⼀次不等式组,并会利⽤数轴正确表⽰出解集.(⼀)课堂学习检测⼀、填空题:1.解不等式组?>--<+)2(223)1(,423x x 时,解⑴式,得______,解(2)式,得______.于是得到不等式组的解集是______.2.解不等式组-≥--≥-)2(21)1(,3212x x 时,解⑴式,得______,解(2)式,得______,于是得到不等式组的解集是______.3.⽤字母x 的范围表⽰下列数轴上所表⽰的公共部分: (1)________________________;(2)_______________________; (3)________________________.⼆、选择题:4.不等式组+<+>-5312,243x x x 的解集为( ).(A)x <-4 (B)x >2 (C)-4<x <2 (D)⽆解5.不等式组?>+<-023,01x x 的解集为( ).(A)x >1(B)132<<-x(C)32-三、解下列不等式组,利⽤数轴确定不等式组的解集.6.≥-≥-.04,012x x7.?>+≤-.074,03x x8.??+>-≤-.3342,121x x x x9.-5<6-2x <3.四、解答题:10.解不等式组??<-+≤+321),2(352x x x x 并写出不等式组的整数解.(⼆)综合运⽤诊断⼀、填空题:11.当x 满⾜______时,235x-的值⼤于-5⽽⼩于7. 12.不等式组≤-+<25 12,912x x x x 的整数解为______.⼆、选择题:13.如果a >b ,那么不等式组?<<.,b x a x 的解集是( ).(A)x <a(B)x <b(C)b <x <a(D)⽆解14.不等式组?+>+≤+1,159m x x x 的解集是x >2,则m 的取值范围是( ).(A)m ≤2(B)m ≥2 (C)m <1 (D)m >1三、解答题:15.求不等式组73123<--≤x 的整数解.16.解不等式组??-<-->-->+.3273,4536,7342x x x x x x17.当k 取何值时,⽅程组-=+=-52,53y x k y x 的解x 、y 都是负数?18.已知?+=+=+122,42k y x k y x 中的x 、y 满⾜且0<y -x <1,求k 的取值范围.(三)拓⼴、探究、思考19.已知a 是⾃然数,关于x 的不等式组?>-≥-.02,43x a x 的解集是x >2,求a 的值.20.关于x 的不等式组?->-≥-.123,0x a x 的整数解共有5个.求a 的取值范围.测试6 ⼀元⼀次不等式组(⼆)学习要求:进⼀步掌握⼀元⼀次不等式组.(⼀)课堂学习检测1.直接写出解集:(1)->>3,2x x 的解集是______;(2)-<<3,2x x 的解集是______;(3)??-><32x x 的解集是______;(4)??-<>3,2x x 的解集是______.2.⼀个两位数,它的⼗位数字⽐个位数字⼩2,如果这个数⼤于20且⼩于40,那么此数为______.⼆、选择题:3.如果式⼦7x -5与-3x +2的值都⼩于1,那么x 的取值范围是( ).(A)76<x (B)31>x (C)7631<4.已知不等式组?->--+-≤-).23(2)1(53,1)1(3)3(2x x x x x 它的整数解⼀共有( ).(A)1个(B)2个(C)3个(D)4个5.若不等式组?>≤1有解,则k 的取值范围是( ).(A)k <2 (B)k ≥2 (C)k <1三、解下列不等式组,并把解集在数轴上表⽰出来:6.??>-<-322,352x x x x7.??->---->-.6)2(3)3(2,132x x xx8.+>-≤+).2(28,142x x x9..234512x x x -≤-≤-(⼆)综合运⽤诊断⼀、填空题:10.不等式组<->+233,152x x 的所有整数解的和是______,积是______.11.k 满⾜______时,⽅程组?=-=+.4,2y x k y x 中的x ⼤于1,y ⼩于1.⼆、解下列不等式组:12.<+->+--.1)]3(2[21,312233x x x x x13.>-->-->-24,255,13x x x x x x三、解答题:14.k 取哪些整数时,关于x 的⽅程5x +4=16k -x 的根⼤于2且⼩于10? 15.已知关于x 、y 的⽅程组?-=-+=+3472m y x m y x ,的解为正数.(2)化简|3m +2|-|m -5|.(三)拓⼴、探究、思考16.若关于x 的不等式组+<+->+a x x x x 322,3215只有4个整数解,求a 的取值范围.测试7 利⽤不等关系分析实际问题学习要求:利⽤不等式(组)解决较为复杂的实际问题;感受不等式(组)在实际⽣活中的作⽤.(⼀)课堂学习检测列不等式(组)解应⽤题:1.⼀个⼯程队原定在10天内⾄少要挖掘600m 3的⼟⽅.在前两天共完成了120m 3后,接到要求要提前2天完成掘⼟任务.问以后⼏天内,平均每天⾄少要挖掘多少⼟⽅?2.某城市平均每天产⽣垃圾700吨,由甲、⼄两个垃圾⼚处理.如果甲⼚每⼩时可处理垃圾55吨,需花费550元;⼄⼚每⼩时处理45吨,需花费495元,如果规定该城市每天⽤于处理垃圾的费⽤的和不能超过7150元,问甲⼚每天⾄少要处理多少吨垃圾?3.若⼲名学⽣,若⼲间宿舍,若每间住4⼈将有20⼈⽆法安排住处;若每间住8⼈,则有⼀间宿舍的⼈不空也不满,问学⽣有多少⼈?宿舍有⼏间?4.今年5⽉12⽇,汶川发⽣了⾥⽒8.0级⼤地震,给当地⼈民造成了巨⼤的损失.某中学全体师⽣积极捐款,其中九年级的3个班学⽣的捐款⾦额如下表:⽼师统计时不⼩⼼把墨⽔滴到了其中两个班级的捐款⾦额上,但他知道下⾯三条信息:信息⼀:这三个班的捐款总⾦额是7700元;信息⼆:(2)班的捐款⾦额⽐(3)班的捐款⾦额多300元;信息三:(1)班学⽣平均每⼈捐款的⾦额⼤于..51元...48元,⼩于请根据以上信息,帮助⽼师解决:①(2)班与(3)班的捐款⾦额各是多元;②(1)班的学⽣⼈数.(⼆)综合运⽤诊断5.某学校计划组织385名师⽣租车旅游,现知道出租公司有42座和60座客车,42座客车的租⾦为每辆320元,60座客车的租⾦为每辆460元.(1)若学校单独租⽤这两种客车各需多少钱?(2)若学校同时租⽤这两种客车8辆(可以坐不满),⽽且⽐单独租⽤⼀种车辆节省租⾦,请选择最节省的租车⽅案.(三)拓⼴、探究、思考A,B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建⼀间A型板房和⼀间B型板房所需板材及能安置的⼈数板房型号甲种板材⼄种板材安置⼈数A型板房54m226m2 5B型板房78m241m28问:这400间板房最多能安置多少灾民?全章测试(⼀)⼀、填空题:1.⽤“>”或“<”填空:(1)m +3______m -3;(2)4-2x ______5-2x ;(3);23______13--yy (4)a <b <0,则a 2______b 2;(5)若23yx -<-,则2x ______3y . 2.若使3233->-yy 成⽴,则y ______. 3.不等式x >-4.8的负整数解是______.⼆、选择题:4.x 的⼀半与y 的平⽅的和⼤于2,⽤不等式表⽰为( ).(A)2212>+y x (B)2212>++y x (C)222>+y x(D)221>+y x5.因为-5<-2,所以( ). (A)-5x <-2x (B)-5x >-2x (C)-5x =-2x (D)三种情况都可能 6.若a ≠0,则下列不等式成⽴的是( ). (A)-2a <2a (B)-2a <2(-a )(C)-2-a <2-a(D)aa 2(D)x >-1三、解不等式(组),并把解集在数轴上表⽰出来:9..11252476312-+≥---x x x10.<+-+--≤+.121331),3(410)8(2x x x x四、解答题:11.x 取何整数时,式⼦729+x 与2143-x 的差⼤于6但不⼤于8.12.当k 为何值时,⽅程1)(5332+-=-k x k x 的解是(1)正数;(2)负数;(3)零.13.已知⽅程组?-=+=-k y x k y x 513,2的解x 与y 的和为负数.求k 的取值范围.14.不等式m m x ->-2)(31的解集为x >2.求m 的值.15.某车间经过技术改造,每天⽣产的汽车零件⽐原来多10个,因⽽8天⽣产的配件超过200个.第⼆次技术改造后,每天⼜⽐第⼀次技术改造后多做配件27个,这样只做了4天,所做配件个数就超过了第⼀次改造后8天所做配件的个数.求这个车间原来每天⽣产配件多少个?16.仔细观察下图,认真阅读对话:根据对话的内容,试求出饼⼲和⽜奶的标价各是多少?全章测试(⼆) ⼀、填空题1.当m______时,⽅程5(x-m)=-2有⼩于-2的根.2.满⾜5(x-1)≤4x+8<5x的整数x为______.3.若11=--xx,则x的取值范围是______.4.已知b<0<a,且a+b<0,则按从⼩到⼤的顺序排列a、-b、-|a|、-|-b|四个数为______.⼆、选择题5.若0<a<b<1,则下列不等式中,正确的是( ).,11;11;1;1babababa<><>④③②①(A)①、③(B)②、③(C)①、④(D)②、④6.下列命题结论正确的是( ).(A)(1)、(2)、(3)(B)(2)、(3)(C)(3)(D)没有⼀个正确7.若不等式(a+1)x>a+1的解集是x<1,则a必满⾜( ).(A)a<0 (B)a>-1 (C)a<-1 (D)a<18.已知x<-3,那么|2+|3+x||的值是( ).(A)-x-1 (B)-x+1 (C)x+1 (D)x-19.如下图,对a、b、c三种物体的重量判断正确的是( ).(A)a<c(B)a<b(C)a>c(D)b<c三、解不等式(组):10.3(x+2)-9≥-2(x-1).11..57321<+<-x12.>--+<-.041131xxxx13.求≤-->32,134xxx的整数解.14.如果关于x的⽅程3(x+4)-4=2a+1的解⼤于⽅程3)43(41xa的解,求a的取值范围.15.某单位要印刷⼀批北京奥运会宣传资料,在需要⽀付制版费600元和每份资料0.3元印刷费的前提下,甲、⼄两个印刷⼚分别提出了不同的优惠条件,甲印刷⼚提出:凡印刷数量超过2000份的,超过部分的印刷费可按9折收费,⼄印刷⼚提出:凡印刷数量超过3000份的,超过部分印刷费可按8折收费。
人教版数学七年级下册第九章不等式与不等式组 单元测试(含答案)

人教版数学七年级下册第九章不等式与不等式组一、单选题1.以下表达式:①4x+3y≤0;②a>3;③x2+xy;④a2+b2=c2;⑤x≠5.其中不等式有()A.4个B.3个C.2个D.1个2.关于m的不等式−m>1的解为().A.m>0B.m<0C.m<−1D.m>−13.若(m−2)x2m+1−1>5是关于x的一元一次不等式,则该不等式的解集为()A.m=0B.x<−3C.x>−3D.m≠24.设a、b、c表示三种不同物体的质量,用天枰称两次,情况如图所示,则这三种物体的质量从小到大排序正确的是【】A.c<b<a B.b<c<a C.c<a<b D.b<a<c5.若式子3a−4的值不小于2,则a的取值范围是()A.a≥−23B.a≥2C.a<−23D.a<26.已知x<y,则下列不等式一定成立的是().A.x+5<y+2B.−2x+5<−2y+5C.x3>y3D.2x−3<2y−37.规定[x]为不大于x的最大整数,如[3.6]=3,[−2.1]=−3,若[x+12]=3且[3−2x]=−4,则x的取值范围为()A.52<x<72B.3<x<72C.3<x≤72D.52≤x<728.八年级某小组同学去植树,若每人平均植树7棵,则还剩9棵,若每人平均植树9棵,则有1位同学有植树但植树棵数不到3棵.则同学人数为()A.8人B.9人C.10人D.11人9.若不等式组{x +a−22≥−1,3x−22<x−12无解,则实数a 的取值范围是( )A .a ≥−1B .a <−1C .a ≤1D .a ≤−110.对一实数x 按如图所示程序进行操作,规定:程序运行从“输入一个实数x ”到“判断结果是否大于190?”为一次操作,如果操作恰好进行两次后停止,则x 的取值范围是( )A .x <64B .x >22C .22<x ≤64D .22<x <64二、填空题11.不等式3x +22<x 的解集是 .12.不等式2x>3的最小整数解是 .13.不等式组{2x−4≥0x 3<2的解集是.14.已知a <b,用“<”或“>”号填空: a−3 b−3; −4a −4b .15.用不等式表示“x 的一半减去3所得的差不大于1” .16.某品牌衬衫的进价为120元,标价为240元,如果商店打折销售但要保证利润不低于30%,则最少可以打折出售.17.若不等式组{2x +a−1>02x−a−1<0的解集为0<x <1,则a 的值为 .18.若整数m 使得关于x 的不等式组{2x +1≥5x +m ≤2无解,且使得关于x ,y 二元一次方程组{x +2y =2,3x−y =m +1 的解x ,y 均为正数,则符合条件的整数m 的和是 .三、解答题19.(1)解不等式:x +12−x−13≤1,并把它的解集在数轴上表示出来.(2)解不等式组:{3x +2≥4x−54x−3<2120.已知二元一次方程组{x+y=3a+9x−y=5a+1的解x,y均为正数.(1)求a的取值范围;(2)化简:|5a+5|−|a−4|21.如图,有一高度为20cm的容器,在容器中倒入100cm3的水,此时刻度显示为5cm,现将大小规格不同的两种玻璃球放入容器内,观察容器的体积变化测量玻璃球的体积.若每放入一个大玻璃球水面就上升0.5cm.(1)求一个大玻璃球的体积;(2)放入27个大玻璃球后,开始放入小玻璃球,若放入5颗,水面没有溢出,再放入一颗,水面会溢出容器,求一个小玻璃球体积的范围.22.关于x,y的二元一次方程组ax+by=c(a,b,c是常数),b=a+1,c=b+1.(1)当{x=3y=1时,求c的值.(2)当a=1时,求满足|x|<5,|y|<5的方程的整数解.2(3)若a是正整数,求证:仅当a=1时,该方程有正整数解.23.为了防控甲型H1N1流感,某校积极进行校园的环境消毒,为此购买了甲、乙两种消毒液,现已知过去两次购买这两种消毒液的瓶数和总费用如表所示:甲种消毒液(瓶)乙种消毒液(瓶)总费用(元)第一次4060660第二次8030690(1)求每瓶甲种消毒和每瓶乙种消毒液各多少元?(2)现在学校决定购买甲乙两种消毒液共300瓶,要求甲乙两种的数量都不少于100瓶,,请你帮助学校计算购买时最低费用为多少?并且甲的数量不少于乙数量的3224.5月22日是第28个国际生物多样性日,为联合国《生物多样性公约》第十五次缔约方大会(COP15)在昆明顺利召开.营造良好氛围,昆明市在植物园举办主题宣传活动.某班开展了此项活动的知识竞赛.小明为班级购买奖品后与小颖对话如下:(1)请用方程的知识帮助小明计算一下,为什么小颖说他搞错了;(2)小明连忙拿出发票,发现自己的确错了,因为他还买了一本笔记本,但笔记本的单价已模糊不清,只能辨认出单价是小于10元的整数,那么笔记本的单价可能是多少元?参考答案1.B 2.C 3.B 4.A 5.B 6.D 7.B 8.A 9.D 10.C 11.x <-212.213.2≤x <614.< >15.12x−3≤116.6.517.118.1019.(1)x ≤1(2)x <620.(1)−54<a <4;(2)当−5<a ≤−1时,−4a−9;当−1<a <4时,6a +121.(1)一个大玻璃球的体积为10cm 3;(2)一个小玻璃球体积的大于5cm 3且不大于6cm 3.22.c =73;(2){x =2y =1 ,{x =−1y =2 {x =−4y =323.(1)甲种消毒每瓶6元,乙种消毒液每瓶7元;(2)最低费用1900元.24.2元或6元。
人教版数学七年级下册第九章不等式与不等式组测试卷附解析

人教版数学七年级下册第九章不等式与不等式组测试卷附解析一、单选题(共10题;共30分)1.x =3是下列不等式( )的一个解.A. x +1<0B. x +1<4C. x +1<3D. x +1<5 2.下列不等式求解的结果,正确的是( )A. 不等式组 {x ≤−3x ≤−5 的解集是 x ≤−3B. 不等式组 {x >−5x ≥−4 的解集是 x ≥−5C. 不等式组 {x >5x <−7 无解 D. 不等式组 {x ≤10x >−3 的解集是 −3≤x ≥103.在数轴上表示-2≤x <1正确的是( ) A.B.C. D.4.关于x 的不等式 2x +m >−6 的解集是 x >−3 ,则m 的值为( ) A. 1. B. 0. C. -1. D. -25.若m >n ,则下列不等式正确的是( )A. m -4<n -4B. m4>n4 C. 4m <4n D. -2m >-2n 6.已知关于x 、y 的方程组 {x +y =1−a x −y =3a +5 ,满足 x ≥12y ,则下列结论:① a ≥−2 ;② a =−53时, x =y ;③当 a =−1 时,关于x 、y 的方程组 {x +y =1−ax −y =3a +5 的解也是方程 x +y =2 的解;④若 y ≤1 ,则 a ≤−1 ,其中正确的有( )A. 1个B. 2个C. 3个D. 4个 7.若代数式4x - 32 的值不大于代数式3x +5的值,则x 的最大整数值是( ) A. 4 B. 6 C. 7 D. 88.如果关于x 的不等式组 {5x −2a >07x −3b ≤0 的整数解仅有7,8,9,那么适合这个不等式组的整数a ,b 的有序数对(a ,b )共有( )A. 4对B. 6对C. 8对D. 9对9.某种商品的进价为1200元,标价为1575元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于5%,则至多可打( )A. 6折B. 7折C. 8折D. 9折10.运行程序如图所示,从“输入实数 x”到“结果是否<18”为一次程序操作,若输入 x 后程序操作仅进行了三次就停止,那么 x 的取值范围是( )A. x ≥329B. 329≤x ≤143C. 329<x ≤143D. x ≤143二、填空题(共8题;共24分)11.如果关于 x 的不等式 2x −m <0 的正整数解恰有2个,则 m 的取值范围是________. 12.“x 与y 的平方和大于8. ”用不等式表示: ________. 13.若 y =2x −6 ,当 x ________时, y >0 ;14.某校规定把期中考试成绩的40%与期末考试成绩的60%的和作为学生的总成绩.该校李红同学在期中考试中数学考了86分,她希望自己这学期数学总成绩不低于92分,她在期末考试中数学至少应得多少分?设她在期末考试中数学考了 x 分,则可列不等式________.15.关于 x 的不等式 bx <a 的解集为 x >−2 ,写出一组满足条件的实数 a ,b 的值:a= ________,b= ________.16.如果不等式组 {x2+a ≥22x −b <3的解集是 0≤x <1 ,那么 a +b 的值为________.17.按下面的程序计算,若开始输入的值 x 为正整数:规定:程序运行到“判断结果是否大于10”为一次运算,例如当 x =2 时,输出结果等于11,若经过2次运算就停止,则 x 可以取的所有值是________.18.关于 x,y 的方程组 {x −y =1+3mx +3y =1+m 的解 x 与 y 满足条件 x +y ≤2 ,则 4m +3 的最大值是________.三、计算题(共1题;共10分)19.解下列不等式(1)4x-2+1x−5>1x−5+3x +2 (2)7x−62x+3>2四、解答题(共7题;共54分)20.(6分)解不等式组: {x −3(x −2)≥42x−15<x+12 并求该不等式组的非负整数解.21.(7分)解不等式 1−2x 3+x+22≥1 ,并把解集在数轴上表示出来.22.(7分)已知关于x ,y 的二元一次方程组 {3x −y =ax −3y =5−4a 的解满足 x <y ,试求a 的取值范围.23.(7分)某居民小区污水管道里积存污水严重,物业决定请工人清理.工人用每分钟可抽30吨水的抽水机来抽污水管道里积存的污水,估计积存的污水不少于1200吨且不超过1500吨,若工人抽污水每小时的工钱是60元,那么抽完污水最少需要支付多少元?24.(8分)新冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂共同完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天,问至少应安排两个工厂共同工作多少天才能完成任务25.(9分)北京奥运会期间,某旅行社组团去北京观看某场足球比赛,入住某宾馆.已知该宾馆一楼房间比二楼房间少5间,该旅游团有48人,若全部安排在一楼,每间住4人,房间不够,每间住5人,有房间没住满.若全部安排在二楼,每间住3人,房间不够,每间住4人,则有房间没住满.你能根据以上信息确定宾馆一楼有多少房间吗?26(10分).对x,y定义了一种新运算T,规定T(x,y)= ax+by2x+y(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= a×0+b×12×0+1,已知T(1,﹣1)=﹣2,T(4,2)=1.(1)求a,b的值;(2)若关于m的不等式组{T(2m,5−4m)≤4T(m,3−2m)>p恰好有3个整数解,求p的取值范围.答案解析部分一、单选题 1.【答案】 D【解析】【解答】解:A 、3+1=4>0,故A 不成立; B 、3+1=4,故B 不成立; C 、3+1=4>3,故C 不成立; D 、3+1=4<5,故D 成立; 故答案为:D.【分析】直接将x=3代入各个不等式,不等式成立的即为所选. 2.【答案】 C【解析】【解答】解:A 、不等式组 {x ≤−3x ≤−5 的解集根据“同小取较小”的原则可知,此不等式组的解集为x≤-5;B 、不等式组 {x >−5x ≥−4 的解集是根据“同大取较大”的原则可知,此不等式组的解集为x≥-4;C 、不等式组 {x >5x <−7 根据“大大小小解为空”的原则可知,此不等式组无解;D 、不等式组 {x ≤10x >−3 的解集根据“小大大小中间找”的原则可知,-3<x≤10.故答案为:C .【分析】根据不等式组解集的确定方法分别求出各不等式组的解集即可. 3.【答案】 D【解析】【解答】解:解:x≥-2表示-2右边的部分,含-2这点,应为实心点,x<1表示1左边的部分,不含1这点,应为空心点,则正确的是D .【分析】根据不等式解集的表示法,在数轴上表示出两个不等式即可. 4.【答案】 B【解析】【解答】解: 2x +m >−6 , 2x >−6−m ,x >−6+m2由题知x >-3, 则 −6+m 2=−3 ,解得:m=0, 故答案为:B .【分析】解不等式求出 x >−6+m 2,结合 x >−3 ,从而得出 −6+m 2=−3 ,解之可得.5.【答案】 B【解析】【解答】解:A 、∵m >n ∴m-4>n-4,故A 不符合题意; B 、∵m >n ∴m4>n4 , 故B 符合题意; C 、∵m >n∴4m >4n ,故C 不符合题意; D 、∵m >n∴-2m <-2n ,故D 不符合题意; 故答案为:B.【分析】利用不等式的性质1,可对A 作出判断;利用不等式的性质2可对B ,C 作出判断,利用不等式的性质3,可对D 作出判断。
人教版初中数学七年级下册第9章《不等式与不等式组》测试题及答案

人教版初中数学七年级下册第9章《不等式与不等式组》测试题(一)一、选择题:1,下列各式中,是一元一次不等式的是( ) A.5+4>8 B.2x -1 C.2x ≤5D.1x-3x ≥0 2,已知a<b,则下列不等式中不正确的是( )A. 4a<4bB. a+4<b+4C. -4a<-4bD. a-4<b-4 3,下列数中:76, 73,79, 80, 74.9, 75.1, 90, 60,是不等式23x >50的解的有( ) A.5个 B.6个 C.7个 D.8个 4,若t>0,那么12a+12t 与a 的大小关系是( ) A .2a +t>2a B .12a+t>12a C .12a+t ≥12a D .无法确定5,如图,a 、b 、c 分别表示苹果、梨、桃子的质量.同类水果质量相等 则下列关系正确的是( )A .a >c >bB .b >a >cC .a >b >cD .c >a >b6,若a<0关于x 的不等式ax+1>0的解集是( )A .x>1a B .x<1a C .x>-1a D .x<-1a7,不等式组31027x x +>⎧⎨<⎩的整数解的个数是( )A .1个B .2个C .3个D .4个8,从甲地到乙地有16千米,某人以4千米/时~8千米/时的速度由甲到乙,则他用的时间大约为( )A 1小时~2小时 B2小时~3小时 C3小时~4小时 D2小时~4小时9,某种出租车的收费标准:起步价7元(即行使距离不超过3千米都须付7元车费),超过3千米以后,每增加1千米,加收2.4元(不足1千米按1千米计).某人乘这种出租车从甲地到乙地共付车费19元,那么甲地到乙地路程的最大值是( )A .5千米 B.7千米 C.8千米 D.15千米 10,在方程组2122x y mx y +=-⎧⎨+=⎩中若未知数x 、y 满足x+y ≥0,则m 的取值范围在数轴上表示应是( )二、填空题11,不等号填空:若a<b<0 ,则5a -5b -;a1 b 1;12-a 12-b .12,满足2n-1>1-3n 的最小整数值是________.13,若不等式ax+b<0的解集是x>-1,则a 、b 应满足的条件有______.14,满足不等式组122113x x x -⎧>-⎪⎪⎨-⎪-≥⎪⎩的整数x 为__________.15,若|12x --5|=5-12x -,则x 的取值范围是________.16,某种品牌的八宝粥,外包装标明:净含量为330g ±10g ,表明了这罐八宝粥的净含量x 的范围是 .17,小芳上午10时开始以每小时4km 的速度从甲地赶往乙地,•到达时已超过下午1时,但不到1时45分,则甲、乙两地距离的范围是_________. 18,代数式x-1与x-2的值符号相同,则x 的取值范围________.三、解答题19,解不等式组,并把它的解集在数轴上表示出来.(1)9-4(x-5)<7x+4; (2)0.10.81120.63x x x ++-<-;(3)523(1),317;22x x x x ->+⎧⎪⎨-≤-⎪⎩ (4)6432,2111.32x x x x +≥+⎧⎪+-⎨>+⎪⎩20,代数式213 1--x的值不大于321x-的值,求x的范围21,方程组3,23x yx y a-=⎧⎨+=-⎩的解为负数,求a的范围.22,已知,x满足3351,11.4x xx+>-⎧⎪⎨+>-⎪⎩化简:52++-xx.23,已知│3a+5│+(a-2b+52)2=0,求关于x的不等式3ax-12(x+1)<-4b(x-2)的最小非负整数解.24,是否存在这样的整数m,使方程组24563x y mx y m+=+⎧⎨-=+⎩的解x、y为非负数,若存在,求m•的取值?若不存在,则说明理由.25,有一群猴子,一天结伴去偷桃子.分桃子时,如果每只猴子分3个,那么还剩下59个;如果每个猴子分5个,就都分得桃子,但有一个猴子分得的桃子不够5个.你能求出有几只猴子,几个桃子吗?参考答案一、1,C;2,C;3,A;4,A.解:不等式t>0利用不等式基本性质1,两边都加上12a得12a+t>12a.5,C.6,D.解:不等式ax+1>0,ax>-1,∵a<0,∴x<-1a因此答案应选D.7,D.解:先求不等式组解集-13<x<72,则整数x=0,1,2,3共4个.8,D;9,C.10,D.解:2122x y m x y+=-⎧⎨+=⎩①+②,得3x+3y=3-m,∴x+y=33m-,∵x+y≥0,∴33m-≥0,∴m≤3在数轴上表示3为实心点.射线向左,因此选D.二、11,>、>、<;12,1.解:先求解集n>25,再利用数轴找到最小整数n=1.13,a<0,a=b 解析:ax+b<0,ax<-b,而不等式解集x>-1不等号改变了方向.因此可以确定运用不等式性质3,所以a<0,而-ab=-1,∴b=a.14,-2,-1,0,1 解析:先求不等式组解集-3<x≤1,故整数x=0,1,-1,-2.15,x≤11 解析:∵│a│=-a时a≤0,∴12x--5≤0,解得x≤11.16,320≤x≤340.17,(12~15)km.解:设甲乙两地距离为xkm,依题意可得4×(13-10)<x<4•×(134560-10),即12<x<15.18,x>2或x<1 解析:由已知可得10102020 x xx x->-<⎧⎧⎨⎨->-<⎩⎩或者.三、19,(1)9-4(x-5)<7x+4.解:去括号9-4x+20<7x+4,移项合并11x>25,化系数为1,x>2511.(2)0.10.81120.63x x x++-<-.解:811263x x x++-<-,去分母 3x-(x+8)<6-2(x+1),去括号 3x-x-8<6-2x-2,移项合并 4x<12,化系数为1,x<3.(3)523(1)31722x xxx->+⎧⎪⎨-≤-⎪⎩解:解不等式①得 x>52,解不等式②得 x≤4,∴不等式组的解集52<x ≤4. (4)6432211132x x x x+≥+⎧⎪+-⎨>+⎪⎩解:解不等式①得x ≥-23,解不等式②得x>1,∴不等式组的解集为x>1. 20,57≥x ;21,a<-3;22,7; 23,解:由已知可得535035520212a a ab b ⎧+==-⎧⎪⎪⎪⎨⎨-+=⎪⎪=⎩⎪⎩解得代入不等式得-5x-12(x+1)<-53(x-2),解之得 x>-1,∴最小非负整数解x=0.24,解:24563x y m x y m +=+⎧⎨-=+⎩得11139529m x m y +⎧=⎪⎪⎨-⎪=⎪⎩∵x ,y 为非负数00x y ≥⎧⎨≥⎩∴1113095209m m +⎧≥⎪⎪⎨-⎪≥⎪⎩解得-1311≤m ≤52,∵m 为整数,∴m=-1,0,1,2.答:存在这样的整数m=-1,0,1,2,可使方程24563x y m x y m +=+⎧⎨-=+⎩的解为非负数.点拨:先求到方程组的解,再根据题意设存在使方程组的解00x y ≥⎧⎨≥⎩的m ,•从而建立关于m 为未知数的一元一次不等式组,求解m 的取值范围,选取整数解.25,设有x 只猴子,则有(3x+59)只桃子,根据题意得:0<(3x+59)-5(x-1)<5,解得29.5<x<32,因为x 为整数,所以x=30或x=31,当x=30时,(3x+59)=149,当x=31时,(3x+59)=152.答:有30只猴子,149只桃子或有31只猴子,152只桃子.1. 将不等式组13x x ⎧⎨⎩≥≤的解集在数轴上表示出来,应是 ( )2. 下面给出的不等式组中①23x x >-⎧⎨<⎩②020x x >⎧⎨+>⎩③22124x x x ⎧>+⎪⎨+>⎪⎩④307x x +>⎧⎨<-⎩⑤101x y x +>⎧⎨-<⎩其中是一元一次不等式组的个数是( ) A.2个B.3个C.4个D.5个3. 不等式组24030x x ->⎧⎨->⎩,的解集为( )A.23x << B. 3x > C. 2x <D. 23x x ><-或4. 下列不等式中哪一个不是一元一次不等式( )A.3x >B.1y y -+>C.12x> D.21x >5. 下列关系式是不等式的是( )A.25x += B.2x + C.25x +>D.235+=6. 若使代数式312x -的值在1-和2之间,x 可以取的整数有( ) A.1个B.2个C.3个D.4个7. 不等式组2030x x -<⎧⎨->⎩的正整数解是( )A.0和1 B.2和3 C.1和3 D.1和2 8. 下列选项中,同时适合不等式57x +<和220x +>的数是( )A.3 B.3- C.1- D.19. 不等式211133x ax +-+>的解集是53x <,则a 应满足( ) A.5a > B.5a = C.5a >- D.5a =-10. a 是一个整数,比较a 与3a 的大小是( )C1DA3BA.3a a >B.3a a <C.3a a =D.无法确定二、填空题(每题3分,共30分) 11. 不等式(3)1a x ->的解集是13x a <-,则a 的取值范围 . 12. 某商品进价是1000元,售价为1500元.为促销,商店决定降价出售,但保证利润率不低于5%,则商店最多降 元出售商品.13. 一个两位数,十位数字与个位数字的和为6,且这个两位数不大于42,则这样的两位数有 ______个. 14. 若a b >,则22____ac bc .15. 关于x 的方程32x k +=的解是非负数,则k 的取值范围是 . 16. 若(1)20mm x++>是关于x 的一元一次不等式,则m 的取值是 .17. 关于x 的方程4132x m x -+=-的解是负数,则m 的取值范围 .18. 若0m n <<,则222x m x n x n >⎧⎪>-⎨⎪<⎩的解集为 .19. 不等式15x +<的正整数解是 .20. 不等式组⎩⎨⎧-<+<632a x a x 的解集是32+<a x ,则a 的取值 .三、解答题(21、22每小题8分,23、24第小题10分,共36分) 21. 解不等式5(1)33x x x +->+22. 解不等式组3(2)41214x x x x --⎧⎪⎨-<-⎪⎩≤23. 关于x ,y 的方程组322441x y k x y k +=+⎧⎨+=-⎩的解x ,y 满足x y >,求k 的取值范围.24.有学生若干人,住若干间宿舍,若每间住4人,则有20人无法安排住宿;若每间住8 人,则有一间宿舍不满也不空,问宿舍间数和学生人数分别是多少?25.喷灌是一种先进的田间灌水技术.雾化指标P是它的技术要素之一.当喷嘴的直径d(mm).喷头的工作压强为h(kPa)时.雾化指标P=100hd.如果树喷灌时要求3000≤P≤4000.若d=4mm.求h的范围.四、解答题(本题共2小题,每题12分,共24分)26.某同学在A,B两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包的单价的4倍少8元.(1)求该同学看中的随身听和书包的单价各是多少元?(2)某一天该同学上街,恰好赶上商家促销,超市A所有商品打八折销售,超市B全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样商品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?27.在“512大地震”灾民安置工作中,某企业接到一批生产甲种板材240002m和乙种板材120002m的任务.(1)已知该企业安排140人生产这两种板材,每人每天能生产甲种板材302m或乙种板材202m .问:应分别安排多少人生产甲种板材和乙种板材,才能确保他们用相同的时间完成各自的生产任务?(2)某灾民安置点计划用该企业生产的这批板材搭建A B ,两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间A 型板房和一间B 型板房所需板材问:这400间板房最多能安置多少灾民?参考答案:一、选择题:1. B2. B.3. A4. C.5. C.6. B7. D.8. D.9. B.10. D. 二、填空题:11. 3a <. 12. 450元. 13. 4个. 14. ≥. 15. 2k ≤. 16. 1m =.17. 3m <. 18. 无解. 19. 1,2,3. 20..a ≤ -9 三、解不等式(组):21. 2x >-. 22. 312x <≤ 23. 1k > 24.解:设宿舍间数为x ,学生人数为y. 由题意得⎪⎩⎪⎨⎧>--<--+=0)1(88)1(8204x y x y x y解得: 5 < x < 7∵x 是正整数 ∴ x = 6 故y=44 答:宿舍间数为6,学生人数为44 . 24.解:把d=4代入公式P=100h d 中得P=1004h,即P=25h ,又∵3000≤P≤4000,∴3000≤25h≤4000,120≤h≤160,故h 的范围为120~160(kPa )26. (1)随身听的单价为360元,书包单价为92元.(2)在超市A 购买更省钱. 27.(1)设安排x 人生产甲种板材,应安排80人生产甲种板材,60人生产乙种板材.(2)设建造A 型板房m 间,则建造B 型板房为(400)m -间,由题意有:5478(400)240002641(400)12000m m m m +-⎧⎨+-⎩≤≤,.解得300m ≥.又0400m ≤≤,300400m ∴≤≤.这400间板房可安置灾民58(400)33200w m m m =+-=-+. ∴当300m =时,w 取得最大值2300名.答:这400间板房最多能安置灾民2300名.。
人教版数学第九章不等式与不等式组测试题
6.下列四个命题中,正确的有()
①若a<b,则a+1<b+1;②若a<b,则a-1<b-1;③若a<b,则-2a>-2b;
④若a<b,则2a>2b.
A.1个B. 2个C. 3个D. 4个
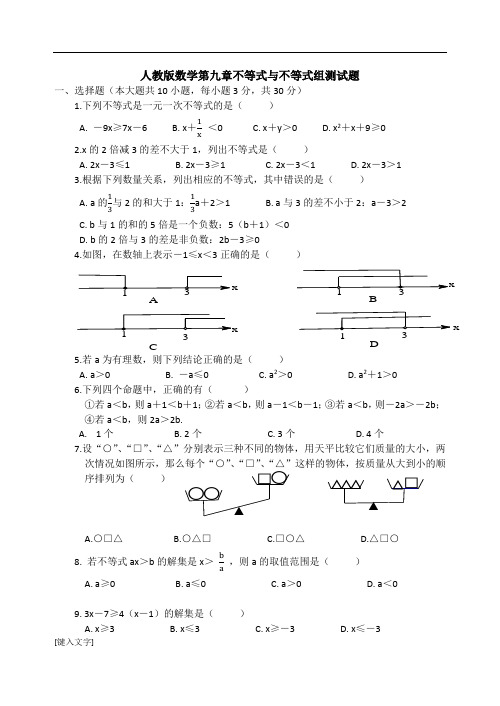
7.设“○”、“□”、“△”分别表示三种不同的物体,用天平比较它们质量的大小,两次情况如图所示,那么每个“○”、“□”、“△”这样的物体,按质量从大到小的顺序排列为()
三、解答题(本大题共60分)
21.(本小题4分)x是什么值时,代数式5x+15的值不小于代数式4x-1的值?
22.(每小题4分,计16分)解下列不等式,并把它们的解集在数轴上表示出来:
⑴3(2x+5)>2(4x+3)⑵10-4(x-4)≤2(x-1)
⑶ < ⑷ ≥ +1
23.(每小题5分,计15分)解下列不等式组:
人教版数学第九章不等式与不等式组测试题
一、选择题(本大题共10小题,每小题3分,共30分)
1.下列不等式是一元一次不等式的是()
A.-9x≥7x-6 B. x+ <0 C. x+y>0 D. x2+x+9≥0
2.x的2倍减3的差不大于1,列出不等式是()
A. 2x-3≤1B. 2x-3≥1C. 2x-3<1D. 2x-3>1
3.根据下列数量关系,列出相应的不等式,其中错误的是()
A. a的 与2的和大于1: a+2>1 B. a与3的差不小于2:a-3>2
C. b与1的和的5倍是一个负数:5(b+1)<0
D. b的2倍与3的差是非负数:2b-3≥0
4.如图,在数轴上表示-1≤x<3正确的是()
5.若a为有理数,则下列结论正确的是()
27、(8分)某公司为了扩大经营,决定购进6台机器用于生产某种活塞。现有甲,乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示。经过预算,本次购买机器所耗资金不能超过34万元。
不等式与不等式组全章测试题含答案

第九章不等式与不等式组全章测试题一、选择题1.以下变形错误的选项是 ()A.若 a-c>b-c,则 a> b11B.若2a<2b,则 a< bC.若- a-c>- b-c,则 a>b11D.若-2a<-2b,则 a>bx x-12.不等式2-3≤1的解集是 ()A.x≤4B.x≥4C.x≤- 1D.x≥- 1133.将不等式组2x-1≤7-2x,的解集表示在数轴上,正确的选项是( )5x- 2> 3( x+ 1)4.若对于 x 的方程 3(x +k) =x+6 的解是非负数,则 k 的取值范围是 () A.k≥2B. k>2C.k≤2D. k<25.若对于 x 的一元一次不等式组x-1<0,)无解,则 a 的取值范围是 (x-a>0A.a≥1B. a>1 C.a≤- 1D.a<- 16.若不等式组x- b< 0,的解集为 2<x<3,则 a, b 的值分别为 ( ) x+ a> 0A.- 2,3B.2,-3C. 3,- 2D.-3,27.三个连续正整数的和小于39,这样的正整数中,最大一组的和是( )A. 39B. 36C.35D.348.某天然气企业在一些居民小区安装天然气管道时,采纳一种鼓舞居民使用天然气的收费办法,若整个小区每户都安装,收整体初装费10000 元,再对每户收费 500 元.某小区住户按这类收费方法所有安装天然气后,每户均匀支付不足1000 元,则这个小区的住户数 ( ) A.起码 20 户B.至多 20 户C.起码 21 户D.至多 21 户9.某种出租车的收费标准是:起步价 7 元 ( 即行驶距离不超出 3 千米都收 7 元车资 ) ,超出 3千米此后,超出部分每增添 1 千米,加收元 ( 不足 1 千米按 1 千米计 ) .某人乘这类出租车从甲地到乙地共支付19 元,设这人从甲地到乙地经过的行程是x 千米,那么 x 的取值范围是( )A. 1<x≤11B. 7<x≤8C. 8<x≤9D. 7< x< 8二、填空题2是非负数,用不等式表示 ____;已知 x 的 5 倍与 3 的差大于 10,且不大于 20,用10.已知 x不等式组表示 ____________.11.若 |x +1| = 1+ x 建立,则 x 的取值范围是 __________.12.若对于 x , y 的二元一次方程组 3x -2y =m +2,中 x 的值为正数, y 的值为负数,则 m的取值范围为 ____________. 2x +y =m -513.在平面直角坐标系中,已知点 A(7-2m ,5-m)在第二象限内,且 m 为整数,则点 A 的坐 标为 _________.14.一种药品的说明书上写着:“每天用量 60~120 mg ,分 4 次服用”,则一次服用这类药品的用量 x(mg) 的范围是 ____________.15.按以下程序 ( 如图 ) ,进行运算规定:程序运转到“判断结果能否大于 244”为一次运算. 若x = 5,则运算进行 ______次才停止;若运算进行了 5 次才停止,则 x 的取值范围是 __________.16.为了增强学生的交通安全意识, 某中学和交警大队结合举行了“我当一日小交警”活动,礼拜天选派部分学生到交通路口值勤, 辅助交通警察保护交通次序. 若每一个路口安排 4 人,那么还剩下 78 人;若每一个路口安排 8 人,那么最后一个路口不足 8 人,但许多于 4 人.则这其中学共选派值好学生 _______人,共有 ______个交通路口安排值勤. 三、解答题17.解以下不等式 ( 组) ,并把解集在数轴上表示出来:5x -1(1)-x >1;3x 7-x(2) 2-1≤ 3 ;4x +6>1- x ,(3)3(x -1)≤ x + 5; 2x +5≤3( x +2),(4) 1- 2x 13 +5>0.2x +3>3x ,18.解不等式组 x + 3 x - 1 1 并求出它的整数解的和.3 -6≥2,19.阅读理解:解不等式 (x + 1)(x - 3) >0.x +1>0, x +1<0, 解:依据两数相乘,同号得正,原不等式能够转变为或x -3>0x -3<0.解不等式组 x + 1> 0,得 x >3;x - 3> 0 解不等式组 x + 1< 0,得 x <- 1.x - 3< 0因此原不等式的解集为x>3 或 x<- 1.问题解决:依据以上资料,解不等式(x -2)(x +3) <0.20.某商场进了一批价值 8 万元的衣服,每件零售价为 180 元时,卖出了 250 件,但发现销售量不大,营业部决定每件降价 40 元,那么商场起码要再卖出多少件后才能回收成本21.某小区前方有一块空地,现想建成一块面积大于 48 平方米,周长小于 34 米的长方形绿化草地,已知一边长为 8 米,设其邻边长为 x 米,求 x 的整数值.22.为增强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识比赛,为奖赏在比赛中表现优秀的班级,学校准备从体育用品商场一次性购置若干个足球和篮球( 每个足球的价钱同样,每个篮球的价钱同样 ) ,购置 1 个足球和 1 个篮球共需 159 元;足球单价是篮球单价的 2 倍少 9 元.(1)求足球和篮球的单价各是多少元(2) 依据学校实质状况,需一次性购置足球和篮球共20 个,但要求购置足球和篮球的总花费不超出 1550 元,则学校最多能够购置多少个足球23.某地域为筹办一项庆典,利用现有的 3490 盆甲栽花卉和 2950 盆乙栽花卉搭配 A,B 两种园艺造型共 50 个摆放在迎宾大道双侧,已知搭配一个 A 种造型需甲栽花卉 80 盆,乙栽花卉 40 盆;搭配一个 B 种造型需甲栽花卉 50 盆,乙栽花卉 90 盆,且搭配一个 A 种造型的成本是 200 元,搭配一个 B 种造型的成本是 300 元,则有多少种搭配方案这些方案中成本最低的是多少元答案 :1---9 CAACA ABCB10. x2≥05x- 3> 10 5x-3≤2011.x≥- 1812.3<m<1913.( - 1,1)14.15≤x≤3015.42<x≤416.1582017.(1)解: x> 2,数轴略(2)解: x≤4,数轴略(3)解:- 1<x≤4,数轴略4(4)解:- 1≤x<5,数轴略18.解:不等式组的解集为- 4≤x< 3 ∴这个不等式组的整数解为- 4,- 3,- 2,- 1, 0,1,2其和为- 4-3- 2- 1+ 0+ 1+ 2=- 7x- 2> 0,x- 2< 0,19. 解:由题意得或x+ 3< 0x+ 3> 0,x- 2> 0,解不等式组不等式组无解;x+ 3< 0,x- 2< 0,解不等式组解得-3<x<2,则原不等式的解集是-3<x<2x+ 3> 0,20.解:设商场起码要再卖出 x 件后才能回收成本由题意得 180×250+ (180 -40)x ≥80000解得 x≥250即商场起码要再卖出 250 件后才能回收成本8x>48,21.解:依据题意得2( x+ 8)< 34,解得 6< x< 9又∵x为整数∴x 的值为 7 或 8x+y=159,解:(1)设足球的单价是x元,篮球的单价是y元,依据题意得解得x=2y-9,x=103,则足球的单价是103 元,篮球的单价是56 元y=56,(2)设最多能够购置足球 m个,则购置篮球 (20 -m)个,依据题意得 103m+ 56(20 -m)≤1550,7解得 m≤9,∵ m为整数,∴ m最大取 9,则学校最多能够购置9 个足球4723.解:设搭配 A 种造型 x 个,则 B 种造型为 (50 - x) 个,依题意得80x+ 50(50- x)≤ 3490,解得 31≤x≤33,∵ x 是整数,∴ x 可取 31, 32,33,40x+ 90(50- x)≤ 2950,∴可设计三种搭配方案:① A 种的造型 31 个, B 种造型 19 个;②A 种造型 32 个, B 种造型 18 个;③A种造型 33 个, B 种造型 17 个.因为 B 种造型的成本高于 A 种造型成本,因此 B种造型越少,成本越低,故应选择方案③,成本最低,最低成本为 33× 200+17×300=11700( 元)。
2022年春人教版七年级数学下册第9章《不等式与不等式组》测试卷(带答案)

《不等式与不等式组》测试卷满分100分姓名:___________班级:___________考号:___________题号一二三总分得分一.选择题(共10小题,满分30分)1.下列为一元一次不等式的是()A.x+y>5B.+3<2C.﹣x=3D.+≥12.甲种蔬菜保鲜适宜的温度是2℃~6℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是()A.2℃~3℃B.2℃~8℃C.3℃~6℃D.6℃~8℃3.若x﹣3<0,则()A.x﹣2>0B.2x>﹣1C.2x<3D.18﹣3x>0 4.如果不等式组的解集是x>5,则a的取值范围是()A.a≥5B.a≤5C.a=5D.a<55.在数轴上表示不等式﹣2≤x<4,正确的是()A.B.C.D.6.已知点P(1+m,3)在第二象限,则m的取值范围是()A.m<﹣1B.m>﹣1C.m≤﹣1D.m≥﹣17.若关于x的不等式3x﹣2m≥0的负整数解为﹣1,﹣2,则m的取值范围是()A.﹣6≤m<﹣B.﹣6<m≤﹣C.﹣≤m<﹣3D.﹣<m≤﹣3 8.某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打()A.六折B.七折C.八折D.九折9.不等式组的解集为()A.﹣4<x<﹣1B.﹣4≤x<﹣1C.﹣4≤x≤﹣1D.﹣4<x≤﹣1 10.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?若设小明答对了x道题,则由题意可列出的不等式为()A.10x+5(20﹣x)>90B.10x+5(20﹣x)<90C.10x﹣5(20﹣x)>90D.10x﹣5(20﹣x)<90二.填空题(共8小题,满分24分)11.一种饮料重约300克,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量为克.12.若a<b,则﹣5a﹣5b(填“>”“<”或“=”).13.不等式3x﹣6>0的解集为.14.用不等式表示“x的5倍不大于3”为:.15.如图,数轴上所表示的关于x的不等式是.16.不等式组的解集是x>4,那么m的取值范围是.17.已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为.18.不等式1﹣4x≥x﹣8的非负整数解为.三.解答题(共7小题,满分46分)19.(5分)解不等式,并把它的解集表示在数轴上:5x﹣2>3(x+1)20.(6分)设a为不超过1的正整数,b为与2之间的整数,求的值.21.(6分)解不等式+1≥,并把它的解集在数轴上表示出来.22.(7分)如果关于x的方程x+2+m=0的解也是不等式组的一个解,求m 的取值范围.23.(7分)解不等式组:并将解集在数轴上表示.24.(7分)若不等式3(x﹣2)+5<4(x﹣1)+6的最小整数解为方程2x﹣ax=3的解,求a的值.25.(8分)某校为了开展“阳光体育运动”,计划购买篮球和足球,已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.(1)每个篮球、每个足球的价格分别为多少元?(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?答案一.选择题(共10小题)1.下列为一元一次不等式的是()A.x+y>5B.+3<2C.﹣x=3D.+≥1【解答】解:A、含有2个未知数,故A不符合题意;B、未知数在分母位置,故B不符合题意;C、是一元一次方程,故C不符合题意;D、是一元一次不等式,故D符合题意.故选:D.2.甲种蔬菜保鲜适宜的温度是2℃~6℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,将这两种蔬菜放在一起同时保鲜,适宜的温度是()A.2℃~3℃B.2℃~8℃C.3℃~6℃D.6℃~8℃【解答】解:∵甲种蔬菜保鲜适宜的温度是2℃~6℃,乙种蔬菜保鲜适宜的温度是3℃~8℃,∴将这两种蔬菜放在一起同时保鲜,适宜的温度是3℃~6℃,故选:C.3.若x﹣3<0,则()A.x﹣2>0B.2x>﹣1C.2x<3D.18﹣3x>0【解答】解:A、若x﹣3<0,则x﹣2<1,故此选项错误;B、若x﹣3<0,则2x<6,故此选项错误;C、若x﹣3<0,则2x<6,故此选项错误;D、若x﹣3<0,则9﹣3x>0,所以18﹣3x>0,此选项正确.故选:D.4.如果不等式组的解集是x>5,则a的取值范围是()A.a≥5B.a≤5C.a=5D.a<5【解答】解:∵不等式组的解集是x>5,∴a≤5,故选:B.5.在数轴上表示不等式﹣2≤x<4,正确的是()A.B.C.D.【解答】解:在数轴上表示不等式﹣2≤x<4的解集为:故选:A.6.已知点P(1+m,3)在第二象限,则m的取值范围是()A.m<﹣1B.m>﹣1C.m≤﹣1D.m≥﹣1【解答】解:点P(1+m,3)在第二象限,则1+m<0,解可得m<﹣1.故选:A.7.若关于x的不等式3x﹣2m≥0的负整数解为﹣1,﹣2,则m的取值范围是()A.﹣6≤m<﹣B.﹣6<m≤﹣C.﹣≤m<﹣3D.﹣<m≤﹣3【解答】解:不等式3x﹣2m≥0,解得:x≥m,∵不等式的负整数解只有﹣1,﹣2,∴﹣3<m≤﹣2,∴﹣<m≤﹣3.故选:D.8.某种商品的进价为80元,出售时标价为120元,后来由于该商品积压,商店准备打折出售,但要保证利润率不低于5%,则至多可打()A.六折B.七折C.八折D.九折【解答】解:设打x折,根据题意得120•﹣80≥80×5%,解得x≥7.所以最低可打七折.故选:B.9.不等式组的解集为()A.﹣4<x<﹣1B.﹣4≤x<﹣1C.﹣4≤x≤﹣1D.﹣4<x≤﹣1【解答】解:解不等式x+5≥1得x≥﹣4,解不等式>,得:x<﹣1,则不等式组的解集为﹣4≤x<﹣1,故选:B.10.某次知识竞赛共有20道题,每一题答对得10分,答错或不答都扣5分.小明得分要超过90分,他至少要答对多少道题?若设小明答对了x道题,则由题意可列出的不等式为()A.10x+5(20﹣x)>90B.10x+5(20﹣x)<90C.10x﹣5(20﹣x)>90D.10x﹣5(20﹣x)<90【解答】解:由题意可列出的不等式为10x﹣5(20﹣x)>90,故选:C.二.填空题(共8小题)11.一种饮料重约300克,罐上注有“蛋白质含量≥0.5%”,其中蛋白质的含量为不少于1.5克.【解答】解:∵某种饮料重约300g,罐上注有“蛋白质含量≥0.5%”,∴蛋白质含量的最小值=300×0.5%=1.5克,∴白质的含量不少于1.5克.故答案是:不少于1.512.若a<b,则﹣5a>﹣5b(填“>”“<”或“=”).【解答】解:∵a<b,∴﹣5a>﹣5b;故答案为:>.13.不等式3x﹣6>0的解集为x>2.【解答】解:移项得:3x>6,解得:x>2,故答案为:x>2.14.用不等式表示“x的5倍不大于3”为:5x≤3.【解答】解:x的5倍表示为5x,不大于3表示为5x≤3,故答案为:5x≤3.15.如图,数轴上所表示的关于x的不等式是x≤2.【解答】解:一元一次不等式的解集是2左边的部分(包含2),因而解集是x≤2.故答案为:x≤2.16.不等式组的解集是x>4,那么m的取值范围是m≤4.【解答】解:∵﹣x+2<x﹣6,解之得x>4,而x>m,并且不等式组解集为x>4,∴m≤4.17.已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为4.【解答】解:∵(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,∴|m|﹣3=1,m+4≠0,解得:m=4,故答案为:418.不等式1﹣4x≥x﹣8的非负整数解为1、0.【解答】解:∵1﹣4x≥x﹣8,∴﹣4x﹣x≥﹣8﹣1,﹣5x≥﹣9,x≤,则该不等式的非负整数解为1和0,故答案为:1、0.三.解答题(共7小题)19.解不等式,并把它的解集表示在数轴上:5x﹣2>3(x+1)【解答】解:5x﹣2>3x+3,2x>5,∴.20.设a为不超过1的正整数,b为与2之间的整数,求的值.【解答】解:∵a为不超过1的正整数,b为与2之间的整数,∴a=1,b=1或2,∴=1或.21.解不等式+1≥,并把它的解集在数轴上表示出来.【解答】解:去分母,得2(1+2x)+6≥3(1+x)去括号得,2+4x+6≥3+3x,再移项、合并同类项得,x≥﹣5.在数轴上表示为:.22.如果关于x的方程x+2+m=0的解也是不等式组的一个解,求m的取值范围.【解答】解:不等式组整理得:,解得:x≤﹣2,由x+2+m=0,得到x=﹣2﹣m,可得﹣2﹣m≤﹣2,解得:m≥0.23.解不等式组:并将解集在数轴上表示.【解答】解:,解①得x≥﹣4,解②得x<1,所以不等式组的解集为﹣4≤x<1,用数轴表示为.24.若不等式3(x﹣2)+5<4(x﹣1)+6的最小整数解为方程2x﹣ax=3的解,求a的值.【解答】解:解不等式3(x﹣2)+5<4(x﹣1)+6,去括号,得:3x﹣6+5<4x﹣4+6,移项,得3x﹣4x<﹣4+6+6﹣5,合并同类项,得﹣x<3,系数化成1得:x>﹣3.则最小的整数解是﹣2.把x=﹣2代入2x﹣ax=3得:﹣4+2a=3,解得:a=.25.某校为了开展“阳光体育运动”,计划购买篮球和足球,已知购买20个篮球和40个足球的总金额为4600元;购买30个篮球和50个足球的总金额为6100元.(1)每个篮球、每个足球的价格分别为多少元?(2)若该校购买篮球和足球共60个,且购买篮球的总金额不超过购买足球的总金额,则该校最多可购买多少个篮球?【解答】解:(1)设每个篮球、足球的价格分别是x元,y元,根据题意得:,解得:,答:每个篮球、足球的价格分别是70元,80元;(2)设购买了篮球m个,根据题意得:70m≤80(60﹣m),解得:m≤32,∴m最多取32,答:最多可购买篮球32个.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
不等式与不等式组
一、选择题(每小题5分,共30分)
1. 若m >n ,则下列不等式中成立的是( )
A .m + a <n + b
B .ma <nb
C .ma 2>na 2
D .a -m <a -n
2.不等式4(x -2)>2(3x + 5)的非负整数解的个数为( )
A .0个
B .1个
C .2个
D .3个
3.若不等式组的解集为-1≤x ≤3,则图中表示正确的是( )
A .
B .
C .
D . 4.若方程()()31135m x m x x ++=--的解是负数,则m 的取值范围是( )
A .54m >-
B .54
m <- C .54m > D .54
m < 5.不等式()123x m m ->-的解集为2x >,则m 的值为( ) A .4 B .2
C .32
D .12
6.不等式组123
x x -≤⎧⎨-<⎩的解集是( )
A .x ≥-1
B .x <5
C .-1≤x <5
D .x ≤-1或x <5
二、填空题(每小题5分,共20分)
7.已知x 的12
与5的差不小于3,用不等式表示这一关系式为 。
8.某饮料瓶上有这样的字样:Eatable Date 18 months. 如果用x (单位:月)表示Eatable Date (保质期),那么该饮料的保质期可以用不等式表示为 。
9.当x 时,式子3x -5的值大于5x + 3的值。
10.阳阳从家到学校的路程为2400米,他早晨8点离开家,要在8点30分到8点40分之间到学校,如果用x 表示他的速度(单位:米/分),则x 的取值范围为 。
三、做一做(每小题6分,共12分)
11.、解不等式
11237
x x --≤,并把它的解集表示在数轴上。
12.解不等式组
513(1) 13
17
22 x x
x x
->+⎧
⎪
⎨
-≤-
⎪⎩
四、想一想(每小题9分,共18分)
13.已知方程组
321
21
x y m
x y m
+=+
⎧
⎨
+=-
⎩
,m为何值时,x>y
14.有一个两位数,其十位数字比个位数字大2,这个两位数在50和70之间,你能求出这个两位数吗
五、实际应用(每小题10分,共20分0
15.小颖家每月水费都不少于15元,自来水公司的收费标准如下:若每户每月用水不超过5立方米,则每立方米收费1. 8元;若每户每月用水超过5立方米,则超出部分每立方米收费2元,小颖家每月用水量至少是多少
16.学校将若干间宿舍分配给七年级一班的女生住宿,已知该班女生少于35人,若每个房间住5人,则剩下5人没处住;若每个房间住8人,则空一间房,并且还有一间房也不满。
有多少间宿舍,多少名女生
参考答案——不等式与不等式组
1.D
2.A
3.D
4.A
5.B
6.C
7.1
5
2
x-≥3.
8.x≤18
9.x<-4
10. 60<x<80
11.x≥4,数轴表示略。
12.2<x≤4
13.m>4
14.53,64
15.8立方米
16.5间房,30名女生。
