北京市海淀区2014年高三一模数学(理科)试题及答案
北京市海淀区2014届高三上期中考试数学试题(理)及答案

海淀区高三年级第一学期期中练习数学(理科) 答案2013.11一、选择题1、A2、C3、B4、C5、B6、B7、D8、C二、填空题:本大题共6小题,每小题5分,共30分。
9.210..211. a b c >> 12..2π3,π613..2λ>14. 4;6(31)n -三、解答题: 本大题共6小题,共80分。
解答应写出文字说明, 演算步骤或证明过程。
15.解:(Ⅰ)由60A = 和332ABC S ∆=可得133sin6022bc = , ---------------------------2分 所以6bc =, --------------------------------------3分又32,b c =所以2,3b c ==. ------------------------------------5分(Ⅱ)因为2,3b c ==,60A = ,由余弦定理2222cos a b c bc A =+-可得 ------------------------------------7分2222367a =+-=,即7a =. ------------------------------------9分 由正弦定理sin sin a b A B=可得------------------------------------11分 72sin sin60B= ,------------------------------------12分 所以21sin 7B =.------------------------------------13分 16. 解:(I )π()3cos4cos(4)2f x x x =-+------------------------------------2分 3cos4sin 4x x =+------------------------------------4分π2sin(4)3x =+------------------------------------6分()f x 最小正周期为πT 2=,------------------------------------8分 (II )因为ππ64x -≤≤,所以ππ4π4333x -≤+≤-----------------------------------10分 所以3πsin(4)123x -≤+≤-----------------------------------12分 所以π32sin(4)23x -≤+≤, -----------------------------------13分 所以()f x 取值范围为[3,2]-. ------------------------------------14分17.解:(I )由已知11,1AH t PH t =-=+ -------------------------------------1分所以APH ∆的面积为1()(11)1,1112f t t t t =-+-<<. ---------------------4分 (II )解法1. 111'()1(11)2221f t t t t =-++⨯-⨯+ 3(3)41t t -=+ -------------------------------------7分 由'()0f t =得3t =, -------------------------------------8分 函数()f t 与'()f t 在定义域上的情况下表: t(1,3)- 3 (3,11) '()f t+ 0 - ()f t ↗ 极大值 ↘-----------------------------------12分所以当3t =时,函数()f t 取得最大值8. ------------------------------------13分解法2.由211()(11)1(11)(1),11122f t t t t t t =-+=-+-<< 设2()(11)(1),111g t t t t =-+-<<, -------------------------------------6分 则2'()2(11)(1)(11)(11)(1122)3(3)(11)g t t t t t t t t t =--++-=--++=--.-------7分 函数()g t 与'()g t 在定义域上的情况下表: t(1,3)- 3 (3,11) '()g t+ 0 - ()g t ↗ 极大值 ↘------------------------------------11分所以当3t =时,函数()g t 取得最大值, -----------------------------------12分所以当3t =时,函数()f t 取得最大值1(3)82g =.------------------------------------13分 18.解:(I )由②可得2112a a ⋅=,3122a a ⋅= -------------------------------2分由①可得12a =. -------------------------------3分(II )由②可得112n n a a +⋅=, ------------------------------6分所以数列{}n a 的通项公式2n n a =. ------------------------------7分(III )由(II )可得21(1)421n n n n b a +=+=++,易得1{4},{2}n n +分别为公比是4和2的等比数列,------------------------------8分 由等比数列求和公式可得124(14)4(12)1(416)214123n n n n n S n n ++--=++=-++--.--13分19.解:(I )因为1a =,2()42ln f x x x x=-+, 所以2242'()(0)x x f x x x-+=>, ------------------------------1分 (1)3f =-,'(1)0f =, ------------------------------3分 所以切线方程为3y =-. ------------------------------4分(II )222(1)22(1)()'()(0)x a x a x x a f x x x x-++--==>, ----------------------------5分 由'()0f x =得12,1x a x ==, ------------------------------6分 当01a <<时,在(0,)x a ∈或(1,)x ∈+∞时'()0f x >,在(,1)x a ∈时'()0f x <,所以()f x 的单调增区间是(0,)a 和(1,)+∞,单调减区间是(,1)a ; ---------------7分 当1a =时,在(0,)x ∈+∞时'()0f x ≥,所以()f x 的单调增区间是(0,)+∞;-----8分 当1a >时,在(0,1)x ∈或(,)x a ∈+∞时'()0f x >,在(1,)x a ∈时'()0f x <.所以()f x 的单调增区间是(0,1)和(,)a +∞,单调减区间是(1,)a . ---------------10分 (III )由(II )可知()f x 在区间[1,e]上只可能有极小值点,所以()f x 在区间[1,e]上的最大值在区间的端点处取到,-------------------------12分 即有(1)12(1)0f a =-+≤且2(e)e 2(1)e 20f a a =-++≤, 解得2e 2e 2e 2a -≥-. ---------------------14分 20.解:(I )27,9,3;8,9,3;6,2,3. --------------------------------------3分(II )若k a 被3除余1,则由已知可得11k k a a +=+,2312,(2)3k k k k a a a a ++=+=+; 若k a 被3除余2,则由已知可得11k k a a +=+,21(1)3k k a a +=+,31(1)13k k a a +≤++;若k a 被3除余0,则由已知可得113k k a a +=,3123k k a a +≤+; 所以3123k k a a +≤+, 所以312(2)(3)33k k k k k a a a a a +-≥-+=- 所以,对于数列{}n a 中的任意一项k a ,“若3k a >,则3k k a a +>”. 因为*k a ∈N ,所以31k k a a +-≥.所以数列{}n a 中必存在某一项3m a ≤(否则会与上述结论矛盾!)若3m a =,则121,2m m a a ++==;若2m a =,则123,1m m a a ++==,若1m a =,则122,3m m a a ++==, 由递推关系易得{1,2,3}A ⊆. ---------------------------------------8分 (III )集合A 中元素个数()Card A 的最大值为21.由已知递推关系可推得数列{}n a 满足:当{1,2,3}m a ∈时,总有3n n a a +=成立,其中,1,2,n m m m =++ .下面考虑当12014a a =≤时,数列{}n a 中大于3的各项:按逆序排列各项,构成的数列记为{}n b ,由(I )可得16b =或9,由(II )的证明过程可知数列{}n b 的项满足:3n n b b +>,且当n b 是3的倍数时,若使3n n b b +-最小,需使2112n n n b b b ++=-=-, 所以,满足3n n b b +-最小的数列{}n b 中,34b =或7,且33332k k b b +=-, 所以33(1)13(1)k k b b +-=-,所以数列3{1}k b -是首项为41-或71-的公比为3的等比数列, 所以131(41)3k k b --=-⨯或131(71)3k k b --=-⨯,即331k k b =+或3231k k b =⨯+, 因为67320143<<,所以,当2014a ≤时,k 的最大值是6,所以118a b =,所以集合A 重元素个数()Card A 的最大值为21.---------------13分。
2014年北京市高考理科数学试卷及答案解析(word版)
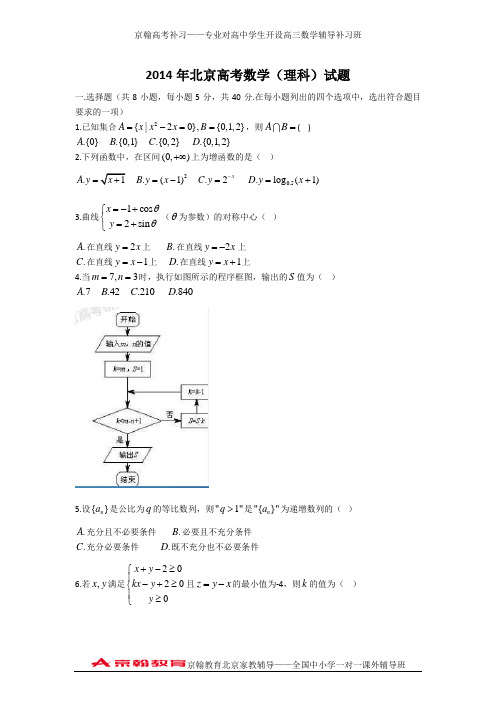
2014年北京高考数学(理科)试题一.选择题(共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项)1.已知集合2{|20},{0,1,2}A x x x B =-==,则AB =( ).{0}A .{0,1}B .{0,2}C .{0,1,2}D2.下列函数中,在区间(0,)+∞上为增函数的是( ).1A y x =+ 2.(1)B y x =- .2x C y -= 0.5.log (1)D y x =+3.曲线1cos 2sin x y θθ=-+⎧⎨=+⎩(θ为参数)的对称中心( ).A 在直线2y x =上 .B 在直线2y x =-上.C 在直线1y x =-上 .D 在直线1y x =+上4.当7,3m n ==时,执行如图所示的程序框图,输出的S 值为( ).7A .42B .210C .840D5.设{}n a 是公比为q 的等比数列,则"1"q >是"{}"n a 为递增数列的( ).A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件6.若,x y 满足20200x y kx y y +-≥⎧⎪-+≥⎨⎪≥⎩且z y x =-的最小值为-4,则k 的值为( ).2A .2B - 1.2C 1.2D -7.在空间直角坐标系Oxyz 中,已知()2,0,0A ,()2,2,0B ,()0,2,0C ,(2D ,若1S ,2S ,3S 分别表示三棱锥D ABC -在xOy ,yOz ,zOx 坐标平面上的正投影图形的 面积,则( )(A )123S S S == (B )12S S =且 31S S ≠ (C )13S S =且 32S S ≠ (D )23S S =且 13S S ≠8.有语文、数学两学科,成绩评定为“优秀”“合格”“不合格”三种.若A 同学每科成绩不 低于B 同学,且至少有一科成绩比B 高,则称“A 同学比B 同学成绩好.”现有若干同学,他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样 的.问满足条件的最多有多少学生( )(A )2 (B )3 (C )4 (D )5 二、填空题(共6小题,每小题5分,共30分)9.复数211i i +⎛⎫= ⎪-⎝⎭________.10.已知向量a 、b 满足1a =,()2,1b =,且()0a b R λλ+=∈,则λ=________.11.设双曲线C 经过点()2,2,且与2214y x -=具有相同渐近线,则C 的方程为________; 渐近线方程为________.12.若等差数列{}n a 满足7890a a a ++>,7100a a +<,则当n =________时{}n a 的前n 项和最大.13. 把5件不同产品摆成一排,若产品A 与产品C 不相邻,则不同的摆法有_______种. 14. 设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且 ⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛6322πππf f f ,则)(x f 的最小正周期为________.三.解答题(共6题,满分80分)15. (本小题13分)如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin(2)求AC BD ,的长16. (本小题13分).李明在10场篮球比赛中的投篮情况如下(假设各场比赛互相独立):(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过6.0的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过6.0,一 场不超过6.0的概率.(3)记x 是表中10个命中次数的平均数,从上述比赛中随机选择一场,记X 为李明 在这比赛中的命中次数,比较)(X E 与x 的大小(只需写出结论)17.(本小题14分)如图,正方形AMDE 的边长为2,C B ,分别为MD AM ,的中点,在五棱锥ABCDE P -中,F 为棱PE 的中点,平面ABF 与棱PC PD ,分别交于点H G ,. (1)求证:FG AB //;(2)若⊥PA 底面ABCDE ,且PE AF ⊥,求直线BC 与平面ABF 所成角的大小,并 求线段PH 的长.18.(本小题13分)已知函数()cos sin ,[0,]2f x x x x x π=-∈,(1)求证:()0f x ≤; (2)若sin xa b x<<在(0,)2π上恒成立,求a 的最大值与b 的最小值.19.(本小题14分) 已知椭圆22:24C xy +=,(1)求椭圆C 的离心率. (2)设O 为原点,若点A 在椭圆C 上,点B 在直线2y =上,且OA OB ⊥,求直线AB 与圆222x y +=的位置关系,并证明你的结论.20.(本小题13分)对于数对序列1122(,),(,),,(,)n n P a b a b a b ,记111()T P a b =+,112()max{(),}(2)k k k k T P b T P a a a k n -=++++≤≤,其中112max{(),}k k T P a a a -+++表示1()k T P -和12k a a a +++两个数中最大的数,(1)对于数对序列(2,5),(4,1)P P ,求12(),()T P T P 的值.(2)记m 为,,,a b c d 四个数中最小值,对于由两个数对(,),(,)a b c d 组成的数对序列(,),(,)P a b c d 和'(,),(,)P a b c d ,试分别对m a =和m d =的两种情况比较2()T P 和2(')T P 的大小.(3)在由5个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中,写出一个数对序列P 使5()T P 最小,并写出5()T P 的值.(只需写出结论).2014北京高考(理科)数学题解析1.集合{}{}2|2002A x x x =-==,.故{}02AB =,,选C .2. A .1y x =+[)1-+∞,上为增函数,符合题意. B .2(1)y x =-在(01),上为减函数,不合题意. C .2x y -=为()-∞+∞,上的减函数,不合题意. D .0.5log (1)y x =+为(1)-+∞,上的减函数,不合题意. 故选A .3. 参数方程1cos 2sin x y θθ=-+⎧⎨=+⎩所表示的曲线为圆心在(12)-,,半径为1的圆.其对称中心为圆心(12)-,.逐个代入选项可知,(12)-,在直线2y x =-上,即选项B .4. 当m 输入的7m =,3n =时,判断框内的判断条件为5k <.故能进入循环的k 依次为7,6,5.顺次执行S S k =⋅,则有765210S =⋅⋅=,故选C . 5.D对于等比数列{}n a ,若1q >,则当10a <时有{}n a 为递减数列. 故“1q >”不能推出“{}n a 为递增数列”.若{}n a 为递增数列,则{}n a 有可能满足10a <且01q <<,推不出1q >. 综上,“1q >”为“{}n a 为递增数列”的既不充分也不必要条件,即选D . 6.D若0k ≥,z y x =-没有最小值,不合题意. 若0k <,则不等式组所表示的平面区域如图所示.由图可知,z y x =-在点20k ⎛⎫- ⎪⎝⎭,处取最小值.故204k ⎛⎫--=- ⎪⎝⎭,解得12k =-,即选项D 正确.7.D (23S S =且13S S ≠)D ABC -在xOy 平面上的投影为ABC △,故12S =,设D 在yOz 和zOx 平面上的投影分别为2D 和3D ,则D ABC -在yOz 和zOx 平面上的投影分别为2OCD △和3OAD △.∵(2012D ,,,(3102D ,,.D 1O D 3D 2DCB A zyx +y -2=0-2kkx -y +2=022O y x故232S S == 综上,选项D 正确. 8.B用ABC 分别表示优秀、及格和不及格。
数学理卷·2014届北京市海淀区高三上学期期末考试(2014.01)扫描版

---------------------------------------------4 分
(Ⅱ)由题意可得点 A(−2,0), M (1, 3) , 2
------------------------------------------6 分
所以由题意可设直线 l : y = 1 x + n , n ≠ 1 .------------------------------------------7 分 2Leabharlann +1>0
,解得
a > −e2 ,-------------------9 分
所以此时 −e2 < a < 0 ;
-----------------------------------------------10 分
②当 a > 0 时, F(x), F '(x) 的情况如下表:
第 8 页 共 11 页
=
1 2
x1
+
n
−
3 2
+
1 2
x2
+n− 3 2
=1+
n −1
+
n −1
x1 − 1
x2 −1
x1 − 1 x2 − 1
= 1 + (n − 1)(x1 + x2 − 2) x1x2 − ( x1 + x2 ) + 1
=1−
(n − 1)(n + 2) n2 + n − 2
=
0,
---------------------------------13 分
所以 sin A = 1 − cos2 A = 4 ,------------------------------------7 分 5
2014北京市海淀区高三(一模)数 学(理)

2014北京市海淀区高三(一模)数学(理)一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.(5分)已知集合A={1,2,},集合B={y|y=x2,x∈A},则A∩B=()A.{} B.{2} C.{1} D.∅2.(5分)复数z=(1+i)(1﹣i)在复平面内对应的点的坐标为()A.(1,0)B.(0,2)C.(0,1)D.(2,0)3.(5分)下列函数f(x)图象中,满足f()>f(3)>f(2)的只可能是()A.B.C.D.4.(5分)已知直线l的参数方程为(t为参数),则直线l的普通方程为()A.x﹣y﹣2=0 B.x﹣y+2=0 C.x+y=0 D.x+y﹣2=05.(5分)在数列{a n}中,“a n=2a n﹣1,n=2,3,4,…”是“{a n}是公比为2的等比数列”的()A.充分不必要条件B.必要不充分条件C.充要条件 D.既不充分也不必要条件6.(5分)小明有4枚完全相同的硬币,每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有()A.4种B.5种C.6种D.9种7.(5分)某购物网站在2013年11月开展“全场6折”促销活动,在11日当天购物还可以再享受“每张订单金额(6折后)满300元时可减免100元”.某人在11日当天欲购入原价48元(单价)的商品共42件,为使花钱总数最少,他最少需要下的订单张数为()A.1 B.2 C.3 D.48.(5分)已知A(1,0),点B在曲线G:y=ln(x+1)上,若线段AB与曲线M:y=相交且交点恰为线段AB的中点,则称B为曲线G关于曲线M的一个关联点.记曲线G关于曲线M的关联点的个数为a,则()A.a=0 B.a=1 C.a=2 D.a>2二、填空题:本大题共6小题,每小题5分,共30分.9.(5分)一个空间几何体的三视图如图所示,该几何体的体积为.10.(5分)函数y=x﹣x2的图象与x轴所围成的封闭图形的面积等于.11.(5分)如图,AB切圆O于B,AB=,AC=1,则AO的长为.12.(5分)已知圆x2+y2+mx﹣=0与抛物线y2=4x的准线相切,则m= .13.(5分)如图,已知△ABC中,∠BAD=30°,∠CAD=45°,AB=3,AC=2,则= .14.(5分)已知向量序列:,,,…,,…满足如下条件:||=4||=2,2•=﹣1且﹣=(n=2,3,4,…).若•=0,则k= ;||,||,||,…,||,…中第项最小.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知函数f(x)=2sin xcos x,过两点A(t,f(t)),B(t+1,f(t+1))的直线的斜率记为g (t).(Ⅰ)求g(0)的值;(Ⅱ)写出函数g(t)的解析式,求g(t)在[﹣,]上的取值范围.16.(13分)为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如图:每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(Ⅰ)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;(Ⅱ)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;(Ⅲ)根据表中数据估算两公司的每位员工在该月所得的劳务费.17.(14分)如图1,在Rt△ABC中,∠ACB=30°,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F,将△ABD沿BD折起,使平面ABD⊥平面BCD,如图2所示.(Ⅰ)求证:AE⊥平面BCD;(Ⅱ)求二面角A﹣DC﹣B的余弦值.(Ⅲ)在线段AF上是否存在点M使得EM∥平面ADC?若存在,请指明点M的位置;若不存在,请说明理由.18.(13分)已知曲线C:y=e ax.(Ⅰ)若曲线C在点(0,1)处的切线为y=2x+m,求实数a和m的值;(Ⅱ)对任意实数a,曲线C总在直线l:y=ax+b的上方,求实数b的取值范围.19.(14分)已知A,B是椭圆C:2x2+3y2=9上两点,点M的坐标为(1,0).(Ⅰ)当A,B两点关于x轴对称,且△MAB为等边三角形时,求AB的长;(Ⅱ)当A,B两点不关于x轴对称时,证明:△MAB不可能为等边三角形.20.(13分)在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)A (n):A1,A2,A3,…,A n与B(n):B1,B2,B3,…,B n,其中n≥3,若同时满足:①两点列的起点和终点分别相同;②线段A i A i+1⊥B i B i+1,其中i=1,2,3,…,n﹣1,则称A(n)与B(n)互为正交点列.(Ⅰ)求A(3):A1(0,2),A2(3,0),A3(5,2)的正交点列B(3);(Ⅱ)判断A(4):A1(0,0),A2(3,1),A3(6,0),A4(9,1)是否存在正交点列B(4)?并说明理由;(Ⅲ)∀n≥5,n∈N,是否都存在无正交点列的有序整点列A(n)?并证明你的结论.数学试题答案一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.【解答】当x=1时,y=1;当x=2时,y=4;当x=时,y=,∴B={1,4,},∴A∩B={1}.故选:C.2.【解答】∵z=(1+i)(1﹣i)=1﹣i2=2,∴复数z=(1+i)(1﹣i)在复平面内对应的点的坐标为(2,0).故选:D.3.【解答】由所给的不等式可得,函数是先减后增型的,故排除A,B,由于C的图象关于x=1对称,左减右增,有f()=f()<f(3),故排除CD图象在(0,1)上递减且递减较快,在(1,+∞)递增,递增较慢,可能满足f()>f(3)>f(2),故选D.4.【解答】将直线l的参数方程为(t为参数),利用代入法,化成普通方程为x﹣y﹣2=0.故选:A.5.【解答】若“{a n}是公比为2的等比数列,则当n≥2时,a n=2a n﹣1,成立.当a n=0,n=1,2,3,4,…时满足a n=2a n﹣1,n=2,3,4,但此时{a n}不是等比数列,∴“a n=2a n﹣1,n=2,3,4,…”是“{a n}是公比为2的等比数列”的必要不充分条件.故选:B.【解答】记反面为1,正面为2;则正反依次相对有12121212,21212121两种;有两枚反面相对有21121212,21211212,6.21212112;共5种摆法,故选B7.【解答】∵原价是:48×42=2016(元),2016×0.6=1209.6(元),∵每张订单金额(6折后)满300元时可减免100,∴若分成10,10,11,11,由于48×10=480,480×0.6=288,达不到满300元时可减免100,∴应分成9,11,11,11.∴只能减免3次,故答案选:C.8.【解答】设点B(x,ln(x+1)),则点A,B的中点的坐标是(,),由于此点在曲线M:y=上,故有=,即ln(x+1)=,此方程的根即两函数y=ln(x+1)与y=的交点的横坐标,由于此二函数一为增函数,一为减函数,故两函数y=ln(x+1)与y=的交点个数为1,故符合条件的关联点仅有一个,所以a=1故选:B.二、填空题:本大题共6小题,每小题5分,共30分.9.【解答】由三视图知:几何体为三棱柱,且三棱柱的高为8,底面三角形的一条边长为6,该边上的高为4,∴几何体的体积V=×6×4×8=96.故答案为:96.10.【解答】由方程组,解得,x1=0,x2=1.故所求图形的面积为S=( x﹣x2)dx=(x2﹣x3)=.故答案为:.11.【解答】设圆的半径为r,则∵AB切圆O于B,∴AB2=AC•(AC+2r),∵AB=,AC=1,∴3=1+2r,∴r=1,∴AO=AC+1=2.故答案为:2.12.【解答】抛物线y2=4x的准线为x=﹣1,圆x2+y2+mx﹣=0的圆心O(﹣,0),半径r=,∵圆x2+y2+mx﹣=0与抛物线y2=4x的准线相切,∴圆心O(﹣,0)到准线为x=﹣1的距离d=r,∴d=|﹣1|=,解得m=,故答案为:.13.【解答】过C作CE∥AB,与AD的延长线相交于E,则∠AEC=30°.在△AEC中,∵∠CAD=45°,∴,∴CE=2,∵CE∥AB,AB=3,∴===.故答案为:.14.【解答】∵﹣=,∴=+(k﹣1),又∵||=4||=2,2•=﹣1∴||=2,||=,•=∴•=•[+(k﹣1)]=+(k﹣1)•=22+(k﹣1)()=0,解得k=9∴=[+(k﹣1)]2=+(k﹣1)2+2(k﹣1)•=22+(k﹣1)2﹣(k﹣1)=(k﹣3)2+3,故当k=3时,上式取最小值,即||最小,故答案为:9;3三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.【解答】(Ⅰ)∵f(x)=2sin xcos x,∴﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)∴=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(Ⅱ)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(7分)=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)∵,∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)∴,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(12分)∴g(t)在上的取值范围是﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)16.【解答】(Ⅰ)甲公司员工A投递快递件数的平均数为:=(32+33+33+38+35+36+39+33+41+40)=36,众数为33.(2分)(Ⅱ)设a为乙公司员工B投递件数,则当a=34时,X=136元,当a>35时,X=35×4+(a﹣35)×7元,∴X的可能取值为136,147,154,189,203,(4分)P(X=136)=,P(X=147)=,P(X=154)=,P(X=189)=,P(X=203)=,X的分布列为:X 136 147 154 189 203P(9分)=.(11分)(Ⅲ)根据图中数据,由(Ⅱ)可估算:甲公司被抽取员工该月收入=36×4.5×30=4860元,乙公司被抽取员工该月收入=165.5×30=4965元.(13分)17.【解答】(Ⅰ)证明:∵平面ABD⊥平面BCD,交线为BD,又在△ABD中,AE⊥BD于E,AE⊂平面ABD∴AE⊥平面BCD.(3分)(Ⅱ)解:由(Ⅰ)结论AE⊥平面BCD,∴AE⊥EF.由题意知EF⊥BD,又AE⊥BD.如图,以E为坐标原点,分别以EF,ED,EA所在直线为x轴,y轴,z轴,建立空间直角坐标系E﹣xyz,(4分)不妨设AB=BD=DC=AD=2,则BE=ED=1.由图1条件计算得,,,EF=,则,.∵AE⊥平面BCD,∴平面DCB的法向量为=(0,0,).(6分)设平面ADC的法向量为=(x,y,z),则,即令z=1,得=(﹣1,,1).(8分)∴cos<>==,∴二面角A﹣DC﹣B的余弦值为.(9分)(Ⅲ)解:设,其中λ∈[0,1].∵,∴,其中λ∈[0,1],(10分)∴,(11分)由,即,(12分)解得,(13分)∴在线段AF上存在点M,使,且.(14分)18.【解答】(Ⅰ)y'=ae ax,因为曲线C在点(0,1)处的切线为L:y=2x+m,所以1=2×0+m且y'|x=0=2.解得m=1,a=2(Ⅱ)法1:对于任意实数a,曲线C总在直线的y=ax+b的上方,等价于∀x,a∈R,都有e ax>ax+b,即∀x,a∈R,e ax﹣ax﹣b>0恒成立,令g(x)=e ax﹣ax﹣b,①若a=0,则g(x)=1﹣b,所以实数b的取值范围是b<1;②若a ≠0,g'(x )=a (e ax﹣1),由g'(x )=0得x=0,g'(x ),g (x )的情况如下: x (﹣∞,0)0 (0,+∞) g'(x )﹣ 0 + g (x ) ↘ 极小值 ↗ 所以g (x )的最小值为g (0)=1﹣b ,所以实数b 的取值范围是b <1;综上,实数b 的取值范围是b <1.法2:对于任意实数a ,曲线C 总在直线的y=ax+b 的上方,等价于∀x ,a ∈R ,都有e ax >ax+b ,即∀x ,a ∈R ,b <e ax ﹣ax 恒成立,令t=ax ,则等价于∀t ∈R ,b <e t ﹣t 恒成立,令g (t )=e t ﹣t ,则 g'(t )=e t ﹣1,由g'(t )=0得t=0,g'(t ),g (t )的情况如下: t (﹣∞,0)0 (0,+∞) g'(t )﹣ 0 + g (t ) ↘极小值 ↗所以 g (t )=e t ﹣t 的最小值为g (0)=1,实数b 的取值范围是b <1.19.【解答】(Ⅰ)解:设A (x 0,y 0),B (x 0,﹣y 0),﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(1分)因为△ABM 为等边三角形,所以.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(2分)又点A (x 0,y 0)在椭圆上, 所以 消去y 0,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(3分)得到 ,解得x 0=2或,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)当x0=2时,;当时,.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(Ⅱ)证明:设A(x1,y1),则,且x1∈[﹣,],所以,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)设B(x2,y2),同理可得,且x2∈[﹣,]﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)因为在[﹣,]上单调所以,有x1=x2⇔|MA|=|MB|,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(11分)因为A,B不关于x轴对称,所以x1≠x2.所以|MA|≠|MB|,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)所以△ABM不可能为等边三角形.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)20.【解答】(Ⅰ)设点列A1(0,2),A2(3,0),A3(5,2)的正交点列是B1,B2,B3,由正交点列的定义可知B1(0,2),B3(5,2),设B2(x,y),,,由正交点列的定义可知,,即,解得所以点列A1(0,2),A2(3,0),A3(5,2)的正交点列是B1(0,2),B2(2,5),B3(5,2).(3分)(Ⅱ)由题可得,设点列B1,B2,B3,B4是点列A1,A2,A3,A4的正交点列,则可设,λ1,λ2,λ3∈Z因为A1与B1,A4与B4相同,所以有因为λ1,λ2,λ3∈Z,方程(2)显然不成立,所以有序整点列A1(0,0),A2(3,1),A3(6,0),A4(9,1)不存在正交点列;﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)(Ⅲ)∀n≥5,n∈N,都存在整点列A(n)无正交点列.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(9分)∀n≥5,n∈N,设,其中a i,b i是一对互质整数,i=1,2,3…,n﹣1若有序整点列B1,B2,B3,…B n是点列A1,A2,A3,…A n正交点列,则,则有①当n为偶数时,取A1(0,0),.由于B1,B2,B3,…B n是整点列,所以有λi∈Z,i=1,2,3,…,n﹣1.等式(2)中左边是3的倍数,右边等于1,等式不成立,所以该点列A1,A2,A3,…A n无正交点列;②当n为奇数时,取A1(0,0),a1=3,b1=2,,由于B1,B2,B3,…B n是整点列,所以有λi∈Z,i=1,2,3,…,n﹣1.等式(2)中左边是3的倍数,右边等于1,等式不成立,所以该点列A1,A2,A3,…A n无正交点列.综上所述,∀n≥5,n∈N,都不存在无正交点列的有序整数点列A(n)﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)。
2014年北京市高考理科数学试卷及答案解析(word版).wps

6. D
若 k ≥ 0 , z y x 没有最小值,不合题意.
若 k 0 ,则不等式组所表示的平面区域如图所示.
由图可知,
z
y
x
在点
2 k
,0
处取最小值.
故
0
2 k
4
,解得
k
1 2
,即选项
D
正确.
7. D( S2 S3 且 S1 ≠ S3 )
y
2
kx-y+2=0
x+y-2=0
O
2
2x -
CD 2, cos ADC 1 7
(1)求 sin BAD (2)求 BD, AC 的长
16. (本小题 13 分). 李明在 10 场篮球比赛中的投篮情况如下(假设各场比赛互相独立):
(1)从上述比赛中随机选择一场,求李明在该场比赛中投篮命中率超过 0.6 的概率. (2)从上述比赛中选择一个主场和一个客场,求李明的投篮命中率一场超过 0.6 ,一
学,
他们之间没有一个人比另一个成绩好,且没有任意两个人语文成绩一样,数学成绩也一样
的.问满足条件的最多有多少学生( )
(A) 2
(B) 3
(C) 4
(D) 5
二、填空题(共 6 小题,每小题 5 分,共 30 分)
9.复数
1 1
i i
2
________.
10.已知向量 a 、 b 满足 a 1, b 2,1 ,且 a b 0 R,则 ________.
求线段 PH 的长.
18.(本小题 13 分)
已知函数 f (x) x cos x sin x, x [0, ], 2
(1)求证: f (x) 0 ;
海淀区2014一模数学答案

此为过程稿,请以纸质版为准! 海淀区九年级第二学期期中测评数学试卷答案及评分参考2014.5一、选择题(本题共32分,每小题4分)二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分)13. 解:0(3π)-++︒60tan 211()3-=13+-…………………………………………………………………4分 =4 ……………………………………………………………………………5分14. 解:49132. 2x x x x >-⎧⎪⎨+>⎪⎩, ①②由①,得3x >-, ……………………………………………………………………2分由②,得1x <, ……………………………………………………………………4分 ∴原不等式组的解集为31x -<<. …………………………………………………5分15. 解: 2(3)(3)(23)x x x +++-22=69239x x x x ++++- 2=39.x x + ……………………………………………………………………………3分2340,x x +-= 23 4.x x ∴+=∴原式()233x x =+=34=12.⨯ ………………………………………………………5分16. 证明:∵∠EAB =90º,EDCBA∴∠EAD+∠CAB =90º. ∵∠ACB =90º, ∴∠B+∠CAB =90º.∴∠B =∠EAD . ……………………………………………………………………1分 ∵ED ⊥AC , ∴∠EDA =90º.∴∠EDA =∠ACB . ………………………………………………………………2分 在△ACB 和△EDA 中, ,,,B EAD BC AD ACB EDA ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ACB ≌△EDA . ……………………………………………………………4分 ∴AB=AE . …………………………………………………………………………5分17. 解:设原计划每年建造保障性住房x 万套. ………………………………………1分根据题意可得:80802(125%)x x-=+ . ……………………………………………2分 解方程,得 8x =. …………………………………………………………………3分 经检验:8x =是原方程的解,且符合题意. ………………………………………4分答:原计划每年建造保障性住房8万套. ……………………………………………5分18.解:(1)∵B (1)m ,在2(0)y x x=>的图象上, ∴2m =.∴B (2, 1). …………………………………………………………………………1分 ∵B (2, 1)在直线y ax a =-(a 为常数)上, ∴12,a a =-∴ 1.a = ……………………………………………………………………………2分 ∴一次函数的解析式为 1.y x =- …………………………………………………3分 (2)P 点的坐标为(0,1)或(0,3). ……………………………………………5分四、解答题(本题共20分,每小题5分)19. 解:(1)∵在△ABC 中,∠ACB =90º,∠ABC =30º,BD =3∴1cos ,2BC ABC AC AB AB ∠==,90903060BAC ABC ∠=-∠=-=.∴14,42cos 2BC AB AC ABC ====⨯=∠. …………………………1分∵△ACD 为等边三角形,∴2AD CD AC ===,60DAC ∠=. 过点D 作DE AC ⊥于E , 则sin 2sin603DE AD DAC =∠=⨯=∴ABC ACD ABCD S S S =+△△四边形1122AC BC AC DE=⋅+⋅112222=⨯⨯⨯= ………………………………………3分 (2)过点D 作DF AB ⊥于F .∵180180606060DAF BAC DAC ∠=-∠-∠=--=, ∴sin 2sin603DF AD DAF =⋅∠==cos 2cos601AF AD DAF =⋅∠==. ………………………………………4分∴415BF AB AF =+=+=. ∵DF AB ⊥,∴在Rt BDF △中,22222528BD DF BF =+=+=.∴BD = …………………………………………………………………5分20. 解:(1)20.0%; ……………………………………………………………………1分(2)8365; ……………………………………………………………………………2分………………………………………………3分(3)9%,2016. …………………………………………………………………………5分53106229 69007703 总额/亿元 年份北京市2009至2013年社会消费品零售总额统计图836521. 解:(1)连接,OD AD .∵AB 是⊙O 的直径, ∴90ADB ∠=. 又∵AB AC =,∴D 为BC 的中点. 又∵O 为AB 的中点, ∴OD //AC .∵DF ⊥AC , ∴DF ⊥OD .又∵OD 为⊙O 的半径,∴DF 为⊙O 的切线.………………………………………………………………2分 (2)∵DF ⊥AC ,9CF =,∴cos CFC CD =. ∴3915cos 5CF CD C ==÷=.…………………3分 ∵90ADB ∠=, ∴90ADC ∠=. ∴cos CDC AC =. ∴31525cos 5CD AC C ==÷=. . ……………………………………………………4分 连接BE .∵AB 是⊙O 的直径,∴90AEB ∠=. 又∵DF ⊥AC , ∴DF //BE .∴1CF CDEF BD ==. ∴9EF CF ==.∴25997AE AC EF CF =--=--=. ……………………………………5分22. 解:①6;………………………………………………………………………………1分 ②不变. ……………………………………………………………………………2分(1) ……………………………………………………………………3分 (2)4+4sin α. ………………………………………………………………5分5五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23. 解:(1)令2()=0mx m n x n -++,则22=()4=()m n mn m n ∆+--. ………………………………………………………1分∵二次函数图象与y 轴正半轴交于A 点,∴(0,)A n ,且0n >. 又0m <,∴0m n -<. ∴2=()0m n ∆->.∴该二次函数的图象与x 轴必有两个交点.………………………………………2分(2)令2()=0mx m n x n -++,解得:121,nx x m==.由(1)得0nm<,故B 的坐标为(1,0). ………………………………………3分 又因为45ABO ∠=,所以(0,1)A ,即=1n .则可求得直线AB 的解析式为1y x =-+.再向下平移2个单位可得到直线:1l y x =--. …………………………………4分 (3)由(2)得二次函数的解析式为2(1)1y mx m x =-++∵M (,)p q 为二次函数图象上的一个动点, ∴2(1)1q mp m p =-++.∴点M 关于x 轴的对称点M '的坐标为(,)p q -. ∴点M '在二次函数2(1)1y mx m x =-++-上.∵当30p -<<时,点M 关于x 轴的对称点都在直线l 的下方,当0p =时,1q =;当3p =-时,124q m =+; ……………………………5分 结合图象可知:(124)2m -+≤,解得:12m ≥-,………………………………………………………………………6分∴m 的取值范围为102m -≤<.……………………………………………………7分24.解:(1)30°;……………………………… ………………………………………1分 (2)如图作等边△AFC ,连结DF 、BF .∴AF=FC=AC , ∠F AC=∠AFC=60°. ∵∠BAC =100°,AB=AC ,∴∠ABC =∠BCA =40°. ∵∠ACD =20°,∴∠DCB=20°. ∴∠DCB=∠FCB=20°. ① ∵AC=CD ,AC=FC , ∴DC=FC . ②2∵BC=BC ,③∴由①②③,得 △DCB ≌△FCB ,∴DB=BF , ∠DBC=∠FBC. ∵∠BAC =100°, ∠F AC=60°,∴∠BAF =40°. ∵∠ACD =20°,AC=CD ,∴∠CAD=80°. ∴∠DAF=20°. ∴∠BAD=∠F AD=20°. ④ ∵AB=AC , AC=AF , ∴AB= AF . ⑤ ∵AD= AD ,⑥∴由④⑤⑥,得 △DAB ≌△DAF . ∴FD= BD . ∴FD= BD=FB .∴∠DBF=60°. ∴∠CBD=30°. ………………………………………………………………………4分 (3)120m α=︒-, α=60° 或 240m α=︒- . ……………………………7分 25. 解:(1)①(-2,-4); ……………………………………………………………1分②答案不唯一,只需横、纵坐标之和为3即可,如(1,2) .……………3分(2)±1; ……………………………………………………………………………5分 (3)设B (a ,b ).∵B 的“属派生点”是A ,∴A (a -b +). ………………6分∵点A 还在反比例函数y =的图象上,∴a b +()∴212b ()=.∵0b >∴b =∴b +∴B 在直线y =+上.…………………7分过Q 作y =+的垂线Q B 1,垂足为B 1,∵(Q ,且线段BQ 最短, ∴1B 即为所求的B 点,∴易求得3(2B .…………………………………………………………8分注:其他解法请参照给分.7。
_2014北京市海淀区高考理综一模试题(附答案)_

北京市海淀区2014届高三下学期期中练习理科综合生物部分2014.41. 下列生命活动过程中,不消耗ATP的是A. 叶绿体基质中将C3还原为糖B. 突触前膜向胞外释放神经递质C. 线粒体内膜上[H]与氧结合生成水D. 植物根细胞逆浓度吸收矿质离子2. 在细胞的生命历程中,不可能发生的是A. 细胞通过表面的蛋白质接收来自其他细胞的信号B. 基因的选择性表达使分化的细胞遗传物质发生改变C. 以亲代DNA为模板合成相同的两个子代DNAD. 细胞的生理功能减退和紊乱引起细胞衰老3. 研究者探究不同光照条件下,两种不同浓度CO2对某种蓝藻生长的影响,结果如下图所示。
下列关于实验的叙述,不正确的是A. “●”和“▲”分别表示高浓度和低浓度CO2下的测量结果B. 若相同条件下测量O2的释放量,可得到相似的实验结果C. 低光强时,不同的CO2浓度对干重增加的影响不显著D. 高浓度CO2时,不同的光强对干重增加的影响不显著4. 沟酸浆属植物中有两个亲缘关系很近的物种,一种开粉红花,被红色的蜂鸟传粉,另一种开黄花,被大黄蜂传粉。
将两物种控制花色的一对基因互换,两物种的传粉者也会随之互换。
由此无法推断出的是A. 花色是其传粉者长期自然选择的结果B. 传粉者在传粉时被捕食的概率较低C. 传粉者不同是两种植物间隔离的形式之一D. 两物种的性状差异一定不是少数基因决定的5. 下列生物学实验操作,能够顺利达到实验目的的是A. 在固体培养基上涂布稀释的大肠杆菌培养液获得单菌落B. 在接种酵母菌的新鲜葡萄汁中通入无菌空气制作果酒C. 土壤浸出液接种于牛肉膏蛋白胨培养基上筛选分解尿素的细菌D. 将切下的胡萝卜外植体直接接种在培养基上获得愈伤组织29. (16分)为研究某种蛇毒阻遏神经递质的机理,研究者进行了如下实验。
(1)该蛇毒的主要成分是蛋白质,其基本组成单位是________________。
(2)大鼠的呼吸中枢发出两条传出神经M和N支配膈肌收缩。
2014年高考理科数学北京卷(含详细答案)

.
设平面ABF的法向量为 ,则 ,即 .
令 ,则 .所以 ,设直线BC与平面ABF所成角为 ,
则 .
设点H的坐标为
因为点H在棱PC上,所以可设 ,即 ,
所以 .
因为 是平面ABF的法向量,所以 ,即 .
解得 ,所以点H的坐标为ቤተ መጻሕፍቲ ባይዱ
所以 .
【提示】由线面平行推出线线平行,利用线面垂直、线线垂直这个条件,作出有关辅助线,建立空间直角坐标系求解.
圆心 到直线AB的距离 .此时直线AB与圆 相切.
当 时,直线AB的方程为 ,即 ,
圆心 到直线AB的距离 .
又 , ,故 ,
此时直线AB与圆 相切.
【提示】根据给出的椭圆方程找出离心率,然后利用椭圆方程与直线的关系及两线垂直,求出直线与圆的位置关系.
【考点】圆与圆锥曲线的综合,椭圆的简单性质
20.【答案】(1)
A.2人
B.3人
C.4人
D.5人
第Ⅱ卷(非选择题共110分)
二、填空题:本大题共6小题,每小题5分.共30分,把答案填写在题中的横线上.
9.复数 .
10.已知向量a,b满足 a ,b ,且 a b 0 ,则 .
11.设双曲线 经过点 ,且与 具有相同渐近线,则 的方程为;渐近线方程为.
12.若等差数列 满足 , ,则当 时, 的前 项和最大.
【提示】由循环语句、条件语句执行程序,直至结束.
【考点】循环结构
5.【答案】D
【解析】当 时,数列 递减;当 ,数列 递增时, ,故选D.
【提示】根据等比数列的性质,结合充分条件和必要条件的定义进行判断即可得到结论.
【考点】充分、必要条件,等比数列的性质
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海淀区高三年级第二学期期中练习数 学 (理科) 2014.4本试卷共4页,150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合11,2,2A ⎧⎫=⎨⎬⎩⎭,集合{}2,B y y x x A ==∈,则A B = ( )A.12⎧⎫⎨⎬⎩⎭B.{}2C.{}1D.ϕ 2.复数()()1i 1i z =+-在复平面内对应的点的坐标为( ) A. (1,0) B. (0,2) C.()0,1 D. (2,0) 3.下列函数()f x 图象中,满足1()(3)(2)4f f f >>的只可能是( )A B C D 4.已知直线l 的参数方程为1,1x t y t=+⎧⎨=-+⎩(t 为参数),则直线l 的普通方程为( )A.20x y --=B.20x y -+=C.0x y +=D.20x y +-=5.在数列{}n a 中,“12,2,3,4,n n a a n -== ”是“{}n a 是公比为2的等比数列”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 6. 小明有4枚完全相同的硬币,每个硬币都分正反两面.他想把4个硬币摆成一摞,且满足相邻两枚硬币的正面与正面不相对,不同的摆法有( )A. 4种B.5种C.6种D.9种7.某购物网站在2013年11月开展“全场6折”促销活动,在11日当天购物还可以再享受“每张订单金额(6折后)满300元时可减免100元”.某人在11日当天欲购入原价48元(单价)的商品共42件,为使花钱总数最少,他最少需要下的订单张数为( ) A.1 B.2 C.3 D.4 8. 已知(1,0)A ,点B 在曲线:G ln(1)y x =+上,若线段AB 与曲线:M 1y x=相交且交点恰为线段AB 的中点,则称B 为曲线G 关于曲线M 的一个关联点.记曲线G 关于曲线M 的关联点的个数为a ,则二、填空题:本大题共6小题,每小题5分,共30分.9.一个空间几何体的三视图如图所示,该几何体的体积为______.10. 函数2y x x =-的图象与x 轴所围成的封闭图形的面积等于_______.11.如图,AB 切圆O 于B,AB =1AC =,则AO 的长为_______.12. 已知圆22104x y mx ++-=与抛物线24y x =的准线相切,则m =_______.13.如图,已知△ABC 中,30BAD ∠= ,45CAD ∠= ,3,2AB AC ==, 则BDDC=_____________.14.已知向量序列:123,,,,,n a a a a 满足如下条件:1||4||2==a d ,121⋅=-a d 且1n n --=a a d , (2,3,4,n = ).若10k ⋅=a a ,则k =________;123||,||,||,,||,n a a a a 中第_____项最小.三、解答题: 本大题共6小题,共80分.解答应写出文字说明, 演算步骤或证明过程.15.(本小题满分13分)已知函数ππ()2sin cos 66f x x x =,过两点(,()),(1,(1))A t f t B t f t ++的直线的斜率记为()g t . (Ⅰ)求(0)g 的值;(II )写出函数()g t 的解析式,求()g t 在33[,]22-上的取值范围.AB俯视图主视图侧视图为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如下:每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.(Ⅰ)根据表中数据写出甲公司员工A 在这10天投递的快递件数的平均数和众数;(Ⅱ)为了解乙公司员工B 的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X (单位:元),求X 的分布列和数学期望; (Ⅲ)根据表中数据估算两公司的每位员工在该月所得的劳务费.17. (本小题满分14分)如图1,在Rt △ABC 中,∠ACB =30°,∠ABC =90°,D 为AC 中点,AE BD ⊥于E ,延长AE 交BC 于F ,将△ABD 沿BD 折起,使平面ABD ⊥平面BCD ,如图2所示. (Ⅰ)求证:AE ⊥平面BCD ;(Ⅱ)求二面角A–DC –B 的余弦值.(Ⅲ)在线段AF 上是否存在点M 使得//EM 平面ADC ?若存在,请指明点M 的位置;若不存在,请说明理由.1图 图 2B F已知曲线:e ax C y =.(Ⅰ)若曲线C 在点(0,1)处的切线为2y x m =+,求实数a 和m 的值;(Ⅱ)对任意实数a ,曲线C 总在直线l :y ax b =+的上方,求实数b 的取值范围.19. (本小题满分14分)已知,A B 是椭圆22:239C x y +=上两点,点M 的坐标为(1,0).(Ⅰ)当,A B 两点关于x 轴对称,且△MAB 为等边三角形时,求AB 的长; (Ⅱ)当,A B 两点不关于x 轴对称时,证明:△MAB 不可能为等边三角形.20. (本小题满分13分)在平面直角坐标系中,对于任意相邻三点都不共线的有序整点列(整点即横纵坐标都是整数的点)()A n :123,,,,n A A A A 与()B n :123,,,,n B B B B ,其中3n ≥,若同时满足:①两点列的起点和终点分别相同;②线段11i i i i A A B B ++⊥,其中1,2,3,,1i n =- , 则称()A n 与()B n 互为正交点列.(Ⅰ)求(3)A :123(0,2),(3,0),(5,2)A A A 的正交点列(3)B ;(Ⅱ)判断(4)A :12340,0),3,1),6,0)(((,9,1)(A A A A 是否存在正交点列(4)B ?并说明理由; (Ⅲ)5n n ∀≥∈,N ,是否都存在无正交点列的有序整点列()A n ?并证明你的结论.海淀区高三年级第二学期期中练习参考答案数 学 (理科) 2014.4阅卷须知:1.评分参考中所注分数,表示考生正确做到此步应得的累加分数。
2.其它正确解法可以参照评分标准按相应步骤给分。
一、选择题:本大题共8小题,每小题5分,共40分.1. C2. D3. D4. A5. B6. B7. C8. B二、填空题:本大题共6小题,每小题5分,共30分.9. 96 10.16 11. 2 12. 3413. 14. 9;3 (本题第一空3分,第二空2分)三、解答题: 本大题共6小题,共80分.15.解:(Ⅰ)π()sin 3f x x = ---------------------------2分(1)(0)(0)1f f g -=------------------------------3分πsin sin 03=-=-------------------------------5分 (Ⅱ)(1)()π()sin()sin 1333f t f t g t t t t t ππ+-==+-+- ------------------------------6分πππsin cos cos sin sin 3333t t t ππ=+- ------------------------------7分1ππsin 233t t =- ------------------------------8分ππsin()33t =-- ------------------------------10分因为33[,]22t ∈-,所以ππ5ππ[,]3366t -∈-, ------------------------------11分所以 π1s i n ()[1,]332t π-∈-, -----------------------------12分 所以()g t 在33[,]22-上的取值范围是1[,1]2- -----------------------------13分16.解:(Ⅰ)甲公司员工A 投递快递件数的平均数为36,众数为33. --------------------------------2分(Ⅱ)设a 为乙公司员工B 投递件数,则当a =34时,X =136元,当a >35时,354(35)7X a =⨯+-⨯元,X 的可能取值为136,147,154,189,203 -------------------------------4分{说明:X 取值都对给4分,若计算有错,在4分基础上错1个扣1分,4分扣完为止} X分{说明:每个概率值给1分,不化简不扣分,随机变量值计算错误的此处不再重复扣分}13231()1361471541892031010101010E X =⨯+⨯+⨯+⨯+⨯1655==165.5()10元 --------------------------------------11分(Ⅲ)根据图中数据,可估算甲公司被抽取员工该月收入4860元,乙公司被抽取员工该月收入4965元.17.(Ⅰ)因为平面ABD ⊥平面BCD ,交线为BD ,又在ABD ∆中,AE BD ⊥于E ,AE ⊂平面ABD所以AE ⊥平面BCD . --------------------------------------3分(Ⅱ)由(Ⅰ)结论AE ⊥平面BCD 可得AE EF ⊥.由题意可知EF BD ⊥,又AE ⊥BD . 如图,以E 为坐标原点,分别以,,EF ED EA 所在直线为x 轴,y 轴,z 轴,建立空间直角坐标系E xyz - --------------------------4分 不妨设2AB BD DC AD ====,则1BE ED ==. 由图1条件计算得,AEBC =,BF =则(0,0,0),(0,1,0),(0,1,0),E D B A F C --------5分(0,1,DC AD == . 由AE ⊥平面BCD 可知平面DCB 的法向量为EA. -----------------------------------6分 设平面ADC 的法向量为(,,)x y z =n ,则0,0.DC AD ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.y y +==⎪⎩令1z =,则1y x ==,所以1)=-n .------------------------------------8分平面DCB 的法向量为EA所以cos ,||||EA EA EA ⋅<>==⋅n n n, 所以二面角A DC B --------------------------------9分(Ⅲ)设AM AF λ=,其中[0,1]λ∈.由于AF = ,所以AM AF λλ== ,其中[0,1]λ∈ --------------------------10分所以,0,(1EM EA AM λ=+=-⎝--------------------------11分 由0EM ⋅=n0λ=-(1- ---------------------------12分解得3=(0,1)4λ∈.-----------------------------13分所以在线段AF 上存在点M 使EM ADC ∥平面,且34AM AF =.-------------14分(Ⅰ)e ax y a '=, -----------------------------------2分因为曲线C 在点(0,1)处的切线为L :2y x m =+,所以120m =⨯+且0|2x y ='=. ----------------------------------4分 解得1m =,2a = -----------------------------------5分(Ⅱ)法1:对于任意实数a ,曲线C 总在直线的y ax b =+的上方,等价于∀x ,a R ∈,都有e ax ax b >+,即∀x ,a ∈R ,e 0ax ax b -->恒成立, --------------------------------------6分 令()e ax g x ax b =--, ----------------------------------------7分 ①若a=0,则()1g x b =-,所以实数b 的取值范围是1b <; ----------------------------------------8分 ②若0a ≠,()(e 1)ax g x a '=-,由'()0g x =得0x =, ----------------------------------------9分 '(),()g x g x 的情况如下:-----------------------------------------11分所以()g x 的最小值为(0)1g b =-, -------------------------------------------12分 所以实数b 的取值范围是1b <;综上,实数b 的取值范围是1b <. --------------------------------------13分法2:对于任意实数a ,曲线C 总在直线的y ax b =+的上方,等价于∀x ,a R ∈,都有e ax ax b >+,即∀x ,a ∈R ,e ax b ax <-恒成立, -------------------------------------------6分 令t ax =,则等价于∀t ∈R ,e t b t <-恒成立,令()e t g t t =-,则 ()e 1t g t '=-, -----------------------------------------7分 由'()0g t =得0t =, ----------------------------------------9分 '(),()g t g t 的情况如下:分 所以 ()e t g t t =-的最小值为(0)1g =, ------------------------------------------12分 实数b 的取值范围是1b <. --------------------------------------------13分(Ⅰ) 设00(,)A x y ,00(,)B x y -, ---------------------------------------1分因为ABM ∆为等边三角形,所以00|||1|y x =-. ---------------------------------2分 又点00(,)A x y 在椭圆上,所以002200|||1|,239,y x x y ⎧=-⎪⎨⎪+=⎩ 消去0y , -----------------------------------------3分 得到 2003280x x --=,解得02x =或043x =-,----------------------------------4分当02x =时,||AB =; 当043x =-时,||AB =. -----------------------------------------5分{说明:若少一种情况扣2分}(Ⅱ)法1:根据题意可知,直线AB 斜率存在.设直线AB :y kx m =+,11(,)A x y ,22(,)B x y ,AB 中点为00(,)N x y ,联立22239,x y y kx m⎧+=⎨=+⎩ 消去y 得222(23)6390k x kmx m +++-=, ------------------6分由0∆>得到 222960m k --< ① ----------------------------7分所以122623kmx x k +=-+,121224()223my y k x x m k+=++=+, ----------------------------8分 所以2232(,)2323km mN k k -++,又(1,0)M如果ABM ∆为等边三角形,则有MN AB ⊥, --------------------------9分所以1MNk k ⨯=-, 即222313123mkk km k +⨯=---+, ------------------------------10分 化简2320k km ++=,② ------------------------------11分由②得232k m k +=-,代入① 得2222(32)23(32)0k k k +-+<,化简得 2340k +<,不成立, -------------------------------------13分{此步化简成42291880k k k++<或4291880k k ++<或22(32)(34)0k k ++<都给分} 故ABM ∆不能为等边三角形. -------------------------------------14分法2:设11(,)A x y ,则2211239x y +=,且1[3,3]x ∈-,所以||MA ----------------8分 设22(,)B x y,同理可得||MB =2[3,3]x ∈- -----------------9分 因为21(3)13y x =-+在[3,3]-上单调所以,有12x x =⇔||||MA MB =, ---------------------------------11分 因为,A B 不关于x 轴对称,所以12x x ≠.所以||||MA MB ≠, ---------------------------------13分 所以ABM ∆不可能为等边三角形. ---------------------------------14分20.解:(Ⅰ)设点列123(0,2),(3,0),(5,2)A A A 的正交点列是123,,B B B ,由正交点列的定义可知13(0,2),(5,2)B B ,设2(,)B x y ,1223(3,2),(2,2)A A A A =-= ,1223(,2)(5,2)B B x y B B x y =-=-- ,,由正交点列的定义可知 12120A A B B ⋅= ,23230A A B B ⋅=,即32(2)0,,2(5)2(2)0x y x y --=⎧⎨-+-=⎩ 解得25x y =⎧⎨=⎩所以点列123(0,2),(3,0),(5,2)A A A 的正交点列是123(0,2),(2,5),(5,2)B B B .------3分 (Ⅱ)由题可得 122334(3,1),(3,1)(3,1)A A A A A A ==-=,, 设点列1234,,,B B B B 是点列1234,,,A A A A 的正交点列,则可设121232343(1,3),(1,3)(1,3)B B B B B B λλλ=-==-,,123λλλ∈,,Z 因为1144,A B A B 与与相同,所以有123123-+-=9,13+3+3=1.2λλλλλλ⎧⎨⎩()() 因为123λλλ∈,,Z ,方程(2)显然不成立,(Ⅲ)5n n ∀≥∈,N ,都存在整点列()A n 无正交点列. -------------------------9分5n n ∀≥∈,N ,设1(,),i i i i A A a b +=其中,i i a b 是一对互质整数,1,2,3,1i n =-若有序整点列123,,,n B B B B 是点列123,,,n A A A A 正交点列, 则1(,),1,2,3,,1i i i i i B B b a i n λ+=-=-,则有 11=1111=11,(1).(2)n n i i i i i n n i i i i i b a a b λλ--=--=⎧-=⎪⎪⎨⎪=⎪⎩∑∑∑∑ ①当n 为偶数时,取1,(0,0)A 1,=3=,1,2,3,,1-1i i i a b i n i ⎧=-⎨⎩为奇数,,为偶数.由于123,,,n B B B B 是整点列,所以有i λ∈Z ,1,2,3,,1i n =- . 等式(2)中左边是3的倍数,右边等于1,等式不成立, 所以该点列123,,,n A A A A 无正交点列; ②当n 为奇数时,取1,(0,0)A 11=3,2a b =,1,=3=,2,3,,1-1i i i a b i n i ⎧=-⎨⎩ 为奇数,,为偶数,由于123,,,n B B B B 是整点列,所以有i λ∈Z ,1,2,3,,1i n =- . 等式(2)中左边是3的倍数,右边等于1,等式不成立, 所以该点列123,,,n A A A A 无正交点列.综上所述,5n n ∀≥∈,N ,都不存在无正交点列的有序整数点列()A n ----------13分。
