G_M法解析公式在T形梁桥横隔梁弯矩计算中的应用

合集下载

#20m整体简支T型梁桥计算书

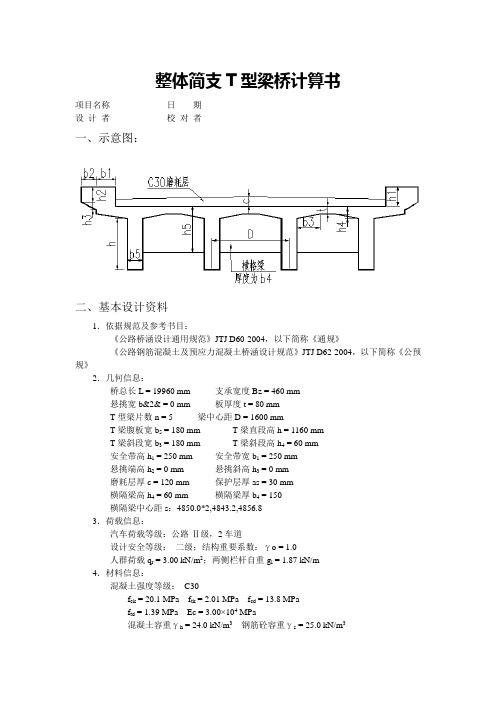
整体简支T型梁桥计算书项目名称_____________日期_____________设计者_____________校对者_____________一、示意图：二、基本设计资料1．依据规范及参考书目：《公路桥涵设计通用规范》JTJ D60-2004，以下简称《通规》《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTJ D62-2004，以下简称《公预规》2．几何信息：桥总长L = 19960 mm 支承宽度Bz = 460 mm悬挑宽b&2& = 0 mm 板厚度t = 80 mmT型梁片数n = 5 梁中心距D = 1600 mmT梁腹板宽b5 = 180 mm T梁直段高h = 1160 mmT梁斜段宽b3 = 180 mm T梁斜段高h4 = 60 mm安全带高h1 = 250 mm 安全带宽b1 = 250 mm悬挑端高h2 = 0 mm 悬挑斜高h3 = 0 mm磨耗层厚c = 120 mm 保护层厚as = 30 mm横隔梁高h4 = 60 mm 横隔梁厚b4 = 150横隔梁中心距s：4850.0*2,4843.2,4856.83．荷载信息：汽车荷载等级：公路-Ⅱ级，2车道设计安全等级：二级；结构重要系数：γo = 1.0人群荷载q r = 3.00 kN/m2；两侧栏杆自重g l = 1.87 kN/m4．材料信息：混凝土强度等级：C30f ck = 20.1 MPa f tk = 2.01 MPa f cd = 13.8 MPaf td = 1.39 MPa Ec = 3.00×104 MPa混凝土容重γh = 24.0 kN/m3钢筋砼容重γs = 25.0 kN/m3钢筋强度等级：HRB335f sk = 335 MPa f sd = 280 MPa Es = 2.0×105 MPa三、计算跨径及截面特性1．计算跨径：计算跨径l o = min（l，1.05×l n）l = L - b = 19960 - 460 = 19500 mml n = L - 2b = 19960 - 2×460 = 19040 mml o = min（19500，1.05×19040）= min（19500，19992）= 19500 mm四、主梁的荷载横向分布系数计算1．跨中荷载弯矩横向分布系数（按G-M法）（1）、计算主梁截面的抗弯惯性矩I x及抗扭惯性矩I Tx主梁截面的重心位置：a x = [（1600-180）×1132/2+180×13002/2]/[（1600-180）×113+180×1300]= 408.2 mmI x = （1600-180）×1133/12+（1600-180）×113×（408.2-113/2）2= +180×13003/12+180×1300×（1300/2-408.2）2 = 66701.1826×106 mm4 T型截面抗扭惯性矩近似等于各个矩形截面抗扭惯性矩之和，即：I Tx = ∑c i×b i×t i3式中：c i -- 矩形截面抗扭惯性矩刚度系数（查表得到）b i、t i -- 相应各矩形截面的宽度及厚度查表可知：t1/b1 = 113/1600 = 0.071，c1 = 0.333t2/b2 = 180/1187 = 0.152，c2 = 0.301故：I Tx = 0.333×1600×1133+0.301×1187×1803= 2863.5910×106 mm4单位宽度抗弯惯性矩J&x&及抗扭惯性矩J&Tx&J x = I x/b'f = 66701.1826×106/1600 = 41688.2391×103 mm3J Tx = I Tx/b'f = 2863.5910×106/1600 = 1789.7443×103 mm3（2）、计算横隔梁截面的抗弯惯性矩I y及抗扭惯性矩I Ty横隔梁翼板有效宽度λ计算：横隔梁长度取为两边主梁的轴线间距，即：l = 4×1600 = 6400 mmc = （4850 - 150）/ 2 = 2350 mmc / l = 2350 / 6400 = 0.367，查表得：λ/ c = 0.548故：λ= 0.548 ×2350 = 1287 mm横梁截面的重心位置：a y = （2×1287×1132/2+150×10002/2）/（2×1287×113+150×1000）= 207.2 mmI y = 2×1287×1133/12+2×1287×113×（207.2-113/2）2= +150×10003/12+150×1000×（1000/2-207.2）2 = 32284.1751×106 mm4查表可知：t1/b1 = 113/4850 = 0.023，c1 = 0.167t2/b2 = 150/887 = 0.169，c2 = 0.893故：I Ty = 0.167×4850×1133+0.893×887×1503= 2069.1399×106 mm4单位宽度抗弯惯性矩J&y&及抗扭惯性矩J&Ty&J x = I x/b = 32284.1751×106/4850 = 6656.5310×103 mm3J Ty = I Ty/b = 2069.1399×106/4850 = 426.6268×103 mm3（3）、计算抗弯参数θ及抗扭参数αθ= B' / lo ×（J x / J y）1/4式中：B' -- 桥宽的一半；θ= 4000 / 19500 ×（41688239 / 6656531）1/4 = 0.325α= G×（J Tx + J Ty）/ [2Ec×（J x × J y）1/2]按《公预规》3.1.6条，取G = 0.4Ec，则：α= 0.4×（1789744 + 426627）/ [2×（41688239 ×6656531）1/2] = 0.027 （4）、跨中弯矩横向分布影响线坐标据θ= 0.325，α= 0.027，查G-M表并插值得到：表中：K=K o+（K1-K o）×α1/2；η= K/5梁号项 b 3b/4 b/2 b/4 0 -b/4 -b/2 -3b/4 -b1号K1 1.392 1.290 1.181 1.074 0.975 0.887 0.811 0.746 0.686 1号K o 3.471 2.831 2.190 1.563 0.956 0.369 -0.205 -0.770 -1.332 1号K 3.132 2.580 2.026 1.484 0.959 0.453 -0.039 -0.523 -1.003 1号η0.626 0.516 0.405 0.297 0.192 0.091 -0.008 -0.105 -0.201 2号K1 1.154 1.133 1.107 1.065 1.011 0.954 0.899 0.850 0.804 2号K o 2.073 1.868 1.612 1.324 1.020 0.710 0.398 0.086 -0.226 2号K 1.923 1.749 1.529 1.282 1.019 0.750 0.480 0.210 -0.058 2号η0.385 0.350 0.306 0.256 0.204 0.150 0.096 0.042 -0.012 3号K10.957 0.979 1.002 1.022 1.031 1.022 1.002 0.979 0.957 3号K o0.922 0.965 1.006 1.038 1.052 1.038 1.006 0.965 0.922 3号K 0.928 0.967 1.005 1.036 1.049 1.036 1.005 0.967 0.928 3号η0.186 0.193 0.201 0.207 0.210 0.207 0.201 0.193 0.186 按《通规》4.3.1条和4.3.5条规定：汽车荷载距人行道板边缘不小于0.5m，人行道板以集中力作用在一块板上。

midas梁格法t梁经典算例

梁格法是工程力学中常用的一种分析方法，用于计算梁的内力和挠度。

在工程实践中，梁格法被广泛应用于桥梁、建筑物和机械结构等工程项目的设计和分析中。

本文将通过具体的案例分析，探讨梁格法在工程实践中的应用和价值。

一、梁格法的基本原理梁格法是一种基于力学原理的计算方法，其基本原理包括静定性原理和虚位移原理。

静定性原理指出，在结构静定的状态下，结构的所有部分都处于平衡状态，即内力和外力相互抵消。

而虚位移原理则是假设结构发生微小位移后，结构的内部工作做功为零，即结构在平衡状态下满足力与位移的乘积为零。

二、梁格法的基本步骤使用梁格法进行梁的内力和挠度计算主要包括以下步骤：1. 建立梁的受力模型在进行梁的内力和挠度计算前，需要对梁的受力情况进行分析，包括受力的位置、作用力的大小和方向等。

通过建立梁的受力模型，可以清楚地描述梁在受力下的变形和内力分布情况。

2. 划分梁的小段将梁划分为若干个小段，每个小段之间的长度相对较小，可以近似认为是直线段。

通过对梁进行划分，可以简化梁的分析和计算，同时也为后续的计算提供了便利。

3. 建立梁的受力方程针对每个小段，建立其在受力下的平衡方程，包括受力平衡方程和弯矩平衡方程。

通过对小段的受力方程进行建立和求解，可以得到该小段内力的大小和分布情况。

4. 求解梁的挠度根据虚位移原理，可以利用小段内力的大小和分布情况，通过积分的方法求解梁的挠度。

通过对梁的挠度进行求解，可以了解梁在外载荷作用下的变形情况。

5. 综合分析综合考虑各个小段的内力和挠度情况，得出整个梁的内力和挠度分布情况。

三、梁格法的经典算例下面将通过一个具体的案例，展示梁格法在工程实践中的应用和价值。

案例：简支梁的内力和挠度分析考虑一个简支梁，长度为L，受均布载荷q作用。

根据梁格法的基本步骤，进行简支梁的内力和挠度分析。

1. 建立梁的受力模型根据简支梁的受力情况，可以建立梁的受力模型，包括受力位置、作用力大小和方向等。

考虑梁在均布载荷q作用下的受力情况，可以建立梁的受力模型。

梁格分析在梁桥计算中的应用

梁格分析在梁桥计算中的应用摘要：本文论述了梁格法在梁桥结构分析中的应用，并以简支T梁为例进行分析说明。

关键词：梁格法，T梁，横向分布系数Abstract: This paper discusses how to apply the grillage method to analyze the structure of the bridges, and takes the T beam for example.Key words: grillage method , T beam , lateralloaddistributionfactors1. 概述梁格法[1]是将分散的梁板或箱梁某一段内的弯曲和抗扭刚度假定集中于最邻近的等效梁格内，实际结构纵向刚度集中于纵向梁格内，横向刚度集中于横向梁格；原型实际结构和对应的等效梁格承受相同荷载时，两者的挠曲是恒等的；任一梁格内的弯矩、剪力和扭矩应等于该梁格所代表的实际结构部分的内力。

梁格法的难点是刚度等效和荷载等效，如若处理不当，则难得到想要的计算结果。

但是梁格法易于理解和使用，利用计算机计算很方便，计算结果精确有效，被广泛应用。

2. 梁格分析本文只分析梁板式上部结构的梁格分析，并以T梁为例加为详细说明；对于闭口箱梁，这里不作论述。

2.1 梁格划分（1）纵梁与每片T梁中心线重合。

梁格须重合于设计受力线，纵梁间距不宜过大，对于纵梁间距较大，可在纵梁间距中心设置虚拟梁，使结构受力连续，也便于荷载模拟。

（2）对于有横隔板部位，必须设一根梁格与之重合。

若横格板间距较密，可仅在横格板处设横梁，但横梁的间距与纵梁间距须相当，以使结构受力灵敏；若横格板间距较稀，参照纵梁设置原则设置。

（3）对于斜桥，纵梁与横梁一般是正交的，但对于支点处，端横隔梁一般为斜交的，故需根据实际受力和构造进行布设。

2.2 截面特性（1）纵梁梁格惯性矩通常按截面的形心计算。

内梁和边梁是处于不同的水平线，采用二维梁格分析，通常这种差距略而不计；但是考虑板的薄膜作用[1]时，建议采用空间梁格分析，纵梁与横梁间采用刚度很大的构件连接。

装配式钢筋混凝土简支T型梁桥实例详解

13M装配式钢筋混凝土简支T型梁桥装配式钢筋混凝土简支型梁桥计算题目：装配式钢筋混凝土简支T梁桥计算一、基本设计资料1．跨度和桥面宽度（1）标准跨径：13m（墩中心距）。

（2）计算跨径：12.6m。

（3）主梁全长：12.96m。

（4）桥面宽度（桥面净空）：净-9+2×0.75m2．技术标准设计荷载：公路—II级，人行道和栏杆自重线密度按照单侧6kN/m计算，人群荷载为3kN/㎡。

环境标准：I类环境。

设计安全等级：二级。

3．主要材料（1）混凝土：混凝土简支T形梁及横梁采用C50混凝土；桥面铺装上层采用0.03m沥青混凝土，下层为厚0.06～0.13m的C30混凝土，沥青混凝土重度按23kN/3m计。

m计，混凝土重度按25kN/3（2）刚材：采用R235钢筋、HRB335钢筋。

4．构造形式及截面尺寸如图8-1所示，全桥共由5片T形梁组成，单片T形梁高为1.4m，宽1.8m；桥上横坡为双向2％，坡度由C30混凝土桥面铺装控制；设有五根横梁。

（五）设计依据（1）《公路桥涵设计通用规范》（JTG D60-2004）,简称“桥规”（2）《公路钢筋混凝土及预应力混凝土桥涵设计规范》（JTG 62-2004），简称“公预规”（3）《公路工程技术标准》（JTG B01-2003）（六）参考资料（1）结构设计原理：叶见曙，人民交通出版社（2）桥梁工程：姚玲森，人民交通出版社（3）公路桥梁设计手册《梁桥》（上、下册）人民交通出版社（4）桥梁计算示例丛书《混凝土简支梁（板）桥》（第三版）易建国主编。

人民交通出版社；（5）《钢筋混凝土及预应力混凝土简支梁结构设计》闫志刚主编，机械工业出版社。

二、主梁的计算1、主梁的荷载横向分布系数1．跨中荷载横向分布系数（按G-M 法）承重机构的宽跨比为：B/L=12/12.6=0.95（1）主梁的抗弯及抗扭惯矩Ix 和ITX1）求主梁截面的重心位置 (图2)xa翼缘板厚按平均厚度计算，其平均板厚度为：h1=1/2(10+16)=13cm 则1813011)18160(21001810021313)18220(⨯+⨯-⨯⨯+⨯⨯-=x a=24.19cm2）抗弯惯性矩Ix 为：42423231078.35501.3557834)19.242100(1001810018121)21319.24(13)18220(13)18220(121[m cm I X -⨯==-⨯⨯+⨯⨯+-⨯⨯-+⨯-⨯=对于T 形梁截面，抗扭惯性矩可近似按下式计算T 形抗扭惯矩近似等于各个矩形截面的抗扭惯矩之和，即： ITX=∑3ii i t b c式中：Ci 为矩形截面抗扭刚度系数（查附表1）；ti t2/b2=0.18/(1.3-0.11)=0.151,c2=0.301 故 ITX=1.6×0.113/3+0.301×1.19×0.183 =0.71×10-3=2.80×10-3m4 单位抗弯及抗扭惯矩：JX=Ix/b=6.628×10-2/160=4.142×10-4m4/cm JTX=ITx/b=2.280×10-3/160=3.15×10-5m4/cm（2）计算抗扭修正系数β：221112Ti it it Gl I E a I β=+∑∑计算得β=0.99（3）按修正的刚性横梁法计算横向影响线竖坐标值5211i ij i i a e na ηβ==+∑式中，n=5，521ii a=∑=48.4m2ij η表示单位荷载p=1作用于J 号梁轴上时，i 号梁轴上所受的作用。

桥梁工程实验-T型梁桥荷载横向分布系数试验(教学)

• 六、实验报告要求 1、对实验中测得的各工况原始的挠度数据进行整理； 2、将各工况荷载作用下的各梁实测挠度值列表； 3、根据实测数据绘制每种工况下每级荷载下T梁的挠度横向分布曲线； 4、将实测结果与教材所讲几种横向分布系数理论计算结果进行比较分析。
• 2、测试内容测试在集中荷载作用下各种横向连接形式的T梁桥模型各梁跨中截面及L/4截面的挠度变形变化规律。
• 3、测点布置由于本模型是架设在刚度很大的钢梁上，实验施加荷载又较小，所以支座变位可以忽略不计。因此挠度测点布置在跨中断面及L/4截面上，测点布置如图所示。
• 4、实验步骤 (1)检查模型和实验装置，安装百分表； (2)首先进行预加载，检查仪表是否工作正常，如发现异常及时排除； (3)正式试验，用加载设备缓慢加载，加载到最大荷载后持荷5分钟后采集各测点读数； (4) 加载读数完毕以后缓慢卸载，卸载完毕后采集各测点残余值；接着完成其余两个工况测试。
• 5、注意事项 (1)实验前注意检查百分表是否接触牢靠、垂直； (2)正式加载前需采用全部荷载的40%进行预加载； (3)在每一工况测试前需进行平衡清零且初读，在数据都基本归零的情况下再加载；
(4)在每一工况荷载卸载完以后还需采样读取结构的残余数据，因为结构的弹性变位（应变）是加载稳定后测量值与卸载稳定后的测量值的差值； (5)只能在加（卸）载完成5分钟之后再开始采样读数，确保结构弹性变形完全； (6)每次采样读数需采集组数据，每组间隔至少10秒，每组数据之间应差别不大才能结束本次采样；分析处理时采用三组数据的平均值。
桥梁工程实验
T型梁桥荷载横向分布系数实实验目的 • 在桥梁工程中，梁桥的荷载横向分布效应是一个复杂的理论问题。为了增强学生对荷载横向分布系数计算理论的理解，验证桥梁荷载横向分布系数的计算方法，加深对课堂所学理论知识的掌握,培养试验研究动手能力及结构分析能力，本实验室安排了此次实验。

G-M法在小半径曲线箱形梁桥受力分析中的应用与研究

进行划分，曲线式梁格构件与直线式梁格构件相比，在精度上的改善并不明显，此本文研究采用因直线梁格分析。通过文献［０可知，常翘曲作用１］通
（实际箱梁结构ａ１
（纵截面图ｂ）
对弯矩、剪力的影响较小，对扭矩的影响较大，。而因此本文考虑翘曲作用的影响。
箱梁的截面形式如图１ａ所示，梁的相邻（）箱腹板之问的距离为ａ截面的抗弯刚度Ｄ；截面，纵如图１ｂ）示，邻横隔板之间的距离为ｂ截面（所相，
抗弯刚度为Ｄ； ’ 横截面如图１ｃ所示；（）根据经典弹
；代入通过构造异性板理论［导再７］
出的，Ｄ函数关系表示的公式。根据诸刚Ｄ，ＡＤ
度公式，用梁格有限元分析『梁结构。对比采８箱｜９拟的正交异性板，根据板式结构的梁格划分原则
性理论，可以将箱梁比拟成正交异厚均质板，如
图１ｄ所示，中Ｘ向板厚用虚线表示，明比拟（）其方说板在两方向具有不同厚度。对构造上的正交异性
独特优点，选择箱梁桥跨结构比拟法的难点Ｄ．，的
１理论基础
１１正交异性板挠曲微分方程．通常所指的正交异性板，其特点是结构材料在两个方向的弹性性质不同，如以弹性性质对称面为坐标面，挠曲微分方程为：板】桥跨结构静力分析上的在

桥梁工程GM法计算横向分布系数表格

1+μ 2 1.200 1.200 1.200 1.200 1.200
qk3 10.500 10.500 10.500 10.500 10.500
w04 4.213 4.213 4.213 4.213 4.213
pk5 353.760 353.760 353.760 353.760 353.760
yk6 0.500 0.500 0.500 0.500 0.500
1汽 2汽 3汽 4汽 5汽
0.518 0.444 0.370 0.328 0.302
η η η η η
1’汽 2’汽 3’汽 4’汽 5’汽
0.306 0.500 0.639 0.639 0.639
η η η η η
1人 2人 3人 4人 5人
0.394 0.323 0.253 0.223 0.222
Q0(kN) w0 16.850 16.850 16.850 16.850 16.850
qw0 451.735 463.411 463.078 463.078 463.078
公路I级产生的弯矩梁号内力 M l/2 1 M l/4 M l/2 2 M l/4 M l/2 3 M l/4 M l/2 4 M l/4 M l/2 5 M l/4 人群产生的弯矩梁号内力 M l/2 1 M l/4 M l/2 2 M l/4 M l/2 3 M l/4 M l/2 4 M l/4 M l/2 5 M l/4 弯矩基本组合表内力梁号 1 M l/2 1 M l/4
组合值 8307.468 6230.665
2 3 4 5
M M M M M M M M
l/2 l/4 l/2 l/4 l/2 l/4 l/2 l/4
3904.201 2928.151 3901.396 2926.047 3901.396 2926.047 3901.396 2926.047

梁桥维修与加固中应用G技术有何应用

梁桥维修与加固中应用G技术有何应用在现代交通基础设施中，梁桥作为重要的组成部分，承担着繁重的交通运输任务。

随着时间的推移和交通流量的不断增加，梁桥可能会出现各种病害和损伤，影响其安全性和使用性能。

为了延长梁桥的使用寿命，保障交通安全，对梁桥进行及时有效的维修与加固至关重要。

近年来，随着科技的不断进步，G 技术在梁桥维修与加固领域得到了广泛的应用，为提高维修与加固效果提供了有力的支持。

一、G 技术在梁桥检测中的应用1、三维激光扫描技术三维激光扫描技术是一种非接触式的测量技术，能够快速、高精度地获取梁桥的三维点云数据。

通过对这些数据的处理和分析，可以准确地获取梁桥的几何形状、变形情况等信息。

例如，在检测梁桥的挠度时，通过在不同位置设置扫描点，对比不同时间点的扫描数据，可以直观地了解梁桥的挠度变化情况，为评估梁桥的承载能力提供重要依据。

2、无损检测技术无损检测技术包括超声波检测、雷达检测、磁粉检测等。

这些技术可以在不破坏梁桥结构的前提下，检测出梁桥内部的缺陷，如裂缝、空洞、锈蚀等。

其中，超声波检测技术利用超声波在材料中的传播特性，能够检测出混凝土内部的裂缝深度和位置；雷达检测技术则通过发射电磁波并接收反射波，来探测梁桥结构中的钢筋分布、混凝土厚度等信息。

二、G 技术在梁桥结构分析中的应用1、有限元分析有限元分析是一种基于数值计算的结构分析方法。

通过将梁桥结构离散化为有限个单元，并对每个单元进行力学分析，最终得到整个结构的应力、应变和位移等结果。

利用 G 技术强大的计算能力，可以快速、准确地完成复杂梁桥结构的有限元分析。

在维修与加固前，通过有限元分析可以预测梁桥在不同荷载作用下的响应，为制定合理的维修与加固方案提供理论支持。

2、模型修正技术由于实际梁桥结构存在材料性能的不确定性、施工误差等因素，有限元模型往往与实际结构存在一定的差异。

模型修正技术通过将现场检测数据与有限元分析结果进行对比，对有限元模型中的参数进行调整和优化，使其更接近实际结构。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

繁琐 . 采用解析方法并利用 Excel 软件，可直接计算横向弯矩影响系数，为进一步求得横隔梁弯矩影响线并计算活载弯矩提供方便 .
Application of GM theory analysis in calculation of Tbeam bridge diaphragm moment
ZHANG Yue
β 为与计算截面位置有关的参数： πy β= ； B
槡
Jx ； Jy
（ 26 ）
（ 27 ）
276 y 为计算截面的横坐标； ψ 为与荷载作用位置有关的参数： ψ= πe ； B
内蒙古科技大学学报
2011 年 9 月
第 30 卷第 3 期
T 形梁，计算跨径 L = 19. 5 m，桥梁构造见图 2 ，相关（ 28 ） 4，计算参数及 Excel 计算书界面见图 3 ，计算结果的 1 ，，比较见表可见两者计算结果吻合很好 .
Fig． 3 图3 计算书界面（基本数据）
Interface of calculation sheet（ basic data）
张
M 法解析公式在 T 形梁桥横隔梁弯矩计算中的应用王月： G-
277
3
结论
M 法的横隔采用解析方法，利用 Excel 进行 G可形成通用的计算表，只需在图梁弯矩影响线计算， 3 所示的界面中输入相关的基本数据即可得到计算结果，如需加密插值点，可在图 4 所示界面右侧增加单元格以完成相应计算，摆脱了传统计算图表的限制，简单易用，计算精度较高，可用于专业教学和工程设计 . 参考文献：
2011 年 9 月第 30 卷 3 期
内蒙古科技大学学报 Journal of Inner Mongolia University of Science and Technology
September， 2011 No．3 Vol．30 ，
文章编号： 2095 － 2295 （ 2011 ） 03 － 0274 － 04
－ 0 ． 241 － 0 ． 121 － 0 ． 001 － 0 ． 101 － 0 ． 040 － 0 ． 218 － 0 ． 108 0 ． 027 0 ． 004
本文
μ1 μα
横隔梁弯矩，一般只需计算跨中截面，则 y = 0， β = 0，与 β 有关的各参数变为： B0 = 2shλπ·sinλπ， D1 = M1 － Q1 ， G1 = 0 ，（ 32 ）（ 34 ）（ 35 ） D0 = chλπ·sinλπ － shλπ·cosλπ，（ 33 ）
Comparison of calculation results
－B
－ 3 B /4
－ B /2
－ 0 ． 240 － 0 ． 120 － 0 ． 001 － 0 ． 098 － 0 ． 040 － 0 ． 216 － 0 ． 107 0 ． 028 0 ． 004
μ1 μα μ0
ρ = π － |β － ψ|， σ = θπ.
成的混凝土梁桥，可采用“弹性等效法 ” 进行分析，将其换算为等效的宽度为 2 B 、两端简支、两侧边自由的比拟正交异性板，如图 1 所示 . GM 法的计算原理和方法在相关文献中已有本文不赘述，在此仅列出相应的解析计算详细介绍，［1 ， 2 ］ . 公式在正弦分布荷载作用下（图 1 ），横隔梁的弯矩可表示为： M y = p0 sin πx ·a ·B ·μ α ， L （ 1）
M 法，比拟正交异性板法，简称 G是将纵横相交的梁格结构比拟为正交异性平板，按弹性薄板理论进行分析的方法，不仅可用于主梁的横向分布计算，也可用于横隔梁内力计算 . 在具体计算中，直接计算不便，因此，利用弹性挠曲微分方程进行求解，为便于使用，常规方法通常是利用事先编制好的计算图表进行计算，但计算过程仍显繁琐 . 为此可根据解析公式并借助 Excel 软件求解，使得计算更为方便、快捷 .
α=
G （ J Tx + J Ty ）
=
J Tx + J Ty
，
（ 3）
F1 = ［ M1 － N1 + Q1］ shθψ － P1 ·θψ·chθψ，（ 19 ） G1 = M1 ·shθβ － P1 ·θβ·chθβ， H1 = 1 ， Q1 ·chσ + （ 1 － v） ·σ （ 20 ）（ 21 ）（ 22 ）（ 23 ）（ 24 ）（ 25 ）
2
（ 9）（ 10 ）（ 11 ）（ 12 ）（ 13 ）
形式的实际荷载按 Fourier 级数展成正弦函数代入［1 ， 3 ］，即可而 aBμ α 可看作是横向弯矩影响线竖标，可见，计算横隔梁弯矩需先计算横向弯矩系数 μ α ，可用下式计算：（ 2） μ α + μ0 + （ μ1 － μ0 ）槡 α，式中， μ0 ， μ1 分别为 α = 0 和 α = 1 时的横向弯矩影响系数； α 为扭弯参数， 2E 槡 Jx Jy 5 槡 Jx Jy J x 为比拟板纵向单宽抗弯惯矩， m4 / m； J y 为比式中， m / m； J Tx + J Ty 为比拟板拟板横向单宽抗弯惯矩， m4 / m； E 为比拟板的弹横向单宽抗扭惯矩之和，纵、 MPa； G 为比拟板的剪切模量， MPa，性模量，参照文 4］，献［取 G = 0. 4 E. 1， 2］文献［给出了 μ0 ， μ1 的解析公式，由于公式本文引入了多个中间参数，以便于分步计较为繁复，算. B 0 · C 0 + D0 （ E 0 + F 0 ）， μ0 = A0 （ 4）
表1 Table 1
计算方法 5］文献［系数 μ0
计算结果对比
荷载位置－ B /4 0 ． 120 0 ． 110 0 ． 118 0 ． 121 0 ． 110 0 ． 119 0 0 ． 244 0 ． 217 0 ． 240 0 ． 244 0 ． 218 0 ． 240
e 为荷载偏心距，即荷载作用位置距桥梁纵轴；线的横向距离 v 为泊松比 . 其它参数为： λ= θ ， 2 槡（ 29 ）（ 30 ）（ 31 ）
上述各参数与结构的刚度常数、截面位置及荷载位置有关： θ 为弯曲刚度参数： θ= B L
4
（ 6）（ 7）（ 8）
B0 = 2shλ （ π － β） ·sinλ （ π － β）， C0 = M0 ·cosλ （ π － ψ） ·chλ （ π + ψ）－ N0 ·chλ （ π － ψ） ·cosλ （ π + ψ）， D0 = chλ （ π － β） ·sinλ （ π － β）－
（ 36 ） ρ = π － |ψ|． H1 无需计算，相应地，参数 F1 ，式（ 5）也简化为： B 1 + C 1 · D1 · E 1 . （ 37 ） μ1 = － A1 计算横向分布影响线时取插值点（即荷载作用则可根据各插值点的荷载偏心距 e，点）个数为 m，（ 37 ），按上述公式计算必要的参数，最后按式（ 4 ），（ 2 ）计算出各插值点对应的横向弯矩影响系数，进，而求得各插值点处的横向弯矩影响线竖标按最不利情况布置活载并计算得出横隔梁弯矩 . 其中插值点个数 m 应取奇数，习惯上将横截面则 m = 9，如需加密插值点，可按下式确定：分 8 等分， m = 8i + 1（ i = 1， 2， 3， …）．（ 38 ）对于横隔梁跨中截面，其弯矩影响线左右对称，则只需计算一半即可，计算点的个数为： j= m +1 ． 2 （ 39 ）
4
A1 = 4 σsh σ，（ 14 ） B1 = （ M1 － N1 ） chθρ － P1 ·θρ·shθρ，（ 15 ） C1 = （ M1 － N1 ） chθψ － P1 ·θψ·shθψ，（ 16 ） D1 = （ M1 － Q1 ） chθβ － P1 ·θβ·shθβ，（ 17 ） E1 = 1 ， Q1 ·chσ －（ 1 － v） ·σ （ 18 ）
G-M 法解析公式在 T 形梁桥横隔梁弯矩计算中的应用
张王月
（内蒙古科技大学建筑与土木工程学院，内蒙古包头 014010 ）
*
M 法； Excel 软件关键词： T 形梁桥；横隔梁；弯矩；影响线； G中图分类号： U441 摘文献标识码： A M 法进行 T 形梁桥横隔梁弯矩计算时，要：采用 G需先确定横隔梁弯矩影响线，但利用计算图表手工计算较为
（ Architecture and Civil Engineering School， Inner Mongolia University of Science and Technology， Baotou 014010 ， China） Key words： Tbeam bridge； diaphragm， moment； influence line； GM theory， Excel softwar Abstract： In using GM theory to calculate Tbeam bridge diaphragm moment， the diaphragm moment influence line should be firstly the analytic method with Excel software was used to calculate transverse mocalculated． As the manual calculation is too complicated， providing convenience for the calculation of diaphragm moment influence line load moment． ment influence factor directly，