CPK工程能力分析
CPK制程能力分析讲解
CPK为什么要定1,,,这几个值?CPK:Complex Process Capability index 的缩写,是现代企业用于表示的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生。
CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差。
CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常工作状态下的过程控制能力。
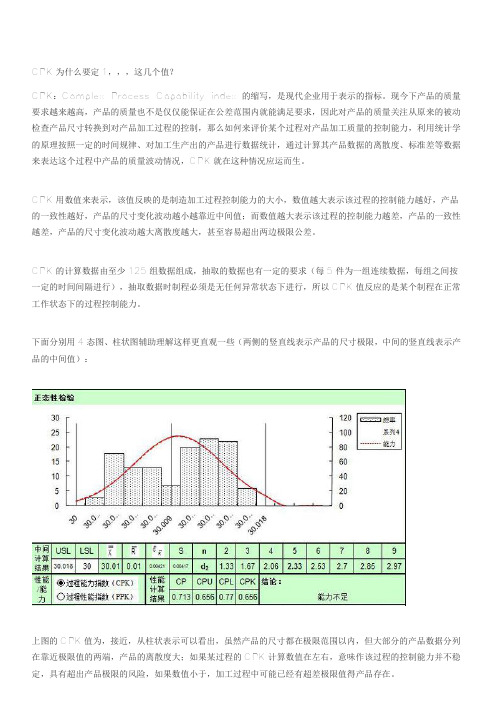
下面分别用4态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):上图的CPK值为,接近,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在左右,意味作该过程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于,加工过程中可能已经有超差极限值得产品存在。
上图的CPK值为,与CPK值为的图形对比可以看出,产品的尺寸的波动范围比前一副图约小一点,更趋近中间值。
因此当CPK值增大时,该图反应出的过程控制能力就比CPK值为的过程控制能力要好,那么产品超差两端极限的情况也就更小。
下面分别为CPK值为和左右的图形从上列4张图片的对比不难看出,当CPK值越大时,过程控制能力越强,加工出的产品越靠近中间值且波动范围越小,产品互换性好质量越高。
CPK制程能力分析

1
名詞介紹
USL:產品之規格上限 LSL:產品之規格下限 u:規格中心值 N X /N 樣本算術平均(平均值): X Σ i=1 N ( X i )2 / N :母體標準差: i 1 n s:樣本標準差: ( X i )2 / n 1 i 1 T:規格公差=規格上限-規格下限(USL-LSL) 平衡公差:18.0 ±0.5 不平衡公差:18.0 +0.5/–0.2 or 18.0 +0.3/ –0.5 PPM(Parts Per Million):每百萬個單位的不合格數
ቤተ መጻሕፍቲ ባይዱ
Cpk = Min ( Cpku ,Cpkl )
= Cp ( 1 - Ca )
Cpku =
USL -X
3σ
LSL
Cpkl =
x u
USL
X - LSL
3σ
-∞ -3σ -2σ -1σ TARGET +1σ +2σ +3σ
+∞
6
Ca/Cp/Cpk等級判定
等級
A B
Ca
0 ≦ Ca < 0.0625
0.0625 < Ca ≦ 0.125
(18.4-18.1)2+(17.6-18.1)2+ (17.9-18.1)2 +….+ (18.3-18.1)2
σ=
9
=0.2981
T=18.5 -17.5=1
Ca = (18.1-18.0)/0.5=0.2……………... B級 Cp = 1/(6× 0.2981)=0.559…………….. D級 Cpk = 0.559 × (1-0.2)=0.4472…………D級 結論:此產品須大大的改善才可符合現代化的要求.
CPK 制程能力分析

– 單邊規格 : 品質特性的合格範圍僅定上限或下 限者稱為單邊規格
•1、 中间高,两边低,左右对称;两边伸向无穷远。 •2、与横坐标所围成区域的面积为 1; •8
制程能力分析的基础
正态分布概率:
•0.34 0.34
•P(u-1σ<X<u+1σ)=0.6827 •P(u-2σ<X<u+2σ)=0.9545 •P(u-3σ<X<u+3σ)=0.9973 •P(u-6σ<X<u+6σ)=0.9999966
CPK值越大表示品质越佳。
•Cpk 基础
1. Cpk的中文定义为:制程能力指数,是某个工程或制程水准的
量化反应,也是工程评估的一类指标。 2. 同Cpk息息相关的两个参数:Ca , Cp.
Ca: 制程准确度。 Cp: 制程精密度。 3. Cpk, Ca, Cp三者的关系: Cpk = Cp * ( 1 - |Ca|),Cpk是
(σ),再计算出规格公差(T),及规格中心值(u). 规格公差=规
格上限-规格下限;规格中心值=(规格上限+规格下限)/2;
•Cpk 基础
7. 依据公式:Ca=(X-U)/(T/2) , 计算出制程准确度:Ca值 (x为7
所有取样数据的平均值) 8. 依据公式:Cp =T/6σ , 计算出制程精密度:Cp值 9. 依据公式:Cpk=Cp(1-|Ca|) , 计算出制程能力指数:Cpk值 10. Cpk的评级标准:(可据此标准对计算出之制程能力指数做
{ } (1) CPK = Min CPU ,CPL
(2)
CPK
=
USL - LSL - 2 ±3
制程能力分析(Cpk)

Confidential
12
穩定製程 vs 不穩定製程
穩定的製程
可以預計未來的品質狀況.
機遇原因
不穩定的製程
可能無法預計未來的品質狀況
機遇原因 非機遇原因
Confidential 13
取樣
取樣原則:系統、隨機、批次、分散
避免影響統計結果
X Sample
X
X
X Sample
X X X X
Sample A C C B B D D
E xp . O v e ra ll P e rf o rm a n c e P P M ?< ?LS L 2 4 5 3 9 .5 4 P P M ?> ?U S L 2 9 0 7 8 .1 5 P P M ?T o ta l 5 3 6 1 7 .6 9
5
基本统计概念
6
常態分配
常態分配特性
須先考慮 製程是否有維持良好"統計管制狀態"的能力
假設製程產出是一個常態分配
Confidential
18
製程能力分析
製程能力分析
Cp:(Capability of Precision) 製程精密度 Ca: (Capability of Accuracy) 製程準確度 Cpk:(Process performance ) 製程績效指標
P r o c e s s C a p a b i l i ty o f te s t
LS L
P ro c e s s D a ta LS L 2 3 0 0 .0 0 0 0 0 T a rg e t * USL 2 5 0 0 .0 0 0 0 0 S a m p le M e a n 2 4 0 1 .9 0 0 0 0 S a m p le ?N 40 S tD e v (W ith in ) 4 2 .2 1 3 5 0 S tD e v (O v e ra ll) 5 1 .7 8 0 9 8
Unit-3测量3.3工程能力研究(CPKPPK)

利用指数平滑公式对过程数 据进行处理,预测未来的 CPK和PPK值。
CPK/PPK分析步骤
数据收集
收集相关的过程数据,确保数据的准确 性和完整性。
计算CPK和PPK值
根据选定的分析方法,利用过程数据 计算CPK和PPK值。
数据处理
对收集到的数据进行整理、清洗和转 换,以满足计算CPK和PPK的要求。
03
PPK计算
PPK计算公式
PPK计算公式:PPK = (USL - T/2) / (T/2) * sqrt((1-T/2)/(T/2))
其中,USL为规格上限,T为总体标准差。
PPK计算步骤
收集数据
收集生产过程中的实际测量数据。
计算PPK
根据PPK计算公式进行计算。
计算平均值和标准差
计算数据的平均值和标准差。
结果分析
对计算得到的CPK和PPK值进行分析, 评估过程的稳定性和能力。
CPK/PPK分析实例
实例一
某机械加工过程的CPK和PPK分析,通过收集加工过程中的数据,计算CPK和PPK值,评估加工过程 的稳定性和能力。
实例二
某电子装配过程的CPK和PPK分析,通过对装配过程中的数据进行处理和分析,计算CPK和PPK值, 评估装配过程的稳定性和能力。
1.2mm、1.3mm、1.4mm、1.5mm、1.6mm、1.7mm、1.8mm、1.9mm、2.0mm。
计算平均值
T = (1.2 + 1.3 + ... + 2.0) / 9 = 1.6mm
计算标准差
σ = sqrt((1/9) * ((1.2 - 1.6)² + (1.3 - 1.6)² + ... + (2.0 - 1.6)²)) = sqrt((1/9) * (0.4² + 0.3² + ... + 0.4²)) = sqrt((1/9) * (0.4² * 9)) = sqrt((1/9) * (0.4² * 9)) = 0.4mm
制程能力分析(CPK定义)

加强质量检测与控制
总结词
质量检测与控制是保障CPK值的重要环节, 通过加强检测和控制,可以及时发现和解决 制程中的问题,避免不良品的产生。
详细描述
加强质量检测与控制包括制定严格的质量检 测计划、采用高效的检测设备和工具、建立 完善的质量信息管理系统等措施。同时,推 行全员质量管理,强化员工的质量意识和技 能培训也是必不可少的。通过持续改进和优 化质量检测与控制体系,可以不断提升CPK 值,提高制程能力和产品质量。
生产过程改进
01
02
03
优化制程参数
通过CPK分析,可以发现 制程参数的不合理之处, 进而优化参数设置,提高 制程效率和产品质量。
改进设备配置
根据CPK分析结果,可以 针对性地改进设备配置, 提高设备利用率和生产效 率。
提升员工技能
通过CPK分析,可以评估 员工的技能水平,进而开 展针对性的培训和技能提 升计划。
详细描述
CPK是制程能力的一种度量,它反映 了制程在满足产品质量要求方面的能 力。CPK值越大,表示制程能力越强, 越能满足产品质量要求。
CPK计算方法
总结词
CPK计算方法包括计算制程的规格界限、计算制程的平均值和标准差、计算制程能力指数等步骤。
详细描述
首先,需要确定产品的规格界限,即产品合格的最大和最小范围。然后,通过收集制程数据,计算制 程的平均值和标准差。最后,利用这些数据计算CPK值,评估制程能力是否满足规格界限的要求。
CPK值的意义
总结词
CPK值的意义在于评估制程能力是否满足产品质量要求,以及发现制程中存在的问题和 改进方向。
详细描述
通过CPK值的大小,可以判断制程能力是否足够满足产品质量要求。如果CPK值较低, 说明制程能力不足,需要采取措施改进制程;如果CPK值较高,说明制程能力较好,但 仍需持续监控和优化制程。同时,CPK值的分析还能帮助发现制程中的瓶颈和问题,为
工序能力指数CPK的计算和分析

工序能力指数CPK的计算和分析CPK的计算公式如下:CPK = min(USL - μ,μ - LSL)/(3 * σ)其中,USL为规格上限,LSL为规格下限,μ为平均值,σ为标准差。
CPK的值越大,表示工序的稳定性和可控性越强。
一般来说,CPK值大于1.33被认为是良好的,大于1.67则被认为是极好的。
而CPK值小于1则表示工序不稳定或者不可控。
CPK的分析可以从以下几个方面进行:1.变异性分析:通过计算标准差和绘制控制图来评估工序的变异性。
如果标准差较小,并且控制图上的数据点在控制界限内,则说明工序具有较小的变异性,可以认为是稳定的。
反之,则说明工序存在较大的变异性,需要进一步改进。
2.规格限值分析:通过比较规格限值和平均值,以及计算CPK值,来评估工序是否能够满足产品的规格要求。
如果CPK值大于1,则说明工序具有足够的能力满足规格要求。
如果CPK值小于1,则需要进行进一步的改进,以提高工序的能力。
3.误差源分析:通过分析工序中可能存在的误差源,找出和改进引起工序不稳定的原因。
误差源可能包括人为因素、设备问题、材料质量等。
通过改进和优化这些误差源,可以提高工序的稳定性和可控性。
4.过程能力改进:通过改进工序中的控制措施和方法,来提高工序的能力。
例如,可以采用六西格玛等质量管理工具,优化工序的流程和参数设定,以减少变异性和提高工序的能力。
总之,CPK是评估工序稳定性和可控性的重要指标,可以通过计算和分析CPK值来评估工序的能力,并通过改进控制措施和优化过程来提高工序的能力。
CPK制程能力分析讲解
CPK为什么要定1 , 1.33 , 1.67,这几个值?CPK : Complex Process Capability index 的缩写,是现代企业用于表示制程能力的指标。
现今下产品的质量要求越来越高,产品的质量也不是仅仅能保证在公差范围内就能满足要求,因此对产品的质量关注从原来的被动检查产品尺寸转换到对产品加工过程的控制,那么如何来评价某个过程对产品加工质量的控制能力,利用统计学的原理按照一定的时间规律、抽样方案对加工生产出的产品进行数据统计,通过计算其产品数据的离散度、标准差等数据来表达这个过程中产品的质量波动情况,CPK就在这种情况应运而生。
CPK用数值来表示,该值反映的是制造加工过程控制能力的大小,数值越大表示该过程的控制能力越好,产品的一致性越好,产品的尺寸变化波动越小越靠近中间值;而数值越大表示该过程的控制能力越差,产品的一致性越差,产品的尺寸变化波动越大离散度越大,甚至容易超出两边极限公差。
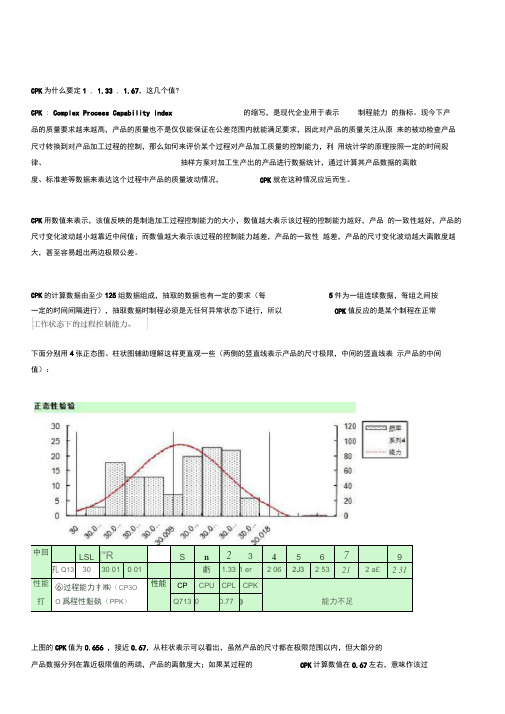
CPK的计算数据由至少125组数据组成,抽取的数据也有一定的要求(每5件为一组连续数据,每组之间按一定的时间间隔进行),抽取数据时制程必须是无任何异常状态下进行,所以CPK值反应的是某个制程在正常下面分别用4张正态图、柱状图辅助理解这样更直观一些(两侧的竖直线表示产品的尺寸极限,中间的竖直线表示产品的中间值):中回LSL["R S n234 5 679孔Q133030 010 01虧 1.331 er 2 062J3 2 5321 2 a£ 2 31性能性能CP CPU CPL CPK⑥过程能力扌㈱(CP3O打O爲程性魁埶(PPK)Q71300.770能力不足上图的CPK值为0.656 ,接近0.67,从柱状表示可以看出,虽然产品的尺寸都在极限范围以内,但大部分的产品数据分列在靠近极限值的两端,产品的离散度大;如果某过程的CPK计算数值在0.67左右,意味作该过0.67,加工过程中可能已经有超差极限值得程的控制能力并不稳定,具有超出产品极限的风险,如果数值小于 产品存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.09 0.17 0.08 0.13 0.02 0.20 0.06 0.73 1.10 0.29
结论
管控在0.15mm,CPK=0.29,工程能力特差,无法保证生
;
置"5"是影响平面度的关键。
建议
平面度0.15mm的稳定性,必须改善现有模具与整平机等。
建议
1.若需保证平面度0.15mm的稳定性,必须改善现有
求0.15mm
最大值 0.12 0.10 0.16 0.17 0.15 0.15 0.17 0.12 0.11 0.16 0.14 0.10 0.17 0.15 0.11 0.12 0.12 0.16 0.12 0.13 0.13 0.16 最小值 0.00 0.00 0.01 0.00 0.00 0.00 0.01 0.01 0.00 0.00 0.01 0.01 0.02 0.00 0.01 0.00 0.02 0.00 0.01 0.01 0.00 0.03 平面度 0.12 0.10 0.15 0.17 0.15 0.15 0.16 0.11 0.11 0.16 0.13 0.09 0.15 0.15 0.10 0.12 0.10 0.16 0.11 0.12 0.13 0.13
0.19 0.14 0.14 0.14 0.13 0.11 0.14 0.16
0.05 0.04 0.05 0.05 0.04 0.04 0.04 0.08
0.04 0.06 0.06 0.04 0.07 0.08 0.02 0.08
1.CP:当Cp越大时,表示制程越稳定,分散度小,分布集中:
CP≥2.0 2.0>CP≥1.8 1.8>CP≥1.5 1.5>CP 工程能力良好。 工程能力较好。 工程能力一般,建议改善。 工程能力特差,必须改善。
0.19 0.14 0.14 0.14 0.13 0.11 0.14 0.16
0.02 0.02 0.02 0.01 0.00 0.01 0.00 0.04 分析
0.17 0.12 0.12 0.13 0.13 0.10 0.14 0.12
最小平面度MIN 最大平面度MAX 极差R 平均值AVE 标准偏差σ 上控制线UCL 下控制线LCL 制程准确度CA 制程精密度CP 随机制程能力指数CPK
2.CPK:当Ca越小,Cp越大时,Cpk也就越大,表示制程的能力也就越强:
CPK≥1.67 1.67>CPK≥1.33 1.33>CPK≥1.0 1.0>CP 工程能力良好。 工程能力较好。 工程能力一般,建议改善。 工程能力ቤተ መጻሕፍቲ ባይዱ差,必须改善。
结论
1.若平面度管控在0.15mm,CPK=0.29,工程能力特 产的稳定性; 2.如图示,位置"5"是影响平面度的关键。
23 24 25 26 27 28 29 30
0.02 0.02 0.02 0.01 0.00 0.01 0.02 0.05
0.02 0.03 0.02 0.02 0.01 0.04 0.00 0.05
0.04 0.07 0.06 0.05 0.08 0.10 0.05 0.06 备注
0.07 0.05 0.05 0.03 0.04 0.05 0.04 0.04
工程能力分析
强网M830500200双向垫片平面度要求0.15mm
序号 个数 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0.00 0.00 0.01 0.01 0.03 0.02 0.02 0.01 0.02 0.00 0.01 0.01 0.02 0.01 0.03 0.00 0.02 0.00 0.01 0.01 0.00 0.04 0.00 0.00 0.01 0.00 0.00 0.00 0.01 0.02 0.00 0.01 0.01 0.02 0.02 0.00 0.01 0.01 0.02 0.00 0.01 0.01 0.00 0.03 0.05 0.04 0.07 0.05 0.07 0.06 0.05 0.11 0.02 0.03 0.06 0.04 0.07 0.04 0.07 0.04 0.07 0.04 0.05 0.06 0.05 0.06 0.04 0.05 0.04 0.04 0.05 0.04 0.07 0.02 0.08 0.04 0.04 0.03 0.06 0.03 0.04 0.04 0.07 0.05 0.03 0.06 0.02 0.07 0.12 0.10 0.16 0.17 0.15 0.15 0.17 0.07 0.11 0.16 0.14 0.10 0.17 0.15 0.11 0.12 0.12 0.16 0.12 0.13 0.13 0.16 0.04 0.04 0.04 0.05 0.04 0.04 0.05 0.03 0.06 0.04 0.04 0.02 0.06 0.05 0.04 0.06 0.04 0.05 0.03 0.04 0.02 0.09 0.06 0.04 0.05 0.06 0.09 0.08 0.08 0.12 0.05 0.04 0.06 0.06 0.07 0.06 0.08 0.04 0.07 0.02 0.05 0.05 0.04 0.05 1 2 3 4 5 6 7
