Topic 3 SRM 1
冗余配置例子

1 引言Controllogix是Rockwell公司在1998年推出AB系列的模块化PLC,代表了当前PLC发展的最高水平,是目前世界上最具有竞争力的控制系统之一,Control- logix将顺序控制、过程控制、传动控制及运动控制、通讯、I/O技术集成在一个平台上,可以为各种工业应用提供强有力的支持,适用于各种场合,最大的特点是可以使用网络将其相互连接,各个控制站之间能够按照客户的要求进行信息的交换。
Controllogix可以提供完善的控制器的冗余功能,采用热备的方式构建控制器,两个控制器框架采用完全相同的配置,它们之间使用同步电缆连接,不仅控制器可以采用热备,通讯网络也可以采用相似的方式进行热备,除以上的部分可以热备外,控制器的电源也可以进行热备,这样大大提高了控制器的运行的可靠性。
2 系统介绍在某焦化厂干熄焦汽轮机发电项目的DCS控制系统中,采用了冗余的Controllogix,系统结构如图1所示。
上位机通过交换机与PLC处理器通讯,远程框架通过冗余的ControlNet连接到控制器框架,同时,远程框架采用了冗余电源配置。
整套系统具有很高的可靠性,满足了汽轮机发电系统对于PLC控制部分需要长期无故障运行的要求。
上位机采用Rsview32软件,用以监控现场设备的运行。
图1 系统结构图本地框架由L1和L2 框架构成,运行时L1和L2互为热备,构成了冗余,L1和L2框架各个槽位的所配置的模块如表1所示。
R1,R2和R3是远程框架,所有的点号都连接到远程框架的模块,远程框架的供电使用了AB的冗余电源(1756-PAR2)。
收藏引用muzi_woody1楼2007-9-21 7:41:00表1 L1和L2框架各个槽位的所配置的模块设置主从控制器框架的1756-CNBR/D的节点地址时应注意,他们的地址拨码应该相同,应该是系统中挂接在冗余ControlNET网上所有节点的最高地址,在本系统里面都设置为4,远程站的节点地址分别为1,2,3。
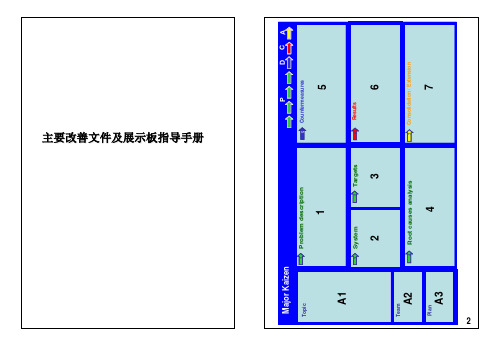
Kaizen_使用说明书中文版
A3
2
4 4
7
A1 – 项目名称及问题识别 识别问题并展示与成本展开的联系(C 矩阵柏拉图中的损失 类型);如果问题与质量相关,按需要细化损失到生产线、 机器或工位,并展示其在QA矩阵中的位置。
A2 – 项目组 展示项目小组成员的名字及角色(项目组必须是多功能的)
Name
700 632 600 524 500 77% 64% 400 48% 300 186 139 100 26% 20% 64 61 33 NVAA Power Supply Defect and reworks Absenteeism AM and PM activity Breakdown 33 Start-up or Shut down 14 Lack of material 11 Tools-prod change 3 Defect qua for Ext comp 1 Minor Stoppage 0% Maint spare parts 40% 383 334 60% 91% 85% 80% 94% 96% 97% 99% 100% 99% 100% 100% 100% 120%
F in a l A s s e m b ly
P r e -P r od u c ti on
S o u rc e
M od el
A n t i-F o g g in g
Problem Description
P o w d er C o a tin g M e t aliz in g M e ta l R ef le c to r
Plant QA Matrix
ቤተ መጻሕፍቲ ባይዱ
Prioritize Matrix
T33 Hond MPV a HL Fogla 3504 3504
维修手册使用

节,组件,图和项目号,对照就可以找到零件的位置。
• 当不知件号时 • 当不知道件号时,进行下列步骤: • - 进入零件所在章的目录 • - 参阅零件应列的主要分组 • - 图按主要名词的字母顺序排列,找到零件所在图的标
题
• - 记下节,组件,和图号 • - 进入章和图找到图解的零件或按零件项目号列出的零
• 如76—11—01/401,这里: • — 76是指ATA章代号 • — 11是子系统或分子系统 • — 01是组件(部件) • — 401是页码区段
3)AMM的有效性
在手册每一页的左下方的有效性栏 (Effectivity Block) 记载了该页的有效性, 有效性为“All”,说明该页适 用于手册所对应机队的所有飞机,注意,维护手册的有 效性是针对特定页的.如下图所示:
5-12章为“总体”类; 20-49章为“系统”类; 51-57章为“结构”类; 60-65章为“螺旋桨/旋翼”类;国内民航客机很少涉及 70-91章为“发动机”类 (1-4章一般是留给航空公司用的)
三,手册的查询途径
1,手册一般有印刷版的,有胶卷胶片的,有磁带光盘的, 有网络版的。
2,在深航,我们可以查询印刷版,光盘,以及网络版的手 册。(如PMA,登陆myboeingfleet网站等)
维修手册使用
一,常用手册构成(以波音为例)
常用的手册有:
1,AMM 飞机维护手册 2,IPC 图解零件目录 3,SSM 系统图册 4,WDM 线路图手册 5,SRM 结构修理手册 6,FIM 故障隔离手册 (波音NG飞机) 7,MEL 最低设备清单 8,CDL,外型缺损清单
二,手册的编写规范
srm软件包用户指南说明书

Package‘srm’November3,2022Type PackageTitle Structural Equation Modeling for the Social Relations ModelVersion0.4-26Date2022-11-0310:20:31Author Steffen Nestler[aut],Alexander Robitzsch[aut,cre],Oliver Luedtke[aut]Maintainer Alexander Robitzsch<**********************.de>Description Provides functionality for structural equation modeling forthe social relations model(Kenny&La V oie,1984;<doi:10.1016/S0065-2601(08)60144-6>;Warner,Kenny,&Soto,1979,<doi:10.1037/0022-3514.37.10.1742>).Maximum likelihoodestimation(Gill&Swartz,2001,<doi:10.2307/3316080>;Nestler,2018,<doi:10.3102/1076998617741106>)andleast squares estimation is supported(Bond&Malloy,2018,<doi:10.1016/B978-0-12-811967-9.00014-X>).Depends R(>=3.1)Imports Rcpp,stats,utilsEnhances amen,TripleRLinkingTo Rcpp,RcppArmadilloLicense GPL(>=2)URL https:///alexanderrobitzsch/srm,https:///site/alexanderrobitzsch2/softwareNeedsCompilation yesRepository CRANDate/Publication2022-11-0310:00:02UTCR topics documented:srm-package (2)data.back (3)12srm-package data.bm (3)data.srm (4)HallmarkKenny (5)Kenzer (6)Malzer (6)srm (7)srm_arbsrm (11)Warner (12)Zero (13)Index15 srm-package Structural Equation Modeling for the Social Relations ModelDescriptionProvides functionality for structural equation modeling for the social relations model(Kenny&La V oie,1984;<doi:10.1016/S0065-2601(08)60144-6>;Warner,Kenny,&Soto,1979,<doi:10.1037/0022-3514.37.10.1742>).Maximum likelihood estimation(Gill&Swartz,2001,<doi:10.2307/3316080>;Nestler,2018,<doi:10.3102/1076998617741106>)and least squares estimation is supported(Bond &Malloy,2018,<doi:10.1016/B978-0-12-811967-9.00014-X>).Author(s)Steffen Nestler[aut],Alexander Robitzsch[aut,cre],Oliver Luedtke[aut]Maintainer:Alexander Robitzsch<**********************.de>ReferencesBond,C.F.,&Malloy,T.E.(2018a).Social relations analysis of dyadic data structure:The gen-eral case.In T.E.Malloy.Social relations modeling of behavior in dyads and groups(Ch.14).Academic Press.doi:10.1016/B9780128119679.00014XGill,P.S.,&Swartz,T.B.(2001).Statistical analyses for round robin interaction data.Canadian Journal of Statistics,29(2),321-331.doi:10.2307/3316080Kenny,D.A.,&La V oie,L.J.(1984).The social relations model.In L.Berkowitz(Ed.),Advances in experimental social psychology(V ol.18,pp.142-182).Orlando,FL:Academic.doi:10.1016/ S0*******(08)601446Nestler,S.(2018).Likelihood estimation of the multivariate social relations model.Journal of Educational and Behavioral Statistics,43(4),387-406.doi:10.3102/1076998617741106Warner,R.M.,Kenny,D.A.,&Soto,M.(1979).A new round robin analysis of variance for social interaction data.Journal of Personality and Social Psychology,37(10),1742-1757.doi:10.1037/ 00223514.37.10.1742See AlsoSee also the R packages amen and TripleR for estimating the social relations model.data.back3 data.back Dataset Back et al.(2011)DescriptionDataset used in Back,Schmukle and Egloff(2011).Usagedata(data.back)Format•The dataset data.back is a round-robin desiogn with54units and has the following structure data.frame :2862obs.of8variables:$Group:num1111111111...$Actor:int1111111111...$Partner:int234567891011...$Dyad:int12345678910...$y:int3322433233...$sex:int1111111111...$age:int22222222222222222222...$n:num-1.17-1.17-1.17-1.17-1.17-1.17-1.17-1.17-1.17-1.17...Sourcehttps://osf.io/zd67x/ReferencesBack,M.D.,Schmukle,S.C.,&Egloff,B.(2011).A closer look atfirst sight:Social relations lens model analysis of personality and interpersonal attraction at zero acquaintance.European Journal of Personality,25(3),225-238.doi:10.1002/per.790data.bm Dataset Bond and Malloy(2018)DescriptionThis is the illustration dataset of Bond and Malloy(2018)for a bivariate social relations model.The round robin design contains16persons and some missing values for one person.Usagedata(data.bm1)data(data.bm2)4data.srmFormat•The dataset data.bm1contains all ratings in a wide format.The two outcomes are arranged one below the other.data.frame :32obs.of16variables:$a:int NA121314151514141313...$b:int10NA10187151481212...$c:int1312NA14131413131112...[...]$p:int111314149817131112...•The dataset data.bm2is a subdataset of data.bm1which contains observations9to16. Source/arbsrm-the-general-social-relations-model/ ReferencesBond,C.F.,&Malloy,T.E.(2018a).Social relations analysis of dyadic data structure:The gen-eral case.In T.E.Malloy.Social relations modeling of behavior in dyads and groups(Ch.14).Academic Press.doi:10.1016/B9780128119679.00014Xdata.srm Example Datasets for the srm PackageDescriptionSome simulated example datasets for the srm package.Usagedata(data.srm01)Format•The dataset data.srm01contains three variables,10round robin groups with10members each.data.frame :900obs.of7variables:$Group:num1111111111...$dyad:num12345678910...$Actor:num1111111112...$Partner:num23456789103...$Wert1:num-0.15-0.950.821.15-1.791.171.79-0.57-0.461.19...$Wert2:num-0.770.170.420.16-0.440.891.67-1.9-0.742.67...$Wert3:num-0.490.08-0.121.16-2.78-0.742.66-1.28-0.451.93...HallmarkKenny5 HallmarkKenny Hallmark and Kenny Round Robin DataDescriptionData from Kenny et al.(1994)Usagedata(HallmarkKenny)FormatA data frame with802measurements of30round-robin groups on the following7round-robinvariables(taken on unnumbered7-point rating scales with higher numbers indicating a higher value of the trait):calm:rating of dimension calm-anxioussociable rating of dimension sociable-withdrawnliking rating of dimension like-do not likecareful rating of dimension careful-carelessrelaxed rating of dimension relaxed-tensetalkative rating of dimension talkative-quietresponsible rating of dimension responsible-undependableThe data frame also contains participants gender(actor.sex;1=F,2=M)and their age in years (actor.age).Note that the data was assessed in two conditions:odd round robin group numbers indicate groups in which participants rated all traits for a person at a time whereas even numbers refer to groups in which participants rated all the people for each trait.Source/srm/srmdata.htmReferencesKenny,D.A.,Albright,L.,Malloy,T.E.,&Kashy,D.A.(1994).Consensus in interpersonal perception:Acquaintance and the bigfive.Psychological Bulletin,116(2),245-258.doi:10.1037/ 00332909.116.2.2456Malzer Kenzer Zero Acquaintance Round Robin Data from KennyDescriptionData from Albright et al.(1988)Study2Usagedata(Kenzer)FormatA data frame with124measurements from7round-robin groups on the following5round-robinvariables(taken on unnumbered7-point rating scales with higher numbers indicating a higher value of the trait):sociable:rating of dimension sociableirritable:rating of dimension good-naturedresponsible:rating of dimension responsibleanxious:rating of dimension calmintellectual:rating of dimension intellectualThe data frame also contains the gender(actor.sex;1=F,2=M)of the participants and their self-ratings on thefive assessed traits(actor.sociable and so on).Source/srm/srmdata.htmReferencesAlbright,L.,Kenny,D.A.,&Malloy,T.E.(1988).Consensus in personality judgments at zero acquaintance.Journal of Personality and Social Psychology,55(3),387-395.doi:10.1037/0022-3514.55.3.387Malzer Zero Acquaintance Round Robin Data from MalloyDescriptionData from Albright et al.(1988)Study1Usagedata(Malzer)srm7FormatA data frame with216measurements from12round-robin groups on the following5round-robinvariables(assessed on numbered7-point rating scales with higher numbers indicating a higher value of the trait with the exception for good and calm):sociable:rating of dimension sociableirritable:rating of dimension good-naturedresponsible:rating of dimension responsibleanxious:rating of dimension calmintellectual:rating of dimension intellectualThe data frame also contains the gender(actor.sex;1=F,2=M)of the participants and their self-ratings on thefive assessed traits(actor.sociable and so on).Source/srm/srmdata.htmReferencesAlbright,L.,Kenny,D.A.,&Malloy,T.E.(1988).Consensus in personality judgments at zero acquaintance.Journal of Personality and Social Psychology,55(3),387-395.doi:10.1037/0022-3514.55.3.387srm Structural Equation Model for the Social Relations ModelDescriptionProvides an estimation routine for a multiple group structural equation model for the social relations model(SRM;Kenny&La V oie,1984;Warner,Kenny,&Soto,1979).The model is estimated by maximum likelihood(Gill&Swartz,2001;Nestler,2018).Usagesrm(model.syntax=NULL,data=NULL,group.var=NULL,rrgroup_name=NULL,person_names=c("Actor","Partner"),fixed.groups=FALSE,var_positive=-1, optimizer="srm",maxiter=300,conv_dev=1e-08,conv_par=1e-06,do_line_search=TRUE,line_search_iter_max=6,verbose=TRUE,use_rcpp=TRUE, shortcut=TRUE,use_woodbury=TRUE)##S3method for class srmcoef(object,...)##S3method for class srmvcov(object,...)##S3method for class srm8srm summary(object,digits=3,file=NULL,layout=1,...)##S3method for class srmlogLik(object,...)Argumentsmodel.syntax Syntax similar to lavaan language,see Examples.data Data frame containing round robin identifier variables and variables in the round robin designgroup.var Name of grouping variablerrgroup_name Name of variable indicating round robin groupperson_names Names for identifier variables for actors and partnersfixed.groups Logical indicating whether groups should be handled withfixed effectsvar_positive Nonnegative value if variances are constrained to be positiveoptimizer Optimizer to be used:"srm"for internal optimization using Fisher scoring and "nlminb"for L-FBGS optimization.maxiter Maximum number of iterationsconv_dev Convergence criterion for change relative devianceconv_par Convergence criterion for change in parametersdo_line_search Logical indicating whether line search should be performedline_search_iter_maxNumber of iterations during line search algorithmverbose Logical indicating whether convergence progress should be displayeduse_rcpp Logical indicating whether Rcpp package should be usedshortcut Logical indicating whether shortcuts for round robin groups with same structure should be useduse_woodbury Logical indicating whether matrix inversion should be simplified by Woodbury identityobject Object of class srmfile Optionalfile name for summary outputdigits Number of digits after decimal in summary outputlayout Different layouts(1or2)for layout of summary...Further arguments to be passedValueList with following entries(selection)parm.table Parameter table with estimated valuescoef Vector of parameter estimatesvcov Covariance matrix of parameter estimatesparm_list List of model matricessigma Model implied covariance matrices...Further valuessrm9ReferencesGill,P.S.,&Swartz,T.B.(2001).Statistical analyses for round robin interaction data.Canadian Journal of Statistics,29(2),321-331.doi:10.2307/3316080Kenny,D.A.,&La V oie,L.J.(1984).The social relations model.In L.Berkowitz(Ed.),Advances in experimental social psychology(V ol.18,pp.142-182).Orlando,FL:Academic.doi:10.1016/ S0*******(08)601446Nestler,S.(2018).Likelihood estimation of the multivariate social relations model.Journal of Educational and Behavioral Statistics,43(4),387-406.doi:10.3102/1076998617741106Warner,R.M.,Kenny,D.A.,&Soto,M.(1979).A new round robin analysis of variance for social interaction data.Journal of Personality and Social Psychology,37(10),1742-1757.doi:10.1037/ 00223514.37.10.1742See AlsoSee also TripleR and amen packages for alternative estimation routines for the SRM.Examples##############################################################################EXAMPLE1:Univariate SRM#############################################################################data(data.srm01,package="srm")dat<-data.srm01#--define modelmf<-%PersonF1@A=~1*Wert1@AF1@P=~1*Wert1@PWert1@A~~0*Wert1@A+0*Wert1@PWert1@P~~0*Wert1@P%DyadF1@AP=~1*Wert1@APF1@PA=~1*Wert1@PAWert1@AP~~0*Wert1@AP+0*Wert1@PAWert1@PA~~0*Wert1@PA#--estimate modelmod1<-srm::srm(mf,data=dat,rrgroup_name="Group",conv_par=1e-4,maxiter=20)summary(mod1)round(coef(mod1),3)##############################################################################EXAMPLE2:Bivariate SRM#############################################################################10srm data(data.srm01,package="srm")dat<-data.srm01#--define modelmf<-%PersonF1@A=~1*Wert1@AF1@P=~1*Wert1@PF2@A=~1*Wert2@AF2@P=~1*Wert2@PWert1@A~~0*Wert1@A+0*Wert1@PWert1@P~~0*Wert1@PWert2@A~~0*Wert2@A+0*Wert2@PWert2@P~~0*Wert2@P%DyadF1@AP=~1*Wert1@APF1@PA=~1*Wert1@PAF2@AP=~1*Wert2@APF2@PA=~1*Wert2@PAWert1@AP~~0*Wert1@AP+0*Wert1@PAWert1@PA~~0*Wert1@PAWert2@AP~~0*Wert2@AP+0*Wert2@PAWert2@PA~~0*Wert2@PA#--estimate modelmod1<-srm::srm(mf,data=dat,rrgroup_name="Group",conv_par=1e-4,maxiter=20)summary(mod1)##############################################################################EXAMPLE3:One-factor model#############################################################################data(data.srm01,package="srm")dat<-data.srm01#--define modelmf<-#definition of factor for persons and dyad%Personf1@A=~Wert1@A+Wert2@A+Wert3@Af1@P=~Wert1@P+Wert2@P+Wert3@P%Dyadf1@AP=~Wert1@AP+Wert2@AP+Wert3@AP#define some constraintsWert1@AP~~0*Wert1@PAWert3@AP~~0*Wert3@PA#--estimate modelmod1<-srm::srm(mf,data=dat,rrgroup_name="Group",conv_par=1e-4)srm_arbsrm11 summary(mod1)coef(mod1)#-use stats::nlminb()optimizermod1<-srm::srm(mf,data=dat,rrgroup_name="Group",optimizer="nlminb",conv_par=1e-4) summary(mod1)srm_arbsrm Least Squares Estimation of the Social Relations Model(Bond&Mal-loy,2018)DescriptionProvides least squares estimation of the bivariate social relations model with missing completely at random data(Bond&Malloy,2018a).The code is basically taken from Bond and Malloy(2018b) and rewritten for reasons of computation time reduction.Usagesrm_arbsrm(data,serror=TRUE,use_srm=TRUE)##S3method for class srm_arbsrmcoef(object,...)##S3method for class srm_arbsrmsummary(object,digits=3,file=NULL,...)Argumentsdata Rectangular dataset currently containing only one round robin group.Bivariate observations are stacked one below the other(see example dataset data.bm1).serror Logical indicating whether standard errors should be calculated.use_srm Logical indicating whether the rewritten code(TRUE)or the original code of Bond and Malloy(2018b)should be used.object Object of class srm_arbsrmfile Optionalfile name for summary outputdigits Number of digits after decimal in summary output...Further arguments to be passedValueList containing entriespar_summary Parameter summary tableest Estimated parameters(as in Bond&Malloy,2018b)se Estimated standard errors(as in Bond&Malloy,2018b)12WarnerNoteIf you use this function,please also cite Bond and Malloy(2018a).Author(s)Rewritten code of Bond and Malloy(2018b).See /arbsrm-the-general-social-relations and /wp-content/uploads/2017/09/arbcodeR.pdf.ReferencesBond,C.F.,&Malloy,T.E.(2018a).Social relations analysis of dyadic data structure:The gen-eral case.In T.E.Malloy.Social relations modeling of behavior in dyads and groups(Ch.14).Academic Press.doi:10.1016/B9780128119679.00014XBond,C.F.,&Malloy,T.E.(2018b).ARBSRM-The general social relations model.http:///arbsrm-the-general-social-relations-model/.See AlsoWithout missing data,ANOV A estimation can be conducted with the TripleR package.Examples##############################################################################EXAMPLE1:Bond and Malloy(2018)illustration dataset#############################################################################data(data.bm2,package="srm")dat<-data.bm2#-estimationmod1<-srm::srm_arbsrm(dat)mod1$par_summarycoef(mod1)summary(mod1)#--estimation with original Bond and Malloy codemod1a<-srm::srm_arbsrm(dat,use_srm=FALSE)summary(mod1a)Warner Round Robin Data Reported in Warner et al.DescriptionData from Warner et al.(1979)Zero13Usagedata(Warner)FormatA data frame with56measurements of a single round-robin group on a single round-robin variablethat was measured at three consecutive time points.The variable reflects the proportion of time an actor spent when speaking to a partner.prop.T1:proportion of time spent in thefirst interactionprop.T2:proportion of time spent in the second interactionprop.T3:proportion of time spent in the third interactionSourceSee Table7(p.1752)of the Warner et al.(1979).ReferencesWarner,R.M.,Kenny,D.A.,&Soto,M.(1979).A new round robin analysis of variance for social interaction data.Journal of Personality and Social Psychology,37(10),1742-1757.doi:10.1037/ 00223514.37.10.1742Zero Zero Acquaintance Round Robin Data From Albirght,Kenny,and Mal-loyDescriptionData from Study3of Albright et al.(1988)Usagedata(Zero)FormatA data frame with636measurements of36round robin groups on the following15round-robinvariables(taken on7-point rating scales with higher values indicating more of the trait):sociable:rating of dimension sociable-reclusivegood:rating of dimension good-natured-irritableresponsible:rating of dimension responsible-undependablecalm:rating of dimension calm-anxiousintellectual:rating of dimension intellectual-unintellectualimaginative:rating of dimension imaginative-unimaginative14Zerotalkative:rating of dimension talkative-silentfussy:rating of dimension fussy-carelesscomposed:rating of dimension composed-excitablecooperative:rating of dimension cooperative-negativisticphysically_attractive:rating of dimension physically attractive-unattractiveformal_dress:rating of dimension formal dress-casual dressneatly_dressed:rating of dimension neatly dressed-sloppy dressathletic:rating of dimension athletic-not athleticyoung:rating of dimension young-oldThe data frame also contains the gender(actor.sex;1=F,2=M)of the participants and their self-ratings on thefive assessed traits(actor.sociable and so on).Source/srm/srmdata.htmReferencesAlbright,L.,Kenny,D.A.,&Malloy,T.E.(1988).Consensus in personality judgments at zero acquaintance.Journal of Personality and Social Psychology,55(3),387-395.doi:10.1037/0022-3514.55.3.387Indexpackagesrm-package,2coef.srm(srm),7coef.srm_arbsrm(srm_arbsrm),11data.back,3data.bm,3data.bm1(data.bm),3data.bm2(data.bm),3data.srm,4data.srm01(data.srm),4 HallmarkKenny,5Kenzer,6logLik.srm(srm),7Malzer,6srm,7srm-package,2srm_arbsrm,11summary.srm(srm),7summary.srm_arbsrm(srm_arbsrm),11vcov.srm(srm),7Warner,12Zero,1315。
欧姆龙术语表

Actual IO Table AddressApplicationASCIIAuxiliary AreaBaud rateBCDBinary Coded Decimal BinaryBitBooleanBridgeBroadcast addressBusCentral Processing Unit ClipboardCommand modifier Common link parameter Compact Flash ComponentsControl bitController Link Counter areaCounterCPU bus link areaCPU typeCPUCS-seriesCJ-seriesCX-ServerCX-Server ProjectCycle timeData areaData bitsData linkData Link EditorData link tableData locationData memory DatagramDDEDDE management library DDE Manager toolDebug modeDecimalDefaultDestination network address Destination node number Destination nodeDevice groupDevice typeDeviceDialogDLLDouble Floating Point DownloadDragDriverDynamic Data Exchange Echo testEEPROMElementsEnd ConnectionEnd network addressError statusEthernetEven parityEvent frameExclusive modeFile Transfer Protocol FINSFinsGatewayFlagFloating PointFolderFrame lengthFTPExpansion memoryFile memoryFile memoryGateway deviceGateway network address Gateway PLCGUIHard disk HexadecimalHierarchyHigh LinkHost computerHost link systemHost link unitIconIDSC device type Import toolInput bit data areaInputInstructionIntel HexInterfaceInternal data type Internode testInvoking applicationIO bitIO Table componentIOIP address tableIP addressIP router tableInput bitInput deviceLocal area network Local network address IPItemLANLink Relay AreaLink systemLink unitLinkLoadLocal network number Local tableLREALLSSMark parityMasterMbMemory areaMemory Card component Memory Card Writer Memory cardMHzMicro host linkMicrosoft ExcelMicrosoft Windows Explorer ModemMonitor modenNative data format Network bridgeNetwork parameters Network Service Board Node numberNodeNSBOdd parityOfflineOLEOnlineOutput Bit data area Output bitOutput deviceOutputPacketParity bitParityPathPeripheralPerformance Monitor tool Ping testPLCPLC Clock toolPLC Error componentPLC Memory component PLC Setup component PointPortProgramProgram memory Program modeProjectPROM writerPROMProtocolPSTNRackRAMRead modeRead/write mode Refresh parameter table Registered IO Table Relay network address Relay node number Relay tableRemote networkRemote TerminalsResetRootRoot groupRotary switchRouting tableRoutingRS232RS422RTsRun ModeSerial ConnectionServerServer application Signed DecimalSIOUSlaveSlotsSoftware switchesSpace paritySpecial Input /Output UnitSRM1 device typeStep AreaStop bitsSymbolSYSMAC LINK SYSMAC NET SYSMAC WAY System areaSystem configuration Tagged databaseTAPITarget PLCTaskbarTCP/IPTemperature Controller Temporary Relay Area Timer areaToolsTopicTransceiverTransfer from PLC TextTransfer to PLC UnknownTransition Area TransmitterUDPUnitsUser Datagram Protocol WordUnit number真正的硬件配置的PLC单元和电源插槽。
SRIM – The stopping and range of ions in matter (2010)

SRIM –The stopping and range of ions in matter (2010)James F.Ziegler a,*,M.D.Ziegler b ,J.P.Biersack caUnited States Naval Academy,Physics Dept.,Annapolis,MD 21402,USA bUniversity of California at Los Angeles,Los Angeles,CA 90066,USA cBerlin,Germanya r t i c l e i n f o Article history:Available online 26February 2010Keywords:SRIMIon stopping Stopping power Stopping force Ion rangea b s t r a c tSRIM is a software package concerning the S topping and R ange of I ons in M atter.Since its introduction in 1985,major upgrades are made about every six years.Currently,more than 700scientific citations are made to SRIM every year.For SRIM-2010,the following major improvements have been made:(1)About 2800new experimental stopping powers were added to the database,increasing it to over 28,000stop-ping values.(2)Improved corrections were made for the stopping of ions in compounds.(3)New heavy ion stopping calculations have led to significant improvements on SRIM stopping accuracy.(4)A self-con-tained SRIM module has been included to allow SRIM stopping and range values to be controlled and read by other software applications.(5)Individual interatomic potentials have been included for all ion/atom collisions,and these potentials are now included in the SRIM package.A full catalog of stopping power plots can be downloaded at .Over 500plots show the accuracy of the stopping and ranges produced by SRIM along with 27,000experimental data points.References to the citations which reported the experimental data are included.Published by Elsevier B.V.1.IntroductionSRIM is a software package concerning the S topping and R ange of I ons in M atter.It has been continuously upgraded since its intro-duction in 1985[1].A recent textbook ‘‘SRIM –The Stopping and Range of Ions in Matter ”describes in detail the fundamental phys-ics of the software [2].Since this time,corrections have been made based on new experimental data [3].Major changes occur in SRIM about every six years.The last major changes were in 1995and 1998and 2003.In 1995a complete overhaul was made of the stop-ping of relativistic light ions with energies above 1MeV/u.In 1998,special attention was made to the Barkas Effect and the theoretical stopping of Li ions.In 2010,significant changes were made to cor-rect the stopping of ions in compounds.All the figures in this paper are also available on the SRIM website,in considerably more detail.2.SRIM-2010stopping accuracyShown in Table 1are the statistical improvements in SRIM’s stopping power accuracy when compared to experimental data and also compared to SRIM-1998.The right two columns show the percentage of data points within 5%and within 10%of the SRIM calculation.The experimental stopping powers for heavy ions contain far more scatter than for light ions,hence there are larger errors for heavy ions,Be–U.The accuracy of SRIM-2010for individual ions or targets can be reviewed by viewing plots which compare experimental values and the equivalent SRIM calculations.Fig.1shows a typical com-parison for a light ion,He,in Ag.Fig.2shows a similar plot for all heavy ions,Be(4)–U(92)in Ag.Here,the various ion stopping powers have been normalized to the stopping of Al ions in Al,(nor-malization means that for any ion,the relative error of its experi-mental value to that calculated by SRIM is plotted with a similar displacement from the stopping of Al ions in Ag).Note that the scatter of data points is much higher than for the case of He ions in Ag,which increases the perceived error of SRIM.Higher resolu-tion figures for each heavy ion and all elemental targets are avail-able at .3.Stopping of ions in compoundsBragg and Kleeman,in 1903,conducted stopping experiments with a radium source in organic gases such as methyl bromide and methyl iodide to find how alpha stopping depended on the atomic weight of the target.They also calculated the stopping contribution of hydrogen and carbon atoms in hydrocarbon target gases by assuming a linear addition based on the chemical composition of H and C atoms in the targets.The concept that the stopping power of a compound may be estimated by the linear combination of the stopping powers of its individual elements has come to be known as Bragg’s Rule [4].This rule is reasonably accurate,and the measured stopping of ions in compounds usually deviates less than 20%from that0168-583X/$-see front matter Published by Elsevier B.V.doi:10.1016/j.nimb.2010.02.091*Corresponding author.E-mail address:Ziegler@ (J.F.Ziegler).Nuclear Instruments and Methods in Physics Research B 268(2010)1818–1823Contents lists available at ScienceDirectNuclear Instruments and Methods in Physics Research Bjournal homepage:www.els ev i e r.c o m /l o c a t e /n i mbpredicted by Bragg’s rule.The accuracy of Bragg’s rule is limited be-cause the energy loss to the electrons in any material depends on the detailed orbital and excitation structure of the matter,and any differences between bonding in elemental materials and in compounds will cause Bragg’s rule to become inaccurate.Further,bonding changes may also alter the charge state of the transitionTable 1Accuracy of SRIM stopping calculations.Approx.data pts.SRIM-1998(%)SRIM-2010(%)SRIM-2010(within 5%)SRIM-2010(within 10%)H ions 9000 4.5 3.968%85%He ions 6800 4.6 3.570%87%Li ions 1700 6.4 4.668%81%Be–U Ions10,6008.1 5.655%78%Overall accuracy28,1006.14.364%85%Notes to Table 1:The above table compares all 28,000data points to SRIM calculations.If wacko points are omitted (those differing from SRIM by more than 25%)then most of the above heavy ion accuracy numbers would be reduced by about 25%.The overall accuracy of SRIM-2010then reduces to 3.9%instead of 4.3%.Approx.data points :Current total data points used in SRIM plots.SRIM-1998:Comparison of SRIM-1998stopping to experimental data.SRIM-1998was the last major change in SRIM stopping powers.SRIM-2010:Current stopping power calculation.SRIM-2010(within 5%):Percentage of experimental data within 5%of the SRIM values.SRIM-2010(within 10%):Percentage of experimental data within 10%of the SRIMvalues.Fig.1.The stopping of He ions in Ag targets.The plot shows experimental values of He ion stopping in Ag targets.It shows the actual stopping,in units of eV/(1015atoms/cm 2).At the right is a listing of the original data citations.As noted,there is a total of 439data points taken from 44papers,and they vary from SRIM calculations by an average of 3.9%.Also noted is the mean ionization potential used for Al (<I >=488eV)and the Fermi velocity ratio for Ag,V /V F =1.254.The <I >value is only used for high energy stopping (>1MeV/u),while the Fermi velocity is important for lower velocities.A higher resolution plot is available at .Fig.2.The stopping of heavy ions in Ag targets.The plot shows experimental stopping values of heavy ions (atomic numbers 4–92)in Ag targets.The plot is organized similar to that of Fig.1.There are 930experimental data points taken from 131citations,and the mean error of SRIM is 4.5%.Ag targets are easy to make and these targets tend to have small grains without texture and contain few contaminants.So the accuracy of SRIM is better than normal when compared to experimental heavy ion data due to the consistency of the targets.A higher resolution plot is available at .J.F.Ziegler et al./Nuclear Instruments and Methods in Physics Research B 268(2010)1818–18231819ion,thus changing the strength of its interaction with the target medium.Detailed experimental studies of Bragg’s rule started in the 1960’s,and wide discrepancies were found from simple additivity of stopping powers.A classic example is shown in Fig.3for targets containing H and C atoms,which show non-additivity of stopping in simple hydrocarbons[5].In thisfigure,the stopping of He ions in various hydrocarbons was measured for pairs of compounds,and the relative contribution of H and C was extracted for each pair (solving two equations with two unknowns).It was found that the relative stopping contributions of H and C differ by almost 2Âover the range of compounds.Similar work studied more com-plex hydrocarbons but instead of adding H and C bonds,they added extra hydrocarbon molecules.In this study,it was found that by adding identical molecules to hydrocarbon strings, stopping linearity returned[6].Adding new molecules to a target just scaled the stopping by the extra number of atoms.These results showed that atomic bonding had large effects on stopping powers in simple molecular targets,while extra agglomeration of molecules to the target compounds had a small stopping effect.Since these early experiments,theorists have shown that extensive calculations can predict the stopping of light ions (usually protons)in hydrocarbon compounds.Much of this work has been based on a seminal paper by Peter Sigmund that devel-oped methods to account for detailed internal motion within a medium[7].This theory allows for arbitrary electronic configura-tions in the target.Sabin and collaborators used this approach to calculate stopping powers for protons in hydrocarbons with good success[8].Sabin’s calculation follows what is sometimes called the‘‘Köln Core and Bond”(CAB)approach which is discussed in detail below.The Core and Bond(CAB)approach suggested that stopping powers in compounds can be predicted using the superposition of stopping by atomic‘‘cores”and then adding the stopping corre-sponding to the bonding electrons[9].The core stopping would simply follow Bragg’s rule for the atoms of the compound,where we linearly add the stopping from each of the atoms in the com-pounds.The chemical bonds of the compound would then contain the necessary stopping correction.They would be evaluated depending on the simple chemical nature of the compound.For example,for hydrocarbons,carbon in C–C,C@C and C…C struc-tures would have different bonding contributions(C@C indicates a double-bond structure and C…C is a triple bond).SRIM uses this CAB approach to generate corrections between Bragg’s rule and compounds containing the common elements in compounds:H,C,N,O,F,S and Cl.These light atoms have the larg-est bonding effect on stopping powers.Heavier atoms are assumed not to contribute anomalously to stopping because of their bonds (discussed later in Stopping of High Energy Heavy Ions).When you use SRIM,you have the option to use the Compound Dictionary which contains the chemical bonding information for about150 common compounds.The compounds with available corrections are shown with a Star symbol,q,next to the name.When these compounds are selected,SRIM shows the chemical bonding dia-gram and calculates the best stopping correction.The correction is a variation from unity(1.0=no correction).Some corrections are quite big:carbon atoms have almost a4Âchange in stopping power from single bonds to triple bonds.This large change indi-cates the importance of making some sort of correction for the stopping of ions in compounds.The CAB corrections that SRIM uses have been extracted from the stopping of H,He and Li ions in more than100compounds, from162experiments.The details of applying this correction are described in Ref.[10].SRIM correctly predicts the stopping of H and He ions in compounds with an accuracy of better than2%at the peak of their stopping power curve,$125keV/u.An example of a large correction for compound targets is the9% correction necessary for a target of water,H2O,see Fig.4.The stop-ping of He ions in gaseous H2and O2is shown with the lower two dotted lines.The stopping in gaseous water vapor is essentially the Bragg’s Rule sum since its bonding correction is only1%,see the upper dotted line.However,for solid water(ice),the sum of stop-ping in H2O is shown as the upper solid line.With the H2O phase correction,which reduces the stopping by9%at the peak,SRIM shows good agreement between predicted stopping and the data from the ten experimental reports[11].The limitations of the CAB approach should be mentioned.A.The most important limitation might be that of the targetband-gap.Experiments on insulating targets dominate the experimental results that we use.For compounds which are conducting,there might be an error with thecalculatedFig.3.Accuracy of Bragg’s Rule in hydrocarbon compounds.In thisfigure,the stopping of He ions(at500keV)in various hydrocarbons is shown for pairs of compounds,with the relative contributions of stopping in H and C extracted assuming Bragg’s Rule and solving using two unknowns[5].This classic paper shows with clarity the errors associated with Bragg’s Rule.The units of the ordinate and abscissa are reduced stopping units,e[18].It is found that the various determinations of stopping by H and C atoms differ by almost2Âover the range of compounds.The result is a clear indication of the importance of including bonding corrections in stopping powers.(Figure from Ref.[5]). 1820J.F.Ziegler et al./Nuclear Instruments and Methods in Physics Research B268(2010)1818–1823stopping correction being too small.Theoretically,band-gap materials are expected to have lower stopping powers than equivalent conductors because the small energy transfers to target electrons are not available in insulators.It is not clear what the magnitude of this effect is,but about 50papers have discussed the stopping of ions in metals and their oxides,e.g.targets of Fe,Fe 2O 3and Fe 3O 4.These exper-iments evaluated similar materials with and without band-gaps.No significant differences were found that could be attributed to the band-gap.Measurements have also been made of the stopping of H and He ions into ice (solid water)with various dopings of salt (NaCl).No change of energy loss was observed for up to 6orders of magnitude change in resistivity of the ice [11].B.The scaling of ion stopping from H to He to Li ions is assumed to be independent of target material.This assump-tion has been evaluated with 27targets which have been measured for two of the three ions (at the same ion velocity)and 6of these targets have been measured for all three ions (see listings in Ref.[11]).In all cases,the stopping scaled identically within 4%.That is,for H (125keV)and He (500keV)and Li (875keV)the scaling of stopping powers was 1:2.7:4.7for the 27targets (average error was <4%).(For those unfamiliar with stopping theory,the primary parameter for the scaling of stopping powers is the ion velocity,which reduces to scaling in units of keV/a.).C.The light elements of He and Ne are missing from the above list of target bonding atoms.No comparative experiments have been done on the stopping into elemental He in solid/gas phases.However studies of stopping into targets of Ne and Ar have been conducted in both gas and solid form.These papers show no significant difference between the stopping in gas and solid phases.It appears that the Van der Waals forces,which hold noble gases together in frozen form,are too weak to effect the energy loss of ions.Of particular note is the extensive work done in a PhD paper by Besenbacher.[12].D.The light target atoms of Li,Be and B are missing from the list of bonding atoms with corrections.This is a serious defect.The number of papers that have looked at com-pounds which contain significant amounts of these three elements is too limited to allow their evaluation.Target atoms of these three elements are considered by SRIM to have no bonding correction,which is clearly not true.But without experimental data,there is no reliable way to eval-uate the contribution of their bonds in compounds.E.Bragg’s Rule and Heavy Target Elements.We have concen-trated on the analysis of the stopping of ions in compounds made up of light elements.For compounds with heavier atoms,many experiments have shown that deviations from Bragg’s rule disappear.In Table 2are shown representative examples of ion stopping in various compounds containing heavy elements.None show measurable deviations from Bragg’s rule.These and other similar results were reviewed in the 1980s [13,14].4.Stopping of high energy heavy ionsThe stopping powers of high energy (E >1MeV/u)heavy ions (Z >3)have two separate components.First is the charge state of these ions,which is traditionally addressed by using the Brandt–Kitagawa approximation,and then the many high velocity effects are combined into modern Bethe–Bloch theory.The Brandt–Kitagawa (BK)theory [15]is easiest to understand relative to the Bohr theory of the average charge state of heavy ions [16].Bohr suggested the simple picture that the energetic heavy ion would lose any of its electrons whose classical velocity was slower than the ion’s velocity.This concept lasted for more than 30years,with remarkable success.The concept was then improved by the suggestion of BK that one should consider instead the loss of any electrons whose velocity was slower than the relative velocity of the ion to the target medium.This lowered the charge state of heavy ions since the relative velocity of the ion was always lower than its absolute velocity.BK then presented a simple method of calculating this relative velocity based on considering the target to be a perfect Fermi conductor.This significantly improved the calculation of stopping powers [1].Modern approaches to Bethe–Bloch stopping equation have been reviewed in detail in Ref.[17].In Bethe–Bloch,twolargeFig.4.Corrections for stopping in compounds:He ions in water.The effects on stopping of target phase are illustrated in the figure for the stopping of He ions in water (solid and gaseous).Data from 14citations are shown.The special bonding of H–O in water is approximately the same for H–H and O–O bonds,so the stopping in the gaseous H 2O is almost the same as found using Bragg’s Rule.However,a large 9%phase correction must be applied to calculate the stopping of H 2O in solid forms,ice and water (see text).A higher resolution plot is available at .J.F.Ziegler et al./Nuclear Instruments and Methods in Physics Research B 268(2010)1818–18231821components are not well described by pure theoretical consider-ations:(1)the mean ionization energy of the target,commonly symbolized using<I>,and(2)the shell corrections for the target, called C/Z2.The<I>value for a target corrects for the quantized en-ergy levels of the target electrons and also any band-gap and target phase correction.The C/Z2term corrects for the Bethe–Bloch assumption that the ion velocity is much larger than the target electron velocities.This term is usually calculated by detailed accounting of the particle’s interaction with each electronic orbit in various elements.Since both of these terms are only dependent on the target,they are assumed to be the same for heavy ions and lighter ions.An example of SRIM’s stopping accuracy for heavy ions is shown in Fig.5.It shows the ratio of experimental stopping values to SRIM calculation for heavy ions in Al targets.(Al targets seem to be the most reliable target to make,since the data scatter about an aver-age value is the least of that for any solid).The data shown are from 135papers,and represents720data points for ion energies over 1MeV/u.There are several heavy ion data points at about 100MeV/u which show about5%higher experimental values than SRIM values.This is of the order of the estimated nuclear reaction losses,and is always a problem with very high energy ions (>10MeV/u).5.Anomalous heavy Ion stopping valuesSRIM uses several different stopping theories to evaluate the accuracy of experimental stopping powers.Specifically,calcula-tions are made for all ions in individual targets(which eliminates common difficulties with target dependent quantities such as shell corrections and mean ionization potentials,discussed above).Cal-culations are also made of one heavy ion in all solids,which elim-inates some of the difficulties with ion dependent quantities such as the degree of ion stripping.Also,calculations are made from fun-damental theories like the Brandt–Kitagawa theory and LSS theory [18].If the experimental values are within reasonable agreement with this set of theoretical calculations,then the experimental val-ues are weighted with the theoretical values to obtainfinal values. However,at times,significant errors occur in experimental stop-ping values and they deviate so far from theoretical values that they are totally ignored.Table2Bragg’s rule accuracy in heavy compounds.Compound Deviation from Bragg’s rule(%)Compound Deviation from Bragg’s rule(%)Compound Deviation from Bragg’s rule(%)Al2O3<1HfSi2<2Si3N4<2Au–Ag alloys<1NbC<2Ta2O5<1Au–Cu alloys<2NbN<2TiO2<1BaCl2<2Nb2O5<1W2N3<2BaF2<2RhSi<2WO3<2Fe2O3<1SiC<2ZnO<1Fe3O4<1Note:For compounds which contain elements with atomic numbers greater than12,it is possible to combine the CAB approach with Bragg’s rule.The CAB approach can beused for the small atomic number cores and bonds,and these can be combined with the normal stopping contribution of the other components of thecompound.Fig.5.Stopping of high energy heavy ions in aluminum.Thefigure shows the ratio of experimental stopping to SRIM calculation for high energy(>1MeV/u)ions in aluminum.The data shown is from135papers,and represents720data points over1MeV/u.The mean error is2.7%.There are several heavy ion data points at about 100MeV/u which show about5%higher experimental values than SRIM values.This is of the order of estimated nuclear reaction losses,and is always a problem with very high energy ions(>10MeV/u).A higher resolution plot is available at .1822J.F.Ziegler et al./Nuclear Instruments and Methods in Physics Research B268(2010)1818–1823Shown in Fig.6is the stopping of Mg ions in all solids.Note the large number of experimental data points below 100keV/u,which diverge from the SRIM stopping by up to 200%.For Mg ions,SRIM has an average accuracy of about 9%,the worst for any ion.Almost lost by the large number of data points which disagree with SRIM are those from seven citations which showed values almost identi-cal to SRIM.All of the deviant experimental stopping values were deter-mined by a technique called ‘‘Inverted Doppler Shift Attenuation ”,IDSA [19].This technique relies on the knowledge of the life-time of an excited nuclear state and is fraught with potential errors.The technique requires a nuclear reaction to occur in the target,result-ing in an emitted gamma ray.The gamma ray energy may be shifted due to motion of the recoiling particle.A particular source of error occurs if the differential of the particle energy loss with ion velocity changes much while the particle is slowing down.Note that in the energy range of 10–100keV/u,the energy loss is chang-ing rapidly with ion velocity,and this is where the maximum devi-ation occurs between IDSA stopping values and SRIM.As also shown,SRIM agrees well with 7papers which measured stopping using other methods.The advantage of the IDSA technique is that it can be used to determine stopping in difficult targets such as liquids and also to evaluate bonding effects in compounds.However,it is often used without full consideration of its sensitivity to non-linear effects.6.SRIM sub-routine moduleA ‘‘module”has been made so that the stopping and ranges of SRIM may be run as a batch sub-program for other applications [20].This allows the user to use SRIM as a sub-routine of another application that needs stopping powers and ranges.The user cre-ates a control file and executes the file ‘‘SRModule.exe”which will generate an output table similar to those normally made by SRIM.The user can generate the standard file (with stopping and ranges)or can generate a file which contains stopping powers for a specific list of energies.AcknowledgementsThe author is particularly indebted to the many users of SRIM who helped debug the first twenty five years of SRIM,leading to SRIM-2010.Without your significant help and enthusiasm,SRIM would not be the robust and versatile program that it is.References[1]J.F.Ziegler,J.Biersack,U.Littmark,‘‘The Stopping and Range of Ions in Matter”,Pergamon Press,1985.[2]J.F.Ziegler,J.P.Biersack,M.D.Ziegler,SRIM –The Stopping and Range of Ions inMatter”,Ion Implantation Press,2008./content/1524197.[3]See .More than 500plots are included showing more than28,000experimental data points as compared to SRIM calculations.[4]W.H.Bragg,R.Kleeman,Phil.Mag.10(1905)318.[5]A.S.Lodhi,D.Powers,Phys.Rev.A10(1974)2131.[6]D.Powers,Acc.Chem.Res.13(1980)433.[7]P.Sigmund,Phys.Rev.A26(1982)2497.[8]J.R.Sabin,J.Oddershede,Nucl.Instrum.Methods B27(1987)280.[9]G.Both,R.Krotz,K.Lohman,W.Neuwirth,Phys.Rev.A28(1983)3212.[10]The most recent core and bond values used in SRIM are shown at: n SRIM n CompoundsCABTheory.htm .The modeling technique used to extract these values was originally described in:J.F.Ziegler,J.M.Manoyan,Nucl.Instrum.Methods,B35(1988)215.[11]The data plotted in Fig.4are from papers listed at: n SRIM n Compounds.htm .This website also describes in detail how corrections are made for target phase changes (solid or gas phases)and for target compound binding.Also,citations are listed for compounds containing heavy atoms,and also the effects of variations of the target band-gap on stopping powers.[12]F.Besenbacher,J.Bottiger,O.Graversen,J.Hanse,H.Sorensen,Nucl.Instrum.Methods 188(1981)657–667.[13]D.I.Thwaites,Nucl.Instrum.Methods B12(1985)84.[14]D.I.Thwaites,Nucl.Instrum.Methods B27(1987)293.[15]W.Brandt,M.Kitagawa,Phys.Rev.25B (1982)5631.[16]N.Bohr,Mat.-Fys.Medd.K.Dan.Selse 18(1948)1.[17]J.F.Ziegler,Applied physics reviews,J.Appl.Phys.85(1999)1249–1272.[18]J.Lindhard,M.Scharff,H.E.Schiott,Kgl.Danske Vid.Sels.Mat.-Fys.Medd.33(1963)1.[19]P.Petkova, A.Dewaldb,P.von Brentano,‘‘A new procedure for lifetimedetermination using the Doppler-shift attenuation method”,Nucl.Instrum.Methods A-560(2006)564–570.[20]Details of using the Stopping and Range module are included in the SRIM-2010package.See the SRIM directory,.../SR Module/HELP SRModule.rtf.Fig.6.The stopping of Mg ions in all solids.The plot shows experimental stopping values for Mg ions in all solids.This plot shows a considerable number of data points which differ from SRIM calculations,especially for low energy ions (<100keV/u).The variation arises from the use of ‘‘Inverted Doppler Shift Attenuation”,IDSA,as a method to measure stopping powers.This technique is quite complex and relies on the knowledge of the life-time of an excited nuclear state (see text)and is fraught with potential errors.As shown,SRIM calculations are in serious disagreement with the lower energy Mg values of which were determined by IDSA,however it agrees with 7papers which measured stopping at the same energies,using other methods.A higher resolution plot is available at .J.F.Ziegler et al./Nuclear Instruments and Methods in Physics Research B 268(2010)1818–18231823。
SRM

◆ “适用性“也是一个不能忽略的问题。
在这个例子中,项目25A后面注着A20003K0002B, 这个号码可以在改装/服务通告( Modification/Service Bulletin List )清单中找到。
A20003K0002B是适用于MSN0012-0999的飞机。 A 20003 K0002 B A - AFTER 20003 – 改装号 K0002 – 设计方案号 B – 后缀 ◆ 页块的安排 这种页块的安排适用于所有的章节 识别页块 -- 1-98页 允许的损伤 -- 101-198页 修理页块 -- 201-998页
结构修理手册介绍
简介: 结构修理手册提供对飞机 结构或结构部件进行修理所需的信 息/数据。该手册没有客户化,也 就是说所有客户都使用同一手册。 手册分为以下7个部分:
◆ 手册中章节的安排: 51章 (结构/修理总述) 52章 (门) 53章 (机身) 54章 (吊架/短舱) 55章 (安定面) 56章 (窗) 57章 (机翼)
手册的内容主要包括:
允许的损伤 结构的材料识别 飞机最易被损伤的结构部件的典型修理 代用材料 紧固件 结构修理的一些程序介绍
其中,52-57章的布局基本相同,可以说也是结构修理手 册的核心部分。它主要包括:
部件的识别 允许的损伤 修理
(1)部件的识别
第一栏是“项目”(ITEM)的编号,例如: 10,10A,10B。后缀A,B,C等表该 部件是装在同一个位置,但有不同的适 用性,改装前或改装后等等。 第 二 栏 是 “ 名 称 ” ( NOMENCLATURE), 也 就 是 说 明 是什么部件,是组件,蒙皮,肋,……。
(b) 在节(SECTION)和分节(SUB-SECTION)部分, 看参考图(FIGUE REFERENCE) (c) 确定相应的图,识别损伤的部件/结构并参考识别页。
SRIM介绍

4.高能粒子慢化,根据入射粒子的能量和所需要的出射粒子的 能量,精确的选定减速靶板的厚度。
5.界面混合。
SRIM的应用
6.可以根据得到的图形的数据估计入射粒子对靶所造成的空缺 损伤,考虑是否产生非晶形层。
7.可以根据得到图形的数据根据入射计量估计入射粒子在靶材 料中的掺杂浓度。
SRIM的应用
1.( Quick )快速计算一定能量粒子打进靶材料中的深度,入 射粒子在靶物质中的分布,粒子的电离效应能量损失,传递给 反冲原子的能量,背散射粒子数和穿透粒子数。
2.( Full )计算入射粒子与靶原子的详细碰撞对靶物质的所 有损伤。比如:溅射产额,入射粒子和反冲原子的能量损失详 细情况。
SRIM简介
TRIM中的相关名词
➢ Stopping power:入射粒子在单位路程上损失的能量(-dE/dx)。
➢ Range:入射粒子从进入靶起到停止点所通过的总的路程,称为射程。
➢ Projected Range: 以Rp表示射程在入射方向投影的长度,称作投影 射程。
SRIM简介
下图是一个能量E,有入射角的入射粒子在物质中的轨迹
❖TRIM (the Transport of Ions in Matter) is a Monte-Carlo
calculation which follows the ion into the target, making detailed calculations of the energy transferred to every target atom collision. (multi-layer complex targets)
SRIM简介
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
SIMPLE REGRESSION MODEL
Y
P4
P1
P2 P3
X1
X2
X3
X4
X
In practice we can see only the P points.
15
SIMPLE REGRESSION MODEL
Y
P4
ˆ Y b1 b 2 X
P1
P2 P3
b1
X1
X2
X3
X4
X
Obviously, we can use the P points to draw a line which is an approximation to the line Y = b1 + b2X +u. If we write this line Y = b1 + b2X, b1 is an estimate of b1 and b2 is an estimate of b2.
16
SIMPLE REGRESSION MODEL
Y (actual value) Y
ˆ Y
(fitted value) R3
P4
ˆ Y b1 b 2 X
P1
R1 b1
R2 P3
R4
P2
X1
X2
X3
X4
X
The line is called the fitted model or sample regression model and the values of Y predicted by it are called the fitted values of Y. They are given by the heights of the R points.
2
The modern interpretation of REGRESSION: Regression analysis is concerned with the study of the dependence of one variable, the dependent variable, on one or more other variables, the explanatory variables, with a view to estimating and/or predicting the (population) mean or average value of the former in terms of the known or fixed (in repeated sampling) values of the latter.
17
SIMPLE REGRESSION MODEL
Y (actual value) Y
ˆ Y
(fitted value) (residual) R3 e1 P1 R1 R2 e2 P2 P3 e3 e4
P4
ˆ Y b1 b 2 X
ˆ Y Y e
R4
b1
X1
X2
X3
X4
X
The discrepancies between the actual and fitted values of Y are known as the residuals, e.
10
1.
2.
3.
5. 6.
SIMPLE REGRESSION MODEL
Some Basic Assumptions on u in SRM
The expected value of u, the disturbance term, in the population is 0. That is,
Y = b 1 + b 2X .
6
SIMPLE REGRESSION MODEL
Y
Y b1 b2X
b1
Q1
Q2
Q3
Q4
X1
X2
X3
X4
X
If the relationship were an exact one, the observations would lie on a straight line and we would have no trouble obtaining accurate estimates of b1 and b2.
8
SIMPLE REGRESSION MODEL
Y
P4
Y b1 b2X
P1
b1
Q1
Q2 P2
Q3 P3
Q4
X1
X2
X3
X4
X
To allow for such divergences, we will write the model as Y = b1 + b2X + u, where u is a disturbance term. A disturbance term is the deviation of an individual Yi around its expected value. It is an unobservabable random variable taking positive or negative values.
Q4
b1
b1 b2X 1
X1
X2
X3
X4
X
Each value of Y thus has a non-random component, b1 + b2X, and a random component, u. The first observation has been decomposed into these two components.
Topic 3. SIMPLE REGRESSION MODEL
(1)
SIMPLE REGRESSION MODEL (简单回归模型 ) LEAST SQUARES REGRESSION (最小二乘法 )
1
Historical origin of the term “Regression”:
This term was introduced by Francis Galton (1886). In a famous paper, Galton found that, although there was a tendency for tall parents to have tall children and for short parents to have short children, the average height of children born of parents of a given height tended to move or “regress” toward the average height in the population as a whole. In other words, the average height of sons of a group of tall fathers was less than their fathers’ height and the average height of sons of a groups of short fathers was greater than their fathers’ height.
E (u) = 0
This assumption means that the factors subsumed in ui do not systematically affect the mean value of Y; so to speak, the positive ui values cancel out the negative ui values so that their average or mean affect on Y is zero.
-1.000
SIMPLE REGRESSION MODEL
Y
Y b1 b2X
b1
X1
X2
X3
X4
X
Suppose that a variable Y is a linear function of another variable X, with unknown parameters b1 and b2 that we wish to estimate. Therefore, as a first approximation, we may write the function as
7
SIMPLE REGRESSION MODEL
Y
P4
Y b1 b2X
P1
b1
Q1
Q2 P2
Q3 P3
Q4
X1
X2
X3
X4
X
In practice, most economic relationships are not exact and the actual values of Y are different from those corresponding to the straight line.
X = independent variable, exogenous variable or regressor Y = dependent or endogenous variable b1 = intercept b2 = slope ui = disturbance term
12
SIMPLE REGRESSION MODEL
18
SIMPLE REGRESSION MODEL
Y (actual value) Y
ˆ Y
