2012年全国各地中考数学压轴题专集反比例函数解答(一)

合集下载

中考数学压轴题----《反比例函数综合》例题讲解

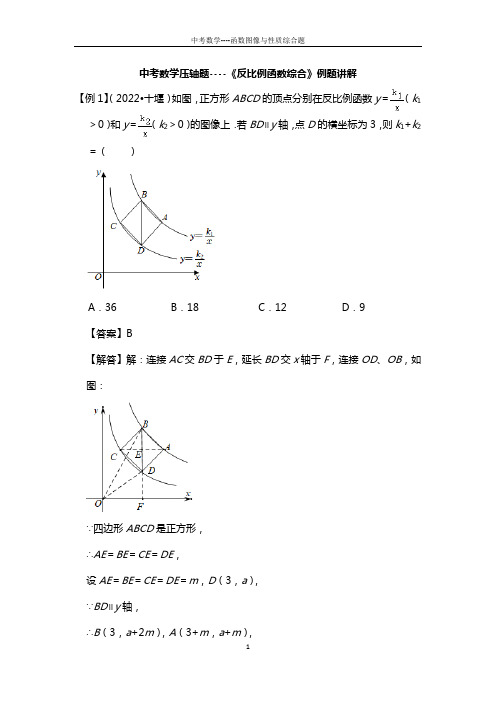
中考数学压轴题----《反比例函数综合》例题讲解【例1】（2022•十堰）如图，正方形ABCD的顶点分别在反比例函数y＝（k1＞0）和y＝（k2＞0）的图像上．若BD∥y轴，点D的横坐标为3，则k1+k2＝（）A．36B．18C．12D．9【答案】B【解答】解：连接AC交BD于E，延长BD交x轴于F，连接OD、OB，如图：∵四边形ABCD是正方形，∴AE＝BE＝CE＝DE，设AE＝BE＝CE＝DE＝m，D（3，a），∵BD∥y轴，∴B（3，a+2m），A（3+m，a+m），∵A，B都在反比例函数y＝（k1＞0）的图像上，∴k1＝3（a+2m）＝（3+m）（a+m），∵m≠0，∴m＝3﹣a，∴B（3，6﹣a），∵B（3，6﹣a）在反比例函数y＝（k1＞0）的图像上，D（3，a）在y＝（k2＞0）的图像上，∴k1＝3（6﹣a）＝18﹣3a，k2＝3a，∴k1+k2＝18﹣3a+3a＝18；故选：B【变式1-1】（2021•鄂州）如图，点A是反比例函数y＝（x＞0）的图像上一点，过点A作AC⊥x轴于点C，AC交反比例函数y＝（x＞0）的图像于点B，点P是y轴正半轴上一点．若△PAB的面积为2，则k的值为．【答案】8【解答】解：连接OA、OB，∵AC⊥x轴，∴AC∥y轴，∴S△AOB＝S△APB，∵S△APB＝2，∴S△AOB＝2，由反比例函数系数k的几何意义可得：S△AOC＝6，S△BOC＝，∴6﹣＝2，解得：k＝8，故答案为8．【变式2-2】（2021•荆州）如图，过反比例函数y＝（k＞0，x＞0）图像上的四点P1，P2，P3，P4分别作x轴的垂线，垂足分别为A1，A2，A3，A4，再过P1，P2，P3，P4分别作y轴，P1A1，P2A2，P3A3的垂线，构造了四个相邻的矩形．若这四个矩形的面积从左到右依次为S1，S2，S3，S4，OA1＝A1A2＝A2A3＝A3A4，则S1与S4的数量关系为．【答案】S1＝4S4【解答】解：∵过双曲线上任意一点、向坐标轴作垂线所围成的矩形面积S是个定值，OA1＝A1A2＝A2A3＝A3A4，∴S1＝k，S2＝k，S3＝k，S4＝k，∴S1＝4S4．故答案为：S1＝4S4．【变式1-3】（2022•毕节市）如图，在平面直角坐标系中，正方形ABCD的顶点A，B分别在x轴、y轴上，对角线交于点E，反比例函数y＝（x＞0，k ＞0）的图像经过点C，E．若点A（3，0），则k的值是．【答案】4【解答】解：设C（m，），∵四边形ABCD是正方形，∴点E为AC的中点，∴E（，），∵点E在反比例函数y＝上，∴，∴m＝1，作CH⊥y轴于H，∴CH＝1，∵四边形ABCD是正方形，∴BA＝BC，∠ABC＝90°，∴∠OBA＝∠HCB，∵∠AOB＝∠BHC，∴△AOB≌△BHC（AAS），∴BH＝OA＝3，OB＝CH＝1，∴C（1，4），∴k＝4，故答案为：4．【变式1-4】（2022•雁塔区校级模拟）如图，正方形ACBE的边长是，点B，C分别在x轴和y轴正半轴上，BO＝2，ED⊥x轴于点D，ED的中点F在反比例函数y＝（x＞0）的图像上，则k＝．【答案】3【解答】解：∵正方形ACBE的边长是，BO＝2，∴BC＝BE＝，∴OC＝＝＝1，∵∠ABC＝90°，∴∠OBC+∠EBD＝90°，∵∠OBC+∠OCB＝90°，∴∠OCB＝∠EBD，在△OBC和△DEB中，，∴△OBC≌△DEB（AAS），∴BD＝OC＝1，DE＝OB＝2，∴OD＝3，∴E（3，2），∵点F是ED的中点，∴F（3，1），∵点F在反比例函数y＝（x＞0）的图像上，∴k＝3×1＝3，故答案为3．【变式1-5】（2021•广元）如图，点A（﹣2，2）在反比例函数y＝的图像上，点M在x轴的正半轴上，点N在y轴的负半轴上，且OM＝ON＝5．点P （x，y）是线段MN上一动点，过点A和P分别作x轴的垂线，垂足为点D 和E，连接OA、OP．当S△OAD＜S△OPE时，x的取值范围是．【答案】1＜x＜4【解答】解：过点B作BF⊥ON于F，连接OB，过点C作CG⊥OM于点G，连接OC，如图，∵点A（﹣2，2）在反比例函数y＝的图像上，∴k＝﹣4．∴y＝．∵点A（﹣2，2），∴AD＝OD＝2．∴．设B（a，b），则ab＝﹣4，OF＝﹣b，BF＝a．∴＝＝2．同理：S△OCG＝2．从图中可以看出当点P在线段BC上时，S△OPE＞S△OBF，即当点P在线段BC上时，满足S△OAD＜S△OPE．∵OM＝ON＝5，∴N（0，﹣5），M（5，0）．设直线MN的解析式为y＝mx+n，则：，解得：．∴直线MN的解析式为y＝x﹣5．∴，解得：，．∴B（1，﹣4），C（4，﹣1）．∴x的取值范围为1＜x＜4．【变式1-6】（2021•荆门）如图，在平面直角坐标系中，Rt△OAB斜边上的高为1，∠AOB＝30°，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A 的对应点C恰好在函数y＝（k≠0）的图像上，若在y＝的图像上另有一点M使得∠MOC＝30°，则点M的坐标为．【答案】（，1）【解答】解：作AE⊥OB于E，MF⊥x轴于F，则AE＝1，∵∠AOB＝30°，∴OE＝AE＝，将Rt△OAB绕原点顺时针旋转90°得到Rt△OCD，点A的对应点C为（1，），∵点C在函数y＝（k≠0）的图像上，∴k＝1×＝，∴y＝，∵∠COD＝∠AOB＝30°，∠MOC＝30°，∴∠DOM＝60°，∴∠MOF＝30°，∴OF＝MF，设MF＝n，则OF＝n，∴M（n，n），∵点M在函数y＝的图像上，∴n＝，∴n＝1（负数舍去），∴M（，1），故答案为（，1）．【变式1-7】（2021•达州）如图，将一把矩形直尺ABCD和一块等腰直角三角板EFG摆放在平面直角坐标系中，AB在x轴上，点G与点A重合，点F在AD上，EF交BC于点M，反比例函数y＝（x＜0）的图像恰好经过点F，M，若直尺的宽CD＝1，三角板的斜边FG＝4，则k＝．【答案】﹣12【解答】解：过点M作MN⊥AD，垂足为N，则MN＝CD＝1，在Rt△FMN中，∠MFN＝45°，∴FN＝MN＝1又∵FG＝4，∴NA＝MB＝FG﹣FN＝4﹣1＝3，设OA＝a，则OB＝a+1，∴点F（﹣a，4），M（﹣a﹣1，3），又∵反比例函数y＝（x＜0）的图像恰好经过点F，M，∴k＝﹣4a＝3（﹣a﹣1），解得，a＝3，∴k＝﹣4a＝﹣12，故答案为：﹣12．a11。

中考压轴题-反比例函数综合(八大题型+解题方法)—冲刺2024年中考数学考点(全国通用)(解析版)

中考压轴题反比例函数综合（八大题型+解题方法）1.求交点坐标联立反比例函数与一次函数图象的解析式进行求解，特别地，反比例函数与正比例函数图象的两个交点关于原点对称.2.结合图象比较函数值的大小如图，一次函数y=k1x+b与反比例函数图象交于A,B 两点，过点A,B分别作y 轴的平行线，连同y 轴，将平面分为I,Ⅱ,Ⅲ,IV 四部分，在I,Ⅲ区域内，y₁<y₂,自变量的取值范围为x<x B或0<x<x A;在Ⅱ,IV区域内，y1>y₂,自变量的取值范围为x B<x<0或x>x A.3.反比例函数系数k的几何意义及常用面积模型目录：题型1：反比例函数与几何的解答证明题型2：存在性问题题型3：反比例函数的代数综合题型4：动态问题、新定义综合题型5：定值问题题型6：取值范围问题题型7：最值问题题型8：情景探究题（含以实际生活为背景题）题型1：反比例函数与几何的解答证明1．（2024·湖南株洲·一模）如图，在平面直角坐标系xOy 中，矩形OABC 的边OA 在x 轴上，OC 在y 轴上，4OA =，2OC =（不与B ，C 重合），反比例函数()0,0k y k x x=＞＞的图像经过点D ，且与AB 交于点E ，连接OD ，OE ，DE ．(1)若点D 的横坐标为1． ①求k 的值；②点P 在x 轴上，当ODE 的面积等于ODP 的面积时，试求点P 的坐标； (2)延长ED 交y 轴于点F ，连接AC ，判断四边形AEFC 的形状【答案】(1)①2；②15,04⎛⎫ ⎪⎝⎭或15,04⎛⎫− ⎪⎝⎭(2)四边形AEFC 是平行四边形，理由见解析【分析】（1）①根据矩形的性质得到90BCO B AOC ∠=∠=∠=︒，得()1,2D ，把()1,2D 代入()0,0ky k x x=＞＞即可得到结论；②由D ，E 都在反比例函数ky x =的图像上，得到1COD AOE S S ==△△，根据三角形的面积公式得到1111315241243222224ODE S =⨯−⨯⨯−⨯⨯−⨯⨯=△，设(),0P x ，根据三角形的面积公式列方程即可得到结论；（2）连接AC ，根据题意得到,22k D ⎛⎫ ⎪⎝⎭，4,4k E ⎛⎫ ⎪⎝⎭，设EF 的函数解析式为y ax b =+，解方程得到84k OF +=，求得24kCF OF AE =−==，根据平行四边形的判定定理即可得到结论．【解析】（1）解：①∵四边形ABCO 是矩形，4OA =， ∴90BCO B AOC ∠=∠=∠=︒，4BC OA ==， ∵2OC =，点D 的横坐标为1， ∴()1,2D ，2AB OC ==，∵反比例函数()0,0ky k x x =＞＞的图像经过点D ，∴122k =⨯=， ∴k 的值为2； ②∵()1,2D ，∴1CD =，∵D ，E 都在反比例函数2y x =的图像上，∴1COD AOE S S ==△△，∴111422AOE S OA AE AE==⋅=⨯△，∴12AE =，∴13222BE AB AE =−=−=， ∴1111315241243222224ODES =⨯−⨯⨯−⨯⨯−⨯⨯=△，∵点P 在x 轴上，ODE 的面积等于ODP 的面积，设(),0P x ，∴115224ODP S x =⨯⨯=△，解得：154x =或154x =−，∴点P 的坐标为15,04⎛⎫ ⎪⎝⎭或15,04⎛⎫− ⎪⎝⎭；（2）四边形AEFC AEFC 是平行四边形．理由：连接AC ，∵4OA =，2OC =，D ，E 都在反比例函数()0,0ky k x x =＞＞的图像上，∴,22k D ⎛⎫ ⎪⎝⎭，4,4k E ⎛⎫⎪⎝⎭，设EF 的函数解析式为：y ax b =+，∴2244k a b k a b ⎧⨯+=⎪⎪⎨⎪+=⎪⎩，解得：1284a kb ⎧=−⎪⎪⎨+⎪=⎪⎩， ∴EF 的函数解析式为：1824k y x +=−+，当0x =时，得：84ky +=，∴84k OF +=， ∴24kCF OF AE =−==，又∵CF AE ∥，∴四边形AEFC 是平行四边形．【点睛】本题是反比例函数与几何的综合，考查待定系数法确定解析式，反比例函数图像上的点的坐标的特征，矩形的性质，平行四边形的判定，三角形的面积等知识点．掌握反比例函数图像上的点的坐标的特征，矩形的性质是解题的关键．题型2：存在性问题2．（2024·四川成都·二模）如图①，O 为坐标原点，点B 在x 轴的正半轴上，四边形OACB 是平行四边形，4sin 5AOB ∠=，反比例函数(0)ky k x =>在第一象限内的图象经过点A ，与BC 交于点F ．(1)若10OA =，求反比例函数解析式；(2)若点F 为BC 的中点，且AOF 的面积12S =，求OA 的长和点C 的坐标；(3)在（2）中的条件下，过点F 作EF OB ∥，交OA 于点E （如图②)，点P 为直线EF 上的一个动点，连接PA ，PO ．是否存在这样的点P ，使以P 、O 、A 为顶点的三角形是直角三角形？若存在，请直接写出所有点P 的坐标；若不存在，请说明理由．【答案】(1)48(0)y x x =>C(3)存在，满足条件的点P 或(或或(【分析】（1）先过点A 作AH OB ⊥，根据4sin 5AOB ∠=，10OA =，求出AH 和OH 的值，从而得出A 点坐标，再把它代入反比例函数中，求出k 的值，即可求出反比例函数的解析式；（2）先设(0)OA a a =>，过点F 作FM x ⊥轴于M ，根据4sin 5AOB ∠=，得出45AH a =，35OH a=，求出AOHS △的值，根据12AOF S =△，求出平行四边形AOBC 的面积，根据F 为BC 的中点，求出6OBF S =△，根据12BF a =，FBM AOB ∠=∠，得出12BMFS BM FM =⋅，23650FOM S a =+△，再根据点A ，F 都在k y x =的图象上，12AOHSk=，求出a ，最后根据AOBC S OB AH =⋅平行四边形，得出OB AC ==C 的坐标；（3）分别根据当90APO ∠=︒时，在OA 的两侧各有一点P ，得出1P ，2P ；当90PAO ∠=︒时，求出3P ；当90POA ∠=︒时，求出4P 即可．【解析】（1）解：过点A 作AH OB ⊥于H ，4sin 5AOB ∠=，10OA =，8AH ∴=，6OH =，A ∴点坐标为(6,8)，根据题意得：86k=，可得：48k =，∴反比例函数解析式：48(0)y x x =>；（2）设(0)OA a a =>，过点F 作FM x ⊥轴于M ，过点C 作CN x ⊥轴于点N ，由平行四边形性质可证得OH BN =，4sin 5AOB ∠=，45AH a ∴=，35OH a=， 2143625525AOHS a a a ∴=⋅⋅=△，12AOF S =△，24AOBC S ∴=平行四边形，F 为BC 的中点，6OBFS∴=，12BF a=，FBM AOB ∠=∠，25FM a ∴=，310BM a =，2112332251050BMF S BM FM a a a ∴=⋅=⋅⋅=△，23650FOMOBFBMFSSSa ∴=+=+，点A ，F 都在ky x =的图象上，12AOH FOM S S k ∴==△△，∴226362550a a =+，a ∴OA ∴=AH ∴=OH =24AOBC S OB AH =⋅=平行四边形，OB AC ∴==ON OB OH ∴=+=C ∴；（3）由（2）可知A ，B 0)，F ．存在三种情况：当90APO ∠=︒时，在OA 的两侧各有一点P ，如图，设PF 交OA 于点J ，则J此时，AJ PJ OJ ==，P ∴，(P '，当90PAO ∠=︒时，如图，过点A 作AK OB ⊥于点K ，交PF 于点L ．由AKO PLA △∽△，可得PLP ，当90POA ∠=︒时，同理可得(P ．综上所述，满足条件的点P 的坐标为或(或或(．【点睛】此题考查了反比例函数的综合，用到的知识点是三角函数、平行四边形、反比例函数、三角形的面积等，解题的关键是数形结合思想的运用．3．（2024·广东湛江·一模）【建立模型】（1）如图1，点B 是线段CD 上的一点，AC BC ⊥，AB BE ⊥，ED BD ⊥，垂足分别为C ，B ，D ，AB BE =．求证：ACB BDE ≌；【类比迁移】（2）如图2，点()3,A a −在反比例函数3y x=图象上，连接OA ，将OA 绕点O 逆时针旋转90︒到OB ，若反比例函数k y x =经过点B ．求反比例函数ky x=的解析式；【拓展延伸】（3）如图3抛物线223y x x +−与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于C 点，已知点()0,1Q −，连接AQ ，抛物线上是否存在点M ，便得45MAQ ∠=︒，若存在，求出点M 的横坐标．【答案】（1）见解析；（2）3y x =−；（3）M 的坐标为39,24⎛⎫ ⎪⎝⎭或()1,4−−．【分析】（1）根据题意得出90C D ABE ︒∠=∠=∠=，A EBD ∠=∠，证明()AAS ACB BDE ≌，即可得证；（2）如图2，分别过点A ，B 作AC x ⊥轴，BD x ⊥轴，垂足分别为C ，D ．求解()3,1A −−，1AC =，3OC =．利用ACO ODB ≌△△，可得()1,3B −；由反比例函数ky x =经过点()1,3B −，可得3k =−，可得答案；（3）如图3，当M 点位于x 轴上方，且45MAQ ∠=︒，过点Q 作QD AQ ⊥，交MA 于点D ，过点D 作DE y⊥轴于点E ．证明AQO QDE ≌，可得AO QE =，OQ DE =，可得()1,2D ，求解1322AM y x =+：，令2132322x x x +=+−，可得M 的坐标为39,24⎛⎫ ⎪⎝⎭；如图，当M 点位于x 轴下方，且45MAQ ∠=︒，同理可得()1,4D −−，AM 为26y x =−−．由22623x x x −−=+−，可得M 的坐标是()1,4−−．【解析】证明：（1）如图，∵AC BC ⊥，AB BE ⊥，ED BD ⊥， ∴90C D ABE ︒∠=∠=∠=，∴90,90ABC A ABC EBD ∠+∠=︒∠+∠=︒， ∴A EBD ∠=∠，又∵AB BE =， ∴()AAS ACB BDE ≌．（2）①如图2，分别过点A ，B 作AC x ⊥轴，BD x ⊥轴，垂足分别为C ，D ．将()3,A a −代入3y x =得：1a =−，∴()3,1A −−，1AC =，3OC =．同（1）可得ACO ODB ≌△△， ∴1OD AC ==，3BD OC ==， ∴()1,3B −，∵反比例函数ky x =经过点()1,3B −，∴3k =−， ∴3y x =−；（3）存在；如图3，当M 点位于x 轴上方，且45MAQ ∠=︒，过点Q 作QD AQ ⊥，交MA 于点D ，过点D 作DE y ⊥轴于点E ．∵45MAQ ∠=︒，QD AQ ⊥， ∴45MAQ ADQ ∠=∠=︒， ∴AQ QD =，∵DE y ⊥轴，QD AQ ⊥，∴90AQO EQD EQD QDE ∠+∠=∠+∠=︒，90AOQ QED ∠=∠=︒， ∴AQO QDE ∠=∠， ∵AQ QD =， ∴AQO QDE ≌， ∴AO QE =，OQ DE =，令2230y x x =+−=，得13x =−，21x =，∴3AO QE ==，又()0,1Q −，∴1OQ DE ==， ∴()1,2D ，设AM 为y kx b =+，则230k b k b +=⎧⎨−+=⎩，，解得：1232k b ⎧=⎪⎪⎨⎪=⎪⎩，∴1322AM y x =+：令2132322x x x +=+−，得132x =，23x =−(舍去)，当32x =时，233923224y ⎛⎫=+⨯−= ⎪⎝⎭， ∴39,24M ⎛⎫⎪⎝⎭；如图，当M 点位于x 轴下方，且45MAQ ∠=︒，同理可得()1,4D −−，AM 为26y x =−−．由22623x x x −−=+−，得11x =−，23x =−(舍去)∴当=1x −时，()()212134y =−+⨯−−=−，∴()1,4M −−．综上：M 的坐标为39,24⎛⎫⎪⎝⎭或()1,4−−．【点睛】本题考查的是全等三角形的判定与性质，反比例函数的应用，二次函数的性质，一元二次方程的解法，熟练的利用类比的方法解题是关键．题型3：反比例函数的代数综合4．（2024·湖南长沙·一模）若一次函数y mx n =+与反比例函数ky x=同时经过点(),P x y 则称二次函数2y mx nx k +=-为一次函数与反比例函数的“共享函数”，称点P 为共享点．(1)判断21y x =−与3y x=是否存在“共享函数”，如果存在，请说明理由；(2)已知：整数m ，n ，t 满足条件8t n m ＜＜，并且一次函数()122=+++y n x m 与反比例函数2024y x=存在“共享函数”()()2102024y m t x m t x ++−=-，求m 的值．(3)若一次函数y x m =+和反比例函数213m y x+=在自变量x 的值满足的6m x m ≤≤+的情况下．其“共享函数”的最小值为3，求其“共享函数”的解析式．【答案】(1)3,22P ⎛⎫ ⎪⎝⎭或()1,3P −−，见解析 (2)2(3)2429y x x =+−或(29155y x x −−−=【分析】（1）判断21y x =−与3y x =是否有交点，计算即可；（2）根据定义，12210n m tm m t +=+⎧⎨+=−⎩，得到39869n m n t +⎧=⎪⎪⎨+⎪=⎪⎩，结合8t n m ＜＜，构造不等式组解答即可．（3）根据定义，得“共享函数”为()22225131324m m y x mx m x ⎛⎫+−+=+−− ⎪⎝⎭=结合6m x m ≤≤+，“共享函数”的最小值为3，分类计算即可．本题考查了新定义，解方程组，解不等式组，抛物线的增减性，熟练掌握定义，抛物线的增减性是解题的关键．【解析】（1）21y x =−与3y x =存在“共享函数”，理由如下：根据题意，得213y x y x =−⎧⎪⎨=⎪⎩，解得322x y ⎧=⎪⎨⎪=⎩，13x y =−⎧⎨=−⎩，故函数同时经过3,22P ⎛⎫ ⎪⎝⎭或()1,3P −−，故21y x =−与3y x =存在“共享函数”．（2）∵一次函数()122=+++y n x m 与反比例函数2024y x =存在“共享函数”()()2102024y m t x m t x ++−=-，∴12210n m tm m t +=+⎧⎨+=−⎩，解得39869n m n t +⎧=⎪⎪⎨+⎪=⎪⎩， ∵8t n m ＜＜， ∴82489869n n m n n +⎧=⎪⎪⎨+⎪⎪⎩＜＞，解得24n 6＜＜， ∴327n +9＜＜， ∴339n +1＜＜，∴13m ＜＜， ∵m 是整数， ∴2m =．（3）根据定义，得一次函数y x m =+和反比例函数213m y x +=的“共享函数”为 ()22225131324m m y x mx m x ⎛⎫+−+=+−− ⎪⎝⎭=，∵()22225131324m m y x mx m x ⎛⎫+−+=+−− ⎪⎝⎭=．∴抛物线开口向上，对称轴为直线2mx =−，函数有最小值25134m −−，且点与对称轴的距离越大，函数值越大，∵6m x m ≤≤+，当62mx m =−+≥时，即4m ≤−时，∵11622m m m m ⎛⎫⎛⎫−−+−− ⎪ ⎪⎝⎭⎝⎭＞， ∴6x m =+时，函数取得最小值，且为2225613182324m m y m m m ⎛⎫=++−−=++ ⎪⎝⎭，又函数有最小值3，∴218233m m ++=，解得99m m =−=−故9m =− ∴“共享函数”为(29155y x x −−−=当2m x m =−≤时，即0m ≥时，∵11622m m m m ⎛⎫⎛⎫−−+−− ⎪ ⎪⎝⎭⎝⎭＜， ∴x m =时，函数取得最小值，且为2225131324m m y m m ⎛⎫=+−−=− ⎪⎝⎭，又函数有最小值3，∴2133m −=，解得4,4m m ==−（舍去）；故4m =，∴“共享函数”为2429y x x =+−；当62mm m −+＜＜时，即40m −＜＜时，∴2mx =−时，函数取得最小值，且为25134m y =−−，又函数有最小值3，∴251334m −−=，方程无解，综上所述，一次函数y x m =+和反比例函数213m y x += 的“共享函数”为2429y x x =+−或(29155y x x −−−=5．（2024·江苏南京·模拟预测）若一次函数y mx n =+与反比例函数ky x=同时经过点(,)P x y 则称二次函数2y mx nx k =+−为一次函数与反比例函数的“共享函数”，称点P 为共享点．(1)判断21y x =−与3y x=是否存在“共享函数”，如果存在，请求出“共享点”．如果不存在，请说明理由； (2)已知：整数m ，n ，t 满足条件8t n m <<，并且一次函数(1)22y n x m =+++与反比例函数2024y x=存在“共享函数” 2()(10)2024y m t x m t x =++−−，求m 的值．(3)若一次函数y x m =+和反比例函数213m y x+=在自变量x 的值满足的6m x m ≤≤+的情况下．其“共享函数”的最小值为3，求其“共享函数”的解析式．【答案】(1)点P 的坐标为：3(2，2)或(1,3)−−；(2)2m =(3)222(13)(9(155y x mx m x x =+−+=+−−+或2429y x x =+−．【分析】（1）联立21y x =−与3y x =并整理得：2230x x −−=，即可求解；（2）由题意得12210n m t m m t +=+⎧⎨+=−⎩，解得39869n m n t +⎧=⎪⎪⎨+⎪=⎪⎩，而8t n m <<，故624n <<，则9327n <+<，故13m <<，m 是整数，故2m =；（3）①当162m m +≤−时，即4m ≤−，6x m =+，函数取得最小值，即22(6)(6)133m m m m +++−−=，即可求解；②当162m m m <−<+，即40m −<<，函数在12x m=−处取得最小值，即22211()13322m m m −−−−=，即可求解；③当0m ≥时，函数在x m =处，取得最小值，即可求解．【解析】（1）解：（1）21y x =−与3y x =存在“共享函数”，理由如下：联立21y x =−与3y x =并整理得：2230x x −−=，解得：32x =或1−，故点P 的坐标为：3(2，2)或(1,3)−−；（2）解：一次函数(1)22y n x m =+++与反比例函数2024y x =存在“共享函数”2()(10)2024y m t x m t x =++−−，依据“共享函数”的定义得： 12210n m tm m t +=+⎧⎨+=−⎩，解得：39869n m n t +⎧=⎪⎪⎨+⎪=⎪⎩， 8t n m <<，∴8698249n n n n +⎧<⎪⎪⎨+⎪<⎪⎩，解得：624n <<；9327n ∴<+<， 13m ∴<<，m 是整数，2m ∴=；（3）解：由y x m =+和反比例函数213m y x +=得：“共享函数”的解析式为22(13)y x mx m =+−+，函数的对称轴为：12x m=−； ①当162m m+≤−时，即4m ≤−， 6x m =+，函数取得最小值，即22(6)(6)133m m m m +++−−=，解得9m =−9−②当162m m m <−<+，即40m −<<，函数在12x m =−处取得最小值，即22211()13322m m m −−−−=，无解；③当0m ≥时，函数在x m =处，取得最小值，即222133m m m +−−=，解得：4m =±（舍去4)−，综上，9m =−4，故“共享函数”的解析式为222(13)(9(155y x mx m x x =+−+=+−−+或2429y x x =+−．【点睛】本题是一道二次函数的综合题，主要考查了一次函数与反比例函数的性质，一次函数与反比例函数图象上点的坐标的特征，二次函数的性质，一元一次不等式组的解法，一元二次方程的解法．本题是阅读型题目，理解题干中的定义并熟练应用是解题的关键．6．（2024·湖南长沙·模拟预测）我们规定：若二次函数2y ax bx c =++（a ，b ，c 为常数，且0a ≠）与x 轴的两个交点的横坐标1x ，2x 满足122x x =−，则称该二次函数为“强基函数”，其中点()1,0x ，()2,0x 称为该“强基函数”的一对“基点”．(1)判断：下列函数中，为“强基函数”的是______（仅填序号）．①228y x x =−−；②21y x x =++．(2)已知二次函数()2221y x t x t t =−+++为“强基函数”，求：当12x −≤≤时，函数22391y x tx t =+++的最大值．(3)已知直线1y x =−+与x 轴交于点C ，与双曲线()20y x x=−<交于点A ，点B 的坐标为()3,0−．若点()1,0x ，()2,0x 是某“强基函数”的一对“基点”，()12,P x x 位于ACB △内部．①求1x 的取值范围；②若1x 为整数，是否存在满足条件的“强基函数”2y x bx c =++？若存在，请求出该“强基函数”的解析式；若不存在，请说明理由．【答案】(1)① (2)当23t =−时函数最大值为8或当13t =−时函数最大值为4；(3)①1x 的取值范围是：120x −<<或110x −<<；②21122y x x =+−【分析】（1）根据抛物线与x 轴的交点情况的判定方法分别判定①与②与x 轴的交点情况，再求解交点坐标，结合新定义，从而可得答案；（2）由()22210y x t x t t =−+++=时，可得1x t=，21x t =+，或11x t =+，2x t=，当122x x =−时，根据新定义可得23t =−或13t =−，再分情况求解函数的最大值即可；（3））①先得到点A 、B 、C 的坐标，然后分122x x =−或212x x =−两种情况，列出关于1x 的不等式组，然后解不等式组即可；②根据1x 为整数，先求出1x 的值，然后根据二次函数的交点式直接得到二次函数的解析式即可．【解析】（1）解：①∵228y x x =−−； ∴()()2Δ2418432360=−−⨯⨯−=+=>，∴抛物线与x 轴有两个交点，∵228=0x x −−，∴14x =，22x =−，∴122x x =−，∴228y x x =−−是“强基函数” ②∵21y x x =++， ∴214111430∆=−⨯⨯=−=−<，∴抛物线与x 轴没有交点，∴21y x x =++不是“强基函数” 故答案为：①；（2）∵二次函数()2221y x t x t t=−+++为“强基函数”，∴()()22Δ21410t t t ⎡⎤=−+−+=>⎣⎦，∵()22210y x t x t t =−+++=时， ∴1x t=，21x t =+，或11x t =+，2x t=，当122x x =−时，∴()21t t =−+或12t t +=−，解得：23t =−或13t =−，当23t =−时，函数为225y x x =−+，如图，∵12x −≤≤，此时当=1x −时，函数最大值为1258y =++=；当13t =−时，函数为22y x x =−+，如图，∵12x −≤≤，此时当=1x −或2x =时，函数最大值为1124y =++=；（3）①联立()201y x x y x ⎧=−<⎪⎨⎪=−+⎩，解得：12x y =−⎧⎨=⎩， ∴点A 的坐标为：()1,2−，把0y =代入 1y x =−+得：10x −+=，解得：1x =，∴点C 的坐标为()1,0，设直线AB 为1y kx b =+，∴11302k b k b −+=⎧⎨−+=⎩，解得：113k b =⎧⎨=⎩，∴直线AB 的解析式为：3y x =+， ∵点()1,0x ，()2,0x 是某“强基函数”的一对“基点”， ()12,P x x 位于ACB △内部．当122x x =−时， ∴111,2P x x ⎛⎫− ⎪⎝⎭， ∴点P 在直线2xy =−上，∵点111,2P x x ⎛⎫− ⎪⎝⎭位于以A 、B 、C 三点所构成的三角形内部，如图，∴1111103212x x x x x ⎧⎪<⎪⎪−+⎨⎪⎪−−+⎪⎩＜＜，解得：120x −<<；当212x x =−时，∵P 点坐标为()11,2x x −，∴点P 在直线2y x =−上，∵点P 位于以A 、B 、C 三点所构成的三角形内部，如图，∴1111102321x x x x x <⎧⎪−<+⎨⎪−<−+⎩，解得：110x −<<；综上分析可知，1x 的取值范围是：120x −<<或110x −<<；②存在；理由如下：∵1x 为整数，∴当120x −<<时，11x =−，∴此时212x =，此时，“强基函数”的一对“基点”为()1,0−，1,02⎛⎫ ⎪⎝⎭， ∴“强基函数”为()21111222y x x x x ⎛⎫=+−=+− ⎪⎝⎭；当110x −<<时，则没有符合条件的整数1x 的值，不存在符合条件的“强基函数”；综上，“强基函数”为21122y x x =+−．【点睛】本题考查的是一次函数，反比例函数，二次函数的综合应用，新定义的含义，本题难度大，灵活应用各知识点，理解新定义的含义是解题的关键．题型4：动态问题、新定义综合7．（2024·山东济南·一模）如图1，直线14y ax =+经过点()2,0A ，交反比例函数2k y x=的图象于点()1,B m −，点P 为第二象限内反比例函数图象上的一个动点．(1)求反比例函数2y 的表达式；(2)过点P 作PC x ∥轴交直线AB 于点C ，连接AP ，BP ，若ACP △的面积是BPC △面积的2倍，请求出点P 坐标；(3)平面上任意一点(),Q x y ，沿射线BA Q '，点Q '怡好在反比例函数2k y x=的图象上；①请写出Q 点纵坐标y 关于Q 点横坐标x 的函数关系式3y =______；②定义}{()()min ,a a b a b b a b ⎧≤⎪=⎨>⎪⎩，则函数{}13min ,Y y y =的最大值为______．【答案】(1)26y x =−(2)点P 坐标为1,122⎛⎫− ⎪⎝⎭或3,42⎛⎫− ⎪⎝⎭ (3)①3621y x =−++；②8【分析】本题考查了反比例函数与一次函数的交点问题，坐标与图形，解题的关键是运用分类讨论的思想．（1）先根据点()2,0A 求出1y 的解析式，然后求出点B 的坐标，最后将点B 的坐标代入2y 中，求出k ，即可求解；（2）分两种情况讨论：当点P 在AB 下方时，当点P 在AB 上方时，结合“若ACP △的面积是BPC △面积的2倍”，求出点C 的坐标，将点C 的纵坐标代入反比例函数解析式，即可求解；（3）①根据题意可得：(),Q x y 向右平移1个单位，再向下平移2个单位得到点Q '，则()1,2Q x y +'−，将其代入26y x =−中，即可求解；②分为：当{}131min ,Y y y y ==时，13y y ≤；当{}133min ,Y y y y ==时，13y y >；分别解不等式即可求解．【解析】（1）解：直线14y ax =+经过点()2,0A ，，∴240x +=，解得：2a =−，∴124y x =−+，点()1,B m −在直线124y x =−+上，∴()2146m =−⨯−+=，∴()1,6B −，∴166k =−⨯=−， ∴26y x =−；（2）①当点P 在AB 下方时，2ACP BPC S S =，∴:2:1AC BC =，过点C 作CH x ⊥轴于点H ，过点B 作BR x ⊥轴于点R ，∴23AC CH AB BR ==， ∴23C B y y =，()1,6B −，∴4C y =，把4C y =代入26y x =−中，得：32C x =−， ∴3,42P ⎛⎫− ⎪⎝⎭； ②当点P 在AB 上方时，2ACP BPC S S =，∴:1:1AB BC =，∴B 为AC 的中点，()2,0A ，()1,6B −，∴()4,12C −，把12y =代入26y x =−中，得：12x =−， ∴1,122P ⎛⎫− ⎪⎝⎭，综上所述，点P 的坐标为1,122⎛⎫− ⎪⎝⎭或3,42⎛⎫− ⎪⎝⎭；（3）① 由(),Q x y ，沿射线BA Q '，得：(),Q x y 向右平移1个单位，再向下平移2个单位得到点Q '，∴()1,2Q x y +'−，点()1,2Q x y +'−恰好在反比例函数26y x =−的图象上， ∴621y x −=−+， ∴3621y x =−++；②a ．当{}131min ,Y y y y ==时，13y y ≤，即62421x x −+≤−++，当1x >−时，()()()2141621x x x x −+++≤−++，解得：2x ≥或2x ≤−（舍去），∴2x =时，函数{}131min ,Y y y y ==有最大值，最大值为2240−⨯+=；当1x <−时，()()()2141621x x x x −+++≥−++，解得：21x −≤<−，∴2x =−时，函数{}131min ,Y y y y ==有最大值，最大值为()2248−⨯−+=；b ．当{}133min ,Y y y y ==时，13y y >，即62421x x −+>−++，当1x >−时，()()()2141621x x x x −+++>−++，解得：2x >或<2x −（舍去）， ∴362021y >−+=+，即0Y >；当1x <−时，()()()2141621x x x x −+++<−++，解得：2<<1x −−，∴328y <<，即28Y <<；综上所述，函数{}13min ,Y y y =的最大值为8，故答案为：8．8．（2024·四川成都·一模）如图，矩形OABC 交反比例函数k y x=于点D ，已知点()0,4A ，点()2,0C −，2ACD S =△．(1)求k 的值；(2)若过点D 的直线分别交x 轴，y 轴于R ，Q 两点，2DRDQ =，求该直线的解析式； (3)若四边形有一个内角为60︒，且有一条对角线平分一个内角，则称这个四边形为“角分四边形”．已知点P在y 轴负半轴上运动，点Q 在x 轴正半轴上运动，若四边形ACPQ 为“角分四边形”，求点P 与点Q 的坐标．【答案】(1)4k =−；(2)26y x =+或22y x =−+；(3)(()020P ,,Q ,−或 ()()04320P ,,−或()()040P ,,Q −【分析】（1）利用面积及矩形的性质，用待定系数法即可求解；（2）分两种情况讨论求解：R 在x 轴正半轴上和在负半轴上两种情况分别求解即可；（3）分三种情况：当AO 平分CAQ ∠，60CPQ ∠=︒时，当CO 平分ACP ∠，60CPQ ∠=︒时，当CO 平分ACP ∠，60AQP ∠=︒时，分别结合图形求解. 【解析】（1）解：2ACD S =△，即122AD OA ⨯⨯=， ()0,4A ，1422AD ∴⨯=，1AD ∴=，()1,4D ∴−， 41k∴=−，4k ∴=−；（2）①如图，当2DR DQ =时，13DQ RQ =，AD OR ，13DQ AD RQ OR ∴==，1AD =，3OR ∴=，()3,0R ∴−，设直线RQ 为11y k x b =+，把()3,0R −，()1,4D −代入11y k x b =+，得1111304k b k b −+=⎧⎨−+=⎩，解得1126k b =⎧⎨=⎩，直线RQ 为26y x =+，②如图，当2DR DQ =时，1DQ RQ =，AD OR ，1DQ AD RQ OR ∴==，1AD =，1OR ∴=，()1,0R ∴，设直线RQ 为22y k x b =+，把()1,0R ，()1,4D −代入22y k x b =+，得222204k b k b +=⎧⎨−+=⎩，解得2222k b =−⎧⎨=⎩，直线RQ 为22y x =−+，综上所述，直线RQ 的表达式为26y x =+或22y x =−+；（3）解：①当AO 平分CAQ ∠，60CPQ ∠=︒时，CAO QAO AO AOAOC AOQ ∠=∠⎧⎪=⎨⎪∠=⎩，()ASA AOC AOQ ∴≌， CO QO ∴=即AP 垂直平分CQ ，()2,0Q ∴，60CPQ ∠=︒，30CPO ∴∠=︒，tan30OC OP ∴===︒，(0,P ∴−，②当CO 平分ACP ∠，60CPQ ∠=︒时，同理ACO PCO ≌，得4OA OP ==，()0,4P ∴−，PC == 作CM PQ ⊥于M ，60CPQ ∠=︒，1cos602PM PC ∴=⨯︒==sin60CM PC =⨯︒== 90POQ CMQ ,PQO PQO ∠=∠=︒∠=∠，CMQ POQ ∴∽，MQ CM OQ OP ∴=，即MQ OQ =，)2222OQ OP PQ MQ +==② ，联立①，②，解得32OQ =或32OQ =(舍），()32,0Q ∴，③当CO 平分ACP ∠，60AQP ∠=︒时，同理 ACO PCO ≌，得4OA OP ==，AC CP = 同理ACQ PCQ ≌，得AQ PQ =∴APQ 是等边三角形()0,4P ∴−，8AP AQ PQ ,===OQ =， ()Q ∴，综上所述，P 、Q 的坐标为(()0,,2,0P Q −或 ()()0,4,32,0P Q −或()()0,4,P Q −.【点睛】此题是反比例函数综合题，主要考查了待定系数法，解直角三角形，求一次函数解析式，相似三角形的性质和判定，正确作出辅助线，解方程组，灵活运用待定系数法求函数解析式是解本题的关键．题型5：定值问题9．（2024·山东济南·模拟预测）如图①，已知点()1,0A −，()0,2B −，ABCD Y 的边AD 与y 轴交于点E ，且E 为AD 的中点，双曲线k y x=经过C 、D 两点．(1)求k 的值；(2)点P 在双曲线k y x=上，点Q 在y 轴上，若以点A 、B 、P 、Q 为顶点的四边形是平行四边形，直接写出满足要求的所有点Q 的坐标；(3)以线段AB 为对角线作正方形AFBH （如图③），点T 是边AF 上一动点，M 是HT 的中点，MN HT ⊥，交AB 于N ，当点T 在AF 上运动时，MN HT 的值是否发生改变？若改变，求出其变化范围：若不改变，请求出其值，并给出你的证明．【答案】(1)4k =(2)()0,6或()0,2或()0,6− (3)12MN HT =，其值不发生改变，证明见解析【分析】（1）根据中点坐标公式可得，1D x =，设()1,D t ，由平行四边形对角线中点坐标相同可知()2,2C t −，再根据反比例函数的性质求出t 的值即可；（2）由（1）知4k =可知反比例函数的解析式为4y x =，再由点P 在双曲线4y x =上，点Q 在y 轴上，设()0,Q q ，4P p p ⎛⎫ ⎪⎝⎭，，再分以AB 为边和以AB 为对角线两种情况求出x 的值，故可得出P 、Q 的坐标；（3）连NH 、NT 、NF ，易证NF NH NT ==，故NTF NFT AHN ∠=∠=∠，90TNH TAH ∠=∠=︒，12MN HT =由此即可得出结论．【解析】（1）解：∵()1,0A −，E 为AD 中点且点E 在y 轴上，1D x ∴=，设()1,D t ，()C m n ，，∵四边形ABCD 是平行四边形，∴AC BD 、的中点坐标相同， ∴101222022m t n +−⎧=⎪⎪⎨−+⎪=⎪⎩， ∴22m n t ==−，()22C t ∴−，，∵C 、D 都在反比例函数4y x =的图象上，()22k t t ∴==−，4t ∴=， 4k ∴=；（2）解：由（1）知4k =，∴反比例函数的解析式为4y x =，点P 在双曲线4x 上，点Q 在y 轴上，∴设()0,Q q ，4P p p ⎛⎫ ⎪⎝⎭，，①当AB 为边时：如图1，若ABPQ 为平行四边形，则1002240422p q p −++⎧=⎪⎪⎨−⎪−=⎪⎩，解得16p q =⎧⎨=⎩，此时()11,4P ，()10,6Q ；如图2，若ABQP 为平行四边形，则1002242022p q p −++⎧=⎪⎪⎨−+⎪+=⎪⎩，解得16p q =−⎧⎨=−⎩，此时()21,4P −−，()20,6Q −；②如图3，当AB 为对角线时，则010*******p q p +−+⎧=⎪⎪⎨+⎪−=⎪⎩解得12p q =−⎧⎨=⎩，()31,4P ∴−−，()30,2Q ；综上所述，满足题意的Q 的坐标为()0,6或()0,2或()0,6−；（3）解：12MN HT =，其值不发生改变，证明如下：如图4，连NH 、NT 、NF ，∵M 是HT 的中点，MN HT ⊥，∴MN 是线段HT 的垂直平分线，NT NH ∴=，四边形AFBH 是正方形，45ABF ABH ∴∠=∠=︒，在BFN 与BHN △中，BF BH NBF NBH BN BN =⎧⎪∠=∠⎨⎪=⎩，()SAS BFN BHN ∴≌，NF NH NT ∴==，BFN BHN ∠=∠，∵90BFA BHA ==︒∠∠，NTF NFT AHN ∴∠=∠=∠，∵180ATN NTF ∠+∠=︒，∴180ATN AHN ∠+∠=︒，∴3601809090TNH ∠=︒−︒−︒=︒．12MN HT ∴=， ∴12MN HT =．三角形的判定与性质、全等三角形的判定与性质等相关知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题.10．（2024·山东济南·二模）如图①，已知点(1,0)A −，(0,2)B −，ABCD Y 的边AD 与y 轴交于点E ，且E 为AD 的中点，双曲线k y x=经过C 、D 两点．(1)求k 的值；(2)点P 在双曲线k y x=上，点Q 在y 轴上，若以点A 、B 、P 、Q 为顶点的四边形是平行四边形，直接写出满足要求的所有点Q 的坐标；(3)以线段AB 为对角线作正方形AFBH （如图③)，点T 是边AF 上一动点，M 是HT 的中点，MN HT ⊥，交AB 于N ，当点T 在AF 上运动时，MN HT的值是否发生改变？若改变，求出其变化范围：若不改变，请求出其值，并给出你的证明．【答案】(1)4k =(2)1(0,6)Q ，2(0,6)Q −，3(0,2)Q(3)结论：MN HT 的值不发生改变，12MN HT =证明见解析【分析】（1）设(1,)D t ，由DC AB ∥，可知(2,2)C t −，再根据反比例函数的性质求出t 的值即可；（2）由（1）知4k =可知反比例函数的解析式为4y x =，再由点P 在双曲线4y x =上，点Q 在y 轴上，设(0,)Q y ，4(,)P x x ，再分以AB 为边和以AB 为对角线两种情况求出x 的值，故可得出P 、Q 的坐标；（3）连NH 、NT 、NF ，易证NF NH NT ==，故NTF NFT AHN ∠=∠=∠，90TNH TAH ∠=∠=︒，12MN HT =由此即可得出结论．【解析】（1）解：(1,0)A −，(0,2)B −，E 为AD 中点， 1D x ∴=，设(1,)D t ，又DC AB ∥，(2,2)C t ∴−，24t t ∴=−，4t ∴=，4k ∴=；（2）解：由（1）知4k =，∴反比例函数的解析式为4y x =，点P 在双曲线4x 上，点Q 在y 轴上，∴设(0,)Q y ，4(,)P x x ， ①当AB 为边时：如图1，若ABPQ 为平行四边形，则102x −+=，解得1x =，此时1(1,4)P ，1(0,6)Q ；如图2，若ABQP 为平行四边形，则122x −=，解得=1x −，此时2(1,4)P −−，2(0,6)Q −；②如图3，当AB 为对角线时，AP BQ =，且AP BQ ∥； ∴122x −=，解得=1x −，3(1,4)P ∴−−，3(0,2)Q ；故1(1,4)P ，1(0,6)Q ；2(1,4)P −−，2(0,6)Q −；3(1,4)P −−，3(0,2)Q ；（3）解：结论：MNHT 的值不发生改变，理由：如图4，连NH 、NT 、NF ，MN 是线段HT 的垂直平分线，NT NH ∴=，四边形AFBH 是正方形，ABF ABH ∴∠=∠，在BFN 与BHN △中，BF BH ABF ABH BN BN =⎧⎪∠=∠⎨⎪=⎩，()BFN BHN SAS ∴≌，NF NH NT ∴==， NTF NFT AHN ∴∠=∠=∠，四边形ATNH 中，180ATN NTF ∠+∠=︒，而NTF NFT AHN ∠=∠=∠，所以，180ATN AHN ∠+∠=︒，所以，四边形ATNH 内角和为360︒，所以3601809090TNH ∠=︒−︒−︒=︒．12MN HT ∴=， ∴12MN HT =．【点睛】此题是反比例函数综合题，主要考查了待定系数法求反比例函数的解析式、正方形的性质、等腰三角形的判定与性质、全等三角形的判定与性质等相关知识，解题的关键是学会用分类讨论的思想思考问题，学会添加常用辅助线，构造全等三角形解决问题.题型6：取值范围问题11．（2024·江苏宿迁·二模）中国象棋棋盘上双方的分界处称为“楚河汉界”，以“楚河汉界”比喻双方对垒的分界线．在平面直角坐标系中，为了对两个图形进行分界，对“楚河汉界线”给出如下定义：点()11,P x y 是图形1G 上的任意一点，点()22,Q x y 是图形2G 上的任意一点，若存在直线()0l y kx b k =+≠∶满足11y kx b ≤+且22y kx b ≥+，则直线(0)y k b k =+≠就是图形1G 与2G 的“楚河汉界线”．例如：如图1，直线4l y x =−−∶是函数6(0)y x x=<的图像与正方形OABC 的一条“楚河汉界线”．(1)在直线①2y x =−，②41y x =−，③23y x =−+，④31y x =−−中，是图1函数6(0)y x x=<的图像与正方形OABC 的“楚河汉界线”的有______；（填序号） (2)如图2，第一象限的等腰直角EDF 的两腰分别与坐标轴平行，直角顶点D 的坐标是()2,1，EDF 与O 的“楚河汉界线”有且只有一条，求出此“楚河汉界线”的表达式；(3)正方形1111D C B A 的一边在y 轴上，其他三边都在y 轴的右侧，点(2,)M t 是此正方形的中心，若存在直线2y x b =−+是函数2)304(2y x x x =−++≤≤的图像与正方形1111D C B A 的“楚河汉界线”，求t 的取值范围．【答案】(1)①④；(2)25y x =−+；(3)7t ≤−或9t ≥．【分析】（1）根据定义，结合图象，可判断出直线为3y x =−或31y x =−−与双曲线6(0)y x x =<及正方形ABCD最多有一个公共点，即可求解；（2）先作出以原点O 为圆心且经过EDF 的顶点D 的圆，再过点D 作O 的切线，求出该直线的解析式即可；（3）先由抛物线与直线组成方程组，则该方程组有唯一一组解，再考虑直线与正方形有唯一公共点的情形，数形结合，分类讨论，求出t【解析】（1）解：如图，从图可知，2y x =−与双曲线6(0)y x x =<和正方形OABC 只有一个公共点，31y x =−−与双曲线6(0)y x x =<和正方形OABC 没有公共点，41y x =−、23y x =−+不在双曲线6(0)y x x =<及正方形ABCD 之间，根据“楚河汉界线”定义可知，直线2y x =−，31y x =−−是双曲线6(0)y x x =<与正方形OABC 的“楚河汉界线”，故答案为：①④；（2）解：如图，连接OD ，以O 为圆心，OD 长为半径作O ，作DG x ⊥轴于点G ，过点D 作O 的切线DM ，则MD OD ⊥，∵MD OD ⊥，DG x ⊥轴， ∴90ODM OGD ∠=∠=︒， ∴90MOD OMD ∠+∠=︒， ∵90MOD DOG ∠+∠=︒， ∴OMD DOG ∠=∠， ∴tan tan OMD DOG ∠=∠， ∵()2,1D ，∴1DG =，2OG =，∴1tan tan 2DG OMD DOG OG ∠=∠==，OG ==∵tan ODOMD DM ∠=，∴12=，∴1122MN DM ∴==⨯=∴5OM =，∴()0,5M ，设直线MD 的解析式为y mx n =+，把()0,5M 、()2,1D 代入得，521n m n =⎧⎨+=⎩，解得25m n =−⎧⎨=⎩，∴25y x =−+，∴EDF 与O 的“楚河汉界线”为25y x =−+；（3）解：由2223y x b y x x =−+⎧⎨=−++⎩得，2430x x b −+−=， ∵直线与抛物线有唯一公共点， ∴0=，∴164120b −+=，解得7b =， ∴此时的“楚河汉界线”为27y x =−+，当正方形1111D C B A 在直线27y x =−+上方时，如图，∵点()2,M t 是此正方形的中心，∴顶点()10,2A t −，∵顶点()10,2A t −不能在直线27y x =−+下方，得27t −≥，解得9t ≥；当正方形1111D C B A 在直线27y x =−下方时，如图，对于抛物线223y x x =−++，当0x =时，3y =；当4x =时，5y =−； ∴直线23y x =−+恰好经过点()0,3和点()4,5−；对于直线23y x =−+，当4x =时，5y =−，由()12,2C t +不能在直线23y x =−+上方，得25t ≤−+，解得7t ≤−；综上所述，7t ≤−或9t ≥．【点睛】此题考查了一次函数、正方形的性质、三角函数、一次函数的应用、二元二次方程组，一元二次方程的根的判别式等知识，解题的关键是理解题意，灵活运用所学知识解决问题，学会用分类讨论的思想思考问题．题型7：最值问题12．（2024·辽宁·一模）【发现问题】随着时代的发展，在现代城市设计中，有许多街道是设计的相互垂直或平行的，因此往往不能沿直线行走到目的地，只能按直角拐弯的方式行走．我们可以按照街道的垂直和平行方向建立平面直角坐标系xOy ，对两点()11,A x y 和()22,B x y ，用以下方式定义两点间的“折线距离”：()1212,d A B x x y y =−+−．【提出问题】（1）①已知点()4,1A ，则(),d O A =______；②函数()2630y x x =+−≤≤的图象如图1，B 是图象上一点，若(),5d O B =，则点B 的坐标为______；（2）函数()30y x x=>的图象如图2，该函数图象上是否存在点C ，使(),2d O C =？若存在，求出其坐标；若不存在，请说明理由；【拓展运用】（3）已知函数()21460y x x x =−+≥和函数()2231y x x =+≥−的图象如图3，D 是函数1y 图象上的一点，E是函数2y 图象上的一点，当(),d O D 和(),d O E 分别取到最小值的时候，请求出(),d D E 的值．【答案】（1）①5；②()14，（2）不存在，理由见解析（3）()15,4d D E =【分析】本题在新定义下考查了一次方程和分式方程的解法，二次函数的最值，关键是紧靠定义来构造方程和函数．（1）①代入定义中的公式求； ②设出函数()2630y x x =+−≤≤的图象上点B 的坐标，通过(),5d O B =建立方程，解方程；（2）设出函数()30y x x =>的图象上点C 的坐标，通过(),2d O C =建立方程，看方程解的情况；（3）设出函数()21460y x x x =−+≥的图象上点D 的坐标，将()d O D ，表示成函数，利用二次函数的性质求函数最值，可求得点D 的坐标；设出函数()2231y x x =+≥−的图象上点E 的坐标，利用一次函数的性质，可求得点E 的坐标；再按定义求得(),d D E 的值即可．【解析】解：（1）①∵点()4,1A ，点()00O ，，∴()40105d O A =−+−=，；故答案为：5； ②设点()26B x x +，，∵(),5d O B =， ∴265x x ++=，∵30x −≤≤， ∴265x x −++=， ∴=1x −， ∴点()14B ，．故答案为：()14，；（2）不存在，理由如下：设点3C m m ⎛⎫ ⎪⎝⎭，， ∵(),2d O C =，∴32m m +=，∵0m >， ∴32m m +=，∴2230m m −+=，∵80∆=−<，∴此方程没有实数根， ∴不存在符合条件的点C ；（3）设点D 为()246n nn −+，，∴()246d O D n n n =+−+，，∵0n ≥，()2246220n n n −+=−+>，∴()222315463624d O D n n n n n n ⎛⎫=+−+=−+=−+⎪⎝⎭，， ∴当32n =时，()d O D ，最小，最小值为154，此时点D 坐标为3924⎛⎫ ⎪⎝⎭，．设点E 为()23e e +，，∴()23d O Ee e =++，，当10e −≤<时，()233d O Ee e e =−++=+，，∴当1e =−时，()d O E ，最小，最小值为2；当0e ≥时，()2333d O Ee e e =++=+，，∴当0e =时，()d O E ，最小，最小值为3；∴此时点E 坐标为()11−，．∴()395515,1124244d D E =−−+−=+=．13．（2024·四川成都·模拟预测）如图，在平面直角坐标系中，已知直线132y x =−与反比例函数ky x=的图象交于点()8,Q t ，与y 轴交于点R ，动直线()08x m m =<<与反比例函数的图象交于点K ，与直线QR 交于点T ．(1)求t 的值及反比例函数的表达式；(2)当m 为何值时，RKT △的面积最大，且最大值为多少？ (3)如图2，ABCO 的顶点C 在反比例函数()0ky x x=>的图象上，点P 为反比例函数图象上一动点，过点P 作MN x ∥轴交OC 于点N ，交AB 于点M ．当点P 的纵坐标为2，点C 的横坐标为1且8OA =时，求PNPM的值．【答案】(1)1t =，反比例函数的表达式为8y x =； (2)当3m =时，RKT △的面积最大，且最大值为254；(3)1517PN PM =【分析】（1）将()8,Q t 代入直线132y x =−，求出t 的值，再将点Q 的坐标代入反比例函数，求出k 的值，即可得到反比例函数解析式；（2）设8,K m m ⎛⎫ ⎪⎝⎭，1,32T m m ⎛⎫− ⎪⎝⎭，则81813322KT m m m m ⎛⎫=−−=−+ ⎪⎝⎭，进而表示出 RKT RTKQTKS SS=+△()2125344m =−−+，结合二次函数的性质，即可求出最值；（3）先求出P 、C 两点的坐标，再利用待定系数法求出直线OC 的解析式，进而得到点N 的坐标，得出PN的长，然后利用平行四边形的性质，得出PM 的长，即可求出PNPM 的值．【解析】（1）解：()8,Q t 在直线132y x =−上，18312t ∴=⨯−=，()8,1Q ∴，()8,1Q 在反比例函数ky x =上，818k ∴=⨯=，。

中考数学——反比例函数的综合压轴题专题复习附答案解析

一、反比例函数真题与模拟题分类汇编（难题易错题）1．在平面直角坐标系内，双曲线：y= （x＞0）分别与直线OA：y=x和直线AB：y=﹣x+10，交于C，D两点，并且OC=3BD．（1）求出双曲线的解析式；（2）连结CD，求四边形OCDB的面积．【答案】（1）解：过点A、C、D作x轴的垂线，垂足分别是M、E、F，∴∠AMO=∠CEO=∠DFB=90°，∵直线OA：y=x和直线AB：y=﹣x+10，∴∠AOB=∠ABO=45°，∴△CEO∽△DEB∴= =3，设D（10﹣m，m），其中m＞0，∴C（3m，3m），∵点C、D在双曲线上，∴9m2=m（10﹣m），解得：m=1或m=0（舍去）∴C（3，3），∴k=9，∴双曲线y= （x＞0）（2）解：由（1）可知D（9，1），C（3，3），B（10，0），∴OE=3，EF=6，DF=1，BF=1，∴S四边形OCDB=S△OCE+S梯形CDFE+S△DFB= ×3×3+ ×（1+3）×6+ ×1×1=17，∴四边形OCDB的面积是17【解析】【分析】（1）过点A、C、D作x轴的垂线，垂足分别是M、E、F，由直线y=x和y=﹣x+10可知∠AOB=∠ABO=45°，证明△CEO∽△DEB，从而可知 = =3，然后设设D（10﹣m，m），其中m＞0，从而可知C的坐标为（3m，3m），利用C、D在反比例函数图象上列出方程即可求出m的值．（2）求分别求出△OCE、△DFB△、梯形CDFE的面积即可求出答案．2．如图．一次函数y=x+b的图象经过点B（﹣1，0），且与反比例函数（k为不等于0的常数）的图象在第一象限交于点A（1，n）．求：（1）一次函数和反比例函数的解析式；（2）当1≤x≤6时，反比例函数y的取值范围．【答案】（1）解：把点B（﹣1，0）代入一次函数y=x+b得： 0=﹣1+b，∴b=1，∴一次函数解析式为：y=x+1，∵点A（1，n）在一次函数y=x+b的图象上，∴n=1+1，∴n=2，∴点A的坐标是（1，2）．∵反比例函数的图象过点A（1，2）．∴k=1×2=2，∴反比例函数关系式是：y=（2）解：反比例函数y= ，当x＞0时，y随x的增大而减少，而当x=1时，y=2，当x=6时，y= ，∴当1≤x≤6时，反比例函数y的值：≤y≤2【解析】【分析】（1）根据题意首先把点B（﹣1，0）代入一次函数y=x+b求出一次函数解析式，又点A（1，n）在一次函数y=x+b的图象上，再利用一次函数解析式求出点A的坐标，然后利用代入系数法求出反比例函数解析式，（2）根据反比例函数的性质分别求出当x=1，x=6时的y值，即可得到答案．3．如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= （k＞0，x＞0）的图象上，点D的坐标为（，2）．（1）求k的值；（2）若将菱形ABCD沿x轴正方向平移，当菱形的一个顶点恰好落在函数y= （k＞0，x ＞0）的图象上时，求菱形ABCD平移的距离．【答案】（1）解：作DE⊥BO，DF⊥x轴于点F，∵点D的坐标为（，2），∴DO=AD=3，∴A点坐标为：（，5），∴k=5 ；（2）解：∵将菱形ABCD向右平移，使点D落在反比例函数y= （x＞0）的图象上D′，∴DF=D′F′=2，∴D′点的纵坐标为2，设点D′（x，2）∴2= ，解得x= ，∴FF′=OF′﹣OF= ﹣ = ，∴菱形ABCD平移的距离为，同理，将菱形ABCD向右平移，使点B落在反比例函数y= （x＞0）的图象上，菱形ABCD平移的距离为，综上，当菱形ABCD平移的距离为或时，菱形的一个顶点恰好落在函数图象上．【解析】【分析】（1）根据菱形的性质和D的坐标即可求出A的坐标，代入求出即可；（2）B和D可能落在反比例函数的图象上，根据平移求出即可．4．已知反比例函数y= 的图象经过点A（﹣，1）．（1）试确定此反比例函数的解析式；（2）点O是坐标原点，将线段OA绕O点顺时针旋转30°得到线段OB．判断点B是否在此反比例函数的图象上，并说明理由；（3）已知点P（m， m+6）也在此反比例函数的图象上（其中m＜0），过P点作x轴的垂线，交x轴于点M．若线段PM上存在一点Q，使得△OQM的面积是，设Q点的纵坐标为n，求n2﹣2 n+9的值．【答案】（1）解：由题意得1= ，解得k=﹣，∴反比例函数的解析式为y=﹣（2）解：过点A作x轴的垂线交x轴于点C．在Rt△AOC中，OC= ，AC=1，∴OA= =2，∠AOC=30°，∵将线段OA绕O点顺时针旋转30°得到线段OB，∴∠AOB=30°，OB=OA=2，∴∠BOC=60°．过点B作x轴的垂线交x轴于点D．在Rt△BOD中，BD=OB•sin∠BOD= ，OD= OB=1，∴B点坐标为（﹣1，），将x=﹣1代入y=﹣中，得y= ，∴点B（﹣1，）在反比例函数y=﹣的图象上（3）解：由y=﹣得xy=﹣，∵点P（m， m+6）在反比例函数y=﹣的图象上，其中m＜0，∴m（ m+6）=﹣，∴m2+2 m+1=0，∵PQ⊥x轴，∴Q点的坐标为（m，n）．∵△OQM的面积是，∴OM•QM= ，∵m＜0，∴mn=﹣1，∴m2n2+2 mn2+n2=0，∴n2﹣2 n=﹣1，∴n2﹣2 n+9=8．【解析】【分析】（1）由于反比例函数y= 的图象经过点A（﹣，1），运用待定系数法即可求出此反比例函数的解析式；（2）首先由点A的坐标，可求出OA的长度，∠AOC的大小，然后根据旋转的性质得出∠AOB=30°，OB=OA，再求出点B的坐标，进而判断点B是否在此反比例函数的图象上；（3）把点P（m， m+6）代入反比例函数的解析式，得到关于m的一元二次方程；根据题意，可得Q点的坐标为（m，n），再由△OQM的面积是，根据三角形的面积公式及m＜0，得出mn的值，最后将所求的代数式变形，把mn的值代入，即可求出n2﹣2 n+9的值．5．已知：如图，正比例函数y=ax的图象与反比例函数y= 的图象交于点C（3，1）（1）试确定上述比例函数和反比例函数的表达式；（2）根据图象回答，在第一象限内，当x取何值时，反比例函数的值大于正比例函数的值？（3）点D（m，n）是反比例函数图象上的一动点，其中0＜m＜3，过点C作直线AC⊥x 轴于点A，交OD的延长线于点B；若点D是OB的中点，DE⊥x轴于点E，交OC于点F，试求四边形DFCB的面积．【答案】（1）解：将点C（3，1）分别代入y= 和y=ax，得：k=3，a= ，∴反比例函数解析式为y= ，正比例函数解析式为y= x；（2）解：观察图象可知，在第二象限内，当0＜x＜3时，反比例函数值大于正比例函数值；（3）解：∵点D（m，n）是OB的中点，又在反比例函数y= 上，∴OE= OA= ，点D（，2），∴点B（3，4），又∵点F在正比例函数y= x图象上，∴F（，），∴DF= 、BC=3、EA= ，∴四边形DFCB的面积为 ×（ +3）× = ．【解析】【分析】（1）利用待定系数法把C坐标代入解析式即可；（2）须数形结合，先找出交点，在交点的左侧与y轴之间，反比例函数值大于正比例函数值.（3）求出DF、BC、EA，代入梯形面积公式即可.6．已知点P在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，将点P向左平移1个单位，再向上平移2个单位得到点Q，点Q也在该函数y=kx+b的图象上．（1）k的值是________；（2）如图，该一次函数的图象分别与x轴、y轴交于A，B两点，且与反比例函数y=图象交于C，D两点（点C在第二象限内），过点C作CE⊥x轴于点E，记S1为四边形CEOB的面积，S2为△OAB的面积，若 = ，则b的值是________．【答案】（1）﹣2（2）3【解析】【解答】解：（1）设点P的坐标为（m，n），则点Q的坐标为（m﹣1，n+2），依题意得：，解得：k=﹣2．故答案为：﹣2．（2）∵BO⊥x轴，CE⊥x轴，∴BO∥CE，∴△AOB∽△AEC．又∵ = ，∴ = = ．令一次函数y=﹣2x+b中x=0，则y=b，∴BO=b；令一次函数y=﹣2x+b中y=0，则0=﹣2x+b，解得：x= ，即AO= ．∵△AOB∽△AEC，且 = ，∴．∴AE= AO= b，CE= BO= b，OE=AE﹣AO= b．∵OE•CE=|﹣4|=4，即 b2=4，解得：b=3 ，或b=﹣3 （舍去）．故答案为：3 ．【分析】（1）设出点P的坐标，根据平移的特性写出Q点的坐标，由点P,Q均在一次函数y=kx+b（k，b为常数，且k＜0，b＞0）的图象上，即可得出关于k,m,n,b的四元次一方程组，两式作差即可求出k的值；（2）由BO⊥x轴，CE⊥x轴，找出△AOB∽△AEC．再由给定图形的面积比即可求出==，根据一次函数的解析式可以用含b的式子表示出OA,OB,由此即可得出线段CE,AE 的长，利用OE=AE﹣AO求出OE的长，再借助反比例函数K的几何意义得出关于b的一元二次方程，解方程即可得出结论。

中考数学与反比例函数有关的压轴题附答案解析

中考数学与反比例函数有关的压轴题附答案解析一、反比例函数1．如图，在平面直角坐标系中，反比例函数y= 的图象与一次函数y=ax+b的图象交于点A（﹣2，3）和点B（m，﹣2）．（1）求反比例函数和一次函数的解析式；（2）直线x=1上有一点P，反比例函数图象上有一点Q，若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，直接写出点Q的坐标．【答案】（1）解：∵点A（﹣2，3）在反比例函数y= 的图形上，∴k=﹣2×3=﹣6，∴反比例函数的解析式为y=﹣，∵点B在反比例函数y=﹣的图形上，∴﹣2m=﹣6，∴m=3，∴B（3，﹣2），∵点A，B在直线y=ax+b的图象上，∴，∴，∴一次函数的解析式为y=﹣x+1（2）解：∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形，∴AB=PQ，AB∥PQ，设直线PQ的解析式为y=﹣x+c，设点Q（n，﹣），∴﹣ =﹣n+c，∴c=n﹣，∴直线PQ的解析式为y=﹣x+n﹣，∴P（1，n﹣﹣1），∴PQ2=（n﹣1）2+（n﹣﹣1+ ）2=2（n﹣1）2，∵A（﹣2，3）．B（3，﹣2），∴AB2=50，∵AB=PQ，∴50=2（n﹣1）2，∴n=﹣4或6，∴Q（﹣4. ）或（6，﹣1）【解析】【分析】（1）先利用待定系数法求出反比例函数解析式，进而求出点B的坐标，再用待定系数法求出直线解析式；（2）先判断出AB=PQ，AB∥PQ，设出点Q的坐标，进而得出点P的坐标，即可求出PQ，最后用PQ=AB建立方程即可得出结论．2．抛物线y= +x+m的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；（3）若射线NM交x轴于点P，且PA•PB= ，求点M的坐标．【答案】（1）解：y= x2+x+m= （x+2）2+（m﹣1）∴顶点坐标为（﹣2，m﹣1）∵顶点在直线y=x+3上，∴﹣2+3=m﹣1，得m=2；（2）解：过点F作FC⊥NB于点C，∵点N在抛物线上，∴点N的纵坐标为： a2+a+2，即点N（a， a2+a+2）在Rt△FCN中，FC=a+2，NC=NB﹣CB= a2+a，∴NF2=NC2+FC2=（ a2+a）2+（a+2）2，=（ a2+a）2+（a2+4a）+4，而NB2=（ a2+a+2）2，=（ a2+a）2+（a2+4a）+4∴NF2=NB2，NF=NB（3）解：连接AF、BF，由NF=NB，得∠NFB=∠NBF，由（2）的思路知，MF=MA，∴∠MAF=∠MFA，∵MA⊥x轴，NB⊥x轴，∴MA∥NB，∴∠AMF+∠BNF=180°∵△MAF和△NFB的内角总和为360°，∴2∠MAF+2∠NBF=180°，∠MAF+∠NBF=90°，∵∠MAB+∠NBA=180°，∴∠FBA+∠FAB=90°，又∵∠FAB+∠MAF=90°，∴∠FBA=∠MAF=∠MFA，又∵∠FPA=∠BPF，∴△PFA∽△PBF，∴ = ，PF2=PA×PB= ，过点F作FG⊥x轴于点G，在Rt△PFG中，PG= = ，∴PO=PG+GO= ，∴P（﹣，0）设直线PF：y=kx+b，把点F（﹣2，2）、点P（﹣，0）代入y=kx+b，解得k= ，b= ，∴直线PF：y= x+ ，解方程 x2+x+2= x+ ，得x=﹣3或x=2（不合题意，舍去），当x=﹣3时，y= ，∴M（﹣3，）．【解析】【分析】（1）利用配方法将二次函数化成顶点式，写出顶点坐标，由顶点再直线y=x+3上，建立方程求出m的值。

中考数学压轴题专项训练反比例函数含解析

2021年中考数学压轴题专项训练《反比例函数》1．如图，反比例函数y1＝和一次函数y2＝mx+n相交于点A（1，3)，B（﹣3，a）,(1)求一次函数和反比例函数解析式;（2)连接OA，试问在x轴上是否存在点P，使得△OAP为以OA为腰的等腰三角形，若存在,直接写出满足题意的点P的坐标；若不存在，说明理由．解:（1）∵点A（1，3）在反比例函数y1＝的图象上，∴k＝1×3＝3，∴反比例函数的解析式为y1＝，∵点B(﹣3,a）在反比例函数y1＝的图象上,∴﹣3a＝3，∴a＝﹣1,∴B（﹣3，﹣1），∵点A(1，3），B(﹣3，﹣1）在一次函数y2＝mx+n的图象上，∴，∴,∴一次函数的解析式为y2＝x+2；（2)如图，∵△OAP为以OA为腰的等腰三角形，∴①当OA＝OP时，∵A（1，3），∴OA＝，∵OP＝,∵点P在x轴上，∴P（﹣，0）或（，0）,②当OA＝AP时，则点A是线段OP的垂直平分线上,∵A（1，3），∴P（2，0)，即：在x轴上存在点P，使得△OAP为以OA为腰的等腰三角形，此时,点P的坐标为(﹣，0）或（2，0）或（，0）．2．在平面直角坐标系xOy中，函数y＝（x＞0）的图象G经过点A（3，2），直线l：y＝kx﹣1（k≠0）与y轴交于点B,与图象G交于点C．(1)求m的值；（2）横、纵坐标都是整数的点叫做整点．记图象G在点A,C 之间的部分与线段BA，BC围成的区域（不含边界）为W．①当直线l过点（2，0)时，直接写出区域W内的整点个数;②若区域W内的整点不少于4个，结合函数图象,求k的取值范围．解:(1）把A（3，2）代入y＝得m＝3×2＝6，(2）①当直线l过点（2，0）时，直线解析式为y＝x﹣1,解方程＝x﹣1得x1＝1﹣（舍去），x2＝1+，则C（1+，），而B（0，﹣1），如图1所示,区域W内的整点有（3，1）一个；②如图2，直线l在AB的下方时，直线l：y＝kx﹣1过(6，1)时，1＝6k﹣1，解得k＝，当直线在OA的上方时，直线经过（1，4）时，4＝k﹣1,解得k＝5，观察图象可知：当k≤或k≥5时，区域W内的整点不少于4个．3．如图，在平面直角坐标系中，四边形OABC的顶点坐标分别为O（0，0）,A（6，0），B（4，3）,C（0,3)．动点P从点O 出发,以每秒个单位长度的速度沿边OA向终点A运动；动点Q从点B同时出发，以每秒1个单位长度的速度沿边BC 向终点C运动，设运动的时间为t秒，PQ2＝y．（1）直接写出y关于t的函数解析式及t的取值范围：；（2）当PQ＝时，求t的值;（3)连接OB交PQ于点D，若双曲线y＝经过点D，问k 的值是否变化？若不变化,请求出k的值；若变化,请说明理由．解：（1）过点P作PE⊥BC于点E，如图1所示．当运动时间为t秒时（0≤t≤4）时，点P的坐标为（t,0），点Q的坐标为（4﹣t，3）,∴PE＝3,EQ＝|4﹣t﹣t|＝|4﹣t|,∴PQ2＝PE2+EQ2＝32+｜4﹣t|2＝t2﹣20t+25,∴y关于t的函数解析式及t的取值范围：；故答案为:．(2）当时，整理，得5t2﹣16t+12＝0，解得：t1＝2，．(3）经过点D的双曲线的k值不变．连接OB，交PQ于点D，过点D作DF⊥OA于点F，如图2所示．∵OC＝3，BC＝4，∴．∵BQ∥OP，∴△BDQ∽△ODP，∴,∴OD＝3．∵CB∥OA,∴∠DOF＝∠OBC．在Rt△OBC中，,，∴，，∴点D的坐标为,∴经过点D的双曲线的k值为．4．如图，一次函数y＝kx+b的图象与反比例函数y＝的图象交于点A（﹣3，m+8)，B(n，﹣6）两点．（1）求一次函数与反比例函数的解析式；（2）求△AOB的面积;（3）若P（x1，y1），Q（x2,y2)是该反比例函数图象上的两点，且当x1＜x2时,y1＞y2，指出点P、Q各位于哪个象限？解：（1)将A（﹣3，m+8）代入反比例函数y＝得﹣3(m+8）＝m，解得m＝﹣6，∴点A的坐标为（﹣3,2）,反比例函数解析式为y＝﹣，将点B（n,﹣6）代入y＝﹣得﹣6n＝﹣6,解得n＝1,∴点B的坐标为（1，﹣6），将点A（﹣3，2），B（1,﹣6）代入y＝kx+b得,解得，∴一次函数解析式为y＝﹣2x﹣4；（2)设AB与x轴相交于点C，如图，当﹣2x﹣4＝0，解得x＝﹣2，则点C的坐标为（﹣2，0），∴S△AOB＝S△AOC+S△BOC，＝×2×2+×2×6,＝2+6，＝8；（3）∵当x1＜x2时，y1＞y2，∴点P和点Q不在同一象限，∴P在第二象限，Q在第四象限．5．如图,平面直角坐标系中，一次函数y＝x﹣1的图象与x轴，y轴分别交于点A，B，与反比例函数y＝的图象交于点C，D，CE⊥x轴于点E，＝．（1)求反比例函数的表达式与点D的坐标；(2）以CE为边作▱ECMN，点M在一次函数y＝x﹣1的图象上，设点M的横坐标为a，当边MN与反比例函数y＝的图象有公共点时，求a的取值范围．解：(1)由题意A(1,0)，B(0，﹣1）,∴OA＝OB＝1，∴∠OAB＝∠CAE＝45°∵AE＝3OA,∴AE＝3,∵EC⊥x轴,∴∠AEC＝90°，∴∠EAC＝∠ACE＝45°,∴EC＝AE＝3，∴C（4,3)，∵反比例函数y＝经过点C（4，3），∴k＝12，由，解得或，∴D（﹣3,﹣4）．（2）如图，设M（a，a﹣1）．当点N在反比例函数的图象上时，N（a，），∵四边形ECMN是平行四边形，∴MN＝EC＝3，∴｜a﹣1﹣｜＝3，解得a＝6或﹣2或﹣1±(舍弃），∴M（6，5）或(﹣2，﹣3），观察图象可知:当边MN与反比例函数y＝的图象有公共点时4＜a≤6或﹣3≤a≤﹣2．6．如图，一次函数y＝kx+2的图象与y轴交于点A，正方形ABCD 的顶点B在x轴上，点D在直线y＝kx+2上，且AO＝OB，反比例函数y＝(x＞0）经过点C．（1）求一次函数和反比例函数的解析式；（2）点P是x轴上一动点，当△PCD的周长最小时，求出P 点的坐标；（3）在（2）的条件下,以点C、D、P为顶点作平行四边形,直接写出第四个顶点M的坐标．解：（1)设一次函数y＝kx+2的图象与x轴交于点E，连接BD，如图1所示．当x＝0时，y＝kx+2＝2，∴OA＝2．∵四边形ABCD为正方形，OA＝OB，∴∠BAE＝90°，∠OAB＝∠OBA＝45°，∴∠OAE＝∠OEA＝45°，∴OE＝2，点E的坐标为(﹣2，0）．将E（﹣2，0）代入y＝kx+2,得：﹣2k+2＝0，解得：k＝1，∴一次函数的解析式为y＝x+2．∵∠OBD＝∠ABD+∠OBA＝90°，∴BD∥OA．∵OE＝OB＝2，∴BD＝2OA＝4,∴点D的坐标为(2,4）．∵四边形ABCD为正方形，∴点C的坐标为（2+2﹣0，0+4﹣2），即（4,2）．∵反比例函数y＝（x＞0）经过点C，∴n＝4×2＝8,∴反比例函数解析式为y＝．（2)作点D关于x轴的对称点D′,连接CD′交x轴于点P,此时△PCD的周长取最小值,如图2所示．∵点D的坐标为（2,4），∴点D′的坐标为（2，﹣4）．设直线CD′的解析式为y＝ax+b（a≠0），将C(4，2），D′（2，﹣4）代入y＝ax+b，得:，解得：，∴直线CD′的解析式为y＝3x﹣10．当y＝0时，3x﹣10＝0,解得：x＝，∴当△PCD的周长最小时，P点的坐标为（,0)．（3)设点M的坐标为（x,y），分三种情况考虑，如图3所示．①当DP为对角线时，，解得：，∴点M1的坐标为（，2）；②当CD为对角线时，,解得:，∴点M2的坐标为(，6）；③当CP为对角线时,,解得：,∴点M3的坐标为(，﹣2）．综上所述：以点C、D、P为顶点作平行四边形，第四个顶点M的坐标为（,2），(，6)或(，﹣2）．7．如图在平面直角坐标系中，一次函数y＝﹣2x﹣4的图象与反比例函数y＝的图象交于点A（1，n)，B（m，2）（1）求反比例函数关系式及m的值；(2)若x轴正半轴上有一点M满足△MAB的面积为16，求点M 的坐标;（3)根据函数图象直接写出关于x的不等式在＜﹣2x﹣4的解集解：（1）∵一次函数y＝﹣2x﹣4的图象过点A（1，n），B(m，2）∴n＝﹣2﹣4,2＝﹣2m﹣4∴n＝﹣6，m＝﹣3，∴A(1，﹣6）把A(1,﹣6）代入y＝得，k＝﹣6，∴反比例函数关系式为y＝﹣；（2）设直线AB与x轴交于N点，则N(﹣2，0），设M(m，0），m＞0，∵S△MAB＝S△BMN+S△AMN，△MAB的面积为16,∴｜m+2｜×（2+6）＝16，解得m＝2或﹣6（不合题意舍去），∴M（2，0）；(3）由图象可知：不等式在＜﹣2x﹣4的解集是x＜﹣3或0＜x＜1．8．如图,在平面直角坐标系中，点A（3,5）与点C关于原点O 对称，分别过点A、C作y轴的平行线，与反比例函数的图象交于点B、D,连结AD、BC，AD与x轴交于点E（﹣2，0)．(1）求直线AD对应的函数关系式;(2)求k的值；(3）直接写出阴影部分图形的面积之和．解：（1)设直线AD对应的函数关系式为y＝ax+b．∵直线AD过点A（3，5），E（﹣2,0），∴解得∴直线AD的解析式为y＝x+2．（2）∵点A（3,5）关于原点O的对称点为点C，∴点C的坐标为（﹣3,﹣5)，∵CD∥y轴，∴设点D的坐标为（﹣3,a），∴a＝﹣3+2＝﹣1，∴点D的坐标为（﹣3,﹣1），∵反比例函数y＝的图象经过点D，∴k＝﹣3×(﹣1）＝3；（3）如图：∵点A和点C关于原点对称，∴阴影部分的面积等于平行四边形CDGF的面积，∴S阴影＝4×3＝12．9．如图，一次函数y＝kx+b的图象分别与反比例函数y＝的图象在第一象限交于点A(4，3），与y轴的负半轴交于点B，且OA＝OB．（1）求函数y＝kx+b和y＝的表达式;(2）已知点C（0,8），试在该一次函数图象上确定一点M，使得MB＝MC，求此时点M的坐标．解：（1）把点A（4，3）代入函数得：a＝3×4＝12，∴y＝,OA＝5，∵OA＝OB，∴OB＝5，∴点B的坐标为（0，﹣5),把B（0,﹣5），A（4,3)代入y＝kx+b得:∴y＝2x﹣5；(2）作MD⊥y轴．∵点M在一次函数y＝2x﹣5上,∴设点M的坐标为（x，2x﹣5）．∵MB＝MC,∴CD＝BD，∴x2+(8﹣2x+5）2＝x2+（﹣5﹣2x+5）2∴8﹣（2x﹣5）＝2x﹣5+5解得：x＝∴2x﹣5＝,∴点M的坐标为（,）．10．如图，矩形OABC的顶点A、C分别在x、y轴的正半轴上，点B在反比例函数y＝（k≠0)的第一象限内的图象上，OA ＝3，OC＝5,动点P在x轴的上方，且满足S△PAO＝S矩形OABC．（1）若点P在这个反比例函数的图象上，求点P的坐标；(2)连接PO、PA，求PO+PA的最小值;（3)若点Q是平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标．解：（1）由题意，可知:点B的坐标为（3，5）．∵点B在反比例函数y＝（k≠0）的第一象限内的图象上，∴k＝3×5＝15，∴反比例函数的解析式为y＝．∵S△PAO＝S矩形OABC，∴×3×y P＝×3×5，∴y P＝3．当y＝3时，＝3，解得：x＝5，∴当点P在这个反比例函数的图象上时，点P的坐标为(5，3)．（2）由（1）可知：点P在直线y＝3上，作点O关于直线y ＝3的对称点O′，连接AO′交直线y＝3于点P，此时PO+PA 取得最小值，如图1所示．∵点O的坐标为（0，0），∴点O′的坐标为（0,6）．∵点A的坐标为（3，0)，∴AO′＝＝3，∴PO+PA的最小值为3．（3）∵AB∥y轴,AB＝5，点P的纵坐标为3，∴AB不能为对角线，只能为边．设点P的坐标为(m，3),分两种情况考虑,如图2所示：①当点Q在点P的上方时，AP＝AB＝5，即(m﹣3)2+(3﹣0）2＝25，解得：m1＝﹣1,m2＝7，∴点P1的坐标为（﹣1,3），点P2的坐标为（7，3)．又∵PQ＝5，且PQ∥AB∥y轴,∴点Q1的坐标为（﹣1,8），点Q2的坐标为（7，8）；②当点Q在点P的下方时，BP＝AB＝5，即（m﹣3)2+（3﹣5）2＝25，解得：m3＝3﹣，m4＝3+,同理，可得出：点Q3的坐标为（3﹣，﹣2）,点Q4的坐标为（3+,﹣2）．综上所述：当以A、B、P、Q为顶点的四边形是菱形时，点Q 的坐标为（﹣1，8），（7，8），(3﹣，﹣2）或（3+，﹣2）．11．如图，已知C，D是反比例函数y＝图象在第一象限内的分支上的两点，直线CD分别交x轴、y轴于A，B两点，设C，D的坐标分别是（x1，y1）、（x2，y2），且x1＜x2，连接OC、OD．（1)若x1+y1＝x2+y2，求证：OC＝OD；（2）tan∠BOC＝，OC＝，求点C的坐标；（3)在(2）的条件下，若∠BOC＝∠AOD,求直线CD的解析式．（1）证明：∵C，D是反比例函数y＝图象在第一象限内的分支上的两点，∴y1＝,y2＝．∵x1+y1＝x2+y2，即x1+＝x2+，∴x1﹣x2＝．又∵x1＜x2，∴＝1，∴＝x2＝y1，＝x1＝y2．∴OC＝＝,OD＝＝，∴OC＝OD．（2）解：∵tan∠BOC＝，∴＝．又∵OC＝,∴+＝10,∴x1＝1,y1＝3或x1＝﹣1，y1＝﹣3．∵点C在第一象限,∴点C的坐标为（1,3）．（3）解：∵∠BOC＝∠AOD，∴tan∠AOD＝，∴＝．∵点C(1，3)在反比例函数y＝的图象上，∴m＝1×3＝3，∴x2•y2＝3，∴x2＝3，y2＝1或x2＝﹣3，y2＝﹣1．∵点D在第一象限,∴点D的坐标为（3，1)．设直线CD的解析式为y＝kx+b（k≠0），将C（1,3）,D（3,1）代入y＝kx+b，得：，解得:，∴直线CD的解析式为y＝﹣x+4．12．如图，在平面直角坐标系中，矩形OABC的两边分别在x 轴、y轴上,D是对角线的交点，若反比例函数y＝的图象经过点D，且与矩形OABC的两边AB,BC分别交于点E，F．（1）若D的坐标为(4，2）①则OA的长是8，AB的长是4；②请判断EF是否与AC平行，井说明理由;③在x轴上是否存在一点P．使PD+PE的值最小，若存在，请求出点P的坐标及此时PD+PE的长；若不存在．请说明理由．(2）若点D的坐标为(m,n），且m＞0，n＞0，求的值．解：（1)①∵点D的坐标为（4,2),∴点B的坐标为（8，4)，∴OA＝8，AB＝4．故答案为：8；4．②EF∥AC，理由如下:∵反比例函数y＝的图象经过点D（4，2)，∴k＝4×2＝8．∵点B的坐标为（8,4)，BC∥x轴，AB∥y轴，∴点F的坐标为（2，4）,点E的坐标为（8，1），∴BF＝6,BE＝3，∴＝，＝，∴＝．∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴∠BCA＝∠BFE，∴EF∥AC．③作点E关于x轴对称的点E′，连接DE′交x轴于点P,此时PD+PE的值最小，如图所示．∵点E的坐标为（8，1），∴点E′的坐标为（8,﹣1），∴DE′＝＝5．设直线DE′的解析式为y＝ax+b(a≠0），将D（4,2），E′（8，﹣1）代入y＝ax+b,得：，解得：，∴直线DE′的解析式为y＝﹣x+5．当y＝0时，﹣x+5＝0，解得：x＝，∴当点P的坐标为(，0)时，PD+PE的值最小，最小值为5．（2）∵点D的坐标为（m，n），∴点B的坐标为（2m，2n）．∵反比例函数y＝的图象经过点D（m,n）,∴k＝mn，∴点F的坐标为（m,2n)，点E的坐标为（2m，n)，∴BF＝m，BE＝n，∴＝，＝，∴＝．又∵∠ABC＝∠EBF，∴△ABC∽△EBF，∴＝＝．13．如图，一次函数y＝kx+b（k≠0）的图象与反比例函数y＝(m ≠0）的图象交于A（﹣3，1），B（1,n）两点．（1）求反比例函数和一次函数解析式;（2)结合图象直接写出不等式﹣kx﹣b＞0的解．解:（1)∵点A（﹣3，1）在反比例函数y＝（m≠0）的图象上,∴m＝（﹣3）×1＝﹣3，∴反比例函数的表达式为y＝﹣，∵点B（1，n）也在反比例函数y＝﹣的图象上，∴n＝﹣＝﹣3，即B（1，﹣3),把点A（﹣3，1），点B（1，﹣3)代入一次函数y＝kx+b中，得,解得，∴一次函数的表达式为y＝﹣x﹣2；（2）如图所示，当＞kx+b时,x的取值范围是﹣3＜x＜0或x ＞1，所以不等式﹣kx﹣b＞0的解是：﹣3＜x＜0或x＞1．14．如图，在平面直角坐标系xOy内，函数y＝的图象与反比例函数y＝（k≠0）图象有公共点A,点A的坐标为(8，a），AB⊥x轴,垂足为点B．(1）求反比例函数的解析式；（2)点P在线段OB上，若AP＝BP+2，求线段OP的长；(3）点D为射线OA上一点,在（2）的条件下，若S△ODP＝S△ABO，求点D的坐标．解：（1）∵函数y＝的图象过点A（8，a），∴a＝×8＝4，∴点A的坐标为（8，4），∵反比例函数y＝（k≠0）图象过点A（8，4），∴4＝，得k＝32,∴反比例函数的解析式为y＝；（2)设BP＝b，则AP＝b+2，∵点A（8，4），AB⊥x轴于点B，∴AB＝4,∠ABP＝90°,∴b2+42＝（b+2）2，解得,b＝3，∴OP＝8﹣3＝5，即线段OP的长是5;（3）设点D的坐标为（d，d)，∵点A（8，4），点B（8，0），点P（5,0），S△ODP＝S△ABO,∴，解得,d＝，∴d＝，∴点D的坐标为（,）．15．阅读理解：如图（1），在平面直角坐标系xOy中,已知点A的坐标是（1,2），点B的坐标是（3，4)，过点A、点B作平行于x轴、y轴的直线相交于点C，得到Rt△ABC，由勾股定理可得,线段AB＝＝．得出结论：（1)若A点的坐标为（x1，y1）,B点的坐标为（x2，y2）请你直接用A、B两点的坐标表示A、B两点间的距离;应用结论：（2)若点P在y轴上运动，试求当PA＝PB时,点P的坐标．（3)如图（2)若双曲线L1：y＝（x＞0）经过A(1，2)点，将线段OA绕点O旋转，使点A恰好落在双曲线L2：y＝﹣（x＞0)上的点D处，试求A、D两点间的距离．解:（1）∵A点的坐标为（x1，y1),B点的坐标为(x2，y2），∴根据两点间的距离公式得,AB＝；(2）设点P（0，a）,∵A的坐标是(1，2），点B的坐标是（3,4），∵PA＝，PB＝，∵PA＝PB，∴＝,∴a＝5,∴P（0，5）；（3）∵双曲线L1：y＝（x＞0）经过A(1,2)点，∴OA＝，k＝1×2＝2，∴双曲线L1：y＝(x＞0），双曲线L2：y＝﹣（x＞0），设点D坐标为（m，﹣）（m＞0），∴OD＝，由旋转知，OA＝OD，∴＝，∴m＝±1或m＝±2,∵m＞0，∴m＝1或m＝2，∴D（1，﹣2）或（2，﹣1）．∵A（1，2),∴AD＝4或．。

中考数学压轴题提升训练一次函数与反比例函数综合题含解析

一次函数与反比例函数综合题【例1】。

如图，直线l：y=ax+b交x轴于点A（3，0）,交y于第一象限的点P，点P的轴于点B(0,-3），交反比例函数y kx横坐标为4.的解析式；（1）求反比例函数y kx（2)过点P作直线l的垂线l1,交反比例函数y k的图象于x点C,求△OPC的面积.【答案】见解析。

【解析】解：（1）∵y=ax+b交x轴于点A(3，0)，交y轴于点B（0，-3)，∴3a+b=0，b=－3,解得：a=1,即l1的解析式为:y=x－3，当x=4时，y=1，即P（4，1），将P点坐标代入y k得：k=4，x；即反比函数的解析式为：y4x（2）设直线l1与x轴、y轴分别交于点E,D，∵OA=OB=3,∴∠OAB=∠OBA=45°，∵l⊥l1，∴∠DPB=90°，∴∠ODP=45°，设直线l1的解析式为：y=－x+b,将点P(4,1）代入得：b=5，联立:y=－x+5，y4x，解得：x=1，y=4或x=4，y=1，即C(1，4），∴S△OPC=S△ODE－S△OCD－S△OPE=12×5×5－12×5×1－12×5×1=152.【变式1—1】.如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A，C分别在坐标轴上，点B的坐标为(4，2）,直线y=–12x+3交AB,BC于点M，N，反比例函数kyx的图象经过点M，N．（1）求反比例函数的解析式；（2)若点P在x轴上，且△OPM的面积与四边形BMON的面积相等，求点P的坐标．【答案】见解析.【解析】解：（1）∵B(4,2)，四边形OABC为矩形，∴OA=BC=2，在y=–12x+3中，y=2时，x=2，即M(2,2),将M（2，2）代入kyx=得：k=4，∴反比例函数的解析式为：4yx=.（2）在4yx=中，当x=4时，y=1，即CN=1，∵S四边形BMON=S矩形OABC－S△AOM－S△CON=4×2－12×2×2－12×4×1=4,∴S△OPM=4,即12·OP·OA=4，∵OA=2，∴OP=4,∴点P 的坐标为（4,0）或(－4，0)。

中考数学压轴题之反比例函数(中考题型整理,突破提升)及详细答案

y1= 中，当 x=1 时，y=4， ∴ P（1，4）．设直线 AP 的函数关系式为 y=mx+n，把点 A（﹣4，﹣1）、P（1，4）代入 y=mx+n，
则
，
解得
．
故直线 AP 的函数关系式为 y=x+3，
则点 C 的坐标（0，3），OC=3，
∴ S△ AOP=S△ AOC+S△ POC
= OC•AR+ OC•PS
又∵ 点 F 在反比例函数
（k＞0）的图象上，∴ k=12，
∴ 该函数的解析式为 y= （x＞0）
（2）解：由题意知 E，F 两点坐标分别为 E（，4），F（6，
∴ 当 k=12 时，S 有最大值．S 最大=3
【解析】【分析】）当 F 为 AB 的中点时，点 F 的坐标为（3，1），由此代入求得函数解
C 与 D 横纵坐标乘积相等，求出 b 的值确定出 B 坐标，进而求出 k 的值，确定出双曲线解析式；（3）抓住两个关键点，将 A 坐标代入双曲线解析式求出 b 的值；将 C 坐标代入双曲线解析式求出 b 的值，即可确定出平行四边形与双曲线总有公共点时 b 的范围．
5．如图，正比例函数和反比例函数的图象都经过点 A（3，3），把直线 OA 向下平移后，与反比例函数的图象交于点 B（6，m），与 x 轴、y 轴分别交于 C、D 两点．
（1）求 m 的值；（2）求过 A、B、D 三点的抛物线的解析式；（3）若点 E 是抛物线上的一个动点，是否存在点 E，使四边形 OECD 的面积 S1
，是四边
形 OACD 面积 S 的？若存在，求点 E 的坐标；若不存在，请说明理由．【答案】（1）解：∵ 反比例函数的图象都经过点 A（3，3），

【免费·中考必备】2012年中考数学试题分类解析专题20 一次(正比例)函数和反比例函数的综合

2012年全国中考数学试题分类解析汇编(159套63专题）专题20：一次(正比例）函数和反比例函数的综合一、选择题1. （2012山西省2分）已知直线y =ax （a ≠0）与双曲线()ky=k 0x≠的一个交点坐标为（2，6），则它们的另一个交点坐标是【】 A ．（﹣2，6） B ．（﹣6，﹣2） C ．（﹣2，﹣6） D ．（6，2）【答案】C 。

【考点】反比例函数图象的对称性，关于原点对称的点的坐标特征。

【分析】∵直线y =ax （a ≠0）与双曲线()ky=k 0x≠的图象均关于原点对称， ∴它们的另一个交点坐标与（2，6）关于原点对称。

∵关于原点对称的点的坐标是横、纵坐标都互为相反数， ∴它们的另一个交点坐标为：（﹣2，﹣6）。

故选C 。

2. （2012海南省3分）如图，正比例函数1y=k x 与反比例函数2k y=x的图象相交于点A 、B 两点，若点A 的坐标为（2，1），则点B 的坐标是【】A ．（1，2）B ．（－2，1）C ．（－1，－2）D ．（－2，－1）【答案】D 。

【考点】正比例函数与反比例函数的对称性，关于原点对称的点的坐标特征。

【分析】根据正比例函数与反比例函数关于原点对称的性质，正比例函数1y=k x 与反比例函数2k y=x的图象的两交点A 、B 关于原点对称；由A 的坐标为（2，1），根据关于原点对称的点的坐标是横、纵坐标都互为相反数的坐标特征，得点B 的坐标是（－2，－1）。

故选D 。

3. （2012广东广州3分）如图，正比例函数y 1=k 1x 和反比例函数22k y =x的图象交于A （﹣1，2）、B （1，﹣2）两点，若y 1＜y 2，则x 的取值范围是【】A．x＜﹣1或x＞1 B．x＜﹣1或0＜x＜1 C．﹣1＜x＜0或0＜x＜1 D．﹣1＜x＜0或x＞1 【答案】D。

【考点】反比例函数与一次函数的交点问题。

【分析】根据图象找出直线在双曲线下方的x的取值范围：由图象可得，﹣1＜x＜0或x＞1时，y1＜y2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2012年全国各地中考数学压轴题专集答案三、反比例函数 1．（北京模拟）如图，直线AB 经过第一象限，分别与x 轴、y 轴交于A 、B 两点，P 为线段AB 上任意一点（不与A 、B 重合），过点P 分别向x 轴、y 轴作垂线，垂足分别为C 、D ．设OC ＝x ，四边形OCPD 的面积为S ．（1）若已知A （4，0），B （0，6），求S 与x 之间的函数关系式；（2）若已知A （a ，0），B （0，b ），且当x ＝34 时，S 有最大值98，求a 、b 的值；（3）在（2）的条件下，在直线AB 上有一点M ，且点M 到x 轴、y 轴的距离相等，点N 在过M 点的反比例函数图象上，且△OAN 是直角三角形，求点N1．解：（1）设直线AB 的解析式为y ＝kx ＋b 由A （4，0），B （0，6），得⎩⎪⎨⎪⎧4k ＋b ＝0b ＝6 解得⎩⎪⎨⎪⎧k ＝－3 2b ＝6∴直线AB 的解析式为y ＝－32x ＋6 ∵OC ＝x ，∴P （x ，－32x ＋6） ∴S ＝x (－32x ＋6) 即S ＝－32x2＋6x （0＜x ＜4）（2）设直线AB 的解析式为y ＝mx ＋n ∵OC ＝x ，∴P （x ，mx ＋n ） ∴S ＝mx2＋nx∵当x ＝34 时，S 有最大值98∴⎩⎨⎧－n 2m＝349 16 m ＋ 3 4 n ＝9 8解得⎩⎪⎨⎪⎧m ＝－2n ＝3∴直线AB 的解析式为为y ＝－2x ＋3∴A （32，0），B （0，3）即a ＝32，b ＝3 （3）设点M 的坐标为（x M，y M ），∵点M 在（2）中的直线AB 上，∴y M ＝－2x M ＋3 ∵点M 到x 轴、y 轴的距离相等， ∴x M ＝y M或x M ＝－y M当x M ＝y M时，易得M 点的坐标为（1，1）∴过M 点的反比例函数的解析式为y ＝1x∵点N 在y ＝1x的图象上，OA 在x 轴上，且△OAN 是直角三角形 ∴点N 的坐标为（32，23）当x M ＝－y M时，M 点的坐标为（3，－3）过M 点的反比例函数的解析式为y ＝－9x∵点N 在y ＝－9x的图象上，OA 在x 轴上，且△OAN 是直角三角形 ∴点N 的坐标为（32，－6）综上，点N 的坐标为（3 2，2 3 ）或（32，－6）2．（北京模拟）已知点A 是双曲线y ＝k 1x（k 1＞0）上一点，点A 的横坐标为1，过点A 作平行于y 轴的直线，与x 轴交于点B ，与双曲线y ＝k 2x（k 2＜0）交于点C ．点D （m ，0）是x轴上一点，且位于直线AC 右侧，E 是AD 的中点．（1）如图1，当m ＝4时，求△ACD 的面积（用含k 1、k 2的代数式表示）；（2）如图2，若点E 恰好在双曲线y ＝k 1x（k 1＞0）上，求m 的值；（3）如图3，设线段EB 的延长线与y 轴的负半轴交于点F ，当m ＝2时，若△BDF 的面积为1，且CF ∥AD ，求k 1的值，并直接写出线段CF 的长．图1图2图3解：（1）由题意得A ，C 两点的坐标分别为A （1，k 1），C （1，k 2） ∵k 1＞0，k 2＜0，∴点A 在第一象限，点C 在第四象限，AC ＝k 1－k 2 当m ＝4时，S △ACD＝12AC ²BD ＝32(k 1－k 2) （2）作EG ⊥x 轴于点G ，则EG ∥AB∵E 是AD 的中点，∴G 是BD 的中点 ∵A （1，k 1），B （1，0），D （m ，0） ∴EG ＝12AB ＝k 1 2 ，BG ＝ 12 BD ＝ m －1 2 ，OG ＝OB ＋BG ＝m ＋1 2∴点E 的坐标为E （m ＋1 2，k 12）∵点E 恰好在双曲线y ＝k 1x（k 1＞0）上∴m ＋1 2 ²k 12＝k 1 ① ∵k 1＞0，∴方程①可化为m ＋14＝1，解得m ＝3 （3）当m ＝2时，点D 的坐标为D （2，0），由（2）可知点E 的坐标为E （3 2，k 12）∵S △BDF＝1，∴12BD ²OF ＝1，∴OF ＝2设直线BE 的解析式为y ＝ax ＋b （a ≠0） ∵B （1，0），E （3 2，k 12）∴⎩⎪⎨⎪⎧a ＋b ＝032a ＋b ＝k 1 2解得⎩⎪⎨⎪⎧k ＝k 1b ＝－k 1 ∴直线BE 的解析式为y ＝k 1x －k 1∵线段EB 的延长线与y 轴的负半轴交于点F ，k 1＞0 ∴点F 的坐标为F （0，－k 1），∴OF ＝k 1 ∴k 1＝2线段CF 的长为53．（上海模拟）Rt △ABC 在直角坐标系中的位置如图所示，tan ∠BAC ＝12，反比例函数y ＝kx（k ≠0）在第一象限内的图象与BC 边交于点D （4，m ），与AB 边交于点E （2，n ），△BDE 的面积为2．（1）求反比例函数和直线AB 的解析式；（2）设直线AB 与y 轴交于点F ，点P 是射线FD 上一动点，是否存在点P 使以E 、F 、P为顶点的三角形与△AEO 相似？若存在，求点P 的坐标；若不存在，请说明理由．解：（1）∵点D （4，m ）、E （2，n ）在反比例函数y ＝kx（k ≠0）的图象上∴⎩⎪⎨⎪⎧4m ＝k 2n ＝k得n ＝2m 过点E 作EH ⊥BC 于H ，连接DE 在Rt △BEH 中，tan ∠BEH ＝tan ∠BAC ＝12，EH ＝2，∴BH ＝1 ∴D （4，m ），E （2，2m ），B （4，2m ＋1） ∵S △BDE＝1 2 BD ²EH ＝ 12(m ＋1)×2＝2，m ＝1∴D （4，1），E （2，2），B （4，3）∵点D （4，1）在反比例函数y ＝kx（k ≠0）的图象上，∴k ＝4∴反比例函数的解析式为y ＝4x设直线AB 的解析式为y ＝k ′x ＋b ，把B （4，3），E （2，2）代入得 ⎩⎪⎨⎪⎧3＝4k ′＋b 2＝2k ′＋b 解得 ⎩⎪⎨⎪⎧k ′＝12b ＝1∴直线AB 的解析式为y ＝12x ＋1 （2）∵直线y ＝12x ＋1与y 轴交于点F （0，1），点D∴FD ∥x 轴，∠EFP ＝∠EAO因此以E、F 、P 为顶点的三角形与△AEO 相似有两种情况： ①若EFFP＝EAAO，则△FEP ∽△AEO ∵E （2，2），F （0，1），∴EF ＝5∵直线y ＝12x ＋1与x 轴交于点A ，∴A （0，－2）∴5FP＝252，∴FP ＝1 ∴P （1，1）②若FPEF ＝AEOA，则△FPE ∽△AEO∴FP5＝252，∴FP ＝5∴P （5，1） 4．（安徽某校自主招生）如图，直角梯形OABC 的腰OC 在y 轴的正半轴上，点A （5n ，0）在x 轴的负半轴上，OA :AB :OC ＝5 :5 :3．点D 是线段OC 上一点，且OD ＝BD ．（1）若直线y ＝kx ＋m （k ≠0）过B 、D 两点，求k 的值；（2）在（1）的条件下，反比例函数y ＝mx的图象经过点B ． ①求证：反比例函数y ＝mx的图象与直线AB 必有两个不同的交点； ②设反比例函数y ＝mx的图象与直线AB 的另一个交点为E ，已知点P （p ，－n －1），Q （q ，－n －2）在线段AB 上，当点E解：（1）∵A （5n ，0），OA :OC ＝5 :3，点C 在y 轴的正半轴上 ∴C （0，－3n ）∵BC ∥OA ，∴点B 的纵坐标为－3n 过点B 作BG ⊥OA 于G ，则BG ＝－3n设OG ＝x ，在Rt △ABG 中，(－5n －x)2＋(－3n)2＝(－5n)2解得x ＝－n 或x ＝－9n （舍去） ∴B （n ，－3n ）设OD ＝t ，∵点D 是线段OC 上一点，且OD ＝BD∴t2＝(－3n －t)2＋(－n)2，∴t ＝－53n ∴D （0，－53n ）把B 、D 的坐标代入y ＝kx ＋m ，得 ⎩⎪⎨⎪⎧nk ＋b ＝－3n b ＝－5 3n解得k ＝－4 3（2）①∵比例函数y ＝m x的图象经过点B ，∴m ＝n (－3n)＝－3n2 ∴y ＝－3n2x由A （5n ，0），B （n ，－3n ）可得直线AB 的解析式为y ＝34x －154n 由y ＝－3n2x 和y ＝ 3 4 x － 15 4n 消去y 并整理得：3x2－15nx ＋12n2＝0∵△＝(－15n)2－4×3×12n2＝9n2＞0∴反比例函数y ＝－3n2x的图象与直线AB 必有两个不同的交点联立 ⎩⎨⎧y ＝－3n2xy ＝3 4 x － 15 4n 解得⎩⎪⎨⎪⎧x 1＝ny 1＝－3n ⎩⎪⎨⎪⎧x 2＝4n y 2＝－ 3 4n∴E （4n ，－34n ）当点E 过点P 时，有－n －1＝－34n ，∴n ＝－4 当点E 过点Q 时，有－n －2＝－34n ，∴n ＝－8 ∴当点E 落在线段PQ 上时，n 的取值范围是：－8≤n≤－45．（浙江杭州）在平面直角坐标系中，反比例函数与二次函数y ＝k (x2＋x －1)的图象交于点A （1，k ）和点B （－1，－k ）．（1）当k ＝－2时，求反比例函数的解析式；（2）要使反比例函数与二次函数都是y 随着x 的增大而增大，求k 应满足的条件以及x 的取值范围；（3）设二次函数的图象的顶点为Q ，当△ABQ 是以AB 为斜边的直角三角形时，求k 的值．解：（1）当k ＝－2时，A （1，－2）设反比例函数为y ＝ k ′x，则k ′＝1×(－2)＝－2∴反比例函数的解析式为y ＝－2x（2）要使反比例函数与二次函数都是y 随着x 的增大而增大则反比例函数只能在二、四象限，k ′＝k＜0此时二次函数开口向下，故x ≤－ b2a ＝－ 12才满足要求综上所述，k ＜0且x ≤－12（3）∵y ＝k (x2＋x －1)＝k ( x ＋12)2－5 4k ，∴Q （－1 2，－5 4k ） ∵A （1，k ），B （－1，－k ），∴A 、B 两点关于原点O 对称，即O 是AB 的中点又∵△ABQ 是以AB 为斜边的直角三角形，∴OQ ＝OA ∴(－12)2＋(－5 4k)2＝12＋k2，解得k ＝±23 36．（浙江义乌）如图，矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上，点D 为对角线OB 的中点，点E （4，n ）在边AB 上，反比例函数y ＝kx在第一象限内的图象经过点D 、E ，且tan ∠BOA ＝12．（1）求反比例函数的解析式；（2）若反比例函数的图象与矩形的边BC 交于点F ，将矩形折叠，使点O 与点F 重合，折痕分别与x 、y 轴正轴交于点H 、G ，求线段OG解：（1）在Rt △BOA 中，∵OA ＝4，tan ∠BOA ＝12∴AB ＝OA ²tan ∠BOA ＝2，∴B （4，2） ∵点D 为对角线OB 的中点，∴D （2，1）∵点D 在反比例函数y ＝kx的图象上，∴1＝k2，∴k ＝2 ∴反比例函数的解析式为y ＝2x（2）设点F （a ，2），则2a ＝2，∴CF ＝a ＝1 连接FG ，设OG ＝t ，则OG ＝FG ＝t ，CG ＝2－t 在Rt △CGF 中，FG 2＝CF 2＋CG 2∴t 2＝12＋(2－t)2，解得t ＝54∴OG ＝t ＝547．（浙江某校自主招生）已知点P 的坐标为（m ，0），在x 轴上存在点Q （不与P 重合），以PQ 为边，∠PQM ＝60°作菱形PQMN ，使点M 落在反比例函数y ＝－23x的图象上．（1）如图所示，若点P 的坐标为（1，0），图中已经画出一个符合条件的菱形PQMN ，若另一个菱形为PQ 1M 1N 1，求点M 1的坐标；（2）探究发现，当符合上述条件的菱形只有两个时，一个菱形的顶点M 在第四象限，另一个菱形的顶点M 1在第二象限．通过改变P 点坐标，对直线MM 1的解析式y ＝kx ＋b 进行探究可得k ＝__________，若点P 的坐标为（m ，0），则b ＝__________（用含m 的代数式表示）；（3）继续探究：①若点P 的坐标为（m ，0），则m 在什么范围时，符合上述条件的菱形分别有两个、三个、四个？②求出符合上述条件的菱形刚好有三个时，点M解：（1）过M 1作M 1H ⊥PQ 1于H ，设Q 1（x ，0），显然点Q 1在x 轴的负半轴上，点M 1在第二象限 ∵P （1，0），∴M 1Q 1＝PQ 1＝1－x ∵∠PQM 1＝60°，∴Q 1H ＝1 2 (1－x)，M 1H ＝3 2(1－x)∴OH ＝－x －1 2 (1－x)＝－12(1＋x)∴M 1（1 2 (1＋x)，32(1－x)）∵点M 1在反比例函数y ＝－23x的图象上 ∴1 2 (1＋x)²32(1－x)＝－23，解得：x ＝3（舍去）或x ＝－∴M 1（－1，23）（2）k ＝－3，b ＝3m提示：连接PM 1、PM ，则∠M 1PQ 1＝∠OPN ＝∠MPN ＝60° ∴∠M 1PM ＝180°，即M1、P 、M 三点共线且∠M 1MN ＝60°可得直线MM 1的解析式为y ＝－3x ＋b ，∴k ＝－3若点P 的坐标为（m ，0），则直线MM 1的解析式为y ＝－3x ∴b ＝3m（3）①若符合条件的菱形有三个，则其中必有一个菱形的一条边PN 或对角线PM 所在直线与双曲线只有一个交点由∠QPM ＝60°或∠PNM ＝60°，P （m ，0），得直线PM 或直线PN m令y ＝3x －3m ＝－23 x，得x2－mx ＋2＝0△＝m2－8＝0，得m ＝±22∴当－2 2＜m ＜2 2时，△＜0，满足条件的菱形有两个当m ＝±2 2时，△＝0，满足条件的菱形有三个当m ＞2 2 或m ＜－2 2时，△＞0，满足条件的菱形有四个 ②由①知，当符合条件的菱形刚好有三个时，m ＝±22 当m ＝2 2 时，点P 的坐标为（22，0）把m ＝22代入x 2－mx ＋2＝0，得x2－22x ＋2＝0 解得x ＝ 2，∴M 1（2，－6）设Q （x ，0），由（1）知，1 2 (22＋x)²32(2 2－x )＝－23解得：x ＝4或x ＝－4∴M 2（2－2，－23－6），M 3（－2＋2，23＋6）当m ＝－22 时，由对称性可得：M 4（－ 2， 6），M 5（－2－ 2，2 3－ 6），M 6（2＋2，－2 3＋6） 8．（浙江模拟）如图，在平面直角坐标系中，△AOB 的顶点O 是坐标原点，点A 坐标为（1，3），A 、B 两点关于直线y ＝x 对称，反比例函数y ＝kx（x ＞0）图象经过点A ，点P 是直线y ＝x 上一动点．（1）填空：B 点的坐标为（______，______）；（2）若点C 是反比例函数图象上一点，是否存在这样的点C ，使得以A 、B 、C 、P 四点为顶点的四边形是平行四边形？若存在，求出点C 坐标；若不存在，请说明理由；（3）若点Q分别作直线OA ，当Q 点坐标．解：（1）（3，1）（2）∵反比例函数y ＝kx（x ＞0）图象经过点A （1，3）∴k ＝1×3＝3∴反比例函数的解析式为y ＝3x∵点P 在直线y ＝x 上，∴设P （m ，m ） ①若PC 为平行四边形的边∵点A 的横坐标比点B 的横坐标小2，点A 的纵坐标比点B 的纵坐标大2 ∴若点C 在点P 下方，则点C 的坐标为（m ＋2，m －2），如图1 若点C 在点P 上方，则点C 的坐标为（m －2，m ＋2），如图2 把C （m ＋2，m －2）代入反比例函数的解析式，得：m －2＝3m ＋2，解得m ＝±7∵m ＞0，∴m ＝7∴C 1（7＋2，7－2）同理可得另一点C 2（7－2，7＋2） ②若PC 为平行四边形的对角线，如图3∵A 、B 关于直线y ＝x 对称，∴OP ⊥AB此时点C 在直线y ＝x 上，且为直线y ＝x 与双曲线y ＝3x的交点由⎩⎪⎨⎪⎧y ＝x y ＝3x解得⎩⎨⎧x 1＝3y 1＝3 ⎩⎨⎧x 2＝－3y 2＝－3（舍去） ∴C 3（3，3）综上所述，满足条件的点C 有三个，坐标分别为： C 1（7＋2，7－2），C 2（7－2，7＋2），C 3（3，3）（3）连接AQ ，设AB 与OP 的交点为D ，如图4 ∵四边形AOBP 是菱形，∴AO ＝AP ∵S △AOP＝S △AOQ＋S △APQ∴1 2OP ²AD ＝1 2 AO ²QE ＋ 12AP ²QF ∴QE ＋QF ＝ OP ²ADAO为定值∴要使QE ＋QF ＋QB 的值最小，只需QB 的值当QB ⊥OP 时，QB 最小，所以D 点即为所求的点 ∵A （1，3），B （3，1），∴D （2，2）∴当QE ＋QF ＋QB 的值最小时，Q 点坐标为（2，2）9．（浙江模拟）已知点P （m ，n ）是反比例函数y ＝6x（x ＞0）图象上的动点，P A ∥x 轴，PB ∥y 轴，分别交反比例函数y ＝3x（x ＞0）的图象于点A 、B ，点C 是直线y ＝2x 上的一点．（1）请用含m 的代数式分别表示P 、A 、B 三点的坐标；（2）在点P 运动过程中，连接AB ，△P AB 的面积是否变化，若不变，请求出△P AB 的面积；若改变，请说明理由；（3）在点P 运动过程中，以点P 、A 、B 、C 为顶点的四边形能否为平行四边形，若能，请求出点P 的坐标；若不能，请说明理由．解：（1）P （m ，6 m ），A （m 2，6 m ），B （m ，3m）（2）∵P A ＝m －m2＝ m 2 ，PB ＝ 6 m － 3 m ＝3 m∴S △P AB＝12P A ²PB ＝1 2 ×m 2 ×3 m＝3 4∴△P AB 的面积不变（3）①若AP 是平行四边形的边，如图1、图2 则AP ∥BQ 且AP ＝BQ得Q （m2，3m）或Q （3m2，3m）∵点Q 在直线y ＝2x 上 ∴3m＝2×m 2 或 3 m＝2×3m 2解得m ＝3或m ＝1（舍去负值） ∴P （3，23）或P （1，6）②若AP 是平行四边形的对角线，如图3 则QA ∥PB 且QA ＝PB得Q （m 2 ，6 m＋3 m）∵点Q 在直线y ＝2x 上 ∴6m＋3 m＝2×m2，解得m ＝3（舍去负值） ∴P （3，2） 10．（江苏徐州）如图，直线y ＝x ＋b （b ＞4）与x 轴、y 轴分别相交于点A 、B ，与反比例函数y ＝－4x的图象相交于点C 、D （点C 在点D 的左侧），⊙O 是以CD 长为半径的圆．CE ∥x轴，DE ∥y 轴，CE 、DE 相交于点E ．（1）△CDE 是______________三角形；点C 的坐标为______________，点D 的坐标为_____________（用含有b 的代数式表示）；（2）b 为何值时，点E 在⊙O 上？（3）随着b 取值逐渐增大，直线y ＝x ＋b 与⊙O 有哪些位置关系？求出相应b 的取值范围．解：（1）等腰直角 C （－b －b 2－16 2 ，b － b 2－16 2 ），D （－b ＋ b 2－16 2 ，b ＋ b2－162）（2）当点E 在⊙O 上时，如图1，连接OE ，则OE ＝CD ∵直线y ＝x ＋b 与x 轴、y 轴相交于点A （－b ，0），B （0，b ），CE ∥x 轴，DE ∥y 轴 ∴△DCE 、△BAO 是等腰直角三角形∵整个图形是轴对称图形，∴OE 平分∠AOB ，∠AOE ＝∠∵CE ∥x 轴，DE ∥y 轴，∴四边形CAOE 、OEDB ∴OE ＝AC ＝BD ∵OE ＝CD ，∴OE ＝AC ＝BD ＝CD 过点C 作CF ⊥x 轴于F ，则△AFC ∽△AOB∴ CF BO ＝ AC AB ＝ 1 3 ，∴y C ＝CF ＝ 1 3 BO ＝ 13b ∴b － b 2－16 2 ＝ 13b ，解得b ＝±3 2∵b ＞4，∴b ＝3 2∴当b ＝32时，点E 在⊙O 上（3）当⊙O 与直线y ＝x ＋b 相切于点G 时，如图2，连接OG ∵整个图形是轴对称图形，∴点O 、E 、G 在对称轴上∴GC ＝GD ＝12CD ＝1 2 OG ＝ 1 2AG ∴AC ＝CG ＝GD ＝DB ，∴AC ＝14AB过点C 作CH ⊥x 轴于H ，则△AHC ∽△AOB ∴CHBO＝ACAB＝14，∴y C ＝CH ＝14BO ＝14b ∴b －b 2－16 2 ＝ 1 4 b ，解得b ＝±83 3∵b ＞4，∴b ＝8 33∴当b ＝833时，直线y ＝x ＋b 与⊙O 相切当4＜b＜833时，直线y ＝x ＋b 与⊙O 相离当b＞833时，直线y ＝x ＋b 与⊙O 相交。