安徽巢湖春晖学校2011-2012学年度第二学期高二年级4月月考数学试题(理科)
2012合肥二模理科数学试题及答案(免费WORD版)
【答案】D
10.定义域为R的偶函数f(x)满足对∀x∈R,有f(x+ 2) =f(x)-f(1),且当x∈[2,3]时f(x) =-2x2+ 12x-18,若函数y=f(x)-loga(x+ 1)在(0,+)上至少有三个零点,则a的取值范围为( )
(1)求证:PC⊥BD
(2)过直线BD且垂直于直线PC的平面交PC于点E,且三棱锥E-BCD的体积取到最大值
(i)求此时四棱锥E-ABCD的高;
(ii)求二面角A-DE-B的余弦值的大小。
解:(1)连接AC,则AC⊥BD
∵PA⊥平面ABCD.
∴PA⊥BD
∴BD⊥平面PAC
∴PC⊥BD
(2) (i)设AC与BD的交点M,连接EM,过点E作EN⊥AC于N,则EN⊥面ABCD,EN是三棱锥E-BCD的高
【答案】128
12.在极坐标系中,点(1,)到直线2cos-sin+2=0的距离为_____.
【答案】
13.若sin(+)=,则sin(+2)=__
【答案】-
14.设函数y=(x∈R,x≠,n∈N*)的最大值和最小值分别为an和bn,且cn=an+bn+anbn-15,Sn=|c1|+|c2|+|c3|+…+ |cn| = ______.
【答案】Sn=
15.函数y=f(x)的定义域为[-1,0)∪(0,1],其图像上任一点P(x,y)满足x2+y2= 1。
①函数y=f(x)一定是偶函数;
②函数y=f(x)可能既不是偶函数,也不是奇函数;
③函数y=f(x)可以是奇函数;
安徽巢湖春晖学校学度第二学期高二级考语文试题

安徽巢湖春晖学校学度第二学期高二级考语文试题————————————————————————————————作者:————————————————————————————————日期:2安徽巢湖春晖学校2011-2012学年度第二学期高二年级4月月考语文试题命题人:高贤军、陈小磊、叶鹏审核:高二语文备课组时间:150分钟总分:150分第Ⅰ卷(阅读题,共68分)一.阅读下面的文字,完成1—3题。
(9分)历史上有一种通行观点:孔子后“儒分为八”,到战国中后期演变为两支。
一支始于子夏,讲文献之学,数传至荀子;一支始于曾参,究义理之学,二传至孟子。
以后,荀子便是汉代经学家所尊信的大部分儒家经传的先师,孟子则成为两宋起道学家所崇敬的不祧之祖。
儒家内部这两派的分野,也就是所谓“学统”与“道统”之别,“汉学”与“宋学”之分。
对这个说法,学界历来意见不同,这里不必细究。
此说至少有一点不错,即孟子其人其书的重要性的确是从两宋开始凸显的。
这以后,“孔孟之道”几乎成了儒家思想的代名词。
孟子去世后,由他为代表的儒家中的一派似无太大发展。
到战国晚期,由荀子代表的一派渐露头角。
荀子稍晚于孟子,他长期居齐,因学问博洽,三次出任“稷下学宫”的“祭酒”。
他精通多种儒经,被认为是儒家经学早期传授中十分重要的人物。
荀子在《非十二子》中,对子思、孟子一派有严厉的批评,说他们“略法先王而不知其统,犹然而材剧志大,闻见博杂。
案往旧造说,谓之五行,甚僻违而无类,幽隐而无说,闭约而无解。
案饰其辞而祗敬之曰:此真先君子之言也。
”荀子的批评只能说是当时儒家内部的派别斗争。
秦汉以降至两宋以前,孟子地位一直不高。
孟子其人,只被视为一般的儒家学者;孟子其书,只能归入“子部”一类。
在官私文献中,多是“周孔”或“孔颜”并提,鲜见有“孔孟”合称的。
值得注意的是,东汉赵岐在注解《孟子》时,曾把孟子尊为“亚圣”,还提到西汉文帝时设置过《孟子》的“传记博士”。
可“亚圣”之名,未被宋朝以前的官方认可过;而“传记博士”即使存在过也为时很短,且不说此事因不见于《史》《汉》记载而颇启后人疑窦。
安徽省巢湖春晖学校11-12学年高二上学期期中考试(数学理)

安徽巢湖春晖学校2011-2012学年第一学期期中考试高二数学试卷(理)命题人:郭荣跃复核人:李其阁考试时间:120分钟总分:150分一选择题(每小题5分,共50分)1 侧面都是直角三角形的正三棱锥,底面边长为a,则此棱锥的全面积是()A B C D 都不对2 一个正三棱柱的三视图如图所示,则这个正三柱的侧面积为3 若直线a和直线b是异面直线,直线b和c异面直线,则直线a和c()A 平行B 异面C 相交 D以上都有可能4 若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成()部分A 5B 6C 7D 85关于直线与平面的命题中,一定正确的是()若,则若,则若,则若,则6.如图,正方体中,分别为BC, CC1中点,则异面直线与所成角的大小为7直线ax+by+c=0同时过第一、第二、第四象限,则a,b,c满足()A ab>0, bc<0B ab<0, bc>0C ab>0, bc>0D ab<0, bc<08设两圆C1、C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|=( )A.4 B.4 C.8 D.89若直线3x+y+a=0过圆x2+y2+2x-4y=0的圆心,则a的值为( ) A.-1 B.1 C.3 D.-310 若直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m=________.A 1B 2C 4D 0.5二填空题(每空5分,共25分)11 以下4个命题其中正确的命题是如果一个几何体的三视图是完全相同的,则这个几何体是正方体;如果一个几何体的主视图和俯视图都是矩形,则这个几何体是长方体;如果一个几何体的三视图都是矩形,则这个几何体是长方体;如果一个几何体的主视图和左视图都是等腰梯形,则这个几何体是圆台。
12.二面角为,是棱上的两点,分别在半平面内,,则长为。
13.一个平面图形的水平放置的斜二测直观图是一个等腰梯形,直观图的底角为,两腰和上底边长均为1,则这个平面图形的面积为。
安徽省巢湖市2011届高三第二次模拟考试(数学理)

巢湖市2011届高三第二次教学质量检测试题数学(理科)一、选择题:本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数12aii++(a R i ∈,是虚数单位)为纯虚数,则a =( ).A.2B.-2C.1D.-12.如图,已知R 是实数集,集合12{|log (1)0}A x x =->,23{|0}x B x x -=<,则阴影部分表示的集合是( ).A.[ 1]0,B.[ 1)0,C. 1)(0,D. 1](0,3.若函数(21)y f x =-是偶函数,则函数(2)y f x =图象的对称轴是直线( ).A.12x =- B.12x =C.1x =-D.1x = 4.已知直线l a b ,,,平面αβγ,,,则下列命题正确的是( ).A .若l a l b a b αα⊥⊥⊂⊂,,,,则l α⊥B .若a l a αβαβ=⊥⊥,,,则l β⊥C .若a b αβαγβγ==,,,则a bD .若αγβγ⊥⊥,,则αβ.5.右图是一次考试结果的频数分布直方图,根据该图可估计,这次考试的平均分数为( ).A.46B.36C.56D.606.已知函数2()sin 22cos 1f x x x =+-,若对于任意x R ∈,都有12()()()f x f x f x ≤≤成立,则12x x -的最小值为( ).A. 2πB.πC.2π D.4π 7.在极坐标系中,已知点2 2A π⎛⎫⎪⎝⎭,,()2B π,,点M 是圆2cos ρθ=上任意一点,则点M到直线AB 的距离的最小值为( ).1-1+8.当x y ,满足约束条件020x y x x y m ≥⎧⎪≤⎨⎪++≤⎩(m 为常数)时,3z x y =+取得最大值12,则此时m 的值等于( ).A.9-B.9C.12-D.129.已知数列{}n a 的前n 项和为n S ,11a =,若2n ≥时,n a 是n S 与1n S -的等差中项,则5a 等于( ).A.18B.54C.162D.8110.自然数1,2,3,…,n 按照一定的顺序排成一个数列:12 n a a a ⋯,,,.若满足12a a -1+-2 4n a n -≤++,则称数列12 n a a a ⋯,,,为一个“优数列”.当6n =时,这样的“优数列”共有( ).A.24个B.23个C.18个D.16个二、填空题:本大题共5小题,每小题5分,共25分.把正确答案直接填写在答题卷中相应的横线上.11.已知21()n x x+展开式的各项系数和为32,则展开式中4x 的系数为 (用数字作答).12.设2[0 1]()1(1]x x f x x e x⎧∈⎪=⎨∈⎪⎩,,,,(其中e 为自然对数的底数),则0()e f x dx ⎰= .13.已知程序框图如图所示,其功能是求一个数列{}n a 的前10项和,则数列{}n a 的一个通项公式n a = .14.设 a b c ,,分别为ABC ∆的三个内角A ,B ,C 所对边的边长,且满足条件4cos cos cos a b cA B C===,则ABC ∆的面积等于 .15.给出下列命题:①已知 a b m ,,都是正数,且a m ab m b+>+,则a b <;②已知()f x '是()f x 的导函数,若()0x R f x '∀∈≥,,则(1)(2)f f <一定成立;③命题“x R ∃∈,使得2210x x -+<”的否定是真命题; ④“1x ≤,且1y ≤”是“2x y +≤”的充分不必要条件.其中正确命题的序号是 .(把你认为正确命题的序号都填上)三、解答题:本大题共6小题,满分75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分13分)已知(sin cos ) (sin sin )m a x x n x b x ==,,,,其中a b x R ∈,,.若()f x m n =⋅满足()26f π=,且()f x 的导函数()f x '的图象关于直线12x π=对称.(Ⅰ)求a b ,的值;(Ⅱ)若关于x 的方程2()log 0f x k +=在区间[0 ]2π,上总有实数解,求实数k 的取值范围.17.(本小题满分12分)如图1,已知四边形ABCD 是上、下底长分别为2和6,高DO为沿DO 折成120的二面角A -DO -B ,如图2,连结AB ,AC ,BD ,OC. (Ⅰ)求三棱锥A -BOD 的体积V ;(Ⅱ)证明:AC ⊥BD ;(Ⅲ)求二面角D -AC -O 的余弦值.18.(本小题满分12分)某学生在上学路上要经过4个路口,假设在各个路口是否遇到红灯是相互独立的.第一个路口遇到红灯的概率是14,其余每个路口遇到红灯的概率都是13.(Ⅰ)求这名学生在上学路上到第二个路口时首次遇到红灯的概率;(Ⅱ)假定这名学生在第二个路口遇到红灯,求这名学生在上学路上遇到红灯的次数X的分布列及期望.19.(本小题满分12分)已知等差数列}{n a 的前n 项和为n S ,且21(21)(21)41n n n S n S n +--+=-)(*N n ∈. (Ⅰ)求数列}{n a 的通项公式; (Ⅱ)11)2a +>.20.(本小题满分13分)已知函数2()ln f x ax x x =++.(Ⅰ)当0a =时,求曲线()y f x =在点(1(1))f ,处的切线方程; (Ⅱ)讨论函数()f x 的单调性.21.(本小题满分13分)设椭圆C: 22221x y a b+=(0a b >>)过点M(1,1),离心率e ,O 为坐标原点.(Ⅰ)求椭圆C 的方程;(Ⅱ)若直线l 是圆O :221x y +=的任意一条切线,且直线l 与椭圆C 相交于A ,B 两点,求证:OA OB ⋅为定值.(Ⅱ)由(Ⅰ)得()1cos 22f x x x =-2sin(2)16x π=-+ ………………………9分∵02x π⎡⎤∈⎢⎥⎣⎦,,52666x πππ-≤-≤,∴12sin(2)26x π-≤-≤,[]()03f x ∈,. ………………………11分 又∵2()log 0f x k +=有解,即2()log f x k =-有解,∴23log 0k -≤≤,解得118k ≤≤,即1[ 1]8k ∈,. ………………………13分17.(本小题满分12分)解:(Ⅰ)13A BOD D AOB AOB V V s OD --∆==⋅=1124sin120432⨯⨯⨯︒⨯=. ……………4分(Ⅱ)()()AC BD AO OD DC BO OD ⋅=++⋅+=2AO BO AO OD OD BO OD DC BO DC OD ⋅+⋅+⋅++⋅+⋅=2124()(23)24(1)02⨯⨯-++⨯⨯-=,∴AC BD ⊥,即AC BD ⊥. ……………………8分 (Ⅲ)由条件知OD AOB ⊥面,以O 为原点,OB 、OD 分别为y 轴、z 轴建立空间直角坐标系(如图),则(0 0 0)1 0)O A -,,,,,(0 2C,(0 0D,∴(AC =,(0 2 0)DC =,,.设平面ACD 的法向量为111( 1)n x y =,,,平面ACO 的法向量为222( 1)n x y =,,, 则1100n AC n DC ⎧⋅=⎪⎨⋅=⎪⎩,得1113020y y ⎧++=⎪⎨=⎪⎩,解得112x y =⎧⎨=⎩,∴1(2 0 1)n =,,. 同理得2(1 3 1)n =--,,, ∴121212cos ,n n n n n n ⋅<>=⋅15=-,由图可知,1n 与2n 的夹角和二面角D-AC-O 的大小相等,∴二面角D-AC-O 的余弦值是15-. ………………………12分18.(本小题满分12分)解:(Ⅰ)设“这名学生在上学路上到第二个路口首次遇到红灯”为事件A ,则所求概率为311()434P A =⨯=. ………………………4分19.(本小题满分12分)(Ⅰ)由21(21)(21)41n n n S n S n +--+=-,得112121n n S Sn n +-=+-, ∴21n S n ⎧⎫⎨⎬-⎩⎭是公差为1的等差数列, ………………………3分 ∴11(1)11211n S Sn S n n =+-⨯=+--,1(21)(1)n S n S n =-+- ① 又∵{}n a 等差数列,∴1322a a a +=,即13221()2()a S S S S +-=-.由①得[][]111115(2)3(1)23(1)a a a a a ++-+=+-,解得11a =,代入①得22n S n n =-. ………………………6分 当2n ≥时,()221221(1)n n n a S S n n n n -⎡⎤=-=-----⎣⎦43n =-,上式对1n =也适用,∴43n a n =-. ………………………8分(Ⅱ)由(Ⅰ)=>12=, ………………………10分a+>1142n++11)2=,故原不等式成立. ………………………12分21.(本小题满分13分)解:(Ⅰ)∵c e a =,∴223a b =,∴椭圆C 的方程为222213x y b b+=.又∵椭圆C 过点(1 1)M ,,代入方程解得22443a b ==,,∴椭圆C 的方程为223144x y +=. ………………………5分(Ⅱ)①当圆O 的切线l 的斜率存在时,设直线l 的方程为y kx m =+,则圆心O 到直线l 的距离1d =,∴221k m +=. ………………………7分将直线l 的方程和椭圆C 的方程联立,得到关于x 的方程为223()4x kx m ++=,即222(13)6340k x kmx m +++-=.由()222222213064(13)(34)4812163640k km k m k m k ⎧+>⎪⎨∆=-+-=-+=+>⎪⎩可设直线l 与椭圆C 相交于11()A x y ,,22()B x y ,两点,则122613kmx x k +=-+,21223413m x x k -=+, ……………………… 9分 ∴OA OB ⋅=12x x +12y y =221212(1)()k x x km x x m ++++22222346(1)()1313m km k km m k k -=+⋅+⋅-+++222444013m k k --==+,………………11分②当圆的切线l的斜率不存在时,验证得OA OB⋅=0.综合上述可得,OA OB⋅为定值0. ………………………13分。
数学_2011年安徽省合肥市高考数学二模试卷(理科)(含答案)

2011年安徽省合肥市高考数学二模试卷(理科)一、选择题(共10小题,每小题5分,满分50分)1. 设集合A ={x|1+log 2|x|≤0},B ={x|14≤x ≤2},则A ∩(C R B)=( ) A [−12, 14] B [−12, 0)∪(0, 14) C (−∞, −12]∪(14, +∞) D [−12, 0)∪(14, 12]2. 双曲线x 2−y 23=1的一个焦点到它的渐近线的距离为( )A 1B √2C √3D 23. a <1是不等式|x −1|+|x|>a (x ∈R)恒成立的( )A 充分不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件 4. △ABC 中,角A ,B ,C 所对的边分别为a ,b ,c 若cb <cosA ,则△ABC 为( ) A 钝角三角形 B 直角三角形 C 锐角三角形 D 等边三角形5. 设复数z =7+i3+4i −i ⋅sinθ,其中i 为虚数单位,θ∈R ,则|z|的取值范围是( ) A [1, √3] B [√2, 3] C [√2,√5] D [1, √5]6. 下列各坐标系中是一个函数与其导函数的图象,其中一定错误的是( )A B C D7. 一个四棱锥的三视图如图所示,其侧视图是等边三角形.该四棱锥的体积等于( )A √3B 2√3C 3√3D 6√38. 在直角坐标系中,以坐标原点为极点x 轴的正半轴为极轴建立极坐标系.直线I 的参数方程是.{x =−1+√22ty =1+√22t (r 为参数),曲线C 的极坐标方程是p =2,直线l 与曲线C 交于A 、B ,则|AB|=( )A √2B 2√2C 4D 4√2 9. 若cos(π4−α)=35,则sin2α=( ) A 725 B 15 C −15 D −72510. 一个盒子内部有如图所示的六个小格子,现有桔子,苹果和香蕉各两个,将这六个水果随机地放入这六个格子里,每个格子放一个,放好之后每行、每列的水果种类各不相同的概率是( ) A 215B 29C 15D 13二、填空题(共5小题,每小题5分,满分25分)11. 随机变量ξ服从正态分布“(0, 1),若P(ξ<1)=0.8413 则P(−1<ξ<0)=________. 12. 小王每月除去所有日常开支,大约结余a 元.小王决定采用零存整取的方式把余钱积蓄起来,每月初存人银行a 元.存期1年(存12次),到期取出本和息.假设一年期零存整取的月利率为r ,每期存款按单利计息.那么,小王存款到期利息为________元.13. 点M(x, y)是不等式组{0≤x ≤√3y ≤3x ≤√3y 表示的平面区域Ω内的一动点,使Z =y −2x 的值取得最小的点为A(x 0, y 0),则OM →⋅OA →(O 为坐标原点)的取值范围是________.14. 程序框图如图,运行此程序,输出结果b =________.15. 下列说法中,正确的有________(把所有正确的序号都填上). ①“∃x ∈R ,使2x >3”的否定是“∀x ∈R ,使2x ≤3”; ②函数y =sin(2x +π3)sin(π6−2x)的最小正周期是π;③命题“函数f(x)在x =x 0处有极值,则f′(x 0)=0”的否命题是真命题;④已知函数f′(x)是函数f(x)在R 上的导函数,若f(x)是偶函数,则f′(x)是奇函数; ⑤∫√1−x 21−1dx 等于π2.三、解答题(共6小题,满分75分)16. 将函数y =f(x)的图象上各点的横坐标缩短为原来的12(纵坐标不变),再向左平移π12个单位后,得到的图象与函数g(x)=sin2x 的图象重合. (1)写出函数y =f(x)的图象的一条对称轴方程;(2)若A 为三角形的内角,且f(A)=13•,求g(A2)的值.17. 如图,四边形ABCD 为正方形,四边形BDEF 为矩形,AB =2BF i DE 丄平面ABCD ,G 为EF 中点. (1)求证:CF // 平面(2)求证:平面ASG 丄平面CDG ; (3)求二面角C −FG −B 的余弦值.18. 已知椭圆C:x 2m +y 2=1的左、右焦点分别为F 1,F 2,若椭圆上总存在点P ,使得点P 在以F 1F 2为直径的圆上;(1)求椭圆离心率的取值范围;(2)若AB 是椭圆C 的任意一条不垂直x 轴的弦,M 为弦AB 的中点,且满足K AB ⋅K OM =−14(其中K AB 、K OM 分别表示直线AB 、OM 的斜率,O 为坐标原点),求满足题意的椭圆C 的方程.19. 已知函数f(x)=ax 3+bx 2+c(a, b, c ∈R, a ≠0)的图象过点P( 1, 2),且在点P 处的切线与直线x −3y =0垂直.(1)若c ∈[0, 1),试求函数f(x)的单调区间;(2)若a >0,b >0且(−∞, m),(n, +∞)是f(x)的单调递增区间,试求n −m −2c 的范围. 20. 高三年级在综合素质评价的某个维度的测评中,依据评分细则,学生之间相互打分,最终将所有的数据合成一个分数,满分100分.按照大于等于80分为优秀,小于80分为合格.为了解学生在该维度的测评结果,从毕业班中随机抽出一个班的数据.该班共有60名学生,得到如下的列联表.(2)能否在犯错误的概率不超过0.10的前提下认为性别与测评结果有关系?(3)如果想了解全年级学生该维度的表现情况,采取简单随机抽样的方式在全校学生中抽取少数一部分人来分析,请你选择一个合适的抽样方法,并解释理由;(4)学生代表、教师代表、家长代表、教务员四人,分别对测评结果是优秀的20名学生进行检查,检查他们是否躲优秀的相4名检查人员各自纖立的舰20学生中随机抽取一名,设其中男生的人数为随机变量x ,求随机变量x 的分布列期望.21. 已知数列{a n }的前n 项和S n 满足S 2=3,2S n =n +na n ,n ∈N ∗. (1)求{a n }的通项公式,并求数列{2n−1⋅a n }的前n 项和T n ; (2)设b n =2a n +1,证明:n 2−17<b 1−1b 2−1+b 2−1b 3−1+...+b n −1bn+1−1<n2.2011年安徽省合肥市高考数学二模试卷(理科)答案1. B2. C3. C4. A5. D6. C7. A8. B9. D 10. A11. 0.3413 12. 78ar 13. [0, 6] 14. 615. ①④⑤16. 解:(1)由题意可知将函数g(x)=sin2x 的图象向右平移π12个单位,再将横坐标伸长到原来的2倍即可得的到f(x)的图象, ∴ f(x)=sin(x −π6) 由x −π6=kπ+π2得x =kπ+2π3,k ∈Z∴ x =kπ+2π3,k ∈Z(2)由f(A)=13可得,sin(A −π6)=13=13∵ 0<A <π,且0<sin(A −π6)=13=13<120<A −π6<π2∴ cos(A −π6)=2√23g(A2)=sinA =sin[(A −π6)+π6]=12cos(A −π6)+√32sin(A −π6)=2√2+√36. 17. 证明:(1)∵ 四边形ABCD 为正方形,四边形BDEF 为矩形,∴ BC // AD ,BF // DE ,∵ 平面BCF 中,有两条相交直线BC ,BF 平行于两一个平面中的两条相交直线AD ,DE , 故有平面BCF // 平面ADE , ∴ CF // 平面ADE .(2)取AB 的中点M ,CD 的中点N . ∵ AB =2BF ,设BF =1,则AB =2.∵ DE 丄平面ABCD , 可得面BDEF ⊥面ABCD .设AC 和BD 交于点O ,则GO ⊥面ABCD .∴ GM =√GO 2+OM 2=√2=GN ,又MN =2, ∴ 由勾股定理可得GM ⊥GN .由G 为EF 中点,可得GC =GD =√2, ∴ GN ⊥CD ,GN ⊥AB .这样面CDG 中的直线GN 垂直于平面GAB 内的两条相交直线AB 和GM , ∴ 平面ABG 丄平面CDG .(3)由已知可得CG ⊥FG ,由(2)GO ⊥EF ∴ ∠CGO 为二面角C −FG −B 的平面角 ∴ cos∠CGO =OG CG=√3318. 解:(1)设点P(x, y),∵ F 1 (−√m −1, 0),F 2 (√m −1, 0), 设椭圆的上顶点为B(0, 1),∵ 点P 在以F 1F 2为直径的圆上,∠F 1PF 2≤∠F 1BF 2,只需满足 BF 1→⋅BF 2→≤0, (−√m −1, −1)⋅(√m −1, −1)=−(m −1)+1=2−m ≤0,m ≥2, e =√m−1m∈[√22, 1). (2)设A(x 1, y 1),B(x 2, y 2 ),M (x 0, y 0),则x 1+x 2=2x 0,y 1+y 2=2y 0. 把A 、B 的坐标代入椭圆方程得 x 12m +y 12=1,x 22m +y 22=1,并相减得:(x 1+x 2)(x 1−x 2)m=−(y 1+y 2)(y 1−y 2),∴ K AB =y 1−y 2x 1−x 2=−x 0my 0,又 K OM =Y 0X 0,再由 K AB ⋅K OM =−14,m =4,此时,椭圆的方程为x 24+y 2=1.19. 解:由f(x)=ax 3+bx 2+c 的图象过点P(−1, 2)可知:−a +b +c =2①,又f′(x)=3ax 2+2bx ,因为f(x)点P 处的切线与直线x −3y =0垂直, 所以f′(−1)=3a −2b =−3②,联立①②解得:a =1−2c ,b =3−3c , 则f′(x)=3(1−2c)x 2+6(1−c)x , (I)当c ∈[0, 12)时,1−2c >0,令f′(x)=0,解得x 1=0,x 2=−2(1−c)1−2c<0,显然,当x >0或x <−2(1−c)1−2c时,f′(x)>0;当−2(1−c)1−2c<x <0时,f′(x)<0, 所以当c ∈[0, 12)时,f(x)的单调递增区间是(−∞, −2(1−c)1−2c)和(0, +∞),f(x)的单调递减区间是(0, −2(1−c)1−2c);(II)当c ∈[12, 1)时,f(x)的单调递减区间是(−2(1−c)1−2c, +∞)和(−∞, 0),f(x)的单调递增区间是(0, −2(1−c)1−2c);(2)当a >0,b >0时,令f′(x)=3ax 2+2bx =x(3ax +2b)=0,解得:x =0或x =−2b 3a<0,由(−∞, m),(n, +∞)是f(x)的单调递增区间,得到m =−2b3a ,n =0, 又a =1−2c >0,b =3−3c >0,得到c <12,即1−2c >0, 则n −m −2c =2b 3a−2c =6−6c 3−6c−2c =11−2c+(1−2c)≥2,当且仅当1−2c =11−2c即c =0或1时取等号,所以n −m −2c 的范围是[2, +∞).20. 解:(1)提出统计假设:性别与测评结果没有关系,则 K 2=60×(6×18−22×14)240×20×32×28=3.348>2.706,P(K 2>2.706)=0.10,因此,在犯错误的概率不超过0.10的前提下认为“性别与测试结果有关系”.(2)有(1)可知性别很有可能对是否优秀有影响,所以采用分层抽样按男女生比例抽取一定的学生,这样得到的结果对学生在该维度总体表现情况会比较符合实际情况;(3)四名抽查人员,从20名学生中随即抽取一名是男生的概率是P =310,随机变量X 的可能取值为:0,1,2,3,4.∴ P(X =0)=C 40(310)0(710)4=(710)4,P(X =1)=C 41(310)1(710)3=12×73104,P(X =2)=C 42(310)2(710)2=6×32×72104,P(X =3)=C 43(310)3(710)1,p(X =4)=C 44(310)4,∴ 随机变量X 的分布列为:∵ 随机变量X 服从二项分布X:B(4, 310) ∴ EX =np =4×310=65.21. 解:(1)当n =1时,2a 1=1+a 1,∴ a 1=1当n ≥2时,2S n =n +na n ,2S n−1=n −1+(n −1)a n−1,相减得2a n =1+na n −(n −1)a n−1,∴ 2a n+1=1+(n +1)a n+1−na n ,相减得(n −1)a n+1+(n −1)a n−1=2(n −1)a n,即当n≥2时,a n+1+a n−1=2a n又S2=3,a1=1,∴ a2=2,∴ 数列{a n}是以1为首项,1为公差的等差数列,∴ a n=n ∴ T n=1+2⋅2+3⋅22++n⋅2n−1,2T n=2+2⋅22++n⋅2n,相减整理得T n=(n−1)⋅2n+1(2)b n=2n+1,∴ b k−1b k+1−1<12,k=1,2,n,∴ b1−1b2−1+b2−1b3−1+⋯+b n−1b n+1−1<n2.b k−1 b k+1−1=12−17⋅2k+2k−2≥12−17⋅12k,k=1,2,n∴ b1−1b2−1+b2−1b3−1+⋯+b n−1b n+1−1>n2−17.∴ n2−17<b1−1b2−1+b2−1b3−1+...+b n−1b n+1−1<n2.。
巢湖春晖学校高二下学期第一次月考数学试卷WENKE (1)

巢湖春晖学校高二下学期第一次月考数学试卷命题:宋燎原 审核:李良勋(时间:120分钟 分数 150分)参考公式:22()K ()()()()n ad bc a b c d a c b d -=++++,回归直线方程:1221ni ii n i i x ynx yb x nx==-=-∑∑,x b y aˆˆ-= 一、选择题(把你认为正确的选项填在答题卷对应的题号下,填在试卷上无效,本大题共10个小题,每小题5分,共50分)1.i 为虚数单位,则201111i i +⎛⎫⎪-⎝⎭=( )A .- i B .-1 C .i D .12.下表中的由平面到空间的三个类比推理正确的个数( )3、两个变量y 与x 的回归模型中,分别选择了4个不同模型,它们的相关指数2R 如下 ,其中拟合效果最好的模型是( )A .模型1的相关指数2R 为0.98 B. 模型2的相关指数2R 为0.80 C. 模型3的相关指数2R 为0.50 D. 模型4的相关指数2R 为0.254、有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线b ⊄平面α,直线a ≠⊂平面α,直线b ∥平面α,则直线b ∥直线a ”的结论显然是错误的,这是因为 ( )A .大前提错误B .小前提错误C .推理形式错误D .非以上错误5 设4,0,0≤+>>b a b a 且,则有( ) A.211≥ab B.2≥ab C.111≥+b a D.411≤+b a 6.设集合{}{}|33,|2,12xA x xB y y x =-<<==≤≤,则()()R RC A C B = ( )A .[)2,3B .()(),23,-∞+∞C .()[),23,-∞+∞D .()(),24,-∞+∞7.函数()34log 21-=x y 的定义域为 ( )A.(43,∞-) B.(1,∞-] C.(43,1] D.(43,1)8、用反证法证明命题:“,,,a b c d R ∈,1a b +=,1c d +=,且1ac bd +>,则,,,a b c d 中至少有一个负数”时的假设为( )A .,,,a b c d 中至少有一个正数B .,,,a b c d 全为正数C .,,,a b c d 全都大于等于0D .,,,a b c d 中至多有一个负数9.执行如右图所示的程序框图,输出的T= ( )A. 11B. 12C. 13D. 1410.设有一回归直线方程为ˆ4 1.5yx =-,则变量x 增加一个单位时( ) A .y 平均增加 1.5 个单位B .y 平均增加 2.5 个单位C .y 平均减少 1.5 个单位D .y 平均减少 2.5 个单位二、填空题(将正确答案填在答题卷的对应题号后的横线上,每小题5分 ,共25分)11、回归直线方程为0.57514.9y x =-,则100x =时,y 的估计值为12、若()()()(,),f a b f a f b a b N +=⋅∈且(1)2f =,则(2)(4)(2010)(1)(3)(2009)f f f f f f +++= 13.设函数(0)()ln (0)x e x g x x x ⎧≤=⎨>⎩,则1(())2g g =__________14. 定义“等和数列”:在一个数列中,如果每一项与它的后一项的和都为同一个常数,这个常数叫做该数列的公和.已知数列{}n a 为等和数列,且12a =,公和为5,则18a 的值为 ; 15.图1是一个水平摆放的小正方体木块,图2,图3是由这样的小正方体木块叠放而成的,按照这样的规律放下去,至第七个叠放的图形中,小正方体木块总数是 .三、解答题:(你有能力正确解答下列题目,解答时要求写出详细的解答过程,解答过程写在答题卷规定的区域内,写在区域外无效)16. 已知2i-3是实系数一元二次方程02=-+q px x 的一个根,求p 和q 值(12分)17、在数列{a n }中,1121,()2nn na a a n N a ++==∈+,试写出这个数列的前4项,并猜想这个数列的通项公式。
安徽省巢湖市春晖学校2011-2012学年高二4月月考物理试题(无答案)
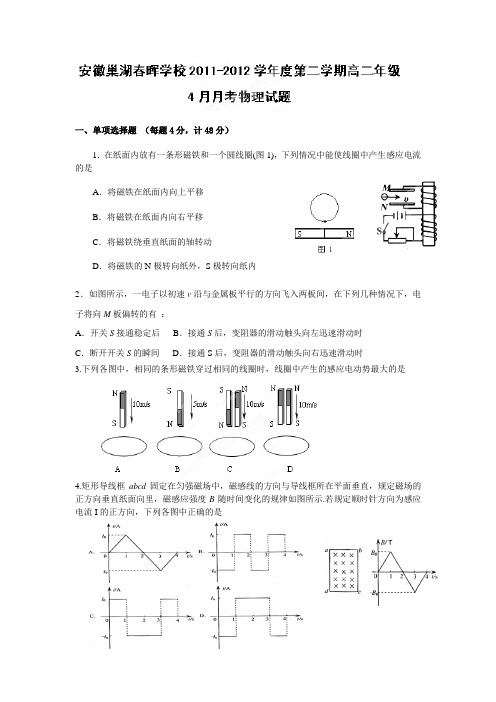
一、单项选择题(每题4分,计48分)1.在纸面内放有一条形磁铁和一个圆线圈(图1),下列情况中能使线圈中产生感应电流的是A.将磁铁在纸面内向上平移B.将磁铁在纸面内向右平移C.将磁铁绕垂直纸面的轴转动D.将磁铁的N极转向纸外,S极转向纸内2.如图所示,一电子以初速v沿与金属板平行的方向飞入两板间,在下列几种情况下,电子将向M板偏转的有:A.开关S接通稳定后B.接通S后,变阻器的滑动触头向左迅速滑动时C.断开开关S的瞬间D.接通S后,变阻器的滑动触头向右迅速滑动时3.下列各图中,相同的条形磁铁穿过相同的线圈时,线圈中产生的感应电动势最大的是4.矩形导线框abcd固定在匀强磁场中,磁感线的方向与导线框所在平面垂直,规定磁场的正方向垂直纸面向里,磁感应强度B随时间变化的规律如图所示.若规定顺时针方向为感应电流I的正方向,下列各图中正确的是5.在地球的北极极点附近,地磁场可看做匀强磁场.假设有一人站在北极极点,他面前有一根重力不计的水平放置的直导线,通有方向自左向右的电流,则此导线受到的安培力方向是A .向前B .向后C .向下 D.向上6.交流发电机在工作时的电动势为e =E m sin ωt ,若将其电枢的转速提高1倍,其他条件不变,则其电动势变为A .E m sin ωt 2B .2E m sin ωt 2C .E m sin 2ωtD .2E m sin 2ωt7.如图11所示,一闭合直角三角形线框以速度v 匀速穿过匀强磁场区域.从BC 边进入磁场区开始计时,到A 点离开磁场区止的过程中,线框内感应电流的情况(以逆时针方向为电流的正方向)是如图12所示中的8.如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是:A .圆盘绕过圆心的竖直轴匀速转动B .圆盘以某一水平直径为轴匀速转动C .圆盘在磁场中向右匀速平移D .圆盘在磁场中竖直向下匀速移动9.如图所示,光滑导轨倾斜放置,其下端连接一个灯泡,匀强磁场垂直于导线所在平面,当ab 棒下滑到稳定状态时,小灯泡获得的功率为0P ,除灯泡外,其它电阻不计,要使灯 泡的功率变为02P ,下列措施正确的是:A .换一个电阻为原来2倍的灯泡B .把磁感应强度B 增为原来的2倍C .换一根质量为原来2倍的金属棒D .把导轨间的距离增大为原来的210.如图,水平桌面上有一质量为m的铜质矩形线圈.当一竖直放置的条形磁铁从线圈中线AB正上方等高快速经过时,若线圈始终不动,则关于线圈受到的支持力F N及在水平方向运动趋势的正确判断是A.F N先小于mg后大于mg,运动趋势向左B.F N先大于mg后小于mg,运动趋势向左C.F N先大于mg后大于mg,运动趋势向右D.F N先大于mg后小于mg,运动趋势向右11.如图所示,在磁感强度为B的匀强磁场中,有半径为r的光滑半圆形导体框架,OC为一能绕O在框架上滑动的导体棒,OC之间连一个电阻R,导体框架与导体棒的电阻均不计,若要使OC能以角速度ω匀速转动,则外力做功的功率是:A.224B rRωB.2242B rRωC.2244B rRωD.2248B rRω12、小型交流发电机中,矩形金属线圈在匀强磁场中匀速转动。
安徽省巢湖市春晖学校2011-2012学年高二4月月考英语试题.pdf

第一部分:听力(共两节,满分0分) 做题时,先将答案标在试卷上,录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题,每小题1分,满分5分) 听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来 回答有关小题和阅读下面一小题,每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B.£9.15.C.£9.18.答案是B。
1. What will the man do next?A. He will find the woman an electrician.B. He will help the woman repair the TV set. C. He will try his best to buy her a new TV set. 2. What does the man mean in the dialogue?A. He can’t believe what he hears.B. He can’t refuse the invitation. C. He can’t admit her to do that. 3. Why is the man making the phone call?A. To say hello to Dr. Black.B. To confirm an appointment with the doctor. C. To have an appointment with the woman. 4. Where do you think this conversation most probably takes place?A. In a restaurant.B. In an office.C. At the airport. 5. Who should be blamed for not turning in the sales report?A. Don.B. His secretary.C. Both Don and his secretary 第二节(共15小题;每小 题1分,满分5分) 听下面5段对话或独白。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安徽巢湖春晖学校2011-2012学年度第二学期高二年级
4月月考数学试(理科)
一、选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只 有一项是符合题目要求的.
1.函数2sin y x x =+的导数为( )
A .'2sin y x x =+
B .'2cos y x x =+
C .'2sin y x x =-
D .'sin y x x =- 2、用反证法证明命题:若整系数一元二次方程20(0)ax bx c a ++=≠有有理根,那么a b c ,,中至少有一个是偶数时,下列假设中正确的是( )
A.假设a b c ,,都是偶数 B.假设a b c ,,都不是偶数 C.假设a b c ,,至多有一个是偶数 D.假设a b c ,,至多有两个是偶数 3.函数x x y 2cos =在点)0,4
(
π
处的切线方程是( )
A .01642
=-+ππy x B .01642
=--ππy x C .0842=-+π
πy x
D .0842
=--π
πy x
4.观察按下列顺序排序的等式:,,31439,21329,11219,1109 =+⨯=+⨯=+⨯=+⨯ 猜想第n(n ∈N*)个等式应为 ( ) 910)1(9.+=++n n n A 910)1(9.-=+-n n n B
110)1(9.-=-+n n n C 1010)1()1(9.-=-+-n n n D
5.用数学归纳法证明
3
12
11
1++
++
+n n n +…)(24
11*
N n n
n ∈≥
++
由k n =到
1+=k n 时,不等式左边应添加的项是( )
A .
)
1(21+k
B .
221121++
+k k
C .
2
21
1
21
++
+k k 1
1+-k D .2
211
21+++k k 1
1+-k 2
1+-k
6、由曲线x y =与直线0,4==y x 围成的曲边梯形的面积为( )
A 、
3
8 B 、
3
16 C 、
3
32 D 、16
7.如图是函数)(x f y =的导函数)('x f y =的图象,给出下列命题: ①3-是函数)(x f y =的极值点;
②1-是函数)(x f y =的最小值点;
③)(x f y =在0=x 处切线的斜率小于零; ④)(x f y =在区间)1,3(-上单调递增。
则正确命题的序号是( ) A .①② B .①④ C .②③ D .③④
8.函数()2
1x
x x f -=
( )
A .在)1,1(-上单调递增
B .在()0,1-上单调递增,在()1,0上单调递减
C .在()1,1-上单调递减
D .在()0,1-上单调递减,在()1,0上单调递增 9.设a,b 为正数,且a +b ≤4,则下列各式中正确的一个是 ( )
A .
111<+b a
B.
111≥+
b
a
C.
211<+
b
a
D.
211≥+
b
a
10.设函数3
2
11()3
2
f x ax bx cx =+
+,且32
b c a <<,(1)2
a f '=-
,则下列结论不正确...
的是( )
A .00a ><且b
B .334
b a
-<<-
C .112
c b
-
<
< D .134
2
c a
-
<
<
二、填空题 11.函数x
x x f ln )(=
单调增区间是 .
12、已知函数f(x)的导函数为)(x f ',且满足f(x)=3x 2+2x )2('f ,则)5('f = 13、计算定积分:⎰+1
3d )e 2(x x x =_______
14.若函数52)(2
3+-+=x ax x x f 在区间(2
1,
31)上不是单调函数......
,则实数a 的取值范围是_ _ _.
15.在平面几何中,有射影定理:“在ABC ∆中,AC AB ⊥,点A 在BC 边上的射影为D ,有BC BD AB
⋅=2
.”类比平面几何定理,研究三棱锥的侧面面积与射影面积、底面面积的
关系,可以得出的正确结论是:“在三棱锥BCD A -中,⊥AD 平面ABC ,点A 在底面BCD 上的射影为O ,则有 .”
C
B
D A
A
D
B
O
三.解答题 16. 已知函数a
x x
x
x f +++-=93)(2
3
.
(Ⅰ)求)(x f 的单调递减区间; (Ⅱ)若
)(x f 在区间]2,2[-上的最大值为
20,求它在该区间上的最小值.
17.设,0,0,0>>>z y x (Ⅰ)比较
2
x
x y
+与
34
x y -的大小;
(Ⅱ)利用(Ⅰ)的结论,证明:3
3
3
2
x
y
z
xy yz zx
x y
y z
z x
+++
+
≥
+++
18. 已知函数.)(,ln )(x x g x x f ==
(1)求函数y =)
()(x g x f 的最大值; (2)若1>x ,求证:).1
1(
2)(+->x x g x f
19、统计表明,某种型号的汽车在匀速行驶中每小时耗油量y (升)关于行驶速度x (千米/小时)的函数解析式可以表示为:
3
138(0120)
128000
80
y x x x =
-
+<≤已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少
升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少
升?
20.是否存在常数b a ,,使等式
2
)
12)(12(5
32
3
11
2
2
2
2
++=
+-+
+⨯+
⨯bn n an n n n
对于一切
*
N n ∈都成立?若存在,用数学归纳法证明之,若不存在,请说明理由。
21、已知a ∈R ,函数()()2
f x x
x a =-.
(1)若函数()x f 在区间20,
3⎛⎫
⎪⎝
⎭
内是减函数,求实数a 的取值范围; (2)求函数()f x 在区间[]1,2上的最小值()h a ;
春晖学校2011-2012学年第二学期高二月考
数学答题卷(理科)
一.选择题(本大题共10小题,每个小题5分,共50分)
二.填空题(本大题共5小题,每小题5分,共25分)把正确的答案填在横线上.11.12.
13.14.
15.
三.解答题(本大题共6小题,共75分)
16.
18.
20.
21.。
