Simotion 路径插补功能介绍
插补方法的总结

插补方法的总结
插补方法是在数学领域中使用的一种技术,它可以用于解决各种数值计算问题。
该方法在计算机领域中也得到了广泛应用,特别是在计算机辅助制造、数控技术和机器人技术等领域。
插补方法通常涉及到使用一些已知的数据来预测其它数据的值。
这些数据可以表示成一个函数,该函数可以用于插值或外推来计算未知数据的值。
插值是指在已知数据点之间插入新的数据点,而外推是指在已知数据点的范围之外推算新的数据点。
在计算机辅助制造中,插补方法通常被用来控制机器人或数控机床的运动轨迹。
这些机器通常会按照一定的速度和方向进行移动,以便完成生产或制造任务。
插补方法可以帮助机器在运动过程中实现高精度的位置控制和运动轨迹规划。
此外,该方法也可以用于图像处理、信号处理和数值模拟等领域。
总之,插补方法是一种强大的数学工具,它在计算机辅助制造、数控技术和机器人技术等领域中发挥了重要作用。
对于需要解决数值计算问题的人来说,学习和掌握插补方法是非常重要的。
- 1 -。
数控系统的实时插补及加减速控制

数控系统的实时插补及加减速控制数控系统实时插补及加减速控制数控系统是一种高精度数控机床控制系统,它通过调节数控机床各轴的运动状态和位置,实现对各种复杂工件的高精度加工。
数控系统的核心控制部分是实时插补及加减速控制。
实时插补数控机床需要根据加工工艺要求,实时调整各电机的运动状态和位置,这就需要数控系统进行实时插补。
数控系统的实时插补是将工件模型翻译为机床加工程序,并计算各轴的运动状态和位置,最终控制数控机床的加工过程。
实时插补最主要的控制参数是各轴的位置、速度和加速度。
根据加工需要,数控系统能够实时调整这些控制参数,以满足各种加工要求。
在实时插补过程中,数控系统需要控制各轴的位置精度和速度精度。
位置精度是指加工工件时各轴运动的精确度,速度精度是指加工运动时各轴的稳定性和准确性。
数控系统需要实时控制这些参数,以确保机床实现高精度加工。
加减速控制加减速控制是数控系统实时控制机床加工过程的关键。
在机床加工中,加减速控制涉及到电机的运动状态和位置变化,以及与原始理论运动轨迹的同步。
数控系统通过分析工件加工过程中的能量分配,调整电机的加减速控制,以实现高质量的加工结果。
加减速控制主要包括加速度控制和速度控制。
加速度控制是指在机床开始运动时,电机的加速度控制,以及在电机停止时的减速度控制。
速度控制是指在机床中间过程中,电机的速度控制。
这两个过程的控制精度对加工质量影响极大。
在加减速控制过程中,数控系统还要考虑到负载变化、机床表面粗糙度等因素。
负载变化会改变加工过程中的能量分配,从而影响加减速度控制;而机床表面粗糙度则会影响工件上的感应机构,从而增加了系统控制的难度。
因此,在加减速控制过程中,数控系统需要保持高度的控制精度和灵活性。
综上所述,数控系统的实时插补及加减速控制是数控机床加工的核心。
数控系统通过实时调整各轴的位置、速度和加速度,确保具有高精度、高稳定性和高效率的加工过程。
对于各种复杂工件,数控系统可以实现高度可靠的加工控制,从而实现高质量、高效率的加工作业。
插补功能说明文档
4.6 插补运动模式插补运动模式可以实现多轴的协调运动,从而完成一定的运动轨迹。
该插补运动模式具有以下一些功能,可以实现直线插补;可以同时有两个坐标系进行插补运动;每个坐标系含有两个缓存区,可以实现缓存区暂停、恢复等功能;具有缓存区延时和缓存区数字量输出的功能;具有前瞻预处理功能,能够实现小线段高速平滑的连续轨迹运动。
4.6.1 指令列表设置插补运动指令列表4.6.2 重点说明4.6.2.1 建立坐标系运动控制器初始状态下,所有的规划轴都处于单轴运动模式下,两个坐标系也是无效的。
所以,当需要进行插补运动时,首先需要建立坐标系,将规划轴映射到相应的坐标系中。
每个坐标系最多支持四维(X-Y-Z-A),用户根据自己的需求,也可以利用二维(X-Y)、三维(X-Y-Z)坐标系描述运动轨迹。
用户通过调用GT_SetCrdPrm()指令将在坐标系内描述的运动通过映射关系映射到相应的规划轴上。
运动控制器根据坐标映射关系,控制各轴运动,实现要求的运动轨迹。
调用GT_SetCrdPrm()指令时,所映射的各规划轴必须处于静止状态。
建立坐标系的例程如下:…… …… ……short rtn;TCrdPrm crdPrm; // 定义坐标系结构体变量memset(&crdPrm,0,sizeof(crdPrm)); // 将变量初始化为全0crdPrm.dimension=2; // 坐标系为二维坐标系图4-6-1 右手坐标系 Z XY OcrdPrm.synVelMax=500; // 最大合成速度:500pulse/mscrdPrm.synAccMax=1; // 最大加速度:1pulse/ms^2crdPrm.evenTime = 50; // 平滑时间:50mscrdPrm.profile[0] = 1; // 规划器1对应到X轴crdPrm.profile[1] = 2; // 规划器2对应到Y轴crdPrm.profile[4] = 1; // 规划器5对应到X轴crdPrm.profile[5] = 2; // 规划器6对应到Y轴rtn = GT_SetCrdPrm(1,&crdPrm); // 建立1号坐标系,设置坐标系参数………………例程说明:dimension:表示所建立的坐标系的维数,取值范围为[1,4],该例程中所建立的坐标系是二维,即X-Y坐标系。
simotion_基本使用手册

simotion_基本使用手册I. 简介1.1 simotion 概述1.2 simotion 的应用领域1.3 simotion 的优势II. 系统组成2.1 simotion 控制器2.2 simotion 运动控制系统2.3 simotion 工程软件III. 基本操作3.1 硬件连接3.1.1 控制器与外部设备连接 3.1.2 模块间的连接方式3.2 系统启动与关闭3.3 菜单操作3.3.1 菜单结构3.3.2 菜单操作步骤3.4 故障排除3.4.1 常见故障与解决方法 3.4.2 故障代码的含义与处理IV. 编程基础4.1 编程环境介绍4.2 编程语言及其特点4.3 编程实例演练4.3.1 简单的运动控制程序编写 4.3.2 系统故障处理的程序编写 4.4 调试与测试4.4.1 程序调试的基本方法4.4.2 程序测试的注意事项V. 运动控制5.1 运动控制原理5.2 运动控制参数设定5.3 运动控制程序设计5.3.1 位置控制程序设计5.3.2 速度控制程序设计5.4 运动学习与优化5.4.1 运动学习的方法5.4.2 运动优化的技巧VI. 系统维护6.1 系统备份与恢复6.1.1 控制器程序的备份方法6.1.2 系统参数的备份与恢复6.2 系统更新与升级6.3 系统性能监控6.3.1 系统各部分性能指标6.3.2 性能监控方法及工具VII. 故障处理7.1 硬件故障处理7.1.1 控制器故障处理7.1.2 模块故障处理7.2 软件故障处理7.2.1 程序故障处理7.2.2 系统故障处理VIII. 安全操作8.1 安全操作规程8.1.1 机器设备安全操作规程8.1.2 simotion 控制系统安全操作规程 8.2 应急处理8.2.1 突发情况的处理步骤8.2.2 安全设备的使用与保养IX. 使用注意事项9.1 温度与湿度要求9.2 电源要求9.3 使用环境要求9.4 维护保养要点结语simotion 控制系统的使用教程至此结束。
数控机床插补原理

终点判别
∑=6+4=10 ∑=10-1=9 ∑=9-1=8 ∑=8-1=7 ∑=7-1=6 ∑=6-1=5 ∑=5-1=4 ∑=4-1=3 ∑=3-1=2 ∑=2-1=1 ∑=1-1=0
3.3逐点比较法第一象限圆弧插补 3.3.1偏差判断
我们以任意加工点Pi(Xi,Yi)与圆弧圆心的距 离同圆弧半径相比较来进行判断。即: Fi=Xi2+Yi2-R2 作为偏差函数
O
5 6
34
12
10 E 89 7
X
步数
0 1 2 3 4 5 6 7 8 9 10
偏差判别
F0=0 F1<0 F2>0 F3<0 F4>0 F5=0 F6<0 F7>0 F8<0 F9>0
坐标进给
+X +Y +X +Y +X +X +Y +X +Y +X
偏差计算
F0=0 F1=F0-ye=0-4=-4 F2=F1+xe=-4+6=2 F3=F2-ye=2-4=-2 F4=F3+xe=-2+6=4 F5=F4-ye=4-4=0 F6=F5-ye=0-4=-4 F7=F6+xe=-4+6=2 F8=F7-ye=2-4=-2 F9=F8+xe=-2+6=4 F10=F9-ye=4-4=0
3、逐点比较法
3.1逐点比较法的基本原理
计算机在刀具按要求轨迹运动加工零件轮廓的过程中,逐点的计算和判别
刀具与被加工零件轮廓之间的相对位置,并根据比较结果决定下一步的进
给方向,使刀具沿着坐标轴向减少偏差的方向进给,且只有一个方向的进
Simotion 路径插补功能介绍
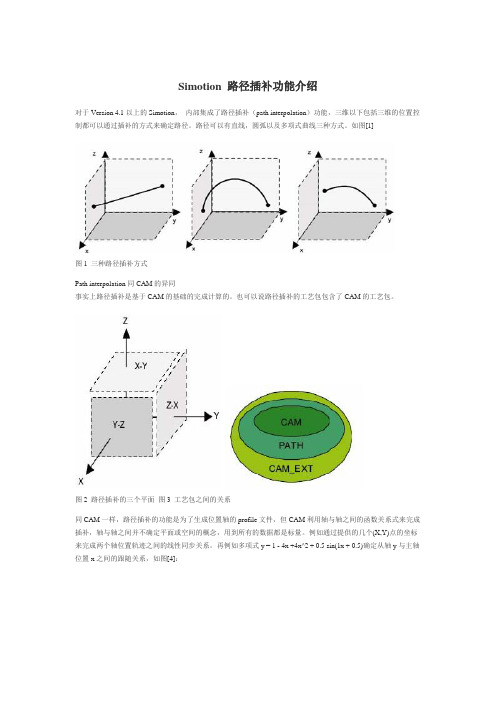
图 14 MCC 编程举例 多项式插补 在高级应用中,圆弧插补可能不能满足设计需求,如椭圆形的插补等,这种情况只有借助多项式来完成计算, 但需要注意,路径插补中用到的多项式变量均为矢量。 1. 根据五阶多项式的系数来完成插补,如下式:
其中,我们在编程时需要提供的数据有目标位置以及四个空间矢量坐标:A2 , A3, A4, A5,方程又可以写成如下 形势:
2. 在两维平面内基于圆心坐标、旋转角度以及方向的平面插补方式,当调用此程序块时,系统会根据当前位 置,圆心坐标以及旋转角度来计算运行轨迹以及目标位置,运行程序块时会根据事先设定的轨迹到达相应位 置。这里不存在大小圆弧的概念,只有方向的设定。如下图所示:
图 11 基于圆心坐标、旋转角度以及方向的平面插补方式 注意这种方式不能用于三维,因为不能确定唯一轨迹。在 ST 编程中相应的指令为 _movePathCircular(),圆弧类 型选择 BY_CENTER_AND_ARC。
图 13 基于中间插补点以及目标位置的插补方式 ST 指令为 _movePathCircular(),圆弧类型选择 BY_CENTER_AND_ARC。 编程举例: retval := _movepathcircular( pathobject := pathIpo, pathplane := X_Y_Z, circulartype := OVER_POSITION_TO_ENDPOSITION, pathmode := RELATIVE, x:=10.0, y:=0.0, z:=0.0, ijkmode := RELATIVE, i:=5.0, j:=5.0, k:=5.0 );
图 10 基于圆弧半径、目标位置以及方向的平面插补方式 注意这种方式不能用于三维,因为不能确定唯一轨迹。在 ST 编程中相应的指令为_movePathCircular(),圆弧类 型选择 WITH_RADIUS_AND_ENDPOSITION。 编程举例: retval := _movepathcircular( pathobject := pathIpo, pathplane := X_Y, circulartype := WITH_RADIUS_AND_ENDPOSITION, circledirection := POSITIVE, pathmode := RELATIVE, x := 10.0, y := 10.0, radius := SQRT(200.0)/2.0 );
什么是插补
什么是插补一、插补的概念在数控机床中,刀具不能严格地根据要求加工的曲线运动,只能用折线轨迹靠近所要加工的曲线。
插补(interpolation)定义:机床数控系统依照肯定方法确定刀具运动轨迹的过程。
也可以说,已知曲线上的某些数据,根据某种算法计算已知点之间的中间点的方法,也称为“数据点的密化”。
数控装置向各坐标供应相互协调的进给脉冲,伺服系统依据进给脉冲驱动机床各坐标轴运动。
数控装置的关键问题:依据掌握指令和数据进行脉冲数目安排的运算(即插补计算),产生气床各坐标的进给脉冲。
插补计算就是数控装置依据输入的基本数据,通过计算,把工件轮廓的外形描述出来,边计算边依据计算结果向各坐标发出进给脉冲,对应每个脉冲,机床在响应的坐标方向上移动一个脉冲当量的距离,从而将工件加工出所需要轮廓的外形。
插补的实质:在一个线段的起点和终点之间进行数据点的密化。
插补工作可由硬件规律电路或执行软件程序来完成,在CNC系统中,插补工作一般由软件完成,软件插补结构简洁、敏捷易变、牢靠性好。
二、插补方法的分类目前普遍应用的两类插补方法为基准脉冲插补和数据采样插补。
1.基准脉冲插补(行程标量插补或脉冲增量插补)特点:每次插补结束,数控装置向每个运动坐标输出基准脉冲序列,每插补运算一次,最多给每一轴一个进给脉冲。
每个脉冲代表了最小位移,脉冲序列的频率代表了坐标运动速度,而脉冲的数量表示移动量。
每发出一个脉冲,工作台移动一个基本长度单位,也叫脉冲当量,脉冲当量是脉冲安排的基本单位。
该方法仅适用于一些中等精度或中等速度要求的计算机数控系统主要的脉冲增量插补方法:数字脉冲乘法器插补法逐点比较法数字积分法矢量判别法比较积分法最小偏差法目标点跟踪法单步追踪法直接函数法加密判别和双判别插补法2. 数字采样插补(数据增量插补)数据采样插补又称时间增量插补,这类算法插补结果输出的不是脉冲,而是标准二进制数。
依据程编进给速度,把轮廓曲线按插补周期将其分割为一系列微小直线段,然后将这些微小直线段对应的位置增量数据进行输出,以掌握伺服系统实现坐标轴的进给。
插补
1、插补英文:interpolation定义:根据给定的数学函数,在理想的轨迹式轮廓上的已知点之间,确定一些中间点的一种方法。
在数控机床中,刀具不能严格地按照要求加工的曲线运动,只能用折线轨迹逼近所要加工的曲线。
插补(interpolation)定义:机床数控系统依照一定方法确定刀具运动轨迹的过程。
也可以说,已知曲线上的某些数据,按照某种算法计算已知点之间的中间点的方法,也称为“数据点的密化”。
数控装置根据输入的零件程序的信息,将程序段所描述的曲线的起点、终点之间的空间进行数据密化,从而形成要求的轮廓轨迹,这种“数据密化”机能就称为“插补”。
插补计算就是数控装置根据输入的基本数据,通过计算,把工件轮廓的形状描述出来,边计算边根据计算结果向各坐标发出进给脉冲,对应每个脉冲,机床在响应的坐标方向上移动一个脉冲当量的距离,从而将工件加工出所需要轮廓的形状。
插补原理:数控车床的运动控制中,工作台(刀具)X、Y、Z轴的最小移动单位是一个脉冲当量。
因此,刀具的运动轨迹是具有极小台阶所组成的折线(数据点密化)。
例如,用数控车床加工直线OA、曲线OB,刀具是沿X轴移动一步或几步(一个或几个脉冲当量Dx),再沿Y轴方向移动一步或几步(一个或几个脉冲当量Dy),直至到达目标点。
从而合成所需的运动轨迹(直线或曲线)。
数控系统根据给定的直线、圆弧(曲线)函数,在理想的轨迹上的已知点之间,进行数据点密化,确定一些中间点的方法,称为插补。
分类:直线插补(Llne Interpolation)这是车床上常用的一种插补方式,在此方式中,两点间的插补沿着直线的点群来逼近,沿此直线控制刀具的运动。
一个零件的轮廓往往是多种多样的,有直线,有圆弧,也有可能是任意曲线,样条线等. 数控机床的刀具往往是不能以曲线的实际轮廓去走刀的,而是近似地以若干条很小的直线去走刀,走刀的方向一般是x和y方向. 插补方式有:直线插补,圆弧插补,抛物线插补,样条线插补等所谓直线插补就是只能用于实际轮廓是直线的插补方式(如果不是直线,也可以用逼近的方式把曲线用一段段线段去逼近,从而每一段线段就可以用直线插补了).首先假设在实际轮廓起始点处沿x方向走一小段(一个脉冲当量),发现终点在实际轮廓的下方,则下一条线段沿y方向走一小段,此时如果线段终点还在实际轮廓下方,则继续沿y方向走一小段,直到在实际轮廓上方以后,再向x方向走一小段,依次循环类推.直到到达轮廓终点为止.这样,实际轮廓就由一段段的折线拼接而成,虽然是折线,但是如果我们每一段走刀线段都非常小(在精度允许范围内),那么此段折线和实际轮廓还是可以近似地看成相同的曲线的--------这就是直线插补.圆弧插补(Circula : Interpolation)这是一种插补方式,在此方式中,根据两端点间的插补数字信息,计算出逼近实际圆弧的点群,控制刀具沿这些点运动,加工出圆弧曲线。
simotion基本使用手册
simotion基本使用手册
Simotion是西门子公司推出的一种先进的运动控制系统,它结合了PLC(可编程逻辑控制器)和运动控制器的功能,适用于各种工业自动化应用。
Simotion的基本使用手册包括以下内容:
1. 系统概述,介绍Simotion系统的基本架构、硬件组成和工作原理,帮助用户了解Simotion系统的整体框架和基本工作原理。
2. 硬件安装,详细介绍Simotion系统的硬件安装步骤,包括各个模块的安装位置、连接方式以及接线方法,帮助用户正确、安全地安装Simotion系统。
3. 软件配置,介绍Simotion系统的软件配置步骤,包括参数设置、控制逻辑编程、运动控制配置等内容,帮助用户进行系统参数设置和控制逻辑编程。
4. 系统调试,介绍Simotion系统的调试方法和步骤,包括硬件连接检查、软件功能测试、运动控制性能调试等内容,帮助用户进行系统调试和性能优化。
5. 故障排除,介绍Simotion系统常见故障的排除方法和步骤,包括故障代码解读、故障现象分析、故障原因判定等内容,帮助用
户快速准确地排除系统故障。
6. 应用实例,提供Simotion系统在不同工业领域的应用实例,包括机床加工、包装输送、物料搬运等各种自动化应用,帮助用户
了解Simotion系统在实际工程中的应用场景和解决方案。
总的来说,Simotion的基本使用手册涵盖了系统概述、硬件安装、软件配置、系统调试、故障排除和应用实例等多个方面,帮助
用户全面了解和掌握Simotion系统的基本使用方法和技巧。
希望以
上内容能够帮助到你对Simotion系统的基本使用有一个全面的了解。
SIMOTIONCAM功能使用入门
SIMOTION CAM功能使用入门 SIMOTION CAM FUNCTION Getting Start摘要 本文介绍SIMOTION CAM功能的使用及编程。
关键词SIMOTION CAM功能Key Words SIMOTION CAMA&D Service & Support Page 2-23目录_Toc2088215861.SIMOTION CAM功能介绍 (4)2.配置主轴和从轴 (4)2.1 建立驱动设备 (4)2.2 轴的插入 (6)2.3 主轴与从轴的耦合 (8)2.4主轴与从轴的同步的设定 (8)2.5 设定CAM曲线 (12)2.5.1 通过插补表设定CAM曲线 (14)2.5.2 通过多项式生成CAM曲线 (16)2.5.3 将CAM曲线与主轴从轴连接 (18)3.编写CAM程序 (18)3.1 轴使能及回零点 (18)3.2使能及解除CAM1 (19)3.3使能及解除CAM2 (20)3.4故障处理程序 (20)3.4.1 工艺对象故障处理程序 (20)3.4.2 外设故障处理程序 (20)3.5程序执行系统的分配 (20)3.6运行CAM时运动轨迹跟踪 (21)3.6.1 CAM1运动轨迹跟踪 (21)3.6.2 CAM2运动轨迹跟踪 (22)3.7示例程序 (22)A&D Service & Support Page 3-231.SIMOTION CAM功能介绍在运动控制应用中,经常需要多个轴的同步控制,例如设定一个轴为主轴,其它的轴为从轴,从轴跟随主轴的运动而作响应的运动,主轴可以是一个实轴也可以是一个虚轴或是一个外接的编码器。
在实际应用中主轴的速度和位置值是一个测量值,容易受到测量周期及外部环境的影响而产生扰动,这样在从轴上产生更大的扰动,这种情况下可以采样虚轴作为主轴,将主轴的值经过优化计算后再传递给从轴,从而从轴减少速度和位置的扰动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Simotion 路径插补功能介绍∙文献∙∙涉及产品∙对于Version 4.1以上的Simotion,内部集成了路径插补(path interpolation)功能,三维以下包括三维的位置控制都可以通过插补的方式来确定路径。
路径可以有直线,圆弧以及多项式曲线三种方式。
如图[1]图1 三种路径插补方式Path interpolation同CAM的异同事实上路径插补是基于CAM的基础的完成计算的。
也可以说路径插补的工艺包包含了CAM的工艺包。
图2 路径插补的三个平面图3 工艺包之间的关系同CAM一样,路径插补的功能是为了生成位置轴的profile文件,但CAM利用轴与轴之间的函数关系式来完成插补,轴与轴之间并不确定平面或空间的概念,用到所有的数据都是标量。
例如通过提供的几个(X,Y)点的坐标来完成两个轴位置轨迹之间的线性同步关系。
再例如多项式y = 1 - 4x +4x^2 + 0.5 sin(1x + 0.5)确定从轴y与主轴位置x之间的跟随关系,如图[4]:图4 用多项式生成的CAM曲线而Path interpolation 功能更突出体现空间路径的概念,如三维空间的多项式插补,如图[2],并不需要确定轴之间的直接函数关系,而是借助矢量矩阵来设定三维变量同第四变量p的关系:P = A0 + A1•p + A2 •p2 + A3•p3 + A4•p4 + A5•p5,p∈[0,1] Path interpolation的激活首先只有Version 4.1以上的simotion才可以激活其路径插补功能,另外PATH的工艺包需要被激活,到simotion 的“select Technology packages”中去选择。
如图[6]所示。
也只有激活PATH工艺包的前提下,才能在编程过程中找到与插补相关的指令[图5]。
图5 Sout 中的插补菜单图6 激活插补工艺包生成带有Path interpolation功能的轴在创建轴的过程中要选择Path interpolation,如图[7]:需要注意的是PATH功能与Synchronous operation并没有直接的联系,因此不必要激活同步功能。
图7 创建Path 轴创建PATH OBJECT在选择了带有Path功能的轴后,我们需要在PATH OBJECTS中创建一个新的object_2, 如下图[8]:图8 创建Path object然后再所创建的path_object_2中的interconnections中将path_object_2链接到相应的轴上去。
图9 将Path 链接到轴上另外,Path_object不但可以链接到轴上,也可以链接到事先生成的CAM,用CAM 定义其速度关系。
三种插补方式直线插补在MCC语言编程中,只需要输入目标位置的坐标值,当调用此程序块时,三维上的三个轴都会到达目标位置的坐标值,而轨迹上的每一个点都在这条空间直线上。
在库文件中提供的指令为_movePathLiner()圆弧插补圆弧插补有三种方式:1. 在二维平面内基于圆弧半径、目标位置以及方向的平面插补方式,当起动此程序块时,系统会根据当前位置,目标位置以及圆弧半径三个数据来计算圆弧轨迹,然后二维方向上的轴会从当前位置按圆弧轨迹运行到目标位置,编程时需要注意半径必需大于两点之间的距离的一半。
另外在编程时还可以定义轨迹的大小圆弧方式,如下图所示。
图10 基于圆弧半径、目标位置以及方向的平面插补方式注意这种方式不能用于三维,因为不能确定唯一轨迹。
在ST编程中相应的指令为_movePathCircular(),圆弧类型选择WITH_RADIUS_AND_ENDPOSITION。
编程举例:retval := _movepathcircular(pathobject := pathIpo,pathplane := X_Y,circulartype := WITH_RADIUS_AND_ENDPOSITION,circledirection := POSITIVE,pathmode := RELATIVE,x := 10.0, y := 10.0,radius := SQRT(200.0)/2.0 );2. 在两维平面内基于圆心坐标、旋转角度以及方向的平面插补方式,当调用此程序块时,系统会根据当前位置,圆心坐标以及旋转角度来计算运行轨迹以及目标位置,运行程序块时会根据事先设定的轨迹到达相应位置。
这里不存在大小圆弧的概念,只有方向的设定。
如下图所示:图11 基于圆心坐标、旋转角度以及方向的平面插补方式注意这种方式不能用于三维,因为不能确定唯一轨迹。
在ST编程中相应的指令为_movePathCircular(),圆弧类型选择BY_CENTER_AND_ARC。
图12 MCC编程举例编程举例:retval := _movepathcircular(pathobject := pathIpo,pathplane := X_Y,circulartype := BY_CENTER_AND_ARC,circledirection := POSITIVE,ijkmode := RELATIVE,i := -10.0, j := 0.0,arc := 90.0 );3. 基于中间插补点以及目标位置的插补方式,与上面两种插补方式不同,这种插补方式有两维也有三维的,因为三点可以确定一个平面,所以轨迹时可以唯一确定的,运行轨迹如下图所示。
如果选择两维平面需要注意中间插补点与目标位置都要保证在此平面上。
否则运行程序时系统会报错。
图13基于中间插补点以及目标位置的插补方式ST指令为_movePathCircular(),圆弧类型选择BY_CENTER_AND_ARC。
编程举例:retval := _movepathcircular(pathobject := pathIpo,pathplane := X_Y_Z,circulartype := OVER_POSITION_TO_ENDPOSITION,pathmode := RELATIVE,x:=10.0, y:=0.0, z:=0.0,ijkmode := RELATIVE,i:=5.0, j:=5.0, k:=5.0 );图14 MCC编程举例多项式插补在高级应用中,圆弧插补可能不能满足设计需求,如椭圆形的插补等,这种情况只有借助多项式来完成计算,但需要注意,路径插补中用到的多项式变量均为矢量。
1. 根据五阶多项式的系数来完成插补,如下式:A5,方程又可以写成如下形势:这种方法的优点是插补比较精确,但缺点是多项式不好确定,即四个矢量的运算难度比较大。
图15 MCC编程举例可供调用的库程序为_movePathPolynomial(),其多项式类型polynomialMode:= SETTING_OF_COEFFICIENTS2. 提供起始位置与目标位置的几何微分图16 根据起始与最终点的微分进行插补其中为起始位置,即当前位置,为一阶微分,为起始位置的二阶微分;为目标位置,为目标位置的一阶微分,为目标位置的二阶微分。
举例如下:图16 插补举例图17 MCC插补举例可供调用的库程序为_movePathPolynomial(),其多项式类型polynomialMode:=SPECIFIC_START_DATA3. 只需提供目标位置的几何微分,不需要提供起始位置,把当前位置作为起始位置,如果当前位置不能获得,则系统会报错50002。
举例:将两段直线通过插补的方式连接起来,并形成路径。
// Determination of derivatives via function// _getLinearPathGeometricData// Derivative in start point of polynomial commandstartPoly := _getLinearPathGeometricData(pathObject := pathIpo,pathPlane := X_Y_Z,pathMode := ABSOLUTE,xEnd := 50.0, yEnd := 0.0, zEnd := 0.0,xStart := 0.0, yStart := 0.0, zStart := 0.0,pathPointType := END_POINT );// Determine derivative in end point of polynomial command endPoly := _getLinearPathGeometricData(pathObject := pathIpo,pathPlane := X_Y_Z,pathMode := ABSOLUTE,xEnd := 150.0, yEnd := 150.0, zEnd := 0.0,xStart := 150.0, yStart := 100.0, zStart := 0.0,pathPointType := START_POINT);// Programming of polynomial command// Use of derivatives in the commandretval := _movePathPolynomial(pathObject := pathIpo,pathPlane := X_Y_Z,pathMode := ABSOLUTE,polynomialMode := ATTACHED_STEADILY,x:=150.0, y:=100.0, z:=0.0,vector1x := startPoly.firstGeometricDerivative.x,vector1y := startPoly.firstGeometricDerivative.y,vector1z := startPoly.firstGeometricDerivative.z,vector2x := startPoly.secondGeometricDerivative.x,vector2y := startPoly.secondGeometricDerivative.y,vector2z := startPoly.secondGeometricDerivative.z,vector3x := endPoly.firstGeometricDerivative.x,vector3y := endPoly.firstGeometricDerivative.y,vector3z := endPoly.firstGeometricDerivative.z,vector4x := endPoly.secondGeometricDerivative.x,vector4y := endPoly.secondGeometricDerivative.y,vector4z := endPoly.secondGeometricDerivative.z,blendingMode := ACTIVE_WITH_DYNAMIC_ADAPTION,mergeMode := SEQUENTIAL,nextCommand := WHEN_BUFFER_READY );停止与继续PATH可用通过_stopPath()编程指令来停止当前的PATH, 但并不清楚,还可以指令_continuePath()来继续PATH。
