数学必修5模块测试一

合集下载

人教B版人教B版高中数学必修五必修模块5测试样题B版答案及评分参考.docx

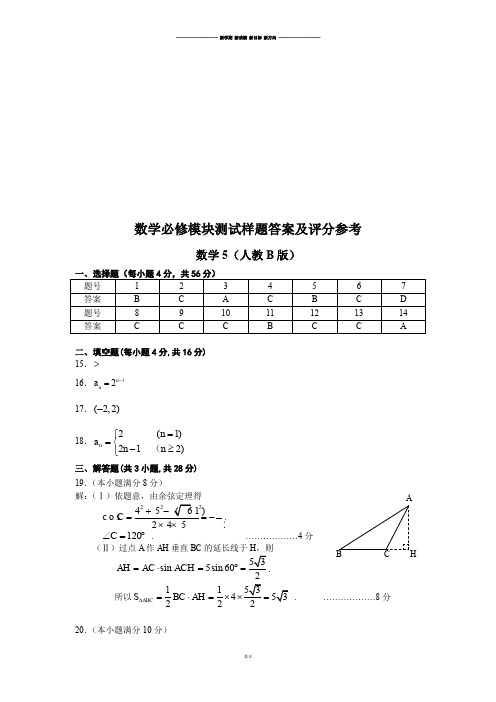
数学必修模块测试样题答案及评分参考数学5（人教B 版）一、选择题（每小题4分，共56分）题号 1 2 3 4 5 6 7 答案 B C A C B C D 题号 8 9 10 11 12 13 14 答案CCCBCCA二、填空题(每小题4分,共16分) 15．> 16．12n n a -= 17．(2,2)-18． 2(1)2 1 2)n n a n n =⎧=⎨-≥⎩（三、解答题(共3小题,共28分) 19．（本小题满分8分）解：（Ⅰ）依题意，由余弦定理得22245(61)1c o s2452C +-==-⨯⨯. 120C ∠=︒ . ………………4分（Ⅱ）过点A 作AH 垂直BC 的延长线于H ，则53sin 5sin 602AH AC ACH =⋅=︒=. 所以1153453222ABCS BC AH ∆=⋅=⨯⨯= . ………………8分20．（本小题满分10分）B C AH解：设水池底面的长为x 米，则宽为48003x米，易知0x >，又设水池总造价为y 元. 根据题意，有48001600150120(2323)3y x x=⨯+⨯+⨯⨯ 1600240000720()x x=++16002400007202x x≥+⨯⋅ 297600=. 当1600,x x=即40x =时，等号成立. 所以，将水池的底面设计成边长为40米的正方形时，总造价最低，最低总造价为297600元..………………10分21．（本小题满分10分）解：（Ⅰ）答案如图所示：………………3分（Ⅱ）易知，后一个图形中的着色三角形个数是前一个的3倍，所以，着色三角形的个数的通项公式为：13n n b -=． ………………6分（Ⅲ）由题意知(1)2n n n a +=，11(1)23231n n n n n c n n --+⨯⨯=⋅+＝，所以 01113233n n S n -=⋅+⋅++⋅ ①12131323(1)33n n n S n n -=⋅+⋅++-⋅+⋅ ② ①－②得 0112(333)3n n n S n --=+++-⋅2n S -＝13313nn n --⋅-．即 (21)31()4n n n S n -+=∈N + ． ………………10分。

浙江省瓯海中学高一数学模块(必修5)测试卷2008.4

浙江省瓯海中学2007学年第二学期高一数学模块（必修5）测试卷2008.4命题人：王春蕾说明：全卷共三大题，19小题，满分100分，考试时间为100分钟。

一、选择题（本大题共10小题，每小题4分，共40分） 1、下列命题正确的是（） A ．22bc ac b a >⇒> B ．320b b a b a >⇒<< C ．01>>⇒>b b a b a 且D ．ba ab b a 110,33<⇒>>2、在△ABC 中，1,6a b A π==∠=，则∠B 等于（）A ．3π B ．3π或23π C ．6π或56πD ．23π3、等差数列{}n a 中,83,a a 是方程0532=--x x 的两个实数根,则此数列的前10项和=10S （）A ．15B ．30C ．50D ．15+4、两灯塔A ，B 与海洋观察站C 的距离都等于100km, 灯塔A 在C 北偏东30︒，B 在C 南偏东60︒，则A ，B 之间的相距约（） A ．100kmB ．173kmC ．141kmD ．180km5、用一个平面去截一个几何体，得到的截面是一个圆面，这个几何体可能是（）A ．圆锥B ．圆柱C ．球体D ．以上都可能6、一个体积为38cm 的正方体的顶点都在球面上，则球的表面积是（） A ．28cm π B ．212cm π C ．216cm π D ．220cm π7、已知,a b 是正实数，A 是,a b 的等差中项，G 是,a b 的等比中项，则（） A ．ab AG ≤B ．ab AG ≥C ．||ab AG ≤D ．||ab AG ≥8、下列函数中，最小值为4的是（）A.4y xx =+ B.2y =C.4xxy e e-=+ D.4sin (0)sin y x x xπ=+<<9、计算机将信息转换成二进制数进行处理时，二进制即“逢二进一”．如2(1101)表示二进制的数，将它转换成十进制的形式是32102(1101)1212021213=⨯+⨯+⨯+⨯=，那么将二进制数16111位转换成十进制数的形式是（）A ．1722-B ．1621-C ．1622-D ．1521-10、小正方形按照下图中的规律排列，每个图形中的小正方形的个数构成数列}{n a 有以下结论：①155=a ；②}{n a 是一个等差数列；③数列}{n a 是一个等比数列；④数列}{n a 的递推公式为),(11*+∈++=N n n a a n n 其中正确的是（）A ．①②④B ．①③④C ．①②D ．①④二、填空题（本大题共5小题，每小题4分，共20分）11、不等式211<x 的解集是．12、如右图为一个几何体的三视图，其中俯视图为正三角形，A 1B 1=2，AA 1=4，则该几何体的表面积为．13、△ABC 的三内角A 、B 、C 成等差数列，所对的三边a 、b 、c 成等比数列，则A C -= ． 14、已知数列{a n }的通项公式a n =n n +⋯++21 ,b n =11+n n a a ,则{b n }的前n 项和为 .15、已知正数,x y 满足21x y +=，则11x y+的最小值为．CAB 1正视图侧视图俯视图17、已知不等式：2860ax x +-<的解集为{}|1x x x b <>或. ⑴求,a b ；⑵解关于x 的不等式:23()30bx a m x am -++<.18、在梯形ABCD 中，AB ∥CD ，∠A=90°，∠B=45°，AB=32CD ，绕AB 边所在直线旋转一周所成的旋转体的表面积是(5π，求这个旋转体的体积。

人教版高中数学必修5第一章解三角形测试题及答案

必修五第一章解三角形测试(总分150)一、选择题(每题5分，共50分)1、在△ABC 中，a ＝3，b ＝7，c ＝2，那么B 等于（）A ． 30°B ．45°C ．60°D ．120°2、在△ABC 中，a ＝10，B=60°,C=45°,则c 等于（）A ．310+B ．()1310-C ．13+D ．3103、在△ABC 中，a ＝32，b ＝22，B ＝45°，则A 等于（）A ．30°B ．60°C ．30°或120°D ． 30°或150°4、在△ABC 中，3=AB ,1=AC ,∠A ＝30°，则△ABC 面积为（）A ．23 B ．43 C ．23或3 D ．43 或23 5、在△ABC 中，已知bc c b a ++=222，则角A 为（）A ．3πB ．6πC ．32πD ． 3π或32π6、在△ABC 中,面积22()Sa b c =--,则sin A 等于（）A ．1517B ．817C ．1315D ．13177、已知△ABC 中三个内角为A 、B 、C 所对的三边分别为a 、b 、c ，设向量(,)p a c b =+ ，(,)q b a c a =-- .若//p q，则角C 的大小为（）A ．6π B ．3π C ．2π D ．23π8、已知锐角三角形的边长分别为1，3，a ，则a 的范围是（）A ．()10,8B ．()10,8C ．()10,8D ．()8,109、在△ABC 中，已知C B A sin cos sin 2=,那么△ABC 一定是 ( )A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．正三角形 10、在△ABC 中,3,4ABBC AC ===,则AC 上的高为（）A ．BC ．32D ．二、填空题（每小题5分，共20分）11、在△ABC 中，若∠A:∠B:∠C=1:2:3,则=c b a :: 12、已知三角形两边长为11，则第三边长为13、若三角形两边长为1和3，第三边上的中线长为1，则三角形的外接圆半径为 14、在△ABC 中BC=1，3Bπ=，当△ABC tan C =三、解答题（本大题共小题6小题，共80分）15、（本小题14分）在△ABC 中，已知210=AB ，A ＝45°，在BC 边的长分别为20，3320，5的情况下，求相应角C 。

高一数学必修5模块测试

高一数学必修5模块测试一、选择题：(本大题共10小题，每小题5分，共50分，在每小题给出的四个选择项中,只有一项是符合题目要求的. 请将选择题答案填入下答题栏内)1．在⊿ABC 中，∠B=300 ，∠C=450，AB=1，则边AC 的长为（）. A ．36 B ．22 C ．21 D ．232．等比数列}{n a 中，公比1>q ，且12,84361==+a a a a ，则116a a 等于A ．21 B ．61 C ．31 D ．31或615、在A B C ∆中，a,b,c 分别是C B A ∠∠∠,,所对应的边，︒=∠90C ，则cb a +的取值范围是（） A ．（1,2） B ．)2,1( C ．]2,1( D ．]2,1[6. 已知变量x 、y 满足条件⎪⎩⎪⎨⎧≤-+≤-≥09201y x y x x 则x+y 的最大值是（）.A ．2B ．5C ．6D ．87、当x>1时不等式a x x ≥-+11恒成立，则实数a 的取值范围是（）A （]3,∞-B [3，+)∞C （]2,∞-D [2，+)∞10．在算式：“4130⨯+⨯= ”的两个、中填入两个正整数，使它们的倒数之和最小，则这两个数构成的数对() ，应为（）Ａ、(4，4) B 、(5，10) C 、(3，18) D 、(6，12)二、填空题（本大题共5小题，每小题4分，共20分。

把答案填在题中横线上。

）。

15. 若A(x,y)的横纵坐标都是整数，则把A 称作“整点”，在下列平面区域 3025000x y x y x y +-≥⎧⎪+-≤⎪⎨≥⎪⎪≥⎩内，整点个数是 . 14、在下列函数中，BAC北①|1|xx y += ；②1222++=xxy ；③1)x ,0(2loglog2≠>+=且x x y x； ④x x y x cot tan ,20+=<<π；⑤xx y -+=33；⑥24-+=xx y ；⑦24-+=xx y ；⑧2log22+=x y ；其中最小值为2的函数是（填入正确命题的序号） 6、将全体正整数排成一个三角形数阵（如图）按照以上排列的规律，第n 行（n ≥3）从左向右的第3 个数为 . 2范围是 .三、解答题（本大题共5小题，共40分。

(完整版)高中数学必修五综合测试题含答案

.绝密★启用前高中数学必修五综合考试卷第I 卷（选择题）一、单选题1．数列的一个通项公式是（）0,23,45,67⋯A ．B ． a n =n -1n +1（n ∈N *)a n =n -12n +1（n ∈N *)C ．D ．a n =2（n -1）2n -1（n ∈N *)a n =2n2n +1（n ∈N *)2．不等式的解集是（）x -12-x ≥0A ．B ．C ．D ． [1,2](-∞,1]∪[2,+∞)[1,2)(-∞,1]∪(2,+∞)3．若变量满足，则的最小值是（）x,y {x +y ≥0x -y +1≥00≤x ≤1x -3y A ．B ．C ．D ． 4-5-314．在实数等比数列{a n }中，a 2，a 6是方程x 2－34x ＋64＝0的两根，则a 4等于( )A ． 8B ．－8C ． ±8D ．以上都不对5．己知数列为正项等比数列，且，则（）{a n }a 1a 3+2a 3a 5+a 5a 7=4a 2+a 6=A ． 1B ． 2C ． 3D ． 46．数列前项的和为（）11111,2,3,4,24816n A ． B ． C ．D ．2122nn n ++21122n n n +-++2122n n n +-+21122n n n +--+7．若的三边长成公差为的等差数列，最大角的正弦值为ΔABC a,b,c 232的面积为（）A ．B ．C ．D ．1541534213435348．在△ABC 中，已知,则B 等于( )a =2,b =2,A =450A ． 30°B ． 60°C ． 30°或150°D ． 60°或120°9．下列命题中正确的是( )A ． a ＞b ⇒ac 2＞bc 2B ． a ＞b ⇒a 2＞b 2C ． a ＞b ⇒a 3＞b 3D ． a 2＞b 2⇒a ＞b.10．满足条件，的的个数是 ( )a =4,b =32,A =45∘A ． 1个B ． 2个C ．无数个D ．不存在11．已知函数满足：则应满足（）f(x)=ax 2-c -4≤f(1)≤-1,-1≤f(2)≤5.f(3)A ．B ．C ．D ．-7≤f(3)≤26-4≤f(3)≤15-1≤f(3)≤20-283≤f(3)≤35312．已知数列{a n }是公差为2的等差数列，且成等比数列，则为（）a 1,a 2,a 5a2A ． -2B ． -3C ． 2D ． 313．等差数列的前10项和，则等于（）{a n }S 10=15a 4+a 7A ． 3B ． 6C ． 9D ． 1014．等差数列的前项和分别为，若，则的值为（）{a n },{b n }n S n ,T nS nT n=2n3n +1a 3b 3A ．B ．C ．D ． 3547581219第II 卷（非选择题）二、填空题15．已知为等差数列，且－2＝－1,＝0,则公差={a n }a 7a 4a3d 16．在中，，，面积为，则边长=_________.△ABC A =60∘b =13c 17．已知中，，，，则面积为_________.ΔABC c =3a =1acosB =bcosA ΔABC 18．若数列的前n 项和，则的通项公式____________{a n }S n =23a n +13{a n }19．直线下方的平面区域用不等式表示为________________．x -4y +9=020．函数的最小值是 _____________．y =x +4x -1(x >1)21．已知，且，则的最小值是______．x ，y ∈R +4x +y =11x +1y三、解答题22．解一元二次不等式（1）（2）-x 2-2x +3>0x 2-3x +5>0.（1）求边上的中线的长；BC AD （2）求△的面积。

湖北省黄冈市2014年高中数学必修5模块测试卷

高中数学必修5模块测试卷本试卷共4页，分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.共150分.考试用时120分钟.第Ⅰ卷（选择题共50分）一、选择题：(本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.)1.已知,,a b c R ∈,则下列选项正确的是（）A.22a b am bm >⇒> B.a ba b c c>⇒> C.11,0a b ab a b >>⇒< D.2211,0a b ab a b>>⇒<2．已知集合M ＝{x |x 2＜4}，N ＝{x |x 2－2x －3＜0}，则集合M ∩N 等于( )A ．{x |x ＜－2}B ．{x |x ＞3}C ．{x |－1＜x ＜2}D ．{x |2＜x ＜3}3．已知△ABC 中，AB ＝3，AC ＝1且B ＝30°，则△ABC 的面积等于( )A.32 B.34 C.32或 3 D.34或324．设S n 是公差为d (d ≠0)的无穷等差数列{a n }的前n 项和，则下列叙述错误．．的是( ) A ．若d ＜0，则数列{S n }有最大项 B ．若数列{S n }有最大项，则d ＜0C ．若数列{S n }是递增数列，则对任意的n ∈N*，均有S n ＞0D ．若对任意的n ∈N*，均有S n ＞0，则数列{S n }是递增数列5．在不等边△ABC 中，a 为最大边，如果a 2＜b 2＋c 2，则A 的取值范围是( )A ．90°＜A ＜180°B ．45°＜A ＜90°C ．60°＜A ＜90°D ．0°＜A ＜90°6．数列{a n }满足a 1＝1，a 2＝2,2a n ＋1＝a n ＋a n ＋2，若b n ＝1a n a n ＋1，则数列{b n }的前5项和等于( ) A ．1 B.56 C.16D.1307.已知点（3 ， 1）和点（－4 ， 6）在直线 3x –2y + m = 0 的两侧，则（）A ．m ＜－7或m ＞24B ．－7＜m ＜24C ．m ＝－7或m ＝24D ．－7≤m ≤ 248．计算机将信息转换成二进制数进行处理，二进制即“逢二进一”．如2(1101)表示二进制的数，将它转换成十进制的形式是32102(1101)1212021213=⨯+⨯+⨯+⨯=，那么将二进制数16111位转换成十进制数的形式是（）A ．1722-B ．1621-C ．1622-D ．15212-9．若数列{a n }满足),3(,2,1*2121N n n a a a a a n n n ∈≥===--，则17a ＝( ) A ．1B ．2 C.12D ．2－98710. 设z y x >>，N n ∈，且z x nz y y x -≥-+-11恒成立，则n 的最大值为（） A ．2B ．3C ．4D ．5第Ⅱ卷（选择题共100分）二、填空题（本大题目共5题，每小题5分，共25分）11．等比数列{a n }中，a 2＝2，a 5＝16，那么数列{a n }的前6项和S 6＝________. 12．若实数x ，y 满足⎩⎪⎨⎪⎧x ＋y －2≥0x ≤4y ≤5，则s ＝y －x 的最小值为________．13．在ABC ∆中，045,B c b ===A ＝_____________; 14．将给定的25个数排成如图所示的数表，若每行5个数按从左至右的顺序构成等差数列，每列的5个数按从上至下的顺序也构成等差数列，且表正中间的一个数33a =1，则表中所以数的和为11a 12a 13a 14a 15a21a 22a 23a 24a 25a31a 32a 33a 34a 35a 41a 42a 43a 44a 45a51a 52a 53a 54a 55a15.已知下列函数， ①|1|xx y += ； ②1)x ,0(2log log 2≠>+=且x x y x ；③24-+=xx y ； ④1222++=x x y ；⑤xx y -+=33 ； ⑥24-+=xx y ；其中最小值为2的函数是（填入所有正确命题的序号）三、解答题(本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤.) 16．（本题满分12分）在△ABC 中，角A 、B 、C 所对的三边长分别为a 、b 、c ，若a 3＋b 3－c 3a ＋b －c ＝c 2，a ＝43，B ＝45°，求△ABC的面积．17．（本题满分12分）已知不等式x 2－2x －3＜0的解集为A ，不等式x 2＋4x －5＜0的解集为B . (1)求A ∪B ；(2)若不等式x 2＋ax ＋b ＜0的解集是A ∪B ，求ax 2＋x ＋b ＜0的解集．18.（满分12分）已知1)1()(2++-=x aa x x f ，（I ）当21=a 时，解不等式0)(≤x f ；（II ）若0>a ，解关于x 的不等式0)(≤x f19．（本小题满分12分）如图，在斜度一定的山坡上的一点A 测得山顶上一建筑物顶端C 对于山坡的斜度为15︒，向山顶前进100m 后，又从点B 测得斜度为45︒，假设建筑物高50m ，设山坡对于地平面的斜度θ，求cos θ的值.20．（本题满分13分）已知等比数列{a n }中，a 1＝64，公比q ≠1，a 2，a 3，a 4又分别是某等差数列的第7项，第3项，第1项．(1)求a n ；(2)设b n ＝log 2a n ，求数列{|b n |}的前n 项和T n .21．（本小题满分14分）设数列{n a }的前n 项和S n ，且24,111+==+n n a S a (n ∈N +).（1）设n n n a a b 21-=+，求证：{n b }是等比数列；（2）设n nn a c 2=，求证：{n c }是等差数列；（3）求S n .2014年春季高中数学必修5模块测试卷参考答案一、选择题二、填空题11. 63 12. －6 13. 15o 或75o 14.25 15. ①③④⑤三、16.解：因为a 3＋b 3－c 3a ＋b －c＝c 2，所以变形得(a ＋b )(a 2＋b 2－c 2－ab )＝0. 因为a ＋b ≠0，所以a 2＋b 2－c 2－ab ＝0，即a 2＋b 2－c 2＝ab .根据余弦定理的推论得cos C ＝a 2＋b 2－c 22ab ＝ab 2ab ＝12.又因为0°<C <180°，所以C ＝60°. ……………………………………6分因为B ＝45°，A ＋B ＋C ＝180°，所以A ＝180°－(60°＋45°)＝75°.根据正弦定理得a sin A ＝bsin B，所以b ＝a sin Bsin A ＝43×226＋24＝12－4 3.……………10分根据三角形的面积公式得S △ABC ＝12ab sin C ＝12×43×(12－43)×32＝36－12 3.…………………12分17．解：(1)解不等式x 2－2x －3＜0，得A ＝{x |－1＜x ＜3} 解不等式x 2＋4x －5＜0，得B ＝{x |－5＜x ＜1}，∴A ∪B ＝{x |－5＜x ＜3}．……………………6分 (2)由x 2＋ax ＋b ＜0的解集是(－5,3)， ∴⎩⎪⎨⎪⎧ 25－5a ＋b ＝09＋3a ＋b ＝0，解得⎩⎪⎨⎪⎧a ＝2b ＝－15， ∴2x 2＋x －15＜0，求得解集为{x |－3＜x ＜52}．………………………12分18.解：（I ）当21=a 时，有不等式25()102f x x x =-+≤， ∴0)2)(21(≤--x x ， ∴不等式的解集为：}221|{≤≤∈x x x …………5分（II ）∵不等式0))(1()(≤--=a x ax x f …………………6分当10<<a 时，有a a >1，∴不等式的解集为}1|{a x a x ≤≤；……………8分当1>a 时，有a a <1，∴不等式的解集为}1|{a x ax ≤≤；……10分当1=a 时，不等式的解为{1}.………12分 19.解：在△ABC 中，∠BAC ＝15°∠CBA ＝180°-45°＝135°，AB ＝100 m∴ ∠ACB ＝30° 由正弦定理，得︒=︒15sin 30sin 100BC∴ BC ＝︒︒30sin 15sin 100………………………6分又在△BCD 中，∠CBD ＝45°，∠CDB ＝90°＋θ， CD ＝50 m∴)90sin(45sin 50θ+︒=︒BC∴ )90sin(30sin 15sin 10045sin 50θ+︒︒︒=︒ 解得cos θ＝3-1 ……………………………12分20．(1)依题意有a 2－a 4＝3(a 3－a 4)，即2a 1q 3－3a 1q 2＋a 1q ＝0， ∴2q 2－3q ＋1＝0.∵q ≠1，∴q ＝12，故a n ＝64×(12)n －1.…………………6分(2)b n ＝log 2[64×(12)n －1]＝7－n .∴|bn |＝⎩⎪⎨⎪⎧7－n nn －7 n，当n ≤7时，T n ＝n (13－n)2；………………9分当n >7时，T n ＝T 7＋(n －7)(n －6)2＝21＋(n －7)(n －6)2. …12分故T n＝⎩⎨⎧n (13－n)2 n(n －7)(n －6)2＋21 n…………………………13分21.解：（1）由S n+1=4a n +2，得a n+1=S n+1-S n =（4a n +2）-（4a n-1+2）（n≥2） ∴a n+1-2a n =2a n -4a n-1=2（a n -2a n-1）故数列{a n+1-2a n } 是以a 2-2a 1为首项，2为公比的等比数列，又a 1=1，a 1+a 2=S 2=4a 1+2，所以a 2=5，∴b n =a n+1-2a n =3·2n-1；即b n 是以3为首项2为公比的等比数列 ………5分（2）将a n+1-2a n=3·2n-1两边同除以2n+1，则，即故{c n}是以为首项，为公差的等差数列；……………10分（3）由（2）知，得a n=（3n-1）·2n-2又S n=4a n-1+2，则S n=4(3n-4)·2n-3+2=(3n-4)·2n-1+2.…………………14分命题人：罗田一中杨德斌审题人：黄冈中学袁晓幼。

高中数学必修5第一二章综合测试

高中数学必修5第一二章综合测试班级：学号：姓名：成绩：一、选择题(本大题共12小题，每小题5分，共60分)1．△ABC 的内角A,B,C 的对边分别为a,b,c ，若c=2,b=6,B=120o，则a 等于（）A． B ．2 CD2．在△ABC 中，已知b=2，B=45°，如果用正弦定理解三角形有两解，则边长a 的取值范围是（）A ．222<<aB ．42<<aC ．22<<aD ．222<<a3．在△ABC 中，角A,B,C 的对边分别为a,b,c,若(a 2+c 2-b 2)tanB=3ac,则角B 的值为（）A.6πB.3πC.6π或56π D.3π或23π4．设等比数列{a n }的前n 项和为S n ，若S 10∶S 5＝1∶2，则S 15∶S 5等于( )A ．3∶4B ．2∶3C ．1∶2D ．1∶35．已知{a n }为等差数列，a 1＋a 3＋a 5＝105，a 2＋a 4＋a 6＝99，以S n 表示{a n }的前n 项和，则使得S n 达到最大值的n 是( )A ．21B ．20C ．19D ．18 6．已知{a n }是等比数列，a 2=2, a 5=41，则a 1a 2+ a 2a 3+…+ a n a n+1=（）A ．16(n --41)B ．16(n --21)C ．332(n --41) D ．332(n --21)7．已知等差数列{a n }中，|a 3|=|a 9|，公差d<0，则使前n 项和S n 取最大值的正整数n 是( )A 、4或5B 、5或6C 、6或7D 、8或98．已知D 、C 、B 三点在地面同一直线上，DC=a ，从C 、D 两点测得A 的点仰角分别为α、β（α＞β）则A 点离地面的高AB 等于（）A ．)sin(sin sin βαβα-a B ．)cos(sin sin βαβα-a C ．)sin(cos cos βαβα-a D ．)cos(cos cos βαβα-a9．已知等差数列{a n }的公差d≠0且a 1，a 3，a 9成等比数列，则a 1＋a 3＋a 9a 2＋a 4＋a 10等于( )A.1514 B.1213 C.1316 D.151610．某纯净水厂在净化过程中，每增加一次过滤可减少水中杂质的20%，要使水中杂质减少到原来的5%以下，则至少需过滤的次数为(lg 2≈0.301 0)( ) A ．5 B ．10 C ．14 D ．1511．在数列{a n }中，a 1＝2，a n ＋1＝a n ＋ln ⎝⎛⎭⎫1＋1n ，则a n 等于( )A ．2＋ln nB ．2＋(n －1)ln nC ．2＋nln nD ．1＋n ＋ln n 12．已知数列1，12，21，13，22，31，14，23，32，41，…，则56是数列中的( )二、填空题(本大题共4小题，每小题4分，共16分)13．在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若(3b – c)cosA=acosC ，则cosA=14．若AB=2, AC=BC ，则S △ABC 的最大值15．已知函数f(x)=2x ,等差数列{a x }的公差为2.若f(a 2+a 4+a 6+a 8+a 10)=4,则log 2[f(a 1)f(a 2)f(a 3)…f(a 10)]= 16．数列{a n }中，S n 是其前n 项和，若a 1＝1，a n ＋1＝13S n (n≥1)，则a n ＝____________.三、解答题(本大题共6小题，共74分)17．(12分) 已知△ABC 的内角C B A ,,所对的边分别为,,,c b a 且53cos ,2==B a .(1) 若4=b , 求A sin 的值; (2) 若△ABC 的面积,4=∆ABC S 求c b ,的值.18．(12分) 已知数列{log 2(a n －1)} (n ∈N *)为等差数列，且a 1＝3，a 3＝9. (1)求数列{a n }的通项公式；(2)证明：1a 2－a 1＋1a 3－a 2＋…＋1a n ＋1－a n <1.19．(12分) 求函数2474sin cos 4cos 4cos y x x x x =-+-的最大值与最小值20．(12分)某市2009年共有1万辆燃油型公交车．有关部门计划于2010年投入128辆电力型公交车，随后电力型公交车每年的投入比上一年增加50%，试问： (1)该市在2016年应该投入多少辆电力型公交车？(2)到哪一年底，电力型公交车的数量开始超过该市公交车总量的13？21．(12分) 在数列{a n }中，已知a 1＝－1，且a n ＋1＝2a n ＋3n －4 (n ∈N *)． (1)求证：数列{a n ＋1－a n ＋3}是等比数列； (2)求数列{a n }的通项公式；(3)求和：S n ＝|a 1|＋|a 2|＋|a 3|＋…＋|a n | (n ∈N *)．22．(14分) 设数列{a n }的首项a 1＝1，前n 项和S n 满足关系式：3tS n －(2t ＋3)S n －1＝3t (t >0，n ＝2,3,4，…)．(1)求证：数列{a n }是等比数列；(2)设数列{a n }的公比为f (t )，作数列{b n }，使b 1＝1，b n ＝f ⎝⎛⎭⎫1b n －1 (n ＝2,3,4，…)．求数列{b n }的通项b n ； (3)求和：b 1b 2－b 2b 3＋b 3b 4－b 4b 5＋…＋b 2n －1b 2n －b 2n b 2n ＋1.。

【数学】第一章《解三角形》测试1(苏教版必修5)

第1章解三角形§1.1正弦定理、余弦定理重难点：理解正、余弦定理的证明，并能解决一些简单的三角形度量问题．考纲要求：①掌握正弦定理、余弦定理，并能解决一些简单的三角形度量问题．经典例题：半径为R 的圆外接于△ABC ，且2R(sin 2A-sin 2C)＝(3a-b)sinB ．(1)求角C ；(2)求△ABC 面积的最大值．当堂练习：1．在△ABC 中，已知a=5 2 , c=10, A=30°, 则∠B= ( )(A) 105° (B) 60° (C) 15° (D) 105°或15° 2．在△ABC 中，若a=2, b=2 2 , c= 6 + 2 ,则∠A 的度数是 ( )(A) 30° (B) 45° (C) 60° (D) 75° 3．在△ABC 中，已知三边a 、b 、c 满足(a+b+c)·(a+b －c)=3ab, 则∠C=( )(A) 15° (B) 30° (C) 45° (D) 60° 4．边长为5、7、8的三角形的最大角与最小角之和为 ( )(A) 90° (B) 120° (C) 135° (D) 150° 5．在△ABC 中，∠A=60°, a= 6 , b=4, 那么满足条件的△ABC ( )(A) 有一个解 (B) 有两个解 (C) 无解 (D)不能确定 6．在平行四边形ABCD 中，AC= 3 BD, 那么锐角A 的最大值为 ( )(A) 30° (B) 45° (C) 60° (D) 75° 7. 在△ABC 中，若cos2a A =cos2b B =cos2c C ，则△ABC 的形状是 ( )(A) 等腰三角形 (B) 等边三角形 (C) 直角三角形 (D) 等腰直角三角形 8．如果把直角三角形的三边都增加同样的长度，则这个新的三角形的形状为（）(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定 9．在△ABC 中，若a=50，b=25 6 , A=45°则B= .10．若平行四边形两条邻边的长度分别是4 6 cm 和4 3 cm ，它们的夹角是45°，则这个平行四边形的两条对角线的长度分别为 .11.在等腰三角形 ABC 中，已知sinA ∶sinB=1∶2，底边BC=10，则△ABC 的周长是。

高中数学苏教版必修5 第1章解三角形单元测试

（时间：120分钟，满分：160分）一、填空题（本大题共14小题，每小题5分，共70分．请把答案填在题中横线上） 1．在△ABC 中，a ＝1，A ＝30°，B ＝60°，则b 等于________．解析：由正弦定理知a sin A ＝b sin B ＝2R ，故1sin 30°＝bsin 60°，解之得b ＝ 3.答案： 32．在三角形中，60°角的两边长分别是16和55，则其对边a 的长是________．解析：由余弦定理得a 2＝162＋552－2×16×55cos 60°＝492，∴a ＝49. 答案：493．在△ABC 中，若a cos A 2＝b cos B 2＝ccos C 2，则△ABC 的形状是________三角形．解析：由正弦定理得sin A cos A 2＝sin B cos B 2＝sin Ccos C 2，即sin A 2＝sin B 2＝sin C 2.由于A 2，C 2均为锐角，故有A 2＝B 2＝C 2，所以△ABC 为等边三角形．答案：等边4．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a 2＋c 2－ac ＝b 2，则角B 的大小为________．解析：∵a 2＋c 2－ac ＝b 2， ∴a 2＋c 2－b 2＝ac ，∴cos B ＝a 2＋c 2－b 22ac ＝12.∴B ＝60°. 答案：60°5．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若1＋tan A tan B ＝2cb，则角A 的大小为________．解析：∵1＋tan A tan B ＝2c b ，∴1＋sin A cos B cos A sin B ＝2sin Csin B，即得sin （A ＋B ）cos A sin B ＝2sin C sin B ，∴1cos A＝2，即得cos A ＝12，解得A ＝π3.答案：π36．△ABC 的三内角A 、B 、C 的对边边长分别为a 、b 、c .若a ＝52b ，A ＝2B ，则cos B＝________．解析：由正弦定理，得sin A a ＝sin Bb，又∵a ＝52b ，A ＝2B ，∴sin 2B 52b ＝sin Bb ，b ≠0，sin B ≠0，∴2cos B 52＝1，∴cos B ＝54.答案：547．在△ABC 中，a ＝1，b ＝2，则角A 的取值范围是________．解析：由a sin A ＝b sin B ，可得sin A ＝12sin B ，又因为0＜sin B ≤1，所以0＜sin A ≤12.所以0°＜A ≤30°或150°≤A ＜180°. 又因为a ＜b ，所以只有0°＜A ≤30°. 答案：0°＜A ≤30°8．在锐角△ABC 中，BC ＝1，B ＝2A ，则ACcos A的值等于__________，AC 的取值范围为________．解析：如图，AC sin B ＝1sin A.又B ＝2A ，∴1sin A ＝AC sin 2A ＝AC 2sin A cos A . ∴AC cos A＝2， ∵在锐角△ABC 中，B ＝2A ，∴0<A <π4.又C ＝π－A －B ＝π－3A ，∴0<π－3A <π2，即π6〈A <π3.∴π6<A <π4，22<cos A <32. ∴AC ＝2cos A ∈(2，3)．答案：2 (2，3)9．△ABC 中，已知a ，b ，c 分别为角A 、B 、C 所对的边，S 为△ABC 的面积．若向量p ＝(4，a 2＋b 2－c 2)，q ＝(3，S ）满足p ∥q ，则C ＝________．解析：由p ∥q ，得3(a 2＋b 2－c 2)＝4S ＝2ab sin C ，即a 2＋b 2－c 22ab ＝33sin C ，由余弦定理的变式，得cos C ＝33sin C ，即tan C ＝3，因为0＜C ＜π，所以C ＝π3.故填π3. 答案：π310．在△ABC 中，三个角A ，B ，C 的对边边长分别为a ＝3，b ＝4，c ＝6，则bc cos A ＋ca cos B ＋ab cos C 的值为________．解析：由余弦定理知：bc cos A ＝12(b 2＋c 2－a 2)①ca cos B ＝12(c 2＋a 2－b 2)②ab cos C ＝12(a 2＋b 2－c 2)③①＋②＋③得：bc cos A ＋ca cos B ＋ab cos C ＝12(a 2＋b 2＋c 2)＝12(32＋42＋62)＝612. 答案：61211．在△ABC 中，若AB ＝2，AC ＝2BC ，则S △ABC 的最大值是________．解析：设BC ＝x ，则AC ＝2x ，根据面积公式，得S △ABC ＝12AB ·BC sin B ＝12×2x 1－cos 2B ，根据余弦定理，得cos B ＝AB 2＋BC 2－AC 22AB ·BC＝4＋x 2－（2x ）24x ＝4－x 24x ，将其代入上式，得S △ABC ＝x 1－（4－x 24x ）2＝128－（x 2－12）216，由三角形三边关系有⎩⎨⎧2x ＋x ＞2，x ＋2＞2x ，解得22－2＜x ＜22＋2，故当x ＝23时，S △ABC 取得最大值2 2. 答案：2 212．设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，且a ＝1，b ＝2，cos C ＝14，则sin B ＝________．解析：法一：由余弦定理c 2＝a 2＋b 2－2ab cos C得c 2＝1＋4－2×1×2×14＝4，∴c ＝2，故△ABC 为等腰三角形．如图所示，过点A 作BC 的高线AE ，在Rt △ABE 中，AE ＝AB 2－BE 2＝ 22－（12）2＝152，∴sin B ＝AE AB ＝1522＝154.法二：由余弦定理c 2＝a 2＋b 2－2ab cos C 得c 2＝1＋4－2×1×2×14＝4，∴c ＝2.∵cos C ＝14，∴sin C ＝ 1－cos 2C ＝154.又由正弦定理c sin C ＝b sin B 得sin B ＝b sin C c ＝sin C ＝154.答案：15413．已知△ABC 的三边a ，b ，c 满足b 2＝ac ，P ＝sin B ＋cos B ，则P 的取值范围为________．解析：由余弦定理知：b 2＝a 2＋c 2－2ac cos B . 又b 2＝ac ，∴ac ＝a 2＋c 2－2ac cos B ， ∴(1＋2cos B )ac ＝a 2＋c 2， ∵(a －c )2≥0，故a 2＋c 2≥2ac ，即（1＋2cos B )ac ≥2ac ，∴cos B ≥12，∴0＜B ≤π3，∴P ＝sin B ＋cos B ＝2sin(B ＋π4)，∵0＜B ≤π3，∴π4＜π4＋B ≤π3＋π4， ∴sin π4＜sin(B ＋π4)≤1，∴22＜sin(B ＋π4)≤1， ∴P 的取值范围为（1， 2 ．答案：1， 2 14．如图，在斜度一定的山坡上一点A 测得山顶上一建筑物顶端C 对于山坡的斜度为α，向山顶前进a m 到达点B ，从B 点测得斜度为β，设建筑物的高为h m ，山坡对于地平面的倾斜角为θ，则cos θ＝________．解析：在△ABC 中，AB ＝a ，∠CAB ＝α，∠ACB ＝β－α，由正弦定理，得AB sin （β－α）＝BCsin α，∴BC ＝a sin αsin （β－α）.在△BDC 中，由正弦定理得 CD sin β＝BCsin ∠BDC， ∴sin ∠BDC ＝BC sin βCD ＝a sin αsin βh sin （β－α）.又∠BDC ＝90°＋θ，∴sin ∠BDC ＝sin(90°＋θ)＝cos θ.∴cos θ＝a sin αsin βh sin （β－α）.答案：a sin αsin βh sin （β－α）二、解答题（本大题共6小题，共90分．解答时应写出文字说明、证明过程或演算步骤）15．（本小题满分14分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且A ＝60°，sin B ∶sin C ＝2∶3.(1）求bc的值；(2）若AB 边上的高为33，求a 的值．解：(1）在△ABC 中，由正弦定理b sin B ＝csin C，得b ∶c ＝sin B ∶sin C .又∵sin B ∶sin C ＝2∶3，∴b ∶c ＝2∶3，即b c ＝23.(2)∵AB 边上的高为33，A ＝60°，由面积相等可求得b ＝6，又b c ＝23，∴c ＝9. 又根据余弦定理a 2＝b 2＋c 2－2bc cos A ，将b ＝6，c ＝9，A ＝60°代入上式，得a 2＝63， ∴a ＝37. 16．（本小题满分14分）在△ABC 中，a ＝3，b ＝26，∠B ＝2∠A ， (1）求cos A 的值； (2）求c 的值．解：(1）因为a ＝3，b ＝26，∠B ＝2∠A ，所以在△ABC 中，由正弦定理得3sin A ＝26sin 2A.所以2sin A cos A sin A ＝263.故cos A ＝63.(2）由（1）知cos A ＝63，所以sin A ＝1－cos 2A ＝33.又因为∠B ＝2∠A ，所以cos B ＝2cos 2A －1＝13.所以sin B ＝1－cos 2B ＝223.在△ABC 中，sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝539.所以c ＝a sin Csin A＝5.17．（本小题满分14分）在△ABC 中，a ＝4，A ＝60°，当b 满足下列条件时，解三角形：(1)b ＝433；(2)b ＝22＋263；(3)b ＝833；(4)b ＝8.解：(1)∵a ＞b ，∴B 为锐角，由正弦定理，得sin B ＝b a sin A ＝12，∴B ＝30°，C ＝90°，由正弦定理，得c ＝a sin A ·sin C ＝833.(2）由正弦定理，得sin B ＝b a ·sin A ＝22＋2634×32＝6＋24，当B 为锐角时，B ＝75°，C ＝45°.由正弦定理，得c ＝a sin A ·sin C ＝463，当B 为钝角时，B ＝105°，C ＝15°，由正弦定理，得c ＝a sin A ·sin C ＝22－263.(3）法一：由正弦定理，得sin B ＝ba·sin A ＝1，∴B ＝90°，C ＝30°，由正弦定理，得c ＝a sin A ·sin C ＝433.法二：由余弦定理a 2＝b 2＋c 2－2bc cos A ，得16＝643＋c 2－833c ，即c 2－833c ＋163＝0.∴(c －433)2＝0.∴c ＝433，由正弦定理，得sin C ＝c a ·sin A ＝12.∵a ＞c ，∴C 为锐角，∴C ＝30°，B ＝90°.(4）由正弦定理，得sin B ＝ba·sin A ＝3＞1，三角形无解．18. （本小题满分16分）如图，△ACD 是等边三角形，△ABC 是等腰直角三角形，∠ACB ＝90°，BD 交AC 于点E ，AB ＝2.求：(1)cos ∠CBE 的值； (2)AE 的长．解：(1）因为∠BCD ＝90°＋60°＝150°，CB ＝AC ＝CD ，所以∠CBE ＝15°.所以cos ∠CBE ＝cos(45°－30°)＝6＋24.(2）在△ABE 中，AB ＝2，由正弦定理知AE sin 30°＝2sin 105°，故AE ＝2sin 30°cos 15°＝6－ 2.19．（本小题满分16分）如图所示的四边形ABCD 中，已知AD ⊥CD ，AD ＝10，AB ＝14，∠BAD ＝60°，∠BCD ＝135°.(1）求sin ∠ADB ； (2）求BC 的长．解：(1）不妨设∠ADB ＝x ，则∠ABD ＝180°－∠BAD －∠ADB ＝120°－x ，由正弦定理得，AB sin ∠ADB ＝ADsin ∠ABD，即14sin x ＝10sin （120°－x ），∴7sin(120°－x )＝5sin x ，整理可得，73cos x ＝3sin x ，结合sin 2 x ＋cos 2 x ＝1及x ∈(0°，90°)．可解得cos x ＝3926，sin x ＝71326.∴sin ∠ADB ＝71326.(2）在△ABD 中利用正弦定理得， AB sin ∠ADB ＝BDsin ∠BAD，即1471326＝BD 32，解得BD ＝239. 在△BDC 中利用正弦定理得， BC sin ∠BDC ＝BDsin ∠BCD，即BC sin （90°－∠ADB ）＝239sin 135°， ∴BC ＝239×cos ∠ADBsin 135°＝239×392622＝3 2.20．（本小题满分16分）在△ABC 中，c ＝2＋6，C ＝30°，求a ＋b 的取值范围．解：由正弦定理有c sin C ＝a sin A ＝bsin B ＝a ＋b sin A ＋sin B.又c ＝2＋6，C ＝30°，∴a ＋b sin A ＋sin B ＝2＋6sin 30°，A ＋B ＝180°－30°＝150°. ∴a ＋b ＝2(2＋6)[sin A ＋sin(150°－A )] ＝2(2＋6)×2sin 75°cos(75°－A )＝2(2＋6)×2×6＋24cos(75°－A )＝(2＋6)2cos(75°－A )．①当A ＝75°时，(a ＋b )max ＝8＋4 3.②∵A ＋B ＝150°，∴0°＜A ＜150°，－150°＜－A ＜0°. ∴cos(75°－A )∈(cos 75°，1．又（2＋6)2cos 75°＝(2＋6)2×6－24＝2＋6，∴2＋6＜a ＋b ≤8＋4 3.综上，a ＋b ∈2＋6，8＋43．。

高中数学必修5《不等式》单元测试题

高中数学必修5《不等式》单元测试题一．选择题：（每小题5分）1. 已知a,b,c ∈R,下列命题中正确的是A 、22bc ac b a >⇒>B 、b a bc ac >⇒>22C 、ba b a 1133<⇒> D 、||22b a b a >⇒> 2.若b ＜0＜a,d ＜c ＜0则下列各不等式中必成立的是（）A 、ac ＞bdB 、db c a < C 、a+c ＞b+d D 、a-c ＞b-d 3.不等式（x-3）（2-x ）＞0的解集是（）A 、{x|x ＜2或x ＞3}B 、{x|2＜x ＜3}C 、{x|x≠2且x≠3}D 、{x|x≠2或x≠3}4.不等式（a-2）x 2+2（a-2）x-4<0对x ∈R 成立，则a 的取值范围是（）A 、]2,(--∞B 、)2,(--∞C 、]2,2(-D 、)2,2(-5.函数)20(),24(22<<-=x x x y 的最大值是（）A 、0B 、21 C 、2 D 、4 6. 已知+∈R b a ,，且3=+b a ，则b a 22+的最小值是（）A 、8B 、6C 、24D 、627. 设b a <<0，且1=+b a ，在下列四个数中最大的是（）A 、21 B 、b C 、ab2 D 、22b a + 8.不等式2x+y+1<0表示的平面区域在直线2x+y+1=0（）A 、右上方B 、右下方C 、左上方D 、右下方9. 目标函数y x z +=2，变量y x ,满足⎪⎩⎪⎨⎧≥<+≤+-12553034x y x y x ，则有（）A 、3,12min max ==z zB 、,12max =z z 无最小值C 、z z ,3min =无最大值D 、z 既无最大值，也无最小值10.有甲、乙两个粮食经销商每次在同一粮食生产地以相同的价格购进粮食，他们共购进粮食两次，各次的粮食价格不同，甲每次购粮10000千克，乙每次购粮食10000元，在两次统计中，购粮的平均价格较低的是（）A 、甲B 、乙C 、一样低D 、不确定二．填空题：（每小题5分）11. 若角α，β满足－2π＜α＜β＜2π，则2α－β的取值范围是。

高中数学必修五第一章《解三角形》单元测试卷及答案

高中数学必修五第一章《解三角形》单元测试卷及答案（2套）单元测试题一一、选择题（本大题共12个小题，每小题5分，共60分，每小题有4个选项，其中有且仅有一个是正确的，把正确的选项填在答题卡中） 1．在ABC △中，::1:2:3A B C =，则::a b c 等于（）A ．1:2:3B ．3:2:1C ．2D ．22．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且A >B ，则一定有（） A ．cos A >cos BB ．sin A >sin BC ．tan A >tan BD ．sin A <sin B3．△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ，2sin sin cos a A B b A +，则ba =（）A ．B ．C D4．在△ABC 中，∠A ＝60°，a =，b ＝4．满足条件的△ABC （） A ．无解B ．有一解C ．有两解D ．不能确定5．在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且222a b c =-，则角B 的大小是（） A ．45°B ．60°C ．90°D ．135°6．在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，若22a b -，sin C B =，则A ＝（） A ．30°B ．60°C ．120°D ．150°7．在△ABC 中，∠A ＝60°，b ＝1，△ABC sin aA为（）A B C D ．8．在△ABC 中，sin 2A ≤sin 2B ＋sin 2C －sin B sin C ，则A 的取值范围是（）A ．0,6π⎛⎤ ⎥⎝⎦B ．,6π⎡⎫π⎪⎢⎣⎭C ．0,3π⎛⎤ ⎥⎝⎦D ．,3π⎡⎫π⎪⎢⎣⎭9．在△ABC 中，已知B ＝45°，c =，b =A 的值是（） A ．15°B ．75°C ．105°D ．75°或15°10．在锐角三角形ABC 中，b ＝1，c ＝2，则a 的取值范围是（）A ．1<a <3B ．1a <<C a <D ．不确定11．在△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，且2cos 22A b cc+=，则 △ABC 的形状为（） A ．直角三角形B ．等腰直角三角形C ．等腰或直角三角形D ．等边三角形12．如图所示，在△ABC 中，已知∠A ∶∠B ＝1∶2，角C 的平分线CD 把三角形面积分为3∶2两部分，则cos A 等于（）A ．13B ．12C ．34D ．0二、填空题（本大题共4个小题，每空5分，共20分，把正确答案填在题中横线上） 13．等腰三角形的底边长为6，腰长为12，其外接圆的半径为________． 14．在△ABC 中，若a 2＋b 2<c 2，且3sin C ，则∠C ＝________． 15．在△ABC 中，a ＝3，26b =B ＝2∠A ，则cos A ＝________．16．某人在C 点测得塔AB 在南偏西80°，仰角为45°，沿南偏东40°方向前进10 m 到O ，测得塔A 仰角为30°，则塔高为________．三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(10分)在△ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ．已知()cos cos 3sin cos 0C A A B +=．（1）求角B 的大小；（2）若a ＋c ＝1，求b 的取值范围．18．(12分)在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ．（1）若sin 2cos 6A A π⎛⎫+= ⎪⎝⎭，求A 的值；（2）若1cos 3A =，b ＝3c ，求sin C 的值．19．(12分)在△ABC 中，角A 、B 、C 对应的边分别是a 、b 、c ，已知cos2A －3cos(B ＋C )＝1．（1）求角A 的大小；（2）若△ABC 的面积S =b ＝5，求sin B sin C 的值．20．(12分)在△ABC 中，内角A 、B 、C 的对边分别是a 、b 、c ，且222a b c +=．（1）求C ；（2）设cos cos A B =，()()2cos cos cos A B ααα++，求tan α的值．21．(12分)在△ABC 中，2C A π-=，1sin 3B =．（1）求sin A 的值；（2）设6AC =，求△ABC 的面积．22．(12分)如图，已知扇形AOB ，O 为顶点，圆心角AOB 等于60°，半径为2，在弧AB 上有一动点P ，过P 引平行于OB 的直线和OA 相交于点C ，设∠AOP ＝θ，求△POC 面积的最大值及此时θ的值．答案一、选择题（本大题共12个小题，每小题5分，共60分，每小题有4个选项，其中有且仅有一个是正确的，把正确的选项填在答题卡中） 1．【答案】C 【解析】6A π=，3B π=，2C π=，132::sin :sin :sin 3222a b c A B C ===，故选C ． 2．【答案】B【解析】∵A B >，∴a b >，由正弦定理，得sin sin A B >，故选B ．3．【答案】D【解析】本小题考查内容为正弦定理的应用．∵2sin sin cos a A B b A +=，∴22sin sin sin cos A B B A A +=，sin B A =，∴b =，∴ba．故选D ． 4．【答案】A【解析】4sin 60⨯︒=<a <b sin A ，∴△ABC 不存在．故选A ． 5．【答案】A【解析】∵222a b c =-，∴222a c b +-=，由余弦定理，得222cos 2a c b B ac +-===0°<B <180°，所以B ＝45°．故选A ． 6．【答案】A【解析】由sin C B =及正弦定理，得c =，∴2226a b b -=，即a 2＝7b 2．由余弦定理，2222222cos2b c a A bc +-===，又∵0°<A <180°，∴A ＝30°．故选A ． 7．【答案】B【解析】由1sin 2bc A =c ＝4．由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝13，故a =sin a A ==B ． 8．【答案】C【解析】本题主要考查正余弦定理，∵sin 2A ≤sin 2B ＋sin 2C －sin B sin C ， ∴由正弦定理得：a 2≤b 2＋c 2－bc ，即b 2＋c 2－a 2≥bc ，由余弦定理得：2221cos 222b c a bc A bc bc +-==≥=，∴03A π<≤，故选C ．9．【答案】D 【解析】∵sin sin b cB C =，∴sin sin c B C b ==． ∵0°＜C ＜180°．∴C ＝60°或120°，∴A ＝75°或15°．故选D ． 10．【答案】C【解析】∵b <c ，△ABC 为锐角三角形，∴边c 与边a 所对的角的余弦值大于0，即b 2＋a 2－c 2>0且b 2＋c 2－a 2>0，∴22140140a a ⎧+->⎪⎨+->⎪⎩．∴3<a 2<5，∴35a <<．故选C ． 11．【答案】A【解析】由21cos cos 222A A b c c ++==，整理得cos bA c=．又222cos 2b c a A bc +-=，联立以上两式整理得c 2＝a 2＋b 2，∴C ＝90°．故△ABC 为直角三角形．故选A ． 12．【答案】C【解析】在△ABC 中，设∠ACD ＝∠BCD ＝β，∠CAB ＝α，由∠A ∶∠B ＝1∶2，得∠ABC ＝2α．∵∠A <∠B ，∴AC >BC ，∴S △ACD >S △BCD ，∴S △ACD ∶S △BCD ＝3∶2，∴1sin 3212sin 2AC DC BC DC ββ⋅⋅⋅=⋅⋅⋅，∴32AC BC =．由正弦定理得sin sin AC BC B A =，sin 2sin 2sin cos sin AC BC AC BCααααα=⇒=， ∴133cos 2224AC BC α==⨯=，即3cos 4A =．故选C ．二、填空题（本大题共4个小题，每空5分，共20分，把正确答案填在题中横线上） 13．815【解析】设△ABC 中，AB ＝AC ＝12，BC ＝6，由余弦定理222222121267cos 2212128AB AC BC A AB AC +-+-===⋅⨯⨯．∵()0,A ∈π，∴15sin A =，∴外接圆半径8152sin BC r A == 14．【答案】23π【解析】∵a 2＋b 2<c 2，∴a 2＋b 2－c 2<0，即cos C <0．又3sin C ，∴23C π∠=． 15．6【解析】∵a ＝3，26b =，∠B ＝2∠A ，由正弦定理326sin sin 2A A=， ∴2sin cos 26sin 3A A A =，∴6cos 3A =． 16．【答案】10 m【解析】画出示意图，如图所示，CO ＝10，∠OCD ＝40°，∠BCD ＝80°，∠ACB ＝45°， ∠AOB ＝30°，AB ⊥平面BCO ，令AB ＝x ，则BC ＝x ，3BO x ，在△BCO 中，由余弦定理得)()223100210cos 8040xx x =+-⨯⨯︒+︒，整理得25500x x -=-，解得10x =，5x =-(舍去)，故塔高为10 m ．三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．【答案】（1）3B π=；（2）112b ≤<．【解析】（1）由已知得()cos cos cos 3cos 0A B A B A B -++-=，即有sin sin 3sin cos 0A B A B =．因为sin A ≠0，所以sin 30B B =．又cos B ≠0，所以tan 3B =．又0<B <π，所以3B π=．（2）由余弦定理，有b 2＝a 2＋c 2－2ac cos B ．因为a ＋c ＝1，1cos 2B =，有2211324b a ⎛⎫=-+ ⎪⎝⎭．又0<a <1，于是有2114b ≤<，即有112b ≤<． 18．【答案】（1）3A π=；（2）1sin 3C =．【解析】（1）由题设知sin cos cos sin 2cos 66A A A ππ+=．从而sin 3A A ，所以cos A ≠0，tan A =．因为0<A <π，所以3A π=．（2）由1cos 3A =，b ＝3c 及a 2＝b 2＋c 2－2bc cos A ，得a 2＝b 2－c 2，故△ABC 是直角三角形，且2B π=．所以1sin cos 3C A ==． 19．【答案】（1）3A π=；（2）5sin sin 7B C =．【解析】（1）由cos2A －3cos(B ＋C )＝1，得2cos 2A ＋3cos A －2＝0，即(2cos A －1)(cos A ＋2)＝0，解得1cos 2A =或cos A ＝－2(舍去)．因为0<A <π，所以3A π=．（2）由11sin sin 223S bc A bc π====bc ＝20，又b ＝5，知c ＝4．由余弦定理得a 2＝b 2＋c 2－2bc cos A ＝25＋16－20＝21，故a =．又由正弦定理得222035sin sin sin sin sin 2147b c bc B C A A A a a a =⋅==⨯=．20．【答案】（1）34C π=；（2）tan α＝1或tan α＝4．【解析】（1）因为222a b c +=，由余弦定理有222cos 2a b c C ab +-===34C π=．（2）由题意得()()2sin sin cos cos sin sin cos cos cos A A B B ααααα--，因此()()tan sin cos tan sin cos A A B B αα--=，()2tan sin sin tan sin cos cos sin cos cos A B A B A B A B αα-++=，()2tan sin sin tan sin cos cos A B A B A B αα-++=因为34C π=，4A B π+=，所以()sin A B +=因为cos(A ＋B )＝cos A cos B －sin A sin B ，即sin sin 52A B -=，解得sin sin 5210A B =-=．由①得tan 2α－5tan α＋4＝0，解得tan α＝1或tan α＝4． 21．【答案】（1）sin A ；（2）ABC S =△．【解析】（1）由2C A π-=和A ＋B ＋C ＝π，得22A B π=-，04A π<<． ∴cos2A ＝sinB ，即2112sin 3A -=，∴sin A =．（2）由（1）得cos A sin sin BC AC A B =，∴sin 31sin 3AC ABC B===∵2C A π-=，∴2C A π=+，∴sin sin cos 2C A A π⎛⎫=+== ⎪⎝⎭，∴11sin 22ABC S AC BC C =⋅⋅==△． 22．【答案】当θ＝30°时，S (θ)．【解析】∵CP ∥OB ，∴∠CPO ＝∠POB ＝60°－θ，∠OCP ＝120°．在△OCP 中，由正弦定理，得sin sin OP CP OCP θ=∠，即2sin120sin CPθ=︒，∴CP θ．又()2sin 60sin120CO θ=︒-︒，∴()60OC θ=︒-．故△POC 的面积是()1sin1202S CP CO θ=⋅⋅︒()()160sin si 2n 60θθθθ=︒-︒-()1sin sin 21cos 2602θθθθ⎫⎤=-︒=-⎪-⎥⎪⎝⎦⎭，()0,60θ∈︒︒， ∴当θ＝30°时，S (θ)单元测试题二一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的）1．在ABC △中，若90C =︒，6a =，30B =︒，则c b -等于（）A ．1B ．1-C ．D ．-2．在ABC △中，3AB =，2AC =，BC =BA ·AC 等于（）A ．32-B ．23-C ．23D ．323．在△ABC 中，已知a =，b =A ＝30°，则c 等于（）A ．BC ．D ．以上都不对4．根据下列情况，判断三角形解的情况，其中正确的是（） A ．a ＝8，b ＝16，A ＝30°，有两解 B ．b ＝18，c ＝20，B ＝60°，有一解 C ．a ＝5，c ＝2，A ＝90°，无解 D ．a ＝30，b ＝25，A ＝150°，有一解5．△ABC 的两边长分别为2,3，其夹角的余弦值为13，则其外接圆的半径为（）A B C D ．6．在△ABC 中，2cos 22A b cc+⋅=(a 、b 、c 分别为角A 、B 、C 的对边)，则△ABC 的形状为（） A ．直角三角形 B ．等腰三角形或直角三角形 C ．等腰直角三角形D ．正三角形7．已知△ABC 中，A 、B 、C 的对边分别为a 、b 、c ．若a c =A ＝75°，则b 等于（）A ．2B -C ．4-D ．4+8．在△ABC 中，已知b 2－bc －2c 2＝0，a =7cos 8A =，则△ABC 的面积S 为（）A B C D ．9．在△ABC 中，AB ＝7，AC ＝6，M 是BC 的中点，AM ＝4，则BC 等于（）A B C D10．若sin cos cos A B Ca b c==，则△ABC 是（） A ．等边三角形 B ．有一内角是30°的直角三角形 C ．等腰直角三角形D ．有一内角是30°的等腰三角形11．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若()222tan 3a c b B ac +-=，则角B 的值为（） A ．6π B ．3π C ．6π或56π D ．3π或23π12．△ABC 中，3A π=，BC ＝3，则△ABC 的周长为（） A ．43sin 33B π⎛⎫++ ⎪⎝⎭B ．43sin 36B π⎛⎫++ ⎪⎝⎭C ．6sin 33B π⎛⎫++ ⎪⎝⎭D ．6sin 36B π⎛⎫++ ⎪⎝⎭二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．在△ABC 中，2sin sin sin a b cA B C--=________． 14．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，若2223a c b ac +-=，则角B 的值为________．15．已知a ，b ，c 分别是△ABC 的三个内角A ，B ，C 所对的边．若a ＝1，3b =， A ＋C ＝2B ，则sin C ＝________．16．钝角三角形的三边为a ，a ＋1，a ＋2，其最大角不超过120°，则a 的取值范围是________．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．(10分)如图所示，我艇在A 处发现一走私船在方位角45°且距离为12海里的B 处正以每小时10海里的速度向方位角105°的方向逃窜，我艇立即以14海里/小时的速度追击，求我艇追上走私船所需要的时间．18．(12分)在△ABC 中，角A 、B 、C 所对的边长分别是a 、b 、c ，且4cos 5A =．（1）求2sin cos22B CA ++的值；（2）若b ＝2，△ABC 的面积S ＝3，求a ．19．(12分)如图所示，△ACD 是等边三角形，△ABC 是等腰直角三角形，∠ACB ＝90°，BD 交AC 于E ，AB ＝2．（1）求cos ∠CBE 的值；（2）求AE ．20．(12分)已知△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c ，且a ＝2，3cos 5B =．（1）若b ＝4，求sin A 的值；（2）若△ABC 的面积S △ABC ＝4，求b ，c 的值．21．(12分)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且2a sin A ＝(2b ＋c )sin B ＋(2c ＋b )sin C ．（1）求A 的大小；（2）若sin B ＋sin C ＝1，试判断△ABC 的形状．22．(12分)已知△ABC 的角A 、B 、C 所对的边分别是a 、b 、c ，设向量(),a b m =， ()sin ,sin B A =n ，()2,2b a --p =．（1）若m ∥n ，求证：△ABC 为等腰三角形；（2）若m ⊥p ，边长c ＝2，角3C π=，求△ABC 的面积．答案一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中只有一个是符合题目要求的） 1．【答案】C【解析】tan 30ba=︒，tan30b a =︒=2c b ==，c b -= 故选C ． 2．【答案】A【解析】由余弦定理得22294101cos 2124AB AC BC A AB AC +-+-===⋅．∴13cos 3242AB AC AB AC A ⋅=⋅⋅=⨯⨯=．∴32BA AC AB AC ⋅=-⋅=-．故选A ．3．【答案】C【解析】∵a 2＝b 2＋c 2－2bc cos A ，∴2515c c =+-．化简得：2100c -+=，即(0c c -=，∴c =c = 故选C ． 4．【答案】D 【解析】A 中，因sin sin a b A B =，所以16sin30sin 18B ⨯︒==，∴90B =︒，即只有一解；B 中，20sin 60sin 18C ︒==c b >，∴C B >，故有两解； C 中，∵A ＝90°，a ＝5，c ＝2，∴b = 故A 、B 、C 都不正确．故选D ． 5．【答案】C【解析】设另一条边为x ，则2221232233x =+-⨯⨯⨯，∴29x =，∴3x =．设1cos 3θ=，则sin θ=．∴32sinR θ==，R =C ． 6．【答案】A【解析】由2cos cos 22A b c b A c c+⋅=⇒⋅=，又222cos 2b c a A bc +-⋅=， ∴b 2＋c 2－a 2＝2b 2⇒a 2＋b 2＝c 2，故选A ． 7．【答案】A【解析】()sin sin 75sin 3045A =︒=︒+︒，由a ＝c 知，C ＝75°，B ＝30°．1sin 2B =．由正弦定理：4sin sin b aB A===．∴b ＝4sin B ＝2．故选A ．8．【答案】A【解析】由b 2－bc －2c 2＝0可得(b ＋c )(b －2c )＝0． ∴b ＝2c ，在△ABC 中，a 2＝b 2＋c 2－2bc cos A ，即22276448c c c =+-⋅．∴c ＝2，从而b ＝4．∴11sin 4222ABCS bc A ==⨯⨯△A ． 9．【答案】B【解析】设BC ＝a ，则2aBM MC ==．在△ABM 中，AB 2＝BM 2＋AM 2－2BM ·AM ·cos ∠AMB ，即22217424cos 42aa AMB =+-⨯⨯⋅∠ ①在△ACM 中，AC 2＝AM 2＋CM 2－2AM ·CM ·cos ∠AMC即22216424cos 42aa AMB =++⨯⨯⋅∠ ②①＋②得：22222176442a +=++，∴a =B ．10．【答案】C 【解析】∵sin cos A Ba b=，∴a cos B ＝b sin A ， ∴2R sin A cos B ＝2R sin B sin A,2R sin A ≠0．∴cos B ＝sin B ，∴B ＝45°．同理C ＝45°，故A ＝90°．故C 选项正确． 11．【答案】D【解析】∵()222tan a c b B +-，∴222tan 2a c b B ac +-⋅=，即cos tan sin B B B ⋅=0<B <π，∴角B 的值为3π或23π．故选D ． 12．【答案】D 【解析】3A π=，BC ＝3，设周长为x ，由正弦定理知2sin sin sin BC AC ABR A B C ===，由合分比定理知sin sin sin sin BC AB BC ACA ABC ++=++，=，∴()sin sin B A B x ⎤+++=⎥⎦，即3sin sin 3sin sin cos cos sin 333x B B B B B π⎤ππ⎛⎫⎫=+++=+++ ⎪⎪⎥⎝⎭⎭⎦133sin sin 3sin 22B B B B B ⎫⎫=+++=++⎪⎪⎪⎪⎭⎭136cos 36sin 26B B B ⎫π⎛⎫=++=++⎪ ⎪⎪⎝⎭⎝⎭．故选D ．二、填空题（本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上） 13．【答案】0 14．【答案】6π【解析】∵222a cb +-=，∴222cos 2a c b B ac +-==6B π=． 15．【答案】1【解析】在△ABC 中，A ＋B ＋C ＝π，A ＋C ＝2B ．∴3B π=．由正弦定理知，sin 1sin 2a B A b ==．又a <b ．∴6A π=，2C π=．∴sin 1C =． 16．【答案】332a ≤< 【解析】由()()()()()()22222212120121212a a a a a a a a a a a ⎧⎪++>+⎪⎪++-+<⎨⎪++-+⎪≥-⎪+⎩，解得332a ≤<．三、解答题（本大题共6个大题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．【答案】2小时．【解析】设我艇追上走私船所需时间为t 小时，则BC ＝10t ，AC ＝14t ，在△ABC 中，由∠ABC ＝180°＋45°－105°＝120°，根据余弦定理知：(14t )2＝(10t )2＋122－2·12·10t cos 120°，∴2t =．答：我艇追上走私船所需的时间为2小时． 18．【答案】（1）5950；（2）a = 【解析】（1）()221cos 1cos 59sin cos2cos22cos 122250B C B C A A A A -++++=+=+-=．（2）∵4cos 5A =，∴3sin 5A =．由1sin 2ABC S bc A =△，得133225c =⨯⨯，解得c ＝5．由余弦定理a 2＝b 2＋c 2－2bc cos A ，可得24425225135a =+-⨯⨯⨯=，∴a = 19．【答案】（1；（2）AE=．【解析】（1）∵∠BCD ＝90°＋60°＝150°，CB ＝AC ＝CD ， ∴∠CBE ＝15°．∴()cos cos 4530CBE ∠=︒-︒= （2）在△ABE 中，AB ＝2，由正弦定理得sin sin AE ABABE AEB=∠∠，即()()2sin 4515sin 9015AE =︒-︒︒+︒，故122sin 30cos15AE ⨯︒===︒20．【答案】（1）2sin 5A =；（2）b =5c =．【解析】（1）∵3cos 05B =>，且0<B <π，∴4sin 5B ==．由正弦定理得sin sin a bA B=，42sin 25sin 45a B Ab ⨯===．（2）∵1sin 42ABC S ac B ==△，∴142425c ⨯⨯⨯=，∴5c =．由余弦定理得2222232cos 25225175b a c ac B =+-=+-⨯⨯⨯=，∴b =21．【答案】（1）120A =︒；（2）△ABC 为等腰钝角三角形．【解析】（1）由已知，根据正弦定理得2a 2＝(2b ＋c )b ＋(2c ＋b )c ，即a 2＝b 2＋c 2＋bc ．由余弦定理得a 2＝b 2＋c 2－2bc cos A ，故1cos 2A =-，120A =︒．（2）方法一由（1）得sin 2A ＝sin 2B ＋sin 2C ＋sin B sin C ，又A ＝120°，∴223sin sin sin sin 4B C B C ++=， ∵sin B ＋sin C ＝1，∴sin C ＝1－sin B ． ∴()()223sin 1sin sin 1sin 4B B B B +-+-=，即21sin sin 04B B -+=．解得1sin 2B =．故1sin 2C =．∴B ＝C ＝30°．所以，△ABC 是等腰的钝角三角形．方法二由（1）A ＝120°，∴B ＋C ＝60°，则C ＝60°－B ， ∴sin B ＋sin C ＝sin B ＋sin(60°－B) 11sin sin sin 22B B B B B =-=＝sin(B ＋60°)＝1， ∴B ＝30°，C ＝30°．∴△ABC 是等腰的钝角三角形．22．【答案】（1）见解析；（2）ABC S =△ 【解析】（1）证明 ∵m ∥n ，∴a sin A ＝b sin B ，即22a ba b R R⋅=⋅，其中R 是△ABC 外接圆半径，∴a ＝b ．∴△ABC 为等腰三角形．（2）解由题意知m ·p ＝0，即a (b －2)＋b (a －2)＝0．∴a ＋b ＝ab ．由余弦定理可知，4＝a 2＋b 2－ab ＝(a ＋b )2－3ab ，即(ab )2－3ab －4＝0．∴ab ＝4(舍去ab ＝－1)，∴11sin 4sin 223ABC S ab C π==⨯⨯=△．。

(必考题)高中数学必修五第一章《数列》测试卷(有答案解析)(1)

一、选择题1．设首项为1的数列{}n a 的前n 项和为n S ，且113,2,23,21,n n n a n k k N a a n k k N *-*-⎧+=∈=⎨+=+∈⎩，若4042m S >，则正整数m 的最小值为（）A ．14B ．15C ．16D ．172．设等差数列{}n a 前n 项和为n S ，等差数列{}n b 前n 项和为n T ，若11n n S n T n -=+．则55a b =（） A ．23B ．45C ．32D ．543．已知数列{}n a 中，12a =，()*,N n m n m a a a n m +=⋅∈，若1234480k k k k a a a a +++++++=，则k =（）A ．3B ．4C ．5D ．64．已知数列{}n a 中，其前n 项和为n S ，且满足2n n S a =-，数列{}2n a 的前n 项和为n T ，若20n n S T λ+>对*n N ∈恒成立，则实数λ的取值范围是（）A ．(3,)+∞B ．(1,3)-C ．93,5⎛⎫⎪⎝⎭D ．(1,)-+∞5．设数列{}n a 满足12a =，26a =，且()*2122n n n a a a n N ++-+=∈，若[]x 表示不超过x 的最大整数（例如[]1.61=，[]1.62-=-），则222122018232019a a a ⎡⎤⎡⎤⎡⎤+++⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦＝（）A ．2018B ．2019C ．2020D ．20216．已知数列{}n a 满足()1341n n a a n ++=≥，且19a =，其前n 项之和为n S ，则满足不等式16125n S n --<的最小整数n 是（） A ．5B ．6C ．7D ．87．已知等差数列{}n a 的前n 和为n S ，若1239a a a ++=，636S =，则12(a = ) A ．23B ．24C ．25D ．268．已知等差数列{}n a 的前n 项和为n S ，55a =，836S =，则数列11{}n n a a +的前n 项和为（）A ．11n + B ．1n n + C ．1n n- D ．11n n -+ 9．已知递增的等差数列{}n a 的前n 项和为n S ，175a a ⋅=，266a a +=，对于n *∈N ，不等式1231111+++⋅⋅⋅+<nM S S S S 恒成立，则整数M 的最小值是（） A ．1B ．2C ．3D ．410．对于数列{}n a ，定义11233n nn a a a T n-+++=为{}n a 的“最优值”，现已知数列{}n a 的“最优值”3n n T =，记数列{}n a 的前n 项和为n S ，则20202020S=（） A ．2019B ．2020C ．2021D ．202211．若a ，b 是函数()()20,0f x x px q p q =-+>>的两个不同的零点，a ，b ，2-这三个数适当排序后可成等比数列，点(),2a b 在直线2100x y +-=上，则p q +的值等于（） A ．6B ．7C ．8D ．912．已知数列{}n a 满足12a =，*11()12n na n N a +=-+∈，则2020a =（） A ．2B ．13 C ．12-D ．3-二、填空题13．设S n 是数列{}n a 的前n 项和，且*1111,20,3n n n a a S S n N ++=+=∈，则1223910S S S S S S ++⋅⋅⋅⋅⋅+=___________.14．在平面直角坐标系xOy 中，点A 在y 轴正半轴上，点n P 在x 轴上，其横坐标为n x ，且{}n x 是首项为1、公比为2的等比数列，记*1,n n n P AP n N θ+∠=∈．若32arctan 9θ=，则点A 的坐标为________．15．设数列{}n a 的前n 项和为n S ，若1sin 12n n a n π+⎛⎫=+ ⎪⎝⎭，则2018S =______. 16．在等比数列{}n a 中，2514,2==a a ，则公比q =__________． 17．已知数列{}n a 的前n 项和是n S ，若111,n n a a a n +=+=，则1916S S -的值为________. 18．设无穷数列{a n }的前n 项和为S n ，下列有三个条件： ①m n m n a a a +⋅＝； ②S n ＝a n +1+1，a 1≠0；③S n ＝2a n +1p（p 是与n 无关的参数）．从中选出两个条件，能使数列{a n }为唯一确定的等比数列的条件是______． 19．等差数列{}n a 的前n 项和为n S ，且4873a a a +-=_________． 20．若等差数列{}n a 中，10a <，n S 为前n 项和，713S S =，则当n S 最小时n =________．三、解答题21．设数列{}n a 满足()121*4n n a n N a +=-∈-，其中11a =. （1）证明：112n a ⎧⎫-⎨⎬-⎩⎭是等比数列；（2）令32n n n a b a -=-，设数列(){}21-⋅n n b 的前n 项和为n S ，求使2021n S <成立的最大自然数n 的值.22．设数列{}n a ，{}n b 是公比不相等的两个等比数列，数列{}n c 满足*,n n n c a b n =+∈N ．（1）若2,3nnn n a b ==，是否存在常数k ，使得数列{}1n n c kc +-为等比数列?若存在，求k 的值；若不存在，说明理由；（2）证明：{}n c 不是等比数列．23．已知数列{}n a 满足11a =，13(1)n n na n a +=+．（1）设nn a b n=，求证:数列{}n b 是等比数列; （2）求数列{}n a 的前n 项和n S ．24．已知递增等比数列{}n a 满足：12a =，416a = ．（1）求数列{}n a 的通项公式；（2）若数列{}n b 为等差数列，且满足221b a =-，3358b a =，求数列{}n b 的通项公式及前10项的和；25．设数列{}n a 的前n 项和为n S ，______．从①数列{}n a 是公比为2的等比数列，2a ，3a ，44a -成等差数列；②22n n S a =-；③122n n S +=-．这三个条件中任选一个，补充在下面问题中，并作答．（1）求数列{}n a 的通项公式；（2）若21log nn na b a +=，求数列{}n b 的前n 项和n T ．26．已知数列{}n a 的前n 项和为21n S n n =++．（1）求这个数列的通项公式；（2）设()11n n n b n a a *+=∈N ，证明：对n *∀∈N ，数列{}n b 的前n 项和524n T <．【参考答案】***试卷处理标记，请不要删除一、选择题 1．C 解析：C 【分析】根据已知递推关系求出数列{}n a 的奇数项加9成等比数列，偶数项加6成等比数列，然后求出2n S 后，检验141615,,S S S 可得．【详解】当n 为奇数时，122232(3)329n n n n a a a a ---=+=++=+，所以292(9)n n a a -+=+，又1910a +=，所以1359,9,9,a a a +++成等比数列，公比为2，1219102n n a --+=⨯，即1211029n n a --=⨯-，当n 为偶数时，122323326n n n n a a a a ---=+=++=+，所以262(6)n n a a -+=+，又2134a a =+=，所以2469,9,9,a a a +++成等比数列，公比为2，126102n n a -+=⨯，即121026n n a -=⨯-，所以210(12)10(12)9620220151212n n n n S n n n --=-+-=⨯----，714202201572435S =⨯--⨯=，816202201584980S =⨯--⨯=， 7151415243510293706S S a =+=+⨯-=，所以满足4042m S >的正整数m 的最小值为16．故选：C ．【点睛】关键点点睛：本题考查由数列的递推关系求数列的和．解题关键是分类讨论，确定数列的奇数项与偶数项分别满足的性质，然后结合起来求得数列的偶数项的和2n S ，再检验n 取具体数值的结论．2．B解析：B 【分析】本题首先可令9n =，得出9945S T =，然后通过等差数列的性质得出959S a =以及959T b =，代入9945S T =中，即可得出结果. 【详解】因为11n n S n T n -=+，所以99914915S T -==+，因为n S 是等差数列{}n a 前n 项和，n T 是等差数列{}n b 前n 项和，所以()1995992a a S a +==，()1995992b b T b +==，则95959459S a T b ==，5545a b =，故选：B. 【点睛】关键点点睛：本题考查等差数列的相关性质的应用，主要考查等差数列前n 项和公式以及等差中项的应用，若等差数列{}n a 前n 项和为n S ，则()12n n n a a S +=，当2m n k +=时，2m n k a a a +=，考查化归与转化思想，是中档题.3．B解析：B 【分析】由已知，取1m =，则112n n n a a a a +=⋅=，得出数列{}n a 是以2为首项，2为公差的等比数列，根据等比数列的通项公式建立方程得可求得解．【详解】因为数列{}n a 中，12a =，()*,N n m n m a a a n m +=⋅∈，所以取1m =，则112n n n a a a a +=⋅=，所以数列{}n a 是以2为首项，2为公差的等比数列，所以2nn a =，又1234480k k k k a a a a +++++++=，即12344220282k k k k +++++++=，即040238k ⨯=，解得4k =，故选：B ．【点睛】关键点点睛：解决本题的问题的关键在于令1m =，得出数列{}n a 是以2为首项，2为公差的等比数列，利用等比数列的通项公式建立方程得解．4．D解析：D【分析】由2n n S a =-利用1112n n n S n a S S n -=⎧=⎨-≥⎩ ，得到数列{}n a 是以1为首项，12为公比的等比数列，进而得到{}2n a 是以1为首项，14为公比的等比数列，利用等比数列前n 项和公式得到n S ，n T ，将20n n S T λ+>恒成立，转化为6321nλ-<-+，从而得出答案. 【详解】当1n =时，112S a =-，得 11a =；当2n ≥时，由2n n S a =-，得112n n S a --=-，两式相减得112n n a a -=，所以数列{}n a 是以1为首项，12为公比的等比数列．因为112n n a a -=，所以22114n n a a -=．又211a =，所以{}2n a 是以1为首项，14为公比的等比数列，所以1112211212n n n S ⎛⎫- ⎪⎡⎤⎛⎫⎝⎭==-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-，11414113414nn n T ⎛⎫- ⎪⎡⎤⎛⎫⎝⎭==-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦-，由20n n S T λ+>，得()()321210nnλ-++>，所以()()321321663212121n nn n n λ-+--<==-+++，所以6332121λ-<-=-=+，所以1λ>-．综上，实数λ的取值范围是(1,)-+∞．故选: D 【点睛】方法点睛：数列与不等式知识相结合的考查方式主要有三种：一是判断数列问题中的一些不等关系；二是以数列为载体，考查不等式的恒成立问题；三是考查与数列问题有关的不等式的证明．在解决这些问题时，往往转化为函数的最值问题.5．B解析：B 【分析】由2122n n n a a a ++-+=，可得()2112n n n n a a a a +++---=，214a a -=．利用等差数列的通项公式、累加求和方法、取整函数即可得出．【详解】2122n n n a a a ++-+=，()2112n n n n a a a a +++∴---=，214a a -=．{}1n n a a +∴-是等差数列，首项为4，公差为2． 142(1)22n n a a n n +∴-=+-=+．2n ∴≥时，()()()112211n n n n n a a a a a a a a ---=-+-+⋯⋯+-+(1)22(1)..2222(1)2n n n n n n +=+-+⋯+⨯+=⨯=+． 2(1)1n n n a n++∴=．∴当2n ≥时，2(1)11⎡⎤++⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦n n n a n ． 222122018232019220172019a a a ⎡⎤⎡⎤⎡⎤∴+++=+=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦. 故选：B ．【点睛】本题考查了数列递推关系、等差数列的通项公式、累加求和方法、取整函数，考查了推理能力与计算能力，属于中档题．6．C解析：C 【分析】首先分析题目已知3a n+1+a n =4（n ∈N*）且a 1=9，其前n 项和为S n ，求满足不等式|S n ﹣n ﹣6|＜1125的最小整数n ．故可以考虑把等式3a n+1+a n =4变形得到111-13n n a a +-=-，然后根据数列b n =a n ﹣1为等比数列，求出S n 代入绝对值不等式求解即可得到答案．【详解】对3a n+1+a n =4 变形得：3（a n+1﹣1）=﹣（a n ﹣1）即：111-13n n a a +-=- 故可以分析得到数列b n =a n ﹣1为首项为8公比为13-的等比数列．所以b n =a n ﹣1=8×11-3n -⎛⎫ ⎪⎝⎭a n =8×11-3n -⎛⎫ ⎪⎝⎭+1所以181********n nnS n n ⎡⎤⎛⎫--⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦=+=-⨯-+ ⎪⎛⎫⎝⎭-- ⎪⎝⎭|S n ﹣n ﹣6|=n11-6-3125⎛⎫⨯< ⎪⎝⎭解得最小的正整数n=7 故选C ．【点睛】此题主要考查不等式的求解问题，其中涉及到可化为等比数列的数列的求和问题，属于不等式与数列的综合性问题，判断出数列a n ﹣1为等比数列是题目的关键，有一定的技巧性属于中档题目．7．A解析：A 【解析】等差数列{}n a 的前n 和为n S ，1239a a a ++=，636S =，11339656362a d a d +=⎧⎪∴⎨⨯+=⎪⎩，解得1a 1,d 2，12111223a =+⨯=，故选A.8．B解析：B 【解析】设等差数列{}n a 的首项为1a ，公差为d . ∵55a =，836S = ∴114582836a d a d +=⎧⎨+=⎩∴111a d =⎧⎨=⎩∴n a n =，则11111(1)1+==-++n n a a n n n n ∴数列11n n a a +⎧⎫⎨⎬⎩⎭的前n 项和为1111111111122334111nn n n n -+-+-+⋅⋅⋅+-=-=+++ 故选B.点睛：裂项相消法是最难把握的求和方法之一，其原因是有时很难找到裂项的方向，突破这一难点的方法是根据式子的结构特点，常见的裂项技巧：(1)()1111n n k k n n k ⎛⎫=- ⎪++⎝⎭；（2）1k =；（3）()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭；（4）()()11122n n n =++ ()()()11112n n n n ⎡⎤-⎢⎥+++⎢⎥⎣⎦；此外，需注意裂项之后相消的过程中容易出现丢项或多项的问题，导致计算结果错误.9．C解析：C 【分析】先求出等差数列的1a 和d ，由等差数列前n 项和公式得n S ，把1nS 拆成两项的差，用裂项相消法求得和12111nS S S +++，在n 变化时，求得M 的范围，得出结论．【详解】∵{}n a 是等差数列，∴17266a a a a +=+=，由171765a a a a +=⎧⎨=⎩解得1715a a =⎧⎨=⎩或1751a a =⎧⎨=⎩，又{}n a 是递增数列，∴1715a a =⎧⎨=⎩，715127163a a d --===-， 1(1)(1)(2)233n n n n n n n S na d n --+=+=+=， 121113331324(2)n S S S n n +++=+++⨯⨯+3111111112324112n n n n ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-++-+- ⎪ ⎪ ⎪ ⎪⎢⎥-++⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦31119311122124212n n n n ⎛⎫⎛⎫=+--=-+ ⎪ ⎪++++⎝⎭⎝⎭94<，由不等式1231111+++⋅⋅⋅+<n M S S S S 恒成立，得94M ≥，∴最小的整数3M =．故选：C ．【点睛】本题考查不等式恒成立问题，考查等差数列的性质，等差数列的通项公式和前n 项和公式，裂项相消法求和，本题属于中档题．10．D解析：D 【分析】根据11233n nn a a a T n-+++=，且3nn T =，得到112333n n n a a a n -+++=⋅，然后利用数列通项与前n 项和的关系求得21n a n =+，再利用等差数列求和公式求解. 【详解】 ∵11233n nn a a a T n-+++=，且3nn T =，∴112333n n n a a a n -+++=⋅，当2n ≥时，有()211213313n n n a a a n ---+++⋅=-⋅，两式相减可得：()()1113313213n n n n n a n n n ---⋅=⋅--⋅=+⋅.∴21n a n =+（2n ≥）. 当1n =时，13a =适合上式. ∴21n a n =+.则数列{}n a 是以3为首项，以2为公差的等差数列. ∴()202032202012020S 202220202+⨯+⨯==⨯.∴202020222020S =. 故选：D . 【点睛】本题主要考查数列通项与前n 项和的关系以及等差数列的定义和求和公式的应用，属于中档题.11．D解析：D 【分析】由零点定义得,a b p ab q +==得0,0a b >>，因此2-只能是等比数列的中间项，从而得4ab =，由点(),2a b 在直线2100x y +-=上，得5a b +=，这样可得,p q 值．从而得出结论．【详解】∵a ，b 是函数()()20,0f x x px q p q =-+>>的两个不同的零点，∴,a b p ab q +==，∴0,0a b >>，而a ，b ，2-这三个数适当排序后可成等比数列，只能是2-是,a b 的等比中项，即4ab =，点(),2a b 在直线2100x y +-=上，则22100a b +-=，得5a b +=，由45ab a b =⎧⎨+=⎩，∴5,4p q ==，9p q +=．故选：D ．【点睛】本题考查函数零点的概念，考查等比数列的定义，考查韦达定理，关键是由题意分析出0,0a b >>．12．D解析：D 【分析】先利用题中所给的首项，以及递推公式，将首项代入，从而判断出数列{}n a 是周期数列，进而求得结果. 【详解】由已知得12a =，2211123a =-=+，32111213a =-=-+， 4213112a =-=--，521213a =-=-，可以判断出数列{}n a 是以4为周期的数列，故2020505443a a a ⨯===-，故选：D. 【点睛】该题考查的是有关数列的问题，涉及到的知识点利用递推公式判断数列的周期性，从而求解数列的某项，属于中档题.二、填空题13．【分析】由代入化简求得再结合求和方法计算可得结果【详解】因为所以所以所以又所以数列是以为首项为公差的等差数列所以所以所以所以故答案为：【点晴】由代入化简求得数列是等差数列是解题的关键解析：17【分析】由11n n n a S S ++=-代入化简求得n S ，再结合求和方法计算可得结果. 【详解】因为1120n n n a S S +++= 所以1120n n n n S S S S ++-+= 所以112n n n n S S S S ++-= 所以1112n nS S +-=又11113S a == 所以数列1n S ⎧⎫⎨⎬⎩⎭是以3为首项，2为公差的等差数列，所以()131221nn n S =+-⨯=+ 所以121n S n =+ 所以111111212322123n n S S n n n n +⎛⎫=⋅=- ⎪++++⎝⎭所以12239101111111111123557192123217S S S S S S ⎛⎫⎛⎫++⋅⋅⋅⋅⋅⋅+=-+-+⋅⋅⋅+-=-=⎪ ⎪⎝⎭⎝⎭ 故答案为：17【点晴】由11n n n a S S ++=-代入化简求得数列1n S ⎧⎫⎨⎬⎩⎭是等差数列是解题的关键. 14．或【分析】设点的坐标利用两角差正切公式求列式解得结果【详解】设因为所以或故答案为：或【点睛】本题考查两角差正切公式等比数列考查综合分析求解能力属中档题解析：(0,2)或(0,16) 【分析】设点A 的坐标，利用两角差正切公式求3tan θ，列式解得结果. 【详解】设(0,),0A a a >,因为233443343,124,128P AP AP OAP O x x θ=-=⨯==⨯=∠∠=∠所以238442284t 21an 39a a a a a a aθ-===∴=++⋅或16 故答案为：(0,2)或(0,16)【点睛】本题考查两角差正切公式、等比数列，考查综合分析求解能力，属中档题.15．【分析】分别计算出进而得出再由可得出的值【详解】由题意可得故答案为：【点睛】本题考查数列求和找出数列的规律是解答的关键考查计算能力属于中等题解析：1008【分析】分别计算出43k a -、42k a -、41k a -、()4k a k N *∈，进而得出43424146k k k k a a a a ---+++=，再由201845042=⨯+可得出2018S 的值.【详解】由题意可得()434243sin 112k k a k π--⎛⎫=-+= ⎪⎝⎭，()424142sin 1342k k a k k π--⎛⎫=-+=- ⎪⎝⎭，()()4141sin 211k a k k π-=-+=，4414sin 1412k k a k k π+⎛⎫=+=+ ⎪⎝⎭，()()43424141341416k k k k a a a a k k ---∴+++=+-+++=，201845042=⨯+，201820172018450534505265046504S a a a a ⨯-⨯-∴=⨯++=⨯++()30241345051008=++-⨯=.故答案为：1008. 【点睛】本题考查数列求和，找出数列的规律是解答的关键，考查计算能力，属于中等题.16．【分析】本题先用表示再建立方程组解题即可【详解】解：∵是等比数列∴∵∴解得：故答案为：【点睛】本题考查等比数列的基本量法是基础题解析：12【分析】本题先用1a ，q 表示2a ，5a ，再建立方程组21451412a a q a a q ==⎧⎪⎨==⎪⎩解题即可. 【详解】解：∵ {}n a 是等比数列，∴ 21a a q =，451a a q∵24a =，512a =，∴ 21451412a a q a a q ==⎧⎪⎨==⎪⎩，解得：1812a q =⎧⎪⎨=⎪⎩，故答案为：12. 【点睛】本题考查等比数列的基本量法，是基础题.17．27【分析】由得相减后得数列的奇数项与偶数项分别成等差数列由此可得通项从而求得结论【详解】∵∴相减得又所以数列的奇数项与偶数项分别成等差数列公差为1故答案为：27【点睛】易错点睛：本题考查等差数列的解析：27 【分析】由1n n a a n ++=得121n n a a n +++=+相减后得数列的奇数项与偶数项分别成等差数列，由此可得通项，从而求得结论．【详解】∵1n n a a n ++=，∴121n n a a n +++=+，相减得21n na a +-=，又1121,1a a a =+=，20a =，211a a -=-，所以数列{}n a 的奇数项与偶数项分别成等差数列，公差为1，21n a n -=，21n a n =-，1916171819981027S S a a a -=++=++=．故答案为：27．【点睛】易错点睛：本题考查等差数列的通项公式，解题时由已知等式中n 改写为1n +，两相减后得21n n a a +-=，这里再计算21a a -，如果2211()22n na a a a +--==，则可说明{}n a 是等差数列，象本题只能说明奇数项与偶数项分别成等差数列．不能混淆，误以为{}n a 是等差数列．这是易错的地方．18．①③【分析】选①②在①中令在②中令联立方程由方程无解推出矛盾；选①③在③中由通项与前项和之间的关系求出公比在①中令在③中用表示出联立方程求出确定数列；选②③由通项与前项和之间的关系即可作出判断【详解解析：①③ 【分析】选①②，在①中令1m n ==，在②中令1n =联立方程，由方程无解推出矛盾；选①③，在③中由通项与前n 项和之间的关系求出公比，在①中令1m n ==，在③中用12,a a 表示出12,S S 联立方程，求出1,a p 确定数列{}n a ；选②③，由通项与前n 项和之间的关系即可作出判断. 【详解】在①中，令1m n ==，得221a a =；在②中，11n n S a +=+，当2n ≥时， 11n n S a -=+，两式相减，得1n n n a a a +=-，即12n n a a +=；在③中，11112,2n n n n S a S a p p++=+=+，两式相减，得 1122n n n a a a ++=-，即 12n n a a +=，若选①②，则22112,1a a a a ⎧=⎨=+⎩即 2211111,10a a a a =--+=， 2(1)41130∆=--⨯⨯=-<，方程无解，故不能选①②作为条件；若选①③，则由12n n a a +=知，数列{}n a 的公比为2，由 221111221212a a a a p a a a p ⎧⎪=⎪⎪=+⎨⎪⎪+=+⎪⎩得1212a p =⎧⎪⎨=-⎪⎩，所以数列 {}n a 是首项为2，公比为2的等比数列；若选②③作为条件，则无法确定首项，数列{}n a 不唯一，故不能选②③作为条件. 综上所述，能使数列{}n a 为唯一确定的等比数列的条件是①③. 故答案为：①③ 【点睛】思路点睛：本题考查利用递推关系求数列中的项，涉及等比数列的判定和通项公式，遇到和与项的递推关系时，一般有两种方法：（1）消去和，得到项的递推关系；（2）消去项，得到和的递推关系.19．【分析】首先设出等差数列的首项和公差根据其通项公式得到再根据其求和公式得到从而得到结果【详解】设等差数列的首项为公差为则有因为所以故答案为：【点睛】思路点睛：该题考查的是有关等差数列的问题解题思路如解析：13313S 【分析】首先设出等差数列的首项和公差，根据其通项公式，得到487733a a a a +-=，再根据其求和公式，得到13713S a =，从而得到结果. 【详解】设等差数列的首项为1a ，公差为d ，则有48711117333(7)(6)318=3a a a a d a d a d a d a +-=+++-+=+，因为11313713()132a a S a +==，所以487133313a a a S +-=，故答案为：13313S . 【点睛】思路点睛：该题考查的是有关等差数列的问题，解题思路如下：（1）首先设出等差数列的首项和公差；（2）利用等差数列的通项公式，得到项之间的关系，整理得出487733a a a a +-=；（3）利用等差数列的求和公式，求得13713S a =；（4）比较式子，求得结果.20．10【分析】根据条件确定中项的符号变化规律即可确定最小时对应项数【详解】单调递增因此即最小故答案为：10【点睛】本题考查等差数列性质等差数列前项和性质考查基本分析求解能力属中档题解析：10 【分析】根据条件确定{}n a 中项的符号变化规律，即可确定n S 最小时对应项数. 【详解】7138910111213101103()0S S a a a a a a a a =∴+++++=∴+= 17130,a S S <=∴{}n a 单调递增，因此10110,0a a <>即10n =，n S 最小故答案为：10 【点睛】本题考查等差数列性质、等差数列前n 项和性质，考查基本分析求解能力，属中档题.三、解答题21．（1）证明见解析；（2）最大自然数6n =. 【分析】（1）根据题中条件，可得1112n a +--的表达式，根据等比数列的定义，即可得证；（2）由（1）可得1122n n a -=-，则可得2n n b =，根据错位相减求和法，可求得n S 的表达式，根据n S 的单调性，代入数值，分析即可得答案. 【详解】解：（1）∵()1621*44n n n n a a n N a a +-=-=∈--， ∴()()1116323346312311122162262822224n n n n n n n n n n n n n n n n a a a a a a a a a a a a a a a a +++----⎛⎫----+--======- ⎪-----+----⎝⎭--即11122112n n a a +--=--， ∴112n a ⎧⎫-⎨⎬-⎩⎭是首项为113132212a a --==--，公比为2的等比数列. （2）由（1）知，1122n n a -=-，即321112222n n n n n n n a a b a a a ---==-==---， ∴()()21212-⋅=-⋅nn n b n ，()123123252212n n S n =⋅+⋅+⋅++-⋅，① ()23412123252212n n S n +=⋅+⋅+⋅++-⋅，②①减②得()()()112311421222222122221212n nn n n S n n +++--=⋅++++--⋅=+⋅--⋅-()13226n n +=-⋅-.∴()12326n n S n +=-⋅+.∴()()()21112122322210++++-=-⋅--⋅=+>n n n n n S S n n n ，∴n S .单调递增.∵7692611582021S =⨯+=<，87112628222021S =⨯+=>.故使2021n S <成立的最大自然数6n =. 【点睛】解题的关键是根据所给形式，进行配凑和整理，根据等比数列定义，即可得证，求和常用的方法有：①公式法，②倒序相加法，③裂项相消法，④错位相减法等，需熟练掌握. 22．（1）存在，2k =或3k =；（2）证明见解析. 【分析】（1）若数列{}1n n c kc +-为等比数列，则有()()()21211n n n n n n c kc c kc c kc +++--=-⋅-，其中2n ≥且*n ∈N ，将23nnn c =+代入上式，整理得1(2)(3)2306n n k k --⋅⋅=化简即可得出答案；（2）证{}n c 不是等比数列只需证2213c c c ≠⋅，验证其不成立即可.【详解】解：（1）由题意知，若数列{}1n n c kc +-为等比数列，则有()()()21211n n n n n n c kc c kc c kc +++--=-⋅-，其中2n ≥且*n ∈N ，将23nnn c =+代入上式，得()()()211221111232323232323n n n n n n n n n n n n k k k ++++++--⎡⎤⎡⎤⎡⎤+-+=+-+⋅+-+⎣⎦⎣⎦⎣⎦，即21111(2)2(3)3(2)2(3)3(2)2(3)3n n n n n n k k k k k k ++--⎡⎤⎡⎤⎡⎤-+-=-+-⋅-+-⎣⎦⎣⎦⎣⎦，整理得1(2)(3)2306n nk k --⋅⋅=，解得2k =或3k =．（2）设数列{}n a ，{}n b 的公比分别为,,p q p q ≠且,0p q ≠，11,0a b ≠，则1111n n n c a pb q --=+，为证{}n c 不是等比数列，只需证2213c c c ≠⋅，事实上()22222221111112c a p b q a p a b pq b q =+=++，()()()222222221311111111c c a b a p b q a p a b p q b q ⋅=+⋅+=+++，由于p q ≠，故222p q pq +>，又11,0a b ≠，从而2213c c c ≠⋅，所以{}n c 不是等比数列. 【点睛】方法点睛：等差、等比数列的证明经常利用定义法和等比中项法，通项公式法和前n 项和公式法经常在选择题、填空题中用来判断数列是否为等差、等比数列不能用来证明．23．（1）证明见解析；（2）(21)3144n n n S -=+.【分析】（1）将13(1)n n na n a +=+变形为131n n a an n+=+，得到{}n b 为等比数列，（2）由（1）得到{}n a 的通项公式，用错位相减法求得n S 【详解】（1）由11a =，13(1)n n na n a +=+，可得131n na a n n+=+，因为nn a b n=则13n n b b +=，11b =，可得{}n b 是首项为1，公比为3的等比数列，（2）由（1）13n n b -=，由13n na n-=，可得13n n a n -=⋅， 01211323333n n S n -=⋅+⋅+⋅++⋅，12331323333n n S n =⋅+⋅+⋅++⋅，上面两式相减可得：0121233333n n n S n --=++++-⋅13313n n n -=-⋅-，则(21)3144n n n S -=+．【点睛】数列求和的方法技巧：(1)倒序相加：用于等差数列、与二项式系数、对称性相关联的数列的求和． (2)错位相减：用于等差数列与等比数列的积数列的求和． (3)分组求和：用于若干个等差或等比数列的和或差数列的求和．(4) 裂项相消法：用于通项能变成两个式子相减，求和时能前后相消的数列求和.24．（1）2nn a =；（2）21n b n =-，数列{}n b 前10项的和10100S =.【分析】（1）利用等比数列的通项公式，结合已知12a =，416a =，可以求出公比，这样就可以求出数列{}n a 的通项公式；（2）由数列{}n a 的通项公式，可以求出21a -和 358a 的值，这样也就求出2b 和 3b 的值，这样可以求出等差数列{}n b 的公差，进而可以求出通项公式，利用前n 项和公式求出数列{}n b 前10项的和.【详解】（1）设等比数列的公比为q ，由已知12a =，34121616q a a q =⇒⋅=⇒=，所以112n n n a q a -=⋅=，即数列{}n a 的通项公式为2n n a =；（2）由（1）知2nn a =，所以2221213b a =-=-=，333552588b a ==⨯=，设等差数列{}n b 的公差为d ，则322d b b -==，12121n d b b n b =-=∴=-，设数列{}n b 前10项的和为10S ，则11010910910101210022S d b ⨯⨯=+⋅=⨯+⨯=，所以数列{}n b 的通项公式21n b n =-，数列{}n b 前10项的和10100S =. 【点睛】方法点睛：数列求和的常用方法：（1）公式法：即直接用等差、等比数列的求和公式求和.（2）错位相减法：若{}n a 是等差数列，{}n b 是等比数列，求1122n n a b a b a b ++⋅⋅⋅. （3）裂项相消法：把数列的通项拆成两项之差，相消剩下首尾的若干项.常见的裂顶有()11111n n n n =-++，()1111222n n n n ⎛⎫=- ⎪++⎝⎭，()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭等.（4）分组求和法：把数列的每一项分成若干项，使其转化为等差或等比数列，再求和. （5）倒序相加法.25．（1）条件性选择见解析，2n n a =；（2）332n nn T +=-．【分析】（1）选①：由题意可得32442a a a =+-，再利用等比数列的公比为2可求1a ，进而可求数列{}n a 的通项公式；选②：22n n S a =-，令1n =可求1a ，当2n ≥时，可得1122n n S a --=-，与已知条件两式相减可求得()122n n a a n -=≥，进而可求数列{}n a 的通项公式；选③：122n n S +=-，当1n =时，112S a ==，当2n ≥时，122n n S -=-，与已知条件两式相减可求得2nn a =，检验12a =也满足，进而可求数列{}n a 的通项公式；（2）由（1）知2nn a =，则221log 1log 2122n n n n n n a n b a +++===，利用乘公比错位相减即可求和. 【详解】（1）选①：因为2a ，3a ，44a -成等差数列，所以32442a a a =+-，又因为数列{}n a 的公比为2，所以2311122242a a a ⨯=+⨯-，即1118284a a a =+-，解得12a =，所以1222n n n a -=⨯=．选②：因为22n n S a =-，当1n =时，1122S a =-，解得12a =．当2n ≥时，1122n n S a --=-，所以()()111222222n n n n n n n a S S a a a a ---=-=---=-．即()122n n a a n -=≥．所以数列{}n a 是首项为2，公比为2的等比数列．故1222n n n a -=⨯=．选③：因为122n n S +=-，所以当1n =时，112S a ==，当2n ≥时，122nn S -=-，所以()()1122222n n nn n n a S S +-=-=---=，当1n =时，1122a ==依然成立．所以2nn a =．（2）由（1）知2nn a =，则221log 1log 2122n n n n n n a n b a +++===，所以2323412222n n n T +=++++， ① 231123122222n n n n n T ++=++++， ② ①－②得23111111122222n n n n T ++⎛⎫=++++- ⎪⎝⎭ 212111111111111121222211111222221122n n n n n n n n n -+++++⎛⎫-- ⎪+++⎝⎭=+-=+-=+---- 13322n n ++=-．所以332n nn T +=-．所以数列{}n b 的前n 项和332n n n T +=-．【点睛】方法点睛：数列求和的方法（1）倒序相加法：如果一个数列{}n a 的前n 项中首末两端等距离的两项的和相等或等于同一个常数，那么求这个数列的前n 项和即可以用倒序相加法（2）错位相减法：如果一个数列的各项是由一个等差数列和一个等比数列的对应项之积构成的，那么这个数列的前n 项和即可以用错位相减法来求；（3）裂项相消法：把数列的通项拆成两项之差，在求和时，中间的一些项可相互抵消，从而求得其和；（4）分组转化法：一个数列的通项公式是由若干个等差数列或等比数列或可求和的数列组成，则求和时可用分组转换法分别求和再相加减；（5）并项求和法：一个数列的前n 项和可以两两结合求解，则称之为并项求和，形如()()1nn a f n =-类型，可采用两项合并求解. 26．（1）*3,(1)2,(2,)n n a n n n N =⎧=⎨≥∈⎩；（2）证明见解析．【分析】（1）利用*1,(1),(2,)n n nn S n a S S n n N -=⎧=⎨-≥∈⎩求解即可；（2）利用n a 求n b ，当1n =时，1151224b =≤显然成立，当2n ≥时，利用列项相消法求和判断即可. 【详解】解：（1）当1n =时，111113a S ==++=；当2n ≥时，1n n n a S S -=-22(1)[(1)(1)1]n n n n =++--+-+2n =，所以*3,(1)2,(2,)n n a n n n N =⎧=⎨≥∈⎩；（2）由（1）易知*1,(1)121(2,),4(1)n n b n n N n n ⎧⎪=⎪=⎨≥∈⎪+⎪⎩ 当1n =时，1151224b =≤显然成立．当2n ≥时，1111()4(1)41n b n n n n ==-++， 123n n T b b b b =+++ 11111111[()()()]12423341n n =+-+-++-+ 1111()12421n =+-+ 515244(1)24n =-<+；故结论成立．【点睛】关键点睛：本题考查数列求通项公式，利用数列求和证明不等式.利用列项相消法求和是解决本题的关键.。

（完整）新课标人教A版高中数学必修五第一章《解三角形》单元测试题

（完整）新课标⼈教A版⾼中数学必修五第⼀章《解三⾓形》单元测试题解三⾓形第Ⅰ卷（选择题共60分）⼀、选择题（共12⼩题，每⼩题5分，只有⼀个选项正确）：1.在△ABC 中，若∠A ＝60°，∠B ＝45°，BC ＝23，则AC ＝( ) A ．43 B ．22 C ．3 D ．32.在△ABC 中，AB ＝5，BC ＝6，AC ＝8，则△ABC 的形状是( )A ．锐⾓三⾓形B ．直⾓三⾓形C ．钝⾓三⾓形D ．⾮钝⾓三⾓形 3.在△ABC 中，已知a ＝11，b ＝20，A ＝130°，则此三⾓形( )A ．⽆解B ．只有⼀解C ．有两解D ．解的个数不确定4. 海上有A 、B 两个⼩岛相距10海⾥，从A 岛望C 岛和B 岛成60ο的视⾓，从B 岛望C 岛和A岛成75ο视⾓，则B 、C 两岛的距离是（）海⾥A. 65B. 35C. 25D. 5 5.边长为3、7、8的三⾓形中，最⼤⾓与最⼩⾓之和为 ( ) A ．90° B ．120° C ．135° D ．150°6.如图，设A ，B 两点在河的两岸，⼀测量者在A 的同侧，在所在的河岸边选定的⼀点C ，测出AC 的距离为502m ，45ACB ∠=?，105CAB ∠=?后，就可以计算出A ，B 两点的距离为 ( )A. 100mB. 3mC. 1002mD. 200mB ．2 C. 2 D. 38.如图，四边形ABCD中，B＝C＝120°，AB＝4，BC＝CD＝2，则该四边形的⾯积等于( )A. 3 B．5 3C．6 3 D．7 39.在△ABC中，A＝120°，AB＝5，BC＝7，则sin Bsin C的值为( )A.85B.58C.53D.3510.某海上缉私⼩分队驾驶缉私艇以40 km/h的速度由A处出发，沿北偏东60°⽅向航⾏，进⾏海⾯巡逻，当⾏驶半⼩时到达B处时，发现北偏西45°⽅向有⼀艘船C，若C船位于A处北偏东30°⽅向上，则缉私艇B与船C的距离是( )A．5(6＋2) km B．5(6－2) kmC．10(6＋2) km D．10(6－2) km11.△ABC 的周长为20，⾯积为A ＝60°，则BC 的长等于( ) A ．5 B.6 C ．7D ．812.在ABC △中，⾓A B C 、、所对的边分别为,,a b c ，若120,C c ∠=?=，则（） A ．a b > B ．a b <C ．a b =D ．a 与b 的⼤⼩关系不能确定第Ⅱ卷（⾮选择题共90分）⼆、填空题（共4⼩题，每⼩题5分）：13.三⾓形的两边分别是5和3，它们夹⾓的余弦值是⽅程06752=--x x 的根，则此三⾓形的⾯积是。

北师大版高二数学必修5单元测试题

高二年级数学学科《必修5》单元质量检测试题第I 卷（选择题，共60分）一、选择题（本大题共12小题，每小题5分，共60分）1、若R c b a ∈,,，且b a >，则下列不等式一定成立的是（）A ．c b c a -≥+B ．bc ac >C ．02>-ba c D ．0)(2≥-cb a2. 不等式11<-x ax的解集为}21|{><x x x 或，则a 值（） A. 21>a B. 21<a C. 21=a D. 以上答案均不正确3.不等式112x <的解集是（）A ．(,2)-∞B ．(2,)+∞C ．(0,2)D ．()0,∞-⋃(2,)+∞4．原点和点（1，1）在直线a y x =+两侧，则a 的取值范围是（）A ．0<a 或2>aB ．20<<aC ．0=a 或2=aD ．20≤≤a5、已知正数x 、y 满足811x y+=，则2x y +的最小值是（）Ａ．18 Ｂ．16 C ．8 D ．106：对任意a ∈[-1,1]，函数f(x)=x 2+(a-4)x+4-2a 的值恒大于零，则x 的取值范围是（） A 1<x<3 B x<1或x>3 C 1<x<2 D a<1或x>27.已知集合M ＝{x|x 2＜4}，N ＝{x|x 2－2x －3＜0}，则集合M ∩N ＝（）（A ）{x|x ＜－2} （B ）{x|x ＞3} （C ）{x|－1＜x ＜2} （D ）{x|2＜x ＜3}8．某高速公路对行驶的各种车辆最大限速为120h km /，行驶过程中，同一车道上的车间距d 不得小于10m ，用不等式表示为（）A ．h km v /120≤或m d 10≥B ．⎩⎨⎧≥≤md h km v 10/120C ．h km v /120<或m d 10>D ．h km v /120≥或m d 10≤9 若对任意∈x R,不等式x ≥ax 恒成立，则实数a 的取值范围是（）(A)a ＜-1 (B)a ≤1 (C) a ＜1 （D ）a ≥110 .已知函数()⎩⎨⎧≥-<+-=0101x x x x x f ，则不等式()()111≤+++x f x x 的解集是（）(A) {}121|-≤≤-x x (B) {}1|≤x x(C) {}12|-≤x x (D) {}1212|-≤≤--x x11、设直角三角形两直角边的长分别为a 和b ，斜边长为c ，斜边上的高为h ，则44b a +和44h c +的大小y 关系是 ( )Ａ．4444h c b a +<+ Ｂ．4444h c b a +>+ C ．4444h c b a +=+ D ．不能确定 12、已知等比数列}{n a 的各项均为正数，公比1≠q ，设293a a P +=，75a a Q ∙=，则P 与Q 的大小关系是（）A ．P > QB ．P < QC ．P = QD ．无法确定第II 卷（非选择题，共90分）二、填空题（本大题共6小题，每小题5分，共30分.把最佳的答案填在该题的横线上） 13．不等式224122x x +-≤的解集为 _________ ． 14．若不等式022>++bx ax 解集为⎭⎬⎫⎩⎨⎧<<-3121|x x ，则b a +的值为。

数学练习题高中数学必修5模块测试

高中数学必修5模块测试一、选择题（每小题5分，10小题，共50分）1、在ABC ∆中，︒===452232B b a ，，，则A 为（）A ．︒︒︒︒︒︒30.15030.60.12060D C B 或或2、在ABC ∆中，bc c b a ++=222，则A 等于（）A ︒︒︒︒30.45.60.120.D C B3、在ABC ∆中，1660=︒=b A ，，面积3220=S ，则a 等于( ) A. 610.B. 75C . 49 D. 514、等比数列{}n a 中293a a =，则313239310log log log log a a a a ++++ 等于（） A ．9 B ．27 C ．81 D ．2435、三个数a ，b ，c 既是等差数列，又是等比数列，则a ，b ，c 间的关系为 ( ) A ．b-a =c-b B ．b 2=a c C ．a =b=c D ．a =b=c ≠06、等比数列{}n a 的首项1a =1，公比为q ，前n 项和是n S ，则数列⎭⎬⎫⎩⎨⎧n a 1的前n 项和是（）A ．1-n S B ．nn qS - C ．nn qS -1 D ．11--n n qS7、在等差数列{}n a 中，前四项之和为40，最后四项之和为80，所有项之和是210，则项数n 为（）A ．12B ．14C ．15D ．16 8、已知,,a b c R ∈,则下列选项正确的是（）A.22a b am bm >⇒> B.a ba b c c>⇒>C .11,0a b ab a b >>⇒< D.2211,0a b ab a b>>⇒<9、已知x y xy +=，则y x +的取值范围是（）A ．]1,0(B ．),2[+∞C ．]4,0(D ．),4[+∞10、⎪⎪⎩⎪⎪⎨⎧≥≥-<-<+0011234x y y x y x 表示的平面区域内的整点的个数是（）A ．8个B ．5个C ．4个D ．2个题号 1 2 3 4 5 6 7 8 9 10 答案第二部分（非选择题）二、填空题（每小题5分，4小题，共20分）11、已知0,0>>y x ，且191=+yx ，求y x +的最小值 _____________ 12、当x 取值范围是_____________ 时，函数122-+=x x y 的值大于零 13、在等比数列}{n a 中，08,204321=+=+a a a a ，则=10S14、不等式组6003x y x y x -+≥⎧⎪+≥⎨⎪≤⎩表示的平面区域的面积是三、解答题15、在△ABC 中，BC ＝a ，AC ＝b ，a ，b 是方程02322=+-x x 的两个根，且()1cos 2=+B A 。

高二上学期数学(必修5)模块测试题

高二上学期数学（必修5）模块测试题姓名：学号：成绩：一选择题(12小题每题3分共36分)1.在数列 ,52,,11,22,5,2中，52是它的 ( )A. 第6项B. 第7项C. 第8项D. 第9项2.已知数列的一个通项公式为,23)1(11-++-=n n n n a 则5a = ( )A.21 B .－21 C.329 D .－329 3. 在△ABC 中，若B A sin sin >，则A 与B 的大小关系为 ( )A. B A >B. B A <C. A ≥BD. A 、B 的大小关系不能确定4.设n S 是等差数列{}n a 的前n 项和，已知23a =，611a =，则7S 等于 ( ) A ．13 B ．35 C ．49 D ． 635.设等比数列{ n a }的前n 项和为n S ，若63S S =3 ，则 69S S ( ) A. 2 B.73 C. 83 D.3 6.下列不等式中与不等式 023≥--xx 同解．．的是（） A.()()023≥--x x B.()()123>--x x a ()10<<a C.0323≥--x x D.023≥--x x7.若不等式ax 2＋bx －2＞0的解集为⎭⎬⎫⎩⎨⎧-<<-412x x 则a ，b 的值分别是（）.A ．10,8-=-=b aB ．9,1=-=b aC ．9,4-=-=b aD ．2,1=-=b a8. 在平面直角坐标系中，不等式组⎪⎩⎪⎨⎧≤≥+≥+2x 02x-y 02y-x ，表示的平面区域的面积是（）A. 24B. 4C. 22D. 2 9.在△ABC 中，已知bc c b a ++=222，则角A 为（）A ． 3πB ．6πC ．32πD ． 3π或32π10.在△ABC 中，若B b A a cos cos =，则△ABC 的形状是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰或直角三角形 11．关于x 的方程22cos cos cos 02Cx x A B -⋅⋅-=有一个根为1，则△ABC 一定（）A. 等腰三角形B. 直角三角形C. 锐角三角形D. 钝角三角形12.已知平面区域D 由以A （1，3）、B （5，2）、C （3，1）为顶点的三角形内部和边界组成若在区域D 内有无穷多个点（x ，y ）可使目标函数m y x z +=取得最小值，则m =（）A. 2-B. 1-C. 1D. 4 二填空题：（共4道小题，每题4分共计16分）13.在等差数列}{n a 中,6,7253+==a a a ,则____________6=a .14. 140,0,1x y x y>>+=若且，则x y +的最小值是．15.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：则第n 个图案中有白色地面砖块 16.观察21211=⨯，32321211=⨯+⨯，43431321211=⨯+⨯+⨯，猜想()=-⨯++⨯+⨯+⨯11431321211n n高二上学期数学（必修5）模块测试卷一.选择题:（每小题3分，共36分）二.填空题:（每小题4分，共16分）13.______________ 14.________________. 15.______________16.__________________.三.解答题（本大题共4小题，共48分）17. (本小题10)设230<<x ，求函数)23(4x x y -=的最大值18.(本小题12分)在∆ABC 中，设,2tan tan bbc B A -=，求A 的值.19. (本小题12) 已知函数862++-=m mx mx y 的定义域为R ，求实数m 的取值范围.20. (本小题14)已知()n n x a x a x a x a x f ++++= 33221，且n a a a a ,,,,321 组成等差数列（n 为正偶数），又()()n f n f =-=1,12；（1）求数列{}n a 的通项n a ；（2）求⎪⎭⎫⎝⎛21f 的值；（3）比较⎪⎭⎫⎝⎛21f 的值与3的大小，并说明理由高二上学期数学（必修5）模块测试题参考答案一.选择题:（每小题3分，共36分）二.填空题:（每小题4分，共16分）13.13 14.9. 15. 4n+2 16. nn 1-三.解答题（本大题共5小题，共48分） 17.(10分)解：∵230<<x∴023>-x2922322)23(22)23(42=⎪⎭⎫⎝⎛-+≤-⋅=-=x x x x x x y 当且仅当,232x x -=即⎪⎭⎫⎝⎛∈=23,043x 时等号成立18.(12分)解：tan 2,tan A c bB b-=根据正弦定理 sin sin 2sin sin sin cos sin A B C B B A B-∴= sin cos sin cos 2sin cos A B B A C A ∴+= sin()2sin cos A B C A ∴+=1sin 2sin cos cos 602C C A A A ∴=⇒=⇒=︒19.(12分)解：当m=0时，有8>0,显然成立；当m ≠0时，有⎩⎨⎧≤∆>00m ，即⎩⎨⎧≤+->0)8(4)6(02m m m m ，解之得 0<m ≤1.综上所述得 0≤m ≤1. 20.(14分)解：（1）设数列的公差为d ，因为f(1)= a 1+a 2+a 3+…+a n =n 2，则na 1+2)1(-n n d=n 2,即2a 1+(n-1)d=2n. 又f(-1)= -a 1+a 2-a 3+…-a n-1+a n =n,即d n⋅2=n,d=2.解得a 1=1.∴a n =1+2(n-1)=2n-1.(2) ⎪⎭⎫ ⎝⎛21f =n n )21)(12()21(5)21(32132-++++ ,把它两边都乘以21，得：n n n n f )21)(12()21)(32()21(3)21()21(21132-+-+++=- 两式相减，得：n n n f )21)(12()21(2)21(2)21(221)21(21132--++++=- =21)21)(12()21(2)21(221212---+++⨯-n n n =21)21)(12()21(2221)21)(12(211])21(1[21211----=-------n n n n n n=n n )21)(32(23+-(3)23)21)(32(23<+-n n∴.3)21(<f。

小学数学必修5第一单元测试题(附答案)

小学数学必修5第一单元测试题(附答案)一、选择题1. 下列哪个数是1.235的百分之一？- A. 0.- B. 0.- C. 0.1235- D. 0.- Answer: B2. 计算：4.2 + (-3.5) = ?- A. 0.7- B. 0.75- C. -0.7- D. -0.75- Answer: C3. 一件商品原价100元，现打8折后出售，打折后的价格是多少元？- A. 20- B. 80- C. 92- D. 120- Answer: C4. 在12小时内，指针会走过12个格子，那么在1小时内，指针会走过几个格子？- A. 6- B. 10- C. 12- D. 24- Answer: B5. 三个相同的珠子平均分给4个人，每人得到的珠子数是多少？- A. 0- B. 0.75- C. 1- D. 1.25- Answer: B二、填空题1. 5 × 2 = ?- Answer: 102. 4.75 ÷ 0.5 = ?- Answer: 9.53. 38.2 × 0.1 = ?- Answer: 3.824. 7.5 ÷ 4 = ?- Answer: 1.8755. (7 + 5) × 3 = ?- Answer: 36三、解答题1. 将14分之1的大片地均匀分给7个人，每人分多少？- Answer: 每人分得2分。

2. 小明去超市买了一件原价50元的衣服，打8折后实付多少钱？- Answer: 小明实付40元。

3. 小红有42块糖，她拿出总数的三分之二分给小明，还剩多少块？- Answer: 小红还剩14块糖。

4. 小华家买了一箱苹果，有20斤，每斤7元，总共花了多少钱？- Answer: 小华家总共花了140元。

5. 小明和小红一起去公园，他们每人带了3个糖果。

他们两人总共带了多少个糖果？- Answer: 小明和小红总共带了6个糖果。