大学物理振动和波习题课
大学物理振动与波练习题与答案
【解】:(1) y 5cos(20 4x) 厘米
(2) y 5cos(3t 11) 厘米
(3) y 5cos3(t 4 x 5) , c 3 (cm/ s)
33
4
(4) y 5cos(3t 9) , yI 15 sin(3t 9) 0
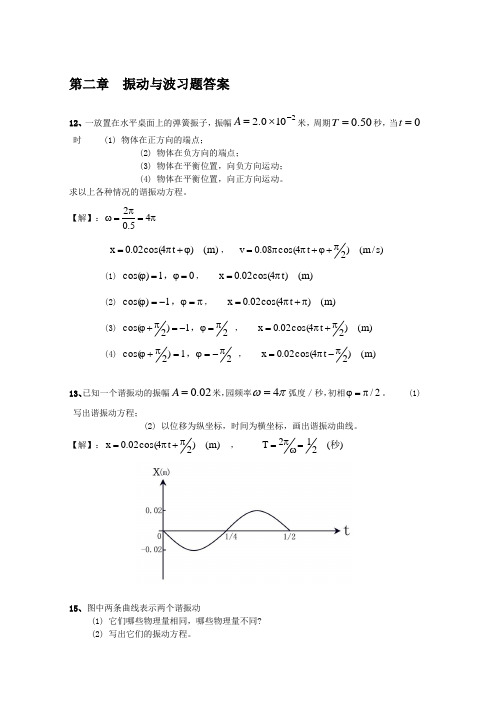
23、一平面简谐波沿 x 轴正方向传播,波速 c=8 m/s, 若 t=0 时的波形曲线如图 2-23 所示 (1)写出波动方程 (2)画出 t=1.25 s 时的波形曲线 【解】:
t=0 时,y=0, v>0 cm T=5s
所以 2 。 波长= 40
y 4.0 cos[0.4t ] (cm) 2
B 点的振动方程
yA
(t)
5 c os [10
(t
20) 300
2
]
5 c os (10t
7 6
)cm
(2)
A,B 相位相同
(3) 或 O 点的振动方程
yo
(t)
5
cos(10t
2
)
(cm)
O 点相位
o
2
OB,OA 间的相位差
oA
oB
2 3
O 比 A 超前
oA
o
A
2 3
A
7 6
同时 B 点
13、已知一个谐振动的振幅 A 0.02 米,园频率 4 弧度/秒,初相 / 2 。 (1)
写出谐振动方程; (2) 以位移为纵坐标,时间为横坐标,画出谐振动曲线。
【解】: x 0.02cos(4 t 2) (m) ,
T
2
1 2
大学物理_波动及课后习题

A 2
2 0 3
取 S点为坐标 原点,以
波的传播方向为 x 轴正方向。
2) 在 x 轴上任取一点 P, OP = x ,
y
o s
x
u
P
x
由于 P点相位落后
S点的时间为—— 于是得到波的表达式为 :
x 2 y 8 10 cos[ (t ) ]m u 3
2
结论:
(1) 质元并未“随波逐流”
波的传播不是媒质质元的传播
(2) “上游”的质元依次带动“下游”的质元振动 (3) 某时刻某质元的振动状态将在较晚时刻 t T /于“下游”某处出现 4 ---波是振动状态的传播
(4) 同相点----质元的振动状态相同
t T / 4 t 5T / 4 t T / 2
x
故
将
p
x
4m
s
D
x y 0.05 cos[3(t ) ](SI ) 2 3
x D 4m 代入波方程,得到 D点的
振动方程:
y D 0.05 cos[3(t 2) ](SI ) 3
(2). 以 S 点左方7m处的 O 点为坐标原点, 取 x 轴正方向向右,写出波方程及 D 点的 振动方程。 u
x / cm
0 0
5 yo cos( t ) 3
5 x y cos[ (t )] 3 10
方法2: 将波形倒退
6
得出 t 0 波形,再写方程! …..
0 0
20.2 解:应用时间落后法,
可得
ξ 0 0.1 x x
x 0.1 y 0.05sin[1.0 4.0(t )] 0.8 0.05sin[(4.0t 5 x 0.5)] 0.05sin[ (4.0t 5 x 0.5)] 0.05sin(4.0t 5 x 2.64)
大学物理 振动与波练习题
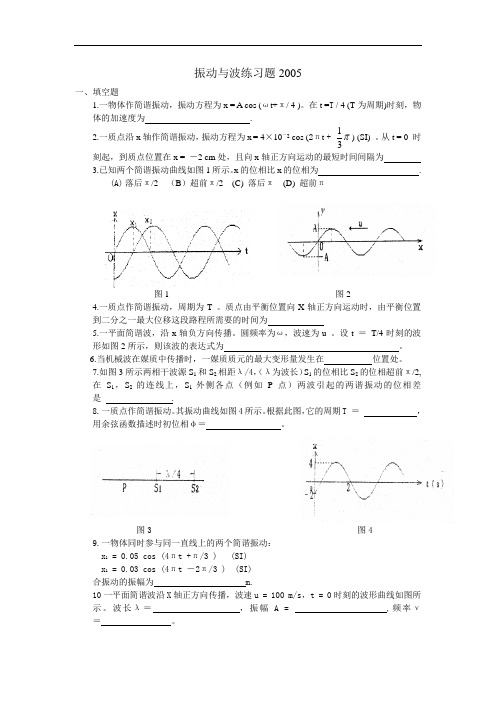
振动与波练习题2005 一、填空题 1.一物体作简谐振动,振动方程为x = A cos (ωt+π/ 4 )。
在t =T / 4 (T 为周期)时刻,物体的加速度为 .2.一质点沿x 轴作简谐振动,振动方程为x = 4×10-2 cos (2πt + 31) (SI) 。
从t = 0 时刻起,到质点位置在x = -2 cm 处,且向x 轴正方向运动的最短时间间隔为3.已知两个简谐振动曲线如图1所示。
x 的位相比x 的位相为 .(A) 落后π/2 (B )超前π/2 (C) 落后π (D) 超前π图1 图24.一质点作简谐振动,周期为T 。
质点由平衡位置向X 轴正方向运动时,由平衡位置到二分之一最大位移这段路程所需要的时间为5.一平面简谐波,沿x 轴负方向传播。
圆频率为ω,波速为u 。
设t = T/4时刻的波形如图2所示,则该波的表达式为 。
6.当机械波在媒质中传播时,一媒质质元的最大变形量发生在 位置处。
7.如图3所示两相干波源S 1和S 2相距λ/4,(λ为波长)S 1的位相比S 2的位相超前π/2,在S 1,S 2的连线上,S 1外侧各点(例如P 点)两波引起的两谐振动的位相差是 .8.一质点作简谐振动。
其振动曲线如图4所示。
根据此图,它的周期T = ,用余弦函数描述时初位相φ= 。
图3 图49.一物体同时参与同一直线上的两个简谐振动:x 1 = 0.05 cos (4πt +π/3 ) (SI)x 1 = 0.03 cos (4πt -2π/3 ) (SI)合振动的振幅为 m.10一平面简谐波沿X 轴正方向传播,波速u = 100 m/s ,t = 0时刻的波形曲线如图所示。
波长λ= ,振幅 A = ,频率ν= 。
11.一平面简谐波(机械波)沿x轴正方向传播,波动方程为y = 0.2 cos (πt –πx/2 )(SI),则x = -3 m 处媒质质点的振动加速度a的表达式为。
振动和波习题课(级)

能量极 小
X
能量极 大
能量极大
能量极 小
16、惠更斯原理:波阵面上的每一点,都是发射 子波的新波源,其后任意时刻,这些子波的包络 面就是新的波阵面。
17、相干条件:两波源应满足:振动方向相同,
频率相同,位相差恒定。
18、波的干涉 在P点引起的合振动的振幅为:
2 1 2 2
S2 S1
r2
p
2 ( 2 1 )+ ( r1 r2 ) A A A 2 A1 A2 cos S1 r1 若波在两种不同介质中传播
2
y a O b u x
[A]
11.一质点同时参与了三个简谐振动,它们的振动 1 5 方程分别为 x1 A cos( t π ) x2 A cos( t π)
x3 A cos( t π ) 其合成运动的运动方程为x = ___ 0 .
3
3
12. 一简谐波沿x轴负方向传播,波速为1 m/s,在 x轴上某质点的振动频率为1 Hz、振幅为0.01 m.t =0 时该质点恰好在正向最大位移处.若以该质点 的平衡位置为x轴的原点.求此一维简谐波的表达 式. 结 果 : y 0 . 01 cos 2π ( t x ) (SI) 13. 当机械波在媒质中传播时,一媒质质元的最大 变形量发生在 : (A) 媒质质元离开其平衡位置最大 位移处. (B) 媒质质元离开其平衡位置( 2 A / 2 )处 (A是振动振幅). (C) 媒质质元在其平衡位置处. 1 [C] (D) 媒质质元离开其平衡位置 2 A 处.
2
2
(C)
3 x2 A cos( t π ) 2
t π ) [B] (D)x2 A cos(
大学物理振动波动例题习题

振动波动一、例题(一)振动1。
证明单摆是简谐振动,给出振动周期及圆频率.2. 一质点沿x 轴作简谐运动,振幅为12cm,周期为2s 。
当t = 0时, 位移为6cm ,且向x 轴正方向运动。
求: (1) 振动表达式;(2) t = 0.5s 时,质点的位置、速度和加速度;(3)如果在某时刻质点位于x =—0.6cm ,且向x 轴负方向运动,求从该位置回到平衡位置所需要的时间。
3。
已知两同方向,同频率的简谐振动的方程分别为:x 1= 0.05cos (10 t + 0.75π) 20.06cos(100.25)(SI)x t π=+求:(1)合振动的初相及振幅.(2)若有另一同方向、同频率的简谐振动x 3 = 0。
07cos (10 t +ϕ 3 ), 则当ϕ 3为多少时 x 1 + x 3 的振幅最大?又ϕ 3为多少时 x 2 + x 3的振幅最小?(二)波动1. 平面简谐波沿x 轴正方向传播,振幅为2 cm ,频率为 50 Hz ,波速为 200 m/s.在t = 0时,x = 0处的质点正在平衡位置向y 轴正方向运动,求:(1)波动方程(2)x = 4 m 处媒质质点振动的表达式及该点在t = 2 s 时的振动速度。
2. 一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播.已知原点的振动曲线如图所示.求:(1)原点的振动表达式;(2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差.3. 两相干波源S 1和S 2的振动方程分别是1cos y A t ω=和2cos(/2)y A t ωπ=+.S 1距P 点3个波长,S 2距P 点21/4个波长。
求:两波在P 点引起的合振动振幅。
4。
沿X 轴传播的平面简谐波方程为:310cos[200(t )]200x y π-=- ,隔开两种媒质的反射界面A 与坐标原点O 相距2。
25m ,反射波振幅无变化,反射处为固定端,求反射波的方程.二、习题课(一)振动1. 一质点在x 轴上作简谐振动,振辐A = 4 cm,周期T = 2 s ,其平衡位置取作坐标原点.若t = 0时刻质点第一次通过x = -2 cm 处,且向x 轴负方向运动,则O 2.25m Ax t O A/2 -A x 1 x 2 质点第二次通过x = -2 cm 处的时刻为[ ](A) 1 s (B) (2/3) s (C ) (4/3) s (D ) 2 s2.已知某简谐振动的振动曲线如图所示,则此简谐振动的振动方程为(A ) ⎪⎭⎫ ⎝⎛+=3232cos 2ππt x ;(B ) ⎪⎭⎫ ⎝⎛-=332cos 2ππt x ;(C) ⎪⎭⎫ ⎝⎛+=3234cos 2ππt x ;(D ) ⎪⎭⎫ ⎝⎛-=334cos 2ππt x 。
2019《大学物理教学课件》振动与波作业答案.ppt

波动(一)
( SI )
3. y 0.1 cos(三、Fra bibliotek算题2
t
3
),
y 0.1 cos(
2
t
2 2 x ) ( SI ) 5 3
1. (1). 2 / T rad / s;
t 0 : y0 A
y 0.01 cos(t )( SI ) x ( 2). u 2ms y 0.01 cos( ( t ) x ) ( SI ) 2 ( 3). uT 4ms y( m )
t 0: y 0
dy 0 dt
x0
2
在2秒内波形移动了 40cm
u 20cm / s
3.2m
2
u
8
)
(1). y 0.01 cos(
8
t
2
( SI ) ( SI )
x ( 2). y 0.01 cos( ( t ) ) 8 0.2 2
0.01 1 3 5
-0.01
X(m)
三、计算题
0.05
y( m )
波动(一)
-0.05
1.5
4.5
7.5
X(m)
2. 2u / 8rad / s;
t 0 : y0 A
x y 0.05 cos(8 ( t )t )( SI ) 24 t 0.25, x1 0 : y 0.05 cos 3 0.05m dy / dt 0.05 8 sin[ 8 (0.25 0) ] 0
2. y 0.01 cos(10t ) 27 y 0.01 cos(10t ) ( SI ) , 1.83m 3 2 2 3. R2 : R1
大学物理热学振动和波动习题课.ppt.ppt

2 k 1 2 1 2k 2 1
A A 1A 2
A A A 1 2
简谐波的波函数
一.描述简谐波的物理量 1.波长—波线上相邻同相点的距离。
2.波速u—振动的相的传播速度。 决定于媒质的惯性和弹性。 3.周期T= /u
1 4.频率 v T 2
u
5.波数k = 2 /
二.平面简谐波的波动方程(波函数) Y 已知:波源O的振动方程
y A c o s t 0
则:ox上所有质点的
振动方程
相位比o 落后了 2x/ 振动时间 x/u 比o晚了
O
x
X
或
2 x y A cos t
x y 3 c o s2 ( t ) a 2 0
u
B2 a
b1
x
5 x y 3 cos 2 ( t ) b 1 20 20 5 x y 3 cos 2 ( t ) b 2 20 20
例4 如图所示,S1、S2为相同振动方向、相同频率v, 相同振幅A的相干波源,且S1的位相较S2超前/2,S1、 S2相距7/4。当两列波以相对速度相向而行时,在S1S2 连线上有哪些合成波为节点?
N n P RT RT VN N 0 0
PV
N RT N0
n1 P RT 1 N0
2 n 1 P RT 2 P 2 1 N 0
P P 3 3 1
P P P P 6 P 1 2 3 1
例2 试说明下列各式的物理意义
Nf vdv dN Nf v dv , v 1
合成后仍然是谐振动。式中A和为:
x A cos t
大学物理振动和波习题课
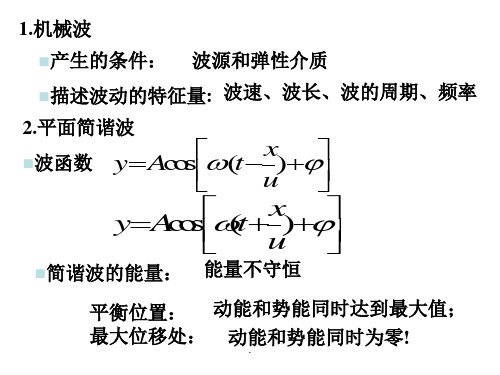
12、一质点作简谐振动,周期为 T。质点由平衡
位置向X轴正方向运动时,由平衡位置到二分之一 最大位移这段路程所需要的时间为( )。
A T 4 B T 1 C 2 T 6 D T 8
解:令简谐振动为 xA si n t
则当 xA2 时, si n t0.5
Acos2(t 1) T2
Acos2T(t 13)
.
7.图中所示为两个简谐振动的振动曲线.若以余弦函数表 示这两个振动的合成结果,则合振动的方程为
xx1x2 0.04cos(t)
x (m)
0.08
O
-0.04
1
x1 t (s)
2 x2
.
8 如果在固定端 x0处反射的反射波方程式是
y2 Aco2stx
设反射波无能量损失,则入射波的方程式是( ) 形成的驻波的表达式是( )。
y1OAcos2vt y2OA cos2vt
形成的驻入 波射 为波 :方 程 y1Acos 2 t x
y y 1 y 2 A c 2 ot s2 x A c 2 ot s2 x
得:
S
wu
1 A22u
2
3.惠更斯原理和波的叠加原理
惠更斯原理:
波阵面上每一点都可以看作是发出球面子波的 新波源,这些子波的包络面就是下一时刻的波阵面。
波的叠加原理:
当几列波在介质中某点相遇时,该质点的
振动位移等于各列波单独传播时在该点引起位 移的矢量和。
.
4.波的干涉: 相干条件: 振动方向相同
频率相同
1.机械波
产生的条件: 波源和弹性介质
描述波动的特征量: 波速、波长、波的周期、频率
2.平面简谐波
波函数 yAcos(tux)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:令简谐振动为 x Asint
则当 x A 2 时, sint 0.5
2 t 2k
k 0,1,2,
T
6
16
由题意知, t T 4 ,所以 t T 12 。
故选(B)。
13、两相干波源 S和 S相距 4 ,S 的位相比
S 2
的位相超前
21,在2两波源的连线上1 ,S1
已知:OA 7 / 8 OB / 2 在t = 0 时,x = 0 处媒质
质元的合振动经平衡位置向负方向运动.求B点处入射 波和反射波的合成振动方程.
解: 设入射波在O点的振动为
y
y1O Acos(2π t )
入射波y1
Acos(2π t
2π
x
)
O
y1A
Acos(2π t
2π
7 8
)
y2 A
因此 mg kx0
+X
k
则 x0 mg k 0.2m
此时物体速度
o
hm
v0 2gh 2.42m s
圆频率
振幅
k m
7 rad s
A
x2 0
v2 0
2
0.4m
Q
x0
A cos
A, 2
v0 0
3
故振动方程为:
x
0.4
cos
7t
3
m
25
17 已知一沿X轴正向传播的平面余弦波,当
(t 1 )13求s时o的点波处形质如点图振所动示的,初且周周相期;(T2)2写s 出。该
外侧
(例如 P点)两波引起的两简谐振动的位相差是:
A0 B C 2 D3 2
解:位相差
2
1
r2
r1
2
4 2 2
P S1
故选(B)。
S2
17
14 一质量 m 0.25kg 的物体,在弹性恢复力的
作用下沿X轴运动,弹簧的倔强系数 k 25Nm1
(1)求振动的周期和圆频率。
(处2,)且如 物果 体振 沿幅 X轴A反 1向5运cm动, t,求0 初时速位移v 及x0初相7.5。cm
情况,列出以O点为原点的波动方程。
解:O点的位相较P点超前
Yc
l
2
2 l 2 c
l
c
l
O PX
所以O点的振动方程为
y
A cos
t
l
c
故以O为原点的波动方程为:
y
A
cos
t
x c
l
c
Acos
t
x
c
l
28
19.振幅为A,频率为 ,波长为 的一简谐波沿弦线传播
在自由端A点反射(如图),假设反射后的波不衰减.
波的波动方程;(3)求 P点处质点振动的初周相
及振动方程。
Y cm
解:(1)先求周相 t
依题意有
10
5
5
10
cos
1 3
o
5
2
10
3
3
P
20 X cm
40cm
又由题意
vo
A sin
3
0
2
3
3 26
即O点处质点振动的初周相为 。
3
(2)因为O点的振动方程为
yo
10cost
12
7.图中所示为两个简谐振动的振动曲线.若以余弦函数表 示这两个振动的合成结果,则合振动的方程为
x x1 x2 0.04 cos(t )
x (m)
0.08
O
-0.04
1
x1 t (s)
2 x2
13
8 如果在固定端 x 0处反射的反射波方程式是
y2
A cos2 t
x
设反射波无能量损失,则入射波的方程式是( )
(3)写出振动的数学表达式。
0
解:(1)
(2)方法一: 依题意,由公式
k 10s1 m
T 2 0.63s
A
x02
v0
2
得:
v0
A2
x2 0
1.3m
s
18
arctg
v0
x0
3
or
4
3
Q x0 Acos 0
3
方法二:
令振动方程为 x Acost ,则
v A sint
若t = 0时质点过x = 0处且朝x轴正方向运动,则振动方程为
x =_____________________________
若t
=
0时质点处于
x
1 2
A
处且向x轴负方向运动,
则振动方程为 x =_____________________________.
Acos(2t 1 ) T2
Acos(2t 1 ) T3
x BA
反射波y2
A cos[2π(t
x
7
u
/8)
2
7 8
]
Acos(2π t 2π x 3 π )
29
2
y
y1
y2
2 A cos(2π
x
3 4
π) cos(2π t
3 4
π
)
在t = 0时,x = 0处,有y = 0和 ( dy / dt ) < 0,故得:
2Acos(3π / 4) cos( 3π / 4) 0
可确定出 2
故波动方程为:y
0.03cos50
t
x 6
2
m 22
16 如图,一平面波在介质中以速度 u 20m s
沿X轴负方向传播,已知A点的振动方程为
y 3cos4t SI
(1)以A点为坐标原点写出波动方程;
(2)以距A点 5m 处的B点为坐标原点,写出波
动方程。
解:如果原点振动方程为
t 0 时,波源振动的位移恰为正的最大值。若
波源处为原点。则沿波传播方向距离波源为 处的
振动方程为(
),当
t
T
2
时,x
4
处2质点
的振动速度为( )。
解: 令波动方程y A cost x
c
2 4
T
c 20
T
y
0.1cos4
t
x 20
10
令
x
2
5
,代入波动方程得振动方程为:
y
c
g
2g
3g
3g
解:复摆 T 2 I
轴的距离。
mgh
,h 为物体重心到
则
T 2
ml 2
3 2
2l
mgl
3g
2
故选(C)。
7
3 已知一平面简谐波的波动方程为 y Acosat bx
(a 、b 为正值)则
(A)波的频率为 a;(B)波的传播速度为b
(C)波长为
b
;(D)波的周期为 2
a
a。
解:
4 cos
2
T
t
3
t 1, x 0且T 2s T 2.4s 故选(B)6 。
2 一长为 l 的均匀细棒悬于通过其一端的光滑水
平轴上,如图示,作成一复摆。已知细棒绕通过其
一端的轴的转动惯量 1 ml 2 ,此摆作微小振动的
周期为( )。
3
o
A 2 l B 2 l C 2 2l D l
' u v0
u mvs 5
机械振动和机械波习题课
一 选择填空题
1 一简谐振动曲线如图示,则振动周期是( )
A2.62s B2.40s C2.20s D2.00s
解:
xm
x Acos t , A 4 4
Q t 0,
x0 4 cos 2,
2
01
ts
v0 A sin
3
0
x
(A)动能为零,势能最大;
(B)动能为零,势能为零;
(C)动能最大,势能最大;
(D)动能最大,势能为零。
( )。
10 质量为 m的物体和一个轻弹簧组成弹簧振子,
其固有振动周期为 T 。当它作振幅为A 的自由简谐 振动时,其振动能量 E =( )。
解: T 2 m
k
k 4 2m
T2
E 1 kA2 2 2mA2
频率相同
相位相同或相位差恒定
干涉相长和干涉相消的条件:
2
1 2 (r2
r1)
2k
(2k
1)
若2=1
k
r1 r2
2k
1
2
,
3
5.驻波: 是由振幅相同,传播方向相反的两列相干波
叠加而成。
驻波特点:
质元分段振动,没有波形的传播,故名驻波; 各质点的振幅各不相同;
波节,波腹; 在空间的位置不动;
下,有一质量为m的物体自高为h 处自由下落至盘
中,并与盘粘在一起作谐振动。设 m 0.1kg,
k 4.9 N m, h 0.3m ,若以物体刚落至盘中时
为计时起点,求系统的振动方程。
解:以平衡位置为坐标原点,向上为X轴正向。
24
依题意,t 0 时,物体的位置 x
等于达平衡位置时弹簧伸长量,0
2
T2
15
11.一弹簧振子作简谐振动,总能量为E1,如果简谐振动
振幅增加为原来的两倍,重物的质量增为原来的四倍,
则它的总能量E2变为
[D ]
( A)E1 / 4 (B)E1 / 2 (C)2E1 (D)4E1
12、一质点作简谐振动,周期为 T。质点由平衡
位置向X轴正方向运动时,由平衡位置到二分之一 最大位移这段路程所需要的时间为( )。
