材料弹性常数E、μ与材料切变模量G的测定
剪切弹性模量g的测定实验报告

剪切弹性模量g的测定实验报告剪切弹性模量G的测定实验报告引言:弹性模量是材料力学性质的重要参数,它描述了材料在受力作用下的变形能力。
剪切弹性模量G是弹性模量的一种,用于描述材料在剪切应力作用下的变形能力。
本实验旨在通过测定剪切弹性模量G的方法,掌握实验技巧,加深对材料力学性质的理解。
实验仪器与材料:1. 剪切弹性模量测定仪器2. 弹性体样品(如橡胶块)实验原理:剪切弹性模量G可以通过测定剪切应力和剪切应变的关系来计算。
实验中,我们将利用剪切弹性模量测定仪器对样品进行测试。
该仪器通过施加剪切力和测量剪切应变,得到剪切弹性模量G的数值。
实验步骤:1. 将弹性体样品放置在剪切弹性模量测定仪器上,并调整仪器使其处于平衡状态。
2. 施加一个恒定的剪切力,记录下施力的数值。
3. 测量样品在施力下产生的剪切应变,记录下剪切应变的数值。
4. 根据施力和剪切应变的数值,计算剪切弹性模量G的数值。
实验结果与分析:根据实验数据计算得到的剪切弹性模量G的数值为X。
通过对实验结果的分析,我们可以得出以下结论:1. 弹性体样品在受力作用下发生剪切变形,剪切弹性模量G描述了材料抵抗剪切应力的能力。
2. 弹性体样品的剪切弹性模量G的数值与材料的性质有关,不同材料的剪切弹性模量G可能存在差异。
3. 实验中所使用的剪切弹性模量测定仪器对于测量剪切弹性模量G具有较高的精确度和准确性。
实验误差与改进:在实验过程中,可能存在一些误差,影响了实验结果的准确性。
可能的误差来源包括:1. 仪器的精度限制:剪切弹性模量测定仪器的精度可能存在一定限制,导致实验结果的误差。
2. 样品的非理想性:实际样品可能存在缺陷或不均匀性,导致实验结果的误差。
3. 实验操作的不精确性:实验过程中操作的不精确性可能导致实验结果的误差。
为了减小误差,提高实验结果的准确性,可以采取以下改进措施:1. 使用更精确的仪器:选择精度更高的剪切弹性模量测定仪器,提高实验结果的准确性。
弹性模量的测定整理

弹性模量的定义及其相互关系材料在弹性变形阶段,其应力和应变成正比例关系(即符合胡克定律),其比例系数称为弹性模量(Elastic Modulus )。
弹性模量的单位是GPa 。
“弹性模量”是描述物质弹性的一个物理量,是一个总称,包括“杨氏模量”、“剪切模量”、“体积模量”等。
所以,“弹性模量”和“体积模量”是包含关系。
一般地讲,对弹性体施加一个外界作用(称为“应力”)后,弹性体会发生形状的改变(称为“应变”),“弹性模量”的一般定义是:应力除以应变。
线应变:对一根细杆施加一个拉力F ,这个拉力除以杆的截面积S ,称为“线应力”,杆的伸长量dL 除以原长L ,称为“线应变”。
线应力除以线应变就等于杨氏模量E=( F/S)/(dL/L)。
剪切应变:对一块弹性体施加一个侧向的力f (通常是摩擦力),弹性体会由方形变成菱形,这个形变的角度a 称为“剪切应变”,相应的力f 除以受力面积S 称为“剪切应力”。
剪切应力除以剪切应变就等于剪切模量G=( f/S)/a 。
体积应变:对弹性体施加一个整体的压强P ,这个压强称为“体积应力”,弹性体的体积减少量(-dV)除以原来的体积V 称为“体积应变”,体积应力除以体积应变就等于体积模量: K=P/(-dV/V)。
意义:弹性模量可视为衡量材料产生弹性变形难易程度的指标,其值越大,使材料发生一定弹性变形的应力也越大,即材料刚度越大,亦即在一定应力作用下,发生弹性变形越小。
弹性模量E 是指材料在外力作用下产生单位弹性变形所需要的应力。
它是反映材料抵抗弹性变形能力的指标,相当于普通弹簧中的刚度。
说明:弹性模量只与材料的化学成分有关,与其组织变化无关,与热处理状态无关。
各种钢的弹性模量差别很小,金属合金化对其弹性模量影响也很小。
泊松比(Poisson's ratio ),以法国数学家 Simeom Denis Poisson 为名,是横向应变与纵向应变之比值它是反映材料横向变形的弹性常数。
材料的三大参数

剪切弹性模量(elastic shear modulus)G,材料的基本物理特性参数之一,与杨氏(压缩、拉伸)弹性模量E、泊松比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
其定义为:G=τ/γ,其中G(M pa)为切变弹性模量;τ为剪切应力(M pa);γ为剪切应变(弧度)。
剪切模量:材料常数,是剪切应力与应变的比值。
又称切变模量或刚性模量。
材料的力学性能指标之一。
是材料在剪切应力作用下,在弹性变形比例极限范围内,切应力与切应变的比值。
它表征材料抵抗切应变的能力。
模量大,则表示材料的刚性强。
剪切模量的倒数称为剪切柔量,是单位剪切力作用下发生切应变的量度,可表示材料剪切变形的难易程度。
剪切应力shear stress物体由于外因(载荷、温度变化等)而变形时,在它内部任一截面的两方出现的相互作用力,称为“内力”。
内力的集度,即单位面积上的内力称为“应力”。
应力可分解为垂直于截面的分量,称为“正应力”或“法向应力”;相切于截面的分量称为“剪切应力”。
作用在构件两侧面上的外力的合力是一对大小相等,方向相反,作用线相距很近的横向集中力。
在这样的外力作用下,构件的变形特点是:以两力之间的横截面为分界线,构件的两部分沿该面发生相对错动。
构件的这种变形形式称为剪切,其截面为剪切面。
截面的单位面积上剪力的大小,称为剪应力。
剪切应力的计算:在实用计算中,假设在剪切面上剪切应力是均匀分布的。
若以A表示剪切面面积,则应力是τ 与剪切面相切,故称:切应力剪切应变shear strain剪切时物体所产生的相对形变量。
即指在简单剪切的情况下,材料受到的力F是与截面A0相平行的大小相等、方向相反的两个力,在此剪切力作用下,材料将发生偏斜。
偏斜角θ的正切定义为剪切应变γ:即γ=tanθ。
当剪切应变足够小时,γ=θ,相应地剪切应力为τ=F/A。
杨氏弹性模量杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量,也是材料力学中的名词。
材料的三大参数

剪切弹性模量(elastic shear modulus)G,材料的基本物理特性参数之一,与杨氏(压缩、拉伸)弹性模量E、泊松比ν并列为材料的三项基本物理特性参数,在材料力学、弹性力学中有广泛的应用。
其定义为:G=τ/γ,其中G(M pa)为切变弹性模量;τ为剪切应力(M pa);γ为剪切应变(弧度)。
剪切模量:材料常数,是剪切应力与应变的比值。
又称切变模量或刚性模量。
材料的力学性能指标之一。
是材料在剪切应力作用下,在弹性变形比例极限范围内,切应力与切应变的比值。
它表征材料抵抗切应变的能力。
模量大,则表示材料的刚性强。
剪切模量的倒数称为剪切柔量,是单位剪切力作用下发生切应变的量度,可表示材料剪切变形的难易程度。
剪切应力shear stress物体由于外因(载荷、温度变化等)而变形时,在它内部任一截面的两方出现的相互作用力,称为“内力”。
内力的集度,即单位面积上的内力称为“应力”。
应力可分解为垂直于截面的分量,称为“正应力”或“法向应力”;相切于截面的分量称为“剪切应力”。
作用在构件两侧面上的外力的合力是一对大小相等,方向相反,作用线相距很近的横向集中力。
在这样的外力作用下,构件的变形特点是:以两力之间的横截面为分界线,构件的两部分沿该面发生相对错动。
构件的这种变形形式称为剪切,其截面为剪切面。
截面的单位面积上剪力的大小,称为剪应力。
剪切应力的计算:在实用计算中,假设在剪切面上剪切应力是均匀分布的。
若以A表示剪切面面积,则应力是τ 与剪切面相切,故称:切应力剪切应变shear strain剪切时物体所产生的相对形变量。
即指在简单剪切的情况下,材料受到的力F是与截面A0相平行的大小相等、方向相反的两个力,在此剪切力作用下,材料将发生偏斜。
偏斜角θ的正切定义为剪切应变γ:即γ=tanθ。
当剪切应变足够小时,γ=θ,相应地剪切应力为τ=F/A。
杨氏弹性模量杨氏模量(Young's modulus)是表征在弹性限度内物质材料抗拉或抗压的物理量,它是沿纵向的弹性模量,也是材料力学中的名词。
材料力学实验报告

1. 了解材料力学实验的基本原理和方法。
2. 掌握材料力学实验的基本操作技能。
3. 通过实验,验证材料力学理论,加深对材料力学基本概念和原理的理解。
4. 培养学生严谨的科学态度和实验操作能力。
二、实验内容1. 金属拉伸实验2. 金属扭转实验3. 材料切变模量G的测定三、实验原理1. 金属拉伸实验:通过拉伸试验,测定材料的弹性模量、屈服强度、极限抗拉强度等力学性能指标。
2. 金属扭转实验:通过扭转试验,测定材料的扭转刚度、剪切强度极限等力学性能指标。
3. 材料切变模量G的测定:通过扭转试验,测定材料的切变模量G,验证圆轴扭转时的虎克定律。
四、实验仪器1. 金属拉伸试验机2. 金属扭转试验机3. 电测仪4. 游标卡尺5. 扭角仪6. 电阻应变仪7. 百分表1. 金属拉伸实验(1)将试样安装在试验机上,调整试验机至适当位置。
(2)启动试验机,逐渐增加拉伸力,记录拉伸过程中的应力、应变数据。
(3)绘制应力-应变曲线,分析材料的力学性能。
2. 金属扭转实验(1)将试样安装在扭转试验机上,调整试验机至适当位置。
(2)启动试验机,逐渐增加扭矩,记录扭转过程中的扭矩、扭角数据。
(3)绘制扭矩-扭角曲线,分析材料的力学性能。
3. 材料切变模量G的测定(1)将试样安装在扭转试验机上,调整试验机至适当位置。
(2)启动试验机,逐渐增加扭矩,记录扭矩、扭角数据。
(3)利用电阻应变仪、百分表等仪器,测量试样表面的应变。
(4)根据虎克定律,计算材料的切变模量G。
六、实验数据及结果分析1. 金属拉伸实验(1)根据应力-应变曲线,确定材料的弹性模量、屈服强度、极限抗拉强度等力学性能指标。
(2)分析材料在不同应力状态下的变形特点。
2. 金属扭转实验(1)根据扭矩-扭角曲线,确定材料的扭转刚度、剪切强度极限等力学性能指标。
(2)分析材料在不同扭角状态下的变形特点。
3. 材料切变模量G的测定(1)根据扭矩、扭角、应变数据,计算材料的切变模量G。
切变模量体变模量

切变模量体变模量切变模量与体变模量是材料力学性质的重要参数,通常用来描述材料在受到外力时的应变特性。
切变模量描述材料在受到剪切力时的应变调节能力,体变模量描述材料在受到体积力时的应变调节能力。
本文将从理论基础、实验测定以及应用领域等方面进行较为详细的介绍。
一、理论基础:切变模量和体变模量均属于弹性模量的范畴,在材料力学领域中具有重要地位。
弹性模量是描述材料抵抗变形能力的一种参数,其中切变模量描述了材料对剪切力的应变调节能力,体变模量描述了材料对体积力的应变调节能力。
切变模量常用符号为G,单位为帕斯卡(Pa),体变模量常用符号为K,单位同样为帕斯卡(Pa)。
切变模量和体变模量的数值通常与物质的性质有关,不同材料具有不同的数值。
根据力学理论的基本方程,切变模量与体变模量可以通过弹性模量E、泊松比ν之间的关系来推导和计算。
具体而言,根据定义,切变模量G与弹性模量E、泊松比ν的关系为G = E / (2(1+ν)),而体变模量K与弹性模量E、泊松比ν的关系为K = E / (3(1-2ν))。
二、实验测定:切变模量和体变模量的实验测定主要通过材料试件在受到外力后的变形实验来完成。
对于切变模量,常见的实验方法包括剪切实验和扭转实验。
剪切实验通常通过加在两个平行表面上的平行力来对试件进行拉伸和剪切,通过测量应力应变曲线,可以得到材料的切变模量。
扭转实验则是通过试件在外力作用下进行旋转,并测量扭转角和扭转力来计算切变模量。
对于体变模量,常见的实验方法包括拉伸实验和压缩实验。
拉伸实验是将试件拉伸并测量拉伸力和伸长量,从而得到材料的体变模量。
而压缩实验则是将试件进行压缩,并测量压缩力和压缩变形来计算体变模量。
实验测定方法通常需要在标准试验条件下进行,以确保结果的准确性和可比性。
三、应用领域:切变模量和体变模量在工程领域广泛应用,对材料的力学性能有重要的影响和指导作用。
在土力学领域,切变模量和体变模量被广泛应用于土体力学参数的确定以及地基工程的设计中。
(4)材料切变模量G的测定
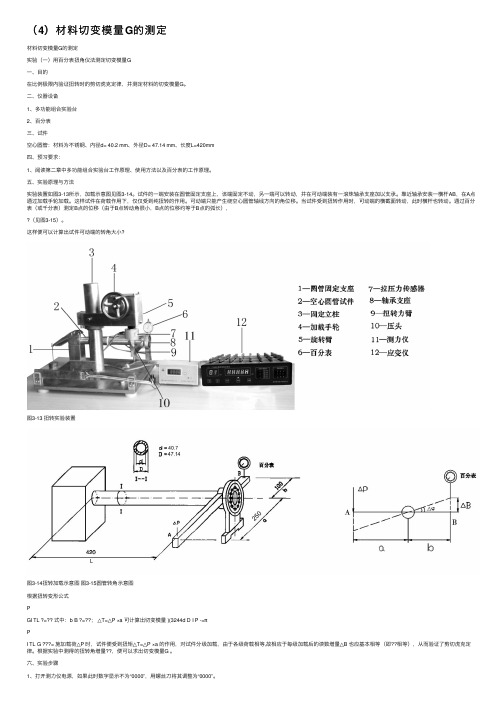
(4)材料切变模量G的测定材料切变模量G的测定实验(⼀)⽤百分表扭⾓仪法测定切变模量G⼀、⽬的在⽐例极限内验证扭转时的剪切虎克定律,并测定材料的切变模量G。
⼆、仪器设备1、多功能组合实验台2、百分表三、试件空⼼圆管:材料为不锈钢、内径d= 40.2 mm、外径D= 47.14 mm、长度L=420mm四、预习要求:1、阅读第⼆章中多功能组合实验台⼯作原理、使⽤⽅法以及百分表的⼯作原理。
五、实验原理与⽅法实验装置如图3-13所⽰,加载⽰意图见图3-14。
试件的⼀端安装在圆管固定⽀座上,该端固定不动,另⼀端可以转动,并在可动端装有⼀滚珠轴承⽀座加以⽀承。
靠近轴承安装⼀横杆AB,在A点通过加载⼿轮加载。
这样试件在荷载作⽤下,仅仅受到纯扭转的作⽤。
可动端只能产⽣绕空⼼圆管轴线⽅向的⾓位移。
当试件受到扭转作⽤时,可动端的横截⾯转动,此时横杆也转动。
通过百分表(或千分表)测定B点的位移(由于B点转动⾓很⼩,B点的位移约等于B点的弧长),(见图3-15)。
这样便可以计算出试件可动端的转⾓⼤⼩?图3-13 扭转实验装置图3-14扭转加载⽰意图图3-15圆管转⾓⽰意图根据扭转变形公式PGI TL ?=?? 式中:b B ?=??;△T=△P ×a 可计算出切变模量 )(3244d D I P -=πPI TL G = 施加载荷△P 时,试件便受到扭矩△T=△P ×a 的作⽤,对试件分级加载,由于各级荷载相等,故相应于每级加载后的读数增量△B 也应基本相等(即??相等),从⽽验证了剪切虎克定律。
根据实验中测得的扭转⾓增量??,便可以求出切变模量G 。
六、实验步骤1、打开测⼒仪电源,如果此时数字显⽰不为“0000”,⽤螺丝⼑将其调整为“0000”。
2、旋转百分表外壳,使⼤指针指到“0”。
3、顺时针转动加载⼿轮加载,分四级加载,每级加载200N ,⼀直加到800N(200N →400N →600N →800N )。
动态法测试弹性模量

动态法测试弹性模量材料的弹性模量的测试⼀、实验⽬的1、掌握拉伸法和动态法测弹性模量的原理。
2、掌握动态弹性模量测定⽅法与实验步骤及对试样的要求。
3、掌握测量结果的计算与数据处理。
⼆、实验原理弹性性能主要指材料在弹性变形范围内的物理量,包括弹性模量(E,⼜称杨⽒模量)、切变模量(G)和泊松⽐(ν),其中弹性模量和切变模量是表征固体材料弹性性质的重要⼒学参数,反映了固体材料抵抗外⼒产⽣形变的能⼒。
弹性模量也是进⾏热应⼒计算、防热与隔热层计算、选⽤机械构件材料的主要依据之⼀。
因此,精确测量弹性模量对理论研究和⼯程技术都具有重要意义。
弹性模量是固体材料在弹性形变范围内正应⼒与相应正应变的⽐值,其表达式为:(1)式中为材料弹性形变范围内的正应⼒,为相应的正应变。
E⼤⼩标志了材料的刚性,与物体的⼏何外形以及外⼒的⼤⼩⽆关,仅与材料的结构、化学成分和加⼯制造⽅法等有关。
对于⼀定的材料⽽⾔,E是⼀个常量。
测量弹性模量有多种⽅法,可分为静态法和动态法两种:①静态法(包括拉伸法、扭转法和弯曲法)通常适⽤于在⼤形变及常温下测量⾦属试样。
静态法测量载荷⼤、加载速度慢并伴有弛豫过程,对脆性材料(如⽯墨、玻璃、陶瓷等)不适⽤,也不能在⾼温状态下测量。
②动态法(⼜称共振法或声频法)包括弯曲(横向)共振法、纵向共振法和扭转共振法,其中弯曲共振法所⽤设备精确易得,理论同实验吻合度好,适⽤于各种⾦属及⾮⾦属(脆性)材料的测量,测定的温度范围极⼴,可从液氮温度⾄3000℃左右。
由于在测量上的优越性,动态法在实际应⽤中已经被⼴泛采⽤,也是国家标准(GB/T2105-91)推荐使⽤的测量弹性弹性模量的⼀种⽅法。
⽬前,测量材料的弹性模量主要有拉伸法和动态法。
1.拉伸法测量原理拉伸法是⽤拉⼒拉伸试样来研究其在弹性限度内受到拉⼒的伸长变形。
由式(1)有:(2)式中各量的单位均为国际单位。
可见,在弹性限度内,对试样施加拉伸载荷F,并测出标距L的相应伸长量,以及试样的原始横截⾯积,即可求得弹性模量E。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 材料弹性常数E 、μ的测定——电测法测定弹性模量E 和泊松比μ预习要求:1、 预习电测法的基本原理;2、 设计本实验的组桥方案;3、 拟定本实验的加载方案;4、 设计本实验所需数据记录表格。
一、实验目的1. 测量金属材料的弹性模量E 和泊松比μ;2. 验证单向受力虎克定律;3. 学习电测法的基本原理和电阻应变仪的基本操作。
二、实验仪器和设备1. 微机控制电子万能试验机;2. 电阻应变仪;3. 游标卡尺。
三、试件中碳钢矩形截面试件,名义尺寸图一 试件示意图bt为b t = (307.5)mm 2。
材料的屈服极限MPa s 360=σ。
四、实验原理和方法1、实验原理材料在比例极限内服从虎克定律,在单向受力状态下,应力与应变成正比:εσE = (1)上式中的比例系数E 称为材料的弹性模量。
由以上关系,可以得到:εεσ0A PE ==(2) 材料在比例极限内,横向应变ε'与纵向应变ε之比的绝对值为一常数:εεμ'=(3) 上式中的常数称为材料的横向变形系数或泊松比。
本实验采用增量法,即逐级加载,分别测量在各相同载荷增量P 作用下,产生的应变增量i。
于是式(2)和式(3)分别变为:ii A PE ε∆∆=0 (4) ii i εεμ∆'∆=(5) 根据每级载荷得到的E i 和i,求平均值:nE E ni i∑==1(6)图二 实验装置图nni i∑==1μμ (7)以上即为实验所得材料的弹性模量和泊松比。
上式中n 为加载级数。
2、增量法增量法可以验证力与变形之间的线性关系,如图三所示。
若各级载荷增量ΔP 相同,相应的应变增量也应大致相等,这就验证了虎克定律。
利用增量法,还可以判断实验过程是否正确。
若各次测出的应变不按线性规律变化,则说明实验过程存在问题,应进行检查。
采用增量法拟定加载方案时,通常要考虑以下情况: (1)初载荷可按所用测力计满量程的10%或稍大于此标准来选定;(本次实验试验机采用50KN 的量程) (2)最大载荷的选取应保证试件最大应力值不能大于比例极限,但也不能小于它的一半,一般取屈服载荷的70%~80%,故通常取最大载荷s P P 8.0max =;(3)至少有4-6级加载,每级加载后要使应变读数有明显的变化。
五、实验步骤1. 设计实验所需各类数据表格;2. 测量试件尺寸;分别在试件标距两端及中间处测量厚度和宽度,将三处测得横截面面积的算术平均值作为试样原始横截面积 。
3. 拟定加载方案;4. 试验机准备、试件安装和仪器调整;εP P P 1P∆ε∆P图三 增量法示意图5.确定组桥方式、接线和设置应变仪参数;6.检查及试车:检查以上步骤完成情况,然后预加载荷至最大值,再卸载至初载荷以下,以检查试验机及应变仪是否处于正常状态。
7.进行试验:加初载荷,记下此时应变仪的读数或将读数清零。
然后逐级加载,记录每级载荷下各应变片的应变值。
同时注意应变变化是否符合线性规律。
重复该过程至少两到三次,如果数据稳定,重复性好即可。
8.数据经检验合格后,卸载、关闭电源、拆线并整理所用设备。
六、试验结果处理σ—坐标系下描出实验点,然后拟合成直线,以验证虎克1.在坐标纸上,在ε定律;2.用逐差法(参考公式(4) ~(7))计算弹性模量E和泊松比。
七、思考题1.电测法测弹性模量E,试提出最佳布片方案?σ—图时,如何确定坐标原点?2.在绘制ε3.本实验如果不采用增量法,应如何拟定加载方案?实验三材料切变模量G的测定预习要求:1、复习电测法;2、预习扭角仪和百分表的使用方法。
3、设计本实验的组桥方案;4、拟定本实验的加载方案;(参照实验二中增量法部分的介绍)5、设计本实验所需数据记录表格。
一.实验目的1.两种方法测定金属材料的切变模量G;2.验证圆轴扭转时的虎克定律。
二.实验仪器和设备1.微机控制电子万能试验机2.扭角仪3.电阻应变仪4.百分表5.游标卡尺三.试件中碳钢圆轴试件,名义尺寸d=40mm, 材料屈服极限MPa s 360=σ。
四. 实验原理和方法1. 电测法测切变模量G材料在剪切比例极限内,切应力与切应变成正比,γτG = (1)上式中的G 称为材料的切变模量。
由式(1)可以得到:γτ=G (2) 圆轴在剪切比例极限内扭转时,圆轴表面上任意一点处的切应力表达式为:P W T=max τ (3) 由式(1)~(3)得到:γ⋅=P W T G (4)由于应变片只能直接测出正应变,不能直接测出切应变,故需找出切应变与正应变的关系。
圆轴扭转时,圆轴表面上任意一点处于纯剪切受力状态,根据图二所示正方形微体的变形分析可知:454522-=-=εεγ (5)由式(2)~(5)得到:454522εεp p W TW T G -==- (6)根据上式,实验时,我们在试件表面沿45o 方向贴应变片(一般贴二向应变花,如图三所示),即可测出材料的切变模量G 。
本实验采用增量法加载,即逐级加载,分别测量在各相同载荷增量T 作用下,产生的应变增量。
于是式(6)变为:454522εε∆⋅∆-=∆⋅∆=-p p W TW T G (7)根据本实验装置,有图一 实验装置图γABC D E D ’τ图二 微体变形示意图图三 应变花示意图a P T ⋅∆=∆ (8)a ——力的作用线至圆轴轴线的距离 最后,我们得到:454522εε∆⋅⋅∆-=∆⋅⋅∆=-p p W aP W a P G (9)2.扭角仪测切变模量G 。
等截面圆轴在剪切比例极限内扭转时,若相距为L 的两横截面之间扭矩为常数,则此梁横截面间的扭转角为:pGI TL=ϕ (10) 由上式可得:pI TLG ϕ=(11) 本实验采用增量法,测量在各相同载荷增量T 作用下,产生的转角增量。
于是式(11)变为:pI LT G ⋅∆⋅∆=ϕ (12)根据本实验装置,按图四所示原理,可以得到:bδϕ∆=∆ (13) δ——百分表杆移动的距离b ——百分表杆触点至试件轴的距离 最后,我们得到:pI b L a P G ⋅∆⋅⋅⋅∆=δ (14)五、实验步骤1.设计实验所需各类数据表格; 2. 测量试件尺寸 3. 拟定加载方案;δbϕ图四 实测ϕ的示意图4. 试验机准备、试件安装和仪器调整; 5. 测量实验装置的各种所需尺寸;6. 确定组桥方式、接线、设置应变仪参数; 7. 安装扭角仪和百分表; 8. 检查及试车;检查以上步骤完成情况,然后预加一定载荷(一般取试验机量程的15%左右),再卸载,以检查试验机、应变仪、扭角仪和百分表是否处于正常状态。
9. 进行试验;加初载荷,记录此时应变仪的读数或将读数清零,并记录百分表的读数。
逐级加载,记录每级载荷下相应的应变值和百分表的读数。
同时检查应变变化和位移变化是否基本符合线性规律。
实验至少重复三到四遍,如果数据稳定,重复性好即可。
10. 数据检查合格后,卸载、关闭电源、拆线、取下百分表并整理所用设备。
六、试验结果处理1. 从几组实验数据中选取线性最好的一组进行处理;在坐标纸上,分别在)(—004545-εεT 坐标系和ϕ—T 坐标系下描出实验点,并拟合成直线,以验证圆轴扭转时的虎克定律;2. 用作图法计算两种实验方法所得切变模量G ; 3. 用逐差法计算两种实验方法所得切变模量G ;七、思考题1. 电测法测切变模量G ,试提出最佳布片方案。
2.在安装扭角仪和百分表时,应注意什么问题?实验四直梁弯曲实验预习要求:1、复习电测法的组桥方法;2、复习纯弯梁理论;3、 设计本实验的组桥方案;4、 拟定本实验的加载方案;5、 设计本实验所需数据记录表格。
一、 实验目的:1. 用电测法测定纯弯梁横截面上的正应力分布规律,并与理论计算结果进行比较,以验证纯弯理论。
2. 用电测法测定纯弯梁载荷作用面附近处横截面上的正应力分布规律,与理论计算结果进行比较,并对实验结果进行分析(选作)。
3.学习电测法的多点测量。
二、实验设备:1. 微机控制电子万能试验机;2. 电阻应变仪;三、实验试件:本实验所用试件为中碳钢矩形截面梁,其横截面设计尺寸为h ×b =(50×30)mm 2,a=50mm (见图一 ), 材料的屈服极限MPa s 360=σ, 弹性模量E=210GPa ,泊松比=0.28。
B ’ B A ’Ahbaa图一 实验装置图四.实验原理及方法:处于纯弯曲状态的梁,在比例极限内,根据平面假设和单向受力假设,其横截面上的正应变为线性分布,距中性层为 y 处的纵向正应变和横向正应变为:()()Z ZM y y E I M y y E I εεμ⋅=⋅⋅'=⋅ (1)距中性层为 y 处的纵向正应力为:()()zM yy E y I σε⋅=⋅=(2) 本实验采用重复加载法,多次测量在一级载荷增量M 作用下,产生的应变增量和’。
于是式(1)和式(2)分别变为:()()()ZZZM y y E I M yy E I M y y I εεμσ∆⋅∆=⋅∆⋅'∆=⋅∆⋅∆=(3) (4)在本实验中,a P M ⋅∆=∆ (5) 最后,取多次测量的平均值作为实验结果:111()()()()()()Nnn Nnn Nnn y y Ny y Ny y Nεεεεσσ===∆∆=∆'∆=∆∆=∑∑∑ (6)本实验采用电测法,在梁纯弯曲段某一横截面A—A的不同高度(梁的顶面、底面、中性层及距中性层±10mm、±20mm)处粘贴纵向电阻应变片(见图一),并在梁的上下表面处粘贴横向应变片。
五、实验步骤1.设计实验所需各类数据表格;2.拟定加载方案(参考P0=5KN,P max=25KN,P=20KN);3.试验机准备、试件安装和仪器调整;4.确定组桥方式、接线、设置应变仪参数;5.检查及试车;检查以上步骤完成情况,然后预加一定载荷,再卸载,以检查试验机和应变仪是否处于正常状态。
6.进行试验;将载荷加至初载荷,记下此时应变仪的读数或将读数清零。
逐级加载,每增加一级,记录一次相应的应变值。
同时检查应变变化是否符合线性。
实验至少重复两次,如果数据稳定,重复性好即可。
7.数据通过后,卸载、关闭电源、拆线并整理所用设备。
六、试验结果处理1.在坐标纸上,在yσ∆—坐标系下描出实验点,然后拟合成直线,与理论结果进行比较,并计算同一y坐标所对应的理论和实验之间的误差;。
2.计算上下表面的横向应变增量ε'∆与纵向应变增量ε∆之比,并于理论结果进行比较。
七.思考题:1. 设计本实验的夹具应考虑哪些因素?2.安装试件时应当注意什么问题?3. 在本次实验中,如何用互补半桥接线法测最大弯曲正应变?试画出桥路图。
4. 如果在试件A-B截面的上表面和下表面(图1),沿纵线方向分别再贴上R2’和R8’两个应变片,如何用全桥接线法测最大弯曲正应变?试画出桥路图。
