通信原理-樊昌信曹丽娜-第六版-第六章-课后答案
通信原理第六版_思考题答案_樊昌信_曹丽娜_编著

第一章绪论1-1 以无线广播与电视为例,说明图1-1模型中信息源,受信者及信道包含的具体内容就是什么?1-2 数字通信有那些特点?答:第一,数字传输抗干扰能力强,尤其在中继时,数字信号可以再生而消除噪声的积累;第二,传输差错可以控制,从而改善了传输质量;第三,便于使用现代数字信号处理技术对数字信息进行处理;第四,数字信息易于做高保密性的加密处理;第五,数字通信可以综合传递各种消息,使通信系统功能增强。
1-3 按消息的物理特征,通信系统如何分类?答:根据消息的特征不同,通信系统可以分为:第一:电报通信系统;第二:电话通信系统;第三:数据通信系统;第四:图像通信系统。
1-4 按调制方式,通信系统如何分类?答:按调制方式,通信系统可以分为:基带传输与频带传输。
1-5 按传输信号的特征,通信系统如何分类?答:按传输信号的特征,通信系统可以分为:模拟通信系统与数字通信系统。
1-6 按传送信号的复用方式,通信系统如何分类?答:按传送信号的复用方式,通信系统可以分为:频分复用,时分复用与码分复用。
1-7 通信方式就是如何确定的?答:通信方式就是根据消息的传送方向与时间关系确定的。
1-8 通信系统的主要性能指标就是什么?答:通信系统的主要性能指标就是:传输速率与差错率。
1-9 什么就是误码率?什么就是误信率?它们之间的关系如何?答:所谓误码率,就是指错误接收的码元数在传送总码元数中所占的比例,或者更确切起的说,误码率即就是码元在传输系统中被传错的概率。
所谓误信率,又称误比特率,就是指错误接收的信息量在传送信息总量中所占的比例,或者更确切地说,它就是码元的信息量在传输系统中被丢失的概率。
二者之间的关系:它们都就是表示差错率的。
1-10 什么就是码元速率?什么就是信息速率? 它们之间的关系如何?答:码元速率就是指每秒钟传送码元的数目,单位为“波特“,常用符号“B”表示。
信息速率就是指每秒钟传递的信息量,单位就是比特/秒。
《通信原理》第六版樊昌信曹丽娜答案

第二章2-1试证明图P2-1中周期性信号可以展开为 (图略)证明:因为所以所以2-2设一个信号S(t)可以表示成试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:功率信号。
由公式有 或者2-3设有一信号如下:试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:是能量信号。
2-4试问下列函数中哪一些满足功率谱密度的性质:(1) (f) cos 2 2 f(2) a (f a)(3) exp(a f)解:功率谱密度P( f)满足条件: P(f )df 为有限值(3)满足功率谱密度条件,(1)和(2)不满足。
2-5试求岀s(t) A COs t 的自相关函数,并从其自相关函数求岀其功率。
解:该信号是功率信号,自相关函数为2-6设信号s(t)的傅里叶变换为 S(f) sin r f ,试求此信号的自相关函数R s ()解:2-7已知一信号s(t)的自相关函数为k kl IR.( ) ^e , k 为常数(1)试求其功率谱密度 P s ( f)和功率P ;(2)试画岀R s ()和P s ( f )的曲线解:(1)l im sin 2 xt (x) 和 sin xt lim (x)(2)略2-8已知一信号S(t)的自相关函数是以2为周期的周期函数:R( ) 1 | | , 1 1试求功率谱密度P s( f ),并画岀其曲线。
解:R()的傅立叶变换为,(画图略)2-9已知一信号S(t)的双边功率谱密度为试求其平均功率。
解:本章练习题:3-1 .设上是-3= =:的高斯随机变量,试确定随机变量-的概率密度函数 /?.,其中均为常数。
查看参考答案3-2 .设一个随机过程」' 可表示成式中,匚是一个离散随机变量,且' 二心…7试求总心及查看参考答案3-3 .设随机过程'''■- ::;' J _ ' 1,若丁丄与「丄是彼此独立且均值为0、方差为的高斯随机变量,试求:(1)……、「■'':(2)-「的一维分布密度函数“;(3)「1 :和「- ' '「。
通信原理(第六版)习题答案

通信原理(第六版)课后答案通信原理第六版(樊昌信曹丽娜著)国防工业出版社课后答案 第一章绪论1-1设英文字母盘出現的概卒药0.105, I 出璇的槪率为0.a02t 试求迓和JT 的信息昼°解:厶=log 2 — = log1-2皐信息源的符号集由Z2D 和E 组咸,设每一符号■独立出现,其出现槪率分别为1炸 1朋・1.岛3/lGi 5/15.徐亲该信息源符号的平均信息壘。
解=平均信息量 疋=Pgbj 恥Ji-LI . 1 V 1 k 1 3 , 3 5 . 5一才叫厂冠吨迈飞呃乔护喝忆 二2.2咖/棉门设駆个消息乩氐C. D 分别以概率lf4、1他1区 ⑴传送 斑一消息的出现是相 互独立的,试计算其平均信息量.M —个由字母直pep 组咸的字,对于告输的每一字囹用二进制眛冲编码,00代替每01 代清即U 代替匚11代替D ,每个脉冲宽度丸%弘⑴不同的宇毎等可能蜩时.试计算传輸的平均信息速率; ⑵ 若霉个字囹出现的等可能性另别光甩=1/5耳=1曲用尸1地山3/10,试计聲传需的平均信 息Jt 率-解;平均信息量用二—£ FUJI 躍」P 〔Gj-10.002解;(1)因一b字母衬翻个二ffi制圖中「属于四进41符号,故一b字母的持剜间为25, 传達宇母的符吕頑率为=1005&4 = ------------ 7聃2x5xl0-3等概时,平均信息速率尽=弘logs 4 = 200^/B ⑵每个符号平均信息量为H= 一工目leg 2 =-丄bg Q 丄1。
呂 2 丄一丄1笔」 --- l og 了——h 5 5 4 2 4 4 S 10 a10-1985边库f号平均信息速率R t=理斗月=100x1.985 = 198.5&/ff1-5国磅尔斯电码用点和划的序列发遊英文字母,划用持续3单位的电臟沖表示,虽用持续1个劉i的电瞒冲表示且到出现的概率是点t±®的概率的1心⑴求点和划的信息墨(刀求点和划的平均信息量-解:⑴由已知条件划出现的概率是点出现的概率的1/3,即PT3巳且P卄Pi所以卩产14 PTA '划的信息量几=-1唱卜加点的信息量厶二-1隅肓=0⑷気左N 1⑵平均信息量/f = -x0.415 + -x2 = 0.81加/符号皿某离散信I.W出忌尬…唧个不同的符号符号遠率为24D逻其中4个符号出现概率为尸财"⑹"MP 兔)=1他利无)="4具余符号等概出BL⑴求该信息源的平均信息率i⑵求传逆“的信息量◎ 解(1由已知条件得巩心)■户(忑訂■用(衍)■刀(花)■—僖耳源航:用(兀)一迟戸(吗)呱尸3” -“丄叱拮!□1D-2.87了加“符号则信忌源的平均信M連率为尺# = x H =2400 x 2. £75 = d?0O bit / $ ⑵舱1血的传亘量酋:f =『X/?』■ 3(500 y tS90D = 2.434 xlO7^1-7设某信息-源以每秒2000个符号的速率发送消息信息源由ARGDE五个信息符号组成发送盘的慨率为12发送其余符号的概率相同,且设每一符号出现是相互独立的。
《通信原理》第六版_樊昌信_曹丽娜答案精编版

第二章2-1 试证明图P2-1中周期性信号可以展开为 (图略)04(1)()cos(21)21nn s t n t n ππ∞=-=++∑证明:因为()()s t s t -= 所以000022()cos cos cos 2k k k k k k kt kt s t c c c kt T πππ∞∞∞======∑∑∑101()00s t dt c -=⇒=⎰1111221111224()cos ()cos cos sin2k k c s t k tdt k tdt k tdt k πππππ----==-++=⎰⎰⎰⎰ 0,24(1)21(21)nk n k n n π=⎧⎪=⎨-=+⎪+⎩所以04(1)()cos(21)21n n s t n t n ππ∞=-=++∑2-2设一个信号()s t 可以表示成 ()2cos(2)s t t t πθ=+-∞<<∞试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:功率信号。
222()cos(2)sin (1)sin (1)[]2(1)(1)j ft j j s f t e dtf f e e f f τπττθθπθτπτπτπτπτ---=+-+=+-+⎰21()lim P f s τττ→∞=2222222222sin (1)sin (1)sin (1)sin (1)lim 2cos 24(1)(1)(1)(1)f f f f f f f f ττπτπτπτπτθπτπτπτ→∞-+-+=++-+-+ 由公式22sin lim ()t xt x tx δπ→∞= 和 sin lim ()t xt x xδπ→∞= 有()[(1)][(1)]441[(1)(1)]4P f f f f f ππδπδπδδ=-++=++-或者001()[()()]4P f f f f f δδ=-++2-3 设有一信号如下: 2exp()0()0t t x t t -≥⎧=⎨<⎩试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
《通信原理》第六版_樊昌信_曹丽娜答案

第二章2-1 试证明图P2-1中周期性信号可以展开为 (图略)04(1)()cos(21)21nn s t n t n ππ∞=-=++∑证明:因为()()s t s t -= 所以000022()cos cos cos 2k k k k k k kt kt s t c c c kt T πππ∞∞∞======∑∑∑101()00s t dt c -=⇒=⎰1111221111224()cos ()cos cos sin2k k c s t k tdt k tdt k tdt k πππππ----==-++=⎰⎰⎰⎰ 0,24(1)21(21)nk n k n n π=⎧⎪=⎨-=+⎪+⎩所以04(1)()cos(21)21n n s t n t n ππ∞=-=++∑2-2设一个信号()s t 可以表示成 ()2cos(2)s t t t πθ=+-∞<<∞试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:功率信号。
222()cos(2)sin (1)sin (1)[]2(1)(1)j ft j j s f t e dtf f e e f f τπττθθπθτπτπτπτπτ---=+-+=+-+⎰21()lim P f s τττ→∞=2222222222sin (1)sin (1)sin (1)sin (1)lim 2cos 24(1)(1)(1)(1)f f f f f f f f ττπτπτπτπτθπτπτπτ→∞-+-+=++-+-+ 由公式22sin lim ()t xt x tx δπ→∞= 和 sin lim ()t xt x xδπ→∞= 有()[(1)][(1)]441[(1)(1)]4P f f f f f ππδπδπδδ=-++=++-或者001()[()()]4P f f f f f δδ=-++2-3 设有一信号如下: 2exp()0()0t t x t t -≥⎧=⎨<⎩试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
通信原理习题及答案第六版樊昌信曹丽娜编着国防工业出版社

第二章2-1 试证明图P2-1中周期性信号可以展开为 (图略)04(1)()cos(21)21nn s t n t n ππ∞=-=++∑证明:因为()()s t s t -= 所以000022()cos cos cos 2k k k k k k kt kt s t c c c kt T πππ∞∞∞======∑∑∑101()00s t dt c -=⇒=⎰1111221111224()cos ()cos cos sin2k k c s t k tdt k tdt k tdt k πππππ----==-++=⎰⎰⎰⎰ 0,24(1)21(21)nk n k n n π=⎧⎪=⎨-=+⎪+⎩所以04(1)()cos(21)21n n s t n t n ππ∞=-=++∑2-2设一个信号()s t 可以表示成 ()2cos(2)s t t t πθ=+-∞<<∞试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
解:功率信号。
22()cos(2)sin (1)sin (1)[]2(1)(1)j ft j j s f t e dtf f e e f f τπττθθπθτπτπτπτπτ---=+-+=+-+⎰21()lim P f s τττ→∞=2222222222sin (1)sin (1)sin (1)sin (1)lim 2cos 24(1)(1)(1)(1)f f f f f f f f ττπτπτπτπτθπτπτπτ→∞-+-+=++-+-+ 由公式22sin lim ()t xt x tx δπ→∞= 和 sin lim ()t xt x xδπ→∞= 有()[(1)][(1)]441[(1)(1)]4P f f f f f ππδπδπδδ=-++=++-或者001()[()()]4P f f f f f δδ=-++2-3 设有一信号如下: 2exp()0()0t t x t t -≥⎧=⎨<⎩试问它是功率信号还是能量信号,并求出其功率谱密度或能量谱密度。
通信原理教程(樊昌形)——第六章答案
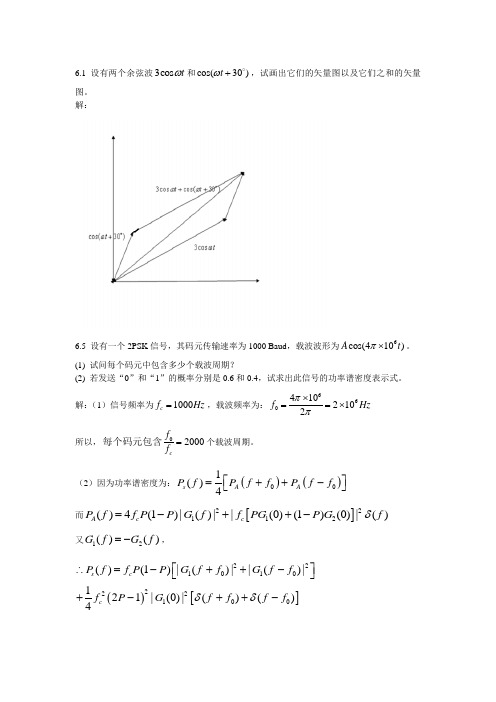
6.1 设有两个余弦波3cos t ω和cos(30)t ω+ ,试画出它们的矢量图以及它们之和的矢量图。
解:6.5 设有一个2PSK 信号,其码元传输速率为1000 Baud ,载波波形为6cos(410)A t π⨯。
(1) 试问每个码元中包含多少个载波周期?(2) 若发送“0”和“1”的概率分别是0.6和0.4,试求出此信号的功率谱密度表示式。
解:(1)信号频率为1000c f Hz =,载波频率为:6604102102f Hz ππ⨯==⨯所以,02000cf f =每个码元包含个载波周期。
(2)因为功率谱密度为:()()001()4s A A P f P f f P f f ⎡⎤=++-⎣⎦而[]22112()4(1)|()||(0)(1)(0)|()A c c P f f P P G f f PG P G f δ=-++- 又12()()G f G f =-,()[]221010222100()(1)|()||()|121|(0)|()()4s c cP f f P P G f f G f f f P G f f f f δδ⎡⎤∴=-++-⎣⎦+-++-又()()()()2011100sin sin (),0,f f TfTG f TG T G f f TfTf f Tππππ+=∴=+=+,()()()20100sin f f TG f f Tf f Tππ--=-将上述式子代入()s P f 得:()()()()()[]220000200sin sin ()(1)121()()4ccs c c cf f Tf f T P f T P P f f T f f T P ff f f ππππδδ⎡⎤+-⎢⎥=-++-⎢⎥⎣⎦+-++-代入6010.4,10,1000c P f T ===得()()()()226626666210210sinsin 24010001000()2102100.01(210)(210)s f fP f f f f f πππδδ⎡⎤+⨯-⨯⎢⎥⎢⎥∴=+⎢⎥+⨯-⨯⎢⎥⎢⎥⎣⎦⎡⎤++⨯+-⨯⎣⎦6.7 设有一个2DPSK 传输系统对信号采用A 方式编码,其码元传输速率为2400 Baud ,载波频率为 1800 Hz 。
通信原理(第六版)樊昌信曹丽娜课后答案

通信原理(第六版)课后习题答案第一章绪论1-1没奨文字母总出视笛⅛S率为O 105, X 的槪奉为0.002,试求总和Jr的信息量“解:I S— IQg 2 —= IOg ? —-—- 3.25 bii> S S 2P 5 1 0.105I X = Iog a—= IOg 2——-——=8.97bitT f30 0021∙2某信息源的符号集由査BCD和E组成,设每一符号独立出现其出现概率分别再1招,1/8» l/Et 3/1, 5/16-试求该信息源苻号的平均信息量Il解:平均信息量H = ~∑Fx) IOg 2 Fu i)J-I1 I 1 I i 1 1 I 1 3 I 3 5 I5=_ —log 3—_ —1Og a———log 3—- Io I g a----------------------------------- ——IGg 3-------4 2A8 e28 S 2 8 16 3 16 16 62 16=2.23 WW 号1-3设有四个消息乩B、C、D分别以M率1练1煤1/& 1门传送4消息的Lt®是相互独立Kh试计算其平均信息量*解:平均信息量j v = -∑¾)iog2¾)i-11.方竝/符号14—个由字母点PCD组成的宇,对于传输的毎一字母用二进制脉冲编码,00代替钉1 代替代替CJl代替D行个脉沖宽度为5沁Ii)不同的字母等可能版时.试计算传输的平均信息速率;⑺若环字母出现的等可能性分删为凡=1∕5∕>%Pe咫防剂W试计算传输的平均信息速率II解:(1X≡→ 字母对应两个二≡制脉沖,属于四进》」符号,故一b字母的持貓间为2× ‰τ 传送字母的符号速率为=——J—=IOO^刖2x5xl0^j等概时,平均信息速率& = Iog2 4 = 200⅛∕s(2)每个符号平均信息量为4 1 Il II 13 3H = -ZRTE=--L IOg 2---Iog3 --^IQg ,---Iog2- h 5 5 4 a 44 2 4 10 3IO=1.985 to/W 号平均信息速率肮=R M H =100xl.9S5 = 198 5⅛∕ff1-5国际莫尔斯电码用点和划的序列发送英文字母,划用持续3单位的电流脉冲表示,点用持续1个单位的电流脉沖表示]且划出现的概率是点出现的嘅率的1/3.⑴求点和划的信®⅛(2)求点和划的平均信S⅛≡解⑴由己知条件划出现的概率是点出现的概率的1/3,即P^∖β P2且Λ+⅛L 所以尸尸1砂Pj=3∕4划的信息量Z l= -IOS3- = 2⅛⅛43点的信息量厶=-Iog 2 - = 0-415⅛ii(2)平均信息量^ = ^XO.415+-^-x2 = 0.31驗/符号M某离散信忌獅出忌心…杯个不同的符号.符号逋率为如迥苴中4个符号出现概率为尸(殆=巩再)= IJg Pg = 1∕3>Fg= IM其余符号等概出现。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6—1解:单极性,双极性,单极性归零,双极性归零,二进制差分,四电平波形分别如下图a,b,c,d,e,f(此图仅作参考)6—2证明:6—36—4解:(1)由图P6-2可以写出故g (t )的傅里叶变换G (f )为()222s s AT T f G f Sa π⎛⎫=⎪⎝⎭6—5 解:图形如6-18所示6—6 解:(1)双极性信号的功率谱密度为()()()()()222241|()|12||s s s ssP f f P p G f f p G mf f mf δ+∞-∞=-+--∑设()()g t G f ⇔,则有()33s s T T fG f Sa π⎛⎫=⎪⎝⎭将P=1/4,/3s T τ=及()G f 代入()s P f 表达式中,可得()()22123183s ss s T T f m P f Sa Sa f mf πππδ+∞-∞⎛⎫⎛⎫=+-⎪ ⎪⎝⎭⎝⎭∑ 功率谱密度图略。
(2)当m=1时,上式中的离散普()()22301838s s m Sa f mf f f ππδδπ+∞-∞⎛⎫-=-≠ ⎪⎝⎭∑ 所以能从该双极性信号中直接提取频率为1/s s f T =的分量,其功率为 238S π=6—7 解:AMI 码:+1 0 -1 +1 0 0 0 0 0 0 0 0 0 -1 0 +1HDB3码:+1 0 -1 +1 0 0 0 +V -B 0 0 -V 0 +1 0 -1 AMI 码形图如下:HDB3码波形图如下:6—8解:双向码:10 01 10 10 01 01 10 01 10CIM 码:11 01 00 11 01 01 00 01 11双向码波形图如下:CIM 码波形图如下:(图形仅供参考) 6—9解:(1)令2(1||)||()20Ts t t g t Ts other - ≤={由图可得()2Ts h t g t ⎛⎫=- ⎪⎝⎭因为()gt 的傅里叶变换为 ()2()24Ts Ts G Sa ωω=所以,系统的传输函数()Hω为 ()()22224Ts Tsjj Ts Ts H G eSa e ωωωωω--⎛⎫== ⎪⎝⎭(2)基带系统的传输函数()H ω由发送滤波器()T G ω,信道()C ω和接收器()R G ω三部分组成,即()()()()T R H G C G ωωωω=因为()1Cω=,()()T R G G ωω=,所以()()()T R H G G ωωω=()2T G ω=()2R G ω=故有()T G ω()R G ω==44Tsj Ts eωω-⎛⎫= ⎪⎝⎭6—10 解:(1)由图可知系统传输函数()H ω为01(1||)||()0H otherωωωωω- ≤={由 1||(1||)()0t Tst g t Tsother≤- ={可得 ()22Ts G TsSa ωω⎛⎫=⎪⎝⎭根据傅里叶变换的对称性 ()()2g G jt πω-↔有()H ω=()g ω()001222t G jt Sa ωωππ⎛⎫↔= ⎪⎝⎭所以,该系统接收滤波器输出基本脉冲时间表示式()ht 为()20022t h t Sa ωωπ⎛⎫=⎪⎝⎭(2)根据奈奎斯特准则,当系统能实现无码间干扰传输时,()H ω应满足12ni i H C Ts πω=⎛⎫+= ⎪⎝⎭∑,||Ts πω≤当传码率01BR Ts ωπ==时,即0||Tsπωω≤=时12ni i H C Ts πω=⎛⎫+≠ ⎪⎝⎭∑此时系统不能实现无码间干扰传输。
6—11解:根据奈奎斯特准则,当最高传码率1B R Ts=时,能够实现无码间串扰传输的基带系统的总特性()Hω应满足12ni i H C Ts πω=⎛⎫+=⎪⎝⎭∑,||Tsπω≤ 因此当2B R Ts=时,基带系统的总特性()H ω应满足14ni i H C Ts πω=⎛⎫+= ⎪⎝⎭∑ 2||Ts πω≤ 所以除c 图外其他均不满足无码间串扰传输的条件。
6—12解:6—13 解:6—14 解:6—15 证明:()H ω可表示为()()()()()224/4/224/4/4/()1cos 12222244s s s s s s s s s T T j j s s s T T T T j j s s sT T T T T T e e H G G T T T G G e G e ωωππωωπππωωωωωωω---⎛⎫+⎛⎫ ⎪=+=+= ⎪ ⎪⎝⎭⎪⎝⎭++ 其中,()4/sT G πω是高为1,宽为4/s T π的门函数,其傅里叶反变换为()4/22s T s s t G Sa T T ππω⎛⎫⇔⎪⎝⎭因此,单位冲激响应=2sin /cos //1(/)s ss s t T t T t T t T ππππ-由上式结果可知,当t=nTs (n 不等于0)时,h (nTs )=0,所以当用1sT 波特速率传送数据时,抽样时刻上不存在码间串扰。
6—16 证明:对于单极性基带信号,在一个码元持续时间内,抽样判决器对接受的合成波形x (t )在抽样时刻的取值为()1()()R R A n kTs transport x kTs n kTs transport + ={因为()Rn t 是均值为0,方差为2n σ的高斯噪声,所以当发送“1”时,A+()R s n kT 的一维概率密度为212()]22n nx A f σπσ-=- 而发送“0”时,()Rs n kT 的一维概率密度函数为202]22nn x f σπσ=- 令判决门限为d V ,则发“1”错判为“0”的概率为212()11()](22222dV d el d n n nx A P P x V f dx dx erf σπσσ-=≤==-=+⎰⎰发“0”错判为“1”的概率为20211()]()22222dd eo d V n n nx P P x V f dx dx erf σπσσ∞=>==-=-⎰⎰发送“1”码和“0”码概率分别为P (1)和P (0),则系统总的误码率为(1)(0)e el eo P P P P P =+令0edP V ∂=∂,则可求得最佳门限电平d V *,即{}2222()(1)exp[]0exp[]}022e d d d n nP V A V P P V σσ**∂-=---=∂ 因为{}2222()(1)exp[]0exp[]22d d n n V A V P P σσ**--=-对上式移项取对数得()22220()ln 22(1)d d n n P V V A P σσ**--= 最佳判决门限 ()20ln 2(1)n d P A V A P σ*=+当p(1)=P(0)=1/2时2d A V *=此时系统误码率(1)(0)e el eo P P P P P =+111222el eo P P erf =+=6—17 解:(1)接收滤波器()G ω输入噪声双边功率谱密度为()0/2P n ω=,则接受滤波器()R G ω输入噪声双边功率谱密度()0P ω为()()()()()20000|()|1cos 2i R i n P P G P H ωωωωωτωτ===+ 0||πωτ≤接受滤波器()R G ω输入噪声功率为 ()()()00//000000//111cos 2222n n S P d d W πτπτπτπτωωτωτωππ--==+=⎰⎰ (2)系统总的误码率为(1)(0)e el eo P P P P P =+在单极性波形情况下,el P 和0e P 分别为 1||exp 2dV el x A P dx λλ-∞-⎛⎫=- ⎪⎝⎭⎰ 01||exp 2de V x P dx λλ∞⎛⎫=- ⎪⎝⎭⎰其中d V 为判决门限,则误码率e P 为1||1||(1)exp (0)exp 22dd Ve V x Ax P P dx P dx λλλλ∞-∞-⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭⎰⎰ 令0e d P V ∂=∂,并考虑P (1)=P (0)= 12,可求得最佳判决门限d V * 即 2d AV *=此时系统总误码率e P 为/2/21||1||(1)exp (0)exp 221||1||1/(4)exp (1/4)exp 22111/(4)exp 1/(4)exp 221/2exp(2d d d d Ve V V V A A x A x P P dx P dx x A x dx dx x A x dx dx Aλλλλλλλλλλλλλλλλ****∞-∞∞-∞∞-∞-⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭-⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭-⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭=-⎰⎰⎰⎰⎰⎰)λ6—18解:6—19解:6—20解:(1)0s T T =的眼图如下(2)02s T T =的眼图如下(3)比较: 0s T T = 02s T T = 最佳抽样判决时刻2s T 即02T 处 2s T 即04T 处 判决门限电平 0 0噪声容限值 1 16—21解:由题意,理想低通滤波器的传输函数为对应的单位冲激响应为 ()()L h t Sa t Tsπ=则系统单位冲击响应为 ()()()()()()2()()(2)L L h t Sa t h t t t Ts h t Sa t Sa t Ts TsTsTsπππδδ==--*=--⎡⎤⎣⎦对h (t )进行傅里叶变换,可得系统传输函数为所以6—22解:第一,四类部分响应信号的相关电平数为(2L-1); 二进制时L=2,相关电平为3; 四进制时L=4,相关电平为7;6—23解:第四类部分响应的预编码公式为 2[mod ]k k k b a b L -=+ 包括方框图:6—24解:6—25解:根据式(C )和2N+1=3,可以列出矩阵方程101210102101010C x x x x x x C x x x C ----⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭将样值Xk 代入,可得方程组 100.20C C -+=1010.30.21C C C --++= 1010.30.21C C C --++=解得1C -=-0.1779 0C =0.8897 1C =0.2847然后通过计算得1y -=0 0y =1 1y =0 3y - =0 2y -=-0.0356 2y =0.0153 3y =0.0285其余k y =0输入峰值失真为1||0.6x kk k D Xx ∞=-∞≠==∑输出峰值失真为1||0.0794y kk k D yy ∞=-∞≠==∑均衡后的峰值失真减少7.5倍。
