PWM整流器的控制器工程化设计方法
PWM整流器直接功率控制系统的设计

Absr c :Ths p p r a p id t o i r t n wih o ti e lo fVDC nd i sd o p o o r ta t i a e p le he c nf gu a i t u sd o p o o a n i e l fp we c nto o de i n PW M e tfe o r lt sg r c iirDPC y t m s d o s se ba e n c r i a e,c o e s t h v l me o n t o dn t h s wic o u fi pu
P WM 整 流 器 直接 功 率 控制 系统 的设 计
郭 宝 宁
( 江苏 海 事 职业 技 术 学 院 , 江苏 南京 217) 1 10
摘
要 : 用 直 流 电压 外 环 、 采 功率 控制 内 环 结 构 , 计 了基 于 ( ) 标 系下 的 P M 整 流 器 直 接 功 率 控 制 器 , 设 坐 W 根
me to c ie p we n e c ie p we .B s d o a lb S mu i k i i tv d l y t m mi — n f t o ra d r a t o r a e n M t / i l t i emo e ,s se i t a v v a n m a a
v l g wi h tbeso e co dn o VAC a d isa tp we o raie t erao a l du t ot ei s t a l trd a c r ig t a n c n n tn o rt el h e sn bea j s— z
浅谈PWM整流器的简单控制方法

浅谈 P WM 整 流 器 的简 单控 制 方法
文/ 黄 雨 鑫
相 电压 型 P WM 整 流器 的主 电路 结构 图 如 图
对P W M整 流 器 工 作 原 理 作 系 统 分 析 , 整 流 器 建 模 ,依 据 瞬 时
个 输出电压 ,此时 ,它体现为逆变器的功能。 但当电网向整流器直流侧的储能元件充 电时 , P WM 变 流器 就 处在 整 流 状态 。 因此 ,P WM
变 流 器 既 是 逆 变 器 也 是 整 流 器 。 由于 电路 直 流
侧有不同的储能元件的不 ,将这些不 同性质的 储能元件为分为 电容的 电压源型 、储能元件为 电感 的 电流 源 型 两 种 ,其 中 , 电压 源 型 整 流 器
主 电路 的储 能 元 件 选 用 前 者 , 由于 电容 的 电压
图2 — 3 : 电流 控 制 环
源 型储 能元件具有优 良的电气特性 ,因此它 的 应用范围很广泛。依据三相 电乐型 P WM 整 流 器 的数 学模 型,根据 控 制 目标推 演 出控 制 规 律。这种控制算法 与原 有的解 耦控 制箅法相 比
要 包 括 功 率 开 关 、 缓 冲 电 路 和 储 能 元 件 。 主 电路中的 P WM 变 流 器 ,其 主 要 功 能 是产 生 一
逆变器的中点 0 和直流侧的 N 点能够由一 电流的控制过程 中,同时还存在 系统电压对 d 电路就能够 简化成单相等效 电路 。如 图 2 一 l 所 示 。其 中采用可控 电压源来代表逆变器的输 出 电压 。
系中,其 中的有功 电流和无功 电流具有耦合 关 联 , 当对 其 中 d轴 或 q轴 电流 进 行 控 制 时 也 会 导 致 另一轴 电流 发生 变化。为 了使 d 、q轴 电
PWM整流器控制策略研究与实现

PWM整流器控制策略研究与实现一、本文概述随着电力电子技术的快速发展,脉冲宽度调制(PWM)整流器在电力系统中扮演着日益重要的角色。
PWM整流器以其高效、可靠和灵活的特性,在电能质量提升、能源节约和环保等方面具有显著优势。
因此,研究和实现PWM整流器的控制策略,对于提高电力系统的稳定性和效率具有重要意义。
本文旨在深入研究和探讨PWM整流器的控制策略,包括传统的控制方法以及新兴的控制策略。
我们将概述PWM整流器的基本原理和工作特性,为后续的控制策略研究提供理论基础。
我们将详细介绍传统的PWM整流器控制方法,如电压控制型PWM整流器和电流控制型PWM 整流器,并分析其优缺点。
在此基础上,我们将进一步探索新兴的控制策略,如基于预测控制的PWM整流器、基于智能算法的PWM整流器等,以期在提高PWM整流器性能、优化系统效率和增强系统稳定性方面取得突破。
本文将通过具体的实验和仿真研究,验证所提出控制策略的有效性和可行性。
通过对比实验数据和分析结果,我们将评估不同控制策略在实际应用中的表现,为PWM整流器的设计和优化提供有力支持。
本文的研究成果将对PWM整流器的进一步发展和应用推广具有重要的指导意义。
二、PWM整流器控制技术基础脉冲宽度调制(PWM)整流器控制技术是现代电力电子领域中的一种重要技术,其核心在于通过控制开关管的导通与关断时间,实现对整流器输出电压或电流的精确控制。
PWM整流器控制技术的基础在于对整流器工作原理、PWM调制原理以及控制策略的理解与掌握。
PWM整流器的工作原理基于电力电子变换器的基本思想,通过控制开关管的通断,实现对整流器输出电压或电流的调节。
与传统的线性整流器相比,PWM整流器具有更高的效率、更好的动态响应能力以及更强的抗干扰能力。
PWM调制原理是PWM整流器控制技术的核心。
PWM调制通过改变开关管在一个周期内的导通时间(即脉冲宽度),从而实现对整流器输出电压或电流的精确控制。
PWM调制具有简单、易实现、调节范围宽等优点,因此在电力电子领域得到了广泛应用。
PWM整流器PI参数设计

PWM整流器PI参数设计一、本文概述随着电力电子技术的快速发展,脉冲宽度调制(PWM)整流器在电力系统中得到了广泛应用。
PWM整流器以其高效、稳定和可控的特点,成为现代电能质量管理和电机驱动领域的重要组成部分。
PI参数设计作为PWM整流器控制策略中的关键环节,对整流器的性能和稳定性起着至关重要的作用。
本文旨在探讨PWM整流器PI参数设计的基本原理、方法及其在实际应用中的优化策略。
本文将简要介绍PWM整流器的基本原理及其在现代电力系统中的应用背景。
接着,重点分析PI参数设计在PWM整流器控制中的重要性,并详细阐述PI参数设计的基本原理和方法,包括比例系数和积分系数的选取原则、参数调整策略等。
还将探讨PI参数设计过程中需要考虑的关键因素,如系统稳定性、动态响应速度以及抗干扰能力等。
本文将结合实际应用案例,分析PI参数设计在实际应用中的优化策略,为PWM整流器的设计与应用提供有益的参考。
通过本文的研究,旨在为相关领域的研究人员和工程师提供PWM整流器PI参数设计的理论支持和实践指导,推动PWM整流器技术的进一步发展。
二、PWM整流器的基本原理PWM整流器,即脉冲宽度调制整流器,是一种先进的电力电子装置,其基本原理是通过对输入电流的脉冲宽度进行调制,实现输入电流波形与电网电压波形的同步,并使其接近正弦波,从而实现高功率因数整流。
PWM整流器通常采用三相桥式电路结构,包括六个开关管,每个开关管由一个绝缘栅双极晶体管(IGBT)或其他类型的全控型器件组成。
通过对这些开关管进行适当的控制,可以实现对输入电流的精确控制。
PWM整流器的工作原理可以分为两个阶段:整流阶段和逆变阶段。
在整流阶段,PWM整流器将输入的交流电转换为直流电,同时实现对输入电流的精确控制。
在逆变阶段,PWM整流器将直流电逆变为交流电,以供给负载使用。
为了实现输入电流的高功率因数,PWM整流器需要采用适当的控制策略。
其中,PI控制是一种常见的控制策略,它通过对输入电流的误差进行积分和比例运算,生成控制信号,从而实现对输入电流的精确控制。
三相电压型PWM整流器控制系统设计方法的研究_丁奇

0 引言
三相电压型 PWM 整流器由于能够提供稳定的 直流电压,实现网侧单位功率因数以及电能的双向 传输,并且结构简单、损耗低、控制方便,成为 PWM 整流器研究的重点。三相电压型 PWM 整流器的控 制方法有间接电流控制和直流电流控制两种,直接 电流控制由于采用网侧电流闭环控制,使网侧电流 动、静态性能得到了提高,增强了电流控制系统的 鲁棒性,是目前控制系统设计的主流[1]。而双闭环 控制结构是实现直接电流控制的主要方式。
上的分量; P 是微分算子。 1.2 三相电压型 PWM 整流器双闭环控制结构
从三相电压型 PWM 整流器在 dq 轴上的数学
模型(式 2)可以看出, id 、 id 相互耦合,从而给
控制器的设计造成困难,对此本文采用了基于前馈 解耦控制策略双闭环控制结构[3(] 图 2),图中Vdc* 是
电压指令值。该控制结构的数学模型为式 3,式中 Kip 、 KiI 是电流环 PI 调解器中的比例增益和积分
摘要:建立了三相电压型 PWM 整流器功率电路在两相旋转坐标系下的数学模型,采用了基于前馈解耦的控制策略,给出了三 相电压型 PWM 器的双闭环控制结构,使用三个 PI 调节器实现网侧单位功率因数和直流侧电压的稳定。根据瞬时功率守恒原 理推导了功率电路的传递函数,建立了从电压环输出到直流侧电压的小信号模型和电流环的结构框图,进而对它们各自的 PI 调节器进行了设计。仿真和实验结果表明,文中提出的设计方案是可行的。 关键词:PWM 整流器;直接电流控制;前馈解耦;双闭环控制;PI 调节器
1.5 Vdc (t
)
(
Em
i*
C dVdc (t) + dt
− LSi*
Vdc (t) RL
di* dt
PWM整流器控制系统的设计与实现的开题报告

PWM整流器控制系统的设计与实现的开题报告
论文题目:PWM整流器控制系统的设计与实现
研究背景和意义:
随着电力电子技术的飞速发展,PWM整流器在现代工业与生活中得到了广泛的应用。
PWM整流器通过对交流电进行整流,将其变成直流电,并通过控制电子开关的开关时间比例来实现直流电的输出电压或电流的
控制。
PWM整流器控制系统的实现,使得PWM整流器在控制上更为灵活,能够更好地满足消费者对电源的需求。
研究内容和方法:
本文主要研究PWM整流器控制系统的设计和实现。
从PWM整流器的基本原理出发,结合电力电子控制理论和数字信号处理技术,设计一
种高效、稳定的PWM整流器控制系统。
具体研究内容包括以下方面:
1. PWM整流器控制系统的基本组成和工作原理
2. 根据需求确定PWM整流器的输出电压或电流
3. 设计一种适用于PWM整流器的控制算法,并利用数字信号处理
技术实现控制算法
4. 设计和实现控制系统的硬件电路
5. 对PWM整流器控制系统进行测试和分析
以上内容将采用文献研究、仿真分析和实验验证等方法进行深入研
究和实现。
预期结论及意义:
本文研究的PWM整流器控制系统设计和实现,能够更好地满足消费者对电源的需求,提高电源的输出性能和稳定性,为工业控制和电力电
子技术的发展提供有力的支持。
同时,本文的研究还可以为类似电力电子控制系统的设计和实现提供参考,具有一定的理论和实践意义。
三相PWM整流器控制器设计(精)
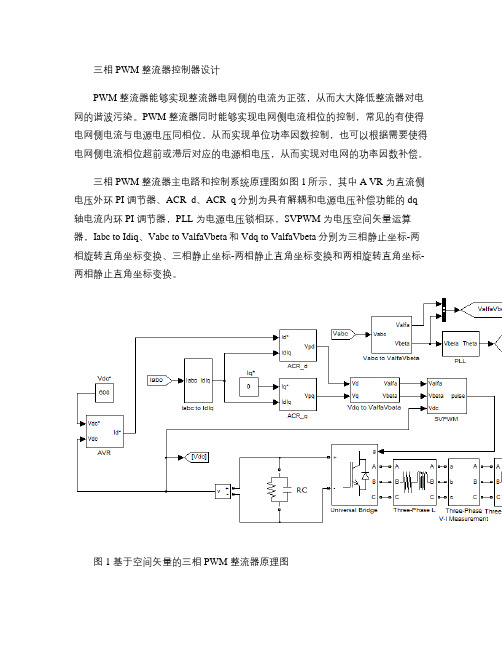
三相PWM 整流器控制器设计PWM 整流器能够实现整流器电网侧的电流为正弦,从而大大降低整流器对电网的谐波污染。
PWM 整流器同时能够实现电网侧电流相位的控制,常见的有使得电网侧电流与电源电压同相位,从而实现单位功率因数控制,也可以根据需要使得电网侧电流相位超前或滞后对应的电源相电压,从而实现对电网的功率因数补偿。
三相PWM 整流器主电路和控制系统原理图如图1所示,其中A VR 为直流侧电压外环PI 调节器、ACR_d、ACR_q分别为具有解耦和电源电压补偿功能的dq 轴电流内环PI 调节器,PLL 为电源电压锁相环,SVPWM 为电压空间矢量运算器,Iabc to Idiq、Vabc to ValfaVbeta和Vdq to ValfaVbeta分别为三相静止坐标-两相旋转直角坐标变换、三相静止坐标-两相静止直角坐标变换和两相旋转直角坐标-两相静止直角坐标变换。
图1 基于空间矢量的三相PWM 整流器原理图根据开关周期平均值概念、三相电压型PWM 整流器开关函数表等,可得到三相电压型PWM 整流器在dq 坐标下微分方程形式和等效电路形式的开关周期平均模型。
经过dq 轴电流解耦和电源电压补偿的控制系统结构图如图2所示,其中小写的变量表示该变量的开关周期平均值,大写的变量表示该变量在工作点的值。
v dc d dcq图2 基于dq 轴电流解耦和电源电压补偿的控制系统结构图对解耦和电源电压补偿之后的dq 轴等效电路进行工作点附近的小信号分析,即可得到小信号下的传递函数如式(1、(2)和(3)所示,其中L 、R 分别为交流侧的滤波电感及其等效电阻,C 为直流侧滤波电容,Dd 为d 轴在工作点的占空比。
~i d (s αd (s ~i q (s αq (s ~v dc (s i d (sV dc(13Ls +3R V dc(2 =-3Ls +3R RD d(3) =-RCs +1=-有了对象的传递函数,根据控制系统校正原则就可整定dq 轴电流环和直流侧电压外环PI 调节器的参数。
变频空调PWM整流器设计

l e = ] l = I l c o s ( C 0 O S 0 e I 1 2 0 " ) I
.-
( 1 ) 电压定 向的直接 功率控 制 (V—DPC);基 于虚拟磁链 定
和 为三 向的矢量控制 ( V F O C);基于虚拟磁链 定向控制的直接
归纳成 四类 :基 于 电压 定 向的矢量 控制 ( V O C);基于
i
.
D C/
= =C Leabharlann L s V6 j |
旦
一
I = o _ 1 l = 叫 5
v 4 v 6 v 2
{ A C
E l ect r i cal Appl i an ces
图2 P W l / 整流主 电路原理 图
技术创新 ・ T e c h n o l o g y a n d I n n o v a t i o n
所示 。
图 4 电流 环 控 制 框 图
V
沈
图 5 电压环控制框图
5 0 2 0 1 3 年O 4 月
日用电器
式 中 :O f= f ,为 a 相 电压相位 角 ,
相输入 电压幅值 与角频率 ,则 由图 2可得如下方程 嘲
功率控制 ( V F - D P C)[ 3 1 。 本 文介 绍基于直接功率控制的 P WM整流器 电流 、电
压双 闭环设计 方法 。
2 . 1 电流环 设 计
[ ] = 一 [ ‘ ÷ R ‘ ] 医 ] + [ 圣 ]
■ 技 术 创 新 ・日 用 电器
1 P 删 整流器的数学模型
C v d . v & d  ̄ = 一P o f
( 5 )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电工电能新技术 Advanced Technology of Electrical Engineering and Energy
Vol. 21, No. 3 Jul. 2002
PWM 整流器的控制器工程化设计方法
熊 健, 张 凯, 陈 坚
( 华中科技大学, 湖北 武汉 430074) 摘要: 在两相同步坐标系中, 引入状态反馈解耦实现了 d 、 q 轴电流的独立控制。 在此基础上, 将 广泛应用的双闭环控制器工程化设计方法应用于整流器 。实验表明 , 这种控制器的设计方法对整 流系统是适合的 。 关键词: 整流器; 双闭环; 开关模式整流器
p= a , b, c
式中 : u rd = S d u dc , u rq= S q u dc 由( 4) 式可见, d 、 q 轴电流除受控制量 u rd 、 u rq 的 影响外, 还受耦合电压 Li q 、 Li d 扰动和电网电 压 u sd 、 u sq 的影响。所以单纯地对 d 、 q 轴电流作负 反馈并没有解除 d 、 q 轴之间的电流耦合, 效果不是 很理想。利用状态反馈 , 可以实现对 d 、 q 轴电流的 解耦。 现假设变换器输出的电压矢量 u rd + ju rq 中包含 三个分量 : u rd = u rd1 + u rd2 + u rd3 u rq = u rq1 + u rq2 + u rq3 如果令: u rd1 = u sd , u rq1 = u sq , u rd2 = u rq2 = Li q Li d ( 5) ( 6)
电流状态反馈的引入实现了电流的解耦控制 , 在此基础上可以应用双闭环控制器的工程化设计方 法。
系统的开环传递函数是 : P ( s) = K ci K pwm K RK if ( c S + 1) s ( T L s + 1) ( T s s + 1) ( T if s + 1) = TL ( 8)
3S q 2C 0
u sd 0 1 - C u sq iL
3
整流器的双闭环控制原理
根据式( 3) 表示的整流器模型, 可知输入电流满
足下式: L di d = - Ri d + dt Li q + u sd - u rd
电流无影响。或者说, 相对于电流变化而言 , 直流电
46
电工电能新技术
第 21 卷
计等同于对图 3 所示的控制对象设计控制器。图 3 中还考虑了变换器的延时和反馈通道的滤波 , 故更 接近于实际情况。 图 3 中 , T L 是电 感时间常 数 ( 等于 L R , 此处 L、 R 的定义与前述数学模型中的相同 ) , K R = 1 R 。 K pwm 表示变换器的放大倍数。而 T s 等于开关周期 的一半, 代表变换器的延时。 T if 是反馈通道的滤波 时间常数。
式中 : K = K ci K pwm K R K if , 二阶系统 :
这时 , 对应的电流闭环传递函数 C ( s ) 为一典型 K T sf P( s) C( s ) = = 2 1+ P ( s ) s + 1 s+ K T sf T sf =
2 n
s + 2 1 2
2
n
s+
n
2 n
( 10) = K T sf
压的变化比较慢。可以认为 , 直流电压在一个开关 周期内基本不变。二是认为 , 开关状态的改变对直 流电流的影响仅通过 d 、 q 轴电流实现, 而没有直接
影响到直流输出电流。所以这里用到的模型还是作 了一定的简化处理 , 这是为了分析问题的方便, 但这 种简化是符合实际情况的。
图 2 双闭环控 制整流器原理框图 Fig. 2 Block diagram of dual close - loop
[ 14,15] [ 6 8] [ 9] [10]
等。
在各种不同的控制方式中 , 以电压反馈作外环 加上以电流反馈作内环的双闭环串级控制结构最为 普遍。事实上 , 实用化的 PWM 整 流装置绝大多数 采用这种控制方法。双闭环控制的主要特点是物理 意义清晰 , 控制结构简单 , 控制性能优良。双闭环控 制的另一个优点也是它特有的优点是: 由于电流内 环的存在 , 只要使电流指令限幅, 可以使整流器工作
2 c
=
c 1
=
Mr =
由于这里 S d 和 S q 是变量 , 所以这里交、 直流电 流之间的关系是时变的。为了能用线性方法设计 , 不得不作一些简化处理。稳态时的 i q 等于零, 由于 电流闭环的作用 , 动态过程中 i q 的变化也很小。或 者这样认为, 在直流电压发生较大变化之前, i q 已 经完成其暂态过程达到零值。从图 2 可看到 , 可将 q 轴电流作为电压环内的扰动处理。所以暂不考虑 q 轴电流的影响。此外, 由于电感电阻 R 很小, 对 整流器矢量图上分析可知 , S d 在全功率范围内的变 化很小。不妨取空载时的 S d 值, 因为这时的 S d 最 大。于是可得图 4 所示电压环控制框。 K =
usp - S c p = a, b , c
S sp u dc
p = a, b , c
du dc C = S a i a + Sb i c + S c i c - i L dt ( 1) 上式中, S a 、 Sb 、 S c 分别表示三相桥臂的开关函数。 其中 : S = 1, 代表对应的桥臂上管导通, 下管关断 ; S = 0, 代表对应的桥臂下管导通, 上管关断。 L 代表输入电感, R 代表包括线路电阻在内的等效 电感电阻。如果三相电网平衡 ( u sa 、 u sb 和 u sc 之和为 零) , 那么 ( 1) 式还可以有所简化。 为便于系统分析与综合, 采用 PARK 变换, 将整 流器模型变换到两相同步旋转的 d 、 q 坐标系, 并使 d 轴定向于电网电压矢量。取变换矩阵为: T abc 2 3
中图分类号 : TM461 文献标识码 : A 文章编号 : 1003 -3076( 2002) 03 - 0044 -05
1
引言
以 PWM 整流器取代传统的相控型整流器是减
于恒流状态, 自然实现了对装置的过载保护。 由于整流系统是非线性的, 通常是通过仿真或 用模型线性化的方法确定控制器参数 , 实际应用中 不方便。双闭环控制 器设计方法
[ 16]
少电网谐波源的积极有效办法。 整流器的控制方法比较多 , 根据对整流器交流 侧电流控制方式的不同, 可分为电流闭环控制和电 流开环控制两大类。 电流开环控制
[1 3]
在 实际系统中
已经得到广泛应用 , 本文研究表明 , 将该方法应用到 PWM 整流器中也是适合的。只需要经过为数不多 的几步简单计算, 就可以确定控制器的参数 , 特别适 合控制器参数的现场整定。该方法的另一特点是在 频域设计控制器, 可以比较方便地将系统中诸如变 换器延时 , 滤波延时等小滞后环节考虑进去。
图 3 电流环原理框 图 Fig. 3 Block diagram of current loop
其中 : =
1 , KT sf
按二阶最优的指标, 令 考虑到参数准确性和漂移等因素, 且一般又希 望电流控制无静差 , 所以选用 PI 调节器。图 3 所示
= 0 707, 则由 ( 10) 式
可算出相应的环路增益 K , 再根据各环节的放大倍 数, 由( 9) 式即可确定电流控制器增益 K ci 。又因为
的整流器具有良好的静态特
性, 其控制思想来源于整流器的稳态相量图或矢量 图。它最显著的优点是结构简单, 无需电流传感器。 但这种控制方式的稳定性很差, 动态响应慢。也有 文献提出过采用动态补偿的方法
[ 4, 5]
加以改进 , 但在
2 PWM 整流器数学模型
图 1 所示是三相 PWM 整流器的主电路及其各 变量的定义。根据整流器的电路拓扑结构, 其数学 模型为:
实际系统和装置中应用不多。从系统的鲁棒性、 抗 干扰能力和系统保护的角度看 , 引入电流反馈是不 可缺少的 , 对于大功率变流器尤其如此。 采用电流闭环的整流器控制方式有: 双闭环控 制 , 状 态反 馈 控制 , 无 差 拍控 制 , 极 点配 [ 11] [ 12] [ 13] 置 , 二次型最优控制 , Lyapunov 方法 , 非线性 状态反馈控制
熊
健 , 等: PWM 整流器的控制器工程化设计方法 di q =dt
45
u sa u sbu sc -
u s p - S ap = a, b , c
S sp u dc
p = a, b , c
L
Li d - Ri q + u sq - u rq
( 4)
u sp - S bp = a, b , c
S sp u dc
dq
将( 5) 和( 6) 式代入 ( 4) 式 , 得 : di d + Ri d = - u rd3 dt di q L + Ri q = - u rq3 dt L
= cos - sin t2 3 cos - sin t+ 2 3
( 7)
cos t - sin t
在( 7) 式表示的 d 、 q 电流子系统中 , d 、 q 轴电流是 独立控制的, 而且控制对象也很简单, 相当于对一个 一阶对象的控制。之所以能形成 ( 7) 式这种简洁形 式, 其主要原因是引入了电流状态反馈 ( u rd2 和 u rq2 ) 对电流子系统解耦。而引入了电网扰动电压( u rd1 和 u rq1 ) 作前馈补偿 , 也使系统的动态性能有进一步提 高。
2 t- 3
2 t+ 3 ( 2)
将( 2) 式作用于 ( 1) 式 , 得到整流器在两相同步 旋转坐标系下的模型为: di d dt di q dt du dc dt 1 L 0 0 = - R L 3Sd 2C 0 1 L 0 R L Sd L Sq L 0 id iq + u dc
