遗传算法流程图
遗传算法遗传算法

(5)遗传算法在解空间进行高效启发式搜索,而非盲 目地穷举或完全随机搜索;
(6)遗传算法对于待寻优的函数基本无限制,它既不 要求函数连续,也不要求函数可微,既可以是数学解 析式所表示的显函数,又可以是映射矩阵甚至是神经 网络的隐函数,因而应用范围较广;
(7)遗传算法具有并行计算的特点,因而可通过大规 模并行计算来提高计算速度,适合大规模复杂问题的 优化。
26
(4)基本遗传算法的运行参数 有下述4个运行参数需要提前设定:
M:群体大小,即群体中所含个体的数量,一般取为 20~100; G:遗传算法的终止进化代数,一般取为100~500; Pc:交叉概率,一般取为0.4~0.99;
Pm:变异概率,一般取为0.0001~0.1。
27
10.4.2 遗传算法的应用步骤
遗传算法简称GA(Genetic Algorithms)是1962年 由美国Michigan大学的Holland教授提出的模拟自然 界遗传机制和生物进化论而成的一种并行随机搜索最 优化方法。
遗传算法是以达尔文的自然选择学说为基础发展起 来的。自然选择学说包括以下三个方面:
1
(1)遗传:这是生物的普遍特征,亲代把生物信息交 给子代,子代总是和亲代具有相同或相似的性状。生 物有了这个特征,物种才能稳定存在。
18
(3)生产调度问题 在很多情况下,采用建立数学模型的方法难以对生
产调度问题进行精确求解。在现实生产中多采用一些 经验进行调度。遗传算法是解决复杂调度问题的有效 工具,在单件生产车间调度、流水线生产车间调度、 生产规划、任务分配等方面遗传算法都得到了有效的 应用。
19
(4)自动控制。 在自动控制领域中有很多与优化相关的问题需要求
10
传统BP与遗传算法简介

计算损失函数: Etotal
1 2
(ta rg et
output)2
Eo1
Eo2
1 2
(ta
rg
eto1
ao1 ) 2
1 2
(ta
rg
eto2
ao2
)2
权值与阈值更新(以w5、b2与w1、b1为例):
输出层 隐含层:
w5对整体损失产生的影响:
Etotal w5
Etotal * ao1 * zo1 ao1 zo1 w5
6. 变异运算 变异的作用,指的是染色体的某个基因片段或者某个
基因点发生突变。例如单点突变可以通过下图进行表示:
突变的作用,是希望能够摆脱局部最优点,往更好的 地方去。但是效果具有很大的随机性。 7. 个体解码
将个体解码为十进制公式为:
xi
1
xt
3 29 1
遗传算法流程图:
效果图:
第一代适应度的平均值为2.025,最大适应度值为3.483,经过97 代遗传选择后适应度平均值达到3.811,最大适应度值为3.843, 可见得到了很好的收敛,并最终稳定在最右侧顶峰。
wi2
n
Neti wij x j si i
w in
j =1
yi ui f (Neti )
其中 f 为激活函数(进行非线性化)
2 传统BP神经网络 BP算法又称为误差反向传播算法,它是一个迭代
算法,其基本思想是梯度下降法。采用梯度搜索技术, 使网络的实际输出值与期望输出值的误差均方值为最 小。
离散点-1到离散点2 ,分别对应于从000000000(0)到111111111 (512)之间的二进制编码
遗传算法流程图

遗传算法流程图遗传算法(Genetic Algorithm,GA)是一种模拟自然进化过程的优化算法,通过模拟生物遗传的过程来寻找最优解。
下面是遗传算法的流程图:1. 初始化群体:设定问题的适应度函数,定义染色体编码方式,并随机生成初始种群。
2. 评估适应度:根据设定的适应度函数,对每个个体进行评估,并计算适应度值。
3. 选择操作:根据适应度值,使用选择算子选择一定数量的个体作为父代。
4. 交叉操作:对选择出的父代,使用交叉算子进行交叉操作,生成新的子代。
5. 变异操作:对交叉产生的子代,使用变异算子进行变异操作,生成新的子代。
6. 更新种群:根据选择、交叉和变异的结果,更新种群中的个体。
7. 判断终止条件:判断是否满足终止条件,如达到指定的迭代次数或找到最优解。
8. 返回最优解:如果满足终止条件,则返回找到的最优解;否则,返回第3步。
遗传算法的核心思想是通过模拟自然选择、遗传和变异的过程,从大量的可能解空间中寻找到最优解。
下面详细介绍遗传算法的流程:首先,需要定义问题的适应度函数,即问题的目标函数。
适应度函数用于评估染色体的好坏程度,从而进行选择操作。
适应度函数越好的个体,被选中的概率越高。
然后,通过染色体编码方式,将问题的解表示为染色体。
染色体可以是二进制编码、整数编码或实数编码,具体根据问题的特点进行选择。
接下来,初始化种群,即随机生成一定数量的初始个体。
种群中的每个个体都表示一个可能解。
然后,对每个个体计算适应度值,并根据适应度值进行选择操作。
选择操作根据设定的选择算子,选择一定数量的个体作为父代。
通常使用轮盘赌选择或锦标赛选择来进行选择操作。
对选择出的父代,进行交叉操作。
交叉操作通过交换染色体的部分基因片段,生成新的子代。
交叉操作有单点交叉、多点交叉、均匀交叉等形式。
接着,对交叉产生的子代进行变异操作。
变异操作通过改变个体染色体中的一些基因值,引入一定的随机性。
再次,根据选择、交叉和变异的结果,更新种群中的个体。
遗传算法简介及sga流程【精品毕业设计】(完整版)

遗传算法:遗传算法(Genetic Algorithm)是一类借鉴生物界的进化规律(适者生存,优胜劣汰遗传机制)演化而来的随机化搜索方法。
遗传算法(Genetic Algorithms简称GA)是由美国Michigan大学的John Holland教授于20世纪60年代末创建的。
它来源于达尔文的进化论和孟德尔、摩根的遗传学理论,通过模拟生物进化的机制来构造人工系统。
遗传算法作为一种全局优化方法,提供了一种求解复杂系统优化问题的通用框架,它不依赖于问题的具体领域,对优化函数的要求很低并且对不同种类的问题具有很强的鲁棒性,所以广泛应用于计算机科学、工程技术和社会科学等领域。
John Holland教授通过模拟生物进化过程设计了最初的遗传算法,我们称之为标准遗传算法。
标准遗传算法流程如下:1)初始化遗传算法的群体,包括初始种群的产生以及对个体的编码。
2)计算种群中每个个体的适应度,个体的适应度反映了其优劣程度。
3)通过选择操作选出一些个体,这些个体就是母代个体,用来繁殖子代。
4)选出的母代个体两两配对,按照一定的交叉概率来进行交叉,产生子代个体。
5)按照一定的变异概率,对产生的子代个体进行变异操作。
6)将完成交叉、变异操作的子代个体,替代种群中某些个体,达到更新种群的目的。
7)再次计算种群的适应度,找出当前的最优个体。
8)判断是否满足终止条件,不满足则返回第3)步继续迭代,满足则退出迭代过程,第7)步中得到的当前最优个体,通过解码,就作为本次算法的近似最优解。
早熟收敛:一般称之为“早熟”,是遗传算法中的一种现象。
指在遗传算法早期,在种群中出现了超级个体,该个体的适应值大大超过当前种群的平均个体适应值。
从而使得该个体很快在种群中占有绝对的比例,种群的多样性迅速降低,群体进化能力基本丧失,从而使得算法较早收敛于局部最优解的现象。
早熟收敛的本质特征是指群体中的各个个体非常相似,群体的多样性急剧减少,当前群体缺乏有效等位基因(最优解位串上的等位基因),在遗传算子作用下不能生成高阶竞争模式。
遗传算法的C语言程序案例
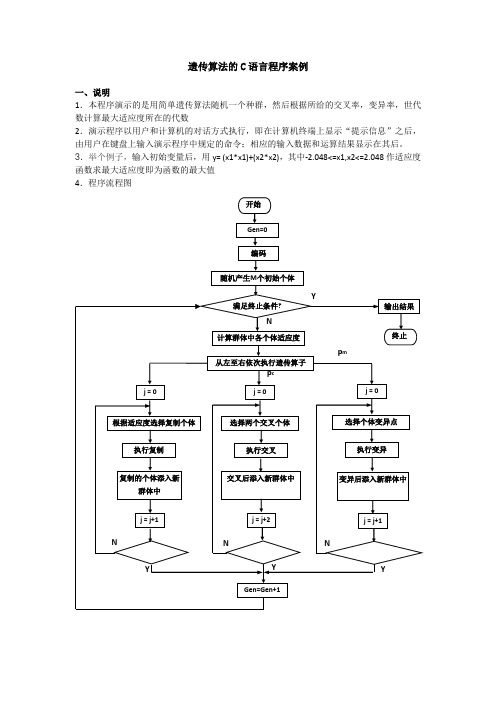
遗传算法的C语言程序案例一、说明1.本程序演示的是用简单遗传算法随机一个种群,然后根据所给的交叉率,变异率,世代数计算最大适应度所在的代数2.演示程序以用户和计算机的对话方式执行,即在计算机终端上显示“提示信息”之后,由用户在键盘上输入演示程序中规定的命令;相应的输入数据和运算结果显示在其后。
3.举个例子,输入初始变量后,用y= (x1*x1)+(x2*x2),其中-2.048<=x1,x2<=2.048作适应度函数求最大适应度即为函数的最大值4.程序流程图5.类型定义int popsize; //种群大小int maxgeneration; //最大世代数double pc; //交叉率double pm; //变异率struct individual{char chrom[chromlength+1];double value;double fitness; //适应度};int generation; //世代数int best_index;int worst_index;struct individual bestindividual; //最佳个体struct individual worstindividual; //最差个体struct individual currentbest;struct individual population[POPSIZE];3.函数声明void generateinitialpopulation();void generatenextpopulation();void evaluatepopulation();long decodechromosome(char *,int,int);void calculateobjectvalue();void calculatefitnessvalue();void findbestandworstindividual();void performevolution();void selectoperator();void crossoveroperator();void mutationoperator();void input();void outputtextreport();6.程序的各函数的简单算法说明如下:(1).void generateinitialpopulation ()和void input ()初始化种群和遗传算法参数。
遗传算法的基本流程

遗传算法的基本流程遗传算法是一种模拟自然进化过程的优化算法,它借鉴了达尔文的进化论思想,通过模拟基因的遗传和变异来寻找问题的最优解。
遗传算法的基本流程包括问题建模、初始化种群、适应度评估、选择操作、交叉操作、变异操作和终止条件等步骤。
1. 问题建模在使用遗传算法解决问题之前,首先需要将问题转化为适合遗传算法求解的形式。
这包括定义问题的目标函数、约束条件以及可行解的表示方法等。
2. 初始化种群在遗传算法中,种群是由一组个体组成的,每个个体代表一个可能的解。
初始化种群是指随机生成一定数量的个体作为初始解集合,这些个体的基因组合形成了种群的初始基因型。
3. 适应度评估适应度评估是为了衡量每个个体的适应度,即它们相对于解决问题的能力。
根据问题的定义,可以计算每个个体的适应度值。
4. 选择操作选择操作是为了从当前种群中选择出适应度较高的个体,使其有更大的概率被选入下一代种群。
常用的选择方法有轮盘赌选择、锦标赛选择等。
5. 交叉操作交叉操作是为了模拟生物个体的基因交换过程,通过将两个个体的基因染色体进行交叉,产生新的个体。
交叉操作可以增加种群的多样性,有助于发现更好的解。
6. 变异操作变异操作是为了模拟基因的突变现象,通过对个体的基因进行随机变动,引入新的基因信息。
变异操作可以增加解的搜索空间,避免算法陷入局部最优解。
7. 终止条件终止条件是指遗传算法的终止条件,即算法何时停止迭代。
可以根据问题的要求设定终止条件,如达到一定的迭代次数、找到满足要求的解等。
通过上述步骤的迭代,遗传算法可以逐步优化种群,使其逐渐接近问题的最优解。
遗传算法的优点是可以在搜索空间较大、问题复杂的情况下找到较好的解,但也存在着收敛速度慢、易陷入局部最优解等问题。
值得注意的是,遗传算法并非适用于所有问题,对于某些问题可能存在更有效的求解方法。
在使用遗传算法解决问题时,需要根据问题的特点和要求合理选择算法参数、运算规模等,以达到较好的求解效果。
遗传算法及其MATLAB实现

Y
输出结果 终止
N
计算群体中各个体适应度 从左至右依次执行遗传算子
pm
j=0 选择个体变异点 执行变异
pc
j=0 根据适应度选择复制个体 执行复制
j=0 选择两个交叉个体 执行交叉 将交叉后的两个新个体 添入新群体中 j = j+2
将复制的个体添入 新群体中
j = j+1
将变异后的个体添入 新群体中
发展
遗传算法——进化计算——计算智能——人工智能 70年代初,Holland提出了“模式定理”(Schema Theorem),一般认为是“遗 传算法的基本定理”,从而奠定了遗传算法研究的理论基础; 1985年,在美国召开了第一届遗传算法国际会议,并且成立了国际遗传算法学会 (ISGA,International Society of Genetic Algorithms); 1989年,Holland的学生D. J. Goldherg出版了“Genetic Algorithms in Search, Optimization, and Machine Learning”,对遗传算法及其应用作了全面而系统的论 述; 1991年,L. Davis编辑出版了《遗传算法手册》,其中包括了遗传算法在工程技术 和社会生活中大量的应用实例。
⑦倒位运算:对一复杂的问题可能需要用到“倒位”。倒位是指 一个染色体某区段正常排列顺序发生 的颠倒造成染色体内的 180
。
DNA序列重新排列,它包括臂内倒位和臂间倒位。 例:染色体S=1001011011101110011010101001划线部分倒位得 ' S =100101100101001110111101001
'
'
首先用随机数产生一个或多个交配点位置,然后两个个体在交配 点位置互换部分基因码形成两个子个体。 例:有两条染色体S 01001011 ,S 10010101 交换后4位基因得 ,S 10011011 S 01000101 可以被看成是原染色体 S1 和S 2 的子代染色体。
Geatpy进化算法遗传算法

算如下:
i−1 F itnessi = 2 − SP + 2 (SP − 1) N ind − 1
线性排序中选择压力SP 的值必须在 [1.0,2.0] 之间。
文献 [1] 中有这种线性排序的详细分析。其选择强度、多样性损失、选择方差 (这些
概念详见下一节) 的计算如下:
选择强度:
SelInt (SP ) = SP√− 1 π
进化算法
序言 进化算法 (Evolutionary Algorithm, EA) 是一类通过模拟自然界生物自然选择和自然
进化的随机搜索算法。与传统搜索算法如二分法、斐波那契法、牛顿法、抛物线法等相 比,进化算法有着高鲁棒性和求解高度复杂的非线性问题 (如 NP 完全问题) 的能力。
在过去的 40 年中,进化算法得到了不同的发展,现主要有三类: 1) 主要由美国 J. H. Holland 提出的的遗传算法 (Genetic Algorithm, GA); 2) 主要由德国 I. Rechenberg 提出的进化策略 (Evolution strategies, ES); 3) 主要由美国的 L. J. Fogel 提出的进化规划 (Evolutionary Programming, EP)。 三种进化算法都是受相同的自然进化原则的启发下创立的,文献 [1] 以及国内的诸 多资料也有详细的介绍。除此之外,进化算法还有差分进化 (Differential Evolution)、基 因表达式编程 (Gene Expression Programming) 等众多分支。本文档只介绍经典的遗传算 法、差分进化算法和多目标进化优化算法,不对众多改进的进化算法以及其他分支作详 细介绍,如有需要进行相关研究的可以参考相关的专业和权威的文献。 文档第一章是有关遗传算法的概述和基本框架;第二章介绍了编码;第三章是关于 适应度的计算;第四章讲述了选择算法;在第五章中,介绍了不同的重组算法;第六章 解释了如何变异;第七章详细讲解了与多目标优化有关的概念。 最后值得一提的是,虽然进化算法在近 20 年来已经得到了快速的发展,在当今已 经比较成熟,在金融、工程、信息学、数学等领域已经有广泛的应用,但是,众多新兴 的进化算法 (如差分进化算法等) 以及不断改进和完善的拥有高维、多目标问题求解能 力的进化优化算法等等,正给进化算法注入源源不断的新活力。与此同时,深度神经网 络的蓬勃发展让进化算法有了一个更加前沿和广阔的前景——神经进化。量子计算机的 出现,也使得拥有高度并行能力的进化算法有着更大的潜能。
