初一数学附加题
初一初中数学试卷附加题

一、解答题(共30分,每题10分)1. 几何证明题:已知在直角三角形ABC中,∠C为直角,AB=5cm,BC=3cm,求证:∠BAC为锐角。
2. 代数题:已知函数f(x) = 2x - 3,求函数f(x)在x=4时的函数值。
3. 应用题:小明骑自行车从家到学校,全程15km。
他骑行的速度在前5km为10km/h,在后10km为15km/h。
求小明从家到学校平均速度是多少km/h?4. 方程题:解方程组:\[\begin{cases}3x + 2y = 12 \\2x - y = 4\end{cases}\]二、探究题(共20分,每题10分)1. 探究题:已知正方形的边长为a,求正方形的周长和面积。
2. 探究题:小明在直角坐标系中画了一个三角形,坐标分别为A(2,3),B(4,6),C(6,3)。
请探究三角形ABC的性质,并给出证明。
三、拓展题(共50分)1. 拓展题:已知函数f(x) = x^2 - 4x + 3,求函数f(x)的顶点坐标和与x轴的交点坐标。
2. 拓展题:在平面直角坐标系中,点P的坐标为(2,5),点Q在x轴上,且PQ的长度为3。
求点Q的坐标。
3. 拓展题:一个长方体的长、宽、高分别为3cm、4cm、5cm,求这个长方体的表面积和体积。
4. 拓展题:小明有一批糖果,他想要将糖果平均分给他的8个朋友,但糖果的数量不能整除。
已知小明至少有49颗糖果,最多有多少颗糖果?四、附加题(共40分)1. 附加题:已知等腰三角形ABC中,AB=AC,BC=8cm,底边BC上的高AD垂直于BC。
求三角形ABC的周长。
2. 附加题:小明在公园里散步,他先向东走了100米,然后向北走了200米,最后向西走了150米。
请问小明最终距离出发点有多远?3. 附加题:一个梯形的上底长为6cm,下底长为10cm,高为4cm。
求这个梯形的面积。
4. 附加题:已知二次函数f(x) = ax^2 + bx + c,其中a、b、c为常数,且a≠0。
初一数学附加题
初一数学附加题:(共计20分)
一.选择题(单项选择,每题3分)
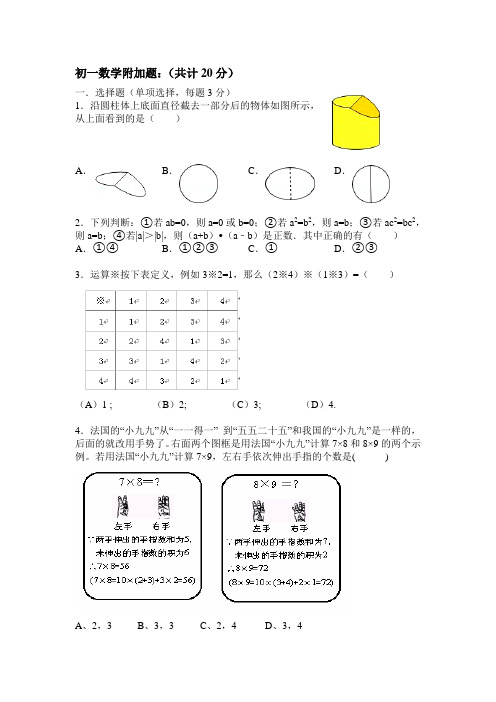
1.沿圆柱体上底面直径截去一部分后的物体如图所示,
从上面看到的是( )
B
2.下列判断:①若ab=0,则a=0或b=0;②若a 2=b 2,则a=b ;③若ac 2=bc 2,则a=b ;
3.运算※按下表定义,例如3※2=1,那么(2※4)※(1※
3)=( )
(A )1 ; (B )2;
(C )3; (D )4.
4.法国的“小九九”从“一一得一” 到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了。
右面两个图框是用法国“小九九”计算7×8和8×9的两个示例。
若用法国“小九九”计算7×9,左右手依次伸出手指的个数是( )
A 、2,3
B 、3,3
C 、2,4
D 、3,4
二、填空题(每空2分)
5.日本福岛核泄漏事故释放的放射性核素碘﹣131,它的放射性每经过8天便降低到原来的一半.若某时测得碘﹣131的放射性为3.2×104msv,那么经过16天其放射性变为msv(用科学记数法表示,注:碘﹣131是一种元素,msv(毫希)是辐射的单位。
)
6.10个同学藏在10个谜宫里面.男同学的谜宫门前写的是一个正数,女同学的谜宫门前写的是一个负数,这10个迷宫门前的数字依次为
则谜宫里面的男同学人,女同学人
7.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意放一条长为2014厘米的木条AB,则木条AB盖住的整点的个数是。
湘教版七年级上册数学附加题(1)

湘教版七年级上册数学附加题(1)例题例1、 已知012=-+a a ,求2018223++a a 的值.例2.若多项式()x y x x x mx 537852222+--++-的值与x 无关,求()[]m m m m +---45222的值.例3.x=-2时,代数式635-++cx bx ax 的值为8,求当x=2时,代数式635-++cx bx ax 的值。
例4、解方程503201320091399551=⨯++⨯+⨯+⨯x x x x例5.问当a 、b 满足什么条件时,方程2x+5-a=1-bx :(1)有唯一解;(2)有无数解;(3)无解。
例6、A 和B 两家公司都准备向社会招聘人才,两家公司招聘条件基本相同,只有工资待遇有如下差异:A 公司,年薪一万元,每年加工龄工资200元;B 公司,半年薪五千元,每半年加工龄工资50元。
从收入的角度考虑,选择哪家公司有利?练习1、如果012=-+x x ,求代数式7223-+x x 的值。
2、已知关于x 的二次多项式()()5233223-++++-x x x b x x x a ,当2=x 时的值为-17,求当2-=x 时该多项式的值。
3、解方程2015201620151262=⨯++++x x x x4、已知关于x 的方程23)12(-=-x x a 无解,试求a 的值。
5、若关于x 的方程2236kx m x nk +-=+,无论K 为何值时,它的解总是1x =,求m 、n 的值。
6.某市剧院举办大型文艺演出,其门票价格为:一等席300元/人,二等席200元/人,三等席150元/人,某公司组织员工26人去观看,计划用5850元购买2种门票,请你帮助公司设计可能的购票方案。
7、(错车问题)在一段双轨铁道上,两列火车同时驶过,A 列车车速为20米/秒,B 列车车速为24米/秒,若A 列车全长180米,B 列车全长160米,两列车错车的时间是多长时间?8、某公园门票价格规定如下:个班都以班为单位购票,则一共应付1240元,问:(1)两班各有多少学生?(2)如果两班联合起来作为一个团体购票,可省多少钱?(3)如果一班单独组织去公园玩儿,如果你是组织者,将如何购票更省钱?9、1+2+3+…+100=?经过研究,这个问题的一般性结论是1+2+3+…+()121+=n n n ,其中n是正整数.现在我们来研究一个类似的问题:1×2+2×3+…= ?观察下面三个特殊的等式()2103213121⨯⨯-⨯⨯=⨯ ()3214323132⨯⨯-⨯⨯=⨯ ()4325433143⨯⨯-⨯⨯=⨯ 将这三个等式的两边相加,可以得到1×2+2×3+3×4=2054331=⨯⨯⨯ 读完这段材料,请你思考后回答:⑴=⨯++⨯+⨯1011003221⑵()()=++++⨯⨯+⨯⨯21432321n n n⑶()()=++++⨯⨯+⨯⨯21432321n n n10、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ =+⨯=+b a ab a b 则符合前面式子的规律,,若…21010 11、《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月计算:那么他当月的工资、薪金所得是多少?12.(2005•烟台)为庆祝第29届北京奥运圣火在泉州站传递,甲、乙两校联合准备文艺汇演.甲、乙两校共92人(其中甲校人数多于乙校人数,且甲校人数不够90人)准备统一购买服装(一人买一套)参加演出,下面是服装厂给出的(1)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?(2)甲、乙两校各有多少学生准备参加演出?(3)如果甲校有9名同学抽调去参加迎奥运书法比赛不能参加演出,那么你有几种购买方案,通过比较,你该如何购买服装才能最省钱?13、如果0abc ≠,求||||||a b c a b c++的值。
初一数学上北京各区附加题

初一数学上北京各区附加题一.选择题 4*5=20分(人大附中期末测试题)1、方程320x +=与关于x 的方程5x +k =20的解相同,那么k 的值为 ( ) A .22 B .143 C .1233 D .21733、图1是分别从不同角度看“由一些相同的小正方体构成的几何体”得到的图形。
这些相同的小正方体的个数是 ( )A .4B .5C .6D .7图1 4、已知:∠AOC =90°,∠AO B :∠AOC =2:3,则∠BOC 的度数是 ( ) A .30° B .60° C .30°或60° D .30°或150°5、若x <0,x y <0,则 15y x x y -+---的值是 ( ) A .- 4 B .4 C .-2x +2y +6 D .不能确定二、填空题(1-4为人大附中期末测试题,5-8为清华附中期末附加题)5*8=40分 1、30°50′23″的角的余角是__________。
2、如果多项式A 减去-3x +5,再加上27x x --后得2531x x --,则A 为__________。
3、若32mm nx yx +与是同类项,那么 n =__________。
4、一个角和它的余角的比是5:4,则这个角的补角是__________。
5、已知一条直线上有A 、B 、C 三点,线段AB 的中点为P ,AB=10,线段BC 的中点为Q ,BC=6,则线段PQ=__________ 7、对整数a 、b 、c ,图形 表示运算b c aa b c -+,已知b a1=2,则x =____________8、如图,一个34⨯的长方形方格,则共有_________个正方形。
三、解答题 (共46分)2、(四中附加题)如果0,0abc a b c <++>,则当||||||a b c x a b c =++时,求32235x x x -++的值。
七年级附加题数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,有理数是()A. √9B. √16C. √25D. √-162. 下列各数中,无理数是()A. 2.5B. √4C. 3/4D. √-43. 已知:a = -3,b = 4,那么a + b的值是()A. 1B. -7C. 7D. 04. 如果一个数的平方是16,那么这个数是()A. 4B. -4C. ±4D. ±25. 已知:x + 2 = 5,那么x的值是()A. 3B. 2C. 1D. -36. 下列各数中,偶数是()A. 3B. 5C. 6D. 77. 下列各数中,质数是()A. 4B. 6C. 7D. 98. 下列各数中,完全平方数是()A. 4B. 5C. 6D. 79. 如果一个数的立方是27,那么这个数是()A. 3B. -3C. ±3D. ±210. 已知:2x - 3 = 7,那么x的值是()A. 5B. 4C. 3D. 2二、填空题(每题5分,共50分)1. 如果一个数的倒数是1/3,那么这个数是__________。
2. 下列各数中,负数是__________。
3. 如果一个数的绝对值是5,那么这个数是__________。
4. 下列各数中,有理数是__________。
5. 下列各数中,无理数是__________。
6. 如果一个数的平方是16,那么这个数是__________。
7. 下列各数中,偶数是__________。
8. 下列各数中,质数是__________。
9. 下列各数中,完全平方数是__________。
10. 如果一个数的立方是27,那么这个数是__________。
三、解答题(每题10分,共40分)1. 已知:a = -2,b = 3,求a - b的值。
2. 已知:x + 4 = 10,求x的值。
3. 已知:√9 - √16 = x,求x的值。
4. 已知:3x - 2 = 7,求x的值。
苏科版七年级上册数学初一期中试卷附加题
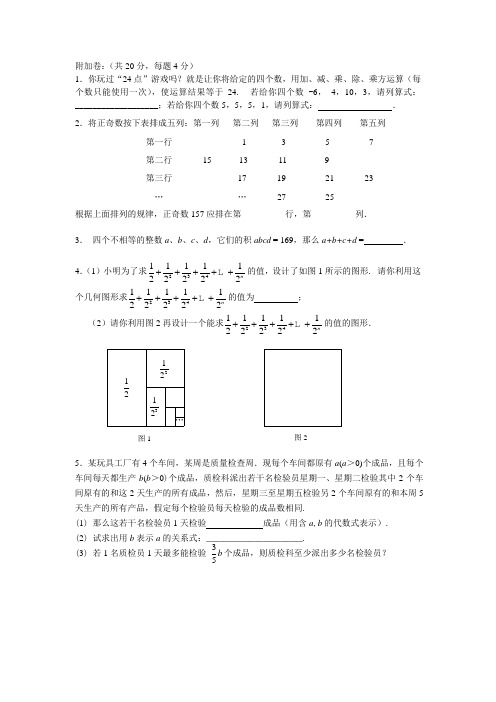
附加卷:(共20分,每题4分)1.你玩过“24点”游戏吗?就是让你将给定的四个数,用加、减、乘、除、乘方运算(每个数只能使用一次),使运算结果等于24. 若给你四个数 -6, 4,10,3,请列算式:___________________;若给你四个数5,5,5,1,请列算式: .2.将正奇数按下表排成五列:第一列 第二列 第三列 第四列 第五列第一行 1 3 5 7第二行 15 13 11 9第三行 17 19 21 23… … 27 25根据上面排列的规律,正奇数157应排在第__________行,第__________列.3. 四个不相等的整数a 、b 、c 、d ,它们的积abcd = 169,那么a+b+c+d = .4.(1)小明为了求2341111122222n +++++的值,设计了如图1所示的图形. 请你利用这个几何图形求2341111122222n +++++的值为 ; (2)请你利用图2再设计一个能求2341111122222n +++++的值的图形.5.某玩具工厂有4个车间,某周是质量检查周.现每个车间都原有a (a >0)个成品,且每个车间每天都生产b (b >0)个成品,质检科派出若干名检验员星期一、星期二检验其中2个车间原有的和这2天生产的所有成品,然后,星期三至星期五检验另2个车间原有的和本周5天生产的所有产品,假定每个检验员每天检验的成品数相同.(1) 那么这若干名检验员1天检验 成品(用含a ,b 的代数式表示).(2) 试求出用b 表示a 的关系式:______________________.(3) 若1名质检员1天最多能检验 个成品,则质检科至少派出多少名检验员? 12 212 312 图1 … 图2b 53。
完整word版,初一数学附加题

附加题:(选做)1、已知|a|=8,|b|=5,且|a+b|=a+b,则a-b=___ ___。
(4分)2、已知x 、y 互为相反数,a 、b 互为倒数,m 的绝对值为3。
求代数式 4(x +y )-ab+m 3的值(4分)()()()()分的值求、已知:41...111020001999...432132000199943322120002000199919994433221x x x x x x x x x x x x x x ++++=-+-++-+-+-+-4、(本小题满分8分)用整体思想解题:为了简化问题,我们往往把一个式子看成一个整体,试试按提示解答下面问题(1)已知A +B =3x 2-5x +1,A -C =3x 2-2x -5,求当x =2时B +C 的值。
(提示:B +C =(A +B )-(A -C ))(2)若代数式2x2+3y+7的值为8,求代数式6x2+9y+8的值。
5、(本小题满分10分)(1)在2009年6月的日历中(见图表),任意圈出一竖列上相邻的三个数,设中间一个为a,则用含a的代数式表示这三个数(从小到大排列)分别是、、。
(2)现将连续自然数1至2009按上图圈中的方式排成一个长方形阵列,用一个正方形框出9个数(如下图)①图中框出的这9个数的和是②在上图中,要使一个正方形框出的9个数之和分别等于2007、2009,是否可能?若不可能,说明理由;若有可能,请求出该正方形框出的9个数中的最小数和最大数。
6、(本小题满分12分)规定:正整数n 的“H 运算”是:①当n 为奇数时,H =3n +13;当n 为偶数时,H =n ×1 2 ×1 2 ×………………(不断乘以1 2 ,直到H 是奇数为止)。
(1)数2经过3次“H 运算”的结果是多少?(2)数7经过2009次“H 运算”的结果是多少?(3)若“H 运算”②结果总是常数a ,求a 的值。
初中数学考试卷附加题

一、解答题(每题20分,共60分)1. 已知等差数列{an}的前三项分别为1,4,7,求该数列的通项公式和第10项的值。
2. 已知函数f(x) = x^2 - 4x + 4,求函数的图像、对称轴、顶点坐标和与x轴的交点。
3. 在直角坐标系中,点A(2,3),点B(4,1),点C(m,n)在直线y=x+1上,求m和n 的值。
二、证明题(每题20分,共40分)4. 证明:在直角三角形ABC中,若∠C=90°,AC=3,BC=4,则AB^2=AC^2+BC^2。
5. 证明:对于任意实数x,都有x^2 ≥ 0。
三、应用题(每题20分,共40分)6. 小明家住在楼层为x的居民楼,他从一楼走到x楼,每层楼之间的距离相同,已知他从一楼走到x楼需要走60秒,求每层楼之间的距离。
7. 一块长方形菜地的长是宽的两倍,如果将宽增加10米,那么面积将增加200平方米,求原来菜地的长和宽。
四、拓展题(每题20分,共40分)8. 设等比数列{an}的首项为a1,公比为q,若a1=1,q=2,求第n项an的值。
9. 已知数列{an}的前三项分别为1,3,5,求该数列的通项公式,并求出第10项的值。
答案:一、解答题1. 解:设等差数列{an}的公差为d,由题意得d=4-1=3,通项公式为an=1+(n-1)×3=3n-2,第10项的值为a10=3×10-2=28。
2. 解:函数f(x) = x^2 - 4x + 4的图像是一个开口向上的抛物线,对称轴为x=2,顶点坐标为(2,-4),与x轴的交点为(2,0)。
3. 解:由题意得n=x+1,代入点B(4,1)得1=4+1,解得x=3,所以m=3,n=4。
二、证明题4. 证明:在直角三角形ABC中,∠C=90°,AC=3,BC=4,根据勾股定理,AB^2=AC^2+BC^2=3^2+4^2=9+16=25。
5. 证明:对于任意实数x,都有x^2 ≥ 0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附加题:(选做)
1、已知|a|=8,|b|=5,且|a+b|=a+b,则a-b=___ ___。
(4分)
2、已知x 、y 互为相反数,a 、b 互为倒数,m 的绝对值为3。
求代数式 4(x +y )-ab+m 3的值(4分)
()()()()
分的值求
、已知:
41...111020001999...432132000199943322120002000199919994433221x x x x x x x x x x x x x x ++++=-+-++-+-+-+-
4、(本小题满分8分)用整体思想解题:为了简化问题,我们往往把一个式子看成一个整体,
试试按提示解答下面问题
(1)已知A +B =3x 2-5x +1,A -C =3x 2-2x -5,求当x =2时B +C 的值。
(提示:B +C =(A +B )-(A -C ))
(2)若代数式2x2+3y+7的值为8,求代数式6x2+9y+8的值。
5、(本小题满分10分)(1)在2009年6月的日历中(见图表),任意圈出一竖列上相邻的
三个数,设中间一个为a,则用含a的代数式表示这三个数(从小到大排列)分别是、、。
(2)现将连续自然数1至2009按上图圈中的方式排成一个长方形阵列,用一个正方形框出9个数(如下图)
①图中框出的这9个数的和是
②在上图中,要使一个正方形框出的9个数之和分别等于2007、2009,是否可能?若
不可能,说明理由;若有可能,请求出该正方形框出的9个数中的最小数和最大数。
6、(本小题满分12分)规定:正整数n 的“H 运算”是:①当n 为奇数时,H =3n +13;
当n 为偶数时,H =n ×1 2 ×1 2 ×………………(不断乘以1 2 ,直到H 是奇数为止)。
(1)数2经过3次“H 运算”的结果是多少?
(2)数7经过2009次“H 运算”的结果是多少?
(3)若“H 运算”②结果总是常数a ,求a 的值。
附加题:(选做)
1、已知|a|=8,|b|=5,且|a+b|=a+b,则a-b=___13或3 _。
(4分)
2、 解: ∵ x 、y 互为相反数,a 、b 互为倒数,m 的绝对值为3
∴ 3,1,
0±===+m ab y x ……………2分
当 3=m 时
原式=33104+-⨯
=26 ……………3分 当 3-=m 时
原式=()33104-+-⨯ =-28 ………………4分 3. 解:∵
()()()2000200019991999443322120001999...4321-+-++-+-+-+-x x x x x x =0 ∴ 2000,1999......,3,2,120001999321=====x x x x x ………1分 原式=2000
19991......431321211⨯++⨯+⨯+⨯ .........2分 =⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-2000119991 (41313121211)
1 ………3分 =200011- =2000
1999 ………4分。
