matlab——大学数学实验报告
MATLAB实验报告

MATLAB实验报告实验报告课程名称 MATLAB基础及应用专业班级电子xxxx姓名学号电气与信息学院实验二 MATLAB 数值计算(一)一实验目的:1.掌握数组的创建与运算方法;2. 掌握矩阵的创建与运算方法;3. 掌握数组的运算方法和矩阵运算方法的区别;4.掌握线性方程的求解方法二实验装置:计算机三实验内容:1.数组的创建和运算创建两个含5个元素的一维数组,并求这两个数组的四则运算。
2.矩阵的创建和运算(1)创建两个3×3的矩阵,并求这两个矩阵的四则运算。
(2)创建一个4×4的矩阵,并求这个矩阵的行列式值。
(3)线性方程的求解解方程组=6613753467294x 。
四实验要求:写出实验程序与仿真结果。
1. >> a=linspace(2,10,5) a =2 4 6 8 10>> b=linspace(1,9,5) b =1 3 5 7 9>> a+bans =3 7 11 15 19>> a-bans =1 1 1 1 1>> a.*bans =2 12 30 56 90>> a./bans =2.0000 1.3333 1.2000 1.1429 1.1111 >> a.\b ans =0.5000 0.7500 0.8333 0.8750 0.9000 2.(1) >> a=[1 1 1;2 2 2;3 3 3];>> b=[4 4 4;5 5 5;6 6 6];>> a+bans =5 5 57 7 79 9 9>> a-bans =-3 -3 -3-3 -3 -3-3 -3 -3>> a*bans =15 15 1530 30 3045 45 45>> a/bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNNaN NaN NaN>> a\bWarning: Matrix is singular to working precision. ans =NaN NaN NaNNaN NaN NaNInf Inf Inf(2).>> a=[1 1 1 1;2 2 2 2;3 3 3 3;4 4 4 4];>> det(a)ans =(3).>> a=[4 9 2;7 6 4;3 5 7];>> b=[13;6;6];>> x=inv(a)*bx =-0.53081.7109-0.1374实验三 MATLAB数值计算(二)一实验目的:1.掌握多项式的创建与运算方法;2. 掌握基本的数据分析方法;二实验装置:计算机三实验内容:1.多项式创建输入系数矢量,创建多项式x^3-2*x^2+5*x+3。
北科大Matlab 数学实验报告

数学实验报告实验名称 Matlab 基础知识学院专业班级姓名学号2014年 6月一、实验目的1.认识熟悉Matlab这一软件,并在此基础上学会基本操作;2.掌握Matlab基本操作和常用命令;3.了解Matlab常用函数,运算符和表达式;4.掌握Matlab工作方式和M文件的相关知识;5.学会Matlab中矩阵和数组的运算;二、实验任务P16 第4题编写函数文件,计算1!nkk =∑,并求出当k=20时表达式的值; P27第2题矩阵A=123456789⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,B=468556322⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦,计算AB,A.B,并比较两者的区别;P27第3题已知矩阵A=5291⎡⎤⎢⎥⎣⎦,B=1292⎡⎤⎢⎥⎣⎦,做简单的关系运算A>B,A==B,A<B,并做逻辑运算A==B&A<B,A==B&A>B; P34 第1题用11114357π=-+-+……公式求π的近似值,直到某一项的绝对值小于-610为止;三、实验程序P16 第4题function sum=jiechengn sum=0;y=1;for k=1:nfor i=1:ky=yi;endsum=sum+y;endsumP27第2题>>A=1 2 3;4 5 6;7 8 9>>B=4 6 8;5 5 6;3 2 2>>AB>>A.BP27第3题>> A=5 2;9 1;B=1 2;9 2;>>A>B>>A==B>>A<B>> A==B&A<B>> A==B&A>BP34 第1题t=1;pi=0;n=1;s=1;while abst>=1e-6pi=pi+t;n=n+2;s=-s;t=s/n;endpi=4pi;四、实验结果P16 第4题P27第2题两者的区别:AB是按正规算法进行矩阵的计算, A.B是对应元素相乘; P27第3题P34 第1题>> pipi=五、实验总结这次实验是第一次接触Matlab这个软件,所以有些生疏,花的时间也比较多,但功夫不怕有心人,而且当一个程序弄出来后感觉也特别开心,以后再继续努力学习;一、实验目的了解并掌握matlab的基本绘图二、实验任务P79页 1,3,5题三、实验程序1.clf;x=0:pi/50:4pi;y1=expx/3.sin3x;y2=expx/3;y3=-expx/3;plotx,y1,'b',x,y2,'r-.',x,y3,'r-.',grid onlegend'y1=expx/3.sin3x','y2=+-expx/3'3.clf;x1=-pi:pi/50:pi;x2=pi:pi/50:4pi;x3=1::8;y1=x1.cosx1;y2=x2.tanx2.^-1.sinx2.^3;y3=expx3.^-1.sinx3;subplot2,2,1,plotx1,y1,'m.',grid on,title'y=xcosx'xlabel'xá',ylabel'yá'gtext'y=xcosx',legend'y=xcosx'subplot2,2,2,plotx2,y2,'r',grid on,title'y=xtan1/xsinx^3' xlabel'xá',ylabel'yá'gtext'y=xtan1/xsinx^3',legend'y=xtan1/xsinx^3'subplot2,2,3,plotx3,y3,'bp',grid on,title'y=e1/x3sinx' xlabel'xá',ylabel'yá'gtext'y=e1/x3sinx',legend'y=e1/x3sinx'5.t=0:pi/50:20pi;x=t.costpi/6;y=t.sintpi/6;z=2t;plot3x,y,z四、实验结果1.3.5.五、实验总结通过本次课程和作业,我初步了解了matlab在绘图方面的优势和重要性;一、 实验目的1. 学会用Matlab 进行三维的曲线绘图;2. 掌握绘图的基本指令和参数设置 二、 实验任务 P79 习题5绘制圆锥螺线的图像并加标注,圆锥螺线的参数方程为;⎪⎪⎪⎩⎪⎪⎪⎨⎧===t z t t y t t x 26sin 6cos ππ )200(π≤≤t ;P79 习题9画三维曲线2)x,y (-2-x -522≤≤=y z 与平面z=3的交线;三、 实验程序 习题5:clf;t=0:pi/100:20pi; x=t.cost.pi/6; y=t.sint.pi/6; z=2t;plot3x,y,z title '圆锥螺线'xlabel 'x 轴',ylabel 'y 轴',zlabel 'z 轴'习题9:clf;t=-2::2;x,y=meshgridt; z1=5-x.^2-y.^2;subplot1,2,1,meshx,y,z1,title '曲面z1=5-x.^2-y.^2' z2=3onessizex;r0=absz1-z2<=;zz=r0.z2;yy=r0.y;xx=r0.x;subplot1,2,2,plot3xxr0~=0,yyr0~=0,zzr0~=0,'.'title'交线'四、实验结果习题5:习题9:五、实验总结这次三维曲线曲面的绘制虽然不算复杂,但还是要注意一些细节,而且要注意弄懂其中的原因,不能硬套书上的,否则很容易不明道理的出错;1. 学会用Matlab 练习使用矩阵的基本运算;2. 掌握用Matlab 运用矩阵的特征值、特征向量、特征多项式;3. 学会用Matlab 解线性方程组;4. 掌握用Matlab 进行数值方法计算定积分 二、 实验任务 P114 习题12随机输入一个六阶方阵,并求其转置、行列式、秩,以及行最简式; P114 习题14求矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2 1 11 2 11 1 2A 的特征多项式、特征值和特征向量;P115 习题20求下列线性方程组的通解:1⎪⎩⎪⎨⎧=+=++=++0-43-203-0-243213214321x x x x x x x x x x x 2⎪⎪⎩⎪⎪⎨⎧=+=+=+21-32--13--0--432143214321x x x x x x x x x x x xP167 习题17用三种方法求下列积分的数值解: 2dx xxx ⎰+π2cos 1sinP167 习题18用多种数值方法计算定积分⎰4sin -11πdx x,并与精确值2进行比较,观察不同方法相应的误差;习题12>> A=1 9 5 3 6 5;2 4 6 8 1 0;3 4 6 9 7 2;4 6 7 8 10 4;5 0 7 3 2 1;3 8 6 3 1 9>> A'>> detA>> rankA>> rrefA习题14:>> B=2 1 1;1 2 1;1 1 2>> p=polyB>> V D=eigB习题20:1>> A=1 1 2 -4;-1 1 3 0;2 -3 4 -1>> rrefA2>> B=1 -1 -1 1;1 -1 1 -3;1 -1 -2 3>> rrefB>> C=1 -1 -1 1 0;1 -1 1 -3 1;1 -1 -2 3 -1/2>> rrefC习题17:2function y=jifenxy=x.sinx./1+cosx.^2;h=;x=0:h:pi;y0=1+cosx.^2;y1=x.sinx./y0;t=lengthx;s1=sumy11:t-1hs2=sumy12:ths3=trapzx,y1s4=quad'jifen',0,pi习题18:function y=jifenxy=1./1-sinx;h=;x=0:h:pi/4;y=1./1-sinx;t=lengthx; format long s1=sumy11:t-1h s2=sumy12:th s3=trapzx,ys4=quad 'jifen',0,pi/4 format short u1=s1-sqrt2 u2=s2-sqrt2 u3=s3-sqrt2 u4=s4-sqrt2四、 实验结果 习题12 习题14 习题201原方程对应的同解方程组为:⎪⎪⎪⎩⎪⎪⎪⎨⎧===434241256572553x x x x x x ,解得方程基础解系为:⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡1256572553,所以方程组的通解为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡4321x x x x =⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡12565725531κ 2解对应的齐次方程组⎩⎨⎧=+=434212x x x x x ,可得一个基础解系:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1212ε原方程组对应的同解方程组为:⎪⎪⎩⎪⎪⎨⎧+=++=2122143421x x x x x ,可找到一个特解为:⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡=125125*η 因此,此方程组的通解为: 习题17: 2 习题18:五、 实验总结在掌握线性代数相关运算和数值积分的理论基础上进行操作,学会了用Matlab 相关指令和编程,并进行计算与误差分析,感觉原来很繁琐的计算用Matlab 很方便一、 实验目的1. 学会用Matlab 进行曲线拟合和使用插值函数;2. 掌握曲线拟合和插值处理的基本指令和参数设置 二、 实验任务 P130 习题9已知在某实验中测得某质点的位移s 和速度v 随时间t 变化如下:、求质点的速度与位移随时间的变化曲线以及位移随速度变化曲线; P130 习题10在某种添加剂的不同浓度之下对铝合金进行抗拉强实验,得到数据如下,现分别使用不同的插值方法,对其中没有测量的浓度进行推测,并估算出浓度X=18及26时的抗压强度Y 的值;P130 习题12利用不同的方法对22169x y z =-在-3,3上的二维插值效果进行比较;三、 实验程序 习题9:clf; t=0::3; v=0 ; s=1 2 3 4;p1=polyfitt,v,2;p2=polyfitt,s,2;p3=polyfits,v,2;disp'速度与时间函数',f1=poly2strp1,'t'disp'位移与时间的函数',f2=poly2strp2,'t'disp'位移与速度的函数',f3=poly2strp3,'s't1=0::3;s1=0::4;y1=polyvalp1,t1;y2=polyvalp2,t1;y3=polyvalp3,s1;subplot1,3,1,plott,v,'b',t1,y1,'-.',title'速度与时间函数',xlabel't轴',ylabel'v轴'subplot1,3,2,plott,s,'x',t1,y2,':',title'位移与时间的函数',xlabel't 轴',ylabel's轴'subplot1,3,3,plots,v,'k',s1,y3,'r--',title'位移与速度的函数',xlabel's轴',ylabel'v轴'习题10:clf;x=10:5:30;y= ;xi=10::30;yi1=interp1x,y,xi,'nearest';yi2=interp1x,y,xi,'linear';yi3=interp1x,y,xi,'spline';yi4=interp1x,y,xi,'cubic';plotx,y,'b',xi,yi1,'--',xi,yi2,'-.',xi,yi3,'k-',xi,yi4,'m:'legend'原始数据','最近点插值','线性插值','样条插值','立方插值'disp'浓度X=18的抗压强度值'a=interp1x,y,18,'spline'disp'浓度X=26的抗压强度值'b=interp1x,y,26,'cubic'习题12:x,y=meshgrid-3:.5:3;z=x.^2/16-y.^2/9;x1,y1=meshgrid-3:.1:3;z1=x1.^2/16-y1.^2/9;figure1subplot1,2,1,meshx,y,z,title'数据点'subplot1,2,2,meshx1,y1,z1,title'函数图象'xi,yi=meshgrid-3:.125:3;zi1=interp2x,y,z,xi,yi,'nearest';zi2=interp2x,y,z,xi,yi,'linear';zi3=interp2x,y,z,xi,yi,'spline';zi4=interp2x,y,z,xi,yi,'cubic';figure2subplot221,meshxi,yi,zi1,title'最近点插值'subplot222,meshxi,yi,zi2,title'线性插值'subplot223,meshxi,yi,zi3,title'样条插值'subplot224,meshxi,yi,zi4,title'立方插值'四、实验结果习题9:习题10:习题12:五、实验总结本次实验是对多项式的表达以及对曲线的拟合方法,在实际操作进一步了认识拟合和插值的方法以及Matlab的简单方便;六、 实验目的1. 学会用Matlab 进行常微分方程的求解、随机试验和统计作图;2. 掌握相关运算处理的基本指令和参数设置 七、 实验任务 P168 习题24 求解微分方程yxx y cos sin ,=; P168 习题27用数值方法求解析下列微分方程,用不同颜色和线形将y 和y ’画在同一个图形窗口里:t y y y 2-1-t ,,,=+初始时间:0t =0;终止时间:π=f t ;初始条件:2.0|1.0|00,====t t y y ;P190 习题15描绘以下数组的频数直方图:, ,,, , , , , , , , , , , , , P190 习题16若样本为85,86,78,90,96,82,80,74 求样本均值、标准差、中位数、极差和方差;八、 实验程序 习题24:>>dsolve'Dy=xsinx/cosy','x' 习题27:function xdot=exft,x u=1-2t;xdot=0,1;1,-tx+0,1'u; clf; t0=0;tf=pi;x0t=;;t,x=ode23'exf',t0,tf,x0t;y=x:,1Dy=x:,2plott,y,'r-', t,Dy,'b'legend'y','Dy'xlabel't轴'习题15:clf;load ;figure1histA,5figure2histA,10figure3histA,20习题16:B=85 86 78 90 96 82 80 74;disp' 样本均值标准差中位数极差方差'C=meanB,stdB,medianB,rangeB,varB九、实验结果习题24:习题27:习题15:习题16:十、实验总结通过这最后一次实验,我学习了怎么用Matlab作常微分方程的求解、概率论与数理统计的相关计算,感受到了Matlab软件的强大与方便;。
Matlab实验报告
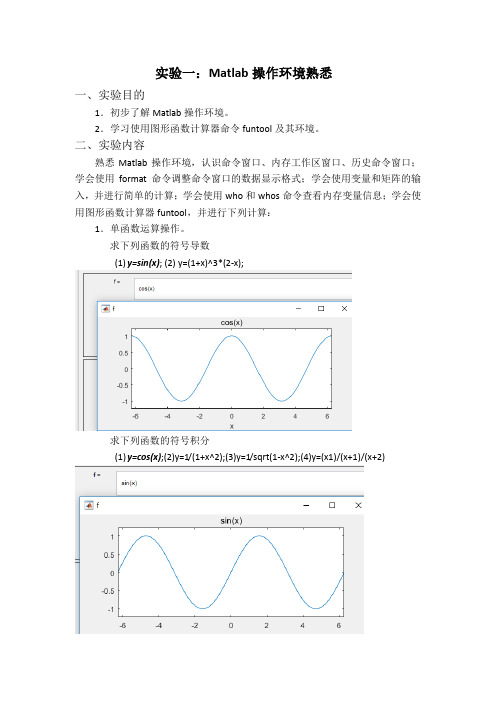
实验一:Matlab操作环境熟悉一、实验目的1.初步了解Matlab操作环境。
2.学习使用图形函数计算器命令funtool及其环境。
二、实验内容熟悉Matlab操作环境,认识命令窗口、内存工作区窗口、历史命令窗口;学会使用format命令调整命令窗口的数据显示格式;学会使用变量和矩阵的输入,并进行简单的计算;学会使用who和whos命令查看内存变量信息;学会使用图形函数计算器funtool,并进行下列计算:1.单函数运算操作。
求下列函数的符号导数(1)y=sin(x); (2) y=(1+x)^3*(2-x);求下列函数的符号积分(1)y=cos(x);(2)y=1/(1+x^2);(3)y=1/sqrt(1-x^2);(4)y=(x1)/(x+1)/(x+2)求反函数(1)y=(x-1)/(2*x+3); (2) y=exp(x); (3) y=log(x+sqrt(1+x^2));代数式的化简(1)(x+1)*(x-1)*(x-2)/(x-3)/(x-4);(2)sin(x)^2+cos(x)^2;(3)x+sin(x)+2*x-3*cos(x)+4*x*sin(x);2.函数与参数的运算操作。
从y=x^2通过参数的选择去观察下列函数的图形变化(1)y1=(x+1)^2(2) y2=(x+2)^2(3) y3=2*x^2 (4) y4=x^2+2 (5) y5=x^4 (6)y6=x^2/23.两个函数之间的操作求和(1)sin(x)+cos(x) (2) 1+x+x^2+x^3+x^4+x^5乘积(1)exp(-x)*sin(x) (2) sin(x)*x商(1)sin(x)/cos(x); (2) x/(1+x^2); (3) 1/(x-1)/(x-2);求复合函数(1)y=exp(u) u=sin(x) (2) y=sqrt(u) u=1+exp(x^2)(3) y=sin(u) u=asin(x) (4) y=sinh(u) u=-x实验二:MATLAB基本操作与用法一、实验目的1.掌握用MATLAB命令窗口进行简单数学运算。
matlab实验报告模板

《高等数学》实验报告(二)实验项目名称:多元函数积分学分组第八组组员姓名学号专业班级实验软件Matlab2010b完成日期实验成绩一、实验目的:加强对Matlab 软件的基本操作,会利用符号计算中int 积分嵌套命令求二重积分、三重积分。
会合理运用int 嵌套命令求解第一类、第二类曲线积分及第一类、第二类曲面积分以及Green 公式及Gauss 公式解题。
结合已经学习的内容,学会分析上述有关内容的综合问题并利用软件给出正确的解答。
二、 实验内容、步骤与结果:8. 计算二重积分 arctan D y d xσ⎰⎰ 其中D 是由圆224x y += 、 及直线y=0, y=x 所围成的在第一象限内的闭区域。
>> syms x y rho theta>> i=int(int(atan(tan(theta))*rho,rho,1,2),theta,0,(0.25)*pi)i =(3*pi^2)/6418. 计算三重积分 e x y z dxdydz ++Ω⎰⎰⎰,其中, 是平面x+y+z=1与三个坐标面围成的立体。
>> syms x y z;>> i=int(int(int(exp(x+y+z),z,0,1),y,0,1-x),x,0,1)i =exp(1) - 128. 计算曲线积分 2()()L x y dx x y dy ++-⎰,其中,L 沿直线从(1,0) 到(0,1), 再沿直线从(0,1)到(-1,0)。
过程syms x y;p=x^2+y;q=x-y;fun=(x^2+y)*diff(p,x)+(x-y)*diff(q,y);I=int(fun,x,1,0);I=int(fun,y,0,1)I =1/2+2*x^3I=int(fun,x,0,-1);I=int(fun,y,1,0)I =-1/2-2*x^3结果由(1,0)到(0,1)I =1/2+2*x^3由(0,1)到(-1,0)I =-1/2-2*x^338求半径为a的球面面积。
Matlab数学实验报告3

a= 311.9546 0.2798
z= Columns 1 through 8
- 6 -MATLAB 作业
3.9000 5.1385 6.7617 8.8828 11.6439 15.2202 19.8224 25.6956 Columns 9 through 16
表 3 美国人口统计数据 年(公元) 1790 1800 1810 1820 1830 1840 1850 人口(百万) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年(公元) 1860 1870 1880 1890 1900 1910 1920 人口(百万) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年(公元) 1930 1940 1950 1960 1970 1980 1990 人口(百万) 123.2 131.7 150.7 179.3 204.0 226.5 251.4 若用非线性回归模型
Optimization terminated: relative function value changing by less than OPTIONS.TolFun.
r=
0.0135
115823
z= 1.0e+005 * Columns 1 through 6 1.0165 1.0304 1.0444 1.0587 1.0731 1.0877 Columns 7 through 12 1.1026 1.1176 1.1328 1.1483 1.1639 1.1798 Columns 13 through 17 1.1958 1.2121 1.2287 1.2454 1.2624
matlab实验报告总结

matlab实验报告总结1.求一份matlab的试验报告计算方法试验报告3【实验目的】检查各种数值计算方法的长期行为【内容】给定方程组x'(t)=ay(t),y'(t)=bx(t), x(0)=0, y(0)=b的解是x-y 平面上的一个椭圆,利用你已经知道的算法,取足够小的步长,计算上述方程的轨道,看看那种算法能够保持椭圆轨道不变。
(计算的时间步长要足够多)【实验设计】用一下四种方法来计算:1. Euler法2. 梯形法3. 4阶RK法4. 多步法Adams公式【实验过程】1. Euler法具体的代码如下:clear;a=2;b=1;A=[0 a; -b0];U=[];u(:,1)=[0;b];n=1000000;h=6*pi/n;fori=1:n delta(i)=((u(1,i)/a)^2+(u(2,i)/b)^2)^0.5; u(:,i+1)=u(:,i)+h*A*u(:,i);endt=1:n+1;subplot(1, 2,1);plot(1:n,delta);gridon;subplot(1,2,2);plot(u(1,:),u(2,:));gridon;max(abs(delta-ones(1,length(delta))));结果如下:2. 梯形法具体的代码如下:clear;a=2;b=1;A=[0 a; -b 0];U=[];u(:,1)=[0;b];n=300;h=6*pi/n;for i=1:n delta(i)=((u(1,i)/a)^2+(u(2,i)/b)^2)^0.5;v1=u(:,i)+h*A*u(:,i);v2=u(:,i)+h*A*(u(:,i)+v1)/2;1u(:,i+1)=u(:,i)+h*A*(u(:,i)+v2)/2;endt=1:n+1;sub plot(1,2,1);plot(1:n,delta);gridon;subplot(1,2,2);结果如下 3. 4阶RK法clear;a=2;b=1;A=[0 a; -b 0];U=[];u(:,1)=[0;b];n=70;h=6*pi/n;for i=1:n delta(i)=((u(1,i)/a)^2+(u(2,i)/b)^2)^0.5;k1=A*u(:,i); k2=A*(u(:,i)+h/2*k2); k3=A*(u(:,i)+h*k3); k4=A*(u(:,i)+h*k3); u(:,i+1)=u(:,i)+h/6*(k1+2*k2+2*k3+k4);endt=1:n+1 ;subplot(1,2,1);plot(1:n,delta);gridon;subplot(1,2,2);结果如下:4. 多步法Adams公式clear;a=2;b=1;A=[0 a; -b 0];U=[];u(:,1)=[0;b];n=200;h=6*pi/n;u(:;2)=u(u,1)+h*A*u(:,1);u(:;3)=u(u,2)+h/2*A*(3*u(:,2)-u(:,1));u(:;4)=u(u,3)+h/12*A*(23*u(:,3)-16*u(:,2)+5*u(:, 1)); delta(1)=((u(1,1)/a)^2+(u(2,1)/b^2)^0.5 delta(2)=((u(1,2)/a)^2+(u(2,2)/b^2)^0.5delta(3)=((u(1,3)/a)^2+(u(2,3)/b^2)^0.5for i=4:n delta(i)=((u(1,i)/a)^2+(u(2,i)/b)^2)^0.5;u(:,i+1)=u(:,i)+h/24*A*(55*u(:,i)-59*u(:,i-1)+37 *u(:,i-1)+37*u(:,i-2)-9*u(:,i-3));endt=1:n+1;sub plot(1,2,1);plot(1:n,delta);gridon;subplot(1,2,2);结果如下:【实验分析】通过这几种方法对比,发现最为稳定的是多步法Adams公式和4阶RK法,其次是梯形法,而欧拉法最为不稳定。
MATLAB数学实验报告

数学实验报告一、实验目的1.学会用软件对矩阵进行一些数值运算。
2.学会用软件解线性方程组。
3.掌握逆矩阵的一种应用:整数逆矩阵加密、解密方法。
4.熟悉三维空间中的线性变换,加深对正交变换保持距离不变性的理解。
5.掌握泰勒级数在近似计算中的应用,从而理解数值逼近思想。
6.了解无理数e和欧拉常数C的由来历史。
7.了解圆周率π的计算历史,掌握计算圆周率π近似值的多种方法。
8.利用幂级数展开式计算无理数e和欧拉常数C的近似值。
9.学会根据实际问题建立线性规划模型。
10.掌握用软件求解线性函数极值问题。
11.学会建立0-1规划模型,掌握用软件求解0-1规划问题。
二、实验内容1.实验五:练习1:1.(1)程序代码[2,11,1;32,13;1,43,5][1;42][]()结果显示特解:(0.8571,-0.7143,0,0)基础解系:ξ1=(0.1429,-1.2857,1,0),ξ2=(0.1429,0.7143,0,1)通解:0.1429 0.1429 0.8571-1.2857 0.7143 -0.7143k1 1 + k2 0 + 0 12єR0 10感想与反思:A.通过解这道题,熟练掌握了用软件解线性方程组的方法B.手工解线性方程组非常繁琐,通过这道题,进一步认识到的强大2.实验五.练习2.24*4的加密锁:程序代码[3 7 15 22;2 5 11 17;3 6 13 21;9 18 36 46](q)(q)[68 105 108 105 103 101 110 99 101 32 105 115 116 32 116 104 101 32 109 111 116 104 101 114 32 111 102 32 115 117 99 99 101 115 115 32](w,4,9)(q)*b结果显示6*6的加密锁代码[2 3 4 2 1 6;7 7 11 9 2 17;4 6 9 5 2 12;8 7 12 9 2 17;3 3 4 2 1 6;6 4 6 6 1 2](q)(q)[68 105 108 105 103 101 110 99 101 32 105 115 116 32 116 104 101 32 109 111 116 104 101 114 32 111 102 32 115 117 99 99 101 115 115 32](w,6,6)*a(q)*b感想与反思:A.通过解这道题,熟练掌握了逆矩阵的一种应用:整数逆矩阵加密、解密方法B.用矩阵就可以完成对于信息的加密和解密,体会到了矩阵和的神奇C.在选择密码锁矩阵时可以对于一个单位矩阵进行多次初等变换,便于找到3.实验七,练习2.1程序代码单数阶导数在0处的值为零。
matlab实验报告

matlab实验报告实验报告:Matlab实验分析1. 实验目的本实验旨在通过Matlab软件完成一系列数值计算和数据分析的任务,包括绘制曲线、解方程、矩阵运算等,以加深对Matlab软件的理解和掌握。
2. 实验内容2.1 绘制函数曲线首先,我们通过在Matlab中输入函数的表达式来绘制函数曲线。
例如,我们可以输入y = sin(x)来绘制正弦函数的曲线。
另外,我们还可以设置曲线的颜色、线型和坐标轴范围等。
2.2 解方程接下来,我们使用Matlab来解方程。
对于一元方程,我们可以使用solve函数来求出方程的解。
例如,我们输入syms x; solve(x^2 - 2*x - 8)来解方程x^2 - 2x - 8 = 0。
而对于多元方程组,我们可以使用solve函数的向量输入形式来求解。
例如,我们输入syms x y; solve(x^2 + y^2 - 1, x - y - 1)来求解方程组x^2 + y^2 - 1 = 0和x - y - 1 = 0的解。
2.3 矩阵运算Matlab也可以进行矩阵运算。
我们可以使用矩阵相乘、相加和取逆等运算。
例如,我们可以输入A = [1 2; 3 4]和B = [5 6;7 8]来定义两个矩阵,然后使用A * B来计算它们的乘积。
3. 实验结果与分析在本实验中,我们成功完成了绘制函数曲线、解方程和矩阵运算等任务。
通过Matlab软件,我们可以快速、准确地进行数值计算和数据分析。
使用Matlab的高级函数和工具箱,我们可以更方便地处理复杂的数值计算和数据分析问题。
4. 实验总结通过本次实验,我们进一步加深了对Matlab软件的理解和掌握。
Matlab提供了丰富的函数库和工具箱,适用于各种不同的数值计算和数据分析任务。
在日常科研和工程实践中,Matlab是一个非常强大和方便的工具,可以帮助我们更高效地完成任务。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
济南大学2012~2013学年第二学期数学实验上机考试题班 级 计科1201 学号 20121222044 姓 名 黄静 考试时间 2014年6 月 17日 授课教师 王新红说明:每题分值20分。
第5题,第6题, 第7题和第8题可以任选其一, 第9题和第10题可以任选其一。
每个同学以自己的学号建立文件夹,把每个题的文件按规定的方式命名存入自己的文件夹。
有多余时间和能力的同学可以多做。
1、自定义函数:x x x ytan ln sin cos ln -=,并求 ?)3(=πy(将总程序保存为test01.m 文件)%%代码区:y=inline('log(cos(x))-sin(x)*log(tan(x))','x'); y(pi/3) %%answerans = -1.16892、将一个屏幕分4幅,选择合适的坐标系在左与右下幅绘制出下列函数的图形。
(1)衰减振荡曲线: x ey x5sin 5.0-=(2)三叶玫瑰线:θρ3sin a = (将总程序保存为test02.m 文件)%%代码区:x=linspace(0,2*pi,30); y=exp(-0.5*x).*sin(5*x);subplot(2,2,1),plot(x,y),title('衰减振荡曲线') hold ontheta=linspace(0,2*pi); r=sin(3*theta); subplot(2,2,4); polar(theta,r); xlabel('三叶玫瑰线')%%answer02468-1-0.500.51衰减振荡曲线三叶玫瑰线3、作马鞍面:22,66,8823x y z x y =--≤≤-≤≤ (将总程序保存为test03.m 文件)%%代码区:[x,y]=meshgrid(linspace(-6,6,70),linspace(-8,8,70)); z=x.^2/2-y.^2/3; mesh(x,y,z)surface(x,y,z)%让曲面光滑并填满 shading interp ;4、建立函数M 文件并作以下计算: (1)求自然数n 的阶乘:!n test04_1(4)%调用%以下代码以text04_1.m 保存在当前文件夹下 function [sum] = test04_1(n) sum=0; if n==0 return end sum=1;for i=[1:n] sum=sum*i; end%%ansser ans=24 (2)求:201!n T n ==∑T=test04_2()%调用%以下代码以text04_2.m 保存在当前文件夹下 function [ sum ] = test04_2( )sum=0;for i = 1:20sum = sum + test04_1(i);end%%answer T=2.5613e+018C(3)求n中取m的组合:nmtest04_3(2,5)%以下代码以text04_1.m保存在当前文件夹下function [ sum ] = test04_3( n,m )sum=(test04_1(m))/(test04_1(n)*test04_1(m-n));%%answer ans=10(将总程序保存为test04.m文件)5、下表给出的x、y数据位于机翼端面的轮廓线上,Y1和Y2分别对应轮廓的上下线。
假设需要得到x坐标每改变0.1时的y坐标,试完成加工所需数据,画出曲线,求加工端面的(将总程序保存为test05.m文件)%%代码区%初值x0=[0 3 5 7 9 11 12 13 14 15];y0=[0 1.8 2.2 2.7 3.0 3.1 2.9 2.5 2.0 1.6];y00=[0 1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6];%步长x=0:0.1:15;%三次样条插值y10=interp1(x0,y0,x,'spline');y100=interp1(x0,y00,x,'spline');%分段线性插值y20=interp1(x0,y0,x,'linear');y200=interp1(x0,y00,x,'linear');plot(x,y10,'.r',x,y100,'.g')s=trapz(x,y10)-trapz(x,y100)%三次样条插值积分值l=trapz(x,y20)-trapz(x,y200)%分段线性插值积分值%%ans——s =11.3444;l =10.7500%s=11.3444更合理些0510156、在农业生产试验研究中,对某地区土豆的产量与化肥的关系做了一实验,得到了氮肥、磷肥的施肥量与土豆产量的对应关系如下表:根据上表数据分别给出土豆产量与氮、磷肥的关系式。
(将总程序保存为test06m文件)%%代码区%%氮肥x1=[0,34,67,101,135,202,259,336,404,471];y1=[15.18,21.36,25.72,32.29,34.03,39.45,43.15,43.46,40.83,30.75]; plot(x1,y1,'r+')%由散点图可发现大致呈二次函数关系aa=polyfit(x1,y1,2)%二次拟合xx=0:471;yy=polyval(aa,xx);%yy=aa(1)*xx.*xx+aa(2)*xx+aa(3);此式与其等价subplot(2,1,1);plot(xx,yy,x1,y1,'r+')grid ;title('氮肥N施肥量与土豆的关系');hold on%%磷肥x2=[0,24,49,73,98,147,196,245,294,342];y2=[33.46,32.47,36.06,37.96,41.04,40.09,41.26,42.17,40.36,42.73]; subplot(2,1,2);plot(x2,y2,'r+')%由散点图可发现大致呈线性关系%x2_0=[0,24,49,73,98];y2_0=[33.46,32.47,36.06,37.96,41.04];%x2_1=[98,147,196,245,294,342];y2_1=[41.04,40.09,41.26,42.17,40.3 6,42.73];%a1=polyfit(x2_0,y2_0,1)a1=polyfit(x2(1:5),y2(1:5),1)%一次拟合a2=polyfit(x2(5:10),y2(5:10),1)x0=(a2(2)-a1(2))/(a1(1)-a2(1))xx1=0:x0; yy1=a1(1)*xx1+a1(2);xx2=x0:342; yy2=a2(1)*xx2+a2(2);subplot(2,1,2);plot(x2,y2,'r+',xx1,yy1,xx2,yy2)grid ;title('磷肥P施肥量与土豆的关系');50100150200250300350400450500氮肥N 施肥量与土豆的关系050100150200250300350磷肥P 施肥量与土豆的关系%%程序运行结果%aa =-0.0003 0.1971 14.7416 %a1 =0.0844 32.0771 %a2 =0.0059 39.9685 %x0 =100.5075建模分析:使用 Matlab 语言首先画出土豆产量与氮施肥量的散点图,从图可看出土豆产量与氮肥量的关系是二次函数关系,因此可选取拟合函数为:,其中 x 和 y 分别为氮肥量和土豆产量,a 、b 和 c 为待定系数。
再画出磷肥量与土豆产量的散点图,从图可看出从 0 到 98、从 98 到 342 之间分别呈明显的线性关系。
由此可选取所求拟合函数为一分段的线性函数,换言之,用前 5 点作一线性拟合函数,再用后 6 个点也作一线性拟合函数,最后用两个线性函数求出其分界点即可得分段线性函数。
数学模型:对氮肥的拟合函数为:7416.141971.00003.0y 2++-=x x对磷肥的拟合函数为:7、红铃虫的产卵数与温度有关,试根据下表数据,建立棉花红铃虫产卵数与温度的回归方(将总程序保存为test07文件)%不会,蒙的%clear;clc;x=[21 23 25 27 29 32 35];y=[7 11 21 24 66 115 325];p=polyfit(x,y,2);fprintf('\n关系: y= %f x^2 + %f x + %f \n',p(1),p(2),p(3));%answer关系: y= 2.553049 x^2 + -123.060824 x + 1482.0673878、人口问题”是我国最大社会问题之一,估计人口数量和发展趋势是我们制定一系列相关政策的基础。
有人口统计年鉴,可查的我国从1949年至1994年人口数据智料如下:(1)在直角坐标系上作出人口数的图象。
(2)估计出这图象近似地可看做一条直线。
(3)用最小二乘法确定直线方程,并算出1999年人口数。
(将总程序保存为test08文件)19451950195519601965197019751980198519901995500600700800900100011001200y=14.5101x+-27753.51999: 1252.06%%answerp =1.0e+004 *0.0015 -2.7754num1999 =1.2521e+003(编者注:p 的比较真实的值是14.5100606060607 -2.775354648484860e+04,一定得从workspace 中观察)9营养师想购这三种食物共10千克,使之所含维生素A 不少于4400单位,维生素B 不少于4800单位,问三种食物各购多少时,成本最低?最低成本是多少? (将程序保存为test09m 文件) %%代码区%动态规划f=[7;6;5];A=[-400 -600 -400;-800 -200 -400;-1 0 0;0 -1 0;0 0 -1]; b=[-4400;-4488;0;0;0]; C=[1 1 1]; d=[10];[x,feval]=linprog(f,A,b,C,d,[],[]); xmoney=7*x(1)+6*x(2)+5*x(3)%画图 bar(x);set(gca,'XTickLabel',{'甲','乙','丙'}); text([1,2,3],x-1,num2str(x)); xlabel({'Money:' money});%%程序运行结果%Optimization terminated.%x =2.2200,2.0000,5.7800,money =56.4400甲乙丙123456Money:56.4410、某厂生产A 、B 两种产品,1千克原料在甲类设备上用12小时可生产3件A ,可获净利润64元;在乙类设备上用8小时可生产4件B,可获净利润54元。
