6-第六讲-杆件有限元分析
6-第六讲-杆件有限元分析

3 0 1 2 k ji 2 2 k jj 3
补充-整体分析
补充-整体分析
整体刚度矩阵的建立 (3) 编码法
杆件有限元分析:案例
四 杆 桁 架 结 构
杆件有限元分析:案例
(1) 结构的离散化与编号
四 杆 桁 架 结 构
对该结构进行自然离散,节点编号和单元编号如上图所示,有关节点 和单元的信息见表1至表3。
杆件有限元分析:案例
(1) 结构的离散化与编号
四 杆 桁 架 结 构
对该结构进行自然离散,节点编号和单元编号如上图所示,有关节点 和单元的信息见表1至表3。
杆件有限元分析:案例
(2) 各个单元的矩阵描述
四 杆 桁 架 结 构
由于所分析的结构包括有斜杆,所以必须在总体坐标下对节点 位移进行表达,所推导的单元刚度矩阵也要进行变换,各单元 经坐标变换后的刚度矩阵如下。
基本概念 回顾:杆件有限元分析
(3) 单元应变场的表达 由弹性力学中的几何方程,有1D问题的应变
1D 杆 单 元
其中
叫做几何矩阵(strain-displacement matrix)。
基本概念 回顾:杆件有限元分析
(4) 单元应力场的表达 由弹性力学中的物理方程,有1D问题的应力
1D 杆 其中 单 元 叫做应力矩阵(stress-displacement matrix)
2D 杆 单 元
回顾:杆件有限元分析
(2)整体坐标系下的单元刚度方程
2D 杆 单 元
(3)整体坐标系下的单元应力
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
杆梁结构的有限元分析原理

e
下面考察该简单问题的FEA求解过程。 (1) 离散化
两个杆单元,即:单元①和单元②
(2) 单元的特征及表达
对于二结点杆单元,设该单元的位移场为 么它的两个结点条件为
,那
设该单元的位移场具有模式(考虑两个待定系数)
利用结点条件,可以确定系数a0和a1,即
将系数a0和a1代入
,可将
表达成结点位移(u1, u2)的关系,即
其中, 为整体坐标系下的单元刚度矩阵, 为 整体坐标系下的结点力,即
由最小势能原理(针对该单元),将 对待定的 结点位移向量 取一阶极小值,有整体坐标系中 的刚度方程
对于本节给出的杆单元,具体有
4.3.3 空间问题中杆单元的坐标变换
就空间问题中杆单元,局部坐标系下的结点位移还 是 而整体坐标系中的结点位移为
这时由全部结点位移[0 u2 u3]分段所插值 出的位移场为全场许可位移场。
由最小势能原理(即针对未知位移u2和u3求 一阶导数),有
可解出
(5) 计算每个单元的应变及应力
在求得了所有的结点位移后,由几何方程
可求得各单元的应变
由方程 可求得各单元的应力
(6) 求结点1的支反力
就单元 ①的势能,对相应的结点位移求极值,可以 建立该单元的平衡方程,即
其中
由一维问题几何方程和物理方程,则该单元 的应变和应力为
其中
单元的势能
其中 叫做单元刚度矩阵。
叫做单元结点外载。
在得到“特征单元”的单元刚度矩阵和单元 结点外载后,就可以计算该单元的势能,因 此,计算各单元的矩阵 和 是一个关 键,下面就本题给出了个单元的 和 。
具体就单元①,有 单元①的结点位移向量
(5) 单元的刚度方程
杆梁结构有限元分析
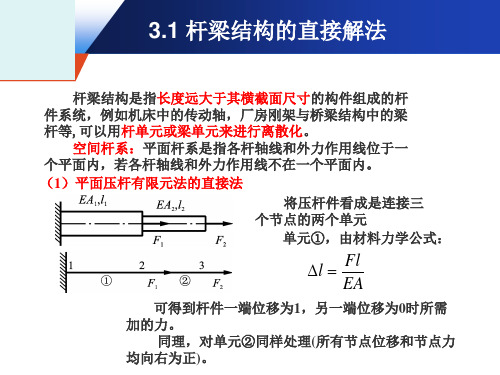
3.1 杆梁结构的直接解法
机械分社
(1)平面压杆有限元法的直接法
由节点平衡有: 即有:
U1(1)u1 U1(1)u2 N1
U
u (1)
21
(U
(2 2
)
U
(1) 2
)u2
U
(2 2
)u3
F1
U
(2 3
)
u2
U
(2 3
)
u3
F2
EA1 l1
u1
EA1 l1
u2
N1
EA1 l1
u1
( EA1 l1
3.1 杆梁结构的直接解法
机械分社
杆梁结构是指长度远大于其横截面尺寸的构件组成的杆 件系统,例如机床中的传动轴,厂房刚架与桥梁结构中的梁 杆等,可以用杆单元或梁单元来进行离散化。
空间杆系:平面杆系是指各杆轴线和外力作用线位于一 个平面内,若各杆轴线和外力作用线不在一个平面内。 (1)平面压杆有限元法的直接法
单元刚度矩阵每一列元素表示一组平衡力系,对于平面 问题,每列元素之和为零。
3.1 杆梁结构的直接解法
机械分社
(2)平面梁单元有限元法的直接法 2)节点位移与节点力之间的关系
Ui
Vi
k11
k21
M i U j
k31
k41
V
j
M j
k51
k61
他们在轴和轴的投影之和等于零:
vi
6EI l2
i
12EI l3
vj
6EI l2
j
M
j
6EI l2
vi
2EI l
i
6EI l2
vj
4EI l
杆梁结构的有限元分析原理

对剪切变形的影响
3.1 理论
只考虑剪切变形
变形后轴线切向与变形前轴角 γxz 其中 ψ (x) 为只考虑梁弯曲理论中的线性单元转角. 假设 : 截面上均匀分布剪应变
弯曲产生的位移:
9
内部力
其中假设
10
实际上τxz采用以下形式:
其中变量与z相关。 为了确定截面的不均匀剪应力分布,引入因素k修正剪应 力:
BEAM44 3-D Elastic Tapered Unsymmetric Beam This element allows a different unsymmetrical geometry at each end and permits the end nodes to be offset from the centroidal axis of the beam
除非ψ是常数(没有弯曲变形),否则, dw/dx-ψ不会为零。这种现象称为剪切闭锁。 shear-locking
17
几种方法避免产生剪切闭锁
减缩积分
数值积分采用比精确积分要求少的积分点数
假设剪切应变 替代插值函数
举例说明
18
19
Timoshenko 梁 (采用精确积分)
20
采用缩减积分
形成总体刚度矩阵
点坐标、约束条件等;
形成结点荷载向量
(3)单元数据:如单元编号、单 元结点序号、单元的材料特性、
引入约束条件
几何特性等;
求解方程组,输出结点位移
(4)载荷数据:包括集中载荷、 计算单元应力,输出结果 分布载荷等。
结束
37
2、单元分析
(1)各单元的bi,ci(i,j,m) , 面积A;
30
连杆机构的有限元分析方法

连杆机构的有限元分析方法连杆机构的有限元分析方法连杆机构是一种常见的机械结构,由多个连杆和铰链连接而成,广泛应用于各行各业的机械装置中。
在设计和优化连杆机构时,有限元分析是一种有效的方法,可以帮助工程师评估其性能和稳定性。
以下是连杆机构有限元分析的一些步骤和方法。
第一步:建立模型在进行有限元分析之前,需要建立连杆机构的几何模型。
这可以通过计算机辅助设计(CAD)软件完成,将连杆和铰链的几何形状和尺寸输入到软件中。
第二步:离散化离散化是指将连续的结构模型分割为有限数量的单元,以便进行有限元分析。
常用的单元类型包括三角形、四边形单元或六面体等。
根据具体的连杆机构结构,选择合适的单元类型进行离散化。
第三步:确定材料属性和边界条件根据实际情况,为连杆和铰链分配合适的材料属性,如弹性模量、泊松比、密度等。
此外,还需要确定边界条件,如约束和外部载荷。
约束是指限制杆件的运动范围,外部载荷是指施加在连杆上的力或力矩。
这些参数对于分析连杆机构的性能至关重要。
第四步:求解有限元方程将连杆机构的模型和边界条件输入有限元分析软件中,通过求解有限元方程来计算连杆机构的应力、位移和变形。
有限元方程是通过应变能原理和位移函数推导得到的。
第五步:评估结果根据有限元分析的结果,评估连杆机构的性能和稳定性。
例如,可以通过应力和位移分布来判断杆件是否会发生破坏或变形。
此外,还可以计算杆件的刚度、自然频率和振动模态等参数。
第六步:优化设计如果连杆机构的性能不符合要求,需要进行设计优化。
可以通过改变连杆和铰链的尺寸、形状或材料来改善连杆机构的性能。
再次进行有限元分析,评估优化后的连杆机构是否满足设计要求。
综上所述,有限元分析是一种对连杆机构进行性能评估和优化设计的有效方法。
通过逐步完成建模、离散化、确定材料属性和边界条件、求解有限元方程、评估结果和优化设计等步骤,可以提高连杆机构的设计质量和工作效率。
有限元分析实例

有限元分析实例引言有限元分析(Finite Element Analysis,简称FEA)是一种工程分析方法,能够将连续体结构分割成有限个小单元,通过在每个小单元内建立方程模型,最终求解整个结构的力学行为。
本文将以一个实例来介绍有限元分析的基本过程和步骤。
实例背景我们将以一个简单的杆件弯曲问题为例来进行有限元分析。
假设有一根长度为L、截面积为A的杆件,材料的弹性模量为E,截面的转动惯性矩为I。
我们希望通过有限元分析来计算杆件在一定加载条件下的弯曲变形。
有限元网格的划分首先,我们需要将杆件划分成有限个小单元,即有限元网格。
常用的网格划分方法有三角形划分、四边形单元划分等。
根据具体问题的要求和复杂度,选择合适的划分方法。
单元的建立划分好网格后,我们需要在每个小单元内建立方程模型。
在弯曲问题中,常见的单元模型有梁单元、壳单元等。
在本实例中,我们选择梁单元作为杆件的单元模型。
对于梁单元,我们需要定义每个节点的位移和约束条件。
根据杆件的几何尺寸和材料属性,可以利用应变能量原理和几何相似原理,得到每个节点的位移和约束条件。
材料特性和加载条件的定义在进行有限元分析之前,我们需要定义材料的特性和加载条件。
对于本实例中的杆件,我们需要定义弹性模量E、截面积A和转动惯性矩I。
加载条件可以包括集中力、均布力、弯矩等。
在本实例中,假设杆件受到均布力,即沿杆件轴向的受力分布是均匀的。
单元方程的建立和求解在定义了材料特性和加载条件之后,我们可以根据每个梁单元的位移和约束条件,建立每个单元的方程模型。
常见的方程模型有刚度矩阵方法、位移法等。
根据所选的单元模型,选择合适的方程模型进行计算。
通过对每个单元的方程模型进行组装,我们可以得到整个结构的方程模型。
将加载条件带入,可以求解出整个结构在给定加载条件下的位移、应力等参数。
结果分析根据求解得到的位移信息,我们可以绘制出结构的变形图。
通过变形图,可以直观地观察到结构在弯曲条件下的变形情况。
杆件结构的有限元法

F1 k11 k12 u1 u F k k 2 21 22 2
杆件结构的有限元法—单个弹簧
单个弹簧的力—位移关系
F1 k F2 k
k u1 k u2
弹簧的节点力向量和节点位移向量
F
F1 F 2
u
u1 u 2
1
2012/5/24
杆件结构的有限元法—单个弹簧
单个弹簧力的刚度(矩阵形式表示)
1 2
k11 k12 k 21 k22
1
2
单个弹簧力和位移关系(矩阵形式)
2012/5/24
杆件结构的有限元法
杆件结构的有限元法
单个弹簧的刚度矩阵 组合弹簧的刚度矩阵 铰支杆系的有限元计算格式 单元坐标系统(局部坐标系)、整体坐标系 刚度、单元刚度矩阵、整体刚度矩阵 自由度
基本概念
杆件结构的有限元法—单个弹簧
单个弹簧力和位移关系(线弹性)
F k
已知力和位移 未知力和位移
F1 K11 X 1 K12 X 2 F2 K 21 X 1 K 22 X 2 X 2 K 22 1 F2 K 21 X 1
4
2012/5/24
杆件结构的有限元法—杆件刚度矩阵
杆件结构的单元划分、节点定义
节点定义 单元划分 节点力和位移
杆件结构的有限元法—杆件刚度矩阵
杆件的力与变形关系
等效刚度
F
A E u L
杆结构 分析的有限元方法(有限元)

杆单元形状函数
杆单元刚度矩阵
平面问题中的坐标变换
梁结构分析的有限元方法
梁:承受横向荷载和弯矩的杆件。
梁的主要变形为挠度v
横截面变形前后都垂直于杆变形前的轴线x轴
中性层变形=0
纯弯曲没有剪力,只有弯矩
梁截面的惯性矩
杆结构分析的有限元方法
杆:承受轴向荷载的杆件
最基本的承力结构件:杆、梁
弹簧--简单的承受轴力的结构件
有限元方法中,每一个处理步骤都是标准化和规范化的,
因而可以在计算机上通过编程来自动实现。
F=kδ
k--刚性系数
位移的绝对变化量/杆件的伸长量δ=u2—u1
应力某截面上单位面积上的内力/内力的分布集度
应变相对伸长量单位长度的伸长量
杆单元的特性是节点位移及节点力的方向都是沿轴线方向。
杆结构的力学分析
铰接的杆结构----杆只受轴力-----杆件拉伸问题---可自然离散
两端为铰接的杆件只承受轴力。
各个单元研究(基于局部坐标系的表达)
各个单元研究
离散单元的集合、组装
杆单元及坐标变换
自由度:描述物体位置状态的每个独立变量。
对于杆单元,其节点位移有两个自由度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本概念 回顾:杆件有限元分析
(5) 单元刚度矩阵
1D 杆 单 元
回顾:杆件有限元分析
(6) 单元的刚度方程
回顾:杆件有限元分析
(1) 变换矩阵
2D 杆 单 元
回顾:杆件有限元分析
(1) 变换矩阵
2D 杆 单 元
回顾:杆件有限元分析
(2)整体坐标系下的单元刚度方程
单元的势能是一个标 量(能量),不会因坐 标系的不同而改变
(1) 位移转换法
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
整体刚度矩阵的建立
(2) 刚度集成法(对号入座法): ①将(1-3)K扩阶,扩大的元素为0,得到单元贡献矩阵
1 2 3 k ii k ij 0 1 单元①: K①= k ji k jj 0 2 0 0 0 3
杆件有限元分析:案例
(4)边界条件的处理及刚度方程求解
四 杆 桁 架 结 构
杆件有限元分析:案例
(5) 各单元应力的计算
四 杆 桁 架 结 构
杆件有限元分析:案例
(6) 支反力的计算
四 杆 桁 架 结 构
杆件有限元分析:作业 作 业
下一节课:连续体结构分析的有限元方法
3 0 1 2 k ji 2 2 k jj 3
补充-整体分析
补充-整体分析
整体刚度矩阵的建立 (3) 编码法
杆件有限元分析:案例
四 杆 桁 架 结 构
杆件有限元分析:案例
(1) 结构的离散化与编号
四 杆 桁 架 结 构
对该结构进行自然离散,节点编号和单元编号如上图所示,有关节点 和单元的信息见表1至表3。
1D 杆 单 元
如图所示为一个在局部坐标系(local coordinate system)中的杆单元 (bar element),由于有两个端节点(Node 1和Node 2),则基本 变量为节点位移(向量)列阵:
将每一个描述物体位置状态的独立变量叫做一个自由度(DOF, degree of freedom),显然,以上的节点位移为两个自由度。 节点力(向量)列阵:
2D 杆 单 元
回顾:杆件有限元分析
(2)整体坐标系下的单元刚度方程
2D 杆 单 元
(3)整体坐标系下的单元应力
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
整体刚度矩阵的建立 (1) 位移转换法
补充-整体分析
整体刚度矩阵的建立
基本概念 回顾:杆件有限元分析
(3) 单元应变场的表达 由弹性力学中的几何方程,有1D问题的应变
1D 杆 单 元
其中
叫做几何矩阵(strain-displacement matrix)。
基本概念 回顾:杆件有限元分析
(4) 单元应力场的表达 由弹性力学中的物理方程,有1D问题的应力
1D 杆 其中 单 元 叫做应力矩阵(stress-displacement matrix)
1 2 3 01 0 0 单元② : K②= 0 k ii k ij 2 0 k ji k jj 3
②将单元贡献矩阵想叠加,形成整体刚度矩阵
1 k ii K= K①+ K②= 1 k ji 0 2 1 k ij k jj
1
k ii
2
2
k ji
基本概念 回顾:杆件ຫໍສະໝຸດ 限元分析(1) 单元的几何及节点描述 单元的描述包括单元的几何及节点描述、位移场、应变场、应力场、 势能,也就是要充分利用描述问题的三大类变量以及三大类方程来 计算单元的势能,然后,由最小势能原理(或虚功原理)来得到单元 的方程。实际上,单元内位移场的描述就是它的试函数的选取。
杆件有限元分析:案例
(2) 各个单元的矩阵描述
四 杆 桁 架 结 构
由于所分析的结构包括有斜杆,所以必须在总体坐标下对节点 位移进行表达,所推导的单元刚度矩阵也要进行变换,各单元 经坐标变换后的刚度矩阵如下。
杆件有限元分析:案例
(3) 建立整体刚度方程
四 杆 桁 架 结 构
将所得到的各个单元刚度矩阵按节点编号进行组装,可以形 成整体刚度矩阵,同时将所有节点载荷也进行组装
基本概念 回顾:杆件有限元分析
(2) 单元位移场的表达 设该单元的位移场为 ,由Taylor级数,它可以表示为
1D 杆 单 元
可取的前两项来作为该单元的位移插值模式(interpolation model): 其中a0和a1为待定系数(unknowns)
则有 其中 N为形状函数矩阵(shape function matrix), 叫做节点位移列阵 (nodal displacement vector),分别为
杆件有限元分析:案例
(1) 结构的离散化与编号
四 杆 桁 架 结 构
对该结构进行自然离散,节点编号和单元编号如上图所示,有关节点 和单元的信息见表1至表3。
杆件有限元分析:案例
(2) 各个单元的矩阵描述
四 杆 桁 架 结 构
由于所分析的结构包括有斜杆,所以必须在总体坐标下对节点 位移进行表达,所推导的单元刚度矩阵也要进行变换,各单元 经坐标变换后的刚度矩阵如下。
