七年级下册数学经典易错题
七年级下册数学易错题50道

七年级下册数学易错题50道一、相交线与平行线1. 判断题:不相交的两条直线叫做平行线。
(错误)解析:必须是在同一平面内不相交的两条直线才叫做平行线,如果不在同一平面内,不相交的直线不一定平行。
2. 若∠1与∠2是同旁内角,∠1 = 50°,则∠2的度数是()A.50°B.130°C.50°或130°D.不能确定答案:D解析:两直线平行,同旁内角互补;两直线不平行,同旁内角的关系不确定,只知道∠1 = 50°,不知道两直线的位置关系,所以∠2的度数不能确定。
3. 如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1 = 72°,求∠2的度数。
解:因为AB∥CD,∠1 = 72°,所以∠BEF = 180°∠1 = 180°-72° = 108°。
因为EG平分∠BEF,所以∠BEG=公式∠BEF=公式。
又因为AB∥CD,所以∠2 = ∠BEG = 54°。
二、实数4. 公式的平方根是()A.2B.±2C.4D.±4答案:B解析:先计算公式,然后求4的平方根,因为公式,所以4的平方根是±2。
5. 下列说法正确的是()A.无限小数都是无理数B.带根号的数都是无理数C.无理数是无限不循环小数D.实数包括正实数和负实数答案:C解析:无限循环小数是有理数,A错误;公式是有理数,B错误;无理数是无限不循环小数,C正确;实数包括正实数、0和负实数,D错误。
6. 计算:公式解:公式,公式,公式。
则原式公式。
三、平面直角坐标系7. 点P(m + 3,m + 1)在x轴上,则点P的坐标为()A.(0,-2)B.(2,0)C.(4,0)D.(0,-4)答案:B解析:因为点P在x轴上,所以P点的纵坐标为0,即m + 1 = 0,解得m=-1。
七年级下册数学易错题

初一年级下学期易错题精选(一)第五章相交线与平行线1.下列判断错误的是().A.一条线段有无数条垂线;B.过线段AB中点有且只有一条直线与线段AB垂直;C.两直线相交所成的四个角中,若有一个角为90°,则这两条直线互相垂直;D.若两条直线相交,则它们互相垂直.2.下列判断正确的是().A.从直线外一点到已知直线的垂线段叫做这点到已知直线的距离;B.过直线外一点画已知直线的垂线,垂线的长度就是这点到已知直线的距离;C.画出已知直线外一点到已知直线的距离;D.连接直线外一点与直线上各点的所有线段中垂线段最短.3.如图所示,图中共有内错角().A.2组;B.3组;C.4组;D.5组.4.下列说法:①过两点有且只有一条直线;②两条直线不平行必相交;③过一点有且只有一条直线与已知直线垂直;④过一点有且只有一条直线与已知直线平行. 其中正确的有().A.1个;B.2个;C.3个;D.4个.5.如图所示,下列推理中正确的有().①因为∠1=∠4,所以BC∥AD;②因为∠2=∠3,所以AB∥CD;③因为∠BCD+∠ADC=180°,所以AD∥BC;④因为∠1+∠2+∠C=180°,所以BC∥AD.A.1个;B.2个;C.3个;D.4个.6.如图所示,直线,∠1=70°,求∠2的度数.7.判断下列语句是否是命题. 如果是,请写出它的题设和结论.(1)内错角相等;(2)对顶角相等;(3)画一个60°的角.正解:(1)是命题. 这个命题的题设是:两条直线被第三条直线所截;结论是:内错角相等. 这个命题是一个错误的命题,即假命题.(2)是命题. 这个命题的题设是:两个角是对顶角;结论是:这两个角相等. 这个命题是一个正确的命题,即真命题.(3)不是命题,它不是判断一件事情的语句.8.“如图所示,△A′B′C′是△ABC平移得到的,在这个平移中,平移的距离是线段AA′”这句话对吗?第六章平面直角坐标系1.点A的坐标满足,试确定点A所在的象限.2.求点A(-3,-4)到坐标轴的距离.第七章三角形1.如图所示,钝角△ABC中,∠B是钝角,试作出BC边上的高AE.2.有四条线段,长度分别为4cm,8cm,10cm,12cm,选其中三条组成三角形,试问可以组成多少个三角形?3.一个三角形的三个外角中,最多有几个角是锐角?4.如图所示,在△ABC中,下列说法正确的是().A.∠ADB>∠ADE;B.∠ADB>∠1+∠2+∠3;C.∠ADB>∠1+∠2;D.以上都对.正解:C.正解解析:∵∠ADB是△ADC的一个外角,∴∠ADB=∠1+∠2+∠3,∴∠ADB>∠1+∠2.5.一个多边形的内角和为1440°,求其边数.第八章二元一次方程组1.已知方程组:①,②,③,④,正确的说法是().A.只有①③是二元一次方程组;B.只有③④是二元一次方程组;C.只有①④是二元一次方程组;D.只有②不是二元一次方程组.2.用加减法解方程组.3.利用加减法解方程组.4.两个车间,按计划每月工生产微型电机680台,由于改进技术,上个月第一车间完成计划的120%,第二车间完成计划的115%,结果两个车间一共生产微型电机798台,则上个月两个车间各生产微型电机多少台?若设两车间上个月各生产微型电机台和台,则列方程组为().A.;B.;C..D..第九章不等式与不等式组1.利用不等式的性质解不等式:.2.某小店每天需水1m³,而自来水厂每天只供一次水,故需要做一个水箱来存水. 要求水箱是长方体,底面积为0.81㎡,那么高至少为多少米时才够用?(精确到0.1m)3.解不等式组.第十章数据的收集、整理与描述1.调查一批药物的药效持续时间,用哪种调查方式?2.2011年4月11日《文汇报》报道:据不完全统计,至今上海自愿报名去西部地区工作的专业技术人员和管理人员已达3600多人,其中硕士、博士占4%,本科生占79%,大专生占13%. 根据上述数据绘制扇形统计图表示这些人员的学历分布情况.正解:如下图所示:3.某班组织25名团员为灾区捐款,其中捐款数额前三名的是10元5人,5元10人,2元5人,其余每人捐1元,那么捐10元的学生出现的频率是__________.4.26名学生的身高分别为(身高:cm ):160; 162; 160; 162; 160; 159; 159; 169; 172; 160;161; 150; 166; 165; 159; 154; 155; 158; 174; 161;170; 156; 167; 168; 163; 162.现要列出频率分布表,请你确定起点和分点数据.正解:起点为149.5,分五组:149.5~154.5,154.5~159.5,159.5~164.5,164.5~169.5,169.5~174.5.方程(组)、不等式(组)易错一、填空题1、关于x 的不等式2x-a ≥-2的解集如图所示,则a 的取值范围为_______2、已知3(2x-1)=2-3x 的解与关于x 的方程6-2k=2(x+3)的解相同,则k=_______3、某品牌商品,按标价8折出售,仍可以获得20%的利润,若该商品的标价为30元,则进价为 元。
七年级下数学-第5章--分式-经典易错题带答案-可直接打印2013浙教版版新教材

七年级下数学-第5章--分式-经典易错题带答案-可直接打印2013浙教版版新教材第5章 分式1.若分式(x +1)(x -2)(x +1)(x +2)的值为0,则x 的值是( C )A .-1B .-1或2C .2D .-2【解析】 依题意(x +1)(x -2)=0,而分母(x +1)(x +2)≠0.由(x +1)(x -2)=0得x +1=0或x -2=0.∴x =-1或x =2.当x =-1时分母为0,当x =2时分母不为0.故x =2.选C.2.如果分式x 2-13x +3的值为0,则x =__1__. 【解析】 依题意得x 2-1=0且3x +3≠0,所以x =1.3.若|x |-3(x -3)(x +1)的值为零,则x 的值是__-3__. 4.[2011·内江]如果分式3x 2-27x -3的值为0,则x 的值应为__-3__. 【解析】 依题意分子3x 2-27=0且分母x -3≠0,所以x =-3.5.已知x +1x =3,求x 2x 4+x 2+1的值. 解:将x +1x=3两边同时乘以x ,得x 2+1=3x , ∴x 2x 4+x 2+1=x 2(x 2+1)2-x 2=x 29x 2-x 2=18. 6.下列化简结果中,正确的是( D )A.x 2-y 2x 2+z 2=-y 2z 2【解析】根据分式的基本性质,分子分母都除以xy ,得5y +1-5x 1y -1-1x=-3×5+1-3-1=72. 9.若1x =1y ,则分式2x +3xy -2y x -2xy -y的值为__-32__. 【解析】由已知1x =1y ,得x =y ,把x =y 代入得2x +3x 2-2x x -2x 2-x=-32. 10.计算:(1)(81-a 4)÷(a 2+9)÷(a -3);(2)(16a 4-b 4)÷(4a 2+b 2)÷(2a -b ).解:(1)原式=(9+a 2)(9-a 2)÷(a 2+9)÷(a -3)=(9-a 2)÷(a -3)=-a -3;(2)原式=(4a 2-b 2)÷(2a -b )=2a +b .11.阅读下列解题过程,然后解题:题目:已知x a -b =y b -c =z c -a(a 、b 、c 互不相等),求x +y +z 的值. 解:设x a -b =y b -c =z c -a =k , 则x =k (a -b ),y =k (b -c ),z =k (c -a ),∴x +y +z =k (a -b +b -c +c -a )=0,∴x +y +z =0.依照上述方法解答下列问题:已知y +z x =z +x y =x +y z ,其中x +y +z ≠0,求x +y -z x +y +z的值. 解:设y +z x =z +x y =x +y z =k ,则⎩⎨⎧y +z =kx , ①x +z =ky , ②x +y =kz , ③①+②+③得:2x +2y +2z =k (x +y +z ),∵x +y +z ≠0,∴k =2,∴原式=2z -z 2z +z =z3z =13.12.先阅读(1)小题的解题过程,再解答第(2)小题.(1)已知a 2-3a +1=0,求a 2+1a 2的值.解:由a 2-3a +1=0,知a ≠0.所以等式两边同除以a ,得a -3+1a =0,即a +1a =3.所以a 2+1a 2=⎝ ⎛⎭⎪⎫a +1a 2-2=7.(2)已知y 2+3y -1=0,求y 4+1y 4的值.解:由y 2+3y -1=0,知y ≠0.所以等式两边同除以y ,得y +3-1y =0,即y -1y =-3.所以y 4+1y 4=(y 2)2+1(y 2)2=⎝ ⎛⎭⎪⎫y 2+1y 22-2=⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫y -1y 2+22-2=[(-3)2+2]2-2=121-2=119.13.计算:x 2-4y 2x 2+2xy +y 2÷x +2y2x 2+2xy .解:原式=(x +2y )(x -2y )(x +y )2·2x (x +y )x +2y=2x (x -2y )x +y =2x 2-4xyx +y .14.先化简,再求值:81-a 2a 2+6a +9÷9-a 2a +6·1a +9,其中a =3.解:原式=(9-a )(9+a )(a +3)2·2(a +3)9-a ·1a +9=2a +3.当a =3时,原式=13.15.化简:(1)[2011·衢州]a -3b a -b +a +ba -b ;(2)[2011·佛山]x 2+4x -2+4x2-x ;(3)x 2x -3-6x x -3+9x -3.解:(1)原式=a -3b +a +b a -b =2a -2ba -b =2(a -b )a -b =2;(2)原式=x 2+4x -2-4x x -2=(x -2)2x -2=x -2;(3)原式=x 2-6x +9x -3=(x -3)2x -3=x -3.16.先化简,再求值:⎝ ⎛⎭⎪⎫x 2x -3-9x -3·1x 2+3x ,其中x =13.解:原式=x 2-9x -3·1x (x +3)=(x -3)(x +3)x -3·1x (x +3)=1x .当x =13时,原式=1x =113=3. 17.已知P =a 2+b 2a 2-b 2,Q =2ab a 2-b 2,用“+”或“-”连结P ,Q 共有三种不同的形式:P +Q ,P -Q ,Q -P ,请选择其中一种进行化简求值,其中a =3,b =2.解:如选P +Q 进行计算:P +Q =a 2+b 2a 2-b 2+2aba 2-b 2=a 2+b 2+2aba 2-b 2=(a +b )2(a +b )(a -b )=a +ba -b .当a =3,b =2时,P +Q =3+23-2=5.18.(1)[2012·泰安]化简:⎝ ⎛⎭⎪⎫2m m +2-m m -2÷mm 2-4=__m -6__.(2)[2012·枣庄]化简⎝ ⎛⎭⎪⎫1-1m +1(m +1)的结果是__m __.(3)[2012·山西]化简x 2-1x 2-2x +1·x -1x 2+x +2x 的结果是__3x __.(4)[2012·聊城]计算⎝ ⎛⎭⎪⎫1+4a 2-4÷a a -2=__aa +2__.19.[2012·黄冈]化简⎝ ⎛⎭⎪⎫x 2-1x 2-2x +1+1-x x +1÷xx -1的结果是__4x +1__.【解析】原式=⎝ ⎛⎭⎪⎫x +1x -1-x -1x +1×x-1x=(x +1)2-(x -1)2(x +1)(x -1)×x -1x =4x (x +1)(x -1)×x -1x =4x +1. 20.化简⎝ ⎛⎭⎪⎫1x -3-x +1x 2-1·(x -3)的结果是 ( B ) A .2 B.2x -1 C.2x -3 D.x -4x -121.[2012·常德]化简:⎝ ⎛⎭⎪⎫x +x x 2-1÷⎝ ⎛⎭⎪⎫2+1x -1-1x +1.解:原式=x 3-x +x()x -1()x +1÷2x 2-2+x +1-x +1()x +1()x -1=x3()x +1()x -1·()x +1()x -12x 2=x 2.22.解方程:(1)[2012·重庆]2x -1=1x -2;(2)[2012·苏州]3x +2+1x =4x 2+2x ;(3)[2012·梅州]4x 2-1+x +21-x =-1.解:(1)2(x -2)=x -1,2x -4=x -1,x =3,检验:当x =3时,(x -1)(x -2)=2≠0,所以原方程的解为x =3.(2)去分母,得3x +x +2=4.解得x =12.经检验,x =12是原方程的解.(3)方程两边都乘以(x +1)(x -1),得4-(x +1)(x +2)=-(x 2-1),整理,得3x =1,解得x =13. 经检验,x =13是原方程的解. 故原方程的解是x =13. 23.[2012·巴中]若关于x 的方程2x -2+x +m 2-x=2有增根,则m 的值是__0__. 【解析】方程两边都乘以(x -2),得2-x -m =2(x -2),∵分式方程有增根,∴x -2=0,解得x =2,∴2-2-m =2×(2-2), 解得m =0.24.[2012·泉州]计算:m m -1-1m -1=__1__. 25.[2012·成都]化简:⎝ ⎛⎭⎪⎫1-b a +b ÷a a 2-b 2. 解:⎝ ⎛⎭⎪⎫1-b a +b ÷a a 2-b 2=a +b -b a +b·a 2-b 2a =a a +b·(a +b )(a -b )a =a -b .26. 化简分式x 2-1x 2+2x +1-x +1x -1.并从-2,-1,0,1,2中选一个能使分式有意义的数代入求值.解:原式=(x -1)(x +1)(x +1)2-x +1x -1=x -1x +1-x +1x -1=(x -1)2-(x +1)2(x -1)(x +1)=-4x x 2-1.把x=0代入,原式=0.或把x=-2代入,原式=-4×(-2)(-2)2-1=83.或把x=2代入,原式=-4×222-1=-83.类型之四解分式方程27.[2012·宜宾]分式方程12x2-9-2x-3=1x+3的解为(C)A.3 B.-3C.无解D.3或-3【解析】方程的两边同乘(x+3)(x-3),得12-2(x+3)=x-3,解得:x=3.检验:把x=3代入(x+3)(x-3)=0,即x=3不是原分式方程的解.28.某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次的54倍,购进数量比第一次少了30支.(1)求第一次每支铅笔的进价是多少元?(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利为420元,问每支铅笔的售价是多少元?解:(1)设第一次每支铅笔的进价为x元,由题意得方程600 x-60054x=30,解得x=4.经检验,x=4是原方程的根.答:第一次每支铅笔的进价是4元.(2)设每支售价为y元,第一次购买了600÷4=150(支),则第二次购买了120枝,由题意得(150+120)y-2×600=420,解得y=6.答:每支铅笔的售价是6元.29.[2012·桂林]李明到离家2.1千米的学校参加班级联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立即步行(匀速)回家,在家拿道具用了1分钟,然后骑自行车(匀速)返回学校,已知李明骑自行车的速度是步行速度的3倍,李明骑自行车到学校比他从学校步行到家少用了20分钟.(1)李明步行的速度是多少米/分?(2)李明能否在联欢会开始前赶到学校?解:(1)设李明步行的速度是x米/分,由题意得2100 x-21003x=20,解得x=70.答:李明步行的速度是70米/分.(2)因为210070+21003×70+1=41<42,所以李明能在联欢会开始前赶到学校.30.[2012·泰安]一项工程,甲,乙两公司合做,12天可以完成,共需付施工费102000元;如果甲,乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元.(1)甲,乙两公司单独完成此项工程,各需多少天?(2)若让一个公司单独完成这项工程,哪个公司的施工费较少?解:(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得1x+11.5x=112,解得x=20,经检验知x=20是方程的解且符合题意.1.5x=30.答:甲,乙两公司单独完成此项工程各需20天,30天.(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y-1500)元,根据题意得12(y+y-1500)=102000,解得y=5000,甲公司单独完成此项工程所需的施工费:20×5000=100000(元);乙公司单独完成此项工程所需的施工费:30×(5000-1500)=105000(元),故甲公司的施工费较少.。
《易错题》初中七年级数学下册第六单元《实数》习题(培优练)

一、选择题1.观察下列运算:81=8,82=64,83=512,84=4 096,85=32 768,86=262 144,…,则81+82+83+84+…+82 017的和的个位数字是( )A .2B .4C .6D .8D 解析:D【分析】根据规律可得底数为8的幂的个位数字依次为8,4,2,6,以4个为周期,个位数字相加为0. 2017除以4余数是1,故得到和的个位数字是8.【详解】解:2017÷4=504…1,循环了504次,还有1个个位数字为8,所以81+82+83+84+…+82017的和的个位数字是504×0+8=8.故选:D .【点睛】本题主要考查了数字的变化类,尾数的特征,得到底数为8的幂的个位数字的循环规律是解决本题的突破点.2 )A .3B .﹣3C .±3D .6A解析:A【分析】9,再利用算术平方根的定义求出答案.【详解】 ∵9,∴3,故选:A .【点睛】. 3.下列说法中,错误的有( )①符号相反的数与为相反数;②当0a ≠时,0a >;③如果a b >,那么22a b >;④数轴上表示两个有理数的点,较大的数表示的点离原点较远;⑤数轴上的点不都表示有理数.A .0个B .1个C .2个D .3个D解析:D【分析】根据相反数、绝对值、数轴表示数以及有理数的乘法运算等知识综合进行判断即可.【详解】解:符号相反,但绝对值不等的两个数就不是相反数,例如5和-3,因此①不正确; a≠0,即a >0或a <0,也就是a 是正数或负数,因此|a|>0,所以②正确;例如-1>-3,而(-1)2<(-3)2,因此③不正确;例如-5表示的点到原点的距离比1表示的点到原点的距离远,但-5<1,因此④不正确; 数轴上的点与实数一一对应,而实数包括有理数和无理数,因此⑤正确;综上所述,错误的结论有:①③④,故选:D .【点睛】本题考查相反数、绝对值、数轴表示数,对每个选项进行判断是得出正确答案的前提.4.若3a =,则a 在( ) A .3-和2-之间 B .2-和1-之间 C .1-和0之间 D .0和1之间C 解析:C【分析】案.【详解】解:∵4<5<9,∴23.∴-1<0.故选:C .【点睛】5.0.31,3π,27-12- 1.212212221…(每两个1之间依次多一个2)中,无理数的个数为( ) A .1B .2C .3D .4C 解析:C【分析】无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数,据此逐一判断即可得.【详解】解∵3=2=,∴在所列的83π,1.212 212 221…(每两个1之间依次多一个2)这3个,【点睛】本题主要考查的是无理数的概念,熟练掌握无理数的三种类型是解题的关键.6 )A .8B .8-C .D .± D 解析:D【分析】8=,再根据平方根的定义,即可解答.【详解】8=,8的平方根是±故选:D .【点睛】8=.7.在1.414,213,5π,2中,无理数的个数是( ) A .1B .2C .3D .4C解析:C【分析】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:1.414是有限小数,属于有理数;213是分数,属于有理数; 5π是无理数;2是无理数,∴无理数的个数是3个,故选:C .【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…等有这样规律的数.8.下列各数中是无理数的是( )A .227B .1.2012001C .2πD 解析:C无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【详解】解:A、227分数,是有理数,选项不符合题意;B、1.2012001是有理数,选项不符合题意;C、2π是无理数,选项符合题意;D、81=9,9是整数是有理数,,选项不符合题意.故选:C.【点睛】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.9.在 -1.414,2,16,π,2+3,3.212212221…,227,3.14这些数中,无理数的个数为()A.2 B.3 C.4 D.5C解析:C【分析】先计算算术平方根,再根据无理数的定义即可得.【详解】164=,223.1428577=小数点后的142857是无限循环的,则在这些数中,无理数有2,,23,3.212212221π+⋯,共4个,故选:C.【点睛】本题考查了算术平方根、无理数,熟记无理数的定义是解题关键.10.如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+p=0,则m,n,p,q四个有理数中,绝对值最大的一个是()A.p B.q C.m D.n B解析:B【分析】根据n+p=0可以得到n和p互为相反数,原点在线段PN的中点处,从而可以得到绝对值最大的数.【详解】解:∵n+p=0,∴n 和p 互为相反数,∴原点在线段PN 的中点处,∴绝对值最大的一个是Q 点对应的q .故选B .【点睛】本题考查了实数与数轴及绝对值.解题的关键是明确数轴的特点.二、填空题11.计算:()214322--⨯-(【分析】利用实数的混合运算法则计算得出答案【详解】解:原式=4+9=4+9=4+93=4+27=31【点睛】本题主要考查了实数的运算正确化简各数是解题的关键解析:【分析】利用实数的混合运算法则计算得出答案.【详解】解:原式=4+9⨯12-(2)2⎡⎤⨯-⎢⎥⎣⎦=4+9⨯[]2+1=4+9⨯3=4+27=31.【点睛】本题主要考查了实数的运算,正确化简各数是解题的关键.12.求出x 的值:()23227x +=x =1或x =﹣5【分析】依据平方根的性质可得到x+2的值然后解关于x 的一元一次方程即可【详解】解:∵3(x+2)2=27∴(x+2)2=9∴x+2=±3解得:x =1或x =﹣5【点睛】本题主要考查的是 解析:x =1或x =﹣5【分析】依据平方根的性质可得到x +2的值,然后解关于x 的一元一次方程即可.【详解】解:∵3(x +2)2=27,∴(x +2)2=9,∴x +2=±3,解得:x =1或x =﹣5.【点睛】本题主要考查的是平方根的性质,熟练掌握平方根的性质是解题的关键.13.计算:(12(2)22(2)8x -=(1)1;(2)【分析】(1)实数的混合运算利用算术平方根和立方根的概念逐个进行化简计算;(2)直接用平方根的概念求解【详解】解:(1)===1(2)∴【点睛】本题考查实数的混合运算及利用平方根解方 解析:(1)1;(2)124,0x x ==【分析】(1)实数的混合运算,利用算术平方根和立方根的概念逐个进行化简计算;(2)直接用平方根的概念求解.【详解】解:(12=4(2)23----=4+223--=1(2)22(2)8x -=2(2)4x -=22x -=±22x =±∴124,0x x ==.【点睛】本题考查实数的混合运算及利用平方根解方程,掌握相关概念和性质正确计算是解题关键.14.计算:(1(2)0(0)|2|π--(3)解方程:4x 2﹣9=0.(1)-8;(2)1﹣;(3)x =±【分析】(1)利用算数平方根立方根及二次根式性质计算即可;(2)利用零指数幂立方根及绝对值的代数意义进行化简即可;(3)方程变形后利用开方运算即可求解【详解】解:解析:(1)-8;(2)13)x =±32. 【分析】(1)利用算数平方根、立方根及二次根式性质计算即可;(2)利用零指数幂、立方根及绝对值的代数意义进行化简即可;(3)方程变形后,利用开方运算即可求解.【详解】解:(1)原式=()935358÷--=--=-;(2)原式=1221-+-=(3)方程变形得:294x =,开方得:32x =±. 【点睛】本题考察实数的运算,熟练掌握运算法则是解题的关键.15.(22-平方根然后进行加减运算即可【详解】解:===【点睛】此题考查了实数的运算熟练掌握算术平方根和立方根的性质是解本题的关键解析:8-【分析】先化简绝对值、立方根、算术平方根,然后进行加减运算即可.【详解】(22=2243--⨯+()=412-=8-【点睛】此题考查了实数的运算,熟练掌握算术平方根和立方根的性质是解本题的关键. 16.一个正方体的木块的体积是3343cm ,现将它锯成8块同样大小的小正方体木块,则每个小正方体木块的表面积是________.5cm3【分析】先根据正方体的体积求出正方体的边长要使它锯成8块同样大小的小正方体木块只需要将正方体的每条棱长平均分为两份即可得到小正方体的棱长即可求出表面积【详解】解:∵一个正方体的木块的体积是∴解析:5cm 3.【分析】先根据正方体的体积求出正方体的边长,要使它锯成8块同样大小的小正方体木块,只需要将正方体的每条棱长平均分为两份即可,得到小正方体的棱长,即可求出表面积.【详解】解:∵一个正方体的木块的体积是3343cm ,∴(cm 3),要将它锯成8块同样大小的小正方体木块,则每个小正方体的棱长为7÷2=3.5(cm 3), ∴每个小正方体的表面积为6×3.52=73.5(cm 3).故答案为73.5cm 3.【点睛】本题考查了立方根.解题的关键是能够通过空间想象得出如何将正方体分成8块同样大小的小正方体木块.17.2-.4【分析】原式利用平方根立方根定义及绝对值化简计算即可得到结果【详解】解:原式【点睛】本题考查了实数的运算熟练掌握平方根立方根定义是解本题的关键解析:4【分析】原式利用平方根、立方根定义及绝对值化简计算即可得到结果.【详解】解:原式282=-+-4=【点睛】本题考查了实数的运算,熟练掌握平方根、立方根定义是解本题的关键.18.规定新运算:()*4a b a ab =+.已知算式()3*2*2x =-,x =_______.【分析】根据新运算可得由得到关于x 的一元一次方程求解即可【详解】解:根据新运算可得∵∴解得故答案为:【点睛】本题考查新定义运算解一元一次方程根据题意得出一元一次方程是解题的关键 解析:43- 【分析】根据新运算可得()3*334x x =+,()()2*22440-=⨯-+=,由()3*2*2x =-得到关于x 的一元一次方程,求解即可.【详解】解:根据新运算可得()3*334x x =+,()()2*22440-=⨯-+=,∵()3*2*2x =-,∴()3340x +=,解得43x =-, 故答案为:43-. 【点睛】本题考查新定义运算、解一元一次方程,根据题意得出一元一次方程是解题的关键.19.计算20201|-+=_________.-5【分析】本题涉及乘方绝对值立方根以及二次根式化简等知识点在计算时需要针对每个知识点分别进行计算然后根据实数的运算法则求得计算结果【详解】解:===-5故答案为:-5【点睛】本题主要考查了实数的综解析:-5【分析】本题涉及乘方、绝对值、立方根以及二次根式化简等知识点.在计算时,需要针对每个知识点分别进行计算,然后根据实数的运算法则求得计算结果.【详解】解:20201|-+=12|2|----=122---=-5.故答案为:-5.【点睛】本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握乘方、二次根式、三次根式、绝对值等知识点的运算.20.一个正数的两个平方根分别是21a -与2a -+,则这个正数是______.9【分析】根据一个正数的两个平方根互为相反数可得关于a 的方程解方程即可求出a 进一步即可求出答案【详解】解:因为一个正数的两个平方根分别是与所以+()=0解得:a=﹣1所以这个正数是故答案为:9【点睛解析:9【分析】根据一个正数的两个平方根互为相反数可得关于a 的方程,解方程即可求出a ,进一步即可求出答案.【详解】解:因为一个正数的两个平方根分别是21a -与2a -+,所以21a -+(2a -+)=0,解得:a =﹣1,所以这个正数是()22119⨯--=⎡⎤⎣⎦.故答案为:9.【点睛】本题考查了平方根的定义,属于基础题型,掌握解答的方法是解题的关键. 三、解答题21.计算:(1)⎛- ⎝;(2|1--解析:(1;(2)12-【分析】(1)先去括号,再利用二次根式加减运算法则进行计算;(2)直接利用绝对值的性质和立方根的性质、二次根式的性质分别化简后再相加减即可;【详解】(1)⎛- ⎝=;(2|1--=914++-=12-【点睛】考查了实数的运算,解题关键是掌握运算法则和运算顺序.22. 1.414≈,于是我们说:的整数部分为1,小数部分则可记为1”.则:(11的整数部分是__________,小数部分可以表示为__________;(22的小数部分是a ,7-b ,那么a b +=__________;(3x 的小数部分为y ,求1(x y --的平方根.解析:(1)21;(2)1;(3)3±.【分析】(11的整数部分和小数部分;(22和7-a 与b 的值,最后代入代数式计算即可;(3的取值范围,再确定x 、y 的值,最后代入代数式计算即可.【详解】解:(1)∵1<2<4∴1<2 ∴1, ∴1的整数部分为212+-1故答案为21;(2)∵1<3<4∴12∴1,∴2的整数部分为3,小数部分为21-;7-的整数部分为5,小数部分为b=75--=2∴1+2=1故答案为1;(3)∵9<11<16∴3<4 ∴x=3,小数部分为-3∴()3211(3==3=9x y --- ∵3±.故答案为3±.【点睛】本题主要考查了估算无理数的大小,掌握运用逼近法比较无理数的大小成为解答本题的关键.23.已知一个正数m 的平方根为2n +1和4﹣3n .(1)求m 的值;(2)|a ﹣3|(c ﹣n )2=0,a +b +c 的立方根是多少?解析:(1)m =121;(2)a +b +c 的立方根是2【分析】(1)由正数的平方根互为相反数,可得2n +1+4﹣3n =0,可求n =5,即可求m ; (2)由已知可得a =3,b =0,c =n =5,则可求解.【详解】解:(1)正数m 的平方根互为相反数,∴2n +1+4﹣3n =0,∴n =5,∴2n +1=11,∴m =121;(2)∵|a ﹣3|(c ﹣n )2=0,∴a =3,b =0,c =n =5,∴a +b +c =3+0+5=8,∴a +b +c 的立方根是2.【点睛】本题考查平方根的性质;熟练掌握正数的平方根的特点,绝对值和偶次方根数的性质是解题的关键.24.(1)小明解方程2x 1x a 332-+=-去分母时,方程右边的−3忘记乘6,因而求出的解为x=2,则原方程正确的解为多少?(2)设x ,y 是有理数,且x ,y 满足等式2x 2y 17++=-x-y 的值. 解析:(1)x =−13;(2)(2)x-y 的值为9或-1.【分析】(1)将错就错把x =2代入计算求出a 的值,即可确定出正确的解;(2)根据题意可以求得x 、y 的值,从而可以求得x−y 的值.【详解】(1)把x =2代入2(2x−1)=3(x +a )−3中得:6=6+3a−3,解得:a =1, 代入方程得:2x 1x 1332-+=-, 去分母得:4x−2=3x +3−18,解得:x =−13;(2)∵x 、y 是有理数,且 x ,y 满足等式2x 2y 17++=-∴22174x y y ⎧+=⎨=-⎩, 解得,54x y =⎧⎨=-⎩或54x y =-⎧⎨=-⎩, ∴当x =5,y =−4时,x−y =5−(−4)=9,当x =−5,y =−4时,原式=−5−(−4)=−1.故x-y 的值为9或-1.【点睛】此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.也考查了实数.25.计算:()214322--⨯-( 解析:【分析】 利用实数的混合运算法则计算得出答案.【详解】解:原式=4+9⨯12-(2)2⎡⎤⨯-⎢⎥⎣⎦=4+9⨯[]2+1=4+9⨯3=4+27=31.【点睛】本题主要考查了实数的运算,正确化简各数是解题的关键.26.求下列各式中x 的值(1)()328x -=(2)21(3)753x -=解析:(1)4x =;(2)18x =或12x =-.【分析】(1)利用立方根的定义得到22x -=,然后解一次方程即可;(2)先变形为()23225x -=,然后利用平方根的定义得到x 的值.【详解】(1)∵()328x -=,∴22x -=,∴4x =;(2)21(3)753x -=,整理得:()23225x -=,∴315x -=或315x -=-,∴18x =或12x =-.【点睛】本题考查了解一元一次方程,平方根和立方根,熟练掌握各自的定义是解本题的关键. 27.解方程:(1)2810x -=;(2)38(1)27x +=. 解析:(1)9x =±;(2)12x =. 【分析】 (1)移项,利用平方根的性质解方程;(2)方程两边同时除以8,然后利用立方根的性质解方程.【详解】(1)2810x -=,移项得:281x =,解得:9x =±;(2)()38127x +=,方程两边同时除以8,得:()32718x +=, ∴312x +=, 解得:31122x =-=. 【点睛】本题考查了平方根和立方根,熟练掌握平方根和立方根的定义与性质是解题关键.--28.计算:(1)225(2)1+解析:(1)-4;(2)1.【分析】(1)根据乘方、开方、绝对值的意义化简,再计算即可;(2)先根据绝对值的意义脱去绝对值,再计算即可求解.【详解】--解:(1)225=-4+6-1-5=-4;(2)1)=++1=+1=-+1=-1+2=1.【点睛】本题考查了实数的性质与运算,熟知实数的运算法则和性质是解题关键.。
七年级数学易错题整理及解析

七年级数学易错题整理及解析
以下是一些常见的七年级数学易错题及其解析:
1. 题目:已知$x = 5$,$y = 3$,则$x - y =$____或____.
【分析】
本题考查了绝对值的性质和代数式求值的知识点,正确理解绝对值的性质,求出$x$的值,即可解答.
【解答】
解:$\becausex = 5$,
$\therefore x = \pm 5$,
当$x = 5$时,$x - y = 5 - 3 = 2$,
当$x = - 5$时,$x - y = - 5 - 3 = - 8$,
故答案为$2$或$- 8$.
2. 题目:下列计算正确的是( )
A.$7a + a = 7a^{2}$
B.$2a \cdot 3a = 6a^{2}$
C.$(2a)^{3} =
8a^{3}$ D.$a^{6} \div a^{2} = a^{3}$
【分析】
本题考查合并同类项,同底数幂相乘,幂的乘方与积的乘方以及同底数幂的除法.根据合并同类项,同底数幂相乘,幂的乘方与积的乘方以及同底数幂的除法运算法则逐一计算即可判断.
【解答】
解:A.$7a + a = 8a$,故A错误;
B.$2a \cdot 3a = 6a^{2}$,故B正确;
C.$(2a)^{3} = 8a^{3}$,故C正确;
D.$a^{6} \div a^{2} = a^{4}$,故D错误.
故选BC.。
七年级下册数学 期末试卷易错题(Word版 含答案)
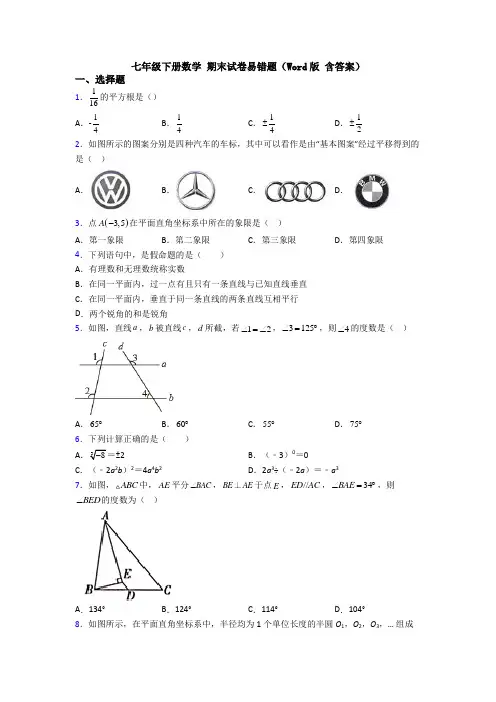
七年级下册数学 期末试卷易错题(Word 版 含答案)一、选择题1.116的平方根是() A .-14B .14C .14±D .12±2.如图所示的图案分别是四种汽车的车标,其中可以看作是由“基本图案”经过平移得到的是( )A .B .C .D .3.点()3,5A -在平面直角坐标系中所在的象限是( ) A .第一象限B .第二象限C .第三象限D .第四象限4.下列语句中,是假命题的是( ) A .有理数和无理数统称实数B .在同一平面内,过一点有且只有一条直线与已知直线垂直C .在同一平面内,垂直于同一条直线的两条直线互相平行D .两个锐角的和是锐角5.如图,直线a ,b 被直线c ,d 所截,若12∠=∠,3125∠=︒,则4∠的度数是( )A .65︒B .60︒C .55︒D .75︒6.下列计算正确的是( ) A .38-=±2B .(﹣3)0=0C .(﹣2a 2b )2=4a 4b 2D .2a 3÷(﹣2a )=﹣a 37.如图,ABC 中,AE 平分BAC ∠,BE AE ⊥于点E ,//ED AC ,34BAE ∠=︒,则BED ∠的度数为( )A .134°B .124°C .114°D .104°8.如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O 1,O 2,O 3,… 组成一条平滑的曲线,点P 从原点O 出发,沿这条曲线向右运动,速度为每秒2π个单位长度,则第2021秒时,点P 的坐标是( )A .(2020,0)B .(2021,-1)C .(2021,1)D .(2022,0)二、填空题9.若,则()m a b +的值为10.点A (-2,1)关于x 轴对称的点的坐标是____________________.11.三角形ABC 中,∠A=60°,则内角∠B ,∠C 的角平分线相交所成的角为_____. 12.如图,//AB EF ,设90C ∠=︒,那么x ,y ,z 的关系式______.13.图,直线//AB CD ,直线l 与直线AB ,CD 相交于点E 、F ,点P 是射线EA 上的一个动.点.(不包括端点E ),将EPF 沿PF 折叠,使顶点E 落在点Q 处.若∠PEF =75°,2∠CFQ =∠PFC ,则EFP ∠=________.14.如图,按照程序图计算,当输入正整数x 时,输出的结果是161,则输入的x 的值可能是__________.15.平面直角坐标系中,已知点A (2,0),B (0,3),点P (m ,n )为第三象限内一点,若△PAB 的面积为18,则m ,n 满足的数量关系式为________.16.在平面直角坐标系中,若干个边长为1个单位长度的等边三角形,按如图中的规律摆放.点P 从原点O 出发,以每秒1个单位长度的速度沿着等边三角形的边“112233445OA A A A A A A A A →→→→”的路线运动,设第n 秒运动到点n P (n 为正整数),则点2021P 的坐标是______.三、解答题17.计算:(1)()4129-⨯- (2)()432054⎛⎫-⨯- ⎪⎝⎭18.求下列各式中的x :(1)3641250x -=; (2)3(1)8x +=; (3)3(21)270x -+=. 19.完成下面的证明.如图,AB ∥CD ,∠B +∠D =180°,求证:BE ∥DF . 分析:要证BE ∥DF ,只需证∠1=∠D . 证明:∵AB ∥CD (已知) ∴∠B +∠1=180°( ) ∵∠B +∠D =180°(已知) ∴∠1=∠D ( ) ∴BE ∥DF ( )20.如图,在平面直角坐标系中,ABC ∆的顶点都在格点上,点C (41)-,. (1)写出点A ,B 的坐标; (2)求ABC ∆的面积.21.已知:31a +的立方根是2-,21b -的算术平方根3,c 是43的整数部分. (1)求,,a b c 的值;(2)求922a b c -+的平方根.二十二、解答题22.教材中的探究:如图,把两个边长为1的小正方形沿对角线剪开,用所得到的4个直角三角形拼成一个面积为2的大正方形.由此,得到了一种能在数轴上画出无理数对应点的方法(数轴的单位长度为1).(1)阅读理解:图1中大正方形的边长为________,图2中点A 表示的数为________; (2)迁移应用:请你参照上面的方法,把5个小正方形按图3位置摆放,并将其进行裁剪,拼成一个大正方形.①请在图3中画出裁剪线,并在图3中画出所拼得的大正方形的示意图.②利用①中的成果,在图4的数轴上分别标出表示数-0.5以及 35-+ 的点,并比较它们的大小.二十三、解答题23.直线AB ∥CD ,点P 为平面内一点,连接AP ,CP .(1)如图①,点P 在直线AB ,CD 之间,当∠BAP =60°,∠DCP =20°时,求∠APC 的度数;(2)如图②,点P 在直线AB ,CD 之间,∠BAP 与∠DCP 的角平分线相交于K ,写出∠AKC 与∠APC 之间的数量关系,并说明理由;(3)如图③,点P 在直线CD 下方,当∠BAK =23∠BAP ,∠DCK =23∠DCP 时,写出∠AKC 与∠APC 之间的数量关系,并说明理由.24.已知,如图①,∠BAD =50°,点C 为射线AD 上一点(不与A 重合),连接BC . (1)[问题提出]如图②,AB ∥CE ,∠BCD =73 °,则:∠B = .(2)[类比探究]在图①中,探究∠BAD 、∠B 和∠BCD 之间有怎样的数量关系?并用平行....线的性质....说明理由. (3)[拓展延伸]如图③,在射线BC 上取一点O ,过O 点作直线MN 使MN ∥AD ,BE 平分∠ABC 交AD 于E 点,OF 平分∠BON 交AD 于F 点,//OG BE 交AD 于G 点,当C 点沿着射线AD 方向运动时,∠FOG 的度数是否会变化?若变化,请说明理由;若不变,请求出这个不变的值.25.在ABC 中,射线AG 平分BAC ∠交BC 于点G ,点D 在BC 边上运动(不与点G 重合),过点D 作//DE AC 交AB 于点E .(1)如图1,点D 在线段CG 上运动时,DF 平分EDB ∠.①若100BAC ︒∠=,30C ︒∠=,则AFD ∠=_____;若40B ︒∠=,则AFD ∠=_____; ②试探究AFD ∠与B 之间的数量关系?请说明理由;(2)点D 在线段BG 上运动时,BDE ∠的角平分线所在直线与射线AG 交于点F .试探究AFD ∠与B 之间的数量关系,并说明理由.26.(生活常识)射到平面镜上的光线(入射光线)和变向后的光线(反射光线)与平面镜所夹的角相等.如图 1,MN 是平面镜,若入射光线AO 与水平镜面夹角为∠1,反射光线OB 与水平镜面夹角为∠2,则∠1=∠2 .(现象解释)如图 2,有两块平面镜OM,ON,且OM⊥ON,入射光线AB 经过两次反射,得到反射光线CD.求证AB∥CD.(尝试探究)如图 3,有两块平面镜OM,ON,且∠MON =55︒,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 相交于点E,求∠BEC 的大小.(深入思考)如图 4,有两块平面镜OM,ON,且∠MON =α ,入射光线AB 经过两次反射,得到反射光线CD,光线AB 与CD 所在的直线相交于点E,∠BED=β , α 与β 之间满足的等量关系是 .(直接写出结果)【参考答案】一、选择题1.C解析:C【分析】根据平方根的定义(如果一个数的平方等于a,那么这个数叫做a的平方根)即可得.【详解】解:因为211416⎛⎫±=⎪⎝⎭,所以116的平方根是14±,故选:C.【点睛】本题考查了平方根,熟练掌握平方根的定义是解题关键.2.C 【分析】根据平移变换的定义可得结论. 【详解】解:由平移变换的定义可知,选项C 可以看作由“基本图案”经过平移得到的. 故选:C . 【点睛】本题考查利用平移设计图案,解题的关键是理解平移变换解析:C 【分析】根据平移变换的定义可得结论. 【详解】解:由平移变换的定义可知,选项C 可以看作由“基本图案”经过平移得到的. 故选:C . 【点睛】本题考查利用平移设计图案,解题的关键是理解平移变换的定义,属于中考基础题. 3.B 【分析】根据坐标的特点即可求解. 【详解】点()3,5A -在平面直角坐标系中所在的象限是第二象限 故选B . 【点睛】此题主要考查坐标所在象限,解题的关键是熟知直角坐标系的特点. 4.D 【分析】根据实数的分类,垂直的性质,平行线的判定,锐角的定义逐项分析即可 【详解】A. 有理数和无理数统称实数,正确,是真命题,不符合题意;B. 在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,是真命题,不符合题意;C. 在同一平面内,垂直于同一条直线的两条直线互相平行,正确,是真命题,不符合题意;D. 两个锐角的和不一定是锐角,例如505010090︒+︒=︒>︒,故D 选项是假命题,符合题意 故选D 【点睛】本题考查了真假命题的判定,实数的分类,垂直的性质,平行线的判定,锐角的定义,掌握相关性质定理是解题的关键.5.C【分析】首先证明a∥b,推出∠4=∠5,求出∠5即可.【详解】解:∵∠1=∠2,∴a∥b,∴∠4=∠5,∵∠5=180°﹣∠3=55°,∴∠4=55°,故选:C.【点睛】本题考查平行线的判定和性质,解题的关键是熟练掌握基本知识,属于中考常考题型.6.C【分析】根据整式的运算法则,立方根的概念,零指数幂的意义即可求出答案.【详解】A.原式=﹣2,故A错误;B.原式=1,故B错误;C、(﹣2a2b)2=4a4b2,计算正确;D、原式=﹣a2,故D错误;故选C.【点睛】本题考查学生的运算能力,解题的关键是熟练运用运算法则,本题属于基础题型.7.B【分析】已知AE平分∠BAC,ED∥AC,根据两直线平行,同旁内角互补可知∠DEA的度数,再由周角为360°,求得∠BED的度数即可.【详解】解:∵AE平分∠BAC,∴∠BAE=∠CAE=34°,∵ED∥AC,∴∠CAE+∠AED=180°,∴∠DEA =180°-34°=146°, ∵BE ⊥AE , ∴∠AEB =90°,∵∠AEB +∠BED +∠AED =360°, ∴∠BED =360°-146°-90°=124°, 故选:B . 【点睛】本题考查了平行线的性质和周角的定义,熟记两直线平行,同旁内角互补是解题的关键.8.C 【分析】根据图象可得移动4次图象完成一个循环,从而可得出点P 的坐标. 【详解】解:半径为1个单位长度的半圆的周长为×2π×1=π,∵点P 从原点O 出发,沿这条曲线向右运动,速度为每秒个单位长解析:C 【分析】根据图象可得移动4次图象完成一个循环,从而可得出点P 的坐标. 【详解】解:半径为1个单位长度的半圆的周长为12×2π×1=π, ∵点P 从原点O 出发,沿这条曲线向右运动,速度为每秒2个单位长度, ∴点P 每秒走12个半圆,∴当点P 从原点O 出发,沿这条曲线向右运动,运动时间为1秒时,点P 的坐标为(1,1),当点P 从原点O 出发,沿这条曲线向右运动,运动时间为2秒时,点P 的坐标为(2,0), 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为3秒时,点P 的坐标为(3,-1), 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为4秒时,点P 的坐标为(4,0), 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为5秒时,点P 的坐标为(5,1), 当点P 从原点O 出发,沿这条曲线向右运动,运动时间为6秒时,点P 的坐标为(6,0), …,∵2021÷4=505余1, ∴P 的坐标是(2021,1), 故选:C . 【点睛】此题考查了点的规律变化,解答本题的关键是仔细观察图象,得到点的变化规律,解决问题.二、填空题9.-1 【解析】解:有题意得,,,,则解析:-1 【解析】 解:有题意得,,,,则()ma b10.(-2,-1) 【分析】根据“关于x 轴对称的点,横坐标相同,纵坐标互为相反数”解答. 【详解】解:点(-2,1)关于x 轴对称的点的坐标是(-2,-1), 故答案为:(-2,-1). 【点睛】 本解析:(-2,-1) 【分析】根据“关于x 轴对称的点,横坐标相同,纵坐标互为相反数”解答. 【详解】解:点(-2,1)关于x 轴对称的点的坐标是(-2,-1), 故答案为:(-2,-1). 【点睛】本题考查了关于x 轴、y 轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:(1)关于x 轴对称的点,横坐标相同,纵坐标互为相反数;(2)关于y 轴对称的点,纵坐标相同,横坐标互为相反数;(3)关于原点对称的点,横坐标与纵坐标都互为相反数.11.120°和60° 【详解】试题分析:因为三角形的内角和是180度,所以∠B+∠C=180°-∠A=180°-60°=120°,又因为∠DFE=∠BFC ,∠BFC=180°-(∠FBC+∠FCB ),解析:120°和60° 【详解】试题分析:因为三角形的内角和是180度,所以∠B+∠C=180°-∠A=180°-60°=120°,又因为∠DFE=∠BFC ,∠BFC=180°-(∠FBC+∠FCB ),因为角平分线CD 、EF 相交于F ,所以∠FBC+∠FCB=(∠B+∠C )÷2=120°÷2=60°,再代入∠DFE=∠BFC=180°-(∠FBC+∠FCB ),即可解答.试题解析:∠B+∠C=180°-∠A=180°-60°=120°, 又因为∠DFE=∠BFC ,∠BFC=180°-(∠FBC+∠FCB ),因为角平分线CD 、EF 相交于F ,所以∠FBC+∠FCB=(∠B+∠C )÷2=120°÷2=60°,∠DFE=180°-(∠FBC+∠FCB ),=180°-60°,=120°;∠DFE 的邻补角的度数为:180°-120°=60°.考点:角的度量.12.【分析】过作,过作,根据平行线的性质可知,然后根据平行线的性质即可求解;【详解】如图,过作,过作,∴,∴,,,∵,∴,∴,∴,∴,∴.故答案为:.【点睛】本题考查了平解析:90x y z +-=︒【分析】过C 作//CN AB ,过D 作//DM AB ,根据平行线的性质可知//////AB CN DM EF ,然后根据平行线的性质即可求解;【详解】如图,过C 作//CN AB ,过D 作//DM AB ,∴//////AB CN DM EF ,∴1x =∠,23∠∠=,4z ∠=,∵90BCD ∠=︒,∴1290∠+∠=︒,∴390x +∠=︒,∴3490x z +∠+∠=︒+,∴90x y z +=︒+,∴90x y z +-=︒.故答案为:90x y z +-=︒.【点睛】本题考查了平行线的性质,两直线平行同位角相等,两直线平行内错角相等,正确理解平行线的性质是解题的关键;13.或【分析】分两种情形:①当点Q在平行线AB,CD之间时.②当点Q在CD下方时,分别构建方程即可解决问题.【详解】解:①当点Q在平行线AB,CD之间时,如图1.∵AB//CD∴∠PEF+解析:35︒或63︒【分析】分两种情形:①当点Q在平行线AB,CD之间时.②当点Q在CD下方时,分别构建方程即可解决问题.【详解】解:①当点Q在平行线AB,CD之间时,如图1.∵AB//CD∴∠PEF+∠CFE=180°设∠PFQ=x,由折叠可知∠EFP=x,∵2∠CFQ=∠CFP,∴∠PFQ=∠CFQ=x,∴75°+3x=180°,∴x=35°,∴∠EFP=35°.②当点Q在CD下方时,如图2设∠PFQ=x,由折叠可知∠EFP=x,∵2∠CFQ=∠CFP,∴∠PFC=2x,3∴75°+2x+x=180°,3解得x=63°,∴∠EFP=63°.故答案为:35︒或63︒【点睛】本题主要考查了平行线的性质以及翻折问题的综合应用,正确掌握平行线的性质和轴对称的性质是解题的关键.14.、、、.【详解】解:∵y=3x+2,如果直接输出结果,则3x+2=161,解得:x=53;如果两次才输出结果:则x=(53-2)÷3=17;如果三次才输出结果:则x=(17-2)÷3=5;解析:53、17、5、1.【详解】解:∵y=3x+2,如果直接输出结果,则3x+2=161,解得:x=53;如果两次才输出结果:则x=(53-2)÷3=17;如果三次才输出结果:则x=(17-2)÷3=5;如果四次才输出结果:则x=(5-2)÷3=1;则满足条件的整数值是:53、17、5、1.故答案为53、17、5、1.点睛:此题的关键是要逆向思维.它和一般的程序题正好是相反的.15.【分析】连接OP,将PAB的面积分割成三个小三角形,根据三个小三角形的面积的和为18进行整理即可解答.【详解】解:连接OP ,如图:∵A (2,0),B (0,3),∴OA=2,OB=3,解析:3230m n +=-【分析】连接OP ,将∆PAB 的面积分割成三个小三角形,根据三个小三角形的面积的和为18进行整理即可解答.【详解】解:连接OP ,如图:∵A (2,0),B (0,3),∴OA=2,OB=3,∵∠AOB=90°, ∴11=23322OAB S OA OB ⋅=⨯⨯=, ∵点P (m ,n )为第三象限内一点,m <0,n <0∴,11y 222OAP P S OA n n ∴=⋅=⨯⋅=-, 1133222OBP P S OB x m m =⋅=⨯⋅=-, 33182PAB OAB OAP OBP S S S S n m ∴=++=--+=, 整理可得:3230m n +=-;故答案为:3230m n +=-.【点睛】本题考查的是平面直角坐标系中面积的求解,要注意在计算面积的时候,可根据题意适当添加辅助线,帮助自己分割图形.16.【分析】通过观察可得,An 每6个点的纵坐标规律:,0,,0,-,0,点An 的横坐标规律:1,2,3,4,5,6,…,n ,点从原点出发,以每秒个单位长度的速度沿着等边三角形的边“…”的路线运动,1 解析:20213,22⎛⎫- ⎪ ⎪⎝⎭ 【分析】 通过观察可得,A n 每6个点的纵坐标规律:32,0,32,0,-32,0,点A n 的横坐标规律:1,2,3,4,5,6,…,n ,点P 从原点O 出发,以每秒1个单位长度的速度沿着等边三角形的边“112233445OA A A A A A A A A →→→→…”的路线运动,1秒钟走一段,P 运动每6秒循环一次,点P 运动n 秒的横坐标规律: 12,1,32,2,52,3,…,2n ,点P 的纵坐标规律:32,0,32,0,032-,0,…,确定P 2021循环余下的点即可. 【详解】解:∵图中是边长为1个单位长度的等边三角形,∴113,22A ⎛⎫ ⎪ ⎪⎝⎭A 2(1,0)333,22A ⎛⎫ ⎪ ⎪⎝⎭A 4(2,0)553,22A ⎛⎫- ⎪ ⎪⎝⎭A 6(3,0)773,22A ⎛⎫ ⎪ ⎪⎝⎭…∴A n 中每6303030, 点P 从原点O 出发,以每秒1个单位长度的速度沿着等边三角形的边“112233445OA A A A A A A A A →→→→…”的路线运动,1秒钟走一段,P 运动每6秒循环一次点P 00,0,…, 点P 的横坐标规律: 12,1,32,2,52,3,…,2n , ∵2021=336×6+5,∴点P 2021的纵坐标为, ∴点P 2021的横坐标为20212,∴点P 2021的坐标20212⎛ ⎝⎭,,故答案为:20212⎛ ⎝⎭,. 【点睛】本题考查点的规律,平面直角坐标系中点的特点及等边三角形的性质,确定点的坐标规律是解题的关键.三、解答题17.(1)-1;(2)-1【分析】(1)根据乘方及二次根式的化简即可求解;(2)根据乘法的分配率计算即可.【详解】(1)(2)【点睛】本题考查的是实数的运算,掌握运算法则及乘法的分配率是解析:(1)-1;(2)-1【分析】(1)根据乘方及二次根式的化简即可求解;(2)根据乘法的分配率计算即可.【详解】(1)()412-⨯ (2)()()()434320=-20--20=-1615=-15454⎛⎫-⨯-⨯⨯+ ⎪⎝⎭【点睛】本题考查的是实数的运算,掌握运算法则及乘法的分配率是关键.18.(1);(2)1;(3)-1.【分析】(1)根据立方根的定义解方程即可;(2)根据立方根的定义解方程即可;(3)根据立方根的定义解方程即可.【详解】解:(1),∴ ,∴,∴;(2解析:(1)54;(2)1;(3)-1. 【分析】(1)根据立方根的定义解方程即可;(2)根据立方根的定义解方程即可;(3)根据立方根的定义解方程即可.【详解】解:(1)3641250x -=,∴ ()334=5x , ∴4=5x , ∴5=4x ; (2)3(1)8x +=∴33(1)2x +=∴12x +=∴1x =;(3)3(21)270x -+=,∴()33(21)3x -=-, ∴213x -=-,∴1x =-.【点睛】本题考查了利用立方根的含义解方程,熟知立方根的定义是解决问题的关键. 19.两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行【分析】要证BE ∥DF ,只需证∠1=∠D ,由AB ∥CD 可知∠B+∠1=180°,又有∠B+∠D=180°,由此即可证得.【详解】解析:两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行【分析】要证BE ∥DF ,只需证∠1=∠D ,由AB ∥CD 可知∠B +∠1=180°,又有∠B +∠D =180°,由此即可证得.【详解】证明:∵AB ∥CD (已知)∴∠B +∠1=180°(两直线平行,同旁内角互补)∵∠B +∠D =180°(已知)∴∠1=∠D (同角的补角相等),∴BE ∥DF (同位角相等,两直线平行)故答案为:两直线平行,同旁内角互补;同角的补角相等;同位角相等,两直线平行.【点睛】本题主要考查了平行线的性质与判定,解题的关键在于能够熟练掌握相关知识进行求解. 20.(1),;(2)9【分析】(1)根据坐标的特性以及C 点坐标,直接可以得出A 、B 的坐标(2)利用面积的和差求解:三角形ABC 的面积等于一个长方形的面积减去三个直角三角形的面积.【详解】解:(解析:(1)(3,4)A ,(0,1)B ;(2)9【分析】(1)根据坐标的特性以及C 点坐标,直接可以得出A 、B 的坐标(2)利用面积的和差求解:三角形ABC 的面积等于一个长方形的面积减去三个直角三角形的面积.【详解】解:(1)(3,4)A ,(0,1)B(2)3ABC S S S =-△长方形个三角形11145241533222=⨯-⨯⨯-⨯⨯-⨯⨯ =9【点睛】本题考查了坐标上的点以及求坐标上图形的面积,熟练掌握网格结构准确找出对应点的位置是解题的关键.21.(1);(2)其平方根为.【分析】(1)根据立方根,算术平方根,无理数的估算即可求出的值;(2)将(1)题求出的值代入,求出值之后再求出平方根.【详解】解:(1)由题得..又,解析:(1)3,5,6a b c =-==;(2)其平方根为4±.【分析】(1)根据立方根,算术平方根,无理数的估算即可求出,,a b c 的值;(2)将(1)题求出的值代入922a b c -+,求出值之后再求出平方根. 【详解】解:(1)由题得318,219a b +=--=.3,5a b ∴=-=. 364349<6437∴<.6c ∴=.3,5,6a b c ∴=-==.(2)当3,5,6a b c =-==时,()99223561622a b c -+=⨯--+⨯=. ∴其平方根为164±±.【点睛】本题考查了立方根,平方根,无理数的估算.正确把握相关定义是解题的关键. 二十二、解答题22.(1);(2)①见解析;②见解析,【分析】(1)设正方形边长为a,根据正方形面积公式,结合平方根的运算求出a值,则知结果;(2)① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②解析:(1)2,2-;(2)①见解析;②见解析,350.5-+<-【分析】(1)设正方形边长为a,根据正方形面积公式,结合平方根的运算求出a值,则知结果;(2)① 根据面积相等,利用割补法裁剪后拼得如图所示的正方形;②由题(1)的原理得出大正方形的边长为5,然后在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M,再把N点表示出来,即可比较它们的大小.【详解】解:设正方形边长为a,∵a2=2,∴a=2±,故答案为:2,2-;(2)解:①裁剪后拼得的大正方形如图所示:②设拼成的大正方形的边长为b,∴b2=5,∴b=±5,在数轴上以-3为圆心,以大正方形的边长为半径画弧交数轴的右方与一点M,则M表示的数为-3+5,看图可知,表示-0.5的N点在M点的右方,∴比较大小:350.5-+<-.【点睛】本题主要考查平方根与算术平方根的应用及实数的大小比较,熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键.二十三、解答题23.(1)80°;(2)∠AKC=∠APC,理由见解析;(3)∠AKC=∠APC,理由见解析【分析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠解析:(1)80°;(2)∠AKC=12∠APC,理由见解析;(3)∠AKC=23∠APC,理由见解析【分析】(1)先过P作PE∥AB,根据平行线的性质即可得到∠APE=∠BAP,∠CPE=∠DCP,再根据∠APC=∠APE+∠CPE=∠BAP+∠DCP进行计算即可;(2)过K作KE∥AB,根据KE∥AB∥CD,可得∠AKE=∠BAK,∠CKE=∠DCK,进而得到∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,同理可得,∠APC=∠BAP+∠DCP,再根据角平分线的定义,得出∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC,进而得到∠AKC=12∠APC;(3)过K作KE∥AB,根据KE∥AB∥CD,可得∠BAK=∠AKE,∠DCK=∠CKE,进而得到∠AKC=∠BAK﹣∠DCK,同理可得,∠APC=∠BAP﹣∠DCP,再根据已知得出∠BAK﹣∠DCK=23∠BAP﹣23∠DCP=23∠APC,进而得到∠BAK﹣∠DCK=23∠APC.【详解】(1)如图1,过P作PE∥AB,∵AB∥CD,∴PE∥AB∥CD,∴∠APE=∠BAP,∠CPE=∠DCP,∴∠APC=∠APE+∠CPE=∠BAP+∠DCP=60°+20°=80°;(2)∠AKC=12∠APC.理由:如图2,过K作KE∥AB,∵AB∥CD,∴KE∥AB∥CD,∴∠AKE=∠BAK,∠CKE=∠DCK,∴∠AKC=∠AKE+∠CKE=∠BAK+∠DCK,过P作PF∥AB,同理可得,∠APC=∠BAP+∠DCP,∵∠BAP与∠DCP的角平分线相交于点K,∴∠BAK+∠DCK=12∠BAP+12∠DCP=12(∠BAP+∠DCP)=12∠APC,∴∠AKC=12∠APC;(3)∠AKC =23∠APC 理由:如图3,过K 作KE ∥AB ,∵AB ∥CD ,∴KE ∥AB ∥CD ,∴∠BAK =∠AKE ,∠DCK =∠CKE ,∴∠AKC =∠AKE ﹣∠CKE =∠BAK ﹣∠DCK ,过P 作PF ∥AB ,同理可得,∠APC =∠BAP ﹣∠DCP ,∵∠BAK =23∠BAP ,∠DCK =23∠DCP , ∴∠BAK ﹣∠DCK =23∠BAP ﹣23∠DCP =23(∠BAP ﹣∠DCP )=23∠APC , ∴∠AKC =23∠APC .【点睛】本题考查了平行线的性质和角平分线的定义,解题的关键是作出平行线构造内错角相等计算.24.(1);(2),见解析;(3)不变,【分析】(1)根据平行线的性质求出,再求出的度数,利用内错角相等可求出角的度数;(2)过点作∥,类似(1)利用平行线的性质,得出三个角的关系; (3)运用解析:(1)23︒;(2)BCD A B ∠=∠+∠,见解析;(3)不变, 25FOG ∠=︒【分析】(1)根据平行线的性质求出50A DCE ∠=∠=︒,再求出BCE ∠的度数,利用内错角相等可求出角的度数;(2)过点C 作CE ∥AB ,类似(1)利用平行线的性质,得出三个角的关系;(3)运用(2)的结论和平行线的性质、角平分线的性质,可求出FOG ∠的度数,可得结论.【详解】(1)因为CE ∥AB ,所以50A DCE ∠=∠=︒,B BCE ∠=∠因为∠BCD =73 °,所以23BCE BCD DCE ∠=∠-∠=︒,故答案为:23︒(2)BCD A B ∠=∠+∠,如图②,过点C 作CE ∥AB ,则A DCE ∠=∠,B BCE ∠=∠.因为BCD DCE BCE ∠=∠+∠,所以BCD BAD B ∠=∠+∠,(3)不变,设ABE x ∠=,因为BE 平分ABC ∠,所以CBE ABE x ∠=∠=.由(2)的结论可知BCD BAD ABC ∠=∠+∠,且50BAD ︒∠=,则:502BCD x ∠=︒+.因为MN ∥AD ,所以502BON BCD x ∠=∠=︒+,因为OF 平分BON ∠, 所以1252COF NOF BON x ∠=∠=∠=︒+. 因为OG ∥BE ,所以COG CBE x ∠=∠=,所以2525FOG COF COG x x ∠=∠-∠=+-=︒︒.【点睛】本题考查了平行线的性质和角平分线的定义,解题关键是熟练运用平行线的性质证明角相等,通过等量代换等方法得出角之间的关系.25.(1)①115°,110°;②,证明见解析;(2),证明见解析.【解析】【分析】(1)①根据角平分线的定义求得∠CAG=∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=解析:(1)①115°,110°;②1902AFD B ︒∠=+∠,证明见解析;(2)1902AFD B ︒∠=-∠,证明见解析. 【解析】【分析】(1)①根据角平分线的定义求得∠CAG=12∠BAC=50°;再由平行线的性质可得∠EDG=∠C=30°,∠FMD=∠GAC=50°;由三角形的内角和定理求得∠AFD 的度数即可;已知AG 平分∠BAC ,DF 平分∠EDB ,根据角平分线的定义可得∠CAG=12∠BAC ,∠FDM=12∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;即可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×140°=70°;再由三角形的内角和定理可求得∠AFD=110°;②∠AFD=90°+12∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=12∠BAC,∠FDM=12∠EDG;由DE//AC,根据平行线的性质可得∠EDG=∠C,∠FMD=∠GAC;由此可得∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;再由三角形的内角和定理可得∠AFD=90°+12∠B;(2)∠AFD=90°-12∠B,已知AG平分∠BAC,DF平分∠EDB,根据角平分线的定义可得∠CAG=12∠BAC,∠NDE=12∠EDB,即可得∠FDM=∠NDE=12∠EDB;由DE//AC,根据平行线的性质可得∠EDB=∠C,∠FMD=∠GAC;即可得到∠FDM=∠NDE=12∠C,所以∠FDM+∠FMD =12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;再由三角形外角的性质可得∠AFD=∠FDM +∠FMD=90°-12∠B.【详解】(1)①∵AG平分∠BAC,∠BAC=100°,∴∠CAG=12∠BAC=50°;∵//DE AC,∠C=30°,∴∠EDG=∠C=30°,∠FMD=∠GAC=50°;∵DF平分∠EDB,∴∠FDM=12∠EDG=15°;∴∠AFD=180°-∠FMD-∠FDM=180°-50°-15°=115°;∵∠B=40°,∴∠BAC+∠C=180°-∠B=140°;∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠FDM=12∠EDG,∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×140°=70°;∴∠AFD=180°-(∠FDM +∠FMD)=180°-70°=110°;故答案为115°,110°;②∠AFD=90°+12∠B,理由如下:∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠FDM=12∠EDG,∵DE//AC,∴∠EDG=∠C,∠FMD=∠GAC;∴∠FDM +∠FMD=12∠EDG +∠GAC=12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;∴∠AFD=180°-(∠FDM +∠FMD)=180°-(90°-12∠B)=90°+12∠B;(2)∠AFD=90°-12∠B,理由如下:如图,射线ED交AG于点M,∵AG平分∠BAC,DF平分∠EDB,∴∠CAG=12∠BAC,∠NDE=12∠EDB,∴∠FDM=∠NDE=12∠EDB,∵DE//AC,∴∠EDB=∠C,∠FMD=∠GAC;∴∠FDM=∠NDE=12∠C,∴∠FDM +∠FMD =12∠C+12∠BAC=12(∠BAC+∠C)=12×(180°-∠B)=90°-12∠B;∴∠AFD=∠FDM +∠FMD=90°-1∠B.2【点睛】本题考查了角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质,根据角平分线的定义、平行线的性质、三角形的内角和定理及三角形外角的性质确定各角之间的关系是解决问题的关键.26.【现象解释】见解析;【尝试探究】BEC 70;【深入思考】2.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠解析:【现象解释】见解析;【尝试探究】∠BEC = 70︒;【深入思考】β= 2α.【分析】[现象解释]根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用∠2+∠3=90°得出∠1+∠2+∠3+∠4=180°,即可得出∠DCB+∠ABC=180°,即可证得AB∥CD;[尝试探究]根据三角形内角和定理求得∠2+∠3=125°,根据平面镜反射光线的规律得∠1=∠2,∠3=∠4,再利用平角的定义得出∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,即可得出∠EBC+BCE=360°-250°=110°,根据三角形内角和定理即可得出∠BEC=180°-110°=70°;[深入思考]利用平角的定义得出∠ABC=180°-2∠2,∠BCD=180°-2∠3,利用外角的性质∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,而∠BOC=∠3-∠2=α,即可证得β=2α.【详解】[现象解释]如图2,∵OM⊥ON,∴∠CON=90°,∴∠2+∠3=90°∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=180°,∴∠DCB+∠ABC=180°,∴AB∥CD;【尝试探究】如图3,在△OBC中,∵∠COB=55°,∴∠2+∠3=125°,∵∠1=∠2,∠3=∠4,∴∠1+∠2+∠3+∠4=250°,∵∠1+∠2+∠EBC+∠3+∠4+∠BCE=360°,∴∠EBC+BCE=360°-250°=110°,∴∠BEC=180°-110°=70°;【深入思考】如图4,β=2α,理由如下:∵∠1=∠2,∠3=∠4,∴∠ABC=180°-2∠2,∠BCD=180°-2∠3,∴∠BED=∠ABC-∠BCD=(180°-2∠2)-(180°-2∠3)=2(∠3-∠2)=β,∵∠BOC=∠3-∠2=α,∴β=2α.【点睛】本题考查了平行线的判定,三角形外角的性质以及三角形内角和定理,熟练掌握三角形的性质是解题的关键.。
七年级下册数学易错题整理附答案(超好)
七年级数学下易错题练习答案第五章相交线与平行线1.如图,将一张含有30°角的三角形纸片的两个顶点叠放在矩形的两条对边上,若∠2=44°,则∠1的大小为()A.14° B.16° C.90°﹣α D.α﹣44°【解答】解:如图,∵矩形的对边平行,∴∠2=∠3=44°,根据三角形外角性质,可得∠3=∠1+30°,∴∠1=44°﹣30°=14°,故选:A.2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边上.如果∠2=44°,那么∠1的度数是()A.14° B.15° C.16° D.17°【解答】解:如图,∵∠ABC=60°,∠2=44°,∴∠EBC=16°,∵BE∥CD,∴∠1=∠EBC=16°,故选:C.3.如图,直线a∥b,直线c分别交a,b于点A,C,∠BAC的平分线交直线b于点D,若∠1=50°,则∠2的度数是()A.50°B.70° C.80° D.110°【解答】∴∠2=180°﹣50°﹣50°=80°.故选:C.4.如图把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=()A.20°B.30° C.40° D.50°【解答】解:∵直尺对边互相平行,故选:C.∴∠3=∠1=50°,∴∠2=180°﹣50°﹣90°=40°.5.如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°【解答】解:∵∠AGE=32°,∴∠DGE=148°,由折叠可得,∠DGH=∠DGE=74°,∵AD∥BC,∴∠GHC=180°﹣∠DGH=106°,故选:D.6.如图,AB∥CD,点E在线段BC上,∠CDE=∠CED.若∠ABC=30°,则∠D为()A.85°B.75° C.60° D.30°【解答】故选:B.7.如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为()A.31° B.28° C.62° D.56°【解答】解:∵四边形ABCD为矩形,∴AD∥BC,∠ADC=90°,∵∠FDB=90°﹣∠BDC=90°﹣62°=28°,∵AD∥BC,∴∠CBD=∠FDB=28°,∵矩形ABCD沿对角线BD折叠,∴∠FBD=∠CBD=28°,∴∠DFE=∠FBD+∠FDB=28°+28°=56°.故选:D.8.如图,在平行线l1、l2之间放置一块直角三角板,三角板的锐角顶点A,B分别在直线l1、l2上,若∠l=65°,则∠2的度数是()A.25° B.35° C.45° D.65°【解答】解:如图,过点C作CD∥a,则∠1=∠ACD.∴∠1+∠2=90°,又∵∠1=65°,∴∠2=25°.故选:A.9.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是()A.相等B.互余或互补C.互补D.相等或互补二、填空题1.如图,把一张长方形的纸片按如图所示的方式折叠,EM 、FM 为折痕,折叠后的C 点落在B ′M 或B ′M 的延长线上,则∠EMF = 90°2.如图,把长方形ABCD 沿EF 对折,若∠1=500,则∠AEF= 115度.3 将长方形纸片ABCD 沿过A 点的直线折叠,折痕为线段AE ,得到图8所示的图形,已知∠CED ′=50º,则∠AED = 65 度.4、改写成如果…那么…形式1、改写:如果三个角是一个三角形的内角,那么这三个角的和是180°。
七年级下册数学易错题100道
七年级下册数学易错题100道1.甲、乙、丙三人在a、b两块地植树,a地要植棵,b地要植棵.已知甲、乙、丙每天分别能植树24,30,32棵,甲在a地植树,丙在b地植树,乙先在a地植树,然后转到b地植树.两块地同时开始同时结束,乙应在开始后第几天从a地转到b地?2.有三块草地,面积分别是5,15,24亩.草地上的草一样厚,而且长得一样快.第一块草地可供10头牛吃30天,第二块草地可供28头牛吃45天,问第三块地可供多少头牛吃80天?3.某工程,由甲、乙两队承揽,2.4天可以顺利完成,须要缴付元;由乙、丙两队承揽,3+3/4天可以顺利完成,须要缴付元;由甲、丙两队承揽,2+6/7天可以顺利完成,须要缴付元.在确保一星期内顺利完成的前提下,挑选哪个队单独承揽费用最少?4.一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水已灌满容器.已知容器的高为50厘米,长方体的高为20厘米,求长方体的底面面积和容器底面面积之比.5.甲、乙两位老板分别以同样的价格供货一种时装,乙供货的套数比甲多1/5,然后甲、乙分别按赢得80%和50%的利润定价出售.两人都全部售罄后,甲仍比乙多赢得一部分利润,这部分利润又恰好这么他再供货这种时装10套,甲原来供货这种时装多少套?6.有甲、乙两根水管,分别同时给a,b两个大小相同的水池注水,在相同的时间里甲、乙两管注水量之比是7:5.经过2+1/3小时,a,b两池中注入的水之和恰好是一池.这时,甲管注水速度提高25%,乙管的注水速度不变,那么,当甲管注满a池时,乙管再经过多少小时注满b池?7.小明早上从家步行回去学校,步上一半路程时,爸爸辨认出小明的数学书偷在家里,随即骑车去给小明送书,甩开时,小明除了3/10的路程未步上,小明随即上了爸爸的车,由爸爸送至学校,这样小明比独自步行提前5分钟回校.小明从家至学校全部步行须要多少时间?8.甲、乙两车都从a地出发经过b地驶往c地,a,b两地的距离等于b,c两地的距离.乙车的速度是甲车速度的80%.已知乙车比甲车早出发11分钟,但在b地停留了7分钟,甲车则不停地驶往c地.最后乙车比甲车迟4分钟到c地.那么乙车出发后几分钟时,甲车就超过乙车.9.甲、乙两辆洁净车继续执行东、西城间的公路打扫任务.甲车单独打扫须要10小时,乙车单独打扫须要15小时,两车同时从东、西城并肩送出,碰面时甲车比乙车多打扫12千米,问东、西两城距离多少千米?10.今有重量为3吨的集装箱4个,重量为2.5吨的集装箱5个,重量为1.5吨的集装箱14个,重量为1吨的集装箱7个.那么最少需要用多少辆载重量为4.5吨的汽车可以一次全部运走集装箱?小学数学应用题综合训练(02)11. 师徒二人共同加工个零件,师傅加工零件个数的1/3比徒弟加工零件个数的1/4还多10个,那么徒弟一共加工了几个零件?12.一辆大轿车与一辆小轿车都从甲地驶向乙地.大轿车的速度就是小轿车速度的80%.未知大轿车比小轿车晚启程17分钟,但在两地中点停在了5分钟,才稳步驶向乙地;而小轿车启程后中途没停在,轻易驶向乙地,最后小轿车比大轿车早4分钟抵达乙地.又言大轿车就是上午10时从甲地启程的.那么小轿车就是在上午什么时候冲上大轿车的.13.一部书稿,甲单独打字要14小时完成,,乙单独打字要20小时完成.如果甲先打1小时,然后由乙接替甲打1小时,再由甲接替乙打1小时.......两人如此交替工作.那么打完这部书稿时,甲乙两人共用多少小时?14. 徐气球2元3个,花掉气球3元2个,学校共买了32个气球,其中花掉气球比黄气球太少4个,学校卖哪种气球用的钱多?15.一只帆船的速度是60米/分,船在水流速度为20米/分的河中,从上游的一个港口到下游的某一地,再返回到原地,共用3小时30分,这条船从上游港口到下游某地共走了多少米?16.甲粮仓装43吨面粉,乙粮仓装37吨面粉,如果把乙粮仓的面粉放入甲粮仓,那么甲粮仓装进后,乙粮仓里剩的面粉占到乙粮仓容量的1/2;如果把甲粮仓的面粉放入乙粮仓,那么乙粮仓装进后,甲粮仓里剩的面粉占到甲粮仓容量的1/3,每个粮仓各可以上装面粉多少吨?17. 甲数除以乙数,乙数除以丙数,商相等,余数都是2,甲、乙两数之和是.那么甲、乙丙三数之和是几?18.一辆车从甲地驶往乙地.如果把车速增加10%,那么必须比原定时间晚1小时抵达,如果以原速高速行驶千米,再把车速提升20%,那么基数排序原定时间早1小时抵达.甲、乙两地之间的距离就是多少千米?19.某校参加军训队列表演比赛,组织一个方阵队伍.如果每班60人,这个方阵至少要有4个班的同学参加,如果每班70人,这个方阵至少要有3个班的同学参加.那么组成这个方阵的人数应为几人?20.甲、乙、丙三台车床加工方形和圆形的两种零件,未知甲车床每加工3个零件中存有2个就是圆形的;乙车床每加工4个零件中存有3个就是圆形的;丙车床每加工5个零件中存有4个就是圆形的.这天三台车床共加工了58个圆形零件,而加工的方形零件个数的比为4:3:3,那么这天三台车床共加工零件几个?小学数学应用题综合训练(03)21.圈金属线长30米,撷取长度为a的金属线3根,长度为b的金属线5根,剩的金属线如果再撷取2根长度为b的金属线还差0.4米,如果再撷取2根长度为a的金属线则还差2米,长度为a的等同于几米?22.某公司要往工地运送甲、乙两种建筑材料.甲种建筑材料每件重千克,共有件,乙种建筑材料每件重千克,共有80件,已知一辆汽车每次最多能运载4吨,那么5辆相同的汽车同时运送,至少要几次?23.从王力家至学校的路程比至体育馆的路程长1/4,一天王力在体育馆看看回去球赛后用17分钟的时间跑到家,稍稍歇息后,他又用了25分钟跑至学校,其速度比从体育馆回去时每分钟快15米,王力家至学校的距离就是多少米?24.师徒两人合作完成一项工程,由于配合得好,师傅的工作效率比单独做时要提高1/10,徒弟的工作效率比单独做时提高1/5.两人合作6天,完成全部工程的2/5,接着徒弟又单独做6天,这时这项工程还有13/30未完成,如果这项工程由师傅一人做,几天完成?25.六年级五个班的同学共植树棵.未知每个班植树的棵数都不相同,且按数量从多至太少的位列恰好就是一、二、三、四、五班.又言一班冈本的棵数就是二、三班冈本的棵数之和,二班冈本的棵数就是四、五班冈本的棵数之和,那么三班最多植树多少棵?26. 甲每小时跑13千米,乙每小时跑11千米,乙比甲多跑了20分钟,结果乙比甲多跑了2千米.乙总共跑了多少千米?27.存有高度成正比的a,b两个圆柱形容器,内口半径分别为6厘米和8厘米.容器a中装满水,容器b就是觑的,把容器a中的水全部放入容器b中,测得容器b中的水深比容器低的7/8还高2厘米.容器的高度就是多少厘米?28. 有吨的货物,用载重为9吨的汽车运送.已知汽车每次往返需要1小时,实际上汽车每次多装了1吨,那么可提前几小时完成.29.师、徒二人第一天共加工零件个,第二天使用了新工艺,师傅加工的零件比第一天减少了24%,徒弟减少了45%,两人共加工零件个,第二天师傅加工了多少个零件?徒弟加工了几个零件?30. 奋斗小学组织六年级同学到百花山进行野营拉练,行程每天增加2千米.去时用了4天,回来时用了3天,问学校距离百花山多少千米?小学数学应用题综合训练(04)31.某地收取电费的标准是:每月用电量不超过50度,每度收5角;如果超出50度,超出部分按每度8角收费.每月甲用户比乙用户多交3元3角电费,这个月甲、乙各用了多少度电?32.王师傅计划用2小时加工一批零件,当还剩个零件时,机器发生故障,效率比原来减少1/5,结果比原计划延后20分钟顺利完成任务,这批零件存有多少个?33.妈妈给了红红一些钱去买贺年卡,有甲、乙、丙三种贺年卡,甲种卡每张1.20元.用这些钱买甲种卡要比买乙种卡多8张,买乙种卡要比买丙种卡多买6张.妈妈给了红红多少钱?乙种卡每张多少钱?34.一位老人存有五个儿子和三间房子,临终前立下遗嘱,将三间房子让给三个儿子各一间.做为补偿,分后至房子的三个儿子每人掏出元,平分给没抽到房子的两个儿子.大家都说道这样的分配公平合理,那么每间房子的价值就是多少元?35.小明和小燕的画册都不足20本,如果小明给小燕a本,则小明的画册就是小燕的2倍;如果小燕给小明a本,则小明的画册就是小燕的3倍.原来小明和小燕各有多少本画册?36.存有白、徐、黑三种球共个.如果抽出红球的1/3,黄球的1/4,白球的1/5,则还剩个;如果抽出红球的1/5,黄球的1/4,白球的1/3,则剩个,问(1)旧有黄球几个?(2)旧有红球、白球各几个?37.爸爸、哥哥、妹妹三人现在的年龄和是64岁,当爸爸的年龄是哥哥年龄的3倍时,妹妹是9岁.当哥哥的年龄是妹妹年龄的2倍时,爸爸是34岁.现在三人的年龄各是多少岁?38.b在a,c两地之间.甲从b地至a地回去写信,启程10分钟后,乙从b地启程回去送来另一封信.乙启程后10分钟,丙辨认出甲乙刚好把两封信拎倒转了,于是他从b地启程骑车去追上甲和乙,以便把信调来.未知甲、乙的速度成正比,丙的速度就是甲、乙速度的3倍,丙从启程至把信调来后回到b地至少必须用多少时间?39.甲、乙两个车间共有94个工人,每天共加工竹椅.由于设备和技术的不同,甲车间平均每个工人每天只能生产15把竹椅,而乙车间平均每个工人每天可以生产43把竹椅.甲车间每天竹椅产量比乙车间多几把?40.甲放学回家东行10分钟,乙放学回家东行14分钟.未知乙回家的路程比甲回家的路程多1/6,甲每分钟比乙多跑12米,那么乙回家的路程就是几米?小学数学应用题综合训练(05)41.某商品每件成本72元,原来按定价出售,每天可以卖出件,每件利润为成本的25%,后来按定价的90%出售,每天销售量提升至原来的2.5倍,照这样排序,每天的利润比原来减少几元?42.甲、乙两列火车的速度比是5:4.乙车先发,从b站开往a站,当走到离b站72千米的地方时,甲车从a站发车往b站,两列火车相遇的地方离a,b两站距离的比是3:4,那么a,b两站之间的距离为多少千米?43.小、小猴子共35只,它们一起回去栽种水蜜桃.猴王无此的时候,一只小猴子一小时可以栽种15千克,一只小猴子一小时可以栽种11千克.猴王到场监督的时候,每只猴子不论大小每小时都可以栽种12千克.一天,栽种了8小时,其中只有第一小时和最后一小时存有猴王到场监督,结果共栽种千克水蜜桃.在这个猴群中,共计小猴子几只?44.某次数学竞赛设一、二等奖.已知(1)甲、乙两校获奖的人数比为6:5.(2)甲、乙来年感校获二等奖的人数总和占两校获奖人数总和的60%.(3)甲、乙两校获二等奖的人数之比为5:6.问甲校获二等奖的人数占该校获奖总人数的百分数是几?45.未知小明与小强步行的速度比是2:3,小强与小刚步行的速度比是4:5.未知小刚10分钟比小明多跑米,那么小明在20分钟里比小强太少跑几米?46.加工一批零件,原计划每天加工15个,若干天可以完成.当完成加工任务的3/5时,采用新技术,效率提高20%.结果,完成任务的时间提前10天,这批零件共有几个?47.甲、乙二人在米的圆形滑行道上展开米比赛.两人从起点同时同向启程,已经开始时甲的速度为8米/秒,乙的速度为6米/秒,当甲每次甩开乙以后,甲的速度每秒增加2米,乙的速度每秒增加0.5米.这样下去,直至甲辨认出乙第一次从后面冲上自己已经开始,两人都把自己的速度每秒减少0.5米,直至终点.那么者抵达终点时,另一人距离终点多少米?48.小明从家去学校,如果他每小时比原来多走1.5千米,他走这段路只需原来时间的4/5;如果他每小时比原来少走1.5千米,那么他走这段路的时间就比原来时间多几分几之?49. 甲、乙、丙、丁现在的年龄和就是64岁.甲21岁时,乙17岁;甲18岁时,丙的年龄就是丁的3倍.丁现在的年龄就是几岁?50.加工一批零件,原计划每天加工30个.当加工完1/3时,由于改进了技术,工作效率提高了10%,结果提前了4天完成任务.问这批零件共有几个?小学数学应用题综合训练(06)51.自动扶梯以均匀的速度向上行驶,一男孩与一女孩同时从自动扶梯向上走,男孩的速度是女孩的2倍,已知男孩走了27级到达扶梯的顶部,而女孩走了18级到达顶部.问扶梯露在外面的部分有多少级?52. 两堆苹果一样轻,第一堆上买进2/3,第二堆上买进50千克,如果第一堆上剩的苹果比第二堆上剩的苹果太少,那么两堆剩的苹果至少存有多少千克?53.甲、乙两车同时从a地出发,不停的往返行驶于a、b两地之间.已知甲车的速度比乙车快,并且两车出发后第一次和第二次相遇都杂途中c地,甲车的速度是乙车的几倍?54.一只小船从甲地至乙地来往一次共用2小时,回去时顺水,比去时的速度每小时多行8千米,因此第二小时比第一小时多行6千米.谋甲、乙两地的距离.55.甲、乙两车分别从a、b两地出发,并在a,b两地间不断往返行驶.已知甲车的速度是15千米/小时,甲、乙两车第三次相遇地点与第四次相遇地点相差千米.求a、b两地的距离.56.某人沿着向上移动的自动扶梯从顶部朝底下用了7分后30秒,而他沿着自动扶梯从底朝上追到顶部就用了1分后30秒.如果此人不跑,那么乘着扶梯从底上浮必须多少时间?如果停水,那么此人沿扶梯从底跑上浮必须多少时间?57.甲、乙两个圆柱体容器,底面积比为5:3,甲容器水深20厘米,乙容器水深10厘米.再往两个容器中注入同样多的水,使得两个容器中的水深相等.这时水深多少厘米?58.a、b两地距离千米,甲、乙两车8:00同时从a地启程至b地,速度分别为60千米/小时,54千米/小时,丙车8:30从b地启程至a地,速度为48千米/小时.丙车与甲、乙两车距离成正比时就是几点几分?59. 一个长方形的周长是厘米,如果它的宽增加1/5,长减少1/8,就得到一个相同周长的新长方形.求原长方形的面积.60. 存有一长方形,它的短与阔的比是5:2,对角线长29厘米,谋这个长方形的面积.小学数学应用题综合训练(07)61.存有一个果园,去年结果的果树比不结果的果树的2倍还多60棵,今年又存有棵果树吴厝庄了果,这时结果的果树刚好就是不结果的果树的5倍.果园里共计多少棵果树?62.小明步行从甲地出发到乙地,李刚骑摩托车同时从乙地出发到甲地.48分钟后两人相遇,李刚到达甲地后马上返回乙地,在第一次相遇后16分钟追上小明.如果李刚不停地往返于甲、乙两地,那么当小明到达乙地时,李刚共追上小明几次?63.同样跑米,小明必须持球,父亲必须持球.父子同时同方向从同一地点启程,如果每跑一步所用的时间相同,那么父亲踏进米后往回跑,还要跑多少步就可以碰到小明?64. 一艘轮船在两个港口间航行,水速为6千米/小时,顺水航行需要4小时,逆水航行需要7小时,求两个港口之间的距离.65.有甲、乙、丙三辆汽车,各以一定的速度从a地驶往b地,乙比丙晚启程10分钟,启程后40分钟甩开丙;甲比乙又晚启程10分钟,启程后60分钟甩开丙,问甲启程后几分钟甩开乙?66.甲、乙合作完成一项工作,由于配合的好,甲的工作效率比单独做时提高1/10,乙的工作效率比单独做时提高1/5,甲、乙合作6小时完成了这项工作,如果甲单独做需要11小时,那么乙单独做需要几小时?67.a、b、c、d、e五名学生排好一纵排,他们的手中共拿着20面小旗.现晓得,东站在c右边的学生共拿着11面小旗,东站在b左边的学生共拿着10面小旗,东站在d左边的学生共拿着8面小旗,东站在e左边的学生共拿着16面小旗.五名学生从左至右依次就是谁?各拎几面小旗?68. 小明在米长的环行的跑道上跑了一圈,已知他前一半时间每秒跑5米,后一半时间每秒跑4米,问他后一半路程用了多少时间?69.小英和小明为了测量直冲而过的火车的长度和速度,他们拎了两块秒表,小英用一块念法下火车从他面前通过所花的时间就是15秒,小明用另一块念法下了从车头过第一根电线杆至车尾过第二根电线杆所花的时间就是18秒,未知两根电线杆之间的距离就是60米,谋火车的全长和速度.70.小明从家到学校时,前一半路程步行,后一半路程乘车;他从学校到家时,前1/3时间乘车,后2/3时间步行.结果去学校的时间比回家的时间多20分钟,已知小明从家到学校的路程是多少千米?小学数学应用题综合训练(08)71. 数学练习共举行了20次,共出试题道,每次出的题数是16,21,24问出16,21,24题的分别有多少次?72. 一个整数除以2余1,用税金的商除以5余4,再用税金的商除以6余1.用这个整数除以60,余数就是多少?73.少先队员在校园里栽的苹果树苗是梨树苗的2倍.如果每人栽3棵梨树苗,则余2棵;如果每人栽7棵苹果树苗,则少6棵.问共有多少名少先队员?苹果和梨树苗共有多少棵?74.某人上开汽车从a城至b城要行千米,已经开始时他以56千米/小时的速度高速行驶,但途中因汽车故障停放维修用回去半小时,为了按时抵达,他必须把速度减少14千米/小时,跑完以后的路程,他洗车的地方距离a城多少千米?75.甲、乙两人分别从a、b两地同时出发,相向而行,乙的速度是甲的2/3,两人相遇后继续前进,甲到达b地,乙到达a地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是米,求a、b两地的距离.76.一条船来往于甲、乙两港之间,未知船在静水中的速度为9千米/小时,平时顺行与逆行所用时间的比为2:1.一天因下雪,水流速度为原来的2倍,这条船来往共用10小时,问甲、乙两港距离多少千米?77.某学校入学考试,确定了录取分数线,报考的学生中,只有1/3被录取,录取者平均分比录取分数线高6分,没有被录取的同学其平均分比录取分数线低15分,所有考生的平均分是80分,问录取分数线是多少分?78.一群学生弄砖,如果存有12人每人各搬7块,其余的每人弄5块,那么最后余下块;如果存有30人每人各搬8块,其余的每人弄7块,那么最后余下20块.问学生共计多少人?砖存有多少块?79.甲、乙两车分别从a、b两地同时相向而行,已知甲车速度与乙车速度之比为4:3,c 地在a、b之间,甲、乙两车到达c地的时间分别是上午8点和下午3点,问甲、乙两车相遇是什么时间?80. 一次棋赛,记分方法就是,胜者得2分后,负者得0分后,和棋两人各得1分后,每位球手都与其他球手各对局一次,现晓得球手中男生就是女后生的10倍,但其总得分只为女生罚球的4.5倍,问共计几名女生参赛?女生共得几分?小学数学应用题综合训练(09)81.存有若干个自然数,它们的算术平均数就是10,如果从这些数中换成的一个,则余下的算术平均数为9;如果换成最轻的一个,则余下的算术平均数为11,这些数最多存有多少个?这些数中的数值就是几?82. 某班有少先队员35人,这个班有男生23人,这个班女生少先队员比男生非少先队员多几人?83.小东计划至周口店参观猿人遗址.如果他坐汽车以40千米/小时的速度高速行驶,那么比骑车去晚至3小时,如果他以8千米/小时的速度步行回去,那么比骑车晚至5小时,小东的出发点至周口店存有多少千米?84. 甲、乙两船在相距90千米的河上航行,如果相向而行,3小时相遇,如果同向而行则15小时甲船追上乙船.求在静水中甲、乙两船的速度.85.二年级两个班共计学生90人,其中少先队员存有71人,一班少先队员占到本班人数的75%,二班少先队员占到本班人数的5/6.一班少先队员人数比二班少先队员人数多几人?86.一个容器中已注满水,有大、中、小三个球.第一次把小球沉入水中,第二次把小球取出,把中球沉入水中,第三次把中球取出,把小球和大球一起沉入水中,现知道每次从容器中溢出水量的情况是:第一次是第二次的1/2,第三次是第二次的1.5倍.求三个球的体积之比.87. 某人翻过一座山用了2小时,回到用了2.5小时,他上山的速度就是米/小时,下山的速度就是米/小时.问翻过这座山必须跑多少米?88.钢筋原材料每根长7.3米,每套钢筋架子用长2.4米、2.1米和1.5米的钢筋各一段.现需要绑好钢筋架子套,至少要用去原材料多少根?89. 存有一块铜锌合金,其中铜和锌的比2:3.现晓得再重新加入6克锌,熔融后共得崭新合金36克,崭新合金中铜和锌的比是多少?90.小明通常总是步行上学,有一天他想锻炼身体,前1/3路程快跑,速度是步行速度的4倍,后一段的路程慢跑,速度是步行速度的2倍.这样小明比平时早35分到校,小明步行上学需要多少分钟?小学数学应用题综合训练(10)91.甲、乙、丙三人,甲的年龄比乙的年龄的2倍还大3岁,乙的年龄比丙的年龄的2倍小2岁,三个人的年龄之和是岁,分别求出甲、乙、丙的年龄.92.快车以60千米/小时的速度从甲站向乙站送出,1.5小时后,慢车以40千米/小时的速度从乙站行甲站送出,.两车碰面时,碰面点距两站的中点70千米.甲、乙两站距离多少千米?93.甲、乙两车先后离开学校以相同的速度开往博物馆,已知8:32分甲车与学校的距离是乙车与学校距离的3倍,8:39分甲车与学校的距离是乙车与学校距离的2倍,求甲车离开学校的时间.94.存有一个工作小组,当每个工人在各自的工作岗位上工作时,7小时可以生产一批零件,如果互换工人甲、乙的岗位,其他人维持不变,那么可以提早1小时,顺利完成这批零件,如果互换工人丙、丁的岗位,其他人维持不变,也可以提早1小时,问如果同时互换甲与乙、丙与丁的岗位,其他人维持不变,那么顺利完成这批零件须要多长的时间.95. 用10块长7厘米、宽5厘米、高3厘米的长方体积木,拼成一个长方体,这个长方体的表面积最小是多少?96.公圆只购两种门票:个人票每张5元,10人一张的团体票每张30元,出售10张以上的团体票的可以优惠10%.(1)甲单位45人月华,按以上规定买票,最少应付多少钱?(2)乙单位人月华,按以上的规定买票,最少应付多少钱?97. 甲、乙、丙三人,参加一次考试,共得分,已知甲得分的1/3,乙得分的1/4与丙得分的一半减去22分都相等,那么丙得分多少?。
初一数学错题整理
初一数学错题整理
一、有理数运算类
1. 计算:
错误答案:
解析:
- 去括号法则错误。
减去一个负数等于加上它的相反数。
- 正确的计算过程是:。
2. 计算:
错误答案:
- 原式
解析:
- 对于幂运算的符号理解错误。
表示的平方的相反数,应该是,而不是。
- 正确计算过程:
- 原式。
二、整式加减类
1. 化简:
错误答案:
- 原式
解析:
- 合并同类项时系数计算错误,正确,但是,而不是。
- 正确答案是:。
2. 先化简,再求值:,其中
错误答案:
- 化简得:
- 原式
- 当时,代入得:
解析:
- 去括号时出现错误,计算正确,但是
,在化简过程中与前面的合并同类项时计算错误。
- 正确化简过程:
- 原式。
- 当时,代入得:(虽然结果相同,但是化简过程存在错误)。
三、一元一次方程类
1. 解方程:
错误答案:
- 移项得:,即,解得
解析:
- 移项错误,移项要变号。
正确的移项应该是。
- 正确答案:。
2. 解方程:
错误答案:
- 去分母得:
- 展开括号得:
- 移项得:
- 合并同类项得:,解得
解析:
- 去分母时错误,等式两边同时乘以6,右边的1也要乘以6。
- 正确的去分母得:
- 展开括号得:
- 移项得:
- 合并同类项得:,解得。
人教版七年级下册数学易错题集合50题含答案(广州)
人教版七年级下册数学易错题集合50题含答案(广州)一、单选题1.一个数的平方等于它本身,这个数是( ). A .1B .1,0C .0D .0,±12.如图所示的图案分别是三菱、大众、奥迪、奔驰汽车的车标,其中可以看成是由“基本图案”经过平移得到的是( )A .B .C .D .3.某班共有学生49人,一天,该班某男生因事请假,当天的男生人数恰为女生人数的一半,若该班男生人数为x ,女生人数为y ,则所列方程组正确的是( )A .()4921x y y x -=⎧⎨=+⎩B .()4921x y y x +=⎧⎨=+⎩C .()4921x y y x -=⎧⎨=-⎩D .()4921x y y x +=⎧⎨=-⎩4.下列各式是二元一次方程的是( ) A .132y x +B .203x yy +-= C .21y x=+ D .20x y +=5.规定用符号[m]表示一个实数m 的整数部分,例如:[23]=0,[3.14]=3.按此规定1]的值为( ) A .3B .4C .5D .66.2008年5月12日,在四川省汶川县发生8.0级特大地震,能够准确表示汶川这个地点位置的是( ) A .北纬31o B .东经103.5oC .金华的西北方向上D .北纬31o ,东经103.5o7.若关于x 的不等式组的解在数轴上如图所示,则这个不等式组的解是( )A .x 2≤B .x 1>C .1x 2≤<D .1x 2<≤8.鸿运旅行社组织了197人到香格里拉和九寨沟旅游,到香格里拉的人数x 比到九寨沟的人数y 的2倍多5人,则下面所列的方程组中符合题意的是( )A .25197x y x y =-⎧⎨+=⎩B .25197x y x y =+⎧⎨+=⎩C .19725x y x y +=⎧⎨=+⎩ D .2(5)197x y x y =+⎧⎨+=⎩9.下列语句中,正确的是( ) A .正整数、负整数统称整数 B .正数、0、负数统称有理数 C .开方开不尽的数和π统称无理数 D .有理数、无理数统称实数 10.频率不可能取到的数为( ) A .0B .0.5C .1D .1.511.不等式1x 0+<的解集在数轴上表示正确的是( ) A .B .C .D .12.为了解中学生获取资讯的主要渠道,设置“A :报纸,B :电视,C :网络,D :身边的人,E :其他”五个选项(五项中必选且只能选一项)的调查问卷,随机抽取50名中学生进行该问卷调查,根据调查的结果绘制成如图所示的条形统计图,该调查的方式与图中a 的值分别是( )A .普查,26B .普查,24C .抽样调查,26D .抽样调查,2413.若方程()2331a a x y -++=是关于x ,y 的二元一次方程,则a 的值为A .-3B .±2C .±3D .314.下列命题不是真命题的是( ) A .0.3是0.09的平方根 B .(-2)2的算术平方根是-2CD .已知a ||a =15.如图,AO ⊥OB 于点O ,⊥BOC =35°,则⊥AOC 的补角等于( )A .55°B .145°C .125°D .135°16.不等式组 21523x x -≤⎧⎨-+<⎩的解集表示在数轴上为( )A .B .C .D .17.在同一平面内,两条直线的位置关系可能是( ) A .相交或垂直 B .垂直或平行 C .平行或相交D .相交或垂直或平行 18.已知关于x 的不等式组3x x a <⎧⎨>⎩有解,则a 的取值范围是( ) A .3a <B .3a ≤C .3a >D .3a ≥19.如果a 是任意实数,则点P (a -2,a -1)一定不在第( )象限 A .一B .二C .三D .四20.已知整数a 1,a 2,a 3,a 4,…满足下列条件:a 1=0,a 2=-|a 1+1|,a 3=-|a 2+2|,a 4=-|a 3+3|,…,依此类推,则a 2022的值为( ) A .-1010B .-1011C .-1012D .-202221.平面直角坐标系内AB ∥x 轴,AB =1,点A 的坐标为(-2,3),则点B 的坐标为( )A .(-1,4)B .(-1,3)C .(-3,3)或(-1,-2)D .(-1,3)或(-3,3)22.2022年我市有37000名初中毕业生参加了毕业考试,为了解37000名考生的中考成绩,从中抽取了200名考生的试卷进行统计分析,以下说法正确的是( ) A .37000名考生是总体 B .每名考生的成绩是个体 C .200名考生是总体的一个样本D .样本容量是37000二、填空题23.在同一平面内,两条直线没有公共点,它们的位置关系是______ ,两条直线有且只有一个公共点,它们的位置关系是_______ .24.已知方程组45ax by bx ay +=⎧⎨+=⎩的解是21x y =⎧⎨=⎩,则a b +的值为____________.25.小于π的自然数有________个.26.如图,直线AB //CD //EF ,且⊥B =40°,⊥C =125°,则⊥CGB =_______.27的所有整数有_____________.28.如图,已知⊥1=⊥2,则图中互相平行的线段是_____.29.一组数据的最大值与最小值的差为3.5cm ,若取组距为0.4cm ,应将该数据应分________ 组.30.若x 3m –3–2yn –1=5是二元一次方程,则mn =__________.31.一个样本含有20个数据:68、69、70、66、68、64、65、65、69、62、67、66、65、67、63、65、64、61、65、66,在列频率分布表时,如果组距为2,那么应分为____组,在64.5~66.5这一小组的频率为________32.在下列实数227,3.1415926,-8 1.103030030003…(两个3之间依次多一个0),π中,无理数有_____________33.2352x x a -≤⎧⎨-+<⎩关于x 的不等式组只有4个整数解,则a 的取值范围是__________.34.以下命题中(1)对顶角相等(2)相等的角是对顶角(3)垂直于同一条直线的两直线互相平行(4)平行于同一条直线的两直线互相平行(5)同位角相等,其中真命题的序号为___________35.关于x 的不等式ax <-b 的解集x <2,则关于y 的不等式by >a 的解集为____ 36.到x 轴距离为6,到y 轴距离为4的坐标为____.37.一个正数的平方根分别是1x -+和2x +5,则这个正数是______38.已知:234x t y t =+⎧⎨=-⎩,则x 与y 的关系式是_______.39.已知x ,y 都是实数,且y 4,则yx =________.40a b ,则2a b ++的值________41.在同一平面内,A ∠与B ∠的两边一边平行,另一边垂直,且A ∠比B ∠的3倍少10°.则B ∠______.42.若⊥A 与⊥B 的两边分别平行,且⊥A 比⊥B 的3倍少40°,则⊥B =_____度. 43.在同一平面内,⊥A 与⊥B 的两边分别垂直,⊥A 比⊥B 的2倍少40°,则⊥B =_____三、解答题44.计算下列各式的值:(1)(2)(﹣3)2﹣|﹣12|+12(3)x2﹣121=0; (4)(x ﹣5)3+8=0.45.甲乙两人同时解方程组832ax by cx y +=⎧⎨-=-⎩ ,甲正确解得11x y =⎧⎨=-⎩ ;乙因为抄错c 的值,解得26x y =⎧⎨=-⎩.求a ,b ,c 的值.46.设a ,b ,c 都是实数,且满足(2﹣a )+|c+8|=0,ax2+bx+c=0,求x2+2x ﹣1的值.47.请你根据萌萌所给的如图所的内容,完成下列各小题.(1)若m※n=1,m※2n=﹣2,分别求m 和n 的值;(2)若m 满足m※2≤0,且3m※(﹣8)>0,求m 的取值范围. 48b a bc -+49.解方程(组) (1)2(21)4x -=(2)1243231y x x y ++⎧=⎪⎨⎪-=⎩ 50.如图,⊥1+⊥2=180°,⊥A =⊥C ,DB 平分⊥AB C .(1)探究AE 与CF 的位置关系,并说明理由. (2)探究AD 与BC 的位置关系,并说明理由. (3)BC 平分⊥DBE 吗?为什么?51.某校计划安排七年级全体师生参观红旗渠风景区,现有36座和48座两种客车(不包括驾驶员座位)供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用48座客车,则能比租36座的客车少租1辆,且有1辆车没有坐满,但超过了30人,该校七年级共有师生多少人?52.如图,平面直角坐标系中,已知点A (-3,3),B (-5,1),C (-2,0),P (a ,b )是⊥ABC 的边AC 上任意一点,⊥ABC 经过平移后得到111A B C △,点P 的对应点为1(6,2)Pab +-(1)直接写出点111,,A B C 的坐标. (2)在图中画出111A B C △.(3)连接11,,AA AO AO ,求1AOA 的面积. (4)连接1BA ,若点Q 在y 轴上,且1QBA 的面积为10,求点Q 的坐标.53.在实施“城乡危旧房改造工程”中,襄城区计划推出A 、B 两种新户型.根据预算,建成10套A 种户型和30套B 种户型住房共需资金480万元,建成30套A 种户型和10套B 种户型住房共需资金400万元.(1)在危旧房改造中建成一套A 种户型和一套B 种户型住房所需的资金分别是多少万元?(2)襄城区有800套住房需要改造,改造资金由国家危旧房补贴和地方财政共同承担.若国家补贴拨付的改造资金不少于2100万,襄城区财政投入额资金不超过7700万元,其中,国家财政投入到A 、B 两种户型的改造资金分别为每套2万元和3万元. ⊥请你计算求出A 种户型至少可以建多少套,最多可以建多少套?⊥这项改造工程总投入资金W 万元,建成A 种户型m 套,写出W 与m 的关系式. 54.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A ,B 的对应点C ,D .连接AC ,BD .(1)写出点C ,D 的坐标及四边形ABDC 的面积.(2)在y 轴上是否存在一点P ,连接P A ,PB ,使S 三角形P AB =S 四边形ABDC ?若存在,求出点P 的坐标,若不存在,试说明理由;(3)点Q 是线段BD 上的动点,连接QC ,QO ,当点Q 在BD 上移动时(不与B ,D重合),给出下列结论:⊥DCQ BOQCQO∠+∠∠的值不变;⊥DCQ COQBQO∠+∠∠的值不变,其中有且只有一个正确,请你找出这个结论并求值.55.如图所示,已知AB∥CD,分别探索下列四个图形中⊥P与⊥A,⊥C的关系,并证明你的结论.参考答案:1.B【详解】解:根据平方的定义可得,1的平方等于1,0的平方等于0,所以一个数的平方等于它本身的数是1和0. 故选B . 2.C【分析】根据平移的性质:不改变物体的大小,朝一个方向移动能够得到的图像. 【详解】解:观察图形可知,图像C 可以看成由“基本图案”经过平移得到. 故选:C .【点睛】此题考查了图形的平移,平移只改变位置,不改变大小和性质,要注意与旋转和翻折的区别. 3.D【分析】根据等量关系:男生数-1=女生数的一半,男生+女生=49,据此即可列出方程组.【详解】由该班一男生请假后,男生人数恰为女生人数的一半,得x -1= 12y ,即y =2(x -1);由该班共有学生49人,得x +y =49, 列方程组为()4921x y y x +=⎧⎨=-⎩, 故选D【点睛】本题考查了二元一次方程组的应用,弄清题意,找准等量关系列出相应的方程是解题的关键. 4.B【详解】A. 3y +12x 是代数式而不是方程,不是二元一次方程,故此选项错误; B. 方程3x y+−2y =0符合二元一次方程的定义,故此选项正确; C. 方程y =2x +1的右边不是整式,不符合二元一次方程的定义,故此选项错误;D. 方程2x +y =0中未知数的项的最高次数是2,不符合二元一次方程的定义,故此选项错误; 故选B.5.B【详解】解:根据91016<<,则34<,即415<<,根据题意可得:14⎤=⎦. 考点:无理数的估算 6.D【详解】本题主要考查了坐标确定位置. 根据在地理上常用经纬度来表示某个点的位置,既有经度,又有纬度.解:根据地理上表示某个点的位的方法可知选项D 符合条件. 故选D . 7.D【分析】不等式组的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.【详解】解:在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.因此,这个不等式组的解是1x 2<≤. 故选D . 8.C【详解】试题解析:根据题意可得等量关系;⊥去香格里拉的人数+去九寨沟的人数=197人;⊥去香格里拉的人数x=到九寨沟的人数y 的2倍+5人,根据等量关系列出方程组:19725x y x y +=⎧⎨=+⎩ 故选C . 9.D【详解】试题解析:A 、正整数、零和负整数统称整数,故A 错误; B 、正有理数、零、负有理数统称有理数,故B 错误; C 、无限不循环小数是无理数,故C 错误; D 、有理数和无理数统称实数,故D 正确; 故选D .10.D【详解】解:频率大于等于0小于等于1,故选D .11.A【详解】不等式1x 0+<的解集为x 1<-,在数轴上表示如下:,故选A.【点睛】本题考查了在数轴上表示一元一次不等式的解集,不等式的解集在数轴上表示的方法:>,≥向右画;<,≤向左画,在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.12.D【详解】根据关键语句“先随机抽取50名中学生进行该问卷调查,”可得该调查方式是抽样调查,调查的样本容量为50,故6+10+6+a+4=50,解即可.解:该调查方式是抽样调查,a=50﹣6﹣10﹣6﹣4=24,故选D .13.D 【分析】试题分析:依题意知a 2-=1且a+3≠0.解得x=3或x=-3(舍去).故选D 考点:二元一次方程点评:本题难度较低,主要考查学生对二元一次方程性质知识点的掌握.【详解】请在此输入详解!14.B【分析】利用有关的性质、定义及定理分别对每个小题判断后即可确定正确的选项.【详解】解:A 、0.3是0.09的平方根,是真命题;B 、()224-=,4的算术平方根是2,是假命题;C 、2-D 、已知a a =,是真命题;故选:B .【点睛】本题考查了命题与定理的知识,解题的关键是理解有关的定义、定理及性质. 15.C【分析】根据题意得90AOB ∠=︒,根据⊥BOC =35°,得55AOC ∠=︒,再根据互补两角和是180°即可得.【详解】解:⊥AO ⊥OB ,⊥90AOB ∠=︒,⊥⊥BOC =35°,⊥903555AOC AOB BOC ∠=∠-∠=︒-︒=︒,⊥⊥AOC 的补角为:180=18055=125AOC ︒-∠︒-︒︒,故选C .【点睛】本题考查了补角,解题的关键是掌握互补的两个角的和是180°.16.B【分析】求出不等式组的解集即可得.【详解】解:21523x x -≤⎧⎨-+<⎩①② 由⊥得,3x ≤,由⊥得,1x >-,⊥不等式组的解集为:13x -<≤,故选:B .【点睛】本题考查了在数轴上表示不等式组的解集,解题的关键是正确求解出不等式组的解集.17.C【分析】根据两条直线有一个交点的直线是相交线,没有交点的直线是平行线,可得答案.【详解】在同一平面内,两条直线有一个交点,两条直线相交;在同一平面内,两条直线没有交点,两条直线平行,故C 正确;故选:C .【点睛】本题主要考查了同一平面内,两条直线的位置关系,注意垂直是相交的一种特殊情况,不能单独作为一类.18.A【分析】先求出不等式组的解集,即可求解.【详解】解:⊥关于x 的不等式组3x x a <⎧⎨>⎩有解, ⊥不等式组的解集为3a x <<,⊥3a <.故选:A【点睛】本题主要考查了解一元一次不等式组,熟练掌握解不等式组解集的口诀:同大取大,同小取小大小小大中间找,大大小小找不到(无解)是解题的关键.19.D【分析】根据题意可得21a a ,然后根据点在第四象限内,横坐标为正,纵坐标为负,即可求解.【详解】解:根据题意得:21a a ,⊥点在第四象限内,横坐标为正,纵坐标为负,⊥点P (a -2,a -1)一定不在第四象限.故选:D【点睛】本题主要考查了平面直角坐标系中各个象限的点的坐标的符号特点,熟练掌握四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-)是解题的关键.20.B【分析】分别求得a 1,a 2,a 3,a 4,…找到规律,当下标为偶数时,其值等于下标的一半的相反数,据此即可求解.【详解】解:⊥a 1=0,a 2=-|a 1+1|=-1,a 3=-|a 2+2|=-1,a 4=-|a 3+3|=-2,5442a a =--+=-,6553a a =--+=-…,当下标为偶数时,其值等于下标的一半的相反数,⊥a 2022的值为-1011.故选B .【点睛】本题考查了数字类规律,找到规律是解题的关键.21.D【分析】根据平行与横轴上的点纵坐标相等分析计算即可.【详解】解:⊥AB∥x轴,⊥A点与B点纵坐标相同,横坐标之差等于其距离,且AB=1,B点横坐标为﹣2+1=-1,或-2-1=-3,故B点坐标为:(-1,3)或(-3,3),故选:D.【点睛】本题考查平行于坐标轴的线上的点的坐标特征,能够掌握数形结合思想是解决本题的关键.22.B【分析】根据总体的定义:要考查的全体对象称为总体;个体的定义:组成总体的每一个考查对象称为个体;样本的定义:被抽取的那些个体组成一个样本;样本容量的定义:样本中个体的数目称为样本容量,进行判断即可得.【详解】解:A、37000名考生的中考成绩是总体,选项说法错误,不符合题意;B、每名考生的成绩是个体,选项说法正确,符合题意;C、200名考生的中考成绩是总体的一个样本,选项说法错误,不符合题意;D、样本容量是200,选项说法错误,不符合题意;故选B.【点睛】本题考查了总体,个体,样本,样本容量,解题的关键是掌握这些知识点.23.平行相交【详解】试题解析:在同一平面内,两条直线没有公共点,它们的位置关系是平行,两条直线有且只有一个公共点,它们的位置关系是相交.故答案为平行,相交.24.3【分析】把21xy=⎧⎨=⎩代入45ax bybx ay+=⎧⎨+=⎩即得关于的a、b二元一次方程组,再把两个方程相加,通过计算即可得到结果.【详解】由题意得,把21xy=⎧⎨=⎩代入45ax bybx ay+=⎧⎨+=⎩得24 25a bb a+=⎧⎨+=⎩2254a b b a +++=+即339a b +=3a b ∴+=故答案为:3.【点睛】本题考查的是二元一次方程组的解的定义及应用,二元一次方程组中两个一次方程的公共解,就是二元一次方程组的解.25.4【详解】试题解析:⊥π≈3.14,⊥小于π的自然数有0,1,2,3共4个.故答案为4.26.15º##15度【分析】根据平行线的性质得出⊥BGF =⊥B =40°,⊥C +⊥CGF =180°,求出⊥CGF =55°,即可得出答案.【详解】解:⊥AB //CD //EF ,⊥B =40°,⊥C =125°,⊥⊥BGF =⊥B =40°,⊥C +⊥CGF =180°,⊥⊥CGF =55°,⊥⊥CGB =⊥CGF -⊥BGF =15°.故答案为:15°【点睛】本题考查了平行线的性质的应用,牢记“两直线平行,内错角相等”等平行线的性质是解题的关键.27.0, 1, 2,-1,-2【分析】先估算出23【详解】解:∴23,⊥2,1,0,-1,-2.故答案为2,1,0,-1,-2.键.28.AD⊥BC【分析】根据内错角相等,两直线平行进行判断.【详解】解:⊥⊥1=⊥2⊥AD⊥BC(内错角相等,两直线平行)故答案为:AD⊥BC.【点睛】本题考查了平行线的判定,解题的关键是记住同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.29.9【详解】试题解析:3.53=80.44,则应该分成9组.故答案是:9.30.169【详解】试题解析由题意得:3m-3=1,n-1=1,解得:m=43,n=2,⊥m n=(43)2=169.故答案为169.31.52 5【分析】⊥根据“组数=(最大值-最小值)÷组距”计算,由于组数为整数,注意小数部分要进位;⊥由频数与总数的比为频率计算即可.【详解】⊥在样本数据中最大值为70,最小值为61,它们的差是7061=9-,已知组距为2,那么由于9=4.52,故可以分成5组.⊥在64.5~66.5这一小组的数为66、65、65、66、65、65、65、66,共8个,这一小组的频率为82 205=.故答案为:5;25.【点睛】本题主要考查数据的收集、整理与描述,解题关键是画频数分布直方图的一般步骤:计算最大值与最小值的差(极差),确定组距与组数,列频数分布表,画出频数分布直方图.32,1.103030030003…(两个3之间依次多一个0),π【分析】根据无理数的定义,“无限不循环的小数是无理数”逐个分析判断即可.【详解】解:在227,3.1415926,-83=,1.103030030003…(两个3之间依次多一个0),π中,227,3.1415926, -83=,1.103030030003…(两个3之间依次多一个0),π是无理数,1.103030030003…(两个3之间依次多一个0),π【点睛】本题考查了无理数,解答本题的关键掌握无理数的三种形式:⊥开方开不尽的数,⊥无限不循环小数,⊥含有π的数.33.23a ≤<【分析】根据题意,分别解不等式,根据不等式组的解只有4个整数解,可得021a ≤-<,解不等式组即可求解.【详解】解:解不等式235x -≤,得4x ≤,解不等式2x a -+<,得2x a >-,x 的不等式组只有4个整数解,1,2,3,4∴021a ≤-<解得23a ≤<故答案为:23a ≤<【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 34.(1)(4)【分析】根据平行线的性质以及对顶角的定义和点、线之间的关系分别判断得出即可.【详解】解:(1)对顶角相等,是真命题,(2)相等的角不一定是对顶角,故原命题不是真命题,(3)在同一平面内,垂直于同一条直线的两直线互相平行, 故原命题不是真命题, (4)平行于同一条直线的两直线互相平行,是真命题,(5)两直线平行,同位角相等,故原命题不是真命题,所以真命题的序号为(1)(4).故答案为:(1)(4)【点睛】本题主要考查了判断命题的真假,平行线的性质以及对顶角的定义和点、线之间的关系,熟练掌握相关知识点是解题的关键.35.12y <- 【分析】根据不等式的性质可得ba -2=,0a >,进而可得0b <,据此即可求解.【详解】解:⊥关于x 的不等式ax <-b 的解集x <2, ⊥b x a<-,b a -2=,0a >, 0b ∴<,∴关于y 的不等式by >a 的解集为a y b<, 2b a=-, ⊥1=2a b - ∴关于y 的不等式by >a 的解集为12y <-. 【点睛】本题考查了解一元一次不等式,确定a b ,的符号以及2b a=-是解题的关键. 36.(4,6),(﹣4,6),(﹣4,﹣6)或(4,﹣6).【分析】根据点到x 轴的距离是纵坐标的绝对值,点到y 轴的距离是横坐标的绝对值,即可得出答案.【详解】解:⊥点到x 轴的距离是6,到y 轴的距离是4,⊥该点的坐标是(4,6),(﹣4,6),(﹣4,﹣6)或(4,﹣6),故答案为:(4,6),(﹣4,6),(﹣4,﹣6)或(4,﹣6).【点睛】本题考查了点的坐标,利用点到x 轴的距离是纵坐标的绝对值,点到y 轴的距离是横坐标的绝对值是解题关键.37.49【分析】根据题意,结合平方根的性质列出方程,求解方程即可得到结论.【详解】解:一个正数的平方根有两个,且互为相反数,∴由一个正数的平方根分别是1x -+和2x +5,可知()()1250x x -+++=, 即60x +=,解得6x =-,∴()221749x -+==, 故答案为:49.【点睛】本题考查平方根的性质,根据题意列出方程求解是解决问题的关键. 38.x +3y =14【分析】用y 把t 表示出来,再利用代入消元法可得到x 与y 的关系式.【详解】解:234x t y t =+⎧⎨=-⎩①② 由⊥得:4,t y =-⊥()234,x y =+-整理得:314,x y +=故答案为:314+=x y39.64【详解】由二次根式有意义的条件得:x =3,⊥y =4,⊥yx =43=64,故答案为:6440的大小,进而求得,a b 的值,代入代数式即可求解.【详解】解:⊥12,12<<<,⊥1,1a b ==,2112a b ∴++=++=【点睛】本题考查了无理数的估算,求得,a b 的值是解题的关键.41.25°或50°【分析】根据平行线的性质以及垂直的定义即可求解.【详解】解:∵A ∠与B ∠的两边一边平行,另一边垂直,∴有两种情况,如下图所示:由题意得,AC∥BD,∠A=3∠B-10°,BC⊥AD ∵AC∥BD∴∠C=∠B∵BC⊥AD∴∠A+∠C=90°∴3∠B-10°+∠B=90°,∴∠B=25°如下图所示:由题意得,AN∥BM,∠A=3∠B-10°,BH⊥AM ⊥AN∥BM∴∠A+∠M=180°,∵BH⊥AM∴∠B+∠M=90°∴∠A-∠B=90°∵∠A=3∠B-10°3∠B﹣10°﹣∠B=90°,∴∠B=50°,综上所述,∠B的度数为25°或50°,故答案:25°或50°.【点睛】本题考查了平行线的性质,解题的关键是根据平行线的性质找出图中角度之间的关系.42.55或20【分析】根据平行线性质得出⊥A+⊥B=180°⊥,⊥A=⊥B⊥,求出⊥A=3⊥B﹣40°⊥,把⊥分别代入⊥⊥求出即可.【详解】解:⊥⊥A与⊥B的两边分别平行,⊥⊥A+⊥B=180°⊥,⊥A=⊥B⊥,⊥⊥A比⊥B的3倍少40°,⊥⊥A=3⊥B﹣40°⊥,把⊥代入⊥得:3⊥B﹣40°+⊥B=180°,⊥B=55°,把⊥代入⊥得:3⊥B﹣40°=⊥B,⊥B=20°,故答案为:55或20.【点睛】本题考查平行线的性质,解题的关键是掌握由⊥A和⊥B的两边分别平行,即可得⊥A=⊥B或⊥A+⊥B=180°,注意分类讨论思想的应用.43.2203或40°【分析】分两种情况讨论,即可求解.【详解】解:如图,⊥ADE=⊥BCE=90°,⊥⊥AED=⊥BEC,⊥⊥A=⊥B,⊥⊥A比⊥B的2倍少40°,即2⊥B-⊥A=40°,⊥2⊥A-⊥A=40°,解得:⊥A=40°,⊥⊥B=40°;如图,连接AB,⊥ADB=⊥ACB=90°,⊥⊥BAD+⊥ABD=90°,⊥BAC+⊥ABC=90°,⊥⊥CAD+⊥DBC=180°,⊥⊥CAD=180°-⊥CBD,⊥⊥CAD比⊥CBD的2倍少40°,即2⊥CBD-⊥CAD=40°,⊥2⊥CBD-(180°-⊥CBD)=40°,解得:2203 CBD;综上所述,⊥B的度数为2203或40°.故答案为:2203或40°【点睛】本题主要考查了余角的性质,三角形的内角和定理,利用分类讨论思想解答是解题的关键.44.(1(2)6;(3)x=±11;(4)x=3.【详解】试题分析:(1)原式去括号合并即可得到结果;(2)原式第一项利用乘方的意义化简,第二项利用绝对值的代数意义化简,最后一项利用算术平方根定义计算即可得到结果;(3)方程变形后,利用平方根定义开方即可求出解;(4)方程变形后,利用立方根定义开立方即可求出解.试题解析::(1)原式(2)原式=9-12+12-3=6;(3)方程变形得:x2=121,开方得:x=±11;(4)方程变形得:(x-5)3=-8,开立方得:x-5=-2,解得:x=3.45.1025 abc=⎧⎪=⎨⎪=-⎩【详解】试题分析:把11xy=⎧⎨=-⎩代入方程组,把26xy=⎧⎨=-⎩代入方程组中的第一个方程,即可得到一个关于a、b、c的方程组,解方程组即可求解.试题解析:根据题意得:832 268a bca b-⎧⎪+-⎨⎪-⎩===,解得:1025 abc=⎧⎪=⎨⎪=-⎩.46.3【详解】试题分析:先依据非负数的性质求得a、b、c的值,再求值即可.试题解析:⊥(2-a)2,⊥a=2,c=-8,b=4.⊥2x2+4x+8=0,⊥x2+2x=4⊥x2+2x﹣1=4-1=3.47.(1)11nm=⎧⎨=⎩;(2)﹣2<m≤32.【详解】试题分析:(1)根据题意列出关于m、n的方程组,求出m、n的值即可;(2)根据题意列出关于m的不等式组,求出m的取值范围即可.试题解析:(1)⊥m⊥n=1,m⊥2n=-2,⊥431462m nm n-⎧⎨--⎩==,解得11nm⎧⎨⎩==;(2)⊥m⊥2≤0,3m⊥(-8)>0,⊥46012240m m -≤⎧⎨+⎩> ,解得-2<m≤32. 点睛:解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则.48.2a -b【分析】由题意得,0a b c <<<,b c <,即0b a ->,0a b +<,0b c +>,根据绝对值的化简性质进行计算即可得.【详解】解:由题意得,0a b c <<<,b c <,⊥0b a ->,0a b +<,0b c +>,,⊥原式=()()()c b a a b b c --++-+=+c b a a b b c -++--=2a -b .【点睛】本题考查了数轴与实数,解题的关键是根据数轴得出各项符号,利用绝对值的化简性质.49.(1)32x =或12x =- (2)373x y =-⎧⎪⎨=-⎪⎩【分析】(1)利用平方根的定义解方程;(2)将方程组整理后,根据加减消元法解二元一次方程组即可求解.(1)解:2(21)4x -=,212x -=±, 解得32x =或12x =-; (2)1243231y x x y ++⎧=⎪⎨⎪-=⎩ 整理得345231y x x y -=⎧⎨-=⎩①②, ⊥+⊥得,26x -=,将3x =-,代入⊥得,()3435y -⨯-=, 解得73y =-,∴方程组的解为373x y =-⎧⎪⎨=-⎪⎩. 【点睛】本题考查了根据平方根解方程,加减消元法解二元一次方程组,正确的计算是解题的关键.50.(1)AE CF ,理由见解析(2)AD BC ∥,理由见解析(3)BC 不一定平分DBE ∠,理由见解析【分析】(1)先根据邻补角定义可得2180CDB ∠+∠=︒,从而可得1CDB ∠=∠,再根据平行线的判定即可得出结论;(2)先根据平行线的性质可得C CBE ∠=∠,从而可得A CBE ∠=∠,再根据平行线的判定即可得出结论;(3)先根据角平分线的定义可得CBD ABD ∠=∠,再根据平行线的性质可得CBE A ∠=∠,然后根据ABD ∠与A ∠不一定相等可得CBD ∠与CBE ∠不一定相等,由此即可得出结论.(1)解:AE CF ,理由如下:⊥12180,2180CDB ∠+∠=︒∠+∠=︒,⊥1CDB ∠=∠,⊥AE CF .(2)解:AD BC ∥,理由如下:⊥AE CF ,⊥C CBE ∠=∠,⊥A C ∠=∠,A CBE ∴∠=∠,⊥AD BC ∥.(3)解:BC 不一定平分DBE ∠,理由如下: DB 平分ABC ∠,CBD ABD ∴∠=∠,AD BC ∥,CBE A ∴∠=∠,ABD ∠与A ∠不一定相等,∴CBD ∠与CBE ∠不一定相等,BC ∴不一定平分DBE ∠.【点睛】本题考查了平行线的判断与性质、角平分线的定义,熟练掌握平行线的判定与性质是解题关键.51.该校七年级共有师生180人.【分析】设需租用36座客车x 辆,则该校七年级共有师生36x 人,根据“若只租用48座客车,则能比租36座的客车少租1辆,且有一辆车没有坐满,但超过了30人”,即可得出关于x 的一元一次不等式组,解之即可得出x 的取值范围,结合x 为整数即可确定x 的值,将其代入36x 中即可求出该校七年级共有师生人数.【详解】解:设需租用36座客车x 辆,则该校七年级共有师生36x 人,由题意得:()()3648230{36481x x x x -+-><, 解得:4112x <<, 又⊥x 为整数,⊥x =5,⊥36x =36×5=180,答:该校七年级共有师生180人.【点睛】本题考查了一元一次不等式组的应用,解题的关键是根据各数量之间的关系,正确列出一元一次不等式组.52.(1)111(3,1),(1,1),(4,2)A B C --(2)见解析(3)6(4)(0,-1.5)或(0,3.5)【分析】(1)根据平移的性质可得⊥ABC 先向右平移6个单位,再向下平移2个单位得到111A B C △,即可求解;(2)根据点111,,A B C 的坐标描点,即可求解;(3)用1AOA 所在的长方形的面积减去三个直角三角形的面积,即可求解;(4)设Q (0,t ),根据三角形的面积公式,即可求解.(1)解:⊥P (a ,b )的对应点为1(6,2)P a b +-.⊥⊥ABC 先向右平移6个单位,再向下平移2个单位得到111A B C △,⊥A (-3,3),B (-5,1),C (-2,0),⊥点111(3,1),(1,1),(4,2)A B C --;(2)解:如图,111A B C △即为所求;(3)解:1AOA 的面积11163333162222=⨯-⨯⨯-⨯⨯-⨯⨯ 9318622=--- =6(4)解:设Q (0,t ),⊥1(5,1),(3,1)B A -,⊥1BA x ∥轴,⊥13(5)8BA =--=,⊥1QBA 的面积为10, ⊥18|1|102t ⨯⨯-=, 解得t =-1.5或t =3.5,⊥Q 点的坐标为(0,-1.5)或(0,3.5).【点睛】本题考查了作图——平移变换:作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形. 53.(1)建成一套A 种户型住房所需的资金是9元,一套B 种户型住房所需的资金是13元(2)⊥100300x ≤≤;⊥410400W m =-+【分析】(1)设建成一套A 种户型住房所需的资金是a 元,一套B 种户型住房所需的资金是b 元,列出方程组即可解决问题.(2)⊥设A 种户型有x 套,则B 种户型有(800-x )套.列出不等式组即可解决问题.⊥根据总投入资金=建A 种户型的费用+建B 种户型的费用,即可解决问题.(1)解:设建成一套A 种户型住房所需的资金是a 元,一套B 种户型住房所需的资金是b 元,根据题意得:10304803010400a b a b +=⎧⎨+=⎩,解得:913a b =⎧⎨=⎩, 答:建成一套A 种户型住房所需的资金是9元,一套B 种户型住房所需的资金是13元; (2)解:⊥设A 种户型可以建x 套,则B 种户型可以建x 套,根据题意得:()()()238002100913800238007700x x x x x x ⎧+-≥⎪⎨⎡⎤+--+-≤⎪⎣⎦⎩, 解得:100300x ≤≤,答:A 种户型至少可以建100套,最多可以建300套;⊥根据题意得:913(800)410400W m m m =+-=-+,即W 与m 的关系式为410400W m =-+.【点睛】本题考查二元一次方程组、一元一次不等式组等知识,解题的关键是学会设未知数,构建方程组、不等式组解决问题,属于中考常考题型.54.(1)C (0,2),D (4,2),S 四边形ABCD =8;(2)存在,点P 的坐标为(0,4)或(0,-4);(3)结论⊥正确,DCQ BOQ CQO∠+∠∠=1. 【分析】(1)根据点平移的规律:左减右加,上加下减,即可得到点C 、D 的坐标,利用平行四边形的面积公式计算面积即可;(2)设点P 的坐标为(0,y ),根据三角形的面积公式底乘以高的一半列式计算即可得到答案;(3)结论⊥正确.过点Q 作QE ⊥AB ,交CO 于点E ,利用平行线的性质:两直线平行内。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年七年级下册数学经典易错题
一、填空题
1.一个数的平方等于它本身,这个数是 ;一个数的平方根等于它本身,这个数是 ;一个数的算术平方根等于它本身,这个数是 ;一个数的立方等于它本身,这个数是 ;一个数的立方根等于它本身,这个数是 ;一个数的倒数是它本身,这个数是 ;一个数的绝对值等于它本身,这个数是。
2.16的平方根为,,的平方根等于 .
3.已知 ; ,则。
4.已知一个正数的两个平方根分别为3x-5和x-7,则这个正数为 .
5. -1的整数部分为 ;小数部分为 ;绝对值为 ;相反数为 .
6. 如图,在数轴上,1,的对应点是A、B, A是
线段BC的中点,则点C所表示的数是。
7.已知,OAOC,且AOB:AOC=2:3,则BOC的度数为。
8.如果1=80,2的两边分别与1的两边平行,那么2= 。
9.已知点A(1+m,2m+1)在x轴上,则点A坐标为。
10.已知AB∥x轴,A点的坐标为(3,2),并且AB=5,则B的坐标为 .
11.点P(a-2,2a+3)到两坐标轴距离相等,则a= .
12.将点A(1,-3)向右平移2个单位,再向下平移2个单位后得到点B(a,b),则ab= .新课标第一网
13.已知平面直角坐标系内点P的坐标为(-1,3),如果将平面直角坐标系向左平移3个单位,再向下平移2个单位,那么平移后点P的坐标为________.
14.在平面直角坐标系中,已知A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P共有个。
15.点P(a+5,a)不可能在第象限。
16.平面直角坐标系内有一点P(x,y),满足,则点P在
17.方程在正整数范围内的解是_____ 。
18.已知x=1,y=﹣8是方程mx+y-1=0的解,则m的平方根是。
19.关于x的不等式(a+1)xa+1的解集为x1,那么a的取值范围是。
20.如果不等式2x-m0的正整数解有3个,则m的取值范围是。
21.一元一次不等式组的解集是xa,则a与b的关系是。
22.若不等式组无解,则m的取值范围是。
23.若不等式组解集是﹣1
24.如果不等式组的整数解有4个,则a的取值范围是。
25.若不等式2x4的解都能使关于x的一次不等式(a-1)x
26.某市出租车的收费标准是:起步价7元,超过3km时,每增加1km加收2.4元(不足1km按1km计).某人乘这种出租车从甲地到乙地共支付车费19元,设此人从甲地到乙地经过的路程是xkm,那么x的最大值是( ).
27.某种品牌的电脑的进价为5000元,按××局定价的9折销售时,利润不低于700元,则此电脑的定价最少为___________元(保留整数)。
28. 有一组数据共60个,最小的数为29,最大的数为98,现在需要做这组数据的频数分布直方图,假若把它们分成7组,则组距应该为。
29.如下图,为了解某新品种黄瓜的生长情况,抽查了部分黄瓜株上长出的黄瓜根数,得到下面的条形图,观察该图,可知共抽查了株黄瓜,并可估计出这个
新品种黄瓜平均每株结根黄瓜
30.下图是市××局公布的十五时期重庆市农村居民人均收入每年比上一年增长率的统计图,下列说法正确的有:
①2019年农村居民人均收入低于2019年;②农村居民人均收入比上年增长率低于9%的有2年;③农村居民人均收入最多时2019年;④农村居民人均收入每年比上一年的增长率有大有小,但农村居民人均收入在持续增加。
第29题图
第30题图
31.某养鱼塘专业户为了估计鱼塘鱼的总数,第一次捞出300条,将每条鱼做上记号后放入水中,当它们完全混于鱼群中后,又捞出200条鱼,发现带有记号的鱼有10条,问该养鱼专业户家的鱼塘中估计有鱼条。
再放入水中使其完全混于鱼群,第三次又捞出500条鱼,估计发现带有记号的鱼有条。
二、解答题:
1.解方程:2(1-x)2=18
2.当m为何值时,方程组的解x,y均为正数?
3.学校为家远的同学安排住宿,现有房间若干间,若每间住5人,则还有14人安排不下,若每间住7人,则有一间房不空也不满,问学校可能有几间房可以安排住宿?可能有多少学生住宿?
4.车站有待运的甲种货物1530吨,乙种货物1150吨,现计划用50节A,B两种型号的车厢将这批货物运至北京,已知每节A型车厢的运费是0.5万元,每节B 车厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨可装满一节B型车厢,按此要求安排A,B两种车厢的节数,共有几种方案?请你设计出来,并说明哪种方案的运费最少?
我国古代的读书人,从上学之日起,就日诵不辍,一般在几年内就能识记几千个汉字,熟记几百篇文章,写出的诗文也是字斟句酌,琅琅上口,成为满腹经纶的文人。
为什么在现代化教学的今天,我们念了十几年书的高中毕业生甚至大学生,竟提起作文就头疼,写不出像样的文章呢?吕叔湘先生早在1978年就尖锐地提
出:“中小学语文教学效果差,中学语文毕业生语文水平低,……十几年上课总时数是9160课时,语文是2749课时,恰好是30%,十年的时间,二千七百多课时,用来学本国语文,却是大多数不过关,岂非咄咄怪事!”寻根究底,其主要原因就是腹中无物。
特别是写议论文,初中水平以上的学生都知道议论文的“三要素”是论点、论据、论证,也通晓议论文的基本结构:提出问题――分析问题――解决问题,但真正动起笔来就犯难了。
知道“是这样”,就是讲不出“为什么”。
根本原因还是无“米”下“锅”。
于是便翻开作文集锦之类的书大段抄起来,抄人家的名言警句,抄人家的事例,不参考作文书就很难写出像样的文章。
所以,词汇贫乏、内容空洞、千篇一律便成了中学生作文的通病。
要解决这个问题,不能单在布局谋篇等写作技方面下功夫,必须认识到“死记硬背”的重要性,让学生积累足够的“米”。
5.图①、图②反映是某综合商场今年1-5月份的商品销售额统计情况.观察图①和图②,解答下面问题:
语文课本中的文章都是精选的比较优秀的文章,还有不少名家名篇。
如果有选择循序渐进地让学生背诵一些优秀篇目、精彩段落,对提高学生的水平会大有裨益。
现在,不少语文教师在分析课文时,把文章解体的支离破碎,总在文章的技巧方面下功夫。
结果教师费劲,学生头疼。
分析完之后,学生收效甚微,没过几天便忘的
一干二净。
造成这种事倍功半的尴尬局面的关键就是对文章读的不熟。
常言道“书读百遍,其义自见”,如果有目的、有计划地引导学生反复阅读课文,或细读、默读、跳读,或听读、范读、轮读、分角色朗读,学生便可以在读中自然领悟文章的思想内容和写作技巧,可以在读中自然加强语感,增强语言的感受力。
久而久之,这种思想内容、写作技巧和语感就会自然渗透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创造和发展。
(1)来自商场财务部的报告表明,商场1-5月份的销售总额一共是370万元,请你根据这一信息补全图①,并写出两条由上两图获得的信息;
教师范读的是阅读教学中不可缺少的部分,我常采用范读,让幼儿学习、模仿。
如领读,我读一句,让幼儿读一句,边读边记;第二通读,我大声读,我大声读,幼儿小声读,边学边仿;第三赏读,我借用录好配朗读磁带,一边放录音,一边幼儿反复倾听,在反复倾听中体验、品味。
(2)商场服装部5月份的销售额是多少万元?
(3)小华观察图②后认为,5月份服装部的销售额比4月份减少了.你同意他的看法吗?为什么?。
