2017届八年级1期末四科成绩分析 (2)
2017秋八上期末试卷质量分析

纳雍县新房彝族苗族乡以角小学2017年秋季学期八年级数学期末考试质量分析为了总结经验,吸取教训,取长补短,改进教学,提升质量,提高成绩,在全面评估2017—2018学年度第一学期期末质量检测八年级数学试卷、学生答题情况以及检测成绩后,做出如下报告剖析。
一、基本情况分析八年级三个班共有学生140人,八(1)班45人,八(2)班40人 ,八(3)班45人,缺考4人。
由于绝大部分学生学习基础较差,成绩参差不齐,多数又都是留守学生,且教师的辅导又不是很到位,导致低分人数多,少部分学生甚至连最简单的化简求值、作轴对称图都不会,平时的考试都是凭运气碰对选择题而得分。
本次考试满分150分。
三个班成绩统计二、试题分析本次考试试卷全卷分值150分,考试时间120分钟。
全卷共四道大题29道小题,包括15道单项选择题,5道填空题,4个计算题,5道解答题。
全卷试题题量融合量较大,难度适中,按7:2:1比例出题。
全面涉及到本学期教学的全部内容,重点考察实数、一次函数、二元一次方程组等。
试卷内容比较灵活多样,对基础知识、生活实践、看图做题等都有考察,尤其是把课本知识融入生活实践中的这类题型,最能体现素质教育,同时也强调了数学教学与现实生活的紧密联系。
三、学生答题情况分析班级 八(1) 八(2) 八(3) 班级人数 45 40 45 本次参加考试人数 44 37 44 优秀人数(120分及以上) 11 0 0 优秀率25% 0 0 及格人数(90分及以上) 25 0 0 及格率 56.81% 0 0 最高分 141 84 82 最低分44891、选择题每小题5分共60分,最高得分为55分,最低分为0分。
错误主要集中在题3、题4、题7、题11、题15上。
题3准确率较低的原因是学生没抓住“确定位置需要两个数据”这一知识点。
题4错误因是勾股定理的知识掌握不牢所致。
题7考察的是最简二次根式,类似于ba3是否是最简二次根式学生没有掌握好。
[精品]镇海区2017-2018学年八年级科学上学期期末考试试题 浙教版
![[精品]镇海区2017-2018学年八年级科学上学期期末考试试题 浙教版](https://img.taocdn.com/s3/m/eefbdf1983c4bb4cf7ecd17a.png)
浙江省镇海区2017-2018学年八年级科学上学期期末考试试题温馨提示:本试卷中g均取10N/kg.可能用到的相对原子质量:H-1 C-12 O-16 N-14一、选择题(本题共15小题,第1~10小题,每小题4分,第11~15小题,每小题3分,共55分。
请选出每小题中一个符合题意的选项,不选、错选均不给分。
)1. 为减少病人疼痛,手术前通常要给病人麻醉,有一种气体麻醉剂通过盖着口鼻的面罩传输给病人。
下列哪个系统不参与麻醉过程?A. 呼吸系统B. 消化系统C. 循环系统D. 神经系统2. 根据生物体的结构与功能相适应的观点,下列关于人体的说法错误的是A.心脏的心房和心室之间有房室瓣,防止血液倒流回心房B.肾小管壁薄且周围缠绕着大量的毛细血管,利于血液滤过形成原尿C.小肠内有胰液、肠液、胆汁等多种消化液,利于消化营养物质D.肺泡壁和毛细血管壁都由一层上皮细胞构成,利于进行气体交换3. 前段时间小明得到了两株相同的花卉幼苗,可她只有一只花盆和一只形状与花盆相同但底部没有小孔的塑料盆,于是她在两个盆里装上等量的同种适合该幼苗生长的泥土,把两株幼苗以相同的方式栽种并放置在合适的环境中,此后浇相等的水、肥料等。
结果一段时间后,种在花盆中的幼苗长得很好,而长在塑料盆中的幼苗长得越来越差。
塑料盆中的幼苗为什么长不好?可能是下列哪个原因造成的A.土壤缺少氧气,影响根的呼吸 B.植物缺少水,影响光合作用C.植物缺少无机盐,影响生长 D.气孔关闭,影响蒸腾作用4. 如图是双子叶植物叶表皮上的气孔。
气孔是氧气、二氧化碳出入及水分散失的门户。
当保卫细胞含水量多时气孔大,含水量少时气孔小甚至关闭。
下列叙述正确的是A.保卫细胞形状能改变是因为没有细胞壁B.植物体光合作用强弱与保卫细胞含水量无关C.蒸腾作用能带走叶片的部分热量,与水的汽化有关D.将叶片浸入浓盐水,气孔会逐渐增大5.一位农民种植的某块农田小麦产量总是比邻近地块的低。
17—18学年度第一学期七八年级期末质量分析报告
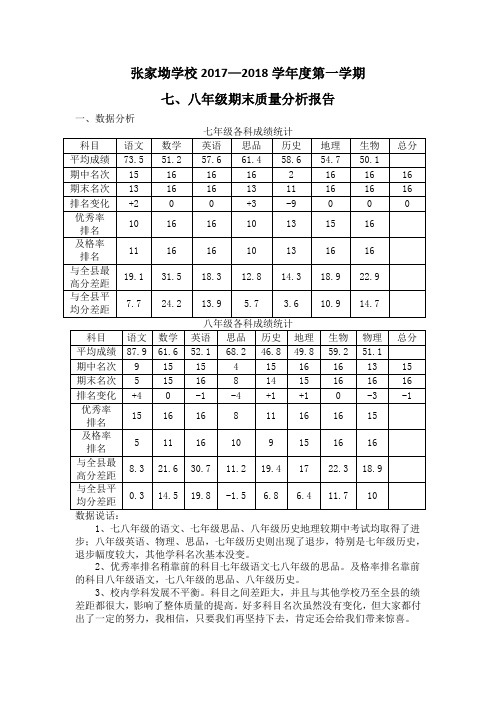
张家坳学校2017—2018学年度第一学期七、八年级期末质量分析报告一、数据分析1、七八年级的语文、七年级思品、八年级历史地理较期中考试均取得了进步;八年级英语、物理、思品,七年级历史则出现了退步,特别是七年级历史,退步幅度较大,其他学科名次基本没变。
2、优秀率排名稍靠前的科目七年级语文七八年级的思品。
及格率排名靠前的科目八年级语文,七八年级的思品、八年级历史。
3、校内学科发展不平衡。
科目之间差距大,并且与其他学校乃至全县的绩差距都很大,影响了整体质量的提高。
好多科目名次虽然没有变化,但大家都付出了一定的努力,我相信,只要我们再坚持下去,肯定还会给我们带来惊喜。
4、前五百名,七年级两人,八年级0人,501—1000名各3人,2000名以后七年级14人,八年级6人。
说明咱们在教学中对尖子生的关注与指导缺位,后进生比重较大。
后进生的转化方面还需多做努力。
实际上,从上学期到这学期,咱们每位老师一直都在努力,都在想方设法提高教学成绩。
除了要一如既往的努力外,我觉得还得在以下几个方面,加大力度:二、后期工作的几点建议1、控辍保学工作已经成为当前各项工作的终点,学生不流失是提高教学质量的前提。
所以咱们老师在工作中要注意方式方法,准确把握学生的思想动向,严防学生流失,特别是相对优秀的学生。
2、继续做好常规教学工作。
深入备课,认真上课,及时批改作业,不断反思总结教学经验。
多相互听课、评课,学习他人先进的教学经验和方法,全力提高教育教学水平。
3、要向课堂教学要效率,要质量。
课堂是学生学习的主阵地,要深入了解学生,想方设法在课堂教学中调动学生学习的积极性,使学生明确学习任务、目标、目的、意义,培养学生学习兴趣,树立信心,增强学习责任感与主人翁意识。
教学过程中要不断强化学生理想、前途教育,树立正确的学习观、人生观和价值观。
变“要我学”为“我要学”,让教学被动转化为主动,学生学起来,才能取得好的教学效果。
4、加强学法指导,提高学习效率。
八年级期末成绩分析会

八年级期末成绩分析会首先,对八年级期末成绩从班级、学科各率情况进行数据分析,并与其他八校各学科优秀及格平均分及两率进行数据比较,可以肯定地说,八年级期末成绩还是不错的,总成绩第四,比期中退了两个名次,但我们的语文、历史、英语、政治四科成绩较好。
1. 各备课组要严格集体备课,不仅关注备课内容,更要关注授课方法,要精选内容,合理设计授课方法。
不能一人备不研讨就上课现象发生,力求课堂教学有针对性,有实效性。
对资料的使用,要合理挑选习题,有目的性,避免大面积重复习题。
2.上好精品课,信托先学后教当堂训练的教学模式,突出学生主体地位,让学生多说,多做,多训练,教师要精讲,精点拨,要将知识讲透,方法讲活,低起点,小步子,大密度。
要让学生集中听讲,听讲时不做笔记,可给学生做笔记的时间。
3.作业要全批全改。
所有作业都要有书面作业。
政治历史地理生物学科不留课后作业,但不是不留作业,作业力争课上高质量完成。
语文数学英语物理作业要精选,适量,保障学生独立完成,巩固本天所学。
作业批改次数按常规要求执行。
4.课堂教学和自习课要候课,教师要早于学生到课堂,早晚自习更要早到课堂。
一是管理学生,避免学生出现意外事故,二是规范学生学习习惯,有些行为就是靠督才养成的。
5.班主任要加强班级管理,除加强常规管理外,重点要抓班级整体学习成绩,要抓好班级学科吻合,不能只顾自己所教学科,及时召开班级成绩分析会。
班级成绩分析会重点分析本班级在期末期初总体成绩在年级的位置,与其他班级的差距,学科的优势,学科的差距,确定本班级到其中考试的成绩目标及对标班级,帮助学生分析成绩,确立下一步努力目标及要达到的分数成绩和努力措施,要鼓励好学生,争取一步一个台阶地进步。
根据提出的具体目标提出具体要求。
并在以后工作中按提出的要求落实到位,严抓学生。
6.任课教师要管学生,要抓学生,特别是要抓学生成绩。
课堂上要管控好课堂纪律,注意学生的听课效率,要留给学生自主学习的时间,要有练习的时间。
初二考试成绩分析

初二考试成绩分析回回考试人相似,次次成绩不相同。
以下就是小编整理的初二考试成绩分析,一起来看看吧!儿子初二上学期期中考试于20xx年10月30日、20xx年11月1日两天举行,每天考四科,考试科目总共为八科。
八科成绩分别如下:语,82;数,86;英,93;理,97;政,88;史,90;地,83;生,92。
语数英理四科总分,358;平均分,89.5。
政史地生四科总分,353;平均分,88.25。
八科总分,711;八科平均分,88.875。
由于此次考试,语数英三科总分均为100分,故此次八科总分为800分,得分系数为八科平均分除以100,即:0.889。
从这个角度来讲,总体而言,此次考试对于儿子而言,是波澜微惊,桃花依旧。
这也再次证明,只要得分系数保持在0.9左右,考试成绩进入优秀之列,那是没有多大问题的。
最大的亮点:政治。
自进入初中起,至今为止的五次大型考试(期中、期末)中,此次政治是考得最好的一次,也是得分系数首次超过0.85。
这其中估计也有偶然因素的原因,但是,这段时间巩固课本知识点、加大案例分析训练以及拓展议论文阅读三点的功劳,也不可抹杀。
很显然,下一阶段,政治的学习还得在这三个方面着手,花工夫。
最有效的学习:物理、英语。
尽管此次物理成绩不是班里的唯一高分,但依然再次证明物理学习方法的有效,也就是在搞清弄透基本概念基本原理的基础上加大习题的投入。
下一阶段,继续发扬之,即可。
而且,此种学习方法完全可以也应该复制到数学学习上!此次英语考试,阅读题一分未丢,再次证明阅读训练的有效:在读懂读透的基础上做题,乃是高效的阅读训练法。
读懂读透为本,做题为末。
不能舍本求末。
但是,一个很好的提醒就是,此次英语考试前面的基本语法题,扣了三分。
这表明,对于包括句型转换之内的基本语法知识的掌握与运用还存在着不少欠缺。
这也再次提醒儿子,单纯地去掌握语法概念绝对是一种事倍功半的学习途径:毕竟英语不是母语,语言的积累还是太少。
人教版八年级(上)期末数学试卷+答案解析

2016-2017学年北京市海淀区八年级(上)期末数学试卷一.选择题(本大题共30分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的.请将正确选项前的字母填在表格中相应的位置.1.第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是()A.B.C.D.2.下列运算中正确的是()A.x2÷x8=x﹣4B.a•a2=a2C.(a3)2=a6D.(3a)3=9a33.石墨烯是从石墨材料中剥离出来,由碳原子组成的只有一层原子厚度的二维晶体.石墨烯(Graphene)是人类已知强度最高的物质,据科学家们测算,要施加55牛顿的压力才能使0.000001米长的石墨烯断裂.其中0.000001用科学记数法表示为()A.1×10﹣6 B.10×10﹣7C.0.1×10﹣5D.1×1064.在分式中x的取值范围是()A.x>﹣2 B.x<﹣2 C.x≠0 D.x≠﹣25.下列各式中,从左到右的变形是因式分解的是()A.2a2﹣2a+1=2a(a﹣1)+1 B.(x+y)(x﹣y)=x2﹣y2C.x2﹣6x+5=(x﹣5)(x﹣1)D.x2+y2=(x﹣y)2+2xy6.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是()A.AD=AE B.DB=AE C.DF=EF D.DB=EC7.下列各式中,计算正确的是()A.(15x2y﹣5xy2)÷5xy=3x﹣5y B.98×102==9996C. D.(3x+1)(x﹣2)=3x2+x﹣28.如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE 的度数是()A.62 B.31 C.28 D.259.在等边三角形ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在()A.△ABC的重心处 B.AD的中点处C.A点处D.D点处10.定义运算=,若a≠﹣1,b≠﹣1,则下列等式中不正确的是()A.×=1 B. +=C.()2=D.=1二.填空题(本大题共24分,每小题3分)11.如图△ABC,在图中作出边AB上的高CD.12.分解因式:x2y﹣4xy+4y=.13.写出点M(﹣2,3)关于x轴对称的点N的坐标.14.如果等腰三角形的两边长分别是4、8,那么它的周长是.15.计算:﹣4(a2b﹣1)2÷8ab2=.16.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A=°.17.教材中有如下一段文字:思考如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC,固定住长木棍,转动短木棍,得到△ABD,这个实验说明了什么?如图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.小明通过对上述问题的再思考,提出:两边分别相等且这两边中较大边所对的角相等的两个三角形全等.请你判断小明的说法.(填“正确”或“不正确”)18.如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.(1)判定△ABD与△AED全等的依据是;(2)∠ACB与∠ABC的数量关系为:.三.解答题(本大题共18分,第19题4分,第20题4分,第21题10分)19.分解因式:(a﹣4b)(a+b)+3ab.20.如图,DE∥BC,点A为DC的中点,点B,A,E共线,求证:DE=CB.21.解下列方程:(1)=;(2)﹣1=.四.解答题(本大题共14分,第22题4分,第23、24题各5分)22.已知a+b=2,求(+)•的值.23.如图,在等边三角形ABC的三边上,分别取点D,E,F,使得△DEF为等边三角形,求证:AD=BE=CF.24.列方程解应用题:老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约千米.然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.五.解答题(本大题共14分,第25、26题各7分)25.在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.26.钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.(1)若AB=AC,点E在AD延长线上.①当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=°,∠BEA=°;②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);(2)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.附加题:(本题最高10分,可计入总分,但全卷总分不超过100分)27.一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?(1)以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有条对称轴;(2)凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;(3)通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是:.2016-2017学年北京市海淀区八年级(上)期末数学试卷参考答案与试题解析一.选择题(本大题共30分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的.请将正确选项前的字母填在表格中相应的位置.1.第24届冬季奥林匹克运动会,将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行.在会徽的图案设计中,设计者常常利用对称性进行设计,下列四个图案是历届会徽图案上的一部份图形,其中不是轴对称图形的是()A.B.C.D.【考点】利用轴对称设计图案.【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.【解答】解:A、是轴对称图形,故此选项错误;B、是轴对称图形,故此选项错误;C、是轴对称图形,故此选项错误;D、不是轴对称图形,故此选项正确;故选:D.2.下列运算中正确的是()A.x2÷x8=x﹣4B.a•a2=a2C.(a3)2=a6D.(3a)3=9a3【考点】同底数幂的除法;同底数幂的乘法;幂的乘方与积的乘方;负整数指数幂.【分析】根据同底数幂相乘,底数不变指数相加;幂的乘方,底数不变指数相乘;同底数幂相除,底数不变指数相减,对各选项分析判断后利用排除法求解.【解答】解:A、底数不变指数相减,故A错误;B、底数不变指数相加,故B错误;C、底数不变指数相乘,故C正确;D、积的乘方等于乘方的积,故D错误;故选:C.3.石墨烯是从石墨材料中剥离出来,由碳原子组成的只有一层原子厚度的二维晶体.石墨烯(Graphene)是人类已知强度最高的物质,据科学家们测算,要施加55牛顿的压力才能使0.000001米长的石墨烯断裂.其中0.000001用科学记数法表示为()A.1×10﹣6 B.10×10﹣7C.0.1×10﹣5D.1×106【考点】科学记数法—表示较小的数.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【解答】解:0.000 001=1×10﹣6,故选A.4.在分式中x的取值范围是()A.x>﹣2 B.x<﹣2 C.x≠0 D.x≠﹣2【考点】分式有意义的条件.【分析】根据分式有意义的条件可得x+2≠0,再解即可.【解答】解:由题意得:x+2≠0,解得:x≠﹣2,故选:D.5.下列各式中,从左到右的变形是因式分解的是()A.2a2﹣2a+1=2a(a﹣1)+1 B.(x+y)(x﹣y)=x2﹣y2C.x2﹣6x+5=(x﹣5)(x﹣1)D.x2+y2=(x﹣y)2+2xy【考点】因式分解的意义.【分析】根据因式分解是将一个多项式转化为几个整式的乘积的形式,根据定义,逐项分析即可.【解答】解:A、2a2﹣2a+1=2a(a﹣1)+1,等号的右边不是整式的积的形式,故此选项不符合题意;B、(x+y)(x﹣y)=x2﹣y2,这是整式的乘法,故此选项不符合题意;C、x2﹣6x+5=(x﹣5)(x﹣1),是因式分解,故此选项符合题意;D、x2+y2=(x﹣y)2+2xy,等号的右边不是整式的积的形式,故此选项不符合题意;故选C.6.如图,已知△ABE≌△ACD,下列选项中不能被证明的等式是()A.AD=AE B.DB=AE C.DF=EF D.DB=EC【考点】全等三角形的性质.【分析】根据全等三角形的性质可得到AD=AE、AB=AC,则可得到BD=CE,∠B=∠C,则可证明△BDF≌△CEF,可得DF=EF,可求得答案.【解答】解:∵△ABE≌△ACD,∴AB=AC,AD=AE,∠B=∠C,故A正确;∴AB﹣AD=AC﹣AE,即BD=EC,故D正确;在△BDF和△CEF中∴△BDF≌△CEF(ASA),∴DF=EF,故C正确;故选B.7.下列各式中,计算正确的是()A.(15x2y﹣5xy2)÷5xy=3x﹣5y B.98×102==9996C. D.(3x+1)(x﹣2)=3x2+x﹣2【考点】分式的加减法;多项式乘多项式;平方差公式;整式的除法.【分析】根据分式的加减法,整式的除法,多项式乘多项式的运算方法和平方差公式,逐项判断即可.【解答】解:∵(15x2y﹣5xy2)÷5xy=3x﹣y,∴选项A不正确;∵98×102==9996,∴选项B正确;∵﹣1=﹣,∴选项C不正确;∵(3x+1)(x﹣2)=3x2﹣5x﹣2,∴选项D不正确.故选:B.8.如图,∠D=∠C=90°,E是DC的中点,AE平分∠DAB,∠DEA=28°,则∠ABE 的度数是()A.62 B.31 C.28 D.25【考点】平行线的判定与性质;角平分线的定义.【分析】过点E作EF⊥AB于F,根据角平分线上的点到角的两边距离相等可得DE=EF,根据线段中点的定义可得DE=CE,然后求出CE=EF,再根据到角的两边距离相等的点在角的平分线上证明即可得出BE平分∠ABC,最后求得∠ABE的度数.【解答】解:如图,过点E作EF⊥AB于F,∵∠D=∠C=90°,AE平分∠DAB,∴DE=EF,∵E是DC的中点,∴DE=CE,∴CE=EF,又∵∠C=90°,∴点E在∠ABC的平分线上,∴BE平分∠ABC,又∵AD∥BC,∴∠ABC+∠BAD=180°,∴∠AEB=90°,∴∠BEC=90°﹣∠AED=62°,∴Rt△BCE中,∠CBE=28°,∴∠ABE=28°.故选:C.9.在等边三角形ABC中,D,E分别是BC,AC的中点,点P是线段AD上的一个动点,当△PCE的周长最小时,P点的位置在()A.△ABC的重心处 B.AD的中点处C.A点处D.D点处【考点】三角形的重心;等边三角形的性质;轴对称﹣最短路线问题.【分析】连接BP,根据等边三角形的性质得到AD是BC的垂直平分线,根据三角形的周长公式、两点之间线段最短解答即可.【解答】解:连接BP,∵△ABC是等边三角形,D是BC的中点,∴AD是BC的垂直平分线,∴PB=PC,△PCE的周长=EC+EP+PC=EC+EP+BP,当B、E、E在同一直线上时,△PCE的周长最小,∵BE为中线,∴点P为△ABC的重心,故选:A.10.定义运算=,若a≠﹣1,b≠﹣1,则下列等式中不正确的是()A.×=1 B. +=C.()2=D.=1【考点】分式的混合运算.【分析】根据定义:=,一一计算即可判断.【解答】解:A、正确.∵=,=.∴×=×=1.B、错误. +=+=.C、正确.∵()2=()2==.D、正确.==1.故选B.二.填空题(本大题共24分,每小题3分)11.如图△ABC,在图中作出边AB上的高CD.【考点】作图—基本作图.【分析】过点C作BA的延长线于点D即可.【解答】解:如图所示,CD即为所求.12.分解因式:x2y﹣4xy+4y=y(x﹣2)2.【考点】提公因式法与公式法的综合运用.【分析】先提取公因式y,再对余下的多项式利用完全平方公式继续分解.【解答】解:x2y﹣4xy+4y,=y(x2﹣4x+4),=y(x﹣2)2.13.写出点M(﹣2,3)关于x轴对称的点N的坐标(﹣2,﹣3).【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可以直接写出答案.【解答】解:∵M(﹣2,3),∴关于x轴对称的点N的坐标(﹣2,﹣3).故答案为:(﹣2,﹣3)14.如果等腰三角形的两边长分别是4、8,那么它的周长是20.【考点】等腰三角形的性质;三角形三边关系.【分析】解决本题要注意分为两种情况4为底或8为底,还要考虑到各种情况是否满足三角形的三边关系来进行解答.【解答】解:∵等腰三角形有两边分别分别是4和8,∴此题有两种情况:①4为底边,那么8就是腰,则等腰三角形的周长为4+8+8=20,②8底边,那么4是腰,4+4=8,所以不能围成三角形应舍去.∴该等腰三角形的周长为20,故答案为:2015.计算:﹣4(a2b﹣1)2÷8ab2=﹣.【考点】整式的除法;幂的乘方与积的乘方;负整数指数幂.【分析】原式利用幂的乘方与积的乘方运算法则,以及整式的除法法则计算即可得到结果.【解答】解:原式=﹣4a4b﹣2÷8ab2=﹣2a3b﹣4=﹣,故答案为:﹣16.如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于D点.若BD平分∠ABC,则∠A=36°.【考点】等腰三角形的性质;线段垂直平分线的性质.【分析】根据线段垂直平分线上的点到两端点的距离相等可得AD=BD,根据等边对等角可得∠A=∠ABD,然后表示出∠ABC,再根据等腰三角形两底角相等可得∠C=∠ABC,然后根据三角形的内角和定理列出方程求解即可.【解答】解:∵AB=AC,∴∠C=∠ABC,∵AB的垂直平分线MN交AC于D点.∴∠A=∠ABD,∵BD平分∠ABC,∴∠ABD=∠DBC,∴∠C=2∠A=∠ABC,设∠A为x,可得:x+x+x+2x=180°,解得:x=36°,故答案为:3617.教材中有如下一段文字:思考如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC,固定住长木棍,转动短木棍,得到△ABD,这个实验说明了什么?如图中的△ABC与△ABD满足两边和其中一边的对角分别相等,即AB=AB,AC=AD,∠B=∠B,但△ABC与△ABD不全等.这说明,有两边和其中一边的对角分别相等的两个三角形不一定全等.小明通过对上述问题的再思考,提出:两边分别相等且这两边中较大边所对的角相等的两个三角形全等.请你判断小明的说法正确.(填“正确”或“不正确”)【考点】全等三角形的判定.【分析】小明的说法正确.如图,△ABC和△DEF中,AB>AC,ED>DF,AB=DE,AC=DF,∠ACB=∠DFE,作AG⊥BC于G,DH⊥EF于H.首先证明△ACG≌△DFH,推出AG=DH,再证明△ABG≌△DEH,推出∠B=∠E,由此即可证明△ABC≌△DEF.【解答】解:小明的说法正确.理由:如图,△ABC和△DEF中,AB>AC,ED>DF,AB=DE,AC=DF,∠ACB=∠DFE,作AG⊥BC于G,DH⊥EF于H.∵∠ACB=∠DFE,∴∠ACG=∠DFH,在△ACG和△DFH中,,∴△ACG≌△DFH,∴AG=DH,在Rt△ABG和Rt△DEH中,,∴△ABG≌△DEH,∴∠B=∠E,在△ABC和△DEF中,,∴△ABC≌△DEF.(当△ABC和△DEF是锐角三角形时,证明方法类似).故答案为正确.18.如图1,△ABC中,AD是∠BAC的平分线,若AB=AC+CD,那么∠ACB与∠ABC有怎样的数量关系?小明通过观察分析,形成了如下解题思路:如图2,延长AC到E,使CE=CD,连接DE.由AB=AC+CD,可得AE=AB.又因为AD是∠BAC的平分线,可得△ABD≌△AED,进一步分析就可以得到∠ACB与∠ABC的数量关系.(1)判定△ABD与△AED全等的依据是SAS;(2)∠ACB与∠ABC的数量关系为:∠ACB=2∠ABC.【考点】等腰三角形的性质;全等三角形的判定.【分析】(1)根据已知条件即可得到结论;(2)根据全等三角形的性质和等腰三角形的性质即可得到结论.【解答】解:(1)SAS;(2)∵△ABD≌△AED,∴∠B=∠E,∵CD=CE,∴∠CDE=∠E,∴∠ACB=2∠E,∴∠ACB=2∠ABC.故答案为:SAS,∠ACB=2∠ABC.三.解答题(本大题共18分,第19题4分,第20题4分,第21题10分)19.分解因式:(a﹣4b)(a+b)+3ab.【考点】因式分解﹣运用公式法.【分析】原式整理后,利用平方差公式分解即可.【解答】解:原式=a2﹣3ab﹣4b2+3ab=a2﹣4b2=(a﹣2b)(a+2b).20.如图,DE∥BC,点A为DC的中点,点B,A,E共线,求证:DE=CB.【考点】全等三角形的判定与性质.【分析】欲证明DE=CB,只要证明△ADE≌△ACB即可.【解答】证明:∵DE∥BC,∴∠D=∠C,∠E=∠B.∵点A为DC的中点,∴DA=CA.在△ADE和△ACB中,,∴△ADE≌△ACB.∴DE=CB.21.解下列方程:(1)=;(2)﹣1=.【考点】解分式方程.【分析】两分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.【解答】解:(1)去分母得:5x+2=3x,解得:x=﹣1,经检验x=﹣1是增根,原方程无解;(2)去分母得:x(x﹣2)﹣(x+2)(x﹣2)=x+2,解得:x=,经检验x=是分式方程的解.四.解答题(本大题共14分,第22题4分,第23、24题各5分)22.已知a+b=2,求(+)•的值.【考点】分式的化简求值.【分析】先化简题目中的式子,然后将a+b的值代入化简后的式子即可解答本题.【解答】解:===,当a+b=2时,原式=.23.如图,在等边三角形ABC的三边上,分别取点D,E,F,使得△DEF为等边三角形,求证:AD=BE=CF.【考点】全等三角形的判定与性质;等边三角形的判定与性质.【分析】只要证明△ADF≌△BED,得AD=BE,同理可证:BE=CF,由此即可证明.【解答】解:在等边三角形ABC中,∠A=∠B=60°.∴∠AFD+∠ADF=120°.∵△DEF为等边三角形,∴∠FDE=60°,DF=ED.∵∠BDE+∠EDF+∠ADF=180°,∴∠BDE+∠ADF=120°.∴∠BDE=∠AFD.在△ADF和△BED中,,∴△ADF≌△BED.∴AD=BE,同理可证:BE=CF.∴AD=BE=CF.24.列方程解应用题:老舍先生曾说“天堂是什么样子,我不晓得,但从我的生活经验去判断,北平之秋便是天堂.”(摘自《住的梦》)金黄色的银杏叶为北京的秋增色不少.小宇家附近新修了一段公路,他想给市政写信,建议在路的两边种上银杏树.他先让爸爸开车驶过这段公路,发现速度为60千米/小时,走了约3分钟,由此估算这段路长约3千米.然后小宇查阅资料,得知银杏为落叶大乔木,成年银杏树树冠直径可达8米.小宇计划从路的起点开始,每a米种一棵树,绘制示意图如下:考虑到投入资金的限制,他设计了另一种方案,将原计划的a扩大一倍,则路的两侧共计减少200棵树,请你求出a的值.【考点】分式方程的应用.【分析】根据题意列出分式方程进行解答即可.【解答】解:这段路长约60×=3千米;由题意可得:.解方程得:a=15.经检验:a=15满足题意.答:a的值是15.故答案为:3五.解答题(本大题共14分,第25、26题各7分)25.在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:(1)非等边的等腰三角形有1条对称轴,非正方形的长方形有2条对称轴,等边三角形有3条对称轴;(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.【考点】四边形综合题;等腰三角形的性质;等边三角形的性质;矩形的性质;轴对称图形.【分析】(1)根据等腰三角形的性质、矩形的性质以及等边三角形的性质进行判断即可;(2)中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,在图1﹣4和图1﹣5中,分别仿照类似的修改方式进行画图即可;(3)长方形具有两条对称轴,在长方形的右侧补出与左侧一样的图形,即可构造出一个恰好有2条对称轴的凸六边形;(4)在等边三角形的基础上加以修改,即可得到恰好有3条对称轴的凸六边形.【解答】解:(1)非等边的等腰三角形有1条对称轴,非正方形的长方形有2条对称轴,等边三角形有3条对称轴,故答案为:1,2,3;(2)恰好有1条对称轴的凸五边形如图中所示.(3)恰好有2条对称轴的凸六边形如图所示.(4)恰好有3条对称轴的凸六边形如图所示.26.钝角三角形ABC中,∠BAC>90°,∠ACB=α,∠ABC=β,过点A的直线l交BC边于点D.点E在直线l上,且BC=BE.(1)若AB=AC,点E在AD延长线上.①当α=30°,点D恰好为BE中点时,补全图1,直接写出∠BAE=60°,∠BEA= 30°;②如图2,若∠BAE=2α,求∠BEA的度数(用含α的代数式表示);(2)如图3,若AB<AC,∠BEA的度数与(1)中②的结论相同,直接写出∠BAE,α,β满足的数量关系.【考点】全等三角形的判定与性质.【分析】(1)①只要证明AE⊥BC,△BCE是等边三角形即可解决问题.②如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN ⊥AE于N.只要证明Rt△BMF≌Rt△BNE,推出∠BEA=∠F,由BF=BC,推出∠F=∠C=α,推出∠BEA=α即可.(2)如图3中,连接EC,由△ADC∽△BDE,推出=,推出=,由∠ADB=∠CDE,推出△ADB∽△CDE,推出∠BAD=∠DCE,∠ABD=∠DEC=β,由BC=BE,推出∠BCE=∠BEC,推出∠BAE=∠BEC=∠BEA+∠DEC=α+β.【解答】解:(1)①补全图1,如图所示.∵AB=AC,BD=DC,∴AE⊥BC,∴EB=EC,∠ADB=90°,∵∠ABC=30°,∴∠BAE=60°∵BC=BE,∴△BCE是等边三角形,∠DEB=∠DEC,∴∠BEC=60°,∠BEA=30°故答案为60,30.②如图2中,延长CA到F,使得BF=BC,则BF=BE=BC,连接BF,作BM⊥AF于M,BN⊥AE于N.∵AB=AC,∴∠ABC=∠C=α,∴∠MAB=2α,∵∠BAN=2α,∴∠BAM=∠BAN,∴BM=BN,在Rt△BMF和Rt△BNE中,,∴Rt△BMF≌Rt△BNE.∴∠BEA=∠F,∵BF=BC,∴∠F=∠C=α,∴∠BEA=α.(2)结论:∠BAE=α+β.理由如下,如图3中,连接EC,∵∠ACD=∠BED=α,∠ADC=∠BDE,∴△ADC∽△BDE,∴=,∴=,∵∠ADB=∠CDE,∴△ADB∽△CDE,∴∠BAD=∠DCE,∠ABD=∠DEC=β,∵BC=BE,∴∠BCE=∠BEC,∴∠BAE=∠BEC=∠BEA+∠DEC=α+β.附加题:(本题最高10分,可计入总分,但全卷总分不超过100分)27.一个多边形如果是轴对称图形,那么它的边数与对称轴的条数之间存在联系吗?(1)以凸六边形为例,如果这个凸六边形是轴对称图形,那么它可能有1,2,3或6条对称轴;(2)凸五边形可以恰好有两条对称轴吗?如果存在请画出图形,并用虚线标出两条对称轴;否则,请说明理由;(3)通过对(1)中凸六边形的研究,请大胆猜想,一个凸多边形如果是轴对称图形,那么它的边数与对称轴的条数之间的联系是:对称轴的条数是多边形边数的约数.【考点】作图﹣轴对称变换.【分析】(1)根据凸六边形进行画图,然后猜想即可;(2)根据题意画出图形,再结合轴对称图形的定义进行分析即可;(3)根据(1)中所得的数据可得答案.【解答】解:(1)凸六边形是轴对称图形,那么它可能有1,2,3或6条对称轴,故答案为:1,2,3或6;(2)不可以.理由如下:根据轴对称图形的定义,若一个凸多边形是轴对称图形,则对称轴与多边形的交点是多边形的顶点或一条边的中点.若多边形的边数是奇数,则对称轴必经过一个顶点和一条边的中点.如图1,设凸五边形ABCDE是轴对称图形,恰好有两条对称轴l1,l2,其中l1经过A和CD的中点.若l2⊥l1,则l2与五边形ABCDE的两个交点关于l1对称,与对称轴必经过一个顶点和一条边的中点矛盾;若l2不垂直于l1,则l2关于l1的对称直线也是五边形ABCDE的对称轴,与恰好有两条对称轴矛盾.所以,凸五边形不可以恰好有两条对称轴.(3)对称轴的条数是多边形边数的约数.2017年3月17日。
初二学生期末成绩分析总结与反思

初二学生期末成绩分析总结与反思初二学生期末成绩分析总结与反思(通用5篇)在我们平凡的日常里,教学是我们的工作之一,所谓反思就是能够迅速从一个场景和事态中抽身出来,看自己在前一个场景和事态中自己的表现。
反思我们应该怎么写呢?下面是店铺帮大家整理的初二学生期末成绩分析总结与反思(通用5篇),供大家参考借鉴,希望可以帮助到有需要的朋友。
初二学生期末成绩分析总结与反思1本次考试完全采用中考模式,卷面分为150,其中选择题14分,非选择题136分。
语文均分121.2,其中农村班级差4.6分,城区班级差5.1分,稍稍超过允许值范围。
130以上人数159人,农村班较多的是6、5、4、8班,城区班较多的是20、17、10班。
试卷最高分为5班宋媛媛140分,最低分李向阳仅有73分。
试题内容基本围绕命题申报表,着重考查学生的双基与能力,现代文阅读选取较好,有助于学生分析水平的提升。
由于不少题目直接来源《同步导学》,各班重视程度不一,因而分差也超过允许值范围。
下面就试卷内容做简要分析:首先选择题,难度不是太大,各班正确率都接近30%。
稍有难度的当数第5题文学常识。
其实这一题不难,只是选项D内容超出教材范围,属于七年级知识点,学生早已淡忘。
正如我问一个学生,选项C明显错误,你为何还选择D?他的回答是:C是错误,但我觉得D也错,我认为《故乡》不是小说。
这是什么逻辑?好笑,这说明我们不少孩子基础知识还不够牢固,在做选择题时存有连猜带蒙的意识。
非选择题,失分率较高的分别是:第9题找出病句,并加以改正;第14题在选文中找出“其”解释与其它不同的句子,如果这一题表述再明确些,学生也不会出现如此高的失误率。
比如,这里的选文,是指甲呢,还是指乙呢?还是两个都指?我个人认为命题者不妨作出明确描述。
第15题第2句翻译,学生不理解“令”“初”“爱”的意思,因而翻译也是牛头不对马嘴,让人啼笑皆非。
现代文阅读,说明文《迎接氢能时代的到来》错误率不是太高。
八年级上学期期末考试结果分析

八年级上学期期末考试结果分析背景八年级上学期期末考试是对学生在这一学期研究成果的一次总结和评估。
为了了解学生的研究情况,分析考试结果是必要的。
考试成绩概况本次期末考试共涉及各科目的考试,包括语文、数学、英语、物理、化学、历史和地理。
下面是各科目的考试成绩概况:- 语文:95- 数学:82- 英语:89- 物理:78- 化学:92- 历史:88- 地理:85考试成绩分析从以上的考试成绩概况来看,各科目的平均成绩都较为理想。
其中语文、化学和历史的平均成绩明显高于其他科目,分别达到了95、92和88分,说明学生在这些科目上取得了较好的成绩。
然而,数学和物理的平均成绩相对较低,分别为82和78分。
这可能意味着学生在数学和物理方面的研究有待加强,有必要进一步关注和辅导学生在这两门科目上的研究。
另外,英语和地理的平均成绩居中,分别为89和85分。
学生成绩差异分析除了平均成绩,还需要注意学生成绩之间的差异。
部分学生的成绩可能与平均水平有较大的差距,这需要找出原因并提供相应的指导和辅导。
下一步措施基于以上的考试结果分析,以下是下一步可行的措施和建议:1. 针对数学和物理成绩较低的学生,开设专门的辅导课程,提供额外的研究资源和辅导指导,帮助他们提高这两门科目的成绩。
2. 对于英语和地理成绩居中的学生,提供更多的研究支持和资源,以帮助他们进一步巩固知识,提升成绩水平。
3. 对于语文、化学和历史成绩较好的学生,鼓励他们继续保持良好的研究状态,并提供更多的挑战性研究机会,以满足他们的需要。
4. 定期进行学生研究情况的跟踪和评估,及时发现问题并采取相应的措施。
以上是八年级上学期期末考试结果的分析和相应的措施建议,希望能为学生的学习进步提供有效的指导和支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
140911张海晨78797869304 163429王浦丞77629768304 11586王霄鹏85699157302 6795赵馨雨83598573300 11313程自立76639665300 117517周晓蕾98705379300 177212潘佳喜926210145300 104515王茜85548179299 11199林崴80866666298 166340李香亿89489665298 190531杨超颖95529259298 8867李宁蒙88478973297 95106王静茹89578368297 9827张钰婷76669758297 12028邢恩豪83658366297 14714马旭86529564297 8173金泽93657068296 134336李佳慧865410056296 76512刘斌斌85787359295 162915胡俊宁76846372295 220345徐若璞83548968294 1501011马婷婷89608361293 152338丁同胜82707368293 1891012裴璟珺89678948293 97327马天龙954110254292 132522王蔚宇83687962292 108330周其越82767459291 179916金雪儿75599859291 159211李全智贤81589754290 6465党安琪90498664289 93326赵王心奕71559070286 129521都彦钦82658355285 13978王君87599643285 156427沈宇轩81835071285 103108李晓青79737755284 170431安欣雨86697353281 109516于赵宁80449066280
330631钱佳琪75193939172 336722薛宇轩66352744172 357634郝澜琪71204536172 362228马海霞70196122172 377731付文聪79213537172 3291023张安琪76263534171 381231折波67343039170 257114唐嘉文82113937169 313827刘欣宇67113457169 387834师超64432041168 343723卢林伟78263033167 364636周鼎鲜60196028167 3851029张银霜75283133167 318630王鹏程65155135166 378230李露晨6886822166 319125金生祥70223636164 348724张运星72363620164 372728王嘉硕65343233164 394835石佳琦55363142164 263442吴占琪57443032163 3001018张浩7426954163 365454李媛67223835162 322828杨玲76174127161 369638乔世豪65382929161 305448王禹桐70312732160 363635祁智刚70244224160 400455郭嘉怡59403526160 306449马帅63323925159 350131董希文61283832159 286117裴玉伟77242828157 333830张宇航59362636157 370549徐佳72174424157 3281022张馨雨67282932156 340930王亦凡77122740156 383134马欣宇71183136156 388135秦嘉辰58243538155 397640杨一博52331951155。
