勾股定理整理 - 360文档中心

勾股定理公式表,勾股定理公式及证明方法

勾股定理公式表,勾股定理公式及证明方法1、勾股计算公式是什么勾股定理公式的计算是a2 b2c2。

设一个直角三角形的两边分别为a和b，斜边为c，关于勾股定理的知识点我整理过了。

让我们一起学习。

定理定义了任意平面直角三角形中两个直角的平方和必等于斜边的平方。

在△abc，∠ c90，则a bc。

勾股定理简介勾股定理是一个基本的几何定理。

在中国，周弼舒静记载勾股定理公式并证明是商代的商高发现的。

三国时期的姜明祖在姜明祖的计算中对勾股定理做了详细的注释，并给出了另一种证明。

也就是说，设一个直角三角形的两个直角为a和b，斜边为c，那么a bc。

勾股定理大约有400个证明，是数学定理中证明最多的一个。

赵双在他的注解《周髀算经》中给出了“赵双仙图”，证明了勾股定理，勾股数组是a bc的正整数群(a，b，c)。

(3，4，5)是毕达哥拉斯数。

2、勾股定理常用11个公式是什么?勾股定理常用公式就一个，即a的平方加上b的平方等于c的平方，如果一个直角三角形的两边分别是a和b，斜边是c，那么公式就是:a bc。

勾股定理是一个基本几何定理。

它是用代数思想解决几何问题的最重要的工具之一，也是联系数与形的纽带之一。

勾股定理:如果一个三角形的三条边a，b，c满足a bc，那么这个三角形是直角三角形，其中c是斜边。

勾股定理常用公式就一个，就是a的平方加上b的平方等于c 的平方，如果一个直角三角形的两边分别是a和b，斜边是c，那么公式就是:a bc。

勾股定理是一个基本几何定理。

它是用代数思想解决几何问题的最重要的工具之一，也是联系数与形的纽带之一。

勾股定理:如果一个三角形的三条边a，b，c满足a bc，那么这个三角形是直角三角形，其中c是斜边。

3、勾股定理公式大全及证明方法勾股定理是一个基本的几何定理，意思是直角三角形的两条右边的平方和等于斜边的平方。

接下来给大家分享一下勾股定理公式，以及证明方法。

勾股定理of公式basic公式在平面上的直角三角形中，两个直角边的平方加起来就是斜边长度的平方。

六年级勾股定理知识点归纳

六年级勾股定理知识点归纳勾股定理是数学中的基础定理，也是学习几何学的重要内容之一。

在六年级数学中，学生将进一步学习和应用勾股定理，深入理解三角形的性质和关系。

本文将对六年级勾股定理的知识点进行归纳和总结。

1. 勾股定理的表述勾股定理又称毕达哥拉斯定理，是指：在直角三角形中，直角边的平方之和等于斜边的平方。

可以用数学语言来表示为：设直角三角形的两条直角边的长度分别为a、b，斜边的长度为c，则有a² + b² = c²。

2. 勾股定理的应用勾股定理可以应用在解决与直角三角形相关的问题中。

一些常见的应用包括：- 通过已知两条直角边的长度求解斜边的长度。

- 判断一个三角形是否为直角三角形，只需验证是否满足勾股定理。

- 利用勾股定理计算建筑物的高度、距离等。

3. 勾股定理的证明勾股定理有多种证明方法，这里简单介绍一种基于几何的证明方法：设直角三角形ABC，其中∠B为直角，边AC为斜边，两直角边分别为AB和BC。

首先，我们将三角形ABC平移使得BC边与原点重合。

此时，点C的坐标为(0,0)，点A的坐标为(a,0)，点B的坐标为(0,b)。

然后，我们通过计算两个向量的内积来证明勾股定理。

向量AB可以表示为(-a,b)，向量AC可以表示为(a,0)。

根据向量的内积公式，有：AB·AC = (-a,b)·(a,0) = -a²。

又因为AB与AC垂直，所以AB与AC的内积为0，即AB·AC = 0。

综上所述：-a² = 0，即a² = b² + (a-b)² = b² + a² - 2ab + b² = a² + b²- 2ab。

整理得：a² + b² = c²。

证明完成。

4. 勾股定理的推广勾股定理不仅适用于直角三角形，还可推广到其他形状的三角形中。

勾股定理、方根专题知识点整理

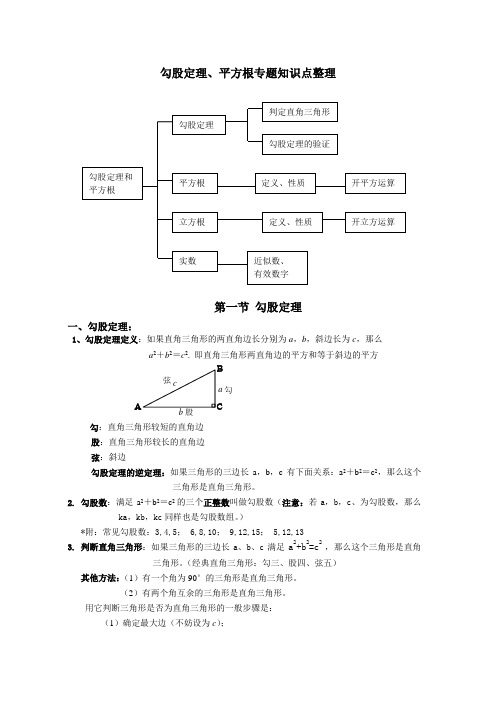
勾股定理、平方根专题知识点整理第一节勾股定理一、勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。

2. 勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）*附：常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,133. 判断直角三角形：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c 2＝a 2＋b 2，则△ABC 是以∠C 为直角的三角形；若a 2＋b 2＜c 2，则此三角形为钝角三角形（其中c 为最大边）；若a 2＋b 2＞c 2，则此三角形为锐角三角形（其中c 为最大边）4.注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

5. 勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n 的线段二、平方根：（11——19的平方）1、平方根定义：如果一个数的平方等于a ，那么这个数就叫做a 的平方根。

勾股定理详解

勾股定理详解勾股定理定义及公式勾股定理是一个基本几何定理，是人类早期发现并证明的重要数学定理之一，用代数思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

勾股定理是余弦定理的一个特例。

勾股定理约有400种证明方法，是数学定理中证明方法最多的定理之一。

“勾三股四弦五”是勾股定理最基本的公式。

勾股数组程a²+ b²= c²的正整数组(a,b,c)。

(3,4,5)就是勾股数。

也就是说，设直角三角形两直角边为a和b，斜边为c，那a²+b²=c²。

勾股定理逆定理勾股定理的逆定理是判断三角形为锐角或钝角的一个简单的方法。

若c为最长边，且a²+b²=c²，则△ABC是直角三角形。

如果a²+b²>c²，则△ABC是锐角三角形。

如果a²+b²<c²，则△ABC是钝角三角形。

勾股定理的证明据不完全统计，勾股定理的证明方法已经多达400多种了。

下面我便向大家介绍几种十分著名的证明方法。

【证法1】赵爽“勾股圆方图”第一种方法：边长为c的正方形可以看作是由4个直角边分别为a、b，斜边为c的直角三角形围在外面形成的。

因为边长为的正方形面积加上4个直角三角形的面积等于外围正方形的面积，所以可以列出等式，化简得。

第二种方法：边长为c的正方形可以看作是由4个直角边分别为a、b，斜边为c的角三角形拼接形成的（虚线表示），不过中间缺出一个边长为(b-a)的正方形“小洞”。

因为边长为的正方形面积等于4个直角三角形的面积加上正方形“小洞”的面积，所以可以列出等式，化简得。

这种证明方法很简明，很直观，它表现了我国古代数学家赵爽高超的证题思想和对数学的钻研精神，是我们中华民族的骄傲。

【证法2】课本的证明做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b，所以面积相等. 即a²+b²+4×1/2ab=c²+4×1/2ab，整理得a²+b²=c²【证法3】1876年美国总统Garfield证明以a、b 为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于2/1ab. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵RtΔEAD ≌RtΔCBE,∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠DEC = 180º―90º= 90º.∴ΔDEC是一个等腰直角三角形，它的面积等于1/2c².又∵∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形，它的面积等于1/2(a+b)².∴1/2(a+b)²=2×1/2ab+1/2c².∴a²+b²=c².【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。

勾股定理笔记整理

勾股定理（又称毕达哥拉斯定理）是数学中著名的定理，它表明了直角三角形的三条边满足特定的关系。

以下是勾股定理的基本概念及相关内容的笔记整理：
一、勾股定理基本概念
1. 直角三角形：一个三角形中有一个内角为$90^\circ$，则这个三角形就是直角三角形。

2. 直角：一个内角为$90^\circ$ 的角。

3. 斜边：直角三角形中，斜边是直角对边的边，即斜边是与直角相对的边。

4. 短边和长边：直角三角形中，直角旁边的两条边叫做短边和长边。

长边位于直角对面，短边则位于直角旁边。

二、勾股定理的表述
直角三角形的斜边的平方等于直角边的平方之和。

即若以$a$、$b$、$c$ 表示直角三角形三边的长度（其中$c$ 表示斜边），则有：
$c^2 = a^2 + b^2$
或者：
$a^2 + b^2 = c^2$
根据勾股定理，如果知道直角三角形的两个直角边长度，可以通过计算求出斜边的长度；如果知道直角三角形的斜边长度和一个直角边的长度，也可以通过计算求出另一个直角边的长度。

三、勾股定理的应用
勾股定理是数学中非常重要的定理，在其它学科中也有着广泛的应用。

1. 建筑学：在建筑设计中，利用勾股定理可以计算建筑中的空间尺寸和角度大小。

2. 物理学：在物理学中，勾股定理经常被用来处理运动和力学问题。

3. 统计学：在统计学中，勾股定理可以用来计算概率分布函数。

4. 计算机图形学：在计算机图形学中，勾股定理可以用来确定图像的位置和大小。

综上所述，勾股定理是一条十分重要的数学定理，在生活、工作和学习中具有着广泛的应用。

勾3股4弦5怎么实际运用

勾3股4弦5怎么实际运用勾三股四弦五的原理(勾3股4弦5是勾股定理的一个特例),本文通过数据整理汇集了勾三股四弦五的原理(勾3股4弦5是勾股定理的一个特例)相关信息，下面一起看看。

欧老师上课说，我来讲，你学。

一：勾股定理1.勾股定理：当一个三角形是直角三角形时，有:斜边的平方等于两条直角边的平方之和。

c=a b例如：勾股定理：比如在直角三角形ABC，a，b中，两边都是直角，C是斜边；甲、乙、丙有如下关系。

c=a b两个直角的平方和等于斜边的平方。

二：勾股定理的逆定理勾股定理逆定理：如果三角形的三条边相交：c=a b那么这个三角形就是直角三角形。

例如：勾股定理逆定理：如果知道三角形中的三条边满足以下条件：c=a b那么能相对的三角形就是直角三角形。

三：挂钩股份的数量如果，三个符合c=a b的数称为一组勾股数，比如3，4，5；5、12、13等。

所以，像3，4，5这样的数字是一组毕达哥拉斯数。

四：勾股定理的实际应用1.下列几组数字中，不属于股票的是()甲：3，4，5乙：6，8，10丙：12，16，20丁：32，42，52解析：满足c=a b的一组数叫做毕达哥拉斯数。

2.图为一棵美丽的毕达哥拉斯树，其中所有四边形都是正方形，所有三角形都是直角三角形。

如果正方形A、B、C和D的面积分别是5、7、3和5，那么最大的正方形E的面积是()甲：108乙：50第20天第12天解析：勾股定理的应用。

因此：ab=fc d=gf g=e因为：A，B，C，D，E，F，G都是正方形。

是a的面积。

b是b的面积。

c是c的面积。

d是d的面积。

f是f的面积。

g是g的面积。

面积的相加，所以是勾股定理的实际运算。

总结:勾股定理主要是关于三角形内角的理解。

一般的计算主要集中在角点之间的关系。

同时，对于角点，有时会巧妙地运用勾股定理的逆定理。

这个网站是个人知识管理的网络存储空间。

所有内容均由用户发布，不代表本网站观点。

请注意甄别内容中的联系方式、诱导购买等信息，谨防诈骗。

勾股定理(毕达哥拉斯定理)及各种证明方法

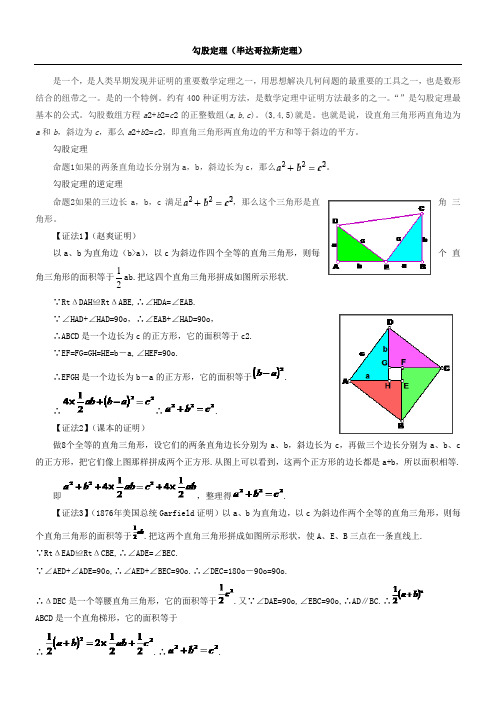
勾股定理（毕达哥拉斯定理）是一个，是人类早期发现并证明的重要数学定理之一，用思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

是的一个特例。

约有400种证明方法，是数学定理中证明方法最多的之一。

“”是勾股定理最基本的公式。

勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。

(3,4,5)就是。

也就是说，设直角三角形两直角边为a 和b ，斜边为c ，那么a 2+b 2=c 2，即直角三角形两直角边的平方和等于斜边的平方。

勾股定理命题1如果的两条直角边长分别为a ，b ，斜边长为c ，那么。

勾股定理的逆定理命题2如果的三边长a ，b ，c 满足，那么这个三角形是直角三角形。

【证法1】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于21ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90o，∴∠EAB+∠HAD=90o，∴ABCD 是一个边长为c 的正方形，它的面积等于c2.∵EF=FG=GH=HE=b―a,∠HEF=90o.∴EFGH 是一个边长为b―a 的正方形，它的面积等于.∴∴.【证法2】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a+b ，所以面积相等.即，整理得.【证法3】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状，使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC.∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o.∴ΔDEC 是一个等腰直角三角形，它的面积等于.又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ABCD 是一个直角梯形，它的面积等于 ∴.∴.【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。

中考备考：数学勾股定理常用的11个公式

【导语】勾股定理是中学数学中⽐较难的部分，下⾯，为⼤家整理⼀下初中数学勾股定理常⽤的11个公式，希望能帮到⼤家。

1、常见的勾股数及⼏种通式有 (1)(3,4,5),(6,8,10)…… 3n,4n,5n(n是正整数) (2)(5,12,13),(7,24,25),(9,40,41)…… 2n+1,2n^2+2n,2n^2+2n+1(n是正整数) (3)(8,15,17),(12,35,37)…… ^2*(n+1),[2(n+1)]^2-1,[2(n+1)]^2+1(n是正整数) (4)m^2-n^2,2mn,m^2+n^2(m、n均是正整数,m>n) 2、勾股定理常见知识点 1、过两点有且只有⼀条直线 2、两点之间线段最短 3、同⾓或等⾓的补⾓相等 4、同⾓或等⾓的余⾓相等 5、过⼀点有且只有⼀条直线和已知直线垂直 6、直线外⼀点与直线上各点连接的所有线段中，垂线段最短 7、平⾏公理经过直线外⼀点，有且只有⼀条直线与这条直线平⾏ 8、如果两条直线都和第三条直线平⾏，这两条直线也互相平⾏ 9、同位⾓相等，两直线平⾏ 10、内错⾓相等，两直线平⾏ 11、同旁内⾓互补，两直线平⾏ 12、两直线平⾏，同位⾓相等 13、两直线平⾏，内错⾓相等 14、两直线平⾏，同旁内⾓互补 15、定理三⾓形两边的和⼤于第三边 16、推论三⾓形两边的差⼩于第三边 17、三⾓形内⾓和定理三⾓形三个内⾓的和等于180" 18、推论1直⾓三⾓形的两个锐⾓互余 19、推论2三⾓形的⼀个外⾓等于和它不相邻的两个内⾓的和 20、推论3三⾓形的⼀个外⾓⼤于任何⼀个和它不相邻的内⾓ 3、勾股定理内容直⾓三⾓形(等腰直⾓三⾓形也算在内)两直⾓边(即“勾”“股”短的为勾，长的为股)边长平⽅和等于斜边(即“弦”)边长的平⽅。

也就是说设直⾓三⾓形两直⾓边为a和b，斜边为c，那么a的平⽅+b的平⽅=c的平⽅a2+b2=c2。

勾股定理现发现约有500种证明⽅法，是数学定理中证明⽅法最多的定理之⼀。

超全勾股定理公式大全

超全勾股定理公式大全我们知道，如果∠C=90°，a 、b 、c 是直角三角形的三边，则由勾股定理，得a 2+b 2=c 2；反之，若三角形的三边a 、b 、c 满足a 2+b 2=c 2，则该三角形是直角三角形，c 为斜边．与此相类似，如果三个正整数a 、b 、c 满足a 2+b 2=c 2，则称a 、b 、c 为勾股数，记为（a ，b ，c ）．勾股数有无数多组，下面向同学们介绍几种：一、三数为连续整数的勾股数（3，4，5）是我们所熟悉的一组三数为连续整数的勾股数，除此之外是否还有第二组或更多组呢？设三数为连续整数的勾股数组为（x －１，x ，x ＋１），则由勾股数的定义，得（x+1）2+x 2=（x+1）2，解得x ＝４或x ＝０（舍去），故三数为连续整数的勾股数只有一组（３，４，５）；类似有3n,4n,5n(n是正整数)都是勾股数。

二、后两数为连续整数的勾股数易知：（５，１２，１３），（９，４０，４１），（１１３，６３３８，６３８５），…，都是勾股数，如此许许多多的后两数为连续整数的勾股数，它的一般形式究竟是什么呢？ a=2n+1,b=2n 2+2n,c=2n 2+2n+1（其特点是斜边与其中一股的差为1）.分别取n ＝１，２，３，…就得勾股数组（３，４，５），（５，１２，１３），（７，２４，２５），…三、前两数为连续整数的勾股数你知道（２０，２１，２９），（１１９，１２０，１６９），（４０５９，４０６０，５７４１）…，这些都是前两数为连续整数的勾股数组。

其公式为：（x ，x ＋１，1222++x x ）（x 为正整数）。

设前两数为连续整数的勾股数组为（x ，x ＋１，y ），y=1222++x x 则()2221y x x =++（＊）整理，得1222++x x ＝2y ，化为()121222-=-+y x ，即()y x 212++()y x 212-+＝－１，又()()2121-+＝－１，∴()1221++n ()1221+-n ＝－１（ｎ∈Ｎ），故取()y x 212++＝()1221++n ，()y x 212-+＝()1221+-n ，解之，得x ＝41〔()1221++n ＋()1221+-n －２〕，y ＝42〔()1221++n －()1221+-n 〕，故前两数为连续整数的勾股数组是（41〔()1221++n ＋()1221+-n －２〕，41〔()1221++n ＋()1221+-n －２〕＋１，42〔()1221++n －()1221+-n 〕）．四、后两数为连续奇数的勾股数如(8，15，17),(12，35，37)…其公式为：4(n+1),4(n+1)2-1,4(n+1)2+1(n 是正整数). 五、其它的勾股数组公式：1.a=2m,b=m 2－1,c=m 2+1（m 大于1的整数）.2.a=21（m 2－n 2）,b=mn,c=21（m 2+n 2）（其中m>n 且是互质的奇数）.3.a=2m,b=m 2－n 2,c=m 2+n 2（m>n,互质且一奇一偶的任意正整数）.下面我们把100以内的勾股数组列出来，供同学们参考：34 5；512 13；6810；72425；81517；9 1215；940 41；102426；116061；12 16 20；12 35 37；13 84 85；14 48 50；15 20 25；15 36 39；15112 113；16 30 34；1663 6517144 145；18 24 30；18 80 82；19 180 181；20 21 29；20 48 52；20 99 101；21 28 3521 72 75；21 220 221；22 120 122；23 264 265；24 32 40；24 45 51；24 70 74；24143 14525 60 65；25 312 313；26 168 170；27 36 45；27120 123；27 364 365；28 45 53；2896 10028 195 197；29 420 421；30 40 50；30 72 78；30 224 226；31 480 481；32 60 68；32126 13032 255 257；33 44 55；33 56 65；33 180 183；33 544 545；34 288 290；35 84 91；35120 12535 612 613；36 48 60；36 77 85；36 105 111；36 160 164；36 323 325；37 684 685；38 360 36239 52 65；39 80 89；39 252 255；39 760 761；40 42 58；40 75 85；40 96 104；40 198 20240 399 401；41 840 841；42 56 70；42 144 150；42 440 442；43 924 925；44 117 125；44 240 24444 483 485；45 60 75；45 108 117；45 200 205；45 336 339；46 528 530；48 55 73；4864 8048 90 102；48 140 148；48 189 195；48 286 290；48 575 577；49 168 175；50 120 130；50 624 62651 68 85；51 140 149；51 432 435；52 165 173；52 336 340；52 675 677；54 72 90；54240 24654 728 730；55 132 143；55 300 305；56 90 106；56 105 119；56 192 200；56 390 394；56 783 78557 76 95；57176 185；57 540 543；58 840 842；60 63 87；60 80 100；60 91 109；60 144 15660 175 185；60 221 229；60 297 303；60 448 452；60 899 901；62 960 962；63 84 105；63 216 22563 280 287；63 660 663；64 120 136；64 252 260；64 510 514；65 72 97；65 156 169；65 420 42566 88 110；66 112 130；66 360 366；68 285 293；68 576 580；69 92 115；69 260 269；69 792 79570 168 182；70 240 250；72 96 120；72 135 153；72 154 170；72 210 222；72 320 328；72 429 43572 646 650；75 100 125；75 180 195；75 308 317；75 560 565；75 936 939；76 357 365；76 720 72477 264 275；77 420 427；78 104 130；78 160 178；78 504 510；80 84 116；80 150 170；80 192 20880 315 325；80 396 404；80 798 802；81 108 135；81 360 369；84 112 140；84 135 159；84 187 20584 245 259；84 288 300；84 437 445；84 585 591；84 880 884；85 132 157；85 204 221；85 720 72587 116 145；87 416 425；88 105 137；88 165 187；88 234 250；88 480 488；88 966 970；90 120 15090 216 234；90 400 410；90 672 678；91 312 325；91 588 595；92 525 533；93 124 155；93 476 48595 168 193；95 228 247；95 900 905；96 110 146；96 128 160；96 180 204；96 247 265；96 280 29696 378 390；96 572 580；96 765 771；98 336 350；99 132 165；99 168 195；99 440 451；99 540 549100 105 145；100240260；100 495 505；100621629.以下是大于100的勾股数：第223组：102 136 170第224组：102 280 298第225组：102 864 870第226组：104 153 185第227组：104 195 221第228组：104 330 346第229组：104 672 680第230组：105 140 175第231组：105 208 233第232组：105 252 273第233组：105 360 375第234组：105 608 617第235组：105 784 791第236组：108 144 180第237组：108 231 255第238组：108 315 333第239组：108 480 492第240组：108 725 733第241组：108 969 975第242组：110 264 286第243组：110 600 610第244组：111 148 185第245组：111 680 689第246组：112 180 212第247组：112 210 238第248组：112 384 400第249组：112 441 455第250组：112 780 788第251组：114 152 190第252组：114 352 370第253组：115 252 277第254组：115 276 299第256组：117 156 195 第257组：117 240 267 第258组：117 520 533 第259组：117 756 765 第260组：119 120 169 第261组：119 408 425 第262组：120 126 174 第263组：120 160 200 第264组：120 182 218 第265组：120 209 241 第266组：120 225 255 第267组：120 288 312 第268组：120 350 370 第269组：120 391 409 第270组：120 442 458 第271组：120 594 606 第272组：120 715 725 第273组：120 896 904 第274组：121 660 671 第275组：123 164 205 第276组：123 836 845 第277组：124 957 965 第278组：125 300 325 第279组：126 168 210 第280组：126 432 450 第281组：126 560 574 第282组：128 240 272 第283组：128 504 520 第284组：129 172 215 第285组：129 920 929 第286组：130 144 194 第287组：130 312 338 第288组：130 840 850 第289组：132 176 220 第290组：132 224 260 第291组：132 351 375 第292组：132 385 407 第293组：132 475 493 第294组：132 720 732 第295组：133 156 205 第296组：133 456 475 第297组：135 180 225 第298组：135 324 351第300组：135 600 615 第301组：136 255 289 第302组：136 273 305 第303组：136 570 586 第304组：138 184 230 第305组：138 520 538 第306组：140 147 203 第307组：140 171 221 第308组：140 225 265 第309组：140 336 364 第310组：140 480 500 第311组：140 693 707 第312组：140 975 985 第313组：141 188 235 第314组：143 780 793 第315组：143 924 935 第316组：144 165 219 第317组：144 192 240 第318组：144 270 306 第319组：144 308 340 第320组：144 420 444 第321组：144 567 585 第322组：144 640 656 第323组：144 858 870 第324组：145 348 377 第325组：145 408 433 第326组：147 196 245 第327组：147 504 525 第328组：150 200 250 第329组：150 360 390 第330组：150 616 634 第331组：152 285 323 第332组：152 345 377 第333组：152 714 730 第334组：153 204 255 第335组：153 420 447 第336组：153 680 697 第337组：154 528 550 第338组：154 840 854 第339组：155 372 403 第340组：155 468 493 第341组：156 208 260 第342组：156 320 356第343组：156 455 481 第344组：156 495 519 第345组：156 667 685 第346组：159 212 265 第347组：160 168 232 第348组：160 231 281 第349组：160 300 340 第350组：160 384 416 第351组：160 630 650 第352组：160 792 808 第353组：161 240 289 第354组：161 552 575 第355组：162 216 270 第356组：162 720 738 第357组：165 220 275 第358组：165 280 325 第359组：165 396 429 第360组：165 532 557 第361组：165 900 915 第362组：168 224 280 第363组：168 270 318 第364组：168 315 357 第365组：168 374 410 第366组：168 425 457 第367组：168 490 518 第368组：168 576 600 第369组：168 775 793 第370组：168 874 890 第371组：170 264 314 第372组：170 408 442 第373组：171 228 285 第374组：171 528 555 第375组：171 760 779 第376组：174 232 290 第377组：174 832 850 第378组：175 288 337 第379组：175 420 455 第380组：175 600 625 第381组：176 210 274 第382组：176 330 374 第383组：176 468 500 第384组：176 693 715 第385组：176 960 976 第386组：177 236 295第388组：180 240 300 第389组：180 273 327 第390组：180 299 349 第391组：180 385 425 第392组：180 432 468 第393组：180 525 555 第394组：180 663 687 第395组：180 800 820 第396组：180 891 909 第397组：182 624 650 第398组：183 244 305 第399组：184 345 391 第400组：184 513 545 第401组：185 444 481 第402组：185 672 697 第403组：186 248 310 第404组：186 952 970 第405组：189 252 315 第406组：189 340 389 第407组：189 648 675 第408组：189 840 861 第409组：190 336 386 第410组：190 456 494 第411组：192 220 292 第412组：192 256 320 第413组：192 360 408 第414组：192 494 530 第415组：192 560 592 第416组：192 756 780 第417组：195 216 291 第418组：195 260 325 第419组：195 400 445 第420组：195 468 507 第421组：195 748 773 第422组：196 315 371 第423组：196 672 700 第424组：198 264 330 第425组：198 336 390 第426组：198 880 902 第427组：200 210 290 第428组：200 375 425 第429组：200 480 520 第430组：200 609 641第432组：203 396 445 第433组：203 696 725 第434组：204 253 325 第435组：204 272 340 第436组：204 560 596 第437组：204 595 629 第438组：204 855 879 第439组：205 492 533 第440组：205 828 853 第441组：207 224 305 第442组：207 276 345 第443组：207 780 807 第444组：207 920 943 第445组：208 306 370 第446组：208 390 442 第447组：208 660 692 第448组：208 819 845 第449组：210 280 350 第450组：210 416 466 第451组：210 504 546 第452组：210 720 750 第453组：213 284 355 第454组：215 516 559 第455组：215 912 937 第456组：216 288 360 第457组：216 405 459 第458组：216 462 510 第459组：216 630 666 第460组：216 713 745 第461组：216 960 984 第462组：217 456 505 第463组：217 744 775 第464组：219 292 365 第465组：220 231 319 第466组：220 459 509 第467组：220 528 572 第468组：220 585 625 第469组：222 296 370 第470组：224 360 424 第471组：224 420 476 第472组：224 768 800 第473组：224 882 910 第474组：225 272 353第476组：225 540 585 第477组：225 924 951 第478组：228 304 380 第479组：228 325 397 第480组：228 665 703 第481组：228 704 740 第482组：230 504 554 第483组：230 552 598 第484组：231 308 385 第485组：231 392 455 第486组：231 520 569 第487组：231 792 825 第488组：232 435 493 第489组：232 825 857 第490组：234 312 390 第491组：234 480 534 第492组：235 564 611 第493组：237 316 395 第494组：238 240 338 第495组：238 816 850 第496组：240 252 348 第497组：240 275 365 第498组：240 320 400 第499组：240 364 436 第500组：240 418 482 第501组：240 450 510 第502组：240 551 601 第503组：240 576 624 第504组：240 700 740 第505组：240 782 818 第506组：240 884 916 第507组：240 945 975 第508组：243 324 405 第509组：245 588 637 第510组：245 840 875 第511组：246 328 410 第512组：248 465 527 第513组：248 945 977 第514组：249 332 415 第515组：250 600 650 第516组：252 275 373 第517组：252 336 420 第518组：252 405 477第519组：252 539 595 第520组：252 561 615 第521组：252 735 777 第522组：252 864 900 第523组：255 340 425 第524组：255 396 471 第525组：255 612 663 第526组：255 700 745 第527组：256 480 544 第528组：258 344 430 第529组：259 660 709 第530组：259 888 925 第531组：260 273 377 第532组：260 288 388 第533组：260 624 676 第534组：260 651 701 第535组：260 825 865 第536组：261 348 435 第537组：261 380 461 第538组：264 315 411 第539组：264 352 440 第540组：264 448 520 第541组：264 495 561 第542组：264 702 750 第543组：264 770 814 第544组：264 950 986 第545组：265 636 689 第546组：266 312 410 第547组：266 912 950 第548组：267 356 445 第549组：270 360 450 第550组：270 648 702 第551组：270 704 754 第552组：272 510 578 第553组：272 546 610 第554组：273 364 455 第555组：273 560 623 第556组：273 736 785 第557组：273 936 975 第558组：275 660 715 第559组：276 368 460 第560组：276 493 565 第561组：276 805 851 第562组：279 372 465第564组：280 294 406 第565组：280 342 442 第566组：280 351 449 第567组：280 450 530 第568组：280 525 595 第569组：280 672 728 第570组：280 759 809 第571组：280 960 1000 第572组：282 376 470 第573组：285 380 475 第574组：285 504 579 第575组：285 684 741 第576组：285 880 925 第577组：287 816 865 第578组：288 330 438 第579组：288 384 480 第580组：288 540 612 第581组：288 616 680 第582组：288 741 795 第583组：288 840 888 第584组：290 696 754 第585组：290 816 866 第586组：291 388 485 第587组：294 392 490 第588组：295 708 767 第589组：296 555 629 第590组：297 304 425 第591组：297 396 495 第592组：297 504 585 第593组：300 315 435 第594组：300 400 500 第595组：300 455 545 第596组：300 589 661 第597组：300 720 780 第598组：300 875 925 第599组：301 900 949 第600组：303 404 505 第601组：304 570 646 第602组：304 690 754 第603组：305 732 793 第604组：306 408 510 第605组：306 840 894 第606组：308 435 533第608组：308 819 875 第609组：309 412 515 第610组：310 744 806 第611组：310 936 986 第612组：312 416 520 第613组：312 459 555 第614组：312 585 663 第615组：312 640 712 第616组：312 910 962 第617组：315 420 525 第618组：315 572 653 第619组：315 624 699 第620组：315 756 819 第621组：318 424 530 第622组：319 360 481 第623组：320 336 464 第624组：320 462 562 第625组：320 600 680 第626组：320 768 832 第627组：321 428 535 第628组：322 480 578 第629组：324 432 540 第630组：324 693 765 第631组：324 945 999 第632组：325 360 485 第633组：325 780 845 第634组：327 436 545 第635组：328 615 697 第636组：330 440 550 第637组：330 560 650 第638组：330 792 858 第639组：333 444 555 第640组：333 644 725 第641组：335 804 871 第642组：336 377 505 第643组：336 385 511 第644组：336 448 560 第645组：336 527 625 第646组：336 540 636 第647组：336 630 714 第648组：336 748 820 第649组：336 850 914 第650组：339 452 565第652组：340 528 628 第653组：340 816 884 第654组：341 420 541 第655组：342 456 570 第656组：344 645 731 第657组：345 460 575 第658组：345 756 831 第659组：345 828 897 第660组：348 464 580 第661组：348 805 877 第662组：350 576 674 第663组：350 840 910 第664组：351 468 585 第665组：351 720 801 第666组：352 420 548 第667组：352 660 748 第668组：352 936 1000 第669组：354 472 590 第670组：355 852 923 第671组：357 360 507 第672组：357 476 595 第673组：360 378 522 第674组：360 480 600 第675组：360 546 654 第676组：360 598 698 第677组：360 627 723 第678组：360 675 765 第679组：360 770 850 第680组：360 864 936 第681组：363 484 605 第682组：363 616 715 第683组：364 585 689 第684组：364 627 725 第685组：365 876 949 第686组：366 488 610 第687组：368 465 593 第688组：368 690 782 第689组：369 492 615 第690组：369 800 881 第691组：370 888 962 第692组：372 496 620 第693组：372 925 997 第694组：375 500 625第696组：376 705 799 第697组：378 504 630 第698组：378 680 778 第699组：380 399 551 第700组：380 672 772 第701组：380 912 988 第702组：381 508 635 第703组：384 440 584 第704组：384 512 640 第705组：384 720 816 第706组：385 552 673 第707组：387 516 645 第708组：387 884 965 第709组：390 432 582 第710组：390 520 650 第711组：390 800 890 第712组：392 630 742 第713组：392 735 833 第714组：393 524 655 第715组：396 403 565 第716组：396 528 660 第717组：396 672 780 第718组：396 847 935 第719组：399 468 615 第720组：399 532 665 第721组：400 420 580 第722组：400 561 689 第723组：400 750 850 第724组：402 536 670 第725组：405 540 675 第726组：406 792 890 第727组：407 624 745 第728组：408 506 650 第729组：408 544 680 第730组：408 765 867 第731组：408 819 915 第732组：411 548 685 第733组：414 448 610 第734组：414 552 690 第735组：416 612 740 第736组：416 780 884 第737组：417 556 695 第738组：420 441 609第740组：420 560 700 第741组：420 637 763 第742组：420 675 795 第743组：420 832 932 第744组：420 851 949 第745组：423 564 705 第746组：424 795 901 第747组：425 660 785 第748组：426 568 710 第749组：429 460 629 第750组：429 572 715 第751组：429 700 821 第752组：429 728 845 第753组：429 880 979 第754组：432 495 657 第755组：432 576 720 第756组：432 665 793 第757组：432 810 918 第758组：435 580 725 第759组：438 584 730 第760组：440 462 638 第761组：440 525 685 第762组：440 825 935 第763组：441 588 735 第764组：444 592 740 第765组：447 596 745 第766组：448 720 848 第767组：448 840 952 第768组：450 544 706 第769组：450 600 750 第770组：451 780 901 第771组：453 604 755 第772组：455 504 679 第773组：455 528 697 第774组：456 608 760 第775组：456 650 794 第776组：456 855 969 第777组：459 612 765 第778组：460 483 667 第779组：462 616 770 第780组：462 784 910 第781组：464 777 905 第782组：464 870 986第784组：468 595 757 第785组：468 624 780 第786组：471 628 785 第787组：473 864 985 第788组：474 632 790 第789组：475 840 965 第790组：476 480 676 第791组：476 765 901 第792组：477 636 795 第793组：480 504 696 第794组：480 550 730 第795组：480 640 800 第796组：480 693 843 第797组：480 728 872 第798组：480 836 964 第799组：481 600 769 第800组：483 644 805 第801组：483 720 867 第802组：486 648 810 第803组：489 652 815 第804组：492 656 820 第805组：495 660 825 第806组：495 840 975 第807组：498 664 830 第808组：500 525 725 第809组：501 668 835 第810组：504 550 746 第811组：504 672 840 第812组：504 703 865 第813组：504 810 954 第814组：507 676 845 第815组：510 680 850 第816组：510 792 942 第817组：513 684 855 第818组：516 688 860 第819组：519 692 865 第820组：520 546 754 第821组：520 576 776 第822组：520 765 925 第823组：522 696 870 第824组：522 760 922 第825组：525 700 875 第826组：528 605 803第828组：528 704 880 第829组：531 708 885 第830组：532 624 820 第831组：533 756 925 第832组：534 712 890 第833组：537 716 895 第834组：540 567 783 第835组：540 629 829 第836组：540 720 900 第837组：540 819 981 第838组：543 724 905 第839组：546 728 910 第840组：549 732 915 第841组：552 736 920 第842组：555 572 797 第843组：555 740 925 第844组：558 744 930 第845组：560 588 812 第846组：560 684 884 第847组：560 702 898 第848组：561 748 935 第849组：564 752 940 第850组：567 756 945 第851组：570 760 950 第852组：573 764 955 第853组：576 660 876 第854组：576 768 960 第855组：579 772 965 第856组：580 609 841 第857组：580 741 941 第858组：582 776 970 第859组：585 648 873 第860组：585 780 975 第861组：588 784 980 第862组：591 788 985 第863组：594 608 850 第864组：594 792 990 第865组：595 600 845 第866组：597 796 995 第867组：600 630 870 第868组：600 800 1000 第869组：612 759 975 第870组：615 728 953第872组：616 735 959 第873组：620 651 899 第874组：621 672 915 第875组：624 715 949 第876组：638 720 962 第877组：640 672 928 第878组：650 720 970 第879组：660 693 957 第880组：680 714 986 第881组：696 697 985。

勾股定理知识点整理

勾股定理知识点整理1：勾股定理直角三角形两直角边a、b的平方和等于斜边c的平方。

即：a²+b²＝c²要点诠释：勾股定理反映了直角三角形三边之间的关系，是直角三角形的重要性质之一。

其主要应用：（1）已知直角三角形的两边求第三边；（2）已知直角三角形的一边与另两边的关系，求直角三角形的另两边；（3）利用勾股定理可以证明线段平方关系的问题。

2：勾股定理的逆定理如果三角形的三边长：a、b、c，则有关系a²+b²＝c²，那么这个三角形是直角三角形。

要点诠释：勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状。

运用这一定理时应注意：（1）首先确定最大边，不妨设最长边长为：c；（2）验证c2与a2+b2是否具有相等关系，若c²＝a²+b²，则△ABC是以∠C为直角的直角三角形（若c²>a²+b²，则△ABC是以∠C为钝角的钝角三角形；若c²<a²+b²，则△ABC为锐角三角形）。

3：勾股定理与勾股定理逆定理的区别与联系区别：勾股定理是直角三角形的性质定理，而其逆定理是判定定理；联系：勾股定理与其逆定理的题设和结论正好相反，都与直角三角形有关。

4：互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

如果把其中一个叫做原命题，那么另一个叫做它的逆命题。

5：勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法用拼图的方法验证勾股定理的思路是：①图形经过割补拼接后，只要没有重叠，没有空隙，面积不会改变；②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理。

勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理（毕达哥拉斯定理）是一个，是人类早期发现并证明的重要数学定理之一，用思想解决几何问题的最重要的工具之一，也是数形结合的纽带之一。

是的一个特例。

约有400种证明方法，是数学定理中证明方法最多的之一。

“”是勾股定理最基本的公式。

勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。

(3,4,5)就是。

也就是说，设直角三角形两直角边为a 和b ，斜边为c ，那么a ²+b ²=c ² ，即直角三角形两直角边的平方和等于斜边的平方。

勾股定理命题1 如果的两条直角边长分别为a ，b ，斜边长为c ，那么。

勾股定理的逆定理命题2 如果的三边长a ，b ，c 满足，那么这个三角形是直角三角形。

【证法1】（赵爽证明）以a 、b 为直角边（b>a ），以c 为斜边作四个全等的直角三角形，则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º，∴ ∠EAB + ∠HAD = 90º，∴ ABCD 是一个边长为c 的正方形，它的面积等于c2.∵ EF = FG =GH =HE = b―a ,∠HEF = 90º.∴ EFGH 是一个边长为b―a 的正方形，它的面积等于.∴∴ .【证法2】（课本的证明）做8个全等的直角三角形，设它们的两条直角边长分别为a 、b ，斜边长为c ，再做三个边长分别为a 、b 、c 的正方形，把它们像上图那样拼成两个正方形.从图上可以看到，这两个正方形的边长都是a + b ，所以面积相等.即，整理得 .【证法3】（1876年美国总统Garfield 证明）以a 、b 为直角边，以c 为斜边作两个全等的直角三角形，则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形，它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形，它的面积等于∴ .∴.【趣闻】：在1876年一个周末的傍晚，在美国华盛顿的郊外，有一位中年人正在散步，欣赏黄昏的美景，他就是当时美国俄亥俄州共和党议员伽菲尔德。

三角形边长定律

三角形边长定律三角形作为初中数学中的基础知识，被广泛学习和应用。

三角形的边长定律，也称为勾股定理，是三角形相关知识中最基础和重要的一个定理。

本文主要探讨三角形边长定律的定义、证明、应用及扩展。

一、定义三角形边长定律又称为勾股定理，它的定义是指：两条边的平方和等于第三边的平方。

具体来说，设三角形ABC的三条边分别为a、b和c，其中c为斜边，则a、b和c的关系可表示为：a²+b²=c²。

其中a、b和c为边长，c为斜边，a、b为与之相邻的两条边。

二、证明三角形边长定律最早可以追溯到古希腊数学家毕达哥拉斯的著名定理。

该定理可以用几何方法和代数方法证明。

几何方法证明勾股定理：如图所示，我们可将三角形ABC利用边长拼成一个正方形。

其中，正方形的边长为c，面积为c²。

而三角形ABC 的面积可以计算为：S=1/2ab。

而正方形与三角形共享的底边形成了高为b的矩形。

因此有：S=cb，即1/2ab=cb，化简得到：a/b=c/b，即a/b=k。

此时，我们可以对三角形进行相似的划分，将大正方形划分成小正方形和两个矩形，如下图所示。

由于三角形ABC和ACB与其相似，因此有：a/b=c/b=k，代入AB分段得到：a=c-b。

将a代入原式中，可得：(c-b)²+b²=c²，整理得到：b²+(c²-2bc+b²)=c²，即2b²-2bc=0，将其化简得到：b(c-b)=0。

由于b不可能为0，因此有c=b。

即我们证明了，当三角形的两边长分别为a和b时，它们所对应的夹角的余弦为c/a，则有a²+b²=c²。

代数方法证明勾股定理：假设在直角三角形ABC中，角A等于90度，斜边长度为c，两条直角边分别为a和b。

不妨假设a为斜边上的较小边，根据正弦定理和余弦定理，可得到：sinB=a/c，cosB=b/c；sinB=b/c，cosB=a/c。

勾股定理知识点总结

第十七章
勾股定理知识点总结
1.勾股定理
如果直角三角形的两条直角边长分别为a,b, 斜边长为c,那么a2+b2=c2.
练习：
1.如图所示，用硬纸板做成的四个全等的直角三角形（两直角边长分别是a，b，斜边长为c）和一个边长为 c的正方形，请你将它们拼成一个能证明勾股定理的图形。
（1）画出拼成的图形的示意图；
8
x
15
y
25
24
1.勾股定理
如果直角三角形的两条直角边长分别为a,b, 斜边长为c,那么a2+b2=c2.
勾股定理的主要应用：（2）已知直角三角形的一边与另两边的关系，求直角三角形的另两边;
练习：
1.若一个直角三角形的一条直角边长是7cm，另一条直角边比斜边短1cm，则斜边的长是___2_5___cm.
么它也是一个定理, 这两个定理叫做互逆定理, 其中一个叫做另一个的逆定理.
练习：
1.下列说法，正确的是（ D ） A.真命题的逆命题是真命题 B.原命题是假命题，它的逆命题也是假命题 C.定理一定有逆定理 D.命题一定有逆命题
练习：
2.下列定理，有逆定理的是（ D ） A.对顶角相等 B.全等三角形的对应角相等 C.两个全等三角形的面积相等 D.平面内，线段的垂直平分线上的点到线段两端点的距离相等
5.分类讨论思想
1.已知：直角三角形的边长分别是3,4, x,
则x2 ___2_5__或__7____.
解：情形一：当斜边为x时，则两直角边分别为3，4. 根据勾股定理
x2 32 42 9 16 25
解：情形二：当斜边为4时，则两直角边分别为x，3.
根据勾股定理
x2 32 42

超全勾股定理公式大全

超全勾股定理公式大全我们知道，如果∠C=90°，a 、b 、c 是直角三角形的三边，则由勾股定理，得a 2+b 2=c 2；反之，若三角形的三边a 、b 、c 满足a 2+b 2=c 2，则该三角形是直角三角形，c 为斜边．与此相类似，如果三个正整数a 、b 、c 满足a 2+b 2=c 2，则称a 、b 、c 为勾股数，记为（a ，b ，c ）．勾股数有无数多组，下面向同学们介绍几种：一、三数为连续整数的勾股数（3，4，5）是我们所熟悉的一组三数为连续整数的勾股数，除此之外是否还有第二组或更多组呢？设三数为连续整数的勾股数组为（x －１，x ，x ＋１），则由勾股数的定义，得（x+1）2+x 2=（x+1）2，解得x ＝４或x ＝０（舍去），故三数为连续整数的勾股数只有一组（３，４，５）；类似有3n,4n,5n(n是正整数)都是勾股数。

二、后两数为连续整数的勾股数易知：（５，１２，１３），（９，４０，４１），（１１３，６３３８，６３８５），…，都是勾股数，如此许许多多的后两数为连续整数的勾股数，它的一般形式究竟是什么呢？ a=2n+1,b=2n 2+2n,c=2n 2+2n+1（其特点是斜边与其中一股的差为1）.分别取n ＝１，２，３，…就得勾股数组（３，４，５），（５，１２，１３），（７，２４，２５），…三、前两数为连续整数的勾股数你知道（２０，２１，２９），（１１９，１２０，１６９），（４０５９，４０６０，５７４１）…，这些都是前两数为连续整数的勾股数组。

其公式为：（x ，x ＋１，1222++x x ）（x 为正整数）。

设前两数为连续整数的勾股数组为（x ，x ＋１，y ），y=1222++x x 则()2221y x x =++（＊）整理，得1222++x x ＝2y ，化为()121222-=-+y x ，即()y x 212++()y x 212-+＝－１，又()()2121-+＝－１，∴()1221++n ()1221+-n ＝－１（ｎ∈Ｎ），故取()y x 212++＝()1221++n ，()y x 212-+＝()1221+-n ，解之，得x ＝41〔()1221++n ＋()1221+-n －２〕，y ＝42〔()1221++n －()1221+-n 〕，故前两数为连续整数的勾股数组是（41〔()1221++n ＋()1221+-n －２〕，41〔()1221++n ＋()1221+-n －２〕＋１，42〔()1221++n －()1221+-n 〕）．四、后两数为连续奇数的勾股数如(8，15，17),(12，35，37)…其公式为：4(n+1),4(n+1)2-1,4(n+1)2+1(n 是正整数). 五、其它的勾股数组公式：1.a=2m,b=m 2－1,c=m 2+1（m 大于1的整数）.2.a=21（m 2－n 2）,b=mn,c=21（m 2+n 2）（其中m>n 且是互质的奇数）.3.a=2m,b=m 2－n 2,c=m 2+n 2（m>n,互质且一奇一偶的任意正整数）.下面我们把100以内的勾股数组列出来，供同学们参考：34 5；512 13；6810；72425；81517；9 1215；940 41；102426；116061；12 16 20；12 35 37；13 84 85；14 48 50；15 20 25；15 36 39；15112 113；16 30 34；1663 6517144 145；18 24 30；18 80 82；19 180 181；20 21 29；20 48 52；20 99 101；21 28 3521 72 75；21 220 221；22 120 122；23 264 265；24 32 40；24 45 51；24 70 74；24143 14525 60 65；25 312 313；26 168 170；27 36 45；27120 123；27 364 365；28 45 53；2896 10028 195 197；29 420 421；30 40 50；30 72 78；30 224 226；31 480 481；32 60 68；32126 13032 255 257；33 44 55；33 56 65；33 180 183；33 544 545；34 288 290；35 84 91；35120 12535 612 613；36 48 60；36 77 85；36 105 111；36 160 164；36 323 325；37 684 685；38 360 36239 52 65；39 80 89；39 252 255；39 760 761；40 42 58；40 75 85；40 96 104；40 198 20240 399 401；41 840 841；42 56 70；42 144 150；42 440 442；43 924 925；44 117 125；44 240 24444 483 485；45 60 75；45 108 117；45 200 205；45 336 339；46 528 530；48 55 73；4864 8048 90 102；48 140 148；48 189 195；48 286 290；48 575 577；49 168 175；50 120 130；50 624 62651 68 85；51 140 149；51 432 435；52 165 173；52 336 340；52 675 677；54 72 90；54240 24654 728 730；55 132 143；55 300 305；56 90 106；56 105 119；56 192 200；56 390 394；56 783 78557 76 95；57176 185；57 540 543；58 840 842；60 63 87；60 80 100；60 91 109；60 144 15660 175 185；60 221 229；60 297 303；60 448 452；60 899 901；62 960 962；63 84 105；63 216 22563 280 287；63 660 663；64 120 136；64 252 260；64 510 514；65 72 97；65 156 169；65 420 42566 88 110；66 112 130；66 360 366；68 285 293；68 576 580；69 92 115；69 260 269；69 792 79570 168 182；70 240 250；72 96 120；72 135 153；72 154 170；72 210 222；72 320 328；72 429 43572 646 650；75 100 125；75 180 195；75 308 317；75 560 565；75 936 939；76 357 365；76 720 72477 264 275；77 420 427；78 104 130；78 160 178；78 504 510；80 84 116；80 150 170；80 192 20880 315 325；80 396 404；80 798 802；81 108 135；81 360 369；84 112 140；84 135 159；84 187 20584 245 259；84 288 300；84 437 445；84 585 591；84 880 884；85 132 157；85 204 221；85 720 72587 116 145；87 416 425；88 105 137；88 165 187；88 234 250；88 480 488；88 966 970；90 120 15090 216 234；90 400 410；90 672 678；91 312 325；91 588 595；92 525 533；93 124 155；93 476 48595 168 193；95 228 247；95 900 905；96 110 146；96 128 160；96 180 204；96 247 265；96 280 29696 378 390；96 572 580；96 765 771；98 336 350；99 132 165；99 168 195；99 440 451；99 540 549100 105 145；100240260；100 495 505；100621629.以下是大于100的勾股数：第223组：102 136 170第224组：102 280 298第225组：102 864 870第226组：104 153 185第227组：104 195 221第228组：104 330 346第229组：104 672 680第230组：105 140 175第231组：105 208 233第232组：105 252 273第233组：105 360 375第234组：105 608 617第235组：105 784 791第236组：108 144 180第237组：108 231 255第238组：108 315 333第239组：108 480 492第240组：108 725 733第241组：108 969 975第242组：110 264 286第243组：110 600 610第244组：111 148 185第245组：111 680 689第246组：112 180 212第247组：112 210 238第248组：112 384 400第249组：112 441 455第250组：112 780 788第251组：114 152 190第252组：114 352 370第253组：115 252 277第254组：115 276 299第256组：117 156 195 第257组：117 240 267 第258组：117 520 533 第259组：117 756 765 第260组：119 120 169 第261组：119 408 425 第262组：120 126 174 第263组：120 160 200 第264组：120 182 218 第265组：120 209 241 第266组：120 225 255 第267组：120 288 312 第268组：120 350 370 第269组：120 391 409 第270组：120 442 458 第271组：120 594 606 第272组：120 715 725 第273组：120 896 904 第274组：121 660 671 第275组：123 164 205 第276组：123 836 845 第277组：124 957 965 第278组：125 300 325 第279组：126 168 210 第280组：126 432 450 第281组：126 560 574 第282组：128 240 272 第283组：128 504 520 第284组：129 172 215 第285组：129 920 929 第286组：130 144 194 第287组：130 312 338 第288组：130 840 850 第289组：132 176 220 第290组：132 224 260 第291组：132 351 375 第292组：132 385 407 第293组：132 475 493 第294组：132 720 732 第295组：133 156 205 第296组：133 456 475 第297组：135 180 225 第298组：135 324 351第300组：135 600 615 第301组：136 255 289 第302组：136 273 305 第303组：136 570 586 第304组：138 184 230 第305组：138 520 538 第306组：140 147 203 第307组：140 171 221 第308组：140 225 265 第309组：140 336 364 第310组：140 480 500 第311组：140 693 707 第312组：140 975 985 第313组：141 188 235 第314组：143 780 793 第315组：143 924 935 第316组：144 165 219 第317组：144 192 240 第318组：144 270 306 第319组：144 308 340 第320组：144 420 444 第321组：144 567 585 第322组：144 640 656 第323组：144 858 870 第324组：145 348 377 第325组：145 408 433 第326组：147 196 245 第327组：147 504 525 第328组：150 200 250 第329组：150 360 390 第330组：150 616 634 第331组：152 285 323 第332组：152 345 377 第333组：152 714 730 第334组：153 204 255 第335组：153 420 447 第336组：153 680 697 第337组：154 528 550 第338组：154 840 854 第339组：155 372 403 第340组：155 468 493 第341组：156 208 260 第342组：156 320 356第343组：156 455 481 第344组：156 495 519 第345组：156 667 685 第346组：159 212 265 第347组：160 168 232 第348组：160 231 281 第349组：160 300 340 第350组：160 384 416 第351组：160 630 650 第352组：160 792 808 第353组：161 240 289 第354组：161 552 575 第355组：162 216 270 第356组：162 720 738 第357组：165 220 275 第358组：165 280 325 第359组：165 396 429 第360组：165 532 557 第361组：165 900 915 第362组：168 224 280 第363组：168 270 318 第364组：168 315 357 第365组：168 374 410 第366组：168 425 457 第367组：168 490 518 第368组：168 576 600 第369组：168 775 793 第370组：168 874 890 第371组：170 264 314 第372组：170 408 442 第373组：171 228 285 第374组：171 528 555 第375组：171 760 779 第376组：174 232 290 第377组：174 832 850 第378组：175 288 337 第379组：175 420 455 第380组：175 600 625 第381组：176 210 274 第382组：176 330 374 第383组：176 468 500 第384组：176 693 715 第385组：176 960 976 第386组：177 236 295第388组：180 240 300 第389组：180 273 327 第390组：180 299 349 第391组：180 385 425 第392组：180 432 468 第393组：180 525 555 第394组：180 663 687 第395组：180 800 820 第396组：180 891 909 第397组：182 624 650 第398组：183 244 305 第399组：184 345 391 第400组：184 513 545 第401组：185 444 481 第402组：185 672 697 第403组：186 248 310 第404组：186 952 970 第405组：189 252 315 第406组：189 340 389 第407组：189 648 675 第408组：189 840 861 第409组：190 336 386 第410组：190 456 494 第411组：192 220 292 第412组：192 256 320 第413组：192 360 408 第414组：192 494 530 第415组：192 560 592 第416组：192 756 780 第417组：195 216 291 第418组：195 260 325 第419组：195 400 445 第420组：195 468 507 第421组：195 748 773 第422组：196 315 371 第423组：196 672 700 第424组：198 264 330 第425组：198 336 390 第426组：198 880 902 第427组：200 210 290 第428组：200 375 425 第429组：200 480 520 第430组：200 609 641第432组：203 396 445 第433组：203 696 725 第434组：204 253 325 第435组：204 272 340 第436组：204 560 596 第437组：204 595 629 第438组：204 855 879 第439组：205 492 533 第440组：205 828 853 第441组：207 224 305 第442组：207 276 345 第443组：207 780 807 第444组：207 920 943 第445组：208 306 370 第446组：208 390 442 第447组：208 660 692 第448组：208 819 845 第449组：210 280 350 第450组：210 416 466 第451组：210 504 546 第452组：210 720 750 第453组：213 284 355 第454组：215 516 559 第455组：215 912 937 第456组：216 288 360 第457组：216 405 459 第458组：216 462 510 第459组：216 630 666 第460组：216 713 745 第461组：216 960 984 第462组：217 456 505 第463组：217 744 775 第464组：219 292 365 第465组：220 231 319 第466组：220 459 509 第467组：220 528 572 第468组：220 585 625 第469组：222 296 370 第470组：224 360 424 第471组：224 420 476 第472组：224 768 800 第473组：224 882 910 第474组：225 272 353第476组：225 540 585 第477组：225 924 951 第478组：228 304 380 第479组：228 325 397 第480组：228 665 703 第481组：228 704 740 第482组：230 504 554 第483组：230 552 598 第484组：231 308 385 第485组：231 392 455 第486组：231 520 569 第487组：231 792 825 第488组：232 435 493 第489组：232 825 857 第490组：234 312 390 第491组：234 480 534 第492组：235 564 611 第493组：237 316 395 第494组：238 240 338 第495组：238 816 850 第496组：240 252 348 第497组：240 275 365 第498组：240 320 400 第499组：240 364 436 第500组：240 418 482 第501组：240 450 510 第502组：240 551 601 第503组：240 576 624 第504组：240 700 740 第505组：240 782 818 第506组：240 884 916 第507组：240 945 975 第508组：243 324 405 第509组：245 588 637 第510组：245 840 875 第511组：246 328 410 第512组：248 465 527 第513组：248 945 977 第514组：249 332 415 第515组：250 600 650 第516组：252 275 373 第517组：252 336 420 第518组：252 405 477第519组：252 539 595 第520组：252 561 615 第521组：252 735 777 第522组：252 864 900 第523组：255 340 425 第524组：255 396 471 第525组：255 612 663 第526组：255 700 745 第527组：256 480 544 第528组：258 344 430 第529组：259 660 709 第530组：259 888 925 第531组：260 273 377 第532组：260 288 388 第533组：260 624 676 第534组：260 651 701 第535组：260 825 865 第536组：261 348 435 第537组：261 380 461 第538组：264 315 411 第539组：264 352 440 第540组：264 448 520 第541组：264 495 561 第542组：264 702 750 第543组：264 770 814 第544组：264 950 986 第545组：265 636 689 第546组：266 312 410 第547组：266 912 950 第548组：267 356 445 第549组：270 360 450 第550组：270 648 702 第551组：270 704 754 第552组：272 510 578 第553组：272 546 610 第554组：273 364 455 第555组：273 560 623 第556组：273 736 785 第557组：273 936 975 第558组：275 660 715 第559组：276 368 460 第560组：276 493 565 第561组：276 805 851 第562组：279 372 465第564组：280 294 406 第565组：280 342 442 第566组：280 351 449 第567组：280 450 530 第568组：280 525 595 第569组：280 672 728 第570组：280 759 809 第571组：280 960 1000 第572组：282 376 470 第573组：285 380 475 第574组：285 504 579 第575组：285 684 741 第576组：285 880 925 第577组：287 816 865 第578组：288 330 438 第579组：288 384 480 第580组：288 540 612 第581组：288 616 680 第582组：288 741 795 第583组：288 840 888 第584组：290 696 754 第585组：290 816 866 第586组：291 388 485 第587组：294 392 490 第588组：295 708 767 第589组：296 555 629 第590组：297 304 425 第591组：297 396 495 第592组：297 504 585 第593组：300 315 435 第594组：300 400 500 第595组：300 455 545 第596组：300 589 661 第597组：300 720 780 第598组：300 875 925 第599组：301 900 949 第600组：303 404 505 第601组：304 570 646 第602组：304 690 754 第603组：305 732 793 第604组：306 408 510 第605组：306 840 894 第606组：308 435 533第608组：308 819 875 第609组：309 412 515 第610组：310 744 806 第611组：310 936 986 第612组：312 416 520 第613组：312 459 555 第614组：312 585 663 第615组：312 640 712 第616组：312 910 962 第617组：315 420 525 第618组：315 572 653 第619组：315 624 699 第620组：315 756 819 第621组：318 424 530 第622组：319 360 481 第623组：320 336 464 第624组：320 462 562 第625组：320 600 680 第626组：320 768 832 第627组：321 428 535 第628组：322 480 578 第629组：324 432 540 第630组：324 693 765 第631组：324 945 999 第632组：325 360 485 第633组：325 780 845 第634组：327 436 545 第635组：328 615 697 第636组：330 440 550 第637组：330 560 650 第638组：330 792 858 第639组：333 444 555 第640组：333 644 725 第641组：335 804 871 第642组：336 377 505 第643组：336 385 511 第644组：336 448 560 第645组：336 527 625 第646组：336 540 636 第647组：336 630 714 第648组：336 748 820 第649组：336 850 914 第650组：339 452 565第652组：340 528 628 第653组：340 816 884 第654组：341 420 541 第655组：342 456 570 第656组：344 645 731 第657组：345 460 575 第658组：345 756 831 第659组：345 828 897 第660组：348 464 580 第661组：348 805 877 第662组：350 576 674 第663组：350 840 910 第664组：351 468 585 第665组：351 720 801 第666组：352 420 548 第667组：352 660 748 第668组：352 936 1000 第669组：354 472 590 第670组：355 852 923 第671组：357 360 507 第672组：357 476 595 第673组：360 378 522 第674组：360 480 600 第675组：360 546 654 第676组：360 598 698 第677组：360 627 723 第678组：360 675 765 第679组：360 770 850 第680组：360 864 936 第681组：363 484 605 第682组：363 616 715 第683组：364 585 689 第684组：364 627 725 第685组：365 876 949 第686组：366 488 610 第687组：368 465 593 第688组：368 690 782 第689组：369 492 615 第690组：369 800 881 第691组：370 888 962 第692组：372 496 620 第693组：372 925 997 第694组：375 500 625第696组：376 705 799 第697组：378 504 630 第698组：378 680 778 第699组：380 399 551 第700组：380 672 772 第701组：380 912 988 第702组：381 508 635 第703组：384 440 584 第704组：384 512 640 第705组：384 720 816 第706组：385 552 673 第707组：387 516 645 第708组：387 884 965 第709组：390 432 582 第710组：390 520 650 第711组：390 800 890 第712组：392 630 742 第713组：392 735 833 第714组：393 524 655 第715组：396 403 565 第716组：396 528 660 第717组：396 672 780 第718组：396 847 935 第719组：399 468 615 第720组：399 532 665 第721组：400 420 580 第722组：400 561 689 第723组：400 750 850 第724组：402 536 670 第725组：405 540 675 第726组：406 792 890 第727组：407 624 745 第728组：408 506 650 第729组：408 544 680 第730组：408 765 867 第731组：408 819 915 第732组：411 548 685 第733组：414 448 610 第734组：414 552 690 第735组：416 612 740 第736组：416 780 884 第737组：417 556 695 第738组：420 441 609第740组：420 560 700 第741组：420 637 763 第742组：420 675 795 第743组：420 832 932 第744组：420 851 949 第745组：423 564 705 第746组：424 795 901 第747组：425 660 785 第748组：426 568 710 第749组：429 460 629 第750组：429 572 715 第751组：429 700 821 第752组：429 728 845 第753组：429 880 979 第754组：432 495 657 第755组：432 576 720 第756组：432 665 793 第757组：432 810 918 第758组：435 580 725 第759组：438 584 730 第760组：440 462 638 第761组：440 525 685 第762组：440 825 935 第763组：441 588 735 第764组：444 592 740 第765组：447 596 745 第766组：448 720 848 第767组：448 840 952 第768组：450 544 706 第769组：450 600 750 第770组：451 780 901 第771组：453 604 755 第772组：455 504 679 第773组：455 528 697 第774组：456 608 760 第775组：456 650 794 第776组：456 855 969 第777组：459 612 765 第778组：460 483 667 第779组：462 616 770 第780组：462 784 910 第781组：464 777 905 第782组：464 870 986第784组：468 595 757 第785组：468 624 780 第786组：471 628 785 第787组：473 864 985 第788组：474 632 790 第789组：475 840 965 第790组：476 480 676 第791组：476 765 901 第792组：477 636 795 第793组：480 504 696 第794组：480 550 730 第795组：480 640 800 第796组：480 693 843 第797组：480 728 872 第798组：480 836 964 第799组：481 600 769 第800组：483 644 805 第801组：483 720 867 第802组：486 648 810 第803组：489 652 815 第804组：492 656 820 第805组：495 660 825 第806组：495 840 975 第807组：498 664 830 第808组：500 525 725 第809组：501 668 835 第810组：504 550 746 第811组：504 672 840 第812组：504 703 865 第813组：504 810 954 第814组：507 676 845 第815组：510 680 850 第816组：510 792 942 第817组：513 684 855 第818组：516 688 860 第819组：519 692 865 第820组：520 546 754 第821组：520 576 776 第822组：520 765 925 第823组：522 696 870 第824组：522 760 922 第825组：525 700 875 第826组：528 605 803第828组：528 704 880 第829组：531 708 885 第830组：532 624 820 第831组：533 756 925 第832组：534 712 890 第833组：537 716 895 第834组：540 567 783 第835组：540 629 829 第836组：540 720 900 第837组：540 819 981 第838组：543 724 905 第839组：546 728 910 第840组：549 732 915 第841组：552 736 920 第842组：555 572 797 第843组：555 740 925 第844组：558 744 930 第845组：560 588 812 第846组：560 684 884 第847组：560 702 898 第848组：561 748 935 第849组：564 752 940 第850组：567 756 945 第851组：570 760 950 第852组：573 764 955 第853组：576 660 876 第854组：576 768 960 第855组：579 772 965 第856组：580 609 841 第857组：580 741 941 第858组：582 776 970 第859组：585 648 873 第860组：585 780 975 第861组：588 784 980 第862组：591 788 985 第863组：594 608 850 第864组：594 792 990 第865组：595 600 845 第866组：597 796 995 第867组：600 630 870 第868组：600 800 1000 第869组：612 759 975 第870组：615 728 953第872组：616 735 959 第873组：620 651 899 第874组：621 672 915 第875组：624 715 949 第876组：638 720 962 第877组：640 672 928 第878组：650 720 970 第879组：660 693 957 第880组：680 714 986 第881组：696 697 985。

勾股定理知识点+对应类型(整理)4.5

勾股定理一、勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。

2. 勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）3. 判断直角三角形：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c2＝a2＋b2，则△ABC是以∠C为直角的三角形；若a2＋b2＜c2，则此三角形为钝角三角形（其中c为最大边）；若a2＋b2＞c2，则此三角形为锐角三角形（其中c为最大边）4.注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

5. 勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n的线段6.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形7.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC∆中，90C∠=︒，则c=，b=，a=②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题8.记住常见的勾股数可以提高解题速度：（黑色为必背熟悉勾股数） 3 、4 、5 5、12、13 6、8 、10 7、24 、25 8、15、17 9 、12、15 9、40、41 10 、24、26 11、60 、61 12、16、20 12 、35、37 13 、84、85 14 、48 、50 15、20 、25 15、36 、39 16 、30 、34 16 、3 、65 18 、24 、30 18、80 、82 20 、21 、29 20、48 、52 21、28 、35 21 、72、75 24、32 、40 24 、45、51 24 、70 、74 25 、60 、65 27、36 、45 28、45、53 30 、40、50 30、72、78 60、80、100 32 、60 、68 33 、44 、55 33、56 、65 35、84、91 36、48 、60 36、77 、85 39 、52 、65 39、80 、89 40、42 、58 40、75 、85 42 、56 、70 45、60 、75 48、55、73 48、64、80 51 、68、85 54 、72、90 57 、76 、9560、63 、8765、72 、97用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）9、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

【数学公式】初中数学勾股定理公式

【数学公式】初中数学勾股定理公式勾股定理是中考数学的重点考查内容，对今后几何的学习也具有举足轻重的作用。

下面整理了数学勾股定理公式，希望对你有所帮助。

1.基本公式在平面上的一个直角三角形中，两个直角边边长的平方加起来等于斜边长的平方。

如果设直角三角形的两条直角边长度分别是a和b，斜边长度是c，那么勾股定理的公式为a2+b2=c2。

2.完全公式a=m，b=(m^2/k-k)/2，c=(m^2/k+k)/2①其中m≥3(1)当m确定为任意一个≥3的奇数时，k={1，m^2的所有小于m的因子}(2)当m确定为任意一个≥4的偶数时，k={m^2/2的所有小于m的偶数因子}3.常用公式（1）(3,4,5),(6,8,10)……3n,4n,5n(n是正整数)。

（2）(5,12,13),(7,24,25),(9,40,41)……2n+1,2n^2+2n,2n^2+2n+1(n是正整数)。

（3）(8,15,17),(12,35,37)……2^2*(n+1),[2(n+1)]^2-1,[2(n+1)]^2+1(n是正整数)。

（4）m^2-n^2,2mn,m^2+n^2(m、n均是正整数,m>n)。

如果三角形三边长a，b，c满足，那么这个三角形是直角三角形，其中c为斜边.①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和a^2+b^2与较长边的平方c^2作比较，若它们相等时，以a，b，c为三边的三角形是直角三角形；若a^2+b^2<c^2时，以a，b，c为三边的三角形是钝角三角形；若a^2+b^2>c^2时，以a，b，c为三边的三角形是锐角三角形；②定理中a，b，c及a^2+b^2=c^2只是一种表现形式，不可认为是唯一的，如若三角形三边长a，b，c满足a^2+b^2=c^2，那么以a，b，c为三边的三角形是直角三角形，但是b为斜边.③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形感谢您的阅读，祝您生活愉快。

超全勾股定理公式大全

超全勾股定理公式大全我们知道，如果∠C=90°，a 、b 、c 是直角三角形的三边，则由勾股定理，得a 2+b 2=c 2；反之，若三角形的三边a 、b 、c 满足a 2+b 2=c 2，则该三角形是直角三角形，c 为斜边．与此相类似，如果三个正整数a 、b 、c 满足a 2+b 2=c 2，则称a 、b 、c 为勾股数，记为（a ，b ，c ）．勾股数有无数多组，下面向同学们介绍几种：一、三数为连续整数的勾股数（3，4，5）是我们所熟悉的一组三数为连续整数的勾股数，除此之外是否还有第二组或更多组呢？设三数为连续整数的勾股数组为（x －１，x ，x ＋１），则由勾股数的定义，得（x+1）2+x 2=（x+1）2，解得x ＝４或x ＝０（舍去），故三数为连续整数的勾股数只有一组（３，４，５）；类似有3n,4n,5n(n是正整数)都是勾股数。

二、后两数为连续整数的勾股数易知：（５，１２，１３），（９，４０，４１），（１１３，６３３８，６３８５），…，都是勾股数，如此许许多多的后两数为连续整数的勾股数，它的一般形式究竟是什么呢？ a=2n+1,b=2n 2+2n,c=2n 2+2n+1（其特点是斜边与其中一股的差为1）.分别取n ＝１，２，３，…就得勾股数组（３，４，５），（５，１２，１３），（７，２４，２５），…三、前两数为连续整数的勾股数你知道（２０，２１，２９），（１１９，１２０，１６９），（４０５９，４０６０，５７４１）…，这些都是前两数为连续整数的勾股数组。

其公式为：（x ，x ＋１，1222++x x ）（x 为正整数）。

设前两数为连续整数的勾股数组为（x ，x ＋１，y ），y=1222++x x 则()2221y x x =++（＊）整理，得1222++x x ＝2y ，化为()121222-=-+y x ，即()y x 212++()y x 212-+＝－１，又()()2121-+＝－１，∴()1221++n ()1221+-n ＝－１（ｎ∈Ｎ），故取()y x 212++＝()1221++n ，()y x 212-+＝()1221+-n ，解之，得x ＝41〔()1221++n ＋()1221+-n －２〕，y ＝42〔()1221++n －()1221+-n 〕，故前两数为连续整数的勾股数组是（41〔()1221++n ＋()1221+-n －２〕，41〔()1221++n ＋()1221+-n －２〕＋１，42〔()1221++n －()1221+-n 〕）．四、后两数为连续奇数的勾股数如(8，15，17),(12，35，37)…其公式为：4(n+1),4(n+1)2-1,4(n+1)2+1(n 是正整数). 五、其它的勾股数组公式：1.a=2m,b=m 2－1,c=m 2+1（m 大于1的整数）.2.a=21（m 2－n 2）,b=mn,c=21（m 2+n 2）（其中m>n 且是互质的奇数）.3.a=2m,b=m 2－n 2,c=m 2+n 2（m>n,互质且一奇一偶的任意正整数）.下面我们把100以内的勾股数组列出来，供同学们参考：34 5；512 13；6810；72425；81517；9 1215；940 41；102426；116061；12 16 20；12 35 37；13 84 85；14 48 50；15 20 25；15 36 39；15112 113；16 30 34；1663 6517144 145；18 24 30；18 80 82；19 180 181；20 21 29；20 48 52；20 99 101；21 28 3521 72 75；21 220 221；22 120 122；23 264 265；24 32 40；24 45 51；24 70 74；24143 14525 60 65；25 312 313；26 168 170；27 36 45；27120 123；27 364 365；28 45 53；2896 10028 195 197；29 420 421；30 40 50；30 72 78；30 224 226；31 480 481；32 60 68；32126 13032 255 257；33 44 55；33 56 65；33 180 183；33 544 545；34 288 290；35 84 91；35120 12535 612 613；36 48 60；36 77 85；36 105 111；36 160 164；36 323 325；37 684 685；38 360 36239 52 65；39 80 89；39 252 255；39 760 761；40 42 58；40 75 85；40 96 104；40 198 20240 399 401；41 840 841；42 56 70；42 144 150；42 440 442；43 924 925；44 117 125；44 240 24444 483 485；45 60 75；45 108 117；45 200 205；45 336 339；46 528 530；48 55 73；4864 8048 90 102；48 140 148；48 189 195；48 286 290；48 575 577；49 168 175；50 120 130；50 624 62651 68 85；51 140 149；51 432 435；52 165 173；52 336 340；52 675 677；54 72 90；54240 24654 728 730；55 132 143；55 300 305；56 90 106；56 105 119；56 192 200；56 390 394；56 783 78557 76 95；57176 185；57 540 543；58 840 842；60 63 87；60 80 100；60 91 109；60 144 15660 175 185；60 221 229；60 297 303；60 448 452；60 899 901；62 960 962；63 84 105；63 216 22563 280 287；63 660 663；64 120 136；64 252 260；64 510 514；65 72 97；65 156 169；65 420 42566 88 110；66 112 130；66 360 366；68 285 293；68 576 580；69 92 115；69 260 269；69 792 79570 168 182；70 240 250；72 96 120；72 135 153；72 154 170；72 210 222；72 320 328；72 429 43572 646 650；75 100 125；75 180 195；75 308 317；75 560 565；75 936 939；76 357 365；76 720 72477 264 275；77 420 427；78 104 130；78 160 178；78 504 510；80 84 116；80 150 170；80 192 20880 315 325；80 396 404；80 798 802；81 108 135；81 360 369；84 112 140；84 135 159；84 187 20584 245 259；84 288 300；84 437 445；84 585 591；84 880 884；85 132 157；85 204 221；85 720 72587 116 145；87 416 425；88 105 137；88 165 187；88 234 250；88 480 488；88 966 970；90 120 15090 216 234；90 400 410；90 672 678；91 312 325；91 588 595；92 525 533；93 124 155；93 476 48595 168 193；95 228 247；95 900 905；96 110 146；96 128 160；96 180 204；96 247 265；96 280 29696 378 390；96 572 580；96 765 771；98 336 350；99 132 165；99 168 195；99 440 451；99 540 549100 105 145；100240260；100 495 505；100621629.以下是大于100的勾股数：第223组：102 136 170第224组：102 280 298第225组：102 864 870第226组：104 153 185第227组：104 195 221第228组：104 330 346第229组：104 672 680第230组：105 140 175第231组：105 208 233第232组：105 252 273第233组：105 360 375第234组：105 608 617第235组：105 784 791第236组：108 144 180第237组：108 231 255第238组：108 315 333第239组：108 480 492第240组：108 725 733第241组：108 969 975第242组：110 264 286第243组：110 600 610第244组：111 148 185第245组：111 680 689第246组：112 180 212第247组：112 210 238第248组：112 384 400第249组：112 441 455第250组：112 780 788第251组：114 152 190第252组：114 352 370第253组：115 252 277第254组：115 276 299第256组：117 156 195 第257组：117 240 267 第258组：117 520 533 第259组：117 756 765 第260组：119 120 169 第261组：119 408 425 第262组：120 126 174 第263组：120 160 200 第264组：120 182 218 第265组：120 209 241 第266组：120 225 255 第267组：120 288 312 第268组：120 350 370 第269组：120 391 409 第270组：120 442 458 第271组：120 594 606 第272组：120 715 725 第273组：120 896 904 第274组：121 660 671 第275组：123 164 205 第276组：123 836 845 第277组：124 957 965 第278组：125 300 325 第279组：126 168 210 第280组：126 432 450 第281组：126 560 574 第282组：128 240 272 第283组：128 504 520 第284组：129 172 215 第285组：129 920 929 第286组：130 144 194 第287组：130 312 338 第288组：130 840 850 第289组：132 176 220 第290组：132 224 260 第291组：132 351 375 第292组：132 385 407 第293组：132 475 493 第294组：132 720 732 第295组：133 156 205 第296组：133 456 475 第297组：135 180 225 第298组：135 324 351第300组：135 600 615 第301组：136 255 289 第302组：136 273 305 第303组：136 570 586 第304组：138 184 230 第305组：138 520 538 第306组：140 147 203 第307组：140 171 221 第308组：140 225 265 第309组：140 336 364 第310组：140 480 500 第311组：140 693 707 第312组：140 975 985 第313组：141 188 235 第314组：143 780 793 第315组：143 924 935 第316组：144 165 219 第317组：144 192 240 第318组：144 270 306 第319组：144 308 340 第320组：144 420 444 第321组：144 567 585 第322组：144 640 656 第323组：144 858 870 第324组：145 348 377 第325组：145 408 433 第326组：147 196 245 第327组：147 504 525 第328组：150 200 250 第329组：150 360 390 第330组：150 616 634 第331组：152 285 323 第332组：152 345 377 第333组：152 714 730 第334组：153 204 255 第335组：153 420 447 第336组：153 680 697 第337组：154 528 550 第338组：154 840 854 第339组：155 372 403 第340组：155 468 493 第341组：156 208 260 第342组：156 320 356第343组：156 455 481 第344组：156 495 519 第345组：156 667 685 第346组：159 212 265 第347组：160 168 232 第348组：160 231 281 第349组：160 300 340 第350组：160 384 416 第351组：160 630 650 第352组：160 792 808 第353组：161 240 289 第354组：161 552 575 第355组：162 216 270 第356组：162 720 738 第357组：165 220 275 第358组：165 280 325 第359组：165 396 429 第360组：165 532 557 第361组：165 900 915 第362组：168 224 280 第363组：168 270 318 第364组：168 315 357 第365组：168 374 410 第366组：168 425 457 第367组：168 490 518 第368组：168 576 600 第369组：168 775 793 第370组：168 874 890 第371组：170 264 314 第372组：170 408 442 第373组：171 228 285 第374组：171 528 555 第375组：171 760 779 第376组：174 232 290 第377组：174 832 850 第378组：175 288 337 第379组：175 420 455 第380组：175 600 625 第381组：176 210 274 第382组：176 330 374 第383组：176 468 500 第384组：176 693 715 第385组：176 960 976 第386组：177 236 295第388组：180 240 300 第389组：180 273 327 第390组：180 299 349 第391组：180 385 425 第392组：180 432 468 第393组：180 525 555 第394组：180 663 687 第395组：180 800 820 第396组：180 891 909 第397组：182 624 650 第398组：183 244 305 第399组：184 345 391 第400组：184 513 545 第401组：185 444 481 第402组：185 672 697 第403组：186 248 310 第404组：186 952 970 第405组：189 252 315 第406组：189 340 389 第407组：189 648 675 第408组：189 840 861 第409组：190 336 386 第410组：190 456 494 第411组：192 220 292 第412组：192 256 320 第413组：192 360 408 第414组：192 494 530 第415组：192 560 592 第416组：192 756 780 第417组：195 216 291 第418组：195 260 325 第419组：195 400 445 第420组：195 468 507 第421组：195 748 773 第422组：196 315 371 第423组：196 672 700 第424组：198 264 330 第425组：198 336 390 第426组：198 880 902 第427组：200 210 290 第428组：200 375 425 第429组：200 480 520 第430组：200 609 641第432组：203 396 445 第433组：203 696 725 第434组：204 253 325 第435组：204 272 340 第436组：204 560 596 第437组：204 595 629 第438组：204 855 879 第439组：205 492 533 第440组：205 828 853 第441组：207 224 305 第442组：207 276 345 第443组：207 780 807 第444组：207 920 943 第445组：208 306 370 第446组：208 390 442 第447组：208 660 692 第448组：208 819 845 第449组：210 280 350 第450组：210 416 466 第451组：210 504 546 第452组：210 720 750 第453组：213 284 355 第454组：215 516 559 第455组：215 912 937 第456组：216 288 360 第457组：216 405 459 第458组：216 462 510 第459组：216 630 666 第460组：216 713 745 第461组：216 960 984 第462组：217 456 505 第463组：217 744 775 第464组：219 292 365 第465组：220 231 319 第466组：220 459 509 第467组：220 528 572 第468组：220 585 625 第469组：222 296 370 第470组：224 360 424 第471组：224 420 476 第472组：224 768 800 第473组：224 882 910 第474组：225 272 353第476组：225 540 585 第477组：225 924 951 第478组：228 304 380 第479组：228 325 397 第480组：228 665 703 第481组：228 704 740 第482组：230 504 554 第483组：230 552 598 第484组：231 308 385 第485组：231 392 455 第486组：231 520 569 第487组：231 792 825 第488组：232 435 493 第489组：232 825 857 第490组：234 312 390 第491组：234 480 534 第492组：235 564 611 第493组：237 316 395 第494组：238 240 338 第495组：238 816 850 第496组：240 252 348 第497组：240 275 365 第498组：240 320 400 第499组：240 364 436 第500组：240 418 482 第501组：240 450 510 第502组：240 551 601 第503组：240 576 624 第504组：240 700 740 第505组：240 782 818 第506组：240 884 916 第507组：240 945 975 第508组：243 324 405 第509组：245 588 637 第510组：245 840 875 第511组：246 328 410 第512组：248 465 527 第513组：248 945 977 第514组：249 332 415 第515组：250 600 650 第516组：252 275 373 第517组：252 336 420 第518组：252 405 477第519组：252 539 595 第520组：252 561 615 第521组：252 735 777 第522组：252 864 900 第523组：255 340 425 第524组：255 396 471 第525组：255 612 663 第526组：255 700 745 第527组：256 480 544 第528组：258 344 430 第529组：259 660 709 第530组：259 888 925 第531组：260 273 377 第532组：260 288 388 第533组：260 624 676 第534组：260 651 701 第535组：260 825 865 第536组：261 348 435 第537组：261 380 461 第538组：264 315 411 第539组：264 352 440 第540组：264 448 520 第541组：264 495 561 第542组：264 702 750 第543组：264 770 814 第544组：264 950 986 第545组：265 636 689 第546组：266 312 410 第547组：266 912 950 第548组：267 356 445 第549组：270 360 450 第550组：270 648 702 第551组：270 704 754 第552组：272 510 578 第553组：272 546 610 第554组：273 364 455 第555组：273 560 623 第556组：273 736 785 第557组：273 936 975 第558组：275 660 715 第559组：276 368 460 第560组：276 493 565 第561组：276 805 851 第562组：279 372 465第564组：280 294 406 第565组：280 342 442 第566组：280 351 449 第567组：280 450 530 第568组：280 525 595 第569组：280 672 728 第570组：280 759 809 第571组：280 960 1000 第572组：282 376 470 第573组：285 380 475 第574组：285 504 579 第575组：285 684 741 第576组：285 880 925 第577组：287 816 865 第578组：288 330 438 第579组：288 384 480 第580组：288 540 612 第581组：288 616 680 第582组：288 741 795 第583组：288 840 888 第584组：290 696 754 第585组：290 816 866 第586组：291 388 485 第587组：294 392 490 第588组：295 708 767 第589组：296 555 629 第590组：297 304 425 第591组：297 396 495 第592组：297 504 585 第593组：300 315 435 第594组：300 400 500 第595组：300 455 545 第596组：300 589 661 第597组：300 720 780 第598组：300 875 925 第599组：301 900 949 第600组：303 404 505 第601组：304 570 646 第602组：304 690 754 第603组：305 732 793 第604组：306 408 510 第605组：306 840 894 第606组：308 435 533第608组：308 819 875 第609组：309 412 515 第610组：310 744 806 第611组：310 936 986 第612组：312 416 520 第613组：312 459 555 第614组：312 585 663 第615组：312 640 712 第616组：312 910 962 第617组：315 420 525 第618组：315 572 653 第619组：315 624 699 第620组：315 756 819 第621组：318 424 530 第622组：319 360 481 第623组：320 336 464 第624组：320 462 562 第625组：320 600 680 第626组：320 768 832 第627组：321 428 535 第628组：322 480 578 第629组：324 432 540 第630组：324 693 765 第631组：324 945 999 第632组：325 360 485 第633组：325 780 845 第634组：327 436 545 第635组：328 615 697 第636组：330 440 550 第637组：330 560 650 第638组：330 792 858 第639组：333 444 555 第640组：333 644 725 第641组：335 804 871 第642组：336 377 505 第643组：336 385 511 第644组：336 448 560 第645组：336 527 625 第646组：336 540 636 第647组：336 630 714 第648组：336 748 820 第649组：336 850 914 第650组：339 452 565第652组：340 528 628 第653组：340 816 884 第654组：341 420 541 第655组：342 456 570 第656组：344 645 731 第657组：345 460 575 第658组：345 756 831 第659组：345 828 897 第660组：348 464 580 第661组：348 805 877 第662组：350 576 674 第663组：350 840 910 第664组：351 468 585 第665组：351 720 801 第666组：352 420 548 第667组：352 660 748 第668组：352 936 1000 第669组：354 472 590 第670组：355 852 923 第671组：357 360 507 第672组：357 476 595 第673组：360 378 522 第674组：360 480 600 第675组：360 546 654 第676组：360 598 698 第677组：360 627 723 第678组：360 675 765 第679组：360 770 850 第680组：360 864 936 第681组：363 484 605 第682组：363 616 715 第683组：364 585 689 第684组：364 627 725 第685组：365 876 949 第686组：366 488 610 第687组：368 465 593 第688组：368 690 782 第689组：369 492 615 第690组：369 800 881 第691组：370 888 962 第692组：372 496 620 第693组：372 925 997 第694组：375 500 625第696组：376 705 799 第697组：378 504 630 第698组：378 680 778 第699组：380 399 551 第700组：380 672 772 第701组：380 912 988 第702组：381 508 635 第703组：384 440 584 第704组：384 512 640 第705组：384 720 816 第706组：385 552 673 第707组：387 516 645 第708组：387 884 965 第709组：390 432 582 第710组：390 520 650 第711组：390 800 890 第712组：392 630 742 第713组：392 735 833 第714组：393 524 655 第715组：396 403 565 第716组：396 528 660 第717组：396 672 780 第718组：396 847 935 第719组：399 468 615 第720组：399 532 665 第721组：400 420 580 第722组：400 561 689 第723组：400 750 850 第724组：402 536 670 第725组：405 540 675 第726组：406 792 890 第727组：407 624 745 第728组：408 506 650 第729组：408 544 680 第730组：408 765 867 第731组：408 819 915 第732组：411 548 685 第733组：414 448 610 第734组：414 552 690 第735组：416 612 740 第736组：416 780 884 第737组：417 556 695 第738组：420 441 609第740组：420 560 700 第741组：420 637 763 第742组：420 675 795 第743组：420 832 932 第744组：420 851 949 第745组：423 564 705 第746组：424 795 901 第747组：425 660 785 第748组：426 568 710 第749组：429 460 629 第750组：429 572 715 第751组：429 700 821 第752组：429 728 845 第753组：429 880 979 第754组：432 495 657 第755组：432 576 720 第756组：432 665 793 第757组：432 810 918 第758组：435 580 725 第759组：438 584 730 第760组：440 462 638 第761组：440 525 685 第762组：440 825 935 第763组：441 588 735 第764组：444 592 740 第765组：447 596 745 第766组：448 720 848 第767组：448 840 952 第768组：450 544 706 第769组：450 600 750 第770组：451 780 901 第771组：453 604 755 第772组：455 504 679 第773组：455 528 697 第774组：456 608 760 第775组：456 650 794 第776组：456 855 969 第777组：459 612 765 第778组：460 483 667 第779组：462 616 770 第780组：462 784 910 第781组：464 777 905 第782组：464 870 986第784组：468 595 757 第785组：468 624 780 第786组：471 628 785 第787组：473 864 985 第788组：474 632 790 第789组：475 840 965 第790组：476 480 676 第791组：476 765 901 第792组：477 636 795 第793组：480 504 696 第794组：480 550 730 第795组：480 640 800 第796组：480 693 843 第797组：480 728 872 第798组：480 836 964 第799组：481 600 769 第800组：483 644 805 第801组：483 720 867 第802组：486 648 810 第803组：489 652 815 第804组：492 656 820 第805组：495 660 825 第806组：495 840 975 第807组：498 664 830 第808组：500 525 725 第809组：501 668 835 第810组：504 550 746 第811组：504 672 840 第812组：504 703 865 第813组：504 810 954 第814组：507 676 845 第815组：510 680 850 第816组：510 792 942 第817组：513 684 855 第818组：516 688 860 第819组：519 692 865 第820组：520 546 754 第821组：520 576 776 第822组：520 765 925 第823组：522 696 870 第824组：522 760 922 第825组：525 700 875 第826组：528 605 803第828组：528 704 880 第829组：531 708 885 第830组：532 624 820 第831组：533 756 925 第832组：534 712 890 第833组：537 716 895 第834组：540 567 783 第835组：540 629 829 第836组：540 720 900 第837组：540 819 981 第838组：543 724 905 第839组：546 728 910 第840组：549 732 915 第841组：552 736 920 第842组：555 572 797 第843组：555 740 925 第844组：558 744 930 第845组：560 588 812 第846组：560 684 884 第847组：560 702 898 第848组：561 748 935 第849组：564 752 940 第850组：567 756 945 第851组：570 760 950 第852组：573 764 955 第853组：576 660 876 第854组：576 768 960 第855组：579 772 965 第856组：580 609 841 第857组：580 741 941 第858组：582 776 970 第859组：585 648 873 第860组：585 780 975 第861组：588 784 980 第862组：591 788 985 第863组：594 608 850 第864组：594 792 990 第865组：595 600 845 第866组：597 796 995 第867组：600 630 870 第868组：600 800 1000 第869组：612 759 975 第870组：615 728 953第872组：616 735 959 第873组：620 651 899 第874组：621 672 915 第875组：624 715 949 第876组：638 720 962 第877组：640 672 928 第878组：650 720 970 第879组：660 693 957 第880组：680 714 986 第881组：696 697 985。