平行四边形提高练习题
【数学】数学平行四边形的专项培优练习题(含答案)含答案

【点睛】
本题考查了矩形的性质,全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,本题中求证DB=DM是解题的关键.
5.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
4.如图所示,矩形ABCD中,点E在CB的延长线上,使CE=AC,连接AE,点F是AE的中点,连接BF、DF,求证:BF⊥DF.
【答案】见解析.
【解析】
【分析】
延长BF,交DA的延长线于点M,连接BD,进而求证△AFM≌△EFB,得AM=BE,FB=FM,即可求得BC+BE=AD+AM,进而求得BD=BM,根据等腰三角形三线合一的性质即可求证BF⊥DF.
在Rt△APE中,(4-BE)2+x2=BE2.
解得BE=2+ ,
∴CF=BE-EM=2+ -x,
∴BE+CF= -x+4= (x-2)2+3.
当x=2时,BE+CF取最小值,
∴AP=2.
考点:几何变换综合题.
3.如图,在△ABC中,∠ACB=90°,∠CAB=30°,以线段AB为边向外作等边△ABD,点E是线段AB的中点,连接CE并延长交线段AD于点F.
∴BM=ME,BM⊥EM.
故答案为BM=ME,BM⊥EM.
(2)ME= MB.
证明如下:连接CM,如解图所示.
∵DC⊥AC,M是边AD的中点,
∴MC=MA=MD.
∵BA=BC,
∴BM垂直平分AC.
∵∠ABC=120°,BA=BC,
∴∠MBE= ∠ABC=60°,∠BAC=∠BCA=30°,∠DCE=60°.
五年级数学上册 平行四边形练习题

五年级数学上册:平行四边形练习题一、填空。
1、平行四边形有()组对边分别平行,梯形有()组对边分别平行。
2、在四边形中,一组对边平行且相等的四边形是();只有一组对边平行的四边形是()3、长方形是特殊的(),正方形是特殊的()。
4、用2个完全一样的梯形,可以拼成一个(),它的底长是原来梯形的()与()之和。
5、一个直角梯形,上底是8厘米,下底是12厘米,直角腰是10厘米,另一条腰是7厘米,这个梯形的面积是()平方厘米。
6、一个平行四边形的底长是10厘米,高是8厘米,它的面积是()平方厘米;一个梯形的上底是10厘米,下底是15厘米,高是8厘米,它的面积是()平方厘米。
7、一个平行四边形,若底增加2厘米,高增加5厘米,则面积增加()平方厘米。
8、一个长方形和一个平行四边形的底边长度相等,且它们的面积也相等。
已知长方形的面积是48平方分米,平行四边形的高是4分米,那么平行四边形的底边长是()分米。
9、两个()的梯形可以拼成一个平行四边形。
二、解答题。
1、一个直角梯形的上底是8厘米,下底是12厘米,腰长为10厘米。
求它的面积?2、一个长方形和一个平行四边形的底边长度相等,并且它们的面积也相等。
已知长方形的面积是48平方分米,平行四边形的高是4分米,求平行四边形的底边长。
3、一个梯形的上底长度不变,下底缩短后与上底长度相等时,它的面积会如何变化?五年级数学平行四边形的面积练习题在五年级的数学学习中,平行四边形的面积计算是一个重要的知识点。
为了帮助学生更好地掌握这一知识点,下面是一组关于平行四边形面积的练习题。
1、计算下列平行四边形的面积:(1)底为6厘米,高为4厘米;(2)底为8厘米,高为3厘米;(3)底为10厘米,高为2厘米。
2.一个平行四边形的底长为12分米,高为8分米,它的面积是多少?3.一个平行四边形的底长为16厘米,高为10厘米,它的面积是多少?4.一个平行四边形的底长为20毫米,高为15毫米,它的面积是多少?5.一个平行四边形的底长为24米,高为18米,它的面积是多少?答案:1、(1)6×4=24(平方厘米)(2)8×3=24(平方厘米)(3)10×2=20(平方厘米)2、12×8=96(平方分米)3、16×10=160(平方厘米)4、20×15=300(平方毫米)5、24×18=432(平方米)通过这组练习题,学生们可以加深对平行四边形面积计算公式的理解和记忆,同时提高他们的计算能力和空间思维能力。
2020—2021学年人教版数学八年级下册第18章《平行四边形》常考题提高练习(一)

人教版数学八年级下册第18章《平行四边形》常考题提高练习(一)1.已知,△ABC、△ADE是等腰三角形,AB=AC,AD=AE,D是BC上一点,∠DAE=∠BAC,过点E作BC的平行线交AB于点F,连接CF.(1)如图1,求证:四边形CDEF是平行四边形;(2)如图2,连接BE、DF,若AD⊥BC,在不添加任何辅助线的情况下,请直接写出图2中长度等于BC的长的的线段.2.如图,在▱ABCD中,点P在对角线AC上一动点,过点P作PM∥DC,且PM=DC,连接BM,CM,AP,BD.(1)求证:△ADP≌△BCM;(2)若P A=PC,设△ABP的面积为S,四边形BPCM的面积为T,求的值.3.如图,四边形ACFD是平行四边形,B,E,C,F在一条直线上,已知BE=CF.(1)求证:四边形ABED是平行四边形.(2)若∠ABC=60°,且AC⊥BF,AB=6,BF=5,求AD的长.4.如图,在▱ABCD中,AE⊥BC于点E,点F在线段DE上,且△ADF∽△DEC,若DC=4cm,AD=cm,AF=cm.(1)求DE的长;(2)求▱ABCD的面积.5.如图,在菱形ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC 到点F,使得CF=BE,连接DF,(1)求证:四边形AEFD是矩形;(2)连接OE,若AB=13,OE=,求AE的长.6.如图,已知菱形ABCD的对角线AC、BD相交于点O,分别过A、D两点作AO、DO的垂线,两垂线交于点E.(1)求证:四边形AODE是矩形;(2)若四边形AODE的面积为12,AD=5,求四边形AODE的周长.7.如图,在矩形ABCD中,E是BC上一点,DF⊥AE于点F,设=λ(λ>0).(1)若λ=1,求证:CE=FE;(2)若AB=3,AD=4,且D、B、F在同一直线上时,求λ的值.8.如图,分别以Rt△ACB的直角边AC和斜边AB向外作等边△ACE,等边△ABD,取AB 的中点F,连接DF、EF,已知∠BAC=30°.(1)求证:四边形ADFE是平行四边形;(2)若BD=4,求四边形BCEF的面积.9.如图,在△ABC中,AB=AC,D是BC中点、F是AC中点,AN是∠ABC的外角∠MAC 的平分线,延长DF交AN于点E,连接CE.(1)求证:四边形ADCE是矩形;(2)若AB=BC=4,则四边形ADCE的面积为多少?(3)直接回答:当△ABC满足时,四边形ADCE是正方形.10.如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD,BC交于M,N两点,连接CM,AN.(1)求证:四边形ANCM为平行四边形;(2)若AD=4,AB=2,且MN⊥AC,求DM的长.11.已知:l∥m∥n∥k,平行线l与m、m与n、n与k之间的距离分别为d1,d2,d3,且d1=d3=2,d2=3.我们把四个顶点分别在l,m,n,k这四条平行线上的四边形称为“线上四边形”.(1)如图1,正方形ABCD为“线上四边形”,BE⊥l于点E,EB的延长线交直线k于点F,求正方形ABCD的边长.(2)如图2,菱形ABCD为“线上四边形”且∠ADC=60°,△AEF是等边三角形,点E在直线k上,连接DF,且直线DF分别交直线l、k于点G、M,求证:EC=DF.12.如图,正方形ABCD,G是BC边上任意一点(不与B、C重合),DE⊥AG于点E,BF ∥DE,且交AG于点F.(1)求证:AF﹣BF=EF;(2)四边形BFDE是否可能是平行四边形,如果可能,请指出此时点G的位置,如不可能,请说明理由.13.如图,在△ABC中,点D,E分别是BC,AC的中点,延长BA至点F,使得AF=AB,连接DE,AD,EF,DF.(1)求证:四边形ADEF是平行四边形;(2)若AB=6,AC=8,BC=10,求EF的长.14.矩形ABCD中,AB=3,BC=4.点E,F在对角线AC上,点M,N分别在边AD,BC 上.(1)如图1,若AE=CF=1,M,N分别是AD,BC的中点.求证:四边形EMFN为矩形.(2)如图2,若AE=CF=0.5,AM=CN=x(0<x<2),且四边形EMFN为矩形,求x 的值.15.如图,四边形ABCD的对角线AC⊥BD于点E,点F为四边形ABCD外一点,且∠FCA =90°,BC平分∠DBF,∠CBF=∠DCB.(1)求证:四边形DBFC是菱形;(2)若AB=BC,∠F=45°,BD=2,求AC的长.参考答案1.(1)如答图1,证明:连接BE,∵∠BAC=∠DAE,∴∠DAC=∠EAB,在△ACD和△ABE中,,∴△ACD≌△ABE(SAS),∴CD=BE,∠ACD=∠ABE,∵EF∥BC,∴∠ABC=∠EFB,∴∠ABE=∠EFB,∴EB=EF,∴EF=CD,∵EF∥BC,∴四边形EDCF是平行四边形;(2)∵AB=AC,AD⊥BC,∴BD=CD=BC,由(1)知CD=BE=EF,∴BD=EF,∵E作BC的平行线交AB于点F,即BD||EF,∴四边形BEFD是平行四边形,∴BD =CD =BE =EF =DF =BC ,故答案为:BD ,CD ,BE ,EF ,DF .2.解:(1)∵PM ∥DC ,且PM =DC ,∴四边形CDPM 是平行四边形,∴PD =MC ,∵AB ∥DC ,且AB =DC ,PM ∥DC ,且PM =DC ,∴AB ∥PM ,且AB =PM ,∴四边形ABMP 是平行四边形,∴AP =BM ,∵四边形ABCD 是平行四边形,∴AD =BC ,∴△ADP ≌△BCM (SSS );(2)由(1)可得S △ADP =S △BCM ,∴S 四边形BMCP =S △BCM +S △BCP =S △ADP +S △BCP =S 平行四边形ABCD , 又∵P A =PC ,∴S △ABP =S △ABC =S 平行四边形ABCD ,∴的值为=.3.证明:(1)∵四边形ACFD 是平行四边形,∴AD ∥CF ,AD =CF ,∵B ,E ,C ,F 在一条直线上,∴AD ∥BE ,∴AD=BE,∴四边形ABED是平行四边形;(2)∵四边形ACFD是平行四边形,∴AD=CF,∵∠ABC=60°,且AC⊥BF,AB=6,∴∠BAC=30°,∴BC=AB=3,∵BF=5,∴CF=BF﹣BC=2,∴AD=2.4.解:(1)∵△ADF∽△DEC,∴,∴,∴DE=6;(2)∵四边形ABCD为平行四边形,∠EAD=∠AEB=90°,∴在Rt△EAD中,,∴AE=3(cm),∴S▱ABCD=BC•AE=.5.(1)证明:∵四边形ABCD是菱形,∴AD∥BC且AD=BC,∵BE=CF,∴BC=EF,∴AD=EF,∵AD∥EF,∴四边形AEFD是平行四边形,∵AE⊥BC,∴∠AEF=90°,∴四边形AEFD是矩形;(2)解:∵四边形ABCD是菱形,AB=13,∴BC=AB=13,AC⊥BD,OA=OC=AC,OB=OD=BD,∵AE⊥BC,∴∠AEC=90°,∴OE=AC=OA=2,AC=2OE=4,∴OB===3,∴BD=2OB=6,∵菱形ABCD的面积=BD×AC=BC×AE,即×6×4=13×AE,解得:AE=12.6.(1)证明:∵四边形ABCD是菱形,∴AC⊥BD,∴∠AOD=90°,∵EA⊥AO,DE⊥DO,∴∠EAO=∠DOA=90°,∴四边形AODE是矩形;(2)解:由(1)知,四边形AODE是矩形,∴∠AED=90°,OA=DE,OD=AE,∵四边形AODE的面积为12,∴OA•OD=12,在Rt△AOD中,根据勾股定理,得OA2+OD2=AD2=25,∴(OA+OD)2=OA2+2OA•OD+OD2=25+24=49,∴OA+OD=7,∴四边形AODE的周长为2(OA+OD)=14.7.解:(1)证明:连接DE,如图:∵四边形ABCD为矩形,∴∠C=90°,AD∥BC,∴∠ADE=∠CED,∵DF⊥AE,∴∠DFE=90°,∴∠DFE=∠C,∵=λ=1,∴AD=AE,∴∠ADE=∠FED,∴∠FED=∠CED,在△DFE和△DCE中,,∴△DFE≌△DCE(AAS),∴CE=FE;(2)当D、B、F在同一直线上时,如图所示:∵四边形ABCD为矩形,∴∠BAD=∠ABC=90°,在Rt△ADB中,AB=3,AD=4,∴tan∠ABD==,∵DF⊥AE,∴∠BFE=90°,∵∠ABD+∠DBC=90°,∠DBC+∠FEB=90°,∴∠FEB=∠ABD,∴=tan∠FEB=tan∠ABD=,∵AB=3,∴BE=,在Rt△ABE中,由勾股定理得,AE==,∴λ====.8.(1)证明:∵Rt△ABC中,∠BAC=30°,∴AB=2BC,又∵△ABD是等边三角形,F是AB的中点,∴AD=AB=BD,AB=2AF,DF⊥AB,∴AF=BC,在Rt△AFD和Rt△BCA中,,∴Rt△AFD≌Rt△BCA(HL),∴DF=AC,∵△ACE是等边三角形,∴∠EAC=60°,AC=AE,∴∠EAB=∠EAC+∠BAC=90°,∴DF=AE,又∵DF⊥AB,∴DF∥AE,∴四边形ADFE是平行四边形;(2)解:由(1)得:△AEF的面积=△ADF的面积=△ABC的面积,AB=BD=4,BC =AB=2,AC=BC=2,∴四边形BCEF的面积=△ACE的面积+△ABC的面积﹣△AEF的面积=△ACE的面积=×(2)2=3.9.(1)证明:∵AN是△ABC外角∠CAM的平分线,∴∠MAE=∠MAC,∵∠MAC=∠B+∠ACB,∵AB=AC,∴∠B=∠ACB,∴∠MAE=∠B,∴AN∥BC,∵F为AC的中点,D为BC的中点,∴FD∥AB,∴四边形ABDE为平行四边形,∴AE=BD,∵BD=CD,∴AE=CD,∴四边形ADCE为平行四边形,∵AB=AC,点D为BC中点,∴AD⊥BC,∴AD⊥AE,∴∠DAE=90°,∴四边形ADCE为矩形;(2)解:由(1)知四边形ADCE是矩形,∵BC=AB=4,AB=AC,∴△ABC是等边三角形,∴AB=AC=BC=4,∵D为BC的中点,∴∠ADC=90°,BD=CD=2,∴AD=2,∴四边形ADCE的面积为CD×AD=2×2=4;(3)解:答案不唯一,如当∠BAC=90°时,四边形ADCE是正方形.∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∵D为BC的中点,∴AD=DC,∵四边形ADCE为矩形,∴四边形ADCE为正方形.故答案为:∠BAC=90°.10.(1)证明:∵在矩形ABCD中,O为对角线AC的中点,∴AD∥BC,AO=CO,∴∠OAM=∠OCN,∠OMA=∠ONC,在△AOM和△CON中,,∴△AOM≌△CON(AAS),∴AM=CN,∵AM∥CN,∴四边形ANCM为平行四边形;(2)解:∵在矩形ABCD中,AD=BC,由(1)知:AM=CN,∴DM=BN,∵四边形ANCM为平行四边形,MN⊥AC,∴平行四边形ANCM为菱形,∴AM=AN=NC=AD﹣DM,∴在Rt△ABN中,根据勾股定理,得AN2=AB2+BN2,∴(4﹣DM)2=22+DM2,解得DM=.11.解:(1)如图1,∵l∥m∥n∥k,BE⊥l,∴BE⊥k,BE⊥m,BE⊥n,∴∠AEB=∠BFC=90°,BE=5,BF=2,∴∠CBF+∠BCF=90°,∵正方形ABCD为“线上四边形”,∴AB=BC,∠ABC=90°,∴∠ABE+∠CBF=90°,∴∠ABE=∠BCF,∴△ABE≌△BCF(AAS),∴FC=BE=5,∴BC===;(2)如图2,连接AC,∵四边形ABCD是菱形,∴AD=CD,∵∠ADC=60°,∴△ADC是等边三角形,∴AD=AC,∠CAD=60°,∵△AEF是等边三角形,∴AE=AF,∠EAF=60°,∴∠EAF=∠CAD,∴∠EAC=∠DAF,∴△EAC≌△F AD(SAS),∴EC=DF.12.解:(1)证明:∵四边形ABCD是正方形,∴AB=AD,∠BAF+∠DAE=90°,∵DE⊥AG,∴∠DAE+∠ADE=90°,∴∠ADE=∠BAF,又∵BF∥DE,∴∠BF A=90°=∠AED,∴△ABF≌△DAE(AAS),∴AE=BF,∴AF﹣BF=AF﹣AE=EF;(2)不可能,理由是:如图,若要四边形BFDE是平行四边形,已知DE∥BF,则当DE=BF时,四边形BFDE为平行四边形,∵DE=AF,∴BF=AF,即此时∠BAF=45°,而点G不与B和C重合,∴∠BAF≠45°,矛盾,∴四边形BFDE不可能是平行四边形.13.(1)证明:∵点D,E分别是BC,AC的中点,∴DE是△ABC的中位线,∴DE∥AB,DE=AB,∵AF=AB,∴DE=AF,DE∥AF,∴四边形ADEF是平行四边形;(2)解:由(1)得:四边形ADEF是平行四边形,∴EF=AD,∵AB=6,AC=8,BC=10,∴AB2+AC2=BC2,∴△ABC是直角三角形,∠BAC=90°,∵点D是BC的中点,∴AD=BC=5,∴EF=AD=5.14.(1)证明:连接MN,如图1所示:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∠B=90°,∴∠EAM=∠FCN,AC===5,∵M,N分别是AD,BC的中点,∴AM=DM=BN=CN,AM∥BN,∴四边形ABNM是平行四边形,又∵∠B=90°,∴四边形ABNM是矩形,∴MN=AB=3,在△AME和△CNF中,,∴△AME≌△CNF(SAS),∴EM=FN,∠AEM=∠CFN,∴∠MEF=∠NFE,∴EM∥FN,∴四边形EMFN是平行四边形,又∵AE=CF=1,∴EF=AC﹣AE﹣CF=3,∴MN=EF,∴四边形EMFN为矩形.(2)解:连接MN,作MH⊥BC于H,如图2所示:则四边形ABHM是矩形,∴MH=AB=3,BH=AM=x,∴HN=BC﹣BH﹣CN=4﹣2x,∵四边形EMFN为矩形,AE=CF=0.5,∴MN=EF=AC﹣AE﹣CF=4,在Rt△MHN中,由勾股定理得:32+(4﹣2x)2=42,解得:x=2±,∵0<x<2,∴x=2﹣.15.(1)证明:∵AC⊥BD,∠FCA=90°,∠CBF=∠DCB.∴BD∥CF,CD∥BF,∴四边形DBFC是平行四边形;∵BC平分∠DBF,∴∠CBF=∠CBD,∵∠CBF=∠DCB,∴∠CBD=∠DCB,∴CD=BD,∴四边形DBFC是菱形;(2)解:∵四边形DBFC是平行四边形,∴CF=BD=2,∵AB=BC,AC⊥BD,∴AE=CE,作CM⊥BF于M,如图:∵BC平分∠DBF,∴CE=CM,∵∠F=45°,∴△CFM是等腰直角三角形,∴CM=CF=,∴AE=CE=,∴AC=2.。
平行四边形、矩形、菱形、正方形提高题
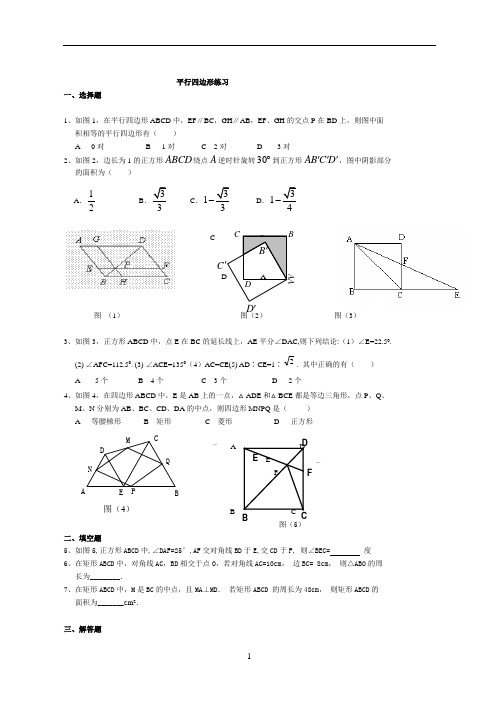
平行四边形练习 一、选择题1、如图1,在平行四边形ABCD 中,EF ∥BC ,GH ∥AB ,EF 、GH 的交点P 在BD 上,则图中面 积相等的平行四边形有( )A 0对B 1对C 2对D 3对 2、如图2,边长为1的正方形ABCD 绕点A 逆时针旋转30︒到正方形AB C D ''',图中阴影部分的面积为( )A .12B .33C .313-D .314-CBD A图 (1) 图(2) 图(3)3、如图3,正方形ABCD 中,点E 在BC 的延长线上,AE 平分∠DAC,则下列结论:(1)∠E=22.50. (2) ∠AFC=112.50. (3) ∠ACE=1350(4)AC=CE(5) AD ∶CE=1∶2. 其中正确的有( ) A 5个 B 4个 C 3个 D 2个4、如图4,在四边形ABCD 中,E 是AB 上的一点,△ADE 和△BCE 都是等边三角形,点P 、Q 、 M 、N 分别为AB 、BC 、CD 、DA 的中点,则四边形MNPQ 是( ) A 等腰梯形 B 矩形 C 菱形 D 正方形A DEFB C图(5)二、填空题5、如图5,正方形ABCD 中,∠DAF=25°,AF 交对角线BD 于E,交CD 于F, 则∠BEC= 度6、在矩形ABCD 中,对角线AC ,BD 相交于点O ,若对角线AC=10cm ,•边BC=•8cm ,•则△ABO 的周 长为________.7、在矩形ABCD 中,M 是BC 的中点,且MA ⊥MD .•若矩形ABCD•的周长为48cm ,•则矩形ABCD 的 面积为_______c m 2.三、解答题C BB '__D C 'D 'DAAQ E PMN DCBA 图(4)_ E _ F_ B_ C8、已知,如图,矩形ABCD 的对角线AC ,BD 相交于点O ,E ,F 分别是OA ,OB 的中点. (1)求证:△ADE ≌△BCF ;(2)若AD=4cm ,AB=8cm ,求OF 的长.10、如图,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF =BE . ⑴求证:CE =CF ;⑵在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? ⑶运用⑴⑵解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =6,E 是AB 上一点, 且∠DCE =45°,BE =2,求DE 的长.6.如图1,在△ABC 中,AB=BC ,P 为AB 边上一点,连接CP ,以PA 、PC 为邻边作□APCD ,AC 与PD 相交于点E ,已知∠ABC=∠AEP=α(0°<α<90°). (1)求证:∠EAP=∠EPA;(2)□APCD 是否为矩形?请说明理由;(3)如图2,F 为BC 中点,连接FP ,将∠AEP 绕点E 顺时针旋转适当的角度,得到∠MEN(点M 、N 分别是∠MEN 的两边与BA 、FP 延长线的交点).猜想线段EM 与EN 之间的数量关系,并证明你的结论.图1ABDCE P 图2ABDCEPM NFB CA G D FEB CA DE图1图2。
平行四边形和特殊四边形提高练习常考题和培优题(供参考)

平行四边形和特殊四边形提高练习常考题和培优题一.选择题(共5小题)1.如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形2.如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H 是AF的中点,那么CH的长是()A.3.5 B.C. D.23.如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O 作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.54.如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.275.如图,在矩形ABCD中,AB=6,AD=8,P是AD上不与A和D重合的一个动点,过点P分别作AC和BD的垂线,垂足为E、F,则PE+PF的值为()A.10 B.4.8 C.6 D.5二.填空题(共4小题)6.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE平分∠BAD交BC 于点E,若∠CAE=15°,则∠BOE的度数等于.7.如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=时,四边形ABEC是矩形.8.如图,在正五边形ABCDE中,连接AC、AD、CE,CE交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是.9.如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是.三.解答题(共31小题)10.如图,正方形ABCD中,AE=AB,直线DE交BC于点F,求∠BEF的度数.11.如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.12.如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.13.如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.14.如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.15.如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=度.16.已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?17.如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.18.如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.19.如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.20.如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG 交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.21.已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.22.如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN 交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:OE=OF;(2)当点O运动到何处时,四边形AECF是矩形?23.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.24.如图1,已知AB∥CD,AB=CD,∠A=∠D.(1)求证:四边形ABCD为矩形;(2)E是AB边的中点,F为AD边上一点,∠DFC=2∠BCE.①如图2,若F为AD中点,DF=1.6,求CF的长度:②如图2,若CE=4,CF=5,则AF+BC=,AF=.25.如图,直线a、b相交于点A,C、E分别是直线b、a上两点且BC⊥a,DE ⊥b,点M、N是EC、DB的中点.求证:MN⊥BD.26.如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形?(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.27.如图,E、F是正方形ABCD的边AD上的两个动点,满足AE=DF.连接CF 交BD于G,连接BE交AG于H.已知正方形ABCD的边长为4cm,解决下列问题:(1)求证:BE⊥AG;(2)求线段DH的长度的最小值.28.如图,点M是矩形ABCD的边AD的中点,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足为E、F.(1)当矩形ABCD的长与宽满足什么条件时,四边形PEMF为矩形?猜想并证明你的结论.(2)在(1)中,当点P运动到什么位置时,矩形PEMF变为正方形,为什么?29.某校数学兴趣小组开展了一次课外活动,过程如下:如图①,正方形ABCD 中,AB=4,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合.三角板的一边交AB于点P,另一边交BC的延长线于点Q.(1)求证:AP=CQ;(2)如图②,小明在图1的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并予以证明;(3)在(2)的条件下,若AP=1,求PE的长.30.如图,在菱形ABCD中,AB=4cm,∠ADC=120°,点E、F同时由A、C两点出发,分别沿AB、CB方向向点B匀速移动(到点B为止),点E的速度为1cm/s,点F的速度为2cm/s,经过t秒△DEF为等边三角形,求t的值.31.如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作∠ADB的角平分线DE交AB于点E,(1)求证:DE∥BC;(2)若AE=3,AD=5,点P为BC上的一动点,当BP为何值时,△DEP为等腰三角形.请直接写出所有BP的值.32.已知:如图,BF、BE分别是∠ABC及其邻补角的角平分线,AE⊥BE,垂足为点E,AF⊥BF,垂足为点F.EF分别交边AB、AC于点M、N.求证:(1)四边形AFBE是矩形;(2)BC=2MN.33.如图,在边长为5的菱形ABCD中,对角线BD=8,点O是直线BD上的动点,OE⊥AB于E,OF⊥AD于F.(1)对角线AC的长是,菱形ABCD的面积是;(2)如图1,当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由;(3)如图2,当点O在对角线BD的延长线上时,OE+OF的值是否发生变化?若不变请说明理由,若变化,请直接写出OE、OF之间的数量关系,不用明理由.34.如图,已知Rt△ABD≌Rt△FEC,且B、D、C、E在同一直线上,连接BF、AE.(1)求证:四边形ABFE是平行四边形.(2)若∠ABD=60°,AB=2cm,DC=4cm,将△ABD沿着BE方向以1cm/s的速度运动,设△ABD运动的时间为t,在△ABD运动过程中,试解决以下问题:(1)当四边形ABEF是菱形时,求t的值;(2)是否存在四边形ABFE是矩形的情形?如果存在,求出t的值,如果不存在,请说明理由.35.已知,矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.(2)如图1,求AF的长.(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止.在运动过程中,点P的速度为每秒1cm,设运动时间为t秒.①问在运动的过程中,以A、P、C、Q四点为顶点的四边形有可能是矩形吗?若有可能,请求出运动时间t和点Q的速度;若不可能,请说明理由.②若点Q的速度为每秒0.8cm,当A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.36.如图1,E,F是正方形ABCD的边上两个动点,满足AE=DF,连接CF交BD 于G,连接BE交AG于点H(1)求证:AG⊥BE;(2)如图2,连DH,若正方形的边长为4,则线段DH长度的最小值是.37.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E时AD边的中点,点M时AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN.(1)求证:四边形AMDN是平行四边形.(2)填空:①当AM的值为时,四边形AMDN是矩形;②当AM的值为时,四边形AMDN是菱形.38.如图,已知正方形OABC的边长为4,顶点A、C分别在x、y轴的正半轴上,M是BC的中点,点P(0,m)是线段oc上的一动点9点P不与点O、C重合0,直线PM交AB的延长线于点D.(1)求点D的坐标;(用含m的代数式表示)(2)若△APD是以AP边为一腰的等腰三角形,求m的值.39.如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;(2)若AC=10,CF=6,求线段AG的长度.40.如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连接EF与边CD相交于点G,连接BE与对角线AC相交于点H,AE=CF,BE=EG.(1)求证:EF∥AC;(2)求∠BEF大小;(3)若EB=4,则△BAE的面积为.初二数学平行四边形和特殊四边形提高练习常考题和培优题参考答案与试题解析一.选择题(共5小题)1.(2012春•炎陵县校级期中)如图,把大小相同的两个矩形拼成如下形状,则△FBD是()A.等边三角形B.等腰直角三角形C.一般三角形D.等腰三角形【分析】根据正方形性质得出FG=BC,∠G=∠C=90°,GB=CD,根据SAS证△FGB ≌△BCD,推出∠FBG=∠BDC,BF=BD,求出∠DBC+∠FBG=90°,求出∠FBD的度数即可.【解答】解:∵大小相同的两个矩形GFEB、ABCD,∴FG=BE=AD=BC,GB=EF=AB=CD,∠G=∠C=∠ABG=∠ABC=90°,∵在△FGB和△BCD中,∴△FGB≌△BCD,∴∠FBG=∠BDC,BF=BD,∵∠BDC+∠DBC=90°,∴∠DBC+∠FBG=90°,∴∠FBD=180°﹣90°=90°,即△FBD是等腰直角三角形,故选B.【点评】本题考查了等腰直角三角形,全等三角形的性质和判定,正方形性质的应用,关键是证出△FGB≌△BCD,主要考查学生运用性质进行推理的能力.2.(2015春•江阴市期中)如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,H是AF的中点,那么CH的长是()A.3.5 B.C. D.2【分析】根据正方形的性质求出AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,求出AM=4,FM=2,∠AMF=90°,根据正方形性质求出∠ACF=90°,根据直角三角形斜边上的中线性质求出CH=AF,根据勾股定理求出AF即可.【解答】解:∵正方形ABCD和正方形CEFG中,点D在CG上,BC=,CE=3,∴AB=BC=,CE=EF=3,∠E=90°,延长AD交EF于M,连接AC、CF,则AM=BC+CE=4,FM=EF﹣AB=2,∠AMF=90°,∵四边形ABCD和四边形GCEF是正方形,∴∠ACD=∠GCF=45°,∴∠ACF=90°,∵H为AF的中点,∴CH=AF,在Rt△AMF中,由勾股定理得:AF==2,∴CH=,故选:C.【点评】本题考查了勾股定理,正方形的性质,直角三角形斜边上的中线的应用,解此题的关键是能正确作出辅助线,并求出AF的长和得出CH=AF,有一定的难度.3.(2015春•泗洪县校级期中)如图,在矩形ABCD中,AB=4,BC=8,对角线AC、BD相交于点O,过点O作OE垂直AC交AD于点E,则AE的长是()A.3 B.5 C.2.4 D.2.5【分析】根据矩形的性质得出∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,根据线段垂直平分线性质得出AE=CE,在Rt△CDE中,由勾股定理得出CE2=CD2+DE2,代入求出即可.【解答】解:∵在矩形ABCD中,AB=4,BC=8,∴∠CDE=90°,AD=BC=8,AB=DC=4,AO=OC,∵OE⊥AC,∴AE=CE,在Rt△CDE中,由勾股定理得:CE2=CD2+DE2,即AE2=42+(8﹣AE)2,解得:AE=5,故选B.【点评】本题考查了矩形的性质,勾股定理,线段垂直平分线性质的应用,解此题的关键是得出关于AE的方程.4.(2015秋•无锡期中)如图,在△ABC中,CF⊥AB于F,BE⊥AC于E,M为BC的中点,EF=7,BC=10,则△EFM的周长是()A.17 B.21 C.24 D.27【分析】根据CF⊥AB于F,BE⊥AC于E,M为BC的中点,利用直角三角形斜边上的中线等于斜边的一半,求出FM和ME的长,即可求解.【解答】解:∵CF⊥AB,M为BC的中点,∴MF是Rt△BFC斜边上的中线,∴FM=BC=×10=5,同理可得,ME=BC=×10=5,又∵EF=7,∴△EFM 的周长=EF +ME +FM=7+5+5=17.故选A .【点评】此题主要考查学生对直角三角形斜边上的中线这个知识点的理解和掌握,解答此题的关键是利用直角三角形斜边上的中线等于斜边的一半,求出FM 和ME 的长.5.(2015春•乌兰察布校级期中)如图,在矩形ABCD 中,AB=6,AD=8,P 是AD 上不与A 和D 重合的一个动点,过点P 分别作AC 和BD 的垂线,垂足为E 、F ,则PE +PF 的值为( )A .10B .4.8C .6D .5【分析】连接OP ,利用勾股定理列式求出BD ,再根据矩形的对角线相等且互相平分求出OA 、OD ,然后根据S △AOD =S △AOP +S △DOP 列方程求解即可.【解答】解:如图,连接OP ,∵AB=6,AD=8,∴BD===10,∵四边形ABCD 是矩形,∴OA=OD=×10=5,∵S △AOD =S △AOP +S △DOP , ∴××6×8=×5•PE +×5•PF ,解得PE +PF=4.8.故选B .【点评】本题考查了矩形的性质,三角形的面积,熟记性质并利用三角形的面积列出方程是解题的关键.二.填空题(共4小题)6.(2016春•东平县期中)如图,在矩形ABCD 中,对角线AC 与BD 相交于点O ,AE 平分∠BAD 交BC 于点E ,若∠CAE=15°,则∠BOE 的度数等于 75° .【分析】由矩形ABCD ,得到OA=OB ,根据AE 平分∠BAD ,得到等边三角形OAB ,推出AB=OB ,求出∠OAB 、∠OBC 的度数,根据平行线的性质和等角对等边得到OB=BE ,根据三角形的内角和定理即可求出答案.【解答】解:∵四边形ABCD是矩形,∴AD∥BC,AC=BD,OA=OC,OB=OD,∠BAD=90°,∴OA=OB,∠DAE=∠AEB,∵AE平分∠BAD,∴∠BAE=∠DAE=45°=∠AEB,∴AB=BE,∵∠CAE=15°,∴∠DAC=45°﹣15°=30°,∠BAC=60°,∴△BAO是等边三角形,∴AB=OB,∠ABO=60°,∴∠OBC=90°﹣60°=30°,∵AB=OB=BE,∴∠BOE=∠BEO=(180°﹣30°)=75°.故答案为75°.【点评】本题主要考查了三角形的内角和定理,矩形的性质,等边三角形的性质和判定,平行线的性质,角平分线的性质,等腰三角形的判定等知识点,解此题的关键是求出∠OBC的度数和求OB=BE.7.(2014春•武昌区期中)如图,将平行四边形ABCD的边DC延长到E,使CE=CD,连接AE交BC于F,∠AFC=n∠D,当n=2时,四边形ABEC是矩形.【分析】首先根据四边形ABCD是平行四边形,得到四边形ABEC是平行四边形,然后证得FC=FE,利用对角线互相相等的四边形是矩形判定四边形ABEC是矩形.【解答】解:当∠AFC=2∠D时,四边形ABEC是矩形.∵四边形ABCD是平行四边形,∴BC∥AD,∠BCE=∠D,由题意易得AB∥EC,AB∥EC,∴四边形ABEC是平行四边形.∵∠AFC=∠FEC+∠BCE,∴当∠AFC=2∠D时,则有∠FEC=∠FCE,∴FC=FE,∴四边形ABEC是矩形,故答案为:2.【点评】此题考查了平行四边形的性质以及矩形的判定.此题难度适中,注意掌握数形结合思想的应用,解题的关键是了解矩形的判定定理.8.(2015春•南长区期中)如图,在正五边形ABCDE中,连接AC、AD、CE,CE 交AD于点F,连接BF,则线段AC、BF、CD之间的关系式是AC2+BF2=4CD2.【分析】首先根据菱形的判定方法,判断出四边形ABCF是菱形,再根据菱形的性质,即可判断出AC⊥BF;然后根据勾股定理,可得OB2+OC2=BC2,据此推得AC2+BF2=4CD2即可.【解答】解:∵五边形ABCDE是正五边形,∴AB∥CE,AD∥BC,∴四边形ABCF是平行四边形,又∵AB=BC=CD=DE=EA,∴四边形ABCF是菱形,∴AC⊥BF,∴OB2+OC2=BC2,∵AC=2OC,BF=2OB,∴AC2+BF2=(2OC)2+(2OB)2=4OC2+4OB2=4BC2,又∵BC=CD,∴AC2+BF2=4CD2.故答案为:AC2+BF2=4CD2.【点评】(1)此题主要考查了菱形的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.(2)此题还考查了勾股定理的应用:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方,要熟练掌握.9.(2015春•株洲校级期中)如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(﹣10,0),C(0,3),点D是OA的中点,点P在BC边上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标是(﹣4,3),或(﹣1,3),或(﹣9,3).【分析】先由矩形的性质求出OD=5,分情况讨论:(1)当OP=OD=5时;根据勾股定理求出PC,即可得出结果;(2)当PD=OD=5时;①作PE⊥OA于E,根据勾股定理求出DE,得出PC,即可得出结果;②作PF⊥OA于F,根据勾股定理求出DF,得出PC,即可得出结果.【解答】解:∵A(﹣10,0),C(0,3),∴OA=10,OC=3,∵四边形OABC是矩形,∴BC=OA=10,AB=OC=3,∵D是OA的中点,∴AD=OD=5,分情况讨论:(1)当OP=OD=5时,根据勾股定理得:PC==4,∴点P的坐标为:(﹣4,3);(2)当PD=OD=5时,分两种情况讨论:①如图1所示:作PE⊥OA于E,则∠PED=90°,DE==4,∴PC=OE=5﹣4=1,∴点P的坐标为:(﹣1,3);②如图2所示:作PF⊥OA于F,则DF==4,∴PC=OF=5+4=9,∴点P的坐标为:(﹣9,3);综上所述:点P的坐标为:(﹣4,3),或(﹣1,3),或(﹣9,3);故答案为:(﹣4,3),或(﹣1,3),或(﹣9,3).【点评】本题考查了矩形的性质、坐标与图形性质、等腰三角形的性质、勾股定理;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.三.解答题(共31小题)10.(2012春•西城区校级期中)如图,正方形ABCD中,AE=AB,直线DE交BC 于点F,求∠BEF的度数.【分析】设∠BAE=x°,根据正方形性质推出AB=AE=AD,根据等腰三角形性质和三角形的内角和定理求出∠AEB和∠AED的度数,根据平角定义求出即可.【解答】解:设∠BAE=x°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∵AE=AB,∴AB=AE=AD,∴∠ABE=∠AEB=(180°﹣∠BAE)=90°﹣x°,∠DAE=90°﹣x°,∠AED=∠ADE=(180°﹣∠DAE)=[180°﹣(90°﹣x°)]=45°+x°,∴∠BEF=180°﹣∠AEB﹣∠AED,=180°﹣(90°﹣x°)﹣(45°+x°),=45°,答:∠BEF的度数是45°.【点评】本题考查了三角形的内角和定理,等腰三角形性质,正方形性质的应用,解此题的关键是如何把已知角的未知角结合起来,题目比较典型,但是有一定的难度.11.(2012秋•高淳县期中)如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别为AB、BC、CD、DA的中点.(1)求证:四边形EFGH为正方形;(2)若AD=1,BC=3,求正方形EFGH的边长.【分析】(1)先由三角形的中位线定理求出四边相等,然后由AC⊥BD入手,进行正方形的判断.(2)连接EG,利用梯形的中位线定理求出EG的长,然后结合(1)的结论求出EH2=2,也即得出了正方形EHGF的边长.【解答】(1)证明:在△ABC中,∵E、F分别是AB、BC的中点,∴EF=同理FG=,GH=,HE=在梯形ABCD中,∵AB=DC,∴AC=BD,∴EF=FG=GH=HE∴四边形EFGH为菱形.设AC与EH交于点M在△ABD中,∵E、H分别是AB、AD的中点,∴EH∥BD,同理GH∥AC又∵AC⊥BD,∴∠BOC=90°.∴∠EHG=∠EMC=∠BOC=90°∴四边形EFGH为正方形.(2)解:连接EG,在梯形ABCD中,∵E、G分别是AB、DC的中点,∴EG=(AD+BC)=(1+3)=2,在Rt△HEG中,EG2=EH2+HG2,4=2EH2,EH2=2,则EH=.即四边形EFGH的边长为.【点评】此题考查了等腰梯形的性质及三角形、梯形的中位线定理,解答本题的关键是根据三角形的中位线定理得出EH=HG=GF=FE,这是本题的突破口.12.(2013秋•青岛期中)如图,点E、F分别是正方形ABCD的边CD和AD的中点,BE和CF交于点P.求证:AP=AB.【分析】延长CF、BA交于点M,先证△BCE≌△CDF,再证△CDF≌△AMF得BA=MA 由直角三角形中斜边中线等于斜边的一半,可得Rt△MBP中AP=BM,即AP=AB.【解答】证明:延长CF、BA交于点M,∵点E、F分别是正方形ABCD的边CD和AD的中点,∴BC=CD,∠BCE=∠CDF,CE=DF,∴△BCE≌△CDF,∴∠CBE=∠DCF.∵∠DCF+∠BCP=90°,∴∠CBE+∠BCP=90°,∴∠BPM=∠CBE+∠BCP=90°.又∵FD=FA,∠CDF=∠MAF,∠CFD=∠MFA,∴△CDF≌△AMF,∴CD=AM.∵CD=AB,∴AB=AM.∴PA是直角△BPM斜边BM上的中线,∴AP=BM,即AP=AB.【点评】本题考查了正方形各边长相等、各内角为直角的性质,全等三角形的判定和对应边相等的性质,直角三角形斜边中线长为斜边长一半的性质,本题中求证△CDF≌△AMF是解题的关键.13.(2015春•禹州市期中)如图,点P为正方形ABCD对角线BD上一点,PE⊥BC于E,PF⊥DC于F.(1)求证:PA=EF;(2)若正方形ABCD的边长为a,求四边形PFCE的周长.【分析】(1)连接PC,证四边形PFCE是矩形,求出EF=PC,证△ABP≌△CBP,推出AP=PC即可;(2)证△CBD是等腰直角三角形,求出BF、PF,求出周长即可.【解答】解:证明:(1)连接PC,∵四边形ABCD是正方形,∴AB=CB,∠ABD=∠CBD=45°,∠C=90°,在△ABP与△CBP中,,∴△ABP≌△CBP(SAS),∴PA=PC,∵PE⊥BC,PF⊥CD,∴∠PFC=90°,∠PEC=90°.又∵∠C=90°,∴四边形PFCE是矩形,∴EF=PC,∴PA=EF.(2)由(1)知四边形PFCE是矩形,∴PE=CF,PF=CE,又∵∠CBD=45°,∠PEB=90°,∴BE=PE,又BC=a,∴矩形PFCE的周长为2(PE+EC)=2(BE+EC)=2BC=2a.【点评】本题主要考查正方形的性质,全等三角形的性质和判定等知识点的连接和掌握,能证出AP=PC是解此题的关键.14.(2015秋•福建校级期中)如图1,在正方形ABCD中,点E为BC上一点,连接DE,把△DEC沿DE折叠得到△DEF,延长EF交AB于G,连接DG.(1)求∠EDG的度数.(2)如图2,E为BC的中点,连接BF.①求证:BF∥DE;②若正方形边长为6,求线段AG的长.【分析】(1)由正方形的性质可得DC=DA.∠A=∠B=∠C=∠ADC=90°,由折叠的性质得出∠DFE=∠C,DC=DF,∠1=∠2,再求出∠DFG=∠A,DA=DF,然后由“HL”证明Rt△DGA≌Rt△DGF,由全等三角形对应角相等得出∠3=∠4,得出∠2+∠3=45°即可;(2)①由折叠的性质和线段中点的定义可得CE=EF=BE,∠DEF=∠DEC,再由三角形的外角性质得出∠5=∠DEC,然后利用同位角相等,两直线平行证明即可;②设AG=x,表示出GF、BG,根据点E是BC的中点求出BE、EF,从而得到GE 的长度,再利用勾股定理列出方程求解即可;【解答】(1)解:如图1所示:∵四边形ABCD是正方形,∴DC=DA.∠A=∠B=∠C=∠ADC=90°,∵△DEC沿DE折叠得到△DEF,∴∠DFE=∠C,DC=DF,∠1=∠2,∴∠DFG=∠A=90°,DA=DF,在Rt△DGA和Rt△DGF中,,∴Rt△DGA≌Rt△DGF(HL),∴∠3=∠4,∴∠EDG=∠3+∠2=∠ADF+∠FDC,=(∠ADF+∠FDC),=×90°,=45°;(2)①证明:如图2所示:∵△DEC沿DE折叠得到△DEF,E为BC的中点,∴CE=EF=BE,∠DEF=∠DEC,∴∠5=∠6,∵∠FEC=∠5+∠6,∴∠DEF+∠DEC=∠5+∠6,∴2∠5=2∠DEC,即∠5=∠DEC,∴BF∥DE;②解:设AG=x,则GF=x,BG=6﹣x,∵正方形边长为6,E为BC的中点,∴CE=EF=BE=×6=3,∴GE=EF+GF=3+x,在Rt△GBE中,根据勾股定理得:(6﹣x)2+32=(3+x)2,解得:x=2,即线段AG的长为2.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、翻折变换的性质;熟练掌握正方形的性质,并能进行推理论证与计算是解决问题的关键.15.(2016春•召陵区期中)如图①,在正方形ABCD中,F是对角线AC上的一点,点E在BC的延长线上,且BF=EF.(1)求证:BF=DF;(2)求证:∠DFE=90°;(3)如果把正方形ABCD改为菱形,其他条件不变(如图②),当∠ABC=50°时,∠DFE=50度.【分析】(1)根据正方形的四条边都相等可得BC=DC,对角线平分一组对角可得∠BCF=∠DCF,然后利用“边角边”证明即可;(2)易证∠FBE=∠FEB,又因为∠FBE=∠FDC,所以可证明∠FEB=∠FDC,进而可证明∠DFE=90°;(3)根据全等三角形对应角相等可得∠CBF=∠CDF,根据等边对等角可得∠CBF=∠E,然后求出∠DFE=∠DCE,再根据两直线平行,同位角相等可得∠DCE=∠ABC,从而得解.【解答】(1)证明:在正方形ABCD中,BC=DC,∠BCF=∠DCF=45°,∵在△BCF和△DCF中,,∴△BCF≌△DCF(SAS);∴BF=DF;(2)证明:∵BF=EF,∴∠FBE=∠FEB,又∵∠FBE=∠FDC,∴∠FEB=∠FDC,又∵∠DGF=∠EGC,∴∠DFG=∠ECG=90°,即∠DFE=90°;(3)证明:由(1)知,△BCF≌△DCF,∴∠CBF=∠CDF,∵EE=FB,∴∠CBF=∠E,∵∠DGF=∠EGC(对顶角相等),∴180°﹣∠DGF﹣∠CDF=180°﹣∠EGC﹣∠E,即∠DFE=∠DCE,∵AB∥CD,∴∠DCE=∠ABC,∴∠DFE=∠ABC=50°,故答案为:50.【点评】本题考查了正方形的性质,全等三角形的判定与性质,菱形的性质,等边对等角的性质,熟记正方形的性质确定出∠BCF=∠DCF是解题的关键.16.(2015秋•泗县期中)已知正方形ABCD中,对角线AC、BD相交于O.①如图1,若E是AC上的点,过A 作AG⊥BE于G,AG、BD交于F,求证:OE=OF②如图2,若点E在AC的延长线上,AG⊥EB交EB的延长线于G,AG延长DB 延长线于点F,其它条件不变,OE=OF还成立吗?【分析】①由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可;②由正方形的性质得出OA=OB,AC⊥BD,得出∠BOE=∠AOF=90°,由角的互余关系得出∠OBE=∠OAF,由ASA证明△BOE≌△AOF,得出对应边相等即可.【解答】①证明:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF;②解:OE=OF还成立;理由如下:∵四边形ABCD是正方形,∴OA=OB,AC⊥BD,∴∠BOE=∠AOF=90°,∴∠OEB+∠OBE=90°,∵AG⊥BE,∴∠AGE=90°,∴∠OEB+∠OAF=90°,∴∠OBE=∠OAF,在△BOE和△AOF中,,∴△BOE≌△AOF(ASA),∴OE=OF.【点评】本题考查了正方形的性质、全等三角形的判定与性质;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.17.(2016春•邳州市期中)如图,点P是菱形ABCD中对角线AC上的一点,且PE=PB.(1)求证:PE=PD;(2)求证:∠PDC=∠PEB;(3)若∠BAD=80°,连接DE,试求∠PDE的度数,并说明理由.【分析】(1)由菱形的性质得出AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,由SAS 证明△CDP≌△CBP,得出PB=PD,再由PE=PB,即可得出结论;(2)由等腰三角形的性质得出∠PBC=∠PEB,由全等三角形的性质得出∠PDC=∠PBC,即可得出∠PDC=∠PEB;(3)由四边形内角和定理得出∠DPE=100°,由等腰三角形的性质和三角形内角和定理即可得出结果.【解答】(1)解:∵四边形ABCD是菱形,∴AB=BC=CD=AD,AB∥CD,∠DCP=∠BCP,在△DCP和△BCP中,,∴△CDP≌△CBP(SAS),∴PB=PD,∵PE=PB,∴PE=PD;(2)证明:∵PE=PB,∴∠PBC=∠PEB,∵△CDP≌△CBP,∴∠PDC=∠PBC,∴∠PDC=∠PEB;(3)解:如图所示:∠PDE=40°;理由如下:在四边形DPEC中,∵∠DPE=360°﹣(∠PDC+∠PEC+∠DCB)=360°﹣(∠PEB+∠PEC+∠DCB)=360°﹣(180°+80°)=100°,∵PE=PD∴∠PDE=∠PED=40°.【点评】本题考查了菱形的性质、全等三角形的判定与性质、等腰三角形的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.18.(2016春•昆山市期中)如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.(1)求证:EF=DF﹣BE;(2)若△ADF的周长为,求EF的长.【分析】(1)由正方形的性质得出AD=AB,证出∠DAF=∠ABE,由AAS证明△ADF ≌△BAE,得出AF=BE,DF=AE,即可得出结论;(2)设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,由已知条件得出DF+AF=,即a+b=,由勾股定理得出a2+b2=1,再由完全平方公式得出a﹣b即可.【解答】(1)证明:∵BE⊥AP,DF⊥AP,∴∠DFA=∠AEB=90°,∠ABE+∠BAE=90°,∵四边形ABCD为正方形,∴AD=AB,∠DAB=90°=∠DAF+∠BAE,∴∠DAF=∠ABE,在△ADF和△BAE中,,∴△ADF≌△BAE(AAS),∴AF=BE,DF=AE,∴EF=AE﹣AF=DF﹣BE;(2)解:设DF=a,AF=b,EF=DF﹣AF=a﹣b>0,∵△ADF的周长为,AD=1,∴DF+AF=,即a+b=,由勾股定理得:DF2+AF2=AD2,即a2+b2=1,∴(a﹣b)2=2(a2+b2)﹣(a+b)2=2﹣=,∴a﹣b=,即EF=.【点评】本题考查了正方形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质,由勾股定理得出a与b的关系式是解决问题(2)的关键.19.(2015春•繁昌县期中)如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.(1)求证:0E=OF;(2)若正方形的边长为4,求EF的最小值.【分析】(1)根据正方形的性质可得∠EAO=∠FBO=45°,OA=OB,再根据同角的余角相等可得∠AOE=∠BOE,然后利用“角边角”证明△AOE和△BOF全等,根据全等三角形对应边相等即可得证;(2)根据等腰直角三角形△EOF,当OE最小时,再根据勾股定理得出EF的最小值.【解答】解:(1)∵四边形ABCD是正方形,∴OA=OB,∠AOB=90°,∠EAO=∠FBO=45°,∴∠AOE+∠BOE=90°,∵OE⊥OF,∴∠BOF+∠BOE=90°,∴∠AOE=∠BOF,在△AOE与△BOF中,,∴△AOE≌△BOF(ASA),∴OE=OF;(2)由(1)可知,△EOF是等腰直角三角形,∠EOF是直角,当OE最小时,EF的值最小,∵OA=OB,OE⊥AB,∴点E是AB的中点,∴OE=AB,∵AB=4,∴OE=2,∴EF=,即EF的最小值是2.【点评】本题考查了正方形的性质,解决此类问题的关键是正确的利用旋转不变量.正确作出辅助线是关键.20.(2016春•江宁区期中)如图,在正方形ABCD中,点E是边AD上任意一点,BE的垂直平分线FG交对角AC于点F.求证:(1)BF=DF;(2)BF⊥FE.【分析】(1)由正方形的性质得出AB=AD,∠BAF=∠DAF=45°,由SAS证明△BAF ≌△DAF,得出对应边相等即可;(2)由线段垂直平分线的性质得出BF=EF,证出EF=DF,得出∠FDE=∠FED,再由全等三角形的性质证出∠ABF=∠FED,由邻补角关系得出∠FED+∠FEA=180°,证出∠ABF+∠FEA=180°,由四边形内角和得出∠BAE+∠BFE=180°,求出∠BFE=90°即可.【解答】证明:如图所示:(1)∵四边形ABCD是正方形,∴AB=AD,∠BAF=∠DAF=45°,∠BAE=90°,在△BAF和△DAF中,,∴△BAF≌△DAF(SAS),∴BF=DF;(2)∵BE的垂直平分线FG交对角AC于点F,∴BF=EF,∵BF=DF,∴EF=DF,∴∠FDE=∠FED,∵△BAF≌△DAF,∴∠ABF=∠FDE,∴∠ABF=∠FED,∵∠FED+∠FEA=180°,∴∠ABF+∠FEA=180°,∴∠BAE+∠BFE=180°,∴∠BFE=90°,∴BF⊥FE.【点评】本题考查了正方形的性质、全等三角形的判定与性质、等腰三角形的判定与性质、四边形内角和定理等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.21.(2015春•台州校级期中)已知:如图所示,四边形ABCD中,∠ABC=∠ADC=90°,M是AC上任一点,O是BD的中点,连接MO,并延长MO到N,使NO=MO,连接BN与ND.(1)判断四边形BNDM的形状,并证明;(2)若M是AC的中点,则四边形BNDM的形状又如何?说明理由.【分析】(1)由对角线互相平分的四边形是平行四边形即可得出结论;(2)由直角三角形斜边上1的中线性质得出BM=AC,DM=AC,得出BM=DM,即可得出结论.【解答】(1)解:四边形BNDM是平行四边形,理由如下:。
最新中考数学总复习:多边形与平行四边形-- 巩固练习(提高)(含答案解析)

中考总复习:多边形与平行四边形-巩固练习(提高)【巩固练习】一、选择题1.如图,四边形ABED和四边形AFCD都是平行四边形,AF和DE相交成直角,AG=3cm,DG=4cm,□ABED 的面积是,则四边形ABCD的周长为()A.49cm B.43cm C.41cm D.46cm2.如图,在△ABC中,已知AB=AC=5,BC=4,点E、F是中线AD上的两点,则图中阴影部分的面积是:( ) A. ; B.2; C.3; D.4.3. 已知点A(2,0)、点B(,0)、点C(0,1),以A、B、C三点为顶点画平行四边形,则第四个顶点不可能在( )A.第一象限B.第二象限 C.第三象限 D.第四象限4.(2011·安徽)如图,在四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=22,CD=2,点P在四边形ABCD的边上,若P到BD的距离为32,则点P的个数为( )A.1 B.2 C.3 D.45.如图,分别以Rt△ABC的斜边AB、直角边AC为边向外作等边△ABD和△ACE,F为AB的中点,DE,AB 相交于点G,若∠BAC=30°,下列结论:①EF⊥AC;②四边形ADFE为平行四边形;③AD=4AG;④△DBF≌△EFA.其中正确结论的是().A.①②③④B.①③④C.②③④ D.①②④6.(2014•杭州模拟)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,①四边形ACED是平行四边形;②△BCE是等腰三角形;③四边形ACEB的周长是10+2;④四边形ACEB的面积是16.则以上结论正确的是()A.①②③B.①②④C.①③④D.②④二、填空题7. 如图,口ABCD中,点E在边AD上,以BE为折痕,将△ABE向上翻折,点A正好落在CD上的点F,若△FDE的周长为8,△FCB的周长为22,则FC的长为________.8.(2015春•淅川县期末)若工人师傅用正三角形、正十边形与正n边形这三种正多边形能够铺成平整的地面,则n的值为.9. 如图,平行四边形ABCD中,∠ABC=60°,AB=4,AD=8,点E、F分别是边BC、AD边的中点,点M是AE与BF的交点,点N是CF与DE的交点,则四边形ENFM的周长是__________.10.(2011•梅州)凸n边形的对角线的条数记作a n(n≥4),例如:a4=2,那么:①a5=_____;②a6-a5=____ ;③a n+1-a n=____.(n≥4,用n含的代数式表示)11.①如图(1),四边形ABCD中,AB∥E1F1∥CD,AD∥BC,则图中共有________个平行四边形;②如图(2),四边形ABCD中,AB∥E1F1∥E2F2∥CD,AD∥BC,则图中共有________个平行四边形;③如图(3),四边形ABCD中,AB∥E1F1∥E2F2∥E3F3∥CD,AD∥BC,则图中共有________个平行四边形;一般地,若四边形ABCD中,E1,E2,E3,…,都是AD上的点,F1,F2,F3,…,都是BC上的点,且AB∥E1F1∥E2F2∥E3F3∥…∥∥CD,AD∥BC,则图中共有________平行四边形.12.如图所示,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为___________.三、解答题13.问题再现:现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题、今天我们把正多边形的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究.我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如图中,用正方形镶嵌平面,可以发现在一个顶点O周围围绕着4个正方形的内角.试想:如果用正六边形来镶嵌平面,在一个顶点周围应该围绕着3个正六边形的内角.问题提出:如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案?问题解决:猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?分析:我们可以将此问题转化为数学问题来解决、从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.验证1:在镶嵌平面时,设围绕某一点有x个正方形和y个正八边形的内角可以拼成一个周角.根据题意,可得方程:90x+(82)1808-⨯•y=360,整理得:2x+3y=8,我们可以找到惟一一组适合方程的正整数解为12 xy=⎧⎨=⎩.结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.验证2:_______;结论2:_______.上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案.问题拓广:请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.猜想3:_______;验证3:_______;结论3:_______.14. 如图,在四边形ABCD中,∠A=90°,∠ABC与∠ADC互补.(1)求∠C的度数;(2)若BC>CD且AB=AD,请在图上画出一条线段,把四边形ABCD分成两部分,使得这两部分能够重新拼成一个正方形,并说明理由;(3)若CD=6,BC=8,S四边形ABCD=49,求AB的值.15. (2015春•苏州校级期末)如图,正方形ABCD中,点P是直线BC上一点,连接PA,将线段PA绕点P逆时针旋转90°得到线段PE,在直线BA上取点F,使BF=BP,且点F与点E在BC同侧,连接EF、CF.(1)如图①,当点P在CB延长线上时,求证:四边形PCFE是平行四边形.(2)如图②,当点P在线段BC上时,四边形PCFE是否还是平行四边形,说明理由.16.(2012•广州)如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).(1)当α=60°时,求CE的长;(2)当60°<α<90°时,①是否存在正整数k ,使得∠EFD=k ∠AEF ?若存在,求出k 的值;若不存在,请说明理由. ②连接CF ,当CE 2-CF 2取最大值时,求tan ∠DCF 的值.【答案与解析】 一.选择题 1.【答案】D. 2.【答案】A.3.【答案】C . 4.【答案】B.【解析】如图所示,作AE ⊥BD 于E ,CF ⊥BD 于F ,由题意得AE =12BD =22AB =2>32,∴在边AB 和AD上各存在一个点P 到BD 的距离为32.∵AB =AD ,∠BAD =90°,∴∠ADB =45°.又∠ADC =90°,∴∠CDF =45°.∴CF =22CD =22×2=1<32,∴在边BC 和CD 上不存在符合题意的点P .综上所述.5.【答案】A.【解析】先证 ΔADF≌ΔABC,可得DF=AC=AE.∵DF ∥AE 且DF=AE ∴四边形ADFE 为平行四边形,即①②③④是正确的. 6.【答案】D .【解析】①∵∠ACB=90°,DE ⊥BC , ∴∠ACD=∠CDE=90°, ∴AC ∥DE , ∵CE ∥AD ,∴四边形ACED是平行四边形,故①正确;②∵D是BC的中点,DE⊥BC,∴EC=EB,∴△BCE是等腰三角形,故②正确;③∵AC=2,∠ADC=30°,∴AD=4,CD=2,∵四边形ACED是平行四边形,∴CE=AD=4,∵CE=EB,∴EB=4,DB=2,∴CB=4,∴AB==2,∴四边形ACEB的周长是10+2故③正确;④四边形ACEB的面积:×2×4+×4×2=8,故④错误,故选:A.二.填空题7.【答案】7.【解析】由题意知x+y+z=8,a+(y+a)+(z+x)=22,所以a=7.8.【答案】十五.【解析】正三边形和正十边形内角分别为60°、144°,正n边形的内角应为360°﹣60°﹣144°=156°,所以正n边形为正十五边形.故答案为:十五.9.【答案】4+4.10.【答案】5;4;n-1.【解析】①五边形有5条对角线;②六边形有9条对角线,9-5=4;③n边形有(3)2n n-条对角线,n+1边形有(1)(2)2n n+-条对角线,a n+1-a n=(1)(2)2n n+--(3)2n n-=n-1.11.【答案】①3 ;②6 ;③10,.12.【答案】n(n+1).【解析】∵①正三边形“扩展”而来的多边形的边数是12=3×4,②正四边形“扩展”而来的多边形的边数是20=4×5,③正五边形“扩展”而来的多边形的边数为30=5×6,④正六边形“扩展”而来的多边形的边数为42=6×7,∴正n边形“扩展”而来的多边形的边数为n(n+1).三.综合题13.【解析】用正六边形来镶嵌平面,在一个顶点周围应该围绕着3个正六边形的内角.验证2:在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角,根据题意,可得方程:60a+120b=360.整理得:a+2b=6,可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩结论2:镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌.猜想3:是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌?验证3:在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角.根据题意,可得方程:60m+90n+120c=360,整理得:2m+3n+4c=12,可以找到惟一一组适合方程的正整数解为121 mnc=⎧⎪=⎨⎪=⎩结论3:镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌.(说明:本题答案不惟一,符合要求即可.)14.【解析】(1)∵∠ABC与∠ADC互补,∴∠ABC+∠ADC=180°.∵∠A=90°,∴∠C=360°-90°-180°=90°;(2)过点A作AE⊥BC,垂足为E.则线段AE把四边形ABCD分成△ABE和四边形AECD两部分,把△ABE以A点为旋转中心,逆时针旋转90°,则被分成的两部分重新拼成一个正方形.过点A作AF∥BC交CD的延长线于F,∵∠ABC+∠ADC=180°,又∠ADF+∠ADC=180°, ∴∠ABC=∠ADF .∵AD=AB ,∠AEC=∠AFD=90°,∴△ABE ≌△ADF . ∴AE=AF .∴四边形AECF 是正方形; (3)解法1:连接BD ,∵∠C=90°,CD=6,BC=8,Rt △BCD 中,BD=2286+=10 又∵S 四边形ABCD =49,∴S △ABD =49-24=25. 过点A 作AM ⊥BD 垂足为M , ∴S △ABD =12×BD ×AM=25.∴AM=5. 又∵∠BAD=90°,∴△ABM ∽△DAM .∴AM BM =MDAM.设BM=x ,则MD=10-x , ∴5x=105x -.解得x=5.∴AB=52.解法2:连接BD ,∠A=90°.设AB=x ,AD=y ,则x 2+y 2=102,① ∵12xy=25,∴xy=50.② 由①,②得:(x-y )2=0. ∴x=y .2x 2=100.∴x=52.15.【解析】(1)证明:∵四边形ABCD 是正方形, ∴AB=BC ,∠ABC=∠PBA=90° 在△PBA 和△FBC 中,,∴△PBA ≌△FBC (SAS ),∴PA=FC ,∠PAB=∠FCB .∵PA=PE,∴PE=FC.∵∠PAB+∠APB=90°,∴∠FCB+∠APB=90°.∵∠EPA=90°,∴∠APB+∠EPA+∠FCP=180°,即∠EPC+∠PCF=180°,∴EP∥FC,∴四边形EPCF是平行四边形;(2)解:结论:四边形EPCF是平行四边形,理由是:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠CBF=90°在△PBA和△FBC中,,∴△PBA≌△FBC(SAS),∴PA=FC,∠PAB=∠FCB.∵PA=PE,∴PE=FC.∵∠FCB+∠BFC=90°,∠EPB+∠APB=90°,∴∠BPE=∠FCB,∴EP∥FC,∴四边形EPCF是平行四边形.16. 【解析】(1)∵α=60°,BC=10,∴sinα=CEBC,即sin60°=10CE=32,解得CE=53;(2)①存在k=3,使得∠EFD=k∠AEF.理由如下:连接CF并延长交BA的延长线于点G,∵F为AD的中点,∴AF=FD,在平行四边形ABCD中,AB∥CD,∴∠G=∠DCF ,在△AFG 和△CFD 中,G DCF AFG DFC AF FD ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△AFG ≌△DFC (AAS ), ∴CF=GF ,AG=CD , ∵CE ⊥AB ,∴EF=GF (直角三角形斜边上的中线等于斜边的一半), ∴∠AEF=∠G ,∵AB=5,BC=10,点F 是AD 的中点, ∴AG=5,AF=12AD=12BC=5, ∴AG=AF ,∴∠AFG=∠G ,在△EFG 中,∠EFC=∠AEF+∠G=2∠AEF , 又∵∠CFD=∠AFG (对顶角相等), ∴∠CFD=∠AEF ,∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF , 因此,存在正整数k=3,使得∠EFD=3∠AEF ; ②设BE=x ,∵AG=CD=AB=5, ∴EG=AE+AG=5-x+5=10-x ,在Rt △BCE 中,CE 2=BC 2-BE 2=100-x 2,在Rt △CEG 中,CG 2=EG 2+CE 2=(10-x )2+100-x 2=200-20x , ∵CF=GF (①中已证),∴CF 2=(12CG )2=14CG 2=14(200-20x )=50-5x ,∴CE 2-CF 2=100-x 2-50+5x=-x 2+5x+50=-(x-52)2+50+254,∴当x=52,即点E 是AB 的中点时,CE 2-CF 2取最大值,此时,EG=10-x=10-52=152,CE=2100x -=251004-=5152, 所以,tan ∠DCF=tan ∠G=CEEG =5152152=153.。
2020-2021太原 备战中考数学(平行四边形提高练习题)压轴题训练
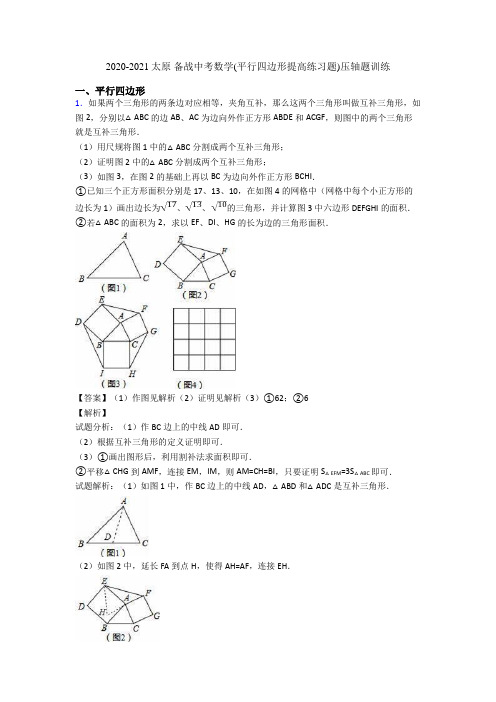
2020-2021太原备战中考数学(平行四边形提高练习题)压轴题训练一、平行四边形1.如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.(1)用尺规将图1中的△ABC分割成两个互补三角形;(2)证明图2中的△ABC分割成两个互补三角形;(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI.①已知三个正方形面积分别是17、13、10,在如图4的网格中(网格中每个小正方形的边长为1)画出边长为、、的三角形,并计算图3中六边形DEFGHI的面积.②若△ABC的面积为2,求以EF、DI、HG的长为边的三角形面积.【答案】(1)作图见解析(2)证明见解析(3)①62;②6【解析】试题分析:(1)作BC边上的中线AD即可.(2)根据互补三角形的定义证明即可.(3)①画出图形后,利用割补法求面积即可.②平移△CHG到AMF,连接EM,IM,则AM=CH=BI,只要证明S△EFM=3S△ABC即可.试题解析:(1)如图1中,作BC边上的中线AD,△ABD和△ADC是互补三角形.(2)如图2中,延长FA到点H,使得AH=AF,连接EH.∵四边形ABDE,四边形ACGF是正方形,∴AB=AE,AF=AC,∠BAE=∠CAF=90°,∴∠EAF+∠BAC=180°,∴△AEF和△ABC是两个互补三角形.∵∠EAH+∠HAB=∠BAC+∠HAB=90°,∴∠EAH=∠BAC,∵AF=AC,∴AH=AB,在△AEH和△ABC中,∴△AEH≌△ABC,∴S△AEF=S△AEH=S△ABC.(3)①边长为、、的三角形如图4所示.∵S△ABC=3×4﹣2﹣1.5﹣3=5.5,∴S六边形=17+13+10+4×5.5=62.②如图3中,平移△CHG到AMF,连接EM,IM,则AM=CH=BI,设∠ABC=x,∵AM∥CH,CH⊥BC,∴AM⊥BC,∴∠EAM=90°+90°﹣x=180°﹣x,∵∠DBI=360°﹣90°﹣90°﹣x=180°﹣x,∴∠EAM=∠DBI,∵AE=BD,∴△AEM≌△DBI,∵在△DBI和△ABC中,DB=AB,BI=BC,∠DBI+∠ABC=180°,∴△DBI和△ABC是互补三角形,∴S△AEM=S△AEF=S△AFM=2,∴S△EFM=3S△ABC=6.考点:1、作图﹣应用与设计,2、三角形面积2.已知:如图,在平行四边形ABCD中,O为对角线BD的中点,过点O的直线EF分别交AD,BC于E,F两点,连结BE,DF.(1)求证:△DOE≌△BOF.(2)当∠DOE等于多少度时,四边形BFDE为菱形?请说明理由.【答案】(1)证明见解析;(2)当∠DOE=90°时,四边形BFED为菱形,理由见解析.【解析】试题分析:(1)利用平行四边形的性质以及全等三角形的判定方法得出△DOE≌△BOF (ASA);(2)首先利用一组对边平行且相等的四边形是平行四边形得出四边形EBFD是平行四边形,进而利用垂直平分线的性质得出BE=ED,即可得出答案.试题解析:(1)∵在▱ABCD中,O为对角线BD的中点,∴BO=DO,∠EDB=∠FBO,在△EOD和△FOB中,∴△DOE≌△BOF(ASA);(2)当∠DOE=90°时,四边形BFDE为菱形,理由:∵△DOE≌△BOF,∴OE=OF,又∵OB=OD,∴四边形EBFD是平行四边形,∵∠EOD=90°,∴EF⊥BD,∴四边形BFDE为菱形.考点:平行四边形的性质;全等三角形的判定与性质;菱形的判定.3.已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.(1)请问EG与CG存在怎样的数量关系,并证明你的结论;(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?(请直接写出结果,不必写出理由)【答案】(1)证明见解析(2)证明见解析(3)结论仍然成立【解析】【分析】(1)利用直角三角形斜边上的中线等于斜边的一半,可证出CG=EG.(2)结论仍然成立,连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点;再证明△DAG≌△DCG,得出AG=CG;再证出△DMG≌△FNG,得到MG=NG;再证明△AMG≌△ENG,得出AG=EG;最后证出CG=EG.(3)结论依然成立.【详解】(1)CG=EG.理由如下:∵四边形ABCD是正方形,∴∠DCF=90°.在Rt△FCD中,∵G为DF的中点,∴CG=12FD,同理.在Rt△DEF中,EG=12FD,∴CG=EG.(2)(1)中结论仍然成立,即EG=CG.证法一:连接AG,过G点作MN⊥AD于M,与EF的延长线交于N点.在△DAG与△DCG中,∵AD=CD,∠ADG=∠CDG,DG=DG,∴△DAG≌△DCG(SAS),∴AG=CG;在△DMG与△FNG中,∵∠DGM=∠FGN,FG=DG,∠MDG=∠NFG,∴△DMG≌△FNG (ASA),∴MG=NG.∵∠EAM=∠AEN=∠AMN=90°,∴四边形AENM是矩形,在矩形AENM中,AM=EN.在△AMG与△ENG中,∵AM=EN,∠AMG=∠ENG,MG=NG,∴△AMG≌△ENG(SAS),∴AG=EG,∴EG=CG.证法二:延长CG至M,使MG=CG,连接MF,ME,EC.在△DCG与△FMG中,∵FG=DG,∠MGF=∠CGD,MG=CG,∴△DCG≌△FMG,∴MF=CD,∠FMG=∠DCG,∴MF∥CD∥AB,∴EF⊥MF.在Rt△MFE与Rt△CBE中,∵MF=CB,∠MFE=∠EBC=90°,EF=BE,∴△MFE≌△CBE∴∠MEF=∠CEB,∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°,∴△MEC为直角三角形.∵MG=CG,∴EG=12MC,∴EG=CG.(3)(1)中的结论仍然成立.理由如下:过F作CD的平行线并延长CG交于M点,连接EM、EC,过F作FN垂直于AB于N.由于G为FD中点,易证△CDG≌△MFG,得到CD=FM,又因为BE=EF,易证∠EFM=∠EBC,则△EFM≌△EBC,∠FEM=∠BEC,EM=EC∵∠FEC+∠BEC=90°,∴∠FEC+∠FEM=90°,即∠MEC=90°,∴△MEC是等腰直角三角形.∵G为CM中点,∴EG=CG,EG⊥CG【点睛】本题是四边形的综合题.(1)关键是利用直角三角形斜边上的中线等于斜边的一半解答;(2)关键是利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质解答.4.如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.(1)连结CG,请判断四边形DBCG的形状,并说明理由;(2)若AE=BD,求∠EDF的度数.【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.【解析】【分析】(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.【详解】解:(1)四边形BCGD是矩形,理由如下,∵四边形ABCD是平行四边形,∴BC∥AD,即BC∥DG,由折叠可知,BC=DG,∴四边形BCGD是平行四边形,∵AD⊥BD,∴∠CBD=90°,∴四边形BCGD是矩形;(2)由折叠可知:EF垂直平分BD,∴BD⊥EF,DP=BP,∵AD⊥BD,∴EF∥AD∥BC,∴AE PD1==BE BP∴AE=BE,∴DE是Rt△ADB斜边上的中线,∴DE=AE=BE,∵AE=BD,∴DE=BD=BE,∴△DBE是等边三角形,∴∠EDB=∠DBE=60°,∵AB∥DC,∴∠DBC=∠DBE=60°,∴∠EDF=120°.【点睛】本题考查了平行四边形的性质,折叠性质,等边三角形的性质和判定,主要考查学生运用定理进行推理和计算的能力,题目综合性比较强,有一定的难度5.如图1,在△ABC中,AB=AC,AD⊥BC于D,分别延长AC至E,BC至F,且CE=EF,延长FE交AD的延长线于G.(1)求证:AE=EG;(2)如图2,分别连接BG,BE,若BG=BF,求证:BE=EG;(3)如图3,取GF的中点M,若AB=5,求EM的长.【答案】(1)证明见解析(2)证明见解析(3)5 2【解析】【分析】(1)根据平行线的性质和等腰三角形的三线合一的性质得:∠CAD=∠G,可得AE=EG;(2)作辅助线,证明△BEF≌△GEC(SAS),可得结论;(3)如图3,作辅助线,构建平行线,证明四边形DMEN是平行四边形,得EM=DN=12AC,计算可得结论.【详解】证明:(1)如图1,过E作EH⊥CF于H,∵AD⊥BC,∴EH∥AD,∴∠CEH=∠CAD,∠HEF=∠G,∵CE=EF,∴∠CEH=∠HEF,∴∠CAD=∠G,∴AE=EG;(2)如图2,连接GC,∵AC =BC ,AD ⊥BC ,∴BD =CD ,∴AG 是BC 的垂直平分线,∴GC =GB ,∴∠GBF =∠BCG ,∵BG =BF ,∴GC =BE ,∵CE =EF ,∴∠CEF =180°﹣2∠F ,∵BG =BF ,∴∠GBF =180°﹣2∠F ,∴∠GBF =∠CEF ,∴∠CEF =∠BCG ,∵∠BCE =∠CEF+∠F ,∠BCE =∠BCG+∠GCE ,∴∠GCE =∠F ,在△BEF 和△GCE 中,CE GCE F CG BF EF =⎧⎪∠=∠⎨⎪=⎩Q , ∴△BEF ≌△GEC (SAS ),∴BE =EG ;(3)如图3,连接DM ,取AC 的中点N ,连接DN ,由(1)得AE=EG,∴∠GAE=∠AGE,在Rt△ACD中,N为AC的中点,∴DN=12AC=AN,∠DAN=∠ADN,∴∠ADN=∠AGE,∴DN∥GF,在Rt△GDF中,M是FG的中点,∴DM=12FG=GM,∠GDM=∠AGE,∴∠GDM=∠DAN,∴DM∥AE,∴四边形DMEN是平行四边形,∴EM=DN=12AC,∵AC=AB=5,∴EM=52.【点睛】本题是三角形的综合题,主要考查了全等三角形的判定与性质,直角三角形斜边中线的性质,等腰三角形的性质和判定,平行四边形的性质和判定等知识,解题的关键是作辅助线,并熟练掌握全等三角形的判定方法,特别是第三问,辅助线的作法是关键.6.现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.(1)求AE、EF的位置关系;(2)求线段B′C的长,并求△B′EC的面积.【答案】(1)见解析;(2)S△B′EC=108 25.【解析】【分析】(1)由折线法及点E是BC的中点,可证得△B'EC是等腰三角形,再有条件证明∠AEF=90°即可得到AE ⊥EF ;(2)连接BB′,通过折叠,可知∠EBB ′=∠EB′B ,由E 是BC 的中点,可得EB′=EC ,∠ECB′=∠EB′C ,从而可证△BB′C 为直角三角形,在Rt △AOB 和Rt △BOE 中,可将OB ,BB′的长求出,在Rt △BB′C 中,根据勾股定理可将B′C 的值求出.【详解】(1)由折线法及点E 是BC 的中点,∴EB =EB ′=EC ,∠AEB =∠AEB ′,∴△B 'EC 是等腰三角形,又∵EF ⊥B ′C∴EF 为∠B 'EC 的角平分线,即∠B ′EF =∠FEC ,∴∠AEF =180°﹣(∠AEB +∠CEF )=90°,即∠AEF =90°,即AE ⊥EF ;(2)连接BB '交AE 于点O ,由折线法及点E 是BC 的中点,∴EB =EB ′=EC ,∴∠EBB ′=∠EB ′B ,∠ECB ′=∠EB ′C ;又∵△BB 'C 三内角之和为180°,∴∠BB 'C =90°;∵点B ′是点B 关于直线AE 的对称点,∴AE 垂直平分BB ′;在Rt △AOB 和Rt △BOE 中,BO 2=AB 2﹣AO 2=BE 2﹣(AE ﹣AO )2将AB =4cm ,BE =3cm ,AE =5cm ,∴AO =165 cm ,∴BO 125cm , ∴BB ′=2BO =245cm ,∴在Rt △BB 'C 中,B ′C 518cm , 由题意可知四边形OEFB ′是矩形,∴EF =OB ′=125, ∴S △B ′EC =*111812108225525B C EF '⨯=⨯⨯=.【点睛】考查图形的折叠变化及三角形的内角和定理勾股定理的和矩形的性质综合运用.关键是要理解折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,只是位置变化.7.如图,在正方形ABCD中,对角线AC与BD交于点O,在Rt△PFE中,∠EPF=90°,点E、F分别在边AD、AB上.(1)如图1,若点P与点O重合:①求证:AF=DE;②若正方形的边长为23,当∠DOE=15°时,求线段EF的长;(2)如图2,若Rt△PFE的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP 时,证明:PE=2PF.【答案】(1)①证明见解析,②2;(2)证明见解析.【解析】【分析】(1)①根据正方形的性质和旋转的性质即可证得:△AOF≌△DOE根据全等三角形的性质证明;②作OG⊥AB于G,根据余弦的概念求出OF的长,根据勾股定理求值即可;(2)首先过点P作HP⊥BD交AB于点H,根据相似三角形的判定和性质求出PE与PF的数量关系.【详解】(1)①证明:∵四边形ABCD是正方形,∴OA=OD,∠OAF=∠ODE=45°,∠AOD=90°,∴∠AOE+∠DOE=90°,∵∠EPF=90°,∴∠AOF+∠AOE=90°,∴∠DOE=∠AOF,在△AOF 和△DOE 中,OAF ODE OA ODAOF DOE ===∠∠⎧⎪⎨⎪∠∠⎩, ∴△AOF ≌△DOE ,∴AF=DE ;②解:过点O 作OG ⊥AB 于G ,∵正方形的边长为23, ∴OG=12BC=3, ∵∠DOE=15°,△AOF ≌△DOE ,∴∠AOF=15°,∴∠FOG=45°-15°=30°,∴OF=OG cos DOG∠=2, ∴EF=22=22OF OE +;(2)证明:如图2,过点P 作HP ⊥BD 交AB 于点H ,则△HPB 为等腰直角三角形,∠HPD=90°,∴HP=BP ,∵BD=3BP ,∴PD=2BP ,∴PD=2HP ,又∵∠HPF+∠HPE=90°,∠DPE+∠HPE=90°,∴∠HPF=∠DPE ,又∵∠BHP=∠EDP=45°,∴△PHF ∽△PDE , ∴12PF PH PE PD ==, ∴PE=2PF .【点睛】 此题属于四边形的综合题.考查了正方形的性质、全等三角形的判定与性质、相似三角形的判定与性质以及勾股定理.注意准确作出辅助线是解此题的关键.8.如图,点O 是正方形ABCD 两条对角线的交点,分别延长CO 到点G ,OC 到点E ,使OG=2OD 、OE=2OC ,然后以OG 、OE 为邻边作正方形OEFG .(1)如图1,若正方形OEFG 的对角线交点为M ,求证:四边形CDME 是平行四边形. (2)正方形ABCD 固定,将正方形OEFG 绕点O 逆时针旋转,得到正方形OE′F′G′,如图2,连接AG′,DE′,求证:AG′=DE′,AG′⊥DE′;(3)在(2)的条件下,正方形OE′F′G′的边OG′与正方形ABCD 的边相交于点N ,如图3,设旋转角为α(0°<α<180°),若△AON 是等腰三角形,请直接写出α的值.【答案】(1)证明见解析;(2)证明见解析;(3)α的值是22.5°或45°或112.5°或135°或157.5°.【解析】【分析】(1)由四边形OEFG 是正方形,得到ME=12GE ,根据三角形的中位线的性质得到CD ∥GE ,CD=12GE ,求得CD=GE ,即可得到结论; (2)如图2,延长E′D 交AG′于H ,由四边形ABCD 是正方形,得到AO=OD ,∠AOD=∠COD=90°,由四边形OEFG 是正方形,得到OG′=OE′,∠E′OG′=90°,由旋转的性质得到∠G′OD=∠E′OC ,求得∠AOG′=∠COE′,根据全等三角形的性质得到AG′=DE′,∠AG′O=∠DE′O ,即可得到结论;(3)分类讨论,根据三角形的外角的性质和等腰三角形的性质即可得到结论.【详解】(1)证明:∵四边形OEFG 是正方形,∴ME=12GE , ∵OG=2OD 、OE=2OC ,∴CD ∥GE ,CD=12GE , ∴CD=GE , ∴四边形CDME 是平行四边形;(2)证明:如图2,延长E′D 交AG′于H ,∵四边形ABCD 是正方形,∴AO=OD ,∠AOD=∠COD=90°,∵四边形OEFG 是正方形,∴OG′=OE′,∠E′OG′=90°,∵将正方形OEFG 绕点O 逆时针旋转,得到正方形OE′F′G′,∴∠G′OD=∠E′OC ,∴∠AOG′=∠COE′,在△AG′O 与△ODE′中,OA OD AOG DOE OG OE ⎧⎪∠'∠'⎨⎪''⎩===,∴△AG′O ≌△ODE′∴AG′=DE′,∠AG′O=∠DE′O ,∵∠1=∠2,∴∠G′HD=∠G′OE′=90°,∴AG′⊥DE′;(3)①正方形OE′F′G′的边OG′与正方形ABCD 的边AD 相交于点N ,如图3,Ⅰ、当AN=AO 时,∵∠OAN=45°,∴∠ANO=∠AON=67.5°,∵∠ADO=45°,∴α=∠ANO-∠ADO=22.5°;Ⅱ、当AN=ON 时,∴∠NAO=∠AON=45°,∴∠ANO=90°,∴α=90°-45°=45°;②正方形OE′F′G′的边OG′与正方形ABCD 的边AB 相交于点N ,如图4,Ⅰ、当AN=AO 时,∵∠OAN=45°,∴∠ANO=∠AON=67.5°,∵∠ADO=45°,∴α=∠ANO+90°=112.5°;Ⅱ、当AN=ON 时,∴∠NAO=∠AON=45°,∴∠ANO=90°,∴α=90°+45°=135°,Ⅲ、当AN=AO 时,旋转角a=∠ANO+90°=67.5+90=157.5°,综上所述:若△AON 是等腰三角形时,α的值是22.5°或45°或112.5°或135°或157.5°.【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质、锐角三角函数、旋转变换的性质的综合运用,有一定的综合性,分类讨论当△AON 是等腰三角形时,求α的度数是本题的难点.9.在平面直角坐标系中,O 为原点,点A (﹣6,0)、点C (0,6),若正方形OABC 绕点O 顺时针旋转,得正方形OA′B′C′,记旋转角为α:(1)如图①,当α=45°时,求BC 与A′B′的交点D 的坐标;(2)如图②,当α=60°时,求点B′的坐标;(3)若P 为线段BC′的中点,求AP 长的取值范围(直接写出结果即可).【答案】(1)(62,6)-;(2)(333,333)+;(3)323323AP 剟.【解析】【分析】(1)当α=45°时,延长OA′经过点B,在Rt△BA′D中,∠OBC=45°,A′B=626-,可求得BD的长,进而求得CD的长,即可得出点D的坐标;(2)过点C′作x轴垂线MN,交x轴于点M,过点B′作MN的垂线,垂足为N,证明△OMC′≌△C′NB′,可得C′N=OM=33,B′N=C′M=3,即可得出点B′的坐标;(3)连接OB,AC相交于点K,则K是OB的中点,因为P为线段BC′的中点,所以PK=1OC′=3,即点P在以K为圆心,3为半径的圆上运动,即可得出AP长的取值范围.2【详解】解:(1)∵A(﹣6,0)、C(0,6),O(0,0),∴四边形OABC是边长为6的正方形,当α=45°时,如图①,延长OA′经过点B,∵OB=62,OA′=OA=6,∠OBC=45°,∴A′B=626-,∴BD=(626-)×21262=-,∴CD=6﹣(1262-,-)=626∴BC与A′B′的交点D的坐标为(662-,6);(2)如图②,过点C′作x轴垂线MN,交x轴于点M,过点B′作MN的垂线,垂足为N,∵∠OC′B′=90°,∴∠OC′M=90°﹣∠B′C′N=∠C′B′N,∵OC′=B′C′,∠OMC′=∠C′NB′=90°,∴△OMC′≌△C′NB′(AAS),当α=60°时,∵∠A′OC′=90°,OC′=6,∴∠C′OM=30°,∴C′N=OM=33,B′N=C′M=3,∴点B′的坐标为333,333+;(3)如图③,连接OB ,AC 相交于点K ,则K 是OB 的中点,∵P 为线段BC′的中点,∴PK =12OC′=3, ∴P 在以K 为圆心,3为半径的圆上运动,∵AK =32,∴AP 最大值为323+,AP 的最小值为323-,∴AP 长的取值范围为323323AP -+剟.【点睛】本题考查正方形性质,全等三角形判定与性质,三角形中位线定理.(3)问解题的关键是利用中位线定理得出点P 的轨迹.10.点P 是矩形ABCD 对角线AC 所在直线上的一个动点(点P 不与点A ,C 重合),分别过点A ,C 向直线BP 作垂线,垂足分别为点E ,F ,点O 为AC 的中点.(1)如图1,当点P 与点O 重合时,请你判断OE 与OF 的数量关系;(2)当点P 运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;(3)若点P 在射线OA 上运动,恰好使得∠OEF =30°时,猜想此时线段CF ,AE ,OE 之间有怎样的数量关系,直接写出结论不必证明.【答案】(1)OE =OF .理由见解析;(2)补全图形如图所示见解析,OE =OF 仍然成立;(3)CF =OE+AE 或CF =OE ﹣AE .【解析】【分析】(1)根据矩形的性质以及垂线,即可判定()AOE COF AAS ∆≅∆,得出OE =OF ; (2)先延长EO 交CF 于点G ,通过判定()AOE COG ASA ∆≅∆,得出OG =OE ,再根据Rt EFG ∆中,12OF EG =,即可得到OE =OF ; (3)根据点P 在射线OA 上运动,需要分两种情况进行讨论:当点P 在线段OA 上时,当点P 在线段OA 延长线上时,分别根据全等三角形的性质以及线段的和差关系进行推导计算即可.【详解】(1)OE =OF .理由如下:如图1.∵四边形ABCD 是矩形,∴ OA =OC .∵AE BP ⊥,CF BP ⊥,∴90AEO CFO ∠=∠=︒.∵在AOE ∆和COF ∆中,AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴()AOE COF AAS ∆≅∆,∴ OE =OF ;(2)补全图形如图2,OE =OF 仍然成立.证明如下:延长EO 交CF 于点G .∵AE BP ⊥,CF BP ⊥,∴ AE //CF ,∴EAO GCO ∠=∠.又∵点O 为AC 的中点,∴ AO =CO .在AOE ∆和COG ∆中,EAO GCO AO CO AOE COG ∠=∠⎧⎪=⎨⎪∠=⎩,∴()AOE COG ASA ∆≅∆,∴ OG =OE ,∴Rt EFG ∆中,12OF EG =,∴ OE =OF ; (3)CF =OE +AE 或CF =OE -AE . 证明如下:①如图2,当点P 在线段OA 上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,由(2)可得:OF =OG ,∴OGF ∆是等边三角形,∴ FG =OF =OE ,由(2)可得:AOE COG ∆≅∆,∴ CG =AE .又∵ CF =GF +CG ,∴ CF =OE +AE ;②如图3,当点P 在线段OA 延长线上时.∵30OEF ∠=︒,90EFG ∠=︒,∴60OGF ∠=︒,同理可得:OGF ∆是等边三角形,∆≅∆,∴CG=AE.∴FG=OF=OE,同理可得:AOE COG又∵CF=GF-CG,∴CF=OE-AE.【点睛】本题属于四边形综合题,主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定,解决问题的关键是构建全等三角形和证明三角形全等,利用矩形的对角线互相平分得全等的边相等的条件,根据线段的和差关系使问题得以解决.11.(问题发现)(1)如图(1)四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为;(拓展探究)(2)如图(2)在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;(解决问题)(3)如图(3)在正方形ABCD中,AB=2,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.【答案】(1)AC垂直平分BD;(2)四边形FMAN是矩形,理由见解析;(3)16+8或16﹣8【解析】【分析】(1)依据点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,即可得出AC 垂直平分BD;(2)根据Rt△ABC中,点F为斜边BC的中点,可得AF=CF=BF,再根据等腰三角形ABD 和等腰三角形ACE,即可得到AD=DB,AE=CE,进而得出∠AMF=∠MAN=∠ANF=90°,即可判定四边形AMFN是矩形;(3)分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,②以点A为旋转中心将正方形ABCD顺时针旋转60°,分别依据旋转的性质以及勾股定理,即可得到结论.【详解】(1)∵AB=AD,CB=CD,∴点A在线段BD的垂直平分线上,点C在线段BD的垂直平分线上,∴AC垂直平分BD,故答案为:AC垂直平分BD;(2)四边形FMAN是矩形.理由:如图2,连接AF,∵Rt△ABC中,点F为斜边BC的中点,∴AF=CF=BF,又∵等腰三角形ABD和等腰三角形ACE,∴AD=DB,AE=CE,∴由(1)可得,DF⊥AB,EF⊥AC,又∵∠BAC=90°,∴∠AMF=∠MAN=∠ANF=90°,∴四边形AMFN是矩形;(3)BD′的平方为16+8或16﹣8.分两种情况:①以点A为旋转中心将正方形ABCD逆时针旋转60°,如图所示:过D'作D'E⊥AB,交BA的延长线于E,由旋转可得,∠DAD'=60°,∴∠EAD'=30°,∵AB=2=AD',∴D'E=AD'=,AE=,∴BE=2+,∴Rt△BD'E中,BD'2=D'E2+BE2=()2+(2+)2=16+8②以点A为旋转中心将正方形ABCD顺时针旋转60°,如图所示:过B作BF⊥AD'于F,旋转可得,∠DAD'=60°,∴∠BAD'=30°,∵AB=2=AD',∴BF=AB=,AF=,∴D'F=2﹣,∴Rt△BD'F中,BD'2=BF2+D'F2=()2+(2-)2=16﹣8综上所述,BD′平方的长度为16+8或16﹣8.【点睛】本题属于四边形综合题,主要考查了正方形的性质,矩形的判定,旋转的性质,线段垂直平分线的性质以及勾股定理的综合运用,解决问题的关键是作辅助线构造直角三角形,依据勾股定理进行计算求解.解题时注意:有三个角是直角的四边形是矩形.12.如图1,若分别以△ABC的AC、BC两边为边向外侧作的四边形ACDE和BCFG为正方形,则称这两个正方形为外展双叶正方形.(1)发现:如图2,当∠C=90°时,求证:△ABC与△DCF的面积相等.(2)引申:如果∠C 90°时,(1)中结论还成立吗?若成立,请结合图1给出证明;若不成立,请说明理由;(3)运用:如图3,分别以△ABC的三边为边向外侧作的四边形ACDE、BCFG和ABMN为正方形,则称这三个正方形为外展三叶正方形.已知△ABC中,AC=3,BC=4.当∠C=_____°时,图中阴影部分的面积和有最大值是________.【答案】(1)证明见解析;(2)成立,证明见解析;(3)18.【解析】试题分析:(1)因为AC=DC ,∠ACB=∠DCF=90°,BC=FC ,所以△ABC ≌△DFC ,从而△ABC 与△DFC 的面积相等;(2)延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q .得到四边形ACDE ,BCFG 均为正方形,AC=CD ,BC=CF ,∠ACP=∠DCQ .所以△APC ≌△DQC . 于是AP=DQ .又因为S △ABC =12BC•AP ,S △DFC =12FC•DQ ,所以S △ABC =S △DFC ; (3)根据(2)得图中阴影部分的面积和是△ABC 的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC 的面积最大,当△ABC 是直角三角形,即∠C 是90度时,阴影部分的面积和最大.所以S 阴影部分面积和=3S △ABC =3×12×3×4=18. (1)证明:在△ABC 与△DFC 中, ∵{AC DCACB DCF BC FC∠∠===,∴△ABC ≌△DFC .∴△ABC 与△DFC 的面积相等;(2)解:成立.理由如下:如图,延长BC 到点P ,过点A 作AP ⊥BP 于点P ;过点D 作DQ ⊥FC 于点Q . ∴∠APC=∠DQC=90°.∵四边形ACDE ,BCFG 均为正方形,∴AC=CD ,BC=CF ,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,∴∠ACP=∠DCQ .∴{APC DQCACP DCQ AC CD∠∠∠∠===,△APC ≌△DQC (AAS ),∴AP=DQ .又∵S△ABC=12BC•AP,S△DFC=12FC•DQ,∴S△ABC=S△DFC;(3)解:根据(2)得图中阴影部分的面积和是△ABC的面积三倍,若图中阴影部分的面积和有最大值,则三角形ABC的面积最大,∴当△ABC是直角三角形,即∠C是90度时,阴影部分的面积和最大.∴S阴影部分面积和=3S△ABC=3×12×3×4=18.考点:四边形综合题13.如图1所示,(1)在正三角形ABC中,M是BC边(不含端点B、C)上任意一点,P 是BC延长线上一点,N是∠ACP的平分线上一点,若∠AMN=60°,求证:AM=MN.(2)若将(1)中“正三角形ABC”改为“正方形ABCD”,N是∠DCP的平分线上一点,若∠AMN=90°,则AM=MN是否成立?若成立,请证明;若不成立,说明理由.(3)若将(2)中的“正方形ABCD”改为“正n边形A1A2…A n“,其它条件不变,请你猜想:当∠A n﹣2MN=_____°时,结论A n﹣2M=MN仍然成立.(不要求证明)【答案】0 (2)180 nn【解析】分析:(1)要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.(2)同(1),要证明AM=MN,可证AM与MN所在的三角形全等,为此,可在AB上取一点E,使AE=CM,连接ME,利用ASA即可证明△AEM≌△MCN,然后根据全等三角形的对应边成比例得出AM=MN.详(1)证明:在边AB上截取AE=MC,连接ME.在正△ABC中,∠B=∠BCA=60°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE,BE=AB-AE=BC-MC=BM,∴∠BEM=60°,∴∠AEM=120°.∵N是∠ACP的平分线上一点,∴∠ACN=60°,∴∠MCN=120°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(2)解:结论成立;理由:在边AB上截取AE=MC,连接ME.∵正方形ABCD中,∠B=∠BCD=90°,AB=BC.∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE,BE=AB-AE=BC-MC=BM,∴∠BEM=45°,∴∠AEM=135°.∵N是∠DCP的平分线上一点,∴∠NCP=45°,∴∠MCN=135°.在△AEM与△MCN中,∠MAE=∠NMC,AE=MC,∠AEM=∠MCN,∴△AEM≌△MCN(ASA),∴AM=MN.(3)由(1)(2)可知当∠A n-2MN等于n边形的内角时,结论A n-2M=MN仍然成立;即∠A n-2MN=()02180nn-时,结论A n-2M=MN仍然成立;故答案为[()02180nn-].点睛:本题综合考查了正方形、等边三角形的性质及全等三角形的判定,同时考查了学生的归纳能力及分析、解决问题的能力.难度较大.14.如图,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合),将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.(1)求证:∠APB=∠BPH;(2)当点P在边AD上移动时,求证:△PDH的周长是定值;(3)当BE+CF的长取最小值时,求AP的长.【答案】(1)证明见解析.(2)证明见解析.(3)2.【解析】试题分析:(1)根据翻折变换的性质得出∠PBC=∠BPH,进而利用平行线的性质得出∠APB=∠PBC即可得出答案;(2)首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8;(3)过F作FM⊥AB,垂足为M,则FM=BC=AB,证明△EFM≌△BPA,设AP=x,利用折叠的性质和勾股定理的知识用x表示出BE和CF,结合二次函数的性质求出最值.试题解析:(1)解:如图1,∵PE=BE,∴∠EBP=∠EPB.又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP.即∠PBC=∠BPH.又∵AD∥BC,∴∠APB=∠PBC.∴∠APB=∠BPH.(2)证明:如图2,过B作BQ⊥PH,垂足为Q.由(1)知∠APB=∠BPH,又∵∠A=∠BQP=90°,BP=BP,在△ABP和△QBP中,,∴△ABP≌△QBP(AAS),∴AP=QP,AB=BQ,又∵AB=BC,∴BC=BQ.又∠C=∠BQH=90°,BH=BH,在△BCH和△BQH中,,∴△BCH≌△BQH(SAS),∴CH=QH.∴△PHD的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.∴△PDH的周长是定值.(3)解:如图3,过F作FM⊥AB,垂足为M,则FM=BC=AB.又∵EF为折痕,∴EF⊥BP.∴∠EFM+∠MEF=∠ABP+∠BEF=90°,∴∠EFM=∠ABP.又∵∠A=∠EMF=90°,在△EFM和△BPA中,,∴△EFM≌△BPA(AAS).∴EM=AP.设AP=x在Rt△APE中,(4-BE)2+x2=BE2.解得BE=2+,∴CF=BE-EM=2+-x,∴BE+CF=-x+4=(x-2)2+3.当x=2时,BE+CF取最小值,∴AP=2.考点:几何变换综合题.15.(本题满分10分)如图1,已知矩形纸片ABCD中,AB=6cm,若将该纸片沿着过点B的直线折叠(折痕为BM),点A恰好落在CD边的中点P处.(1)求矩形ABCD的边AD的长.(2)若P为CD边上的一个动点,折叠纸片,使得A与P重合,折痕为MN,其中M在边AD上,N在边BC上,如图2所示.设DP=x cm,DM=y cm,试求y与x的函数关系式,并指出自变量x的取值范围.(3)①当折痕MN的端点N在AB上时,求当△PCN为等腰三角形时x的值;②当折痕MN的端点M在CD上时,设折叠后重叠部分的面积为S,试求S与x之间的函数关系式【答案】(1)AD=3;(2)y=-其中,0<x<3;(3)x=;(4)S=.【解析】试题分析:(1)根据折叠图形的性质和勾股定理求出AD的长度;(2)根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式;(3)过点N作NQ⊥CD,根据Rt△NPQ 的勾股定理进行求解;(4)根据Rt△ADM的勾股定理求出MP与x的函数关系式,然后得出函数关系式.试题解析:(1)根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得:AD=3.(2)由折叠可知AM=MP,在Rt△MPD中,∴∴y=-其中,0<x<3.(3)当点N在AB上,x≥3,∴PC≤3,而PN≥3,NC≥3.∴△PCN为等腰三角形,只可能NC=NP.过N点作NQ⊥CD,垂足为Q,在Rt△NPQ中,∴解得x=.(4)当点M在CD上时,N在AB上,可得四边形ANPM为菱形.设MP=y,在Rt△ADM中,,即∴ y=.∴ S=考点:函数的性质、勾股定理.。
平行四边形练习题及答案

平行四边形练习题及答案平行四边形是初中数学中的重要概念之一,它具有特殊的性质和特点。
通过练习题的形式,我们可以更好地理解和掌握平行四边形的相关知识。
本文将为大家提供一些平行四边形的练习题及答案,希望能对大家的学习有所帮助。
1. 练习题一:已知平行四边形ABCD中,AB = 6cm,BC = 8cm,角A的度数为60°,求AD的长度。
解答:由平行四边形的性质可知,平行四边形的对边长度相等。
因此,AD = BC =8cm。
2. 练习题二:已知平行四边形EFGH中,EF = 10cm,GH = 15cm,角E的度数为120°,求FG的长度。
解答:由平行四边形的性质可知,平行四边形的对边长度相等。
因此,FG = EH =15cm。
3. 练习题三:已知平行四边形IJKL中,IJ = 12cm,KL = 18cm,角I的度数为135°,求JK的长度。
解答:由平行四边形的性质可知,平行四边形的对边长度相等。
因此,JK = IL = 18cm。
4. 练习题四:已知平行四边形MNOP中,MN = 5cm,NO = 7cm,角M的度数为45°,求OP的长度。
解答:由平行四边形的性质可知,平行四边形的对边长度相等。
因此,OP = MN = 5cm。
5. 练习题五:已知平行四边形QRST中,QR = 9cm,ST = 12cm,角Q的度数为30°,求RS 的长度。
解答:由平行四边形的性质可知,平行四边形的对边长度相等。
因此,RS = QT =9cm。
通过以上练习题,我们可以发现平行四边形的一个重要性质:平行四边形的对边长度相等。
这个性质在解题过程中起到了关键的作用,帮助我们求解未知的边长。
除了对边长度相等外,平行四边形还具有其他一些重要的性质。
例如,平行四边形的对角线互相平分,即对角线互相等长。
这个性质在解题过程中也经常被用到。
练习题只是帮助我们巩固平行四边形的相关知识点,实际问题中,平行四边形的应用非常广泛。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行四边形提高练习
一、基础训练
1、在下列性质中,矩形有而平行四边形不一定具有的性质是()
A、对边相等
B、对角相等
C、对角线相等
D、对边平行
2、已知:菱形的周长等于它的较短对角线长的4倍,则它的各个角是()
A、60°或120°
B、45°或135°
C、30°或150°
D、以上答案都不对
3、同学们都玩过万花筒,它是由三块等宽等长的玻璃片围成的。
如图,看到的是万花筒的一个图案,图中所有的小三角形均是完全一样的等边三角形,其中的菱形AEFG可以看成是把菱形ABCD以A为旋转中心()
A、顺时针旋转60°得到的
B、顺时针旋转120°得到的
C、逆时针旋转60°得到的
D、逆时针旋转120°得到的
4、如图,O是正方形ABCD内的一点,如果△AOB是一个等边三角形,那么∠DCO的度数为________。
5、天河宾馆在重新装修后,准备在大厅的主楼梯铺上某种红色的地毯,已知这种地毯每平方米的售价30元,主楼梯道宽2米,其侧面如图所示,则购买地毯至少需要_________元。
6、如图,在梯形ABCD中,AB=AD=DC,BD⊥CD,则∠C=__________。
7、已知,如图,梯形ABCD中,AD//BE,DM=MC,AF⊥BC,∠B=45°,AF=3,EF=5,则梯形ABCD
的面积为________________。
8、有一条长为1000m的路基,它的横截面是一个等腰梯形ABCD,已知路基基顶AB=6m,路基的高为
2.3m,路基基底比基顶宽0.5m,则要建造这样的一段路基一共需要的土石方数位________________。
9、下列说法不正确的是()
A、等腰梯形的对角线相等
B、平行四边形的对角线互相平分
C、菱形的对角线相等
D、矩形的对角线相等
二、判定一个四边形是特殊的四边形的方法有许多,小明在一次学习时又发现了一种方法,即“有一条
对角线平分一个内角的平行四边形是菱形”,但他还没有验证出这个结论是正确的,你能帮他说明白吗?
三、迎宾大酒楼准备将一个大厅隔成两个小厅,隔屏的正面形态如图所示,阴影部分全是用宽为10cm
的木条拼成,木条的数量如图所示,请计算图中阴影部分的面积。
四、按要求画一个图形:所画的图形中同时要有正方形和圆,并且这个图形既是轴对称图形又是中心对
称图形。
通过画图,你能总结出正确的画出图形的规律吗?
五、如图,平行四边形ABCD中,AQ、BN、CN、DQ分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN交于P,CN与DQ角与M。
在不添加其他条件的情况下,试写出一个由上述条件推出的结论,并说明其
正确性(要求:推导过程中用到“平行四边形”和“角平分线”这两个条件)。
六、有一位小朋友想剪一个等边三角形,可是手上只有一张正方形的纸,如图,你能帮他得到等边三角形吗?如果能,写出你的操作步骤。
七、用一张矩形的纸,不用其他工具,只用双手,你能将直角三等分吗?徐老师是按以下的步骤进行的(如图):
(1)现将矩形纸对折,设折痕为MN;
(2)再把D点叠在折痕MN上,折痕为AE,点D在MN上的对应点为H,得Rt△AHE;
(3)延AH折叠,得到折痕AH。
这样,AE、AH就是直角BAD的三等分线,你能说明这个结论吗?
八、在一次数学课堂上,王老师随意的拿出了一张梯形纸片,然后问学生:“我想不改变这张纸片的面积,而将其形状变化成平行四边形,你能否办到呢?”请画图说明。
九、要剪切如图(尺寸单位:mm)所示甲、乙两种直角梯形零件,且使两种零件的数量相同,有两种面积相等的矩形铝板,第一种长600mm,宽250mm,第二种长500mm,宽300mm可供选用。
(1)填空:为了充分利用材料,应选用第_______种铝板,这是一块铝板最多能剪甲、乙零件共________个,(2)剪下这些零件后,剩余的边角余料的面积是多少平方厘米?
(3)画图:选出你要用的铝板,在上面画出剪切线,并把边角余料用阴影表示出来。
十、如图,把边长为2cm的正方形剪成四个完全相同的直角三角形。
请用这四个完全相同的直角三角形拼成符合下列要求的图形(全部用上,互不重叠且不留空隙),并把你的拚法仿照题中所给的图按实际大小画出:
(1)不是正方形的菱形(一个);
(2)不是正方形的矩形(一个);
(3)梯形(两个);
(4)不是矩形和菱形的平行四边形(一个);
(5)不是梯形和平行四边形的凸四边形;
十一、如图,在矩形ABCD中,横向阴影部分是矩形,另一阴影部分是平行四边形,依照图中标注的数据,计算图中空白部分的面积。
