第六章、数理统计的基本知识解答
第六章 数理统计的基本概念pdf_(一)基本要求

.第六章 数理统计基本概念
一、基本要求、重点与难点
(一)基本要求
1.理解总体、个体、简单随机样本和统计量的概念。掌握样本均值和样本 方差的计算。
(2)设 X ~ χ 2 (n) ,则 E(X)=n,D(X)=2n .
若 X ~ χ 2 (n) ,对于α (0 < α < 1) ,称满足 P( X > χα2 (n)) = α的点χα2 (n) 为 χ 2 (n) 分布的
上侧α 分位点。当 n>45 时,R.A.Fisher 证明了下面的近似公式
( ) χα2
(n)
≈
1 2
uα +
2
2n −1 ,
其中 uα 为标准正态分布的上侧α 分位点。
2、 自由度为 n 的 t 分布:
定义设 X1, X2 独立,X1~N(0,1), X2~ χ 2 (n) ,则称
T (n) = X1 X 2 n
的分布是自由度为 n 的 t 分布,简记为 t(n) ,亦称为学生(student)分布。这种分布是英国人 w.s.Gosset 在 1908 年以笔名”student”发表的,它是数理统计中最重要的分布之一。 命题 设 T(n)是自由度为 n 的 t 分布,则它的概率密度函数为:
2.会列出分组数据统计表。 3.了解X2-分布、t-分布和F-分布的定义及性质。了解分位数的概念并会查
表计算。 4.掌握正态总体的抽样分布规律。
(二)重点
1.样本均值和样本方差的计算。 2.分组数据统计表。 3.正态总体的抽样分布规律。
概率论与数理统计(茆诗松)第二版课后第六章习题参考答案

⎝ 2 2⎠
2
则X
=Y
+θ
−
1 2
,
X (1)
= Y(1)
+θ
−
1 2
, X(n)
= Y(n)
+θ
−
1 2
,即
1 2
(
X
(1)
+
X(n)) =
1 2 (Y(1)
+ Y(n) ) + θ
−1 2
,
可得 E( X ) = E(Y ) + θ − 1 = E(Y ) +θ − 1 = θ , Var(X ) = Var(Y ) = 1 Var(Y ) = 1 ,
n
∑ 由伽玛分布的可加性知 Y = X i 服从伽玛分布 Ga(n, λ),密度函数为 i=1
pY
( y)
=
λn Γ(n)
y n−1 e−λ y
Ι y>0
,
∫ ∫ 则 E⎜⎛ 1 ⎟⎞ = E⎜⎛ n ⎟⎞ = ⎝ X ⎠ ⎝Y ⎠
+∞ n ⋅ λn y n−1 e−λ y dy = nλn
0 y Γ(n)
n
∑ 4. 设总体 X ~ N (µ , σ 2),X1, …, Xn 是来自该总体的一个样本.试确定常数 c 使 c ( X i+1 − X i )2 为σ 2 的无 i=1
偏估计. 解:因 E[(Xi + 1 − Xi )2 ] = Var (Xi + 1 − Xi ) + [E(Xi + 1 − Xi )]2 = Var (Xi + 1) + Var (Xi ) + [E(Xi + 1) − E(Xi )]2 = 2σ 2,
概率论与数理统计 第六章--数理统计的基本概念

F分布性质2 若X ~t(n),则X2~F(1,n)
例4.设X1,X2, …,Xn是来自正态总体N(0,1) 的样本,试问c=( )统计量
c
2 X i 3 i 1 n
X
i 4
2 i
服从F分布?
抽样分布的分位点
设α为给定的常数,且0<α<1.若存在χα2(n)使
P ( n)
分位点的性质
(1) u1 u (2)
t1 (n) t (n)
1 (3) F (m, n) F1 (n, m)
回顾1. 设X1 ,X2 ,X3, X4是来自总体N(0,4)的简单 随机样本,X=a(X1-2 X2)2+b(3X3 -4X4)2,问当 a,b为何值时,统计量X服从 2分布 .
Max=1572, Min=738, 组数=6 组距=(Max-Min)/6=139140 取a0=735, 则分组区间及相关数据如下
组序 1 2 分区区间 (735,875] (875,1015] 频数 6 8 频率 0.2 0.27 累计频率 0.2 0.47
3
4 5 6 合计
(1015,1155]
2
所服从的分布为自由度为 n 的 分布 记为
2
~ (n)
2 2
分布的密度函数为
2
n x 1 1 n2 x2 e 2 f ( x; n ) 2 ( n 2 ) 0
x0 x0
其中伽玛函数 ( x )通过积分
( x ) e t dt, x 0 0 来定义.
(1155,1295] (1295,1435] (1435,1575]
9
4 2 1 30
0.3
数理统计第六章知识点

P 1 n X i . n i 1
注:
样本的 l 阶矩依概率收敛于总体的 l 阶矩.
第六章 参数估计
第10页
(2). 替换原理:
用样本矩替换相应的总体矩;
用样本矩的函数替换相应的总体矩的函数.
ˆ 1 / x. 得参数 的矩估计为
又由于 Var( X ) 1 / 2 , 有 1 / Var( X ), 由替换原理,
ˆ 1 / s. 得参数 的矩估计为
这说明矩估计不唯一, 这是矩估计的一个缺点,此时通常 尽量采取低阶矩给出未知参数的估计.
第六章 参数估计
a 概率 P ( X a ) 例如:X ~ N(, . 3. 总体分布的各种特征数.
2 ),
一、参数的主要类型
例如: 总体均值E(X)、 总体方差Var(X)、 总体中位数 x0.5 等.
第六章 参数估计
第 3页
二、参数空间 1.参数的表示
一般情形下,常用θ 表示参数.
2n2 2n1 n2 (1 )n2 2n3 ,
用求导法求极大似然估计的具体步骤:
①. 写出样本的似然函数L( ; x); ②. 求出对数似然函数 l ( ; x) ; l ( ; x ) 0 1 , ③. 解似然方程组 l ( ; x ) 0 k ④. 判断 ˆ 是否是极大似然估计.
4.非参数假设检验问题
利用样本去检验形式未知的总体的假设.
第六章 参数估计
第 5页
四、参数估计的主要内容 1.点估计
习题解答 - 第六章 数理统计基本概念

么值时, η 服从 χ 分布?并给出自由度。
2
解答:因 ξ1 ,L , ξ 4 是 N (0, 2 ) 的一个样本,所以 a (ξ1 − 2ξ 2 ) 与 b (3ξ3 − 4ξ 4 ) 相互独立,
2
且由例 3.16 可知它们分别服从 N (0, 20a ) 、 N (0,100b) ,要使 η 服从 χ 分布,只要
_ _
σ2
n
, E (S 2 ) = σ 2 。 (1)因
ξ
B(k , p) , 则 E (ξ ) = μ = kp, D (ξ ) =
_
_
_
σ2
n
_
=
kp(1 − p ) , E ( S 2 ) = σ 2 = kp(1 − p ) ; n =
(2)因 ξ
π (λ ) ,则 E (ξ ) = μ = λ , D(ξ ) =
i =1
10
N (0, 0.32 ) ,所以 ξ 0.3
N (0,1) ,即从中抽取的容量为 10 的样本,去
10 10
我们有
∑ (ξ 0.3)2
i =1
10
χ 2 (10) ,所以 0.05 = P{∑ ξ 2 > λ} = P{∑ (ξ / 0.3) 2 >
i =1 i =1
λ
0.09
}
查表可知
_ 1 1 11 [∑ ni ⋅ xi2 − n( x) 2 ] = (8 ⋅ 02 + 5 ⋅12 + 7 ⋅ 32 + 3 ⋅ 42 + 2 ⋅ 62 − 25 ⋅ 22 ) = , 3 24 n −1 _ 1 n − 1 2 24 11 b2 = [∑ ni ⋅ xi2 − n( x) 2 ] = s = ⋅ = 3.52 n n 25 3
数理统计课后答案-第六章
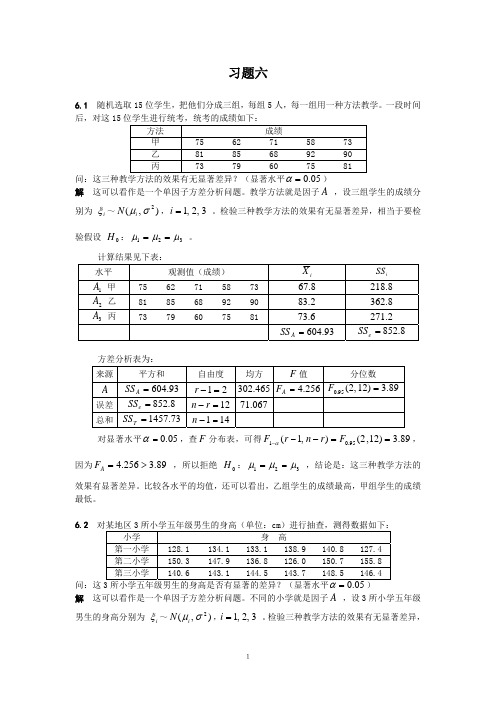
r
,
SST =
∑ j∑ ( i
=1 =1
X ij − X ,SSe =
)
2
∑ j∑ ( i
=1
X ij − X i
)
2
∑ SS i ,SS A =
i =1
ni ( X i ∑ i
r
=1
−X
)
2
可以证明离差分解公式: SST = SS e + SS A ,以及在 H 0 : μ1 = μ2 = ... = μr 成立时有
58 92 75
67.8 83.2 73.6 SS A = 604.93
218.8 362.8 271.2 SS e = 852.8
方差分析表为: 来源 平方和 自由度
A
误差 总和
SS A = 604.93
SS e = 852.8
SS T = 1457.73
r −1 = 2 n − r = 12 71.067 n − 1 = 14
ξ i ~ N ( μ i , σ 2 ) ,i = 1, 2, 3 。 检验三种教学方法的效果有无显著差异,
1
相当于要检验假设 H 0 : μ1 = 计算结果见下表: 水平
μ 2 = μ3 。
Xi
133.7333 144.5833
SS i
观测值(身高) 128.1 134.1 133.1 138.9 140.8 127.4 150.3 147.9 136.8 126.0 150.7 155.8 140.6 143.1 144.5 143.7 148.5 146.4
ξ i j ~ N (μ i j , σ 2 ) , 其中, μi j = μ + αi + β j , i = 1, 2, 3, 4 ,j = 1, 2, 3 。
第六章 数理统计的基本概念

第六章 数理统计的基本概念§6.1基本概念 §6.2样本数字特征一、填空题1. 若12,,n X X X ,为来自总体X 的容量为n 的样本,则样本均值X = ,样本方差2S = ; 2.设总体(4,40)X N , 1210,,X X X ,是X 的简单随机样本,则X 的概率密度()f x = ; .3.某种灯泡的寿命X 服从参数为(0)λλ>的指数分布,12,,n X X X ,是取自总体X 的简单随机样本,则12(,,)n X X X ,的联合密度函数为 ;4.设总体2(,2)X N μ ,12,,n X X X ,为取自总体的一个样本,X 为样本均值,要使2()0.1E X μ-≤成立,则样本容量n 至少应取多大 ;.5.设n X X X ,,21 ,是来自总体2(,)N μσ的随机样本,,a b 为常数,且0a b <<,则随机区间222211()(),n n i i i i X X b a μμ==⎛⎫-- ⎪⎝⎭∑∑的长度的数学期望为 。
.二、选择题1. 设(1,4)X N ,12,,n X X X ,为X 的样本,则(C )(A )1~(01)2X N -,; (B )1~(01)4X N -,; (C~(01)N ,; (D~(01)N ,. 2.设12,,n X X X ,是总体X 的样本,则有(D )(A )()X E X =; (B )()X E X ≈; (C )1()X E X n=; (D )以上三种都不对. 3.设总体(2,9)X N , 1210,,X X X ,是X 的样本,则(B )(A )(20,90)X N ; (B )(2,0.9)X N ; (C )(2,9)X N; (D )(20,9)X N .4.设总体2(,)X N μσ , 其中μ已知, 1234,,X X X X ,是X 的样本,则不是统计量的是(C ) (A )145X X +; (B )41i i X μ=-∑; (C )1X σ-; (D )421i i X =∑.5.设随机变量X 服从正态分布(0,1)N ,对给定的(01)αα<<,数a u 满足{}a P X u α>=,若{||}P X x α<=,则x 等于(C )(A )2a u ; (B )12a u-;(C )12a u -; (D )1a u -.6.设12,,n X X X ,是来自正态总体2(,)N μσ的简单随机样本,X 与2S 分别是样本均值与样本方差,则(C )(A )2222()E X S μσ-=-; (B )2222()D X S μσ+=+; (C )22()E X S μσ-=-; (D )22()D X S μσ+=+.三、 计算题5. 设1234,,,X X X X 是取自正态总体2(,)N μσ中的一个大小为4的样本,其中μ已知,但2σ未知,指出下面随机变量中哪些是统计量? (1)1234X X X X +++;(2)42211()ii Xμσ=-∑; (3)12max{,}X X ;(4)4X μ+; (5)141()2X X +; (6X . 其中4114i i X X ==∑.6. 12,,n X X X ,是取自正态总体2(,)N μσ中的一个样本,12, m U X X X =+++12 m m n V X X X ++=+++ ( )n m >.求,U V 的联合密度函数。
数理统计的基本知识

• 这些观测值仍分别称为样本均值,样本方差,样本标准差,样本k阶原 点矩,样本k阶中心矩。 记作 k 存在,则当n→∞时 • 我们指出,若总体X的k阶原点距 E ( X k ) , p A k , k 1,2,... k • • 即:样本的k阶原点距依概率收敛于总体的k阶原点距。 • 事实上,由于X1,X2,...,Xn相互独立,且与X同分布,故 X1k,X2k,...,Xnk相互独立,且与Xk同分布,故有 • E(X1k)=E(X2k)=E(Xnk)=μk,k=1,2,... • 由第五章的辛钦大数定律知
二· 常用的统计量
• 样本均值
• 样本方差 • 样本标准差
1 n X Xi n i 1 2 n n 2 2 1 1 2 S ( Xi nX ) (Xi X ) n 1 i 1 n 1 i 1 S S2 1 n 2 (Xi X ) n 1 i 1
F (n , n ) f ( x)dx 1 2
• 的点Fɑ(n1,n2)为F(n1,n2)分布的上ɑ分位点 。 • 如图
f(x)
1 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0 0
ɑ
x
0.5 1 1.5
1 • F分布的上分位点具有如下性质:F1 (n1, n2 ) F (n2 , n1 )
如果总体X的分布函数为F(x),则样本X1,X2,...Xn的联合分布函数为 F*(x1,x2,...xn)=F(x1)F(x2)· · · F(xn)= n 如果总体X是离散型随机变量,且概率密度为 F ( xi ) P{X=xi},i=1,2,... i 1 则样本X1,X2,...Xn的联合概率密度为 P*{X1=x1,X2=x2,...Xn=xn}=P{X1=x1}P{X2=x2}· · · P{Xn=xn}=
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章、数理统计的基本知识五、证明题:1.证:因为随机变量12,,,n X X X 相互独立,并且与总体X 服从相同的正态分布2(,)N μσ,所以,它们的线性组合11222111111[,()](,)n ni ii i nni i X X X n nN N nnn σμσμ======⋅⋅=∑∑∑∑即样本均值X 服从正态分布2(,)N nσμ.2.证:因为随机变量12,,,n X X X 相互独立,并且与总体X 服从相同的正态分布2(,)N μσ,所以,它们的线性组合11222111111[,()](,)n ni ii i nni i X X X n nN N nnn σμσμ======⋅⋅=∑∑∑∑即样本均值X 服从正态分布2(,)N nσμ。
所以,将X 标准化,即得~(0,1)u N =. 3.证:因为随机变量12,,,n X X X 相互独立,并且与总体X 服从相同的正态分布2(,)N μσ,即2~(,),1,2,i X N i n μσ=所以得~(0,1),1,2,,i X N i n μσ-=又因为12,,,n X X X 相互独立,所以 12,,,n X X X μμμσσσ--- 也相互独立。
于是,22222111()()~()n ni i i i X X n μμσσ==-χ=-=χ∑∑.4.证:由§5.4定理2知,统计量~(0,1)u N=;又由§5.4定理4知,统计量2222(1)~(1)n Snσ-χ=χ-因为X与2S独立,所以统计量u=222(1)n Sσ-χ=也是独立的。
于是,根据§5.3定理2可知,统计量~(1)t t n===-.5.证:由§5.4定理1知:22121212~(,),~(,)X N Y Nn nσσμμ.因为X与Y独立,所以可知:22121212~(,)X Y Nn nσσμμ--+.于是,得~(0,1)U N=.6.证:由§5.4定理6的推论知,统计量~(0,1)U N=.又由§5.4定理4知:2221111222222222(1)~(1),(1)~(1).n Snn Snσσ-χ=χ--χ=χ-因为21S与22S独立所以21χ与22χ也是独立的,由2χ分布的可加性可知,统计量w s =由§5.4定理4知:X 与21S 独立,Y 与22S 独立,所以统计量U 与2χ也是独立的.于是,由§5.3定理2可知,统计量12~(2)T t n n ==+-.其中w s =7.证: 由§5.4定理3知:2221112112222222121()~(),1()~().nii njj Xn Yn μσμσ==χ=-χχ=-χ∑∑因为所有的1(1,2,)i X i n = 与1(1,2,)i Y j n = 都是相互独立的,所以统计量21χ与22χ也是独立的.于是,由§5.3定理3可知,统计量22211111112222222221()/()/~(,)/()/()ni i njj X n nF F n n n Yn μσμσ==-χ==χ-∑∑.8.证:由§5.4定理4知:222111121222222222(1)~(1),(1)~(2).n S x x n n Sx x n σσ-=--=-因为21S 与22S 独立,所以统计量21x 与22x 也是独立的.于是,由§5.3定理3可知,统计量2221111122222222/(1)/~(1,1)/(1)/x n S F F n n x n S σσ-==--- 9.证:由于127,,,X X X 是取自总体X 的样本,故127,,,X X X 相互独立,且~(0,9)1,2,i X N i=从而有1234567123456~(0,27);~(0,36)/~(0,1);36~(0,1)X X X N X X X X N X X X N X X X N ++++++++++故2221234567222123456711()()2727[/[~(2)X X X X X X X X X X X X X X χ=++++++=++++++χ 10.证:由于1215,,,X X X 是取X 的样本,故1215,,,X X X 相互独立,且~(0,4)1,2,,i X N i = 从而有10152222111~(0,1)1,2,,152()~(10);()~(5)22ii i i i X N i X X ===χχ∑∑故101022111515221111()/102~(10,5)2()/52i ii i i i i i X XY F XX ======∑∑∑∑ 11.证:由于1234,,,X X X X 是取自总体X 的样本,故1234,,,X X X X 相互独立,且 2~(0,)1,2,3,4i X N i σ=从而有 ~(0,1)1,2,3,4iX N i σ=故22223124~(0,1);()()()~(3)X X X X N x σσσσ++~(3)Y t ==12.证:由于1210,,,X X X 是取X 的样本,故1210,,,X X X 相互独立,且~(0,1)1,2,,i X N i= 从而2345345~(0,()~(0,1)X X X N X X X N ++++根据§5. 3定理1可知 2222213453121()~(1),~(2)3Y X X X Y X X =++χ=+χ 根据§5. 4定理4可知1010222661[]~(4)5i i i i Y X X ===-χ∑∑根据2χ分布的可加性,得22123~(142)(7)Z Y Y Y =++χ++=χ 17.证:由题设 ,有222222()[()()][()()][()()2()()]()()2[()()]2(,)D X YE X Y E X Y E X EX Y EY E X EX Y EY X EX Y EY E X EX E Y EY E X EX Y EY DX DY Cov X Y +=+-+=-+-=-+-+--=-+-+--=++18.证:由题设 ,有*][]0E X E X E X =⋅-=22***2*222()()[]11()1DX EX EX EX X EX E E DX E X EX DX DX DX=-=-===-=⋅=19.证:由题设~()X t k ,根据定理2可设 2~(0,1),~()U N V k χ 则有X =从而 22/U Y X V k==又 22~(0,1)~(1)U N U ⇒χ故 2/1~(1,)/U Y F k V k=20.由题设 12~(,)X F k k ,根据定理3可设 2212~(),~()U k V k χχ从而 1122/~(,)/U k X F k k V k =故 2211/1~(,)/V k F k k X U k = 从而1212121211212121{(,)}11{}(,)11{}1(,)1(,)(,)1(,)(,)P X F k k P X F k k P X F k k F k k F k k F k k F k k αααααααααα-->=<=≥=-==三、证明题:.1.设总体~()X N μσ2,,证明:样本均值11~()n i i X X N n nσμ==∑2,。
2. 设总体~()X N μσ2,,证明:统计量~(0,1)u N =。
3. 设总体~()X N μσ2,,证明:统计量222211()~()nii Xn μσ=χ=-χ∑。
4. 设总体~()X N μσ2,,证明:统计量~(1)t t n =-。
5. 设总体211~()X N μσ,,总体222~()Y N μσ,,证明:统计量~(0,1)U N=。
6. 设总体211~()X Nμσ,,总体222~()Y Nμσ,,证明:统计量12~(2)T t n n=+-,其中wS=.7. 设总体211~()X Nμσ,,总体222~()Y Nμσ,,证明:统计量12212111122221221()~(,)1()niinjjXnF F n nYnμσμσ==-=-∑∑.8. 设总体211~()X Nμσ,,总体222~()Y Nμσ,,证明:统计量2211122222/~(1,1)/SF F n nSσσ=--.9. 设总体X ~ N(0,9),127,,,X X X是取自总体X的样本,证明:统计量2222123456711()()~(2)2736X X X X X X Xχ=++++++χ。
10. 设总体X ~ N(0,4),1215,,,X X X是取自总体X的样本,证明:统计量2221210222111215~(10,5)2()X X XY FX X X+++=+++。
11. 设总体~(0)X Nσ2,,1234,,,X X X X是取自总体X的样本,证明:统计量~(3)Y t=12. 设总体X ~ N(0,1),1210,,,X X X是取自总体X的样本,213451()3Y X X X=++,101022661[]5i ii iY X X===-∑∑,22312Y X X=+,123Z Y Y Y=++,证明:统计量2~(7)Zχ。
13. 设随机变量~()X t k ,证明:随机变量函数2~(1,)Y X F k =. 14. 若随机变量12~(,)X F k k ,证明:随机变量121~(,)Y F k k X=,从而有 12121(,)1/(,)F k k F k k αα-=.。
