第28章《圆》中考题集(41):28.2 与圆有关的位置关系
2024中考数学一轮复习核心知识点精讲—圆的基本性质与圆有关的位置关系

2024中考数学一轮复习核心知识点精讲—圆的基本性质与圆有关的位置关系1.探索并了解点和圆、直线和圆以及圆和圆的位置关系.2.知道三角形的内心和外心.3.了解切线的概念,并掌握切线的判定和性质,会过圆上一点画圆的切线.考点1:点与圆的位置关系设⊙O的半径是r,点P到圆心O的距离为d,则有:d<r⇔点P在⊙O内;d=r⇔点P在⊙O上;d>r⇔点P在⊙O外。
考点2:直线与圆的位置关系1、直线与圆相离⇒d r>⇒无交点;2、直线与圆相切⇒d r=⇒有一个交点;3、直线与圆相交⇒d r<⇒有两个交点;r d=r r dd考点3:切线的性质与判定定理1、切线的判定定理:过半径外端且垂直于半径的直线是切线;两个条件:过半径外端且垂直半径,二者缺一不可即:∵MN OA ⊥且MN 过半径OA 外端∴MN 是⊙O 的切线2、性质定理:切线垂直于过切点的半径(如上图)推论1:过圆心垂直于切线的直线必过切点。
推论2:过切点垂直于切线的直线必过圆心。
以上三个定理及推论也称二推一定理:即:①过圆心;②过切点;③垂直切线,三个条件中知道其中两个条件就能推出最后一个。
考点4:切线长定理切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,这点和圆心的连线平分两条切线的夹角。
即:∵PA 、PB 是的两条切线∴PA PB =;PO 平分BPA∠考点5:三角形的内切圆和内心(1)三角形的内切圆与三角形的各边都相切的圆叫做三角形的内切圆。
(2)三角形的内心三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心。
注意:内切圆及有关计算。
(1)三角形内切圆的圆心是三个内角平分线的交点,它到三边的距离相等。
(2)△ABC 中,∠C=90°,AC=b ,BC=a ,AB=c ,则内切圆的半径r=2cb a -+。
(3)S △ABC =)(21c b a r ++,其中a ,b ,c 是边长,r 是内切圆的半径。
中考数学总复习第六单元圆第28课时与圆有关的位置关系

tiáo)角平分线
的交点,三角形的内心到
三边的② 距离( jùlí)
相等
如图,☉I 内切于△ABC,切点分别为 D,E,F.
规律清单
1
则(1)∠BIC=90°+ ∠BAC;
2
1
(2)若△ABC 的三边长分别为 a,b,c,☉I 的半径为 r,则有 S△ABC= r(a+b+c);
由于 EF 与圆心 O 的距离为 1,小于☉O 的半径 5,故直线 EF 与☉O 相交,二者有且只有两个交点 E,F.
因此☉O 上有且只有 3 个点到直线 AB 的距离为 3.
2021/12/9
第十二页,共四十页。
高频考向探究
探究(tànjiū)一
点和圆的位置关系
【命题角度】根据点到圆心的距离判定点和圆的位置关系.
.
高频考向探究
13
[答案] 0<m<
2
5
12
12
5
[解析] 利用待定系数法求 k,再求出与☉O 相切时的 m 的值,直线 AB 的函数表达式为 y=- x+m,A(0,m),B( m,0),
13
13
2
2
过点 O 作 OC⊥AB 于点 C,因为 OC 为半径 6,用三角函数求出 OA= ,所以 m 最大为 .
第八页,共四十页。
课前双基巩固
3. [九上 P73 习题第 4 题改编] 如图 28-2,AB 是☉O 的直径,AD
[答案] 45
是☉O 的弦,过点 B 的切线交 AD 的延长线于点 C.若 AD=DC,
[解析] 由 AB 是☉O 的直径,得 BD⊥
九年级数学下册第28章圆28.2与圆有关的位置关系4圆与圆的位置关系课件华东师大版

∵∠PDB=∠ACB=90°,∠PBD=∠ABC. ∴△PBD∽△ABC. PD PB ,即 PD 4 ,
AC AB 6 10
∴PD=2.4(cm) .…………………………………………5分
当t=1.2时,PQ=2t=2.4(cm). ∴PD=PQ,
即圆心P到直线AB的距离等于⊙P的半径. ∴直线AB与⊙P相切.……………………………………6分
【解析】当点A1在线段AB上时,如
图①所示,设所用时间为x s,
则A1B=AB-A A1=2-2x,
A1B=A1D+DB=1+x,所以2-2x=1+x, x=1当. 点A1在线段AB的延长线上时,
3
如图②所示,则BA1=B B1+B1A1
=x+1,BA1=A A1-AB=2x-2, 那么1+x=2x-2,x=3. 所以x=1 或3.
1.两种判定方法 (1)从两圆公共点的个数;(2)比较两圆半径的和、差与圆心距 的大小. 2.四点注意事项 (1)两圆的五种位置关系按公共点个数可分为三大类,即相切、 相离和相交;
(2)两圆相切包含两种情况,即两圆外切和内切; (3)两圆相离也包含两种情况,即两圆外离和内含; (4)同心圆是两圆内含的特殊情况.
1.若半径为1 cm和2 cm的两圆相外切,那么与这两个圆都相切且
半径为3 cm的圆的个数为( )
(A)5个
(B)4个
(C)3个
(D)2个
【解析】选A.因为与两个圆都内切的有1个;与两个圆都外切的
有2个;与其中一个内切,另一个外切的有2个,共5个.
2.(2012·烟台中考)如图,⊙O1,⊙O,⊙O2的半径均为2 cm,
则⊙O1与⊙O2的位置关系是( )
华东师大版数学九年级下册第28章圆28.2与圆有关的位置关系

知识点 2 确定圆的条件 【例2】为了推进农村新型合作医疗制度改革,准备在某镇新建 一个医疗点P,使P到该镇所属A村、B村、C村的村委会所在地的 距离都相等(A,B,C不在同一直线上,地理位置如图),请你用尺 规作图的方法确定点P的位置. 要求:不写作法,保留作图痕迹.
【思路点拨】分析题意→作AB和AC的垂直平分线→交点为所 求. 【自主解答】如图所示
【总结提升】点与圆的位置关系 若圆的半径为r,点A到圆心的距离为d,则:
点与圆的 位置关系
点在圆内
d和r的 关系
d<r
点在圆上
d=r
点在圆外
d>r
图形
推理过程
点在圆内⇔ d<r
点在圆上⇔ d=r
点在圆外⇔ d>r
利用d和r的关系可以判断点和圆的位置关系,反之,知道了点和 圆的位置关系,也能确定d和r的数量关系,体现了“数”与“形” 的结合.
内接三角形
垂直平分线
(打“√”或“×”) (1)已知☉O的半径为r,点P到点O的距离大于r,那么点P一定在 ☉O的外部.( ) (2)任意一个圆有且只有一个内接三角形.( ) (3)三角形的外√心到三角形各顶点的距离相等.( ) ((45))过 任平 意面三内角的形任都意有三一点个可外以接作圆,一且个圆圆心.在( 三)×角形的内部.( )
2.4 4
【总结提升】d,r和直线与圆的位置关系 1.由d和r可推出直线与圆的位置关系. 2.由直线与圆的位置关系,可比较d和r的大小. 3.已知d和位置关系可求r的范围. 4.已知r和位置关系可求d的范围.
题组一:直线与圆的位置关系
1.已知☉O的面积为9πcm2,若点O到直线l的距离为πcm,则直线
【解析】如图所示
中考数学复习之与圆有关的位置关系,考点过关与基础练习题
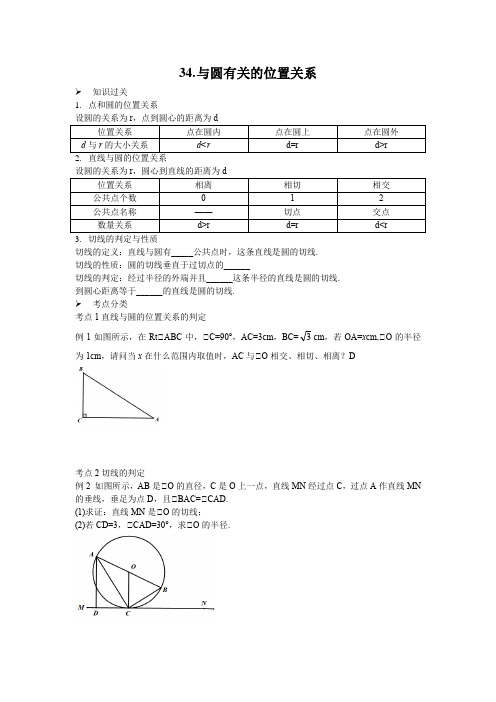
34.与圆有关的位置关系➢知识过关1.点和圆的位置关系2.直线与圆的位置关系3.切线的判定与性质切线的定义:直线与圆有_____公共点时,这条直线是圆的切线.切线的性质:圆的切线垂直于过切点的______切线的判定:经过半径的外端并且______这条半径的直线是圆的切线.到圆心距离等于______的直线是圆的切线.➢考点分类考点1直线与圆的位置关系的判定例1如图所示,在Rt△ABC中,△C=90°,AC=3cm,BC=3cm,若OA=x cm,△O的半径为1cm,请问当x在什么范围内取值时,AC与△O相交、相切、相离?D考点2切线的判定例2 如图所示,AB是△O的直径,C是O上一点,直线MN经过点C,过点A作直线MN 的垂线,垂足为点D,且△BAC=△CAD.(1)求证:直线MN是△O的切线;(2)若CD=3,△CAD=30°,求△O的半径.考点3 切线的性质 例3 如图所示,在△O 中,点C 是直径AB 延长线上一点,过点C 作△O 的切线,切点为D ,连接BD.(1)求证:△A=△BDC(2)若CM 平分△ACD ,且分别交AD 、BD 于点M 、N ,当DM=1时,求MN 的长.➢ 真题演练1.如图,A 、P 、B 、C 是⊙O 上的四点,∠APC =∠BPC =60°,P A =2,PC =4,则△ABC 的面积为( )A .43√3B .32√3C .2√3D .3√32.如图,四边形ABCD 是⊙O 的内接四边形,∠B =90°,∠BCD =120°,AB =4,BC =2,则AD 的长为( )A .2√3B .4−√3C .√3+1D .2+√33.如图,P A 、PB 、CE 分别与⊙O 相切于点A 、B 、D 点,若圆O 的半径为6,OP =10,则△PCE 的周长为( )A .10B .12C .16D .204.如图所示,点P 是⊙O 的半径OC 延长线上的一点,过点P 作⊙O 的切线,切点为A ,AB 是⊙O 的弦,连接AC ,BC ,若∠P AB =70°,则∠ACB 的大小为( )A .70°B .110°C .120°D .140°5.如图,在△ABC 中,∠A =60°,BC =12,若⊙O 与△ABC 的三边分别相切于点D ,E ,F ,且△ABC 的周长为32,则DF 的长为( )A .2B .3C .4D .66.如图,已知DC 是⊙O 的直径,点B 为CD 延长线上一点,AB 是⊙O 的切线,点A 为切点,且∠BAD =35°,则∠ADC =( )A .75°B .65°C .55°D .50°7.如图,PC 、PB 是⊙O 的切线,AB 是⊙O 的直径,延长PC ,与BA 的延长线交于点E ,过C 点作弦CD ,且CD ∥AB ,连接DO 并延长与圆交于点F ,连接CF ,若AE =2,CE =4,则CD 的长度为( )A .3B .4C .185D .2458.如图,四边形ABCD 内接于⊙O ,AE ⊥CB ,交CB 的延长线于点E .若BA 平分∠DBE ,AD =7,CE =√13,则AE 的长度为 .9.如图,四边形ABCD 内接于⊙O ,AB 为直径,AD =CD ,过点D 作DE ⊥AB 于点E ,连接AC 交DE 于点F .若sin ∠CAB =35,DF =5,则AB 的长为 .10.如图,P A、PB分别与⊙O相切于A、B两点,C为⊙O上一点连接AC、BC,若∠C=55°,则∠P的度数是°.11.如图,AB为圆O直径,∠DAB=∠ABC=90°,CD与圆O相切于点E,EF⊥AB于点F,EF交BD于点G,若AD=2,BC=6.(1)求CD的长度.(2)求EG的长度.(3)求FB的长度.12.如图,P A、PB、CD是⊙O的切线,点A、B、E为切点.(1)如果△PCD的周长为10,求P A的长;(2)如果∠P=40°,①求∠COD;②连AE,BE,求∠AEB.13.如图,P A、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.(1)求证:∠POA=2∠PCB;(2)若OA=3,P A=4,求tan∠PCB的值.➢ 课后练习1.如图,P A ,PB 是⊙O 的两条切线,A ,B 是切点,过半径OB 的中点C 作CD ⊥OB 交P A 于点D ,若PD =3,AD =5,则⊙O 的半径长为( )A .2√7B .4√2C .3√3D .2√52.如图,等边三角形ABC 的边长为4,⊙C 的半径为√3,P 为AB 边上一动点,过点P 作⊙C 的切线PQ ,切点为Q ,则PQ 的最小值为( )A .12B .√3C .2√3D .33.如图,点O 是矩形ABCD 对角线BD 上的一点,⊙O 经过点C ,且与AB 边相切于点E ,若AB =4,BC =5,则⊙O 的半径长为( )A .165B .258C .5√419D .44.如图,在△ABC 中,∠ACB =90°,AC =BC =√2,点D 是AB 边上一个动点,以点D 为圆心r 为半径作⊙D ,直线BC 与⊙D 切于点E ,若点E 关于CD 的对称点F 恰好落在AB 边上,则r 的值是( )A .√2−1B .1C .√2D .√2+15.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,如果∠D=30°,AB=4,那么线段CD的长是.6.如图,△ABD内接于⊙O,AD为直径,CD为⊙O的切线,连接BC,若CD=AD,AB =2,BC=2√13,则BD=.7.已知菱形ABCD的边长为4,∠BAD=60°,M是线段AD的中点,点P是对角线AC 上的动点,连接PM,以P为圆心,PM长为半径作⊙P,当⊙P与菱形ABCD的边相切时,AP的长为.8.如图,已知△ABC,以AB为直径的⊙O交AC于点E,交BC于点D,且BD=CD,DF ⊥AC于点F.给出以下四个结论:̂=DÊ;④∠A=2∠FDC.①DF是⊙O的切线;②CF=EF;③AE其中正确结论的序号是.9.如图,在Rt△ABC中,AC=BC=6,点O为边BC上一动点,连接OA.以O为圆心,OB为半径作圆,交OA于D,过D作⊙O的切线,交AC于点E.当⊙O与边AC相切时,CE的长为.10.如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交AB于点D,点Q为CA延长线上一点,延长QD交BC于点P,连接OD,∠ADQ=12∠DOQ.若AQ=AC,AD=4时,写出BP的长为.11.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆交于点D.(1)如图1,连接DB,求证:DB=DE;(2)如图2,若∠BAC=60°,求证:AB+AC=√3AD.12.如图,△ABC的内切圆⊙O与BC、CA、AB分别相切于点D、E、F.(1)若∠ABC=50°,∠ACB=75°,求∠BOC的度数;(2)若AB=13,BC=11,AC=10,求AF的长.➢冲击A+。
中考数学考点知识与题型专题讲解29---与圆有关的位置关系

3 / 20
①若 d>5,则 m=0;②若 d=5,则 m=1;③若 1<d<5,则 m=3;④若 d=1,则 m=2;⑤
⑤若 d<1 时,直线与圆相交,则 m=2,故错误.
故选 C.
Байду номын сангаас
【点睛】考查了直线与圆的位置关系,解题的关键是了解直线与圆的位置关系与 d 与 r
的数量关系.
【举一反三】 在平面直角坐标系 xOy 中,直 线经过点 A(-3,0),点 B(0, 3 ),点 P 的坐标为(1, 0),与 y 轴相切于点 O,若将⊙P 沿 x 轴向左平移,平移后得到(点 P 的对应点为点 P′),
若 d<1,则 m=4.
其中正确命题的个数是( )
A. 1 B. 2 C. 4 D. 5
【答案】C.
【解析】
试题 分析:①若 d>5 时,直线与圆相离,则 m=0,正确;
②若 d=5 时,直线与圆相切,则 m=1,故正确;
③若 1<d<5,则 m=3,正确;
④若 d=1 时,直线与圆相交,则 m=2 正确;
【答案】(1)详见解析;(2)4. 【解析】
5 / 20
过点 O 作 OF⊥AC 于点 F, ∴AF=CF=3, ∴OF= AO2 − AF 2 = 52 − 32 = 4 , ∵∠OFE=∠DEF=∠ODE=90°, ∴四边形 OFED 是矩形, ∴DE=OF=4. 考点:切线的判定;垂径定理;勾股定理;矩形的判定及性质.
中考数学考点一遍过 考点18 圆的性质及与圆有关的位置关系

中考数学考点一遍过考点18 圆的性质及与圆有关的位置关系圆的性质及与圆有关的位置关系是中考数学中的一个重要考点。
在这个考点中,我们需要掌握圆的定义、圆弧、圆心角、弧长和扇形面积的计算方法,以及圆与直线的位置关系。
首先,我们来看一下圆的定义。
圆是由平面上距离圆心相等的点构成的集合。
圆是一种特殊的椭圆,其所有点到圆心的距离都相等。
在圆的性质中,圆弧是一个重要的概念。
圆弧是圆上两个点之间的一段弧线。
我们可以使用圆心角来描述圆弧的大小。
圆心角是以圆心为顶点的角,其对应的弧所对的圆心角大小等于弧所对的圆弧长度的一半。
通过圆心角的大小,我们可以判断圆弧的长度。
根据圆的性质,我们可以计算圆的弧长和扇形面积。
弧长是圆弧的长度,可以通过圆心角的大小和半径的关系来计算。
弧长等于圆心角的弧度数乘以半径。
扇形面积是由圆心角和半径所围成的扇形的面积,可以通过圆心角的大小和半径的关系来计算。
扇形面积等于圆心角的弧度数乘以半径的平方再除以2。
除了圆弧、圆心角、弧长和扇形面积的计算方法,我们还需要了解圆与直线的位置关系。
当直线与圆相交时,可以根据相交的情况判断它们的关系。
如果直线与圆相交于两个不同的点,我们可以得到两条相交弧。
如果直线与圆相切于一个点,那么这条直线被称为切线。
同时,切线与半径垂直。
综上所述,圆的性质及与圆有关的位置关系是中考数学中的一个重要考点。
我们需要掌握圆的定义、圆弧、圆心角、弧长和扇形面积的计算方法,以及圆与直线的位置关系。
通过熟练掌握这些知识,我们可以在中考数学考试中轻松应对相关题目。
希望同学们能够通过不断练习和巩固知识,顺利掌握这个考点,取得好成绩。
中考复习——与圆有关的位置关系

典型例题精析
例1 (2011娄底)若⊙ O 的半径 5cm ,点到圆心 的距离为 4 c m ,那么点 A 与⊙ O 的位置关系 是( C ) A.点 A 在圆外
C.点 A 在圆内
B.点 A 在圆上
D.不能确定
例2 (2011舟山)如图, A B C 中,以 A B于点 D , A C D A B C . (1)求证:
三角形的内心与外心
1.三角形的三个顶点确定一个圆,这个圆叫 做三角形的外接圆,三角形和外接圆的圆心叫外 三边垂直平分线 心,是三角形______________的交点,它到三角 顶点 形_______的中离相等 2.与三角形各边都要相切的圆叫做三角 形的内切圆,内切圆的圆心叫做三角形的内心, 角平分线 是三角形____________的交点,到三角形 三边 _______的距离相等地.
中考总复习—— 与圆有关的位置关系
命题预测
本节主要考查与圆的位置关系、 直线与圆的位置关系、切线的性质及 判定、三角形的内切圆与外接圆的知 识等,其中点与圆的位置关系和切线 性质是江西近年考查重点,题型以选 择题和解答题为主.
中考知识清单
好好记住哦!
与圆有关的位置关系
1.点与圆的位置关系
位置关系 点在圆内 点在圆上 点在圆外
0
1
相交
2
内切
1
内含(同心 圆)
0
两圆公共 点个数 圆心距为d , d 半径分别为, R , r( R > r ) 外公切线的 条数
内公切线的 条数
Rr
Rr d Rr
d Rr
2
d Rr
d Rr d 0
0
2
2
12Βιβλιοθήκη 1000
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第28章《圆》中考题集(41):28.2 与圆有关的位置关系
填空题
511.已知⊙O1和⊙O2的半径分别为3cm和2cm,且O1O2=1cm,则⊙O1与⊙O2的位置关系为.
512.两圆的半径分别为3cm和4cm,圆心距为5cm,则两圆的位置关系为.513.已知两圆的半径分别为5cm和4cm,圆心距是6cm,则这两个圆的位置关系是.514.如图,⊙A、⊙B的半径分别为1cm、2cm,圆心距AB为5cm.如果⊙A由图示位置沿直线AB向右平移3cm,则此时该圆与⊙B的位置关系是.
515.已知⊙O1和⊙O2的半径分别是一元二次方程(x﹣1)(x﹣2)=0的两根,且O1O2=2,则⊙O1和⊙O2的位置关系是.
516.已知两圆的半径分别是2和3,圆心距为6,那么这两圆的位置关系是.517.已知△ABC的三边分别是a、b、c,两圆的半径r1=a,r2=b,圆心距d=c,则这两个圆的位置关系是.
518.已知相切两圆的半径分别为5cm和4cm,这两个圆的圆心距是.
519.若⊙O1和⊙O2外切,O1O2=10cm,⊙O1半径为3cm,则⊙O2半径为cm.520.已知,⊙O1的半径为5,⊙O2的半径为9,且⊙O1与⊙O2相切,则这两圆的圆心距为.
521.已知R和r是两圆半径,且两圆的圆心距为6,已知|R﹣7|与|r﹣2|互为相反数,那么这两圆的位置关系是.
522.如图,奥运五环旗上的五个环可以近似地看成五个圆,这五个圆反映出的圆与圆的位置关系有.
523.两圆有多种位置关系,图中不存在的位置关系是.
524.已知⊙O1和⊙O2内切,且圆心距为10cm,若⊙O1的半径为3cm,则⊙O2的半径为cm.
525.分别以梯形ABCD的上底AD、下底BC的长为直径作⊙O1、⊙O2,若两圆的圆心距等于这个梯形的中位线长,则这两个圆的位置关系是.
526.如图,轮椅车的大小两车轮(在同一平面上)与地面的触点A、B间距离为80cm,两车轮的半径分别为136cm、16cm,则此两车轮的圆心相距cm.
527.如图,在以O为圆心的两个同心圆中,大圆的直径AB交小圆于C、D两点,AC=CD =DB,分别以C、D为圆心,以CD为半径作圆.若AB=6cm,则图中阴影部分的面积为cm2.
528.如图,奥运五环标志里,包含了圆与圆的位置关系中的外离和.
529.已知⊙O1和⊙O2的半径分别为3cm和5cm,且它们内切,则圆心距O1O2等于cm.
530.已知⊙O1与⊙O2的半径分别为2cm和3cm,当⊙O1与⊙O2外切时,圆心距O1O2=cm.
531.若两圆的半径分别为5和2,圆心距为7,则这两个圆的位置关系是.532.⊙O的半径为3cm,点M是⊙O外一点,OM=4cm,则以M为圆心且与⊙O相切的圆的半径是cm.
533.在直角坐标系中,⊙O的圆心在原点,半径为3,⊙A的圆心A的坐标为(,1),
半径为1,那么⊙O与⊙A的位置关系是.
534.两个圆的半径分别为3和4,圆心之间的距离是5,这两个圆的位置关系是.535.如图,已知两圆外切于点P,直线AD依次与两圆相交于点A、B、C、D.若∠BPC =42°,则∠APD=度.
536.已知⊙O1与⊙O2相外切,⊙O1的半径为3cm,圆心距O1O2=7cm,那么⊙O2的半径为cm.
537.如果两个圆的一条外公切线长等于5,另一条外公切线长等于2a+3,那么a=.538.两圆有多种位置关系,图中不存在的位置关系是.
539.如图是一个小熊的图象,图中反映出圆与圆的四种位置关系,但是其中有一种位置关系没有反映出来,请你写出这种位置关系,它是.
540.仔细观察如图所示的卡通脸谱,图中没有出现的两圆的位置关系是.
第28章《圆》中考题集(41):28.2 与圆有关的位置关
系
参考答案
填空题
511.内切;512.相交;513.相交;514.相交;515.相交;516.外离;517.相交;518.1cm或9cm;519.7;520.4或14;521.相交;522.相交和外离;523.内切;524.13;525.外切;526.40;527.4π;528.相交;529.2;530.5;531.外切;532.1或7;533.内切;534.相交;535.138;536.4;537.1;538.相交;539.相交;540.相交;。
