【3年高考】2016届高考数学专题练习2.4指数函数与对数函数
指数函数对数函数专练习题含答案-V1

指数函数对数函数专练习题含答案-V1
本篇文章将针对指数函数和对数函数的专练习题含答案做重新整理,主要分为以下几个部分:
一、指数函数部分练习题
1、简单的指数函数练习题
如:化简y=2^x+2^x
解答:y=2^x+2^x=2*2^x=2^(x+1)
2、指数函数的性质
如:已知y=2^x,求y在x=3处的切线方程
解答:y'=ln2*2^x,当x=3时,y'=ln2*2^3=8ln2
切线方程:y-2^3=8ln2(x-3),即y=8ln2x-16ln2
3、指数函数与对数函数的综合练习
如:已知y=log2x,求y=2^x的解
解答:当y=log2x时,x=2^y
将x=2^y带入y=2^x,得到:y=2^(2^y)
令f(x)=2^x-x,则f'(x)=ln2*2^x-1>0,所以f(x)单增
故f(x)=0的解唯一,即y=2^x的解唯一,即y=log2(2^y)
二、对数函数练习题
1、简单的对数函数练习题
如:化简y=log(a^2b^3/(ab)^2)
解答:y=log(a^2b^3)-log(a^2b^2)=logb
2、对数函数的性质
如:已知y=logax,z=logbx,求y和z的关系式
解答:由对数函数的换底公式,可得y=logbx/logba,z=logbx
式中,x>0,且a、b均大于0且不等于1
3、对数函数与指数函数的综合练习
如:已知y=log2x,求y=2^x的解
解答:将x=2^y带入y=log2x,得到y=y*log2(2),
即y=0或y=1,因此,x=1或x=2
以上是指数函数和对数函数中的一些练习题,希望对大家的学习有所帮助。
(完整版)指数函数对数函数专练习题(含答案).docx
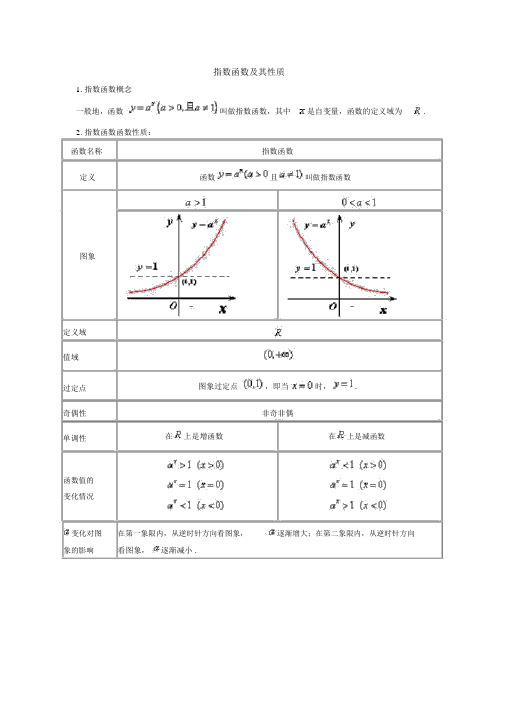
指数函数及其性质1.指数函数概念一般地,函数叫做指数函数,其中是自变量,函数的定义域为.2.指数函数函数性质:函数名称定义图象定义域值域过定点奇偶性单调性函数值的变化情况变化对图象的影响指数函数函数且叫做指数函数图象过定点,即当时,.非奇非偶在上是增函数在上是减函数在第一象限内,从逆时针方向看图象,逐渐增大;在第二象限内,从逆时针方向看图象,逐渐减小 .对数函数及其性质1.对数函数定义一般地,函数叫做对数函数,其中是自变量,函数的定义域.2.对数函数性质:函数名称定义函数对数函数且叫做对数函数图象定义域值域过定点奇偶性图象过定点,即当非奇非偶时,.单调性在上是增函数在上是减函数函数值的变化情况变化对图象的影响在第一象限内,从顺时针方向看图象,看图象,逐渐减小 .逐渐增大;在第四象限内,从顺时针方向指数函数习题一、选择题aa ≤ b,则函数 f ( x ) =1?2x 的图象大致为 ()1.定义运算 a ?b =>b a b2.函数 f ( x ) = x 2-bx + c 满足 f (1 + x ) =f (1 - x ) 且 f (0) =3,则 f ( b x ) 与 f ( c x ) 的大小关系是()xxA . f ( b ) ≤ f ( c ) x xB . f ( b ) ≥ f ( c )xxC . f ( b )> f ( c )D .大小关系随 x 的不同而不同3.函数 y = |2 x - 1| 在区间A . ( - 1,+∞ )C . ( - 1,1)( k - 1, k + 1) 内不单调,则 k 的取值范围是 ()B . ( -∞, 1)D . (0,2)4.设函数 f ( x ) =ln [( x -1)(2 -x)] 的定义域是 ,函数 ( ) = lg(x - 2x -1) 的定义域是 ,Ag xaB若 ?,则正数a 的取值范围 ()ABA . a >3B . a ≥ 3C . a > 5D . a ≥ 5.已知函数 f (x = 3- a x -3, x ≤ 7,若数列 { a n 满足 a n = f (n )(n ∈ * ,且 {a n }是递5 ) a x - 6, x >7. } N) 增数列,则实数a 的取值范围是 ()A . [ 9, 3)B . ( 9, 3) 44C . (2,3)D . (1,3)2x16.已知 a >0 且 a ≠ 1,f ( x ) = x - a ,当 x ∈ ( - 1,1) 时,均有 f ( x )< 2,则实数 a 的取值范围 是( )1 1 A . (0 , 2] ∪ [2 ,+∞ ) B . [ 4, 1) ∪ (1,4]11C . [ 2, 1) ∪ (1,2]D . (0 , 4) ∪ [4 ,+∞ )二、填空题xa7.函数 y = a ( a >0,且 a ≠ 1) 在 [1,2] 上的最大值比最小值大 2,则 a 的值是 ________.8.若曲线 | y | = 2 x + 1 与直线 y =b 没有公共点,则b 的取值范围是 ________.| x|的定义域为9. (2011 ·滨州模拟 ) 定义:区间 [x 1,x 2 ]( x 1<x 2) 的长度为 x 2- x 1. 已知函数 y = 2 [a , b] ,值域为 [1,2] ,则区间 [a , b] 的长度的最大值与最小值的差为 ________.三、解答题10.求函数y=2x2 3x 4 的定义域、值域和单调区间.11.(2011 ·银川模拟 ) 若函数y=a2x+ 2a x-1( a>0 且a≠ 1) 在x∈ [- 1,1]上的最大值为14,求a 的值.12.已知函数f (x) = 3x,(a+ 2) = 18, (x) =λ·3ax-4x的定义域为 [0,1] .f g(1)求 a 的值;(2) 若函数g( x) 在区间 [0,1] 上是单调递减函数,求实数λ的取值范围.1. 解析:由? = a a≤ b x2x x≤0,b a>b x>0 .1答案: A2. 解析:∵f (1 +x) =f (1 -x) ,∴f ( x) 的对称轴为直线x=1,由此得 b=2.又 f (0)=3,∴c=3.∴f ( x)在(-∞,1)上递减,在(1,+∞)上递增.x≥2x≥ 1,∴ (3 x) ≥(2 x) .若 x≥0,则3f f若 x<0,则3x<2x<1,∴f (3x)> f (2x).∴f (3x)≥ f (2x).答案: A3.解析:由于函数 y=|2x-1|在(-∞,0)内单调递减,在(0,+∞)内单调递增,而函数在区间 ( k- 1,k+ 1) 内不单调,所以有答案: Ck-1<0<k+1,解得-1<k<1.4.解析:由题意得: A=(1,2)x x>1x x>1在(1,2)上恒成立,即,a- 2且 a>2,由 A? B知 a- 2x x上恒成立,令x x xln a-2xln2>0 ,所以函数a-2 - 1>0 在 (1,2)u( x)=a- 2- 1,则u′( x) =au ( x ) 在 (1,2) 上单调递增,则 u ( x )> u (1) = a - 3,即 a ≥ 3.答案: B*f ( n ) 为增函数,5. 解析: 数列 { a } 满足 a = f ( n )( n ∈ N ) ,则函数nna >18- 6- ) × 7- 3,所以 3- a >0注意 a>(3,解得 2<a <3.aa8-6> 3- a × 7-3答案: C1 2x1 21 x x21的图象,6. 解析: f ( x )<? x -a < ? x - <a ,考查函数 y = a与 y =x - 2222当 a >1 时,必有 a-1≥1,即 1<a ≤ 2,21 1当 0<a <1 时,必有 a ≥ ,即 ≤a <1,2 2 1 综上, 2≤ a <1 或 1<a ≤ 2. 答案: C7. 解析: 当 a >1 时, y x在 [1,2] 上单调递增,故 2a3x= a a - a = ,得 a = . 当 0<a <1 时, y = a2 22a在 [1,2] 上单调递减,故 a -a = 2,得 a = 2. 故 a =2或 2.1131 3答案: 2或28. 解析: 分别作出两个函数的图象,通过图象的交点个数来判断参数的取值范围.x+1 与直线 y = b 的图象如图所示,由图象可得:如果x+ 1 与直线 y = b曲线 | y | = 2 | y | = 2没有公共点,则 b 应满足的条件是 b ∈ [- 1,1] .答案: [- 1,1]9. 解析: 如图满足条件的区间 [a , b] ,当 a =- 1, b = 0 或 a = 0, b = 1 时区间长度最小,最小值为 1,当 a =- 1,b = 1 时区间长度最大,最大值为2,故其差为 1.答案: 110. 解: 要使函数有意义,则只需- x 2-3x + 4≥ 0,即 x 2+ 3x -4≤ 0,解得- 4≤ x ≤ 1.∴函数的定义域为 { x | -4≤ x ≤ 1} .223225 令 t =- x - 3x + 4,则 t =- x - 3x + 4=- ( x + ) +4,2253∴当-4≤ x ≤ 1 时, t max = 4 ,此时 x =- 2, t min = 0,此时 x =- 4 或 x =1.∴0≤t ≤ 25 . ∴0≤ -x 2- 3x + 4≤ 5 .4 2∴函数 y = ( 1)x 23 x4的值域为 [ 2 , 1] .8223 225由 t =- x - 3x + 4=- ( x + )+4( - 4≤ x ≤ 1) 可知,23当- 4≤ x ≤- 2时, t 是增函数,3当- 2≤ x ≤1 时, t 是减函数.根据复合函数的单调性知:y = ( 1 )x 23 x 4在 [ - 4,- 3 3] 上是减函数,在 [ - ,1] 上是增函数.22 233∴函数的单调增区间是 [ - 2, 1] ,单调减区间是 [ - 4,- 2] . 11. 解: 令x22tt >0y= t+ 2t1= ( t+ 1)2,其对称轴为t =- 1.该二次函数a = ,∴ ,则--在[ - 1,+ ∞ ) 上是增函数.x12①若 a >1,∵x ∈ [ - 1,1] ,∴t = a ∈ [ a , a ] ,故当 t = a ,即 x =1 时, y max =a + 2a - 1=14,解得 a = 3( a =- 5 舍去 ) .②若 0<a <1,∵x ∈ [ - 1,1] ,∴ = x∈1 1=-时,a [ a , ] ,故当 t = ,即 1t a ax12y max = (a + 1) - 2= 14.11∴a =3或- 5( 舍去 ) .1综上可得 a = 3 或 3.12. 解: 法一: (1) 由已知得 a2 aa =log 32.3 += 18? 3 = 2?(2) 此时 g ( x ) = λ·2x - 4 x ,设 0≤ x 1<x 2≤ 1,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以 g ( x ) - g ( x ) = (2 x - 2x )( λ- 2x - 2x )>0 恒成立,即 λ<2x + 2x 恒成立.1 2 1 2 2 1 2 1由于 2x 2+ 2x 1>2 + 2 = 2,所以实数 λ的取值范围是λ≤ 2.法二: (1) 同法一.(2) 此时 g ( x ) = λ·2x - 4x ,因为 g ( x ) 在区间 [0,1] 上是单调减函数,所以有 g ′( x ) = λln2 ·2x - ln4 ·4x = ln2 [- 2 ·(2x )2+ λ·2x] ≤0 成立.x2 设 2 = u ∈ [1,2] ,上式成立等价于-2u+ λu ≤0 恒成立.因为 u ∈ [1,2] ,只需 λ≤2u 恒成立,所以实数 λ的取值范围是λ≤ 2.对数与对数函数同步练习一、选择题1、已知 3a2 ,那么 log3 8 2log 3 6 用 a 表示是()A 、 a 2B 、 5a2C 、 3a (1 a)2D 、 3a a 22、 2log a (M 2N ) log a Mlog a N ,则M的值为()A 、1NB 、4C 、1D 、 4 或 1413 、 已 知 x 2 y 2 1, x0, y 0 , 且 log a (1 x) m,log a n,则 log a y 等 于1 x()A 、 m nB 、 m nC 、 1m nD 、 1m n224、如果方程 lg 2 x (lg5lg 7)lgx lg5 glg 7 0 的两根是 ,,则 g的值是()A 、 lg5 glg 7B 、 lg35C 、 35D 、13515、已知 log 7[log 3 (log 2 x)] 0,那么 x2等于( )A 、1B 、13 C 、1D 、1322 2336、函数 ylg2 1 的图像关于()1 xA 、 x 轴对称B 、 y 轴对称C 、原点对称D 、直线 yx 对称7、函数 ylog (2 x 1) 3x2 的定义域是()A 、 2,1 U 1,B 、 1,1 U 1,32C 、 2,D 、 1,328、函数 ylog 1 (x 2 6x17) 的值域是()2A 、 RB 、 8,C 、, 3D 、 3,9、若 log m 9 log n 9 0 ,那么 m, n 满足的条件是( )A 、 m n 1B 、 n m 1C 、 0 n m 1D 、 0 m n 110、 log a 2 1,则 a 的取值范围是()3A 、 0, 2U 1,B 、 2,C 、 2,1D 、 0, 2U 2,3333 311、下列函数中,在 0,2 上为增函数的是()A 、 ylog 1 ( x1)B 、 y log 2 x 2 12C 、 ylog 2 1D 、 ylog 1 ( x 2 4x 5)x212、已知 g( x) log a x+1 ( a 0且a 1) 在 10, 上有 g( x)0 ,则 f ( x)a x 1 是( )A 、在 ,0上是增加的 B 、在 ,0 上是减少的C 、在, 1 上是增加的D 、在,0 上是减少的二、填空题13、若 log a 2 m,log a 3 n, a 2 m n 。
指数函数与对数函数高考题及答案

指数函数与对数函数(一)选择题(共15题)1.(安徽卷文7)设232555322555a b c ===(),(),(),则a ,b ,c 的大小关系是 (A )a >c >b (B )a >b >c (C )c >a >b (D )b >c >a【答案】A【解析】25y x =在0x >时是增函数,所以a c >,2()5xy =在0x >时是减函数,所以c b >。
【方法总结】根据幂函数与指数函数的单调性直接可以判断出来.2.(湖南卷文8)函数y=ax2+ bx 与y= ||log b ax(ab ≠0,| a |≠| b |)在同一直角坐标系中的图像可能是【答案】D【解析】对于A 、B 两图,|b a |>1而ax2+ bx=0的两根之和为 -b a ,由图知0<-b a <1得-1<ba <0,矛盾,对于C 、D 两图,0<|b a |<1,在C 图中两根之和-b a <-1,即ba >1矛盾,选D 。
3.(辽宁卷文10)设525bm ==,且112a b +=,则m =(A(B )10 (C )20 (D )100 【答案】D解析:选A.211log 2log 5log 102,10,m m m m a b +=+==∴=又0,m m >∴=4.(全国Ⅰ卷理8文10)设a=3log 2,b=In2,c=125-,则A. a<b<cB.b<c<aC. c<a<b D .c<b<a 【答案】C【解析】 a=3log 2=21log 3, b=In2=21log e ,而22log 3log 1e >>,所以a<b,c=125-=,而222log 4log 3>=>,所以c<a,综上c<a<b.【命题意图】本小题以指数、对数为载体,主要考查指数函数与对数函数的性质、实数大小的比较、换底公式、不等式中的倒数法则的应用.5.(全国Ⅰ卷理10)已知函数F(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+2b 的取值范围是(A))+∞(B))+∞ (C)(3,)+∞(D)[3,)+∞【答案】A【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a =+>,从而错选A,这也是命题者的用苦良心之处.【解析】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a +又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞).6.(全国Ⅰ卷文7)已知函数()|lg |f x x =.若a b ≠且,()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞ (C) (2,)+∞ (D) [2,)+∞【答案】C【命题意图】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用苦良心之处. 7.(山东卷文3)函数()()2log 31x f x =+的值域为A.()0,+∞ B. )0,+∞⎡⎣ C. ()1,+∞ D. )1,+∞⎡⎣ 【答案】A【解析】因为311x+>,所以()()22log 31log 10x f x =+>=,故选A 。
(精选试题附答案)高中数学第四章指数函数与对数函数典型例题

(名师选题)(精选试题附答案)高中数学第四章指数函数与对数函数典型例题单选题1、函数y=|lg(x+1)|的图像是()A.B.C.D.答案:A分析:由函数y=lgx的图象与x轴的交点是(1,0)结合函数的平移变换得函数y=|lg(x+1)|的图象与x轴的公共点是(0,0),即可求解.由于函数y=lg(x+1)的图象可由函数y=lgx的图象左移一个单位而得到,函数y=lgx的图象与x轴的交点是(1,0),故函数y=lg(x+1)的图象与x轴的交点是(0,0),即函数y=|lg(x+1)|的图象与x轴的公共点是(0,0),显然四个选项只有A选项满足.故选:A.2、青少年视力是社会普遍关注的问题,视力情况可借助视力表测量.通常用五分记录法和小数记录法记录视力数据,五分记录法的数据L和小数记录表的数据V的满足L=5+lgV.已知某同学视力的五分记录法的数据为10≈1.259)4.9,则其视力的小数记录法的数据为()(√10A .1.5B .1.2C .0.8D .0.6答案:C分析:根据L,V 关系,当L =4.9时,求出lgV ,再用指数表示V ,即可求解.由L =5+lgV ,当L =4.9时,lgV =−0.1,则V =10−0.1=10−110=√1010≈11.259≈0.8. 故选:C. 3、已知函数f (x )={−2x,x <0−x 2+2x,x ≥0若关于x 的方程f (x )=12x +m 恰有三个不相等的实数解,则m 的取值范围是( ) A .[0,34]B .(0,34) C .[0,916]D .(0,916)答案:D分析:根据题意,作出函数f (x )={−2x, x <0,−x 2+2x,x ≥0与y =12x +m 的图像,然后通过数形结合求出答案. 函数f (x )={−2x, x <0,−x 2+2x,x ≥0 的图像如下图所示:若关于x 的方程f (x )=12x +m 恰有三个不相等的实数解, 则函数f (x )的图像与直线y =12x +m 有三个交点,若直线y =12x +m 经过原点时,m =0, 若直线y =12x +m 与函数f (x )=12x +m 的图像相切,令−x 2+2x =12x +m ⇒x 2−32x +m =0,令Δ=94−4m =0⇒m =916.故m ∈(0,916). 故选:D .4、已知函数f (x )=x 2+e x −12(x <0)与g (x )=x 2+ln (x +a )图象上存在关于y 轴对称的点,则a 的取值范围是( )A .√e )B .(−∞,√e )C .√e )D .(0,√e ) 答案:B分析:f (x )=x 2+e x −12(x <0)关于y 轴对称的函数为:f(−x)=x 2+e −x −12(x >0),函数f (x )=x 2+e x −12(x <0)与g (x )=x 2+ln (x +a )图象上存在关于y 轴对称的点, 即f(−x)=g(x)有解,通过数形结合即可得解.f (x )=x 2+e x −12(x <0)关于y 轴对称的函数为:f(−x)=x 2+e −x −12(x >0), 函数f (x )=x 2+e x −12(x <0)与g (x )=x 2+ln (x +a )图象上存在关于y 轴对称的点, 即f(−x)=g(x)有解,即x 2+e −x −12=x 2+ln(x +a),整理的:e −x −12=ln(x +a), y =e −x −12和y =ln(x +a)的图像存在交点,如图:临界值在x=0处取到(虚取),此时a=√e,故当a<√e时y=e−x−12和y=ln(x+a)的图像存在交点,故选:B.5、已知函数f(x)=11+2x,则对任意实数x,有()A.f(−x)+f(x)=0B.f(−x)−f(x)=0C.f(−x)+f(x)=1D.f(−x)−f(x)=13答案:C分析:直接代入计算,注意通分不要计算错误.f(−x)+f(x)=11+2−x +11+2x=2x1+2x+11+2x=1,故A错误,C正确;f(−x)−f(x)=11+2−x −11+2x=2x1+2x−11+2x=2x−12x+1=1−22x+1,不是常数,故BD错误;故选:C.6、已知对数式log(a+1)24−a(a∈Z)有意义,则a的取值范围为()A.(−1,4)B.(−1,0)∪(0,4)C.{1,2,3}D.{0,1,2,3}答案:C分析:由对数的真数大于0,底数大于0且不等于1列出不等式组,然后求解即可.由题意可知:{a +1>0a +1≠124−a>0 ⇔{a >−1a ≠0a <4 ,解之得:−1<a <4且a ≠0. ∵a ∈Z ,∴a 的取值范围为{1,2,3}.故选:C.7、果农采摘水果,采摘下来的水果会慢慢失去新鲜度.已知某种水果失去新鲜度h 与其采摘后时间t (天)满足的函数关系式为ℎ=m ⋅a t .若采摘后10天,这种水果失去的新鲜度为10%,采摘后20天,这种水果失去的新鲜度为20%.那么采摘下来的这种水果在多长时间后失去50%新鲜度(已知lg2≈0.3,结果取整数)( )A .23天B .33天C .43天D .50天答案:B分析:根据题设条件先求出m 、a ,从而得到ℎ=120⋅2110t ,据此可求失去50%新鲜度对应的时间.{10%=m ⋅a 1020%=m ⋅a 20⇒{a 10=2,m =120 ,故a =2110,故ℎ=120⋅2110t , 令ℎ=12,∴2t 10=10,∴t 10lg2=1,故t =100.3≈33,故选:B.8、设2a =5b =m ,且1a +1b =2,则m =( )A .√10B .10C .20D .100答案:A分析:根据指数式与对数的互化和对数的换底公式,求得1a =log m 2,1b =log m 5,进而结合对数的运算公式,即可求解.由2a =5b =m ,可得a =log 2m ,b =log 5m ,由换底公式得1a =log m 2,1b =log m 5,所以1a +1b =log m 2+log m 5=log m 10=2,又因为m >0,可得m =√10.故选:A.9、化简√a3b2√ab23(a 14b12)4⋅√ba3(a>0,b>0)的结果是()A.ba B.abC.a2bD.b2a答案:B分析:直接利用根式与分数指数幕的互化及其化简运算,求解即可. √a3b2√ab23(a 14b12)4⋅√ba3=a32b⋅a16b13(a14b12)4⋅a−13⋅b13=a32+16−1+13b1+13−2−13=ab−1=ab故选:B10、方程log2x=log4(2x+3)的解为()A.−1B.1C.3D.−1或3答案:C分析:根据对数运算性质化为同底的对数方程,结合对数真数大于零可求得结果.∵log2x=log4(2x+3)=12log2(2x+3)=log2√2x+3,∴{x>02x+3>0x=√2x+3,解得:x=3.故选:C.填空题11、函数f(x)=1x+1+lnx的定义域是____________.答案:(0,+∞)分析:根据分母不为零、真数大于零列不等式组,解得结果.由题意得{x>0x+1≠0,∴x>0所以答案是:(0,+∞)小提示:本题考查函数定义域,考查基本分析求解能力,属基础题.]的值域为______.12、函数f(x)=4x−2x+1+3在(−∞,12答案:[2,3)分析:令2x=t,结合二次函数的性质即可得出答案.解:f(x)=(2x)2−2×2x+3=(2x−1)2+2,设2x=t,]时,0<t≤√2,所以2≤(t−1)2+2<3,当x∈(−∞,12]的值域为[2,3).所以f(x)在(−∞,12所以答案是:[2,3).13、若a>0且a≠1,则函数f(x)=a x−4+3的图像恒过的定点的坐标为______.答案:(4,4)分析:任意指数函数一定过定点(0,1),根据该性质求解.令x−4=0,得x=4,所以f(4)=a0+3=4,所以函数f(x)=a x−4+3的图像恒过定点(4,4).所以答案是:(4,4)14、设x>0,y>0,若e x、e y的几何平均值为e(e是自然对数的底数),则x2、y2的算术平均值的最小值为__________.答案:1分析:利用指数的运算性质可得出x+y=2,再利用基本不等式可求得结果.由已知条件可得e x⋅e y=e x+y=e2,所以,x+y=2,因为x>0,y>0,由基本不等式可得x2+y2≥2xy,≥1,即2(x2+y2)≥x2+y2+2xy=(x+y)2=4,所以,x2+y22当且仅当x=y=1时,等号成立.因此,x 2、y 2的算术平均值的最小值为1.所以答案是:1.15、计算:2√3×√126×√323=___________. 答案:6分析:根据根式指数幂的互化,以及指数幂的运算性质,准确运算,即可求解.根据根式指数幂的互化,以及指数幂的运算性质,可得2√3×√126×√323=2⋅312⋅(22⋅3)16⋅(32)13=21+13−13⋅312+16+13=2×3=6. 所以答案是:6解答题16、某化工企业致力于改良工艺,想使排放的废气中含有的污染物数量逐渐减少.设改良工艺前所排放的废气中含有的污染物数量为r 0mg /m 3,首次改良工艺后所排放的废气中含有的污染物数量为r 1mg /m 3,第n 次改良工艺后所排放的废气中含有的污染物数量为r n mg /m 3,则可建立函数模型r n =r 0−(r 0−r 1)⋅50.5n+P (P ∈R ,n ∈N ∗),其中n 是指改良工艺的次数.已知r 0=2,r 1=1.94(参考数据:lg2≈0.3).(1)试求该函数模型的解析式;(2)若该地环保部门要求,企业所排放的废气中含有的污染物数量不能超过0.08mg /m 3,试问至少进行多少次改良工艺才能使该企业所排放的废气中含有的污染物数量达标?答案:(1)r n =2−0.06⋅50.5n−0.5(n ∈N ∗);(2)6.分析:(1)将r 0=2,r 1=1.94代入函数模型解解得答案;(2)结合题意,解出指数不等式即可.(1)根据题意,1.94=2−(2−1.94)⋅50.5+P ⇒P =−0.5,所以该函数模型的解析式为r n =2−0.06⋅50.5n−0.5(n ∈N ∗).(2)由(1),令r n =2−0.06⋅50.5n−0.5≤0.08⇒50.5n−0.5≥32⇒(0.5n −0.5)lg5≥5lg2⇒n ≥10lg2lg5+1, 则n ≥10×0.30.7+1,10×0.30.7+1≈5.3,而n ∈N ∗,则n ≥6.综上:至少进行6次改良工艺才能使该企业所排放的废气中含有的污染物数量达标.17、若函数y =3x 2−5x +a 的两个零点分别为x 1,x 2,且有−2<x 1<0,1<x 2<3,试求出a 的取值范围. 答案:−12<a <0.分析:根据题意,利用二次函数的性质和根的分布,列出不等式组,即可求出实数a 的取值范围.令f (x )=3x 2−5x +a ,则{f(−2)>0f(0)<0f(1)<0f(3)>0得a 的取值范围是−12<a <0. 故实数a 的取值范围为−12<a <0.小提示:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化的数学思想,属于基础题.18、数学运算是指在明晰运算对象的基础上,依据运算法则解决数学问题的素养.因为运算,数的威力无限;没有运算,数就只是一个符号.对数运算与指数幂运算是两类重要的运算.(1)对数的运算性质降低了运算的级别,简化了运算,在数学发展史上是伟大的成就.对数运算性质的推导有很多方法.请同学们根据所学知识推导如下的对数运算性质:如果a >0,且a ≠1,M >0,那么log a M n =nlog a M (n ∈R );(2)请你运用上述对数运算性质计算lg3lg4(lg8lg9+lg16lg27)的值; (3)因为210=1024∈(103,104),所以210的位数为4(一个自然数数位的个数,叫做位数).请你运用所学过的对数运算的知识,判断20192020的位数.(注lg2019≈3.305)答案:(1)见解析(2)1712 (3)20192020的位数为6677解析:(1)根据指数与对数的转换证明即可.(2)根据对数的运算性质将真数均转换成指数幂的形式再化简即可.(3)分析lg20192020的值的范围再判断位数即可.(1)方法一:设x=log a M所以M=a x所以M n=(a x)n=a nx所以log a M n=nx=nlog a M,得证. 方法二:设x=nlog a M所以xn=log a M所以a xn=M所以a x=M n所以x=log a M n所以nlog a M=log a M n方法三:因为a log a M n=M na nlog a M=(a log a M)n=M n 所以a log a M n=a nlog a M所以log a M n=nlog a M得证.(2)方法一:lg3 lg4(lg8lg9+lg16lg27)=lg3lg22(lg23lg32+lg24lg33) =lg32lg2(3lg22lg3+4lg23lg3)=lg32lg2⋅17lg26lg3=1712.方法二:lg3 lg4(lg8lg9+lg16lg27)=log43(log98+log2716) =log223(log3223+log3324)=12log23(32log32+43log32)=12log23⋅176log32=1712.(3)方法一:设10k<20192020<10k+1,k∈N∗所以k<lg20192020<k+1所以k<2020lg2019<k+1所以k<2020×3.305<k+1所以6675.1<k<6676.1因为k∈N∗所以k=6676所以20192020的位数为6677方法二:设20192020=N所以2020lg2019=lgN所以2020×3.305=lgN所以lgN=6676.1所以N=106676.1=100.1×106676因为1<100.1<10,所以N有6677位数,即20192020的位数为6677小提示:本题主要考查了对数的运算以及利用对数的运算求解数字位数的问题,需要取对数分析对数值进行分析,属于中档题.19、(1)计算0.027−13−(−16)−2+810.75+(19)0−3−1;(2)若x 12+x−12=√6,求x2+x−2的值.答案:(1)-5;(2)14.分析:(1)由题意利用分数指数幂的运算法则,计算求得结果.(2)由题意两次利用完全平方公式,计算求得结果.(1)0.027−13−(−16)−2+810.75+(19)0−3−1=0.3﹣1﹣36+33+1−13=103−36+27+1−13=−5.(2)若x 12+x−12=√6,∴x+1x+2=6,x+1x=4,∴x2+x﹣2+2=16,∴x2+x﹣2=14.。
【2年模拟】2016届高考数学专题练习2.4指数函数与对数函数

§ 2.4指数函数与对数函数A组2014—2015年模拟·基础题组限时:25分钟1.(2015山东泰安期中,4)若点(16,2)在函数y=log a x(a>0且a≠1)的图象上,则tan的值为( )A.-B.-C.D.2.(2015黑龙江双鸭山一中期中,9)设x=log510,y=(e是自然对数的底数),z=,则( )A.x<y<zB.y<x<zC.z<x<yD.x<z<y3.(2015北京海淀期中,5)设a=,b=log2,c=log23,则( )A.a>b>cB.c>a>bC.a>c>bD.c>b>a4.(2014河南洛阳一模,3)函数f(x)=a x+log a(x+1)在[0,1]上的最大值和最小值之和为a,则a 的值为( )A. B. C.2 D.45.(2014北京丰台一模)“m>n>1”是“log m2<log n2”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件6.(2014陕西咸阳二模)已知f(x)是定义在R上的奇函数,当x>0时, f(x)=2+flog2x,则f(-2)=( )A.1B.3C.-1D.-37.(2014河南郑州二模)若x∈(e-1,1),a=ln x,b=,c=e ln x,则a,b,c的大小关系为( )A.c>b>aB.b>c>aC.a>b>cD.b>a>c8.(2014江西南昌4月,13)已知函数f(x)满足:当x≥4时, f(x)=;当x<4时, f(x)=f(x+1),则f(2+log23)= .9.(2014北京育才中学质检)已知函数f(x)=ln x,g(x)=lg x,h(x)=log3x,直线y=a(a<0)与这三个函数图象的交点的横坐标分别是x1,x2,x3,则x1,x2,x3的大小关系是.B组2014—2015年模拟·提升题组限时:30分钟1.(2015内蒙古呼和浩特期中,4)下列说法正确的是( )A.函数f(x)=a x+1(a>0,且a≠1)的图象恒过定点(0,1)B.函数f(x)=x-3在其定义域上是减函数C.函数f(x)=的值域为(0,+∞)D.函数f(x)=|log2x|在区间(1,+∞)上单调递增2.(2014山东济宁三模,10)已知函数f(x)=|2x-1|,a<b<c且f(a)>f(c)>f(b),则下列结论中,一定成立的是( )A.a<0,b<0,c<0B.a<0,b≥0,c>0C.2-a<2cD.2a+2c<23.(2014福建龙岩一模,7)已知y=log a(2-ax)(a>0,且a≠1)在区间[0,1]上是减函数,则a的取值范围是( )A.(0,1)B.(0,2)C.(1,2)D.[2,+∞)4.(2014浙江丽水5月,8)当x∈(-∞,-1]时,不等式(m2-m)·4x-2x<0恒成立,则实数m的取值范围是( )A.(-2,1)B.(-4,3)C.(-1,2)D.(-3,4)5.(2014江苏徐州4月,11)函数f(x)=log0.5(3x2-ax+5)在(-1,+∞)上是减函数,则实数a的取值范围是.6.(2014北京丰台一模,12)已知函数f(x)=2x,点P(a,b)在函数y=(x>0)的图象上,那么f(a)·f(b)的最小值是.A组2014—2015年模拟·基础题组1.D∵点(16,2)在函数y=log a x(a>0且a≠1)的图象上,∴2=log a16,∴a2=16,∴a=4,∴tan=tan=tan=.故选D.2.D ∵x=log510=log55+log52<1+log5=1+==z,y===>==z,∴x<z<y,故选D.3.B 对于a=,有0<a<1;对于b=log2,有b<0;对于c=log23,有c>1,∴b<0<a<1<c,即c>a>b,故选B.4.B ∵在[0,1]上y=a x与y=log a(x+1)具有相同的单调性,∴f(x)=a x+log a(x+1)在[0,1]上单调,∴f(0)+f(1)=a,即a0+log a1+a1+log a2=a,化简得1+log a2=0,解得a=.5.A 由函数图象知,若m>n>1,则log m2<log n2,充分性成立.反之,取m=,n=,∵lo2=-1<-=lo2,即log m2<log n2,而n<m<1,∴显然必要性不成立,故选A.6.D 因为f=2+flog2,所以f=1,所以f(2)=2+flog22=3,所以f(-2)=-f(2)=-3.7.B 依题意得a=ln x∈(-1,0),b=∈(1,2),c=x∈(e-1,1),因此b>c>a,选B.8.答案解析因为3<2+log23<4,所以f(2+log23)=f(2+log23+1)=f(3+log23).因为3+log23>4,所以f(3+log23)==·=,即f(2+log23)=.9.答案x2<x3<x1解析在同一直角坐标系中画出f(x)=ln x,g(x)=lg x及h(x)=log3x的图象,直线y=a(a<0)与三个函数图象交点的横坐标如图所示.显然x2<x3<x1.B组2014—2015年模拟·提升题组1.D 对于A,由于当x=0时, f(x)=a0+1=2,故函数f(x)=a x+1(a>0,且a≠1)的图象恒过定点(0,2),故A不正确.对于B,由函数f(x)=x-3的图象可得:在(0,+∞)上, f(x)单调递减,且f(x)>0;在(-∞,0)上, f(x)单调递减,且f(x)<0,故函数f(x)在其定义域(-∞,0)∪(0,+∞)上不是减函数,故B不正确.对于C,由于f(x)=中,≠0,故f(x)≠20,即f(x)≠1,故f(x)=的值域一定不是(0,+∞),故C不正确.对于D,在区间(1,+∞)上, f(x)=|log2x|=log2x,故函数f(x)在区间(1,+∞)上单调递增,故D 正确.2.D 作出函数f(x)=|2x-1|的图象,如图,∵a<b<c,且f(a)>f(c)>f(b),∴结合图象知a<0,c>0,∴0<2a<1.∴f(a)=|2a-1|=1-2a<1,∴f(c)<1,∴0<c<1.∴1<2c<2,∴f(c)=|2c-1|=2c-1,又∵f(a)>f(c),∴1-2a>2c-1,∴2a+2c<2,故选D.3.C 因为y=log a(2-ax)在[0,1]上单调递减,u=2-ax(a>0)在[0,1]上是减函数,所以y=log a u是增函数,所以a>1.又2-a>0,所以1<a<2.4.C 原不等式变形为m2-m<,∵函数y=在(-∞,-1]上是减函数,∴≥=2,当x∈(-∞,-1]时,m2-m<恒成立等价于m2-m<2,解得-1<m<2.5.答案[-8,-6]解析设g(x)=3x2-ax+5,由已知得解得-8≤a≤-6.6.答案 4解析由已知得a>0,b>0,且ab=1,∴f(a)·f(b)=2a·2b=2a+b≥=22=4,当且仅当a=b=1时, f(a)·f(b)取最小值4.。
高中数学指数函数和对数函数练习题(带答案和解释)

高中数学指数函数和对数函数练习题(带答案和解释)一、选择题1.下列函数:①y=3x2(xN+);②y=5x(xN+);③y=3x +1(xN+);④y=32x(xN+),其中正整数指数函数的个数为()A.0B.1C.2D.3【解析】由正整数指数函数的定义知,只有②中的函数是正整数指数函数.【答案】 B2.函数f(x)=(14)x,xN+,则f(2)等于()A.2 B.8C.16 D.116【解析】∵f(x)=(14x)xN+,f(2)=(14)2=116.【答案】 D3.(2019阜阳检测)若正整数指数函数过点(2,4),则它的解析式为()A.y=(-2)x B.y=2xC.y=(12)x D.y=(-12)x【解析】设y=ax(a>0且a1),由4=a2得a=2.【答案】 B4.正整数指数函数f(x)=(a+1)x是N+上的减函数,则a 的取值范围是()A.a B.-10C.01 D.a-1【解析】∵函数f(x)=(a+1)x是正整数指数函数,且f(x)为减函数,0a+11,-10.【答案】 B5.由于生产电脑的成本不断降低,若每年电脑价格降低13,设现在的电脑价格为8 100元,则3年后的价格可降为() A.2 400元 B.2 700元C.3 000元 D.3 600元【解析】1年后价格为8 100(1-13)=8 10023=5 400(元),2年后价格为5 400(1-13)=5 40023=3 600(元),3年后价格为3 600(1-13)=3 60023=2 400(元).【答案】 A二、填空题6.已知正整数指数函数y=(m2+m+1)(15)x(xN+),则m =______.【解析】由题意得m2+m+1=1,解得m=0或m=-1,所以m的值是0或-1.【答案】0或-17.比较下列数值的大小:(1)(2)3________(2)5;(2)(23)2________(23)4.【解析】由正整数指数函数的单调性知,(2)3(2)5,(23)2(23)4.【答案】(1) (2)8.据某校环保小组调查,某区垃圾量的年增长率为b,2019年产生的垃圾量为a吨,由此预测,该区下一年的垃圾量为________吨,2020年的垃圾量为________吨.【解析】由题意知,下一年的垃圾量为a(1+b),从2019年到2020年共经过了8年,故2020年的垃圾量为a(1+b)8. 【答案】a(1+b) a(1+b)8三、解答题9.已知正整数指数函数f(x)=(3m2-7m+3)mx,xN+是减函数,求实数m的值.【解】由题意,得3m2-7m+3=1,解得m=13或m=2,又f(x)是减函数,则01,所以m=13.10.已知正整数指数函数f(x)的图像经过点(3,27),(1)求函数f(x)的解析式;(2)求f(5);(3)函数f(x)有最值吗?若有,试求出;若无,说明原因.【解】(1)设正整数指数函数为f(x)=ax(a0,a1,xN+),因为函数f(x)的图像经过点(3,27),所以f(3)=27,即a3=27,解得a=3,所以函数f(x)的解析式为f(x)=3x(xN +).(2)f(5)=35=243.(3)∵f(x)的定义域为N+,且在定义域上单调递增,f(x)有最小值,最小值是f(1)=3;f(x)无最大值.11.某种细菌每隔两小时分裂一次(每一个细菌分裂成两个,分裂所需时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t).(1)写出函数y=f(t)的定义域和值域;(2)在坐标系中画出y=f(t)(06)的图像;(3)写出研究进行到n小时(n0,nZ)时,细菌的总个数(用关于n的式子表示).【解】(1)y=f(t)的定义域为{t|t0},值域为{y|y=2m,mN+)};(2)06时,f(t)为一分段函数,y=2,02,4,24,8,46.图像如图所示.(3)n为偶数且n0时,y=2n2+1;n为奇数且n0时,y=2n-12+1.。
指数函数和对数函数练习题

指数函数和对数函数练习题指数函数和对数函数练习题一、选择题1.下列函数:①y=3x2(xN+);②y=5x(xN+);③y=3x+1(xN+);④y=32x(xN+),其中正整数指数函数的个数为() A.0B.1C.2D.3【解析】由正整数指数函数的定义知,只有②中的函数是正整数指数函数.【答案】 B2.函数f(x)=(14)x,xN+,则f(2)等于()A.2 B.8C.16 D.116【解析】∵f(x)=(14x)xN+,f(2)=(14)2=116.【答案】 D3.(2013阜阳检测)若正整数指数函数过点(2,4),则它的解析式为()A.y=(-2)x B.y=2xC.y=(12)x D.y=(-12)x【解析】设y=ax(a>0且a1),由4=a2得a=2.【答案】 B4.正整数指数函数f(x)=(a+1)x是N+上的减函数,则a的取值范围是()A.a B.-10C.01 D.a-1【解析】∵函数f(x)=(a+1)x是正整数指数函数,且f(x)为减函数,0a+11,-10.【答案】 B5.由于生产电脑的成本不断降低,若每年电脑价格降低13,设现在的电脑价格为8 100元,则3年后的`价格可降为()A.2 400元 B.2 700元C.3 000元 D.3 600元【解析】 1年后价格为8 100(1-13)=8 10023=5 400(元),2年后价格为5 400(1-13)=5 40023=3 600(元),3年后价格为3 600(1-13)=3 60023=2 400(元).【答案】 A二、填空题6.已知正整数指数函数y=(m2+m+1)(15)x(xN+),则m=______.【解析】由题意得m2+m+1=1,解得m=0或m=-1,所以m的值是0或-1.【答案】 0或-17.比较下列数值的大小:(1)(2)3________(2)5;(2)(23)2________(23)4.【解析】由正整数指数函数的单调性知,(2)3(2)5,(23)2(23)4.【答案】 (1) (2)8.据某校环保小组调查,某区垃圾量的年增长率为b,2012年产生的垃圾量为a吨,由此预测,该区下一年的垃圾量为________吨,2020年的垃圾量为________吨.【解析】由题意知,下一年的垃圾量为a(1+b),从2012年到2020年共经过了8年,故2020年的垃圾量为a(1+b)8.【答案】 a(1+b) a(1+b)8三、解答题9.已知正整数指数函数f(x)=(3m2-7m+3)mx,xN+是减函数,求实数m的值.【解】由题意,得3m2-7m+3=1,解得m=13或m=2,又f(x)是减函数,则01,所以m=13.10.已知正整数指数函数f(x)的图像经过点(3,27),(1)求函数f(x)的解析式;(2)求f(5);(3)函数f(x)有最值吗?若有,试求出;若无,说明原因.【解】 (1)设正整数指数函数为f(x)=ax(a0,a1,xN+),因为函数f(x)的图像经过点(3,27),所以f(3)=27,即a3=27,解得a=3,所以函数f(x)的解析式为f(x)=3x(xN+).(2)f(5)=35=243.(3)∵f(x)的定义域为N+,且在定义域上单调递增,f(x)有最小值,最小值是f(1)=3;f(x)无最大值.11.某种细菌每隔两小时分裂一次(每一个细菌分裂成两个,分裂所需时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t).(1)写出函数y=f(t)的定义域和值域;(2)在坐标系中画出y=f(t)(06)的图像;(3)写出研究进行到n小时(n0,nZ)时,细菌的总个数(用关于n的式子表示).【解】 (1)y=f(t)的定义域为{t|t0},值域为{y|y=2m,mN+)};(2)06时,f(t)为一分段函数,y=2,02,4,24,8,46.图像如图所示.(3)n为偶数且n0时,y=2n2+1;n为奇数且n0时,y=2n-12+1.。
(带答案)高中数学第四章指数函数与对数函数经典大题例题

(每日一练)高中数学第四章指数函数与对数函数经典大题例题高中数学第四章指数函数与对数函数经典大题例题单选题1、化简√a 3b 2√ab 23(a 14b 12)4⋅√b a3 (a >0,b >0)的结果是( )A .b aB .abC .a 2bD .b 2a答案:B分析:直接利用根式与分数指数幕的互化及其化简运算,求解即可.√a 3b 2√ab 23(a 14b 12)4⋅√a3=a 32b⋅a 16b 13(a 14b 12)4⋅a −13⋅b 13=a32+16−1+13b1+13−2−13=ab −1=ab故选:B2、若32是函数f (x )=2x 2−ax +3的一个零点,则f (x )的另一个零点为( ) A .1B .2C .(1,0)D .(2,0) 答案:A分析:由32是函数f (x )=2x 2−ax +3的一个零点,可得a 值,再利用韦达定理列方程解出f (x )的另一个零点.因为32是函数f (x )=2x 2−ax +3的一个零点,所以f (32)=2×(32)2−a ×32+3=0,解得a =5.设另一个零点为x 0,则x 0+32=52,解得x 0=1,所以f (x )的另一个零点为1. 故选:A .3、下列计算中结果正确的是( ) A .log 102+log 105=1B .log 46log 43=log 42=12C .(log 515)3=3log 515=−3D .13log 28=√log 283=√33答案:A分析:直接根据对数的运算性质及换底公式计算可得;解:对于A :log 102+log 105=log 10(2×5)=log 1010=1,故A 正确; 对于B :log 46log 43=log 36,故B 错误;对于C :(log 515)3=(log 55−1)3=(−log 55)3=−1,故C 错误; 对于D :13log 28=13log 223=13×3log 22=1,故D 错误;故选:A4、下列函数中是偶函数且在区间(0,+∞)单调递减的函数是( ) A .f(x)=1|x |B .f(x)=(13)xC .f(x)=lg |x |D .f(x)=x −13 答案:A分析:利用幂指对函数的性质逐一分析给定四个函数的单调性和奇偶性,可得结论.解:f(x)=1|x |是偶函数且在区间(0,+∞)上单调递减,满足条件; f(x)=(13)x是非奇非 偶函数,不满足条件;f(x)=lg |x |是偶函数,但在区间(0,+∞)上单调递增,不满足条件;f(x)=x −13是奇函数不是偶函数,不合题意. 故选:A .5、若函数y =(m 2−m −1)⋅m x 是指数函数,则m 等于( ) A .−1或2B .−1 C .2D .12答案:C分析:根据题意可得出关于实数m 的等式与不等式,即可解得实数m 的值. 由题意可得{m 2−m −1=1m >0m ≠1 ,解得m =2. 故选:C.6、已知函数f(x)=2x −x −1,则不等式f(x)>0的解集是( ). A .(−1,1)B .(−∞,−1)∪(1,+∞) C .(0,1)D .(−∞,0)∪(1,+∞) 答案:D分析:作出函数y =2x 和y =x +1的图象,观察图象可得结果. 因为f (x )=2x −x −1,所以f (x )>0等价于2x >x +1, 在同一直角坐标系中作出y =2x 和y =x +1的图象如图:两函数图象的交点坐标为(0,1),(1,2),不等式2x >x +1的解为x <0或x >1.所以不等式f (x )>0的解集为:(−∞,0)∪(1,+∞). 故选:D.小提示:本题考查了图象法解不等式,属于基础题. 7、设函数f (x )=ln |2x +1|﹣ln |2x ﹣1|,则f (x )( ) A .是偶函数,且在 (12,+∞)单调递增B .是奇函数,且在 (−12,12)单调递增C .是偶函数,且在(−∞,−12)单调递增D .是奇函数,且在 (−∞,−12)单调递增 答案:B分析:先求出f (x )的定义域结合奇偶函数的定义判断f (x )的奇偶性,设t =|2x+12x−1|,则y =ln t ,由复合函数的单调性判断f (x )的单调性,即可求出答案.解:由{2x +1≠02x −1≠0,得x ≠±12.又f (﹣x )=ln |﹣2x +1|﹣ln |﹣2x ﹣1|=﹣(ln |2x +1|﹣ln |2x ﹣1|)=﹣f (x ), ∴f (x )为奇函数,由f (x )=ln |2x +1|﹣ln |2x ﹣1|=ln |2x+12x−1|, ∵2x+12x−1=1+22x−1=1+1x−12.可得内层函数t =|2x+12x−1|的图象如图,在(﹣∞,−12),(12,+∞)上单调递减,在(−12,12)上单调递增,又对数式y =lnt 是定义域内的增函数,由复合函数的单调性可得,f (x )在(−12,12)上单调递增,在(﹣∞,−12),(12,+∞)上单调递减. 故选:B .8、已知f (x )={2x −x 2,x ≥5f(x +3),x <5,则f (4)+f (-4)=( )A .63B .83C .86D .91 答案:C分析:由给定条件求得f (-4)=f (5),f (4)=f (7),进而计算f (5)、f (7)的值,相加即可得解. 依题意,当x <5时,f (x )=f (x +3),于是得f (-4)= f (-1)=f (2)=f (5),f (4)=f (7), 当x ≥5时,f (x )=2x -x 2,则f (5)=25-52=7,f (7)=27-72=79, 所以f (4)+f (-4)=86. 故选:C9、若2x −2y <3−x −3−y ,则( )A .ln(y −x +1)>0B .ln(y −x +1)<0C .ln|x −y|>0D .ln|x −y|<0 答案:A分析:将不等式变为2x −3−x <2y −3−y ,根据f (t )=2t −3−t 的单调性知x <y ,以此去判断各个选项中真数与1的大小关系,进而得到结果.由2x−2y<3−x−3−y得:2x−3−x<2y−3−y,令f(t)=2t−3−t,∵y=2x为R上的增函数,y=3−x为R上的减函数,∴f(t)为R上的增函数,∴x<y,∵y−x>0,∴y−x+1>1,∴ln(y−x+1)>0,则A正确,B错误;∵|x−y|与1的大小不确定,故CD无法确定.故选:A.小提示:本题考查对数式的大小的判断问题,解题关键是能够通过构造函数的方式,利用函数的单调性得到x,y的大小关系,考查了转化与化归的数学思想.10、若ln2=a,ln3=b,则log818=()A.a+3ba3B.a+2b3aC.a+2ba3D.a+3b3a答案:B分析:先换底,然后由对数运算性质可得.log818=ln18ln8=ln(32×2)ln23=2ln3+ln23ln2=2b+a3a.故选:B多选题11、关于函数f(x)=|ln|2−x||,下列描述正确的有()A.f(x)在区间(1,2)上单调递增B.y=f(x)的图象关于直线x=2对称C.若x1≠x2,f(x1)=f(x2),则x1+x2=4D.f(x)有且仅有两个零点答案:ABD分析:作出函数f(x)的图象,由图象观察性质判断各选项.根据图象变换作出函数f(x)的图象(f(x)=|ln|x−2||,作出y=lnx的图象,再作出其关于y轴对称的图象,然后向右平移2个单位,最后把x轴下方的部分关于x轴翻折上去即可得),如图,由图象知f(x)在(1,2)是单调递增,A正确,函数图象关于直线x=2对称,B正确;f(x1)=f(x2)=k,直线y=k与函数f(x)图象相交可能是4个交点,如图,如果最左边两个交点横坐标分别是x1,x2,则x1+x2=4不成立,C错误,f(x)与x轴仅有两个公共点,即函数仅有两个零点,D正确.故选:ABD.12、下列运算法则正确的是()log a bA.log a3b2=23B.(a n)m n=a m(b>0,a>0且a≠1)C.log a b=lnblnaD.a m+n=a m⋅a n(a≠0,m,n∈N+)答案:CD分析:取b<0可判断A选项的正误;取a<0,n=1可判断B选项的正误;利用对数的换底公式可判断C选2项的正误;利用指数的运算性质可判断D 选项的正误. 对于A 选项,若b <0,则log a b 无意义,A 选项错误;对于B 选项,若a <0,n =12,则a n =√a 无意义,B 选项错误;对于C 选项,由换底公式可得log a b =lnb lna(b >0,a >0且a ≠1),C 选项正确;对于D 选项,当a ≠0,m 、n ∈N +时,a m+n =a m ⋅a n ,D 选项正确. 故选:CD.13、设函数f (x )={|x 2+3x |,x ≤1log 2x,x >1,若函数f (x )+m =0有五个零点,则实数m 可取( )A .−3B .1C .−12D .−2 答案:CD分析:函数f (x )+m =0有五个零点等价于y =f(x)与y =−m 有五个不同的交点,作出f(x)图像,利用图像求解即可函数f (x )+m =0有五个零点等价于y =f(x)与y =−m 有五个不同的交点,作出f(x)图像可知,当x =−32时,f (−32)=|(−32)2+3×(−32)|=94若y =f(x)与y =−m 有五个不同的交点, 则−m ∈(0,94),∴m ∈(−94,0), 故选:CD .14、已知函数f(x)=2x2x +1+m(m ∈R)则下列说法正确的是( ) A .f (x )的定义域为R .B .若f(x)为奇函数,则m =−12C .f(x)在R 上单调递减D .若m =0,则f(x)的值域为(0,1) 答案:ABD分析:根据函数的定义域的求法,可判定A 正确;根据函数的奇偶性列出方程,求得m 的值,可判定B 正确,化简f(x)=−12x +1+m +1,结合指数函数的单调性,可判定C 错误;化简函数f(x)=1−12x +1,结合指数函数的值域,可判定D 正确.由题意,函数f(x)=2x 2x +1+m(m ∈R),对于A 中,由2x +1≠0,所以函数f (x )的定义域为R ,所以A 正确; 对于B 中,由函数f (x )为奇函数,则满足f (−x )=−f (x ),即2−x2−x +1+m =−2x 2x +1−m ,所以2m =−2x 2x +1−2−x 2−x +1=−2x2x +1−12x 12x+1=−2x2x +1−12x +1=−1,即m =−12,所以B 不正确;对于C 中,由f(x)=2x2x +1+m =2x +1−12x +1+m =−12x +1+m +1,因为函数y =2x +1为单调递增函数,则y =−12x +1递增函数,所以f (x )函数在R 上单调递减,所以C 不正确;对于D 中,当m =0时,可得f(x)=2x 2x +1=1−12x +1,因为2x +1>1,可得−1<−12x +1<0,所以1−12x +1∈(0,1),即函数f (x )的值域为(0,1),所以D 正确. 故选:ABD.15、函数f (x )=2x +a2x (a ∈R )的图象可能为( )A .B .C .D .答案:ABD解析:根据函数解析式的形式,以及图象的特征,合理给a 赋值,判断选项. 当a =0时,f (x )=2x ,图象A 满足;当a =1时,f (x )=2x +12x ,f (0)=2,且f (−x )=f (x ),此时函数是偶函数,关于y 轴对称,图象B 满足;当a=−1时,f(x)=2x−12x,f(0)=0,且f(−x)=−f(x),此时函数是奇函数,关于原点对称,图象D满足;图象C过点(0,1),此时a=0,故C不成立.故选:ABD小提示:思路点睛:函数图象的辨识可从以下方面入手:(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.(2)从函数的单调性,判断图象的变化趋势;(3)从函数的奇偶性,判断图象的对称性;(4)从函数的特征点,排除不合要求的图象.填空题16、化简:(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)=________.答案:2−1263分析:分析式子可以发现,若在结尾乘以一个(1−12),则可以从后到前逐步使用平方差公式进行计算,为保证恒等计算,在原式末尾乘以(1−12)×2即可﹒原式=(1+1232)(1+1216)(1+128)(1+124)(1+122)(1+12)×(1−12)×2=(1+1232)(1+1216)(1+128)(1+124)(1+122)×(1−122)×2 =(1+1232)(1+1216)(1+128)(1+124)×(1−124)×2=(1+1232)(1+1216)(1+128)×(1−128)×2=(1+1232)(1+1216)×(1−1216)×2=(1+1232)×(1−1232)×2=(1−1264)×2=2−1 263所以答案是:2−1263﹒17、已知a>b>1,若log a b+log b a=52,a b=b a,则a+2b=___________. 答案:8分析:利用指数函数、对数函数的性质、运算法则直接求解.解:由log a b+log b a=52,且log a b⋅log b a=1所以log a b,log b a是方程x2−52x+1=0的两根,解得log b a=2或log b a=12,又a>b>1,所以log b a=2,即a=b2,又a b=b a从而b2b=b a⇒a=2b,且a=b2,则b=2,a=4.所以a+2b=8.所以答案是:8.18、函数f(x)=4x−2x+1+3在(−∞,12]的值域为______.答案:[2,3)分析:令2x=t,结合二次函数的性质即可得出答案.解:f(x)=(2x)2−2×2x+3=(2x−1)2+2,设2x=t,当x∈(−∞,12]时,0<t≤√2,所以2≤(t−1)2+2<3,所以f (x )在(−∞,12]的值域为[2,3).所以答案是:[2,3).解答题19、已知函数f (x )=3x 2-5x +a .(1)若函数f (x )有两个零点,求实数a 的取值范围;(2)若函数f (x )的一个零点在(-2,0)内,另一个零点在(1,3)内,求实数a 的取值范围.答案:(1)(−∞,2512);(2)(-12,0).分析:(1)由判别式大于零求出实数a 的取值范围;(2)画出f(x)的草图,结合零点存在性定理,列出不等式组求出实数a 的取值范围.(1)由题意得Δ=25-4×3×a >0,解得a <2512.所以a 的取值范围是(−∞,2512). (2)由草图可知{f(−2)⋅f(0)<0f(1)⋅f(3)<0得{(22+a)a <0(a −2)(a +12)<0,解得−12<a <0.所以a 的取值范围是(−12,0)小提示:关键点睛:解决问题二的关键在于根据题意画出f(x)的草图,结合零点存在性定理得出实数a 的取值范围.20、声强级L 1(单位:dB )由公式L 1=10lg (I10−12)给出,其中I 为声强(单位:W m 2⁄).(1)一般正常人听觉能忍受的最高声强为1W/m 2,能听到的最低声强为10−12W/m 2.求人听觉的声强级范围.(2)平时常人交谈时的声强约为10−6W/m 2,求其声强级.答案:(1)0 dB−120 dB(2)60dB解析:(1)分别代入I=1与I=10−12求解即可.(2)代入I=10−6求解即可.)=10×lg1012=120(dB).解:(1)10lg(110−1210lg(10−12)=10lg1=0(dB).10−12因此人听觉的声强级范围为0 dB−120 dB.=10×lg106=10×6=60(dB).(2)L1=10lg10−610−12小提示:本题主要考查了对数的实际运用,需要根据题意代入对应的数值进行计算,属于基础题.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【3年高考】(新课标)2016版高考数学2.4指数函数与对数函数
A组2012—2014年高考·基础题组
1.(2014山东,5,5分)已知实数x,y满足a x<a y(0<a<1),则下列关系式恒成立的是( )
A.>
B.ln(x2+1)>ln(y2+1)
C.sin x>sin y
D.x3>y3
2.(2012安徽,3,5分)(log29)×(log34)=( )
A. B. C.2 D.4
3.(2012广东,4,5分)下列函数中,在区间(0,+∞)上为增函数的是( )
A.y=ln(x+2)
B.y=-
C.y=
D.y=x+
4.(2012大纲全国,9,5分)已知x=ln π,y=log52,z=,则( )
A.x<y<z
B.z<x<y
C.z<y<x
D.y<z<x
5.(2012四川,5,5分)函数y=a x-(a>0,且a≠1)的图象可能是( )
6.(2014陕西,11,5分)已知4a=2,lg x=a,则x= .
B组2012—2014年高考·提升题组
1.(2014天津,4,5分)函数f(x)=lo(x2-4)的单调递增区间为( )
A.(0,+∞)
B.(-∞,0)
C.(2,+∞)
D.(-∞,-2)
2.(2014四川,9,5分)已知f(x)=ln(1+x)-ln(1-x),x∈(-1,1).现有下列命题:
①f(-x)=-f(x);②f=2f(x);③|f(x)|≥2|x|.
其中的所有正确命题的序号是( )
A.①②③
B.②③
C.①③
D.①②
3.(2013课标全国Ⅱ,8,5分)设a=log36,b=log510,c=log714,则( )
A.c>b>a
B.b>c>a
C.a>c>b
D.a>b>c
4.(2012山东,3,5分)函数f(x)=+的定义域为( )
A.[-2,0)∪(0,2]
B.(-1,0)∪(0,2]
C.[-2,2]
D.(-1,2]
5.(2014重庆,12,5分)函数f(x)=log2·lo(2x)的最小值为.
6.(2013山东,16,4分)定义“正对数”:
ln+x=现有四个命题:
①若a>0,b>0,则ln+(a b)=bln+a;
②若a>0,b>0,则ln+(ab)=ln+a+ln+b;
③若a>0,b>0,则ln+≥ln+a-ln+b;
④若a>0,b>0,则ln+(a+b)≤ln+a+ln+b+ln 2.
其中的真命题有.(写出所有真命题的编号)
A组2012—2014年高考·基础题组
1.D ∵a x<a y,0<a<1,∴x>y,∴x3>y3.
2.D (log29)×(log34)=×=×=4.
3.A 函数y=ln(x+2)在(-2,+∞)上是增函数,因此在(0,+∞)上是增函数,故选A.
4.D 由2<e<3得<<,∴<z<,即<z<1,y=log52<log5=,x=ln π>ln e=1,故选D.
5.D 令f(x)=a x-,当a>1时, f(0)=1-∈(0,1),所以A与B均错;当0<a<1时, f(0)=1-<0,所以C错D对,故选D.
6.答案
解析∵4a=2=,∴a=,∴lg x=,即x=.
B组2012—2014年高考·提升题组
1.D 由x2-4>0得x<-2或x>
2.又y=lou为减函数,故f(x)的单调递增区间为(-∞,-2).
2.A f(-x)=ln(1-x)-ln(1+x)=-[ln(1+x)-ln(1-x)]=-f(x),①正确. f=ln-ln=ln-ln,∵x∈(-1,1),∴f=2ln(1+x)-2ln(1-x)=2[ln(1+x)-ln(1-x)]=2f(x),②正确.当x∈[0,1)时,|f(x)|=ln(1+x)-ln(1-x)=ln,2|x|=2x,令g(x)=ln-2x,则g'(x)=≥0,∴g(x)在[0,1)上为增函数,∴g(x)≥g(0)=0,即|f(x)|≥2|x|;当x∈(-1,0)时,|f(x)|=ln(1-x)-ln(1+x)=-ln,2|x|=-2x,
令h(x)=2x-ln,则h'(x)=<0,∴h(x)在(-1,0)上为减函数,∴h(x)>0,即|f(x)|>2|x|.
∴当x∈(-1,1)时,|f(x)|≥2|x|,③正确.
3.D由对数运算法则得a=log36=1+log32,b=1+log52,c=1+log72,由对数函数图象得log32>log52>log72,所以a>b>c,故选D.
4.B 要使函数有意义,必有
⇒⇒-1<x<0或0<x≤2.故选B.
5.答案-
解析显然x>0,∴f(x)=log2·lo(2x)=log2x·log2(4x2)=log2x·(log24+2log2x)=log2x+(log2x)2=-≥-.当且仅当x=时,有f(x)min=-.
6.答案①③④
解析对于①:当0<a b<1时,有
此时ln+(a b)=bln+a=0;
当a b=1时,有此时ln+(a b)=bln+a=0;
当a b>1时,有
此时ln+(a b)=ln a b=bln a,
而bln+a=bln a=ln+(a b),
综上,ln+(a b)=bln+a,故①正确.
对于②:令a=2,b=,则ln+(ab)=ln+=0;
而ln+a+ln+b=ln 2>0,故ln+(ab)=ln+a+ln+b不成立,故②错误.
对于③:当0<<1时,有或或
经验证,ln+≥ln+a-ln+b成立;
当>1时,
有或或
经验证,ln+≥ln+a-ln+b成立;
当=1时,ln+≥ln+a-ln+b成立,故③正确.
对于④,分四种情况进行讨论:
当a≥1,b≥1时,不妨令a≥b,有2ab≥2a≥a+b,此时ln+(a+b)≤ln+a+ln+b+ln 2成立;
同理,当a≥1,0<b<1或0<a<1,b≥1或0<a<1,0<b<1时,ln+(a+b)≤ln+a+ln+b+ln 2成立.故④
正确.
综上所述,①③④均正确.。
