临泉一中2014-2015高三上学期竞赛数学(文)试卷
2015年全国高中数学联赛(WORD,含答案)
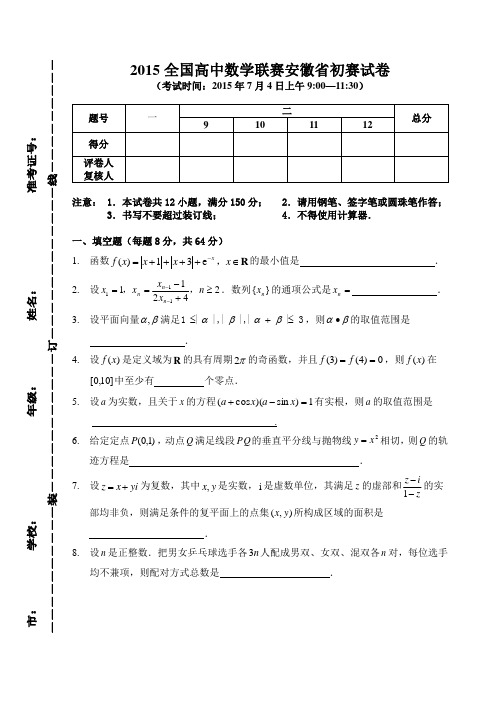
2015全国高中数学联赛安徽省初赛试卷(考试时间:2015年7月4日上午9:00—11:30)注意: 1.本试卷共12小题,满分150分; 2.请用钢笔、签字笔或圆珠笔作答;3.书写不要超过装订线; 4.不得使用计算器.一、填空题(每题8分,共64分)1. 函数R ∈++++=-x x x x f x ,e 31)(的最小值是 .2. 设24211111≥+-==--n x x x x n n n ,.数列}{n x 的通项公式是=n x .3. 设平面向量βα,满足3|||,||,|1≤+≤βαβα,则βα∙的取值范围是.4. 设)(x f 是定义域为R 的具有周期π2的奇函数,并且0)4()3(==f f ,则)(x f 在]10,0[中至少有 个零点.5. 设a 为实数,且关于x 的方程1)sin )(cos (=-+x a x a 有实根,则a 的取值范围是.6. 给定定点)1,0(P ,动点Q 满足线段PQ 的垂直平分线与抛物线2x y =相切,则Q 的轨迹方程是 . 7. 设z x yi =+为复数,其中,x y 是实数,i 是虚数单位,其满足z 的虚部和1z iz--的实部均非负,则满足条件的复平面上的点集(,)x y 所构成区域的面积是.8. 设n 是正整数.把男女乒乓球选手各n 3人配成男双、女双、混双各n 对,每位选手均不兼项,则配对方式总数是 .二、解答题(第9题20分,第10━12题22分,共86分)9. 设正实数b a ,满足1=+b a .求证:31122≥+++bb a a .10. 在如图所示的多面体ABCDEF 中,已知CFBE AD ,,都与平面ABC 垂直.设c CF b BE a AD ===,,,1===BC AC AB .求四面体ABCE 与BDEF 公共部分的体积(用c b a ,,表示).11.设平面四边形ABCD的四边长分别为4个连续的正整数。
证明:四边形ABCD的面积的最大值不是整数。
2018届安徽省阜阳市临泉县第一中学高三上学期第一次模拟考试数学(文)试题

临泉一中 2017-2018学年高三上学期第一次模拟数学(文)(时间:120分钟,满分150分)一、选择题:(本大题共12小题,每小题5分,共60分.) 1.已知全集{1,2,3,4,5}U =,集合{2,3,4}A =,{1,4}B =,则(∁U A ) B 为( ) A. {1} B.{1,5} C.{1,4} D. {1,4,5} 2.命题“存在2,++0x R x x n ∈≤使”的否定是( )A. 存在2,0x R x x n ∈++>使B. 不存在2,++0x R x x n ∈>使C. 对任意2,0x R x x n ∈++>使D. 对任意2,0x R x x n ∈++≤使3.已知△ABC 内角,,A B C 所对的边分别为,,a b c ,若6,6a b A π===,则满足条件的三角形个数为( )A. 0B. 1C. 2D. 不能确定 4.方程0.52|log |10x x -=的不同实根个数为( ) A. 1 B. 2 C. 3 D. 45.已知定义在区间[24,1]()a a a R -+∈上的偶函数()f x ,当0x ≥时,()f x 单调递增,则满足1(21)()3f x f -<的x 的取值范围是( )A. 12(,)23B. 12(,)43C. 11(,)53D. 12(,)336.若,71sin cos sin cos ),,2(=-+∈ααααππα则αcos = ( ) A. 53 B. 54 C. 53- D. 54-7.函数22x y x =-的图像大致是( )A B C D8.△ABC中,若2cos22A b cc+=,则△ABC的形状为()A. 直角三角形B. 等腰三角形C. 正三角形D.等腰直角三角形9.若2ln,4,283===cba,则有()A. bac<< B. abc<< C. cba<< D. cab<<10.定义行列式运算:12142334a aa a a aa a=-,若将函数sin()cosxf xx-=的图像向左平移m个单位后,所得图像对应的函数为偶函数,则m的最小值为()A. 23π B.3π C.6π D. 56π11.△ABC中,若24ac b=,sin sin sinA C p B+=,且B为锐角,则p的取值范围是()A.B.C.D.12.已知R 上的函数()f x 满足'()()2,f x f x +>且(1)24,ef e =+则不等式4()2x f x e>+的解集为( ) A. (,1)-∞ B. (1,)+∞ C. (,0)(1,)-∞+∞ D.(,0)(0,)-∞+∞二、填空题(本大题共4小题,每小题5分,共20分)13.曲线()f x =在x a =处切线与两坐标辆围成的三角形的面积为22,则a =_________. 14.函数()f x 为定义在R 上周期为2的奇函数,当01x <<时,()4x f x =,则12x <<时,()f x =____________.15.已知α的始边在x 轴正半轴上,终边经过点(4,3)P -,则t a n ()4πα+=________.16.有下列四个命题:①若R 上的函数()f x 满足)()(x a f x a f -=+,则()f x 关于x a =对称;②命题“在 △ABC 中,若A B >,则sin sin A B >”的否命题为真命题; ③“'0()0f x =”是“函数()f x 在0x 处取得极值”的充分不必要条件; ④:p 点)0,2(π为函数x x f tan )(=图像的一个对称点。
安徽省阜阳市临泉县第一中学高三语文上学科竞赛(期末)试题(扫描)

临泉一中2018-2019学年第一学期高三年级竞赛语文答案1.C(不同家族的家训、家谱中宣扬的内容不一致)2.D(文中没有突出君子之风的社会价值,也没有深入探究如何以君子之风促成风俗之美) 3.D(家族文化不是以君子文化为思想来源和核心理念)4.B. 图中两条线的交汇处表示在2000年和2010年间农村人口和城市人口出现了等值,即各占一半,这个等值和比例只意味着平均,并不意味着城乡发展均衡。
5.B . 美国着力打造大城市,而非小城镇。
6. ①提升中小城镇质量,增强吸引力。
统筹生产、生活、生态三大布局。
增加就业,改善环境,提升公共服务水平。
②国家层面上要有政策支持。
推动有序设市,改革户籍制度,培育特色优势产业。
③学习发达国家经验,比如美国的做法。
(每点2分)7.C “人物关系复杂,以‘复仇’作为主线贯穿全文”理解有误,小说中人物关系并不复杂,而且前半部分围绕“复仇”来写,后半部分则围绕“输血”“救命”展开。
8.①对读者:运用了倒叙手法,将爷刀刃仇敌后行走于旷野置于开篇,设置悬念,扣人心弦,吸引读者。
(2分)②对环境:使用比喻、比拟、排比等手法强化了风雪之大、哭声之响,写自然环境的死寂荒凉,暗示了社会环境。
(2分)③对人物:烘托了爷的形象,反映了爷的心境。
( 2分)(答“引出下文内容”等酌情给分。
)9.答案示例一:“纯爷们”是爷。
①情节方面:爷是贯穿全文的重要人物,杀敌报仇、救护虎山峪后代等感人故事都集中发生在他的身上。
( 2分)②形象方面:爷是小说重点塑造的形象,他的英勇无畏、疾恶如仇、恩怨分明、敢于自责、重情重义等性格,正与“纯爷们”相符。
( 2分)③主旨方面:爷是文中着墨最多的人物,小说通过爷荡气回肠的故事,弘扬了一种英勇、正义的人格精神。
( 2分)示例二:“纯爷们”是韦二。
①情节方面:韦二收养爷的孩子,危难之中将自己的儿子交给日本人,到死也无人知其苦衷,可见其“纯爷们”特征。
( 2分)②形象方面:在日本人面前表现胆怯、懦弱,实则内心坚毅,虽遭人痛骂,仍忍辱负重,最终献出生命,非“纯爷们”不能做到。
安徽省示范重点高中2014届高三数学上学期第一次联考试题文(扫描版)新人教A版

安徽省示范高中2014 届高三数学上学期第一次联考试题文(扫描版)新人教 A 版2014 届安徽省示范高中高三第一次联考文科数学参照答案一、选择题:本大题共 10 小题,每题 5 分,共 50 分。
在每题给出的四个选项中,只有一项为哪一项切合题目要求的.1.B 【分析】A { x | x 2 2x 0}{ x | 0剟x2} ,B { x | lg x 1, 0}x | 0 x 1, 1 = { x |1 x, 2} ,因此 A B { x |1 x, 2} ,应选 B .2.C 【分析】 f (0) =1,f ( f (0)) =f (1) = 2-1= 1.应选 C .3.C 【分析】若,联合图形可知,2221 2.应选 .1OA OBOA OBABC4.B 【分析】 cos()cos5,∴ cos5,又α∈, ,3325 22.∴sin(2∴sin α= 1cos2= 1π+α) =- sinα=- .应选 B .33 35.D 【分析】圆 C 的标准方程为 x 2 y24 ,直线 l 过定点(0,1 ),代入 x 2 y 1 2,1 4 可知直线过圆上的点,因此直线与圆相切或订交.应选 D .6.D 【分析】函数 y f ( x) c 与 x 轴有两个不一样交点,即方程 f ( x) c0 有两个不一样的 解,由 f ( x) c 知, y f ( x) 与 y c 有两个不一样的交点,联合图形可知c2, 0.51.1,1.8 .应选 D .7.B 【分析】 S -S =a +a +a +a =2( a +a ) =0,又 a =1,∴a =- 1.∴ b 22 ,6234564545又 b 5b 1 4b 22 ,即 b 3 2 4b 2 2 ,∴ q 2 b 3 2 4 , q 2 .因此 b 10 b 2q 8228 29 ,因此b 2 2log 2 b 10 log 2 29 9 .8.A 【分析】f ( x ) 的最小正周期 T 45,故2 2.由 2得,126 T662由图可知 A =2.故函数 f ( x ) 的分析式为 f ( x)2sin 2 x.因此 f (0) 2sin1 .故66选 A .9.B 【分析】 ①样本容量为 93 ,①是假命题; ②数据 1,2,3,3,4,5 的均匀数为 1861(12 33 4 5) 3,中位数为 3,众数为 3,都同样, ②是真命题;5③ x 乙5 6 9 105 7, s 乙21[(5 -7) 2+(6 -7) 2+(9 -7) 2+(10-7) 2+(5 -7) 2 ] =551×(4 +1+4+9+4) =4.4 ,∵s 2>s 2,∴乙稳固, ③是假命题; ④是真命题; ⑤精心整理4数据落在 [114.5,124.5) 内的有: 120,122,116,120共 4 个,故所求 率 10=0.4 ,⑤是真命 .10.B 【分析】由 f ( x ) 是( -∞,+∞ ) 上的减函数,可得 0 a 1,化 得 0 a,1.f (0) a 0 2 3a 3 ,二、填空 :本大 共5 小 ,每小 5 分,共 25 分,把答案填在 中横 上。
2014-2015临泉一中高三上学期竞赛化学试卷

2014~2015届临泉一中高三年级竞赛试题化学试题本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷满分100分,考试时间:90分钟。
考生务必将答案答在答题卷上,在试卷上作答无效。
考试结束后只交答题卷。
可能用到的相对原子质量:H-1 C-12 N-14 O-16 Cl-35.5 Fe-56 Cu-64 S-32 I-127 Na-23 Al-27第I卷(选择题共48分)一、选择题(24小题,每小题只有一个正确选项,每题2分,共48分)1.空气质量指数(Air Quality Index,AQI)是定量描述空气质量状况的非线性无量纲指数。
参与评价的污染物为SO2、NO2、PM10、PM2.5、O3、CO等六项。
下列措施不能有效改善空气质量的是( ) A.调整产业结构,淘汰落后产能B.改善能源结构,使用清洁能源C.控制工业源污染,对钢铁、水泥等行业实行限产、限污D.及时发布AQI指数,提示公众应对污染的措施2.化学在工农业生产和日常生活中都有着重要的应用。
下列叙述正确的是( ) A.K2FeO4是新型净水剂,其净水原理与明矾完全相同B.工业上铝的冶炼是通过电解熔融的AlCl3来实现的C.PM2.5表示每立方米空气中直径小于或等于2.5微米的颗粒物的含量,PM2.5值越高,大气污染越严重,因为PM2.5颗粒物在空气中形成胶体分散系,吸附能力很强D.长期使用(NH4)2SO4化肥使土壤酸化,而过度使用尿素[CO(NH2)2]会使土壤碱化3.下列表述完全正确的是( )A.氮原子最外层电子的排布图表示式:B.氨分子的球棍模型:C.二氧化碳分子的比例模型D.溴化铵的电子式4.N A代表阿伏加德罗常数的值,下列有关叙述正确的是( )A.5.6g铁粉在2.24L氯气中充分燃烧,失去的电子数一定为0.3N AB.标准状况下,15g一氧化氮和5.6L氧气混合后的分子总数为0.5N AC.在标准状况下,22.4LCH4与18gH2O所含有的电子数均为10N AD.78gNa2S和Na2O2的混合物中含有的离子总数大于3N A5)6.下列离子在溶液中能够共存并且在加入少量的Na2O2固体后原离子浓度能基本保持不变的是( ) A.NH4+、Ba2+、Cl-、NO3-B.K+、AlO2-、Cl-、SO42-C.Ca2+、Mg2+、NO3-、HCO3-D.Na+、Cl-、CO32-、NO3-7.常温下,下列各组粒子在指定溶液中能大量共存的是( )A.在酸性KMnO4溶液中:Na+、C2H5OH、NH4+、Cl-B.能溶解CaCO3的溶液中:Fe2+、Ca2+、Cl-、NO3-C.澄清透明的溶液中:Cu2+、Mg2+、SO32-、Cl-D.能使淀粉-KI试纸显蓝色的溶液中:K+、H+、SO32-、Cl28.根据下列实验现象,所得结论错误的是( )9.某无色溶液中可能含有仅由①Na、②Ba、③Cl、④Br、⑨SO3、⑥SO4离子中的若干种组成的溶质,A.肯定含有的离子是①④⑤B.肯定没有的离子是②⑥C.不能确定的离子是①D.不能确定的离子是③⑤1011.下列各组原子中,彼此化学性质一定相似的是( )A.原子核外电子排布式为ls2的X原子与原子核外电子排布式为ls22s2的Y原子B.原子核外M层上仅有两个电子的X原子与原子核外N层上仅有两个电子的Y原子C.2p轨道上有三个未成对电子的X原子与3p轨道上有三个未成对电子的Y原子D.最外层都只有一个电子的X、Y原子12.反应A(g)+B(g)C(g)+D(g)过程中的能量变化如图所示,由此可判断( )A.1molA与1molB充分反应后,能量变化为△EB.加入催化剂后,反应加快,△E减小C.反应物的总键能小于生成物的总键能D.反应达到平衡时,升高温度,A的转化率增大13.某化学小组研究在其他条件不变时,改变密闭容器中某一条件对A 2(g)+3B2(g)2AB3(g)化学平衡状态的影响,得到如上图所示的曲线(图中T表示温度,n表示物质的量)下列判断正确的是( ) A.若T2>T1,则正反应一定是放热反应B.达到平衡时A2的转化率大小为:b>a>cC.若T2>T1,达到平衡时b、d点的反应速率为v d>v bD.在T2和n(A2)不变时达到平衡,AB3的物质的量大小为:c>b>a14.W、X、Y是原子序数依次增大的同一短周期元素。
2016-2017年安徽省阜阳市临泉一中高一(下)竞赛数学试卷和答案(文科)

2016-2017学年安徽省阜阳市临泉一中高一(下)竞赛数学试卷(文科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)一中学有90个班,每班60人,若每班选派3人参加“学代会”,则在这个问题中,样本容量是()A.90 B.60 C.270 D.1802.(5分)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则()A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差3.(5分)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为()A.2,5 B.5,5 C.5,8 D.8,84.(5分)有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12]内的频数为()A.18 B.36 C.54 D.725.(5分)在区间[﹣1,1]上随机取一个数x,的值介于到1之间的概率为()A.B.C.D.6.(5分)要得到函数f(x)=cos2x的图象,只需将函数g(x)=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度7.(5分)按如下程序框图,若输出结果为S=170,则判断框内应补充的条件为()A.i>5 B.i≥5 C.i≥7 D.i>78.(5分)已知圆O的半径为2,圆O的一条弦AB的长是3,P是圆O上的任意一点,则的最大值为()A.9 B.10 C.D.9.(5分)定义运算a*b为执行如图所示的程序框图输出的S值,则(sin)*()的值为()A.B.C.D.10.(5分)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(1)=()A.B.﹣C.1 D.﹣111.(5分)已知直线x+y=a与圆x2+y2=4交于A、B两点,且|+|=|﹣|,其中O为原点,则实数a的值为()A.2 B.﹣2 C.2或﹣2 D.或﹣12.(5分)已知函数的图象与直线y=m有三个交点的横坐标分别为x1,x2,x3(x1<x2<x3),那么x1+2x2+x3的值是()A. B. C. D.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若向量,则=.14.(5分)从集合{1,2,3,4}的所有子集中任取一个集合,它含有2个元素的概率为.15.(5分)已知向量和的夹角为120°,,则=.16.(5分)设当x=θ时,函数f(x)=2sinx﹣3cosx取得最小值,则tanθ=.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100](1)求频率分布图中a 的值,并估计该企业的职工对该部门评分不低于80的概率;(2)从评分在[40,60)的受访职工中,随机抽取2人,求此2人评分都在[50,60)的概率..18.一台机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如表所示:(1)作出散点图;(2)如果y 与x 线性相关,求出回归直线方程.(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?附:对于一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其回归直线y=bx +a 的斜率和截距的最小二乘估计分别为,,.19.设函数.(1)求函数y=f (x )的最小正周期和单调递增区间;(2)当时,求函数f(x)的最大值.20.在边长为3的正△ABC中,设.(1)用向量表示向量,并求的模;(2)求的值;(3)求与的夹角的大小.21.已知α,β均为锐角,满足,求.22.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点对称,且在区间上是单调函数,求ω和φ的值.2016-2017学年安徽省阜阳市临泉一中高一(下)竞赛数学试卷(文科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)一中学有90个班,每班60人,若每班选派3人参加“学代会”,则在这个问题中,样本容量是()A.90 B.60 C.270 D.180【解答】解:由题意,是一个分层抽样,一中学有90个班,每班60人,若每班选派3人参加“学代会,故共抽取270人组成样本所以,样本容量是270人.故选:C.2.(5分)甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则()A.甲的成绩的平均数小于乙的成绩的平均数B.甲的成绩的中位数等于乙的成绩的中位数C.甲的成绩的方差小于乙的成绩的方差D.甲的成绩的极差小于乙的成绩的极差【解答】解:=×(4+5+6+7+8)=6,=×(5+5+5+6+9)=6,甲的成绩的方差为×(22×2+12×2)=2,以的成绩的方差为×(12×3+32×1)=2.4.故选:C.3.(5分)以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为()A.2,5 B.5,5 C.5,8 D.8,8【解答】解:乙组数据平均数=(9+15+18+24+10+y)÷5=16.8;∴y=8;甲组数据可排列成:9,12,10+x,24,27.所以中位数为:10+x=15,∴x=5.故选:C.4.(5分)有一个容量为200的样本,其频率分布直方图如图所示.根据样本的频率分布直方图估计,样本数据落在区间[10,12]内的频数为()A.18 B.36 C.54 D.72【解答】解:观察直方图易得数据落在[10,12)的频率=(0.02+0.05+0.15+0.19)×2=0.82;数据落在[10,12)外的频率=1﹣0.82=0.18;∴样本数落在[10,12)内的频数为200×0.18=36,故选:B.5.(5分)在区间[﹣1,1]上随机取一个数x,的值介于到1之间的概率为()A.B.C.D.【解答】解:由≤≤1,得2kπ﹣≤≤2kπ+,得4k﹣≤x≤4k+,k∈Z,当k=0时,﹣≤x≤,∵﹣1≤x≤1,∴在区间[﹣1,1]上随机取一个数x,的值介于到1之间的概率为P===,故选:D.6.(5分)要得到函数f(x)=cos2x的图象,只需将函数g(x)=sin2x的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度【解答】解:要得到函数f(x)=cos2x=sin(2x+)的图象,只需将函数g(x)=sin2x的图象向左平移个单位长度,故选:A.7.(5分)按如下程序框图,若输出结果为S=170,则判断框内应补充的条件为()A.i>5 B.i≥5 C.i≥7 D.i>7【解答】解:经过第一次循环得到S=2,i=3经过第二次循环得到S=2+23=10,i=5经过第三次循环得到S=10+25=42,i=7经过第四次循环得到S=42+27=170,i=9此时需要输出结果,此时的i满足判断框中的条件i>7.故选:D.8.(5分)已知圆O的半径为2,圆O的一条弦AB的长是3,P是圆O上的任意一点,则的最大值为()A.9 B.10 C.D.【解答】解:以圆心O为原点建立坐标系,不妨设AB与x轴平行,A(﹣,﹣),B(,﹣),P(2cosα,2sinα),则=(3,0),=(2cosα+,2sinα+),∴=6cosα+,∴当cosα=1时,取得最大值.故选:C.9.(5分)定义运算a*b为执行如图所示的程序框图输出的S值,则(sin)*()的值为()A.B.C.D.【解答】解:由已知的程序框图可知:本程序的功能是:计算并输出分段函数S=的值,∵a=sin>b=cos,∴S=(sin)*(cos)=sin×cos=sin=.故选:C.10.(5分)如图所示为函数f(x)=2sin(ωx+φ)(ω>0,≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(1)=()A.B.﹣C.1 D.﹣1【解答】解:如图,由图象可知,A=2.又A,B两点之间的距离为5,A,B两点的纵坐标的差为4,得函数的半个周期,∴T=6.则ω=.∴函数解析式为f(x)=2sin(+φ).由f(0)=1,得2sinφ=1,∴sinφ=.又≤φ≤π,∴φ=.则f(x)=2sin(+).∴f(1)=2sin=2×(﹣)=﹣1.故选:D.11.(5分)已知直线x+y=a与圆x2+y2=4交于A、B两点,且|+|=|﹣|,其中O为原点,则实数a的值为()A.2 B.﹣2 C.2或﹣2 D.或﹣【解答】解:由||=||得||2=||2,•=0,⊥,三角形AOB为等腰直角三角形,圆心到直线的距离为,即=,a=±2,故选C.12.(5分)已知函数的图象与直线y=m有三个交点的横坐标分别为x1,x2,x3(x1<x2<x3),那么x1+2x2+x3的值是()A. B. C. D.【解答】解:函数的图象取得最值有2个x值,分别为x=和x=,由正弦函数图象的对称性可得x1+x2=2×=,x2+x3 =2×=.故x1+2x2+x3=x1+x2+x2+x3==,故选:C.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)若向量,则=(﹣2,6).【解答】解:根据题意,向量,则=+=(﹣2,6);故答案为:(﹣2,6)14.(5分)从集合{1,2,3,4}的所有子集中任取一个集合,它含有2个元素的概率为.【解答】解:从集合{1,2,3,4}的所有子集中任取一个集合,基本事件总数n=24=16,它含有2个元素包含的基本事件个数m==6,∴从集合{1,2,3,4}的所有子集中任取一个集合,它含有2个元素的概率为:p==.故答案为:.15.(5分)已知向量和的夹角为120°,,则=7.【解答】解:由题意得,=,∴=7.故答案为:7.16.(5分)设当x=θ时,函数f(x)=2sinx﹣3cosx取得最小值,则tanθ=.【解答】解:f(x)=2sinx﹣3cosx==,(tanα=),当x﹣α=,k∈Z时,函数f(x)=2sinx﹣3cosx取得最小值,即x=θ=α,k∈Z时,函数f(x)=2sinx﹣3cosx取得最小值,此时tanθ=tan(α)=﹣tanα=.故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50),[50,60),…,[80,90),[90,100](1)求频率分布图中a的值,并估计该企业的职工对该部门评分不低于80的概率;(2)从评分在[40,60)的受访职工中,随机抽取2人,求此2人评分都在[50,60)的概率..【解答】解:(1)由频率分布直方图得:(0.004+a+0.018+0.022×2+0.028)×10=1,解得a=0.006.由频率分布直方图,得:50名受访职工评分不低于80分的频率为:(0.022+0.018)×10=0.4,∴该企业职工对该部门评分不低于80分的概率的估计值为0.4.(2)受访职工中评分在[50,60)的有:50×0.006×10=3人,记为a,b,c,受访职工中评分在[40,50)的有:50×0.006×10=2人,记为A,B,从这5名受访职工中随机抽取2人,所有的可能结果有10种,分别为:{a,b},{a,c},{a,A},{a,B},{b,c},{b,A},{b,B},{c,A},{c,B},{A,B},此2人评分都在[50,60)包含的基本事件有{a,b},{a,c},{b,c},共3个,∴从评分在[40,60)的受访职工中,随机抽取2人,此2人评分都在[50,60)的概率p=.18.一台机器由于使用时间较长,生产的零件有一些会有缺损,按不同转速生产出来的零件有缺损的统计数据如表所示:(1)作出散点图;(2)如果y 与x线性相关,求出回归直线方程.(3)若实际生产中,允许每小时的产品中有缺损的零件最多为10个,那么,机器的运转速度应控制在什么范围内?附:对于一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),其回归直线y=bx +a 的斜率和截距的最小二乘估计分别为,,.【解答】解:(1)画出散点图,如图所示:;(2)计算=×(16+14+12+8)=12.5, =×(11+9+8+5)=8.25, ∴≈0.7286,=﹣=8.25﹣0.7286×12.5=﹣0.8571,∴回归直线方程为:y=0.7286x ﹣0.8571;(3)要使y ≤10,则0.728 6x ﹣0.857 4≤10,解得x ≤14.901 9; 故机器的转速应控制在14.9转/秒以下.19.设函数.(1)求函数y=f (x )的最小正周期和单调递增区间; (2)当时,求函数f (x )的最大值.【解答】解:(1)f(x)=2cos2x+2cosxsinx=1+cos2x+sin2x=1+2sin(2x+),∴f(x)的最小正周期为T==π.令﹣+2kπ≤2x+≤+2kπ,解得:﹣+kπ≤x≤+kπ,∴f(x)的单调递增区间是:[﹣+kπ,+kπ],k∈Z.(2)当x∈[0,]时,2x+∈[,],∴当2x+=时,f(x)取得最大值1+2=3.20.在边长为3的正△ABC中,设.(1)用向量表示向量,并求的模;(2)求的值;(3)求与的夹角的大小.【解答】解:(1),又,∴==1+2+4=7,∴||=.(2)==﹣,∴=(+)•(﹣)=﹣﹣+=﹣3﹣+2=﹣.(3)由△ABE≌△CAD可得BE=AD=,∴,∴与的夹角为120°.21.已知α,β均为锐角,满足,求.【解答】解:∵β=(α+β)﹣α,∴cosβ=cos[(α+β)﹣α]=cos(α+β)cosα+sin(α+β)sinα①∵,∴∵,∵α+β>α∴若α+β为锐角,则根据y=sinx在单调递增,可知sin(α+β)>sinα,与条件矛盾∴,∴,代入①可得:,∴,∵,∴,∴.22.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点对称,且在区间上是单调函数,求ω和φ的值.【解答】解:由f(x)是偶函数,得f(﹣x)=f(x),即sin(﹣ωx+φ)=sin(ωx+φ),所以﹣cosφsinωx=cosφsinωx对任意x都成立,又ω>0,∴cosφ=0,依题设0≤φ≤π,所以解得.由f(x)的图象关于点M对称,得,取x=0,得,所以.∵,∴,又ω>0,得,∴.当k=0时,在上是增函数;当k=1时,在上是增函数;当k≥2时,在上不是单调函数.所以,综合可得或ω=2.。
安徽省阜阳市临泉县第一中学高一数学1月学科竞赛试题

安徽省阜阳市临泉县第一中学2016-2017学年高一数学1月学科竞赛试题理(扫描版)临泉一中2016-2017学年第一学期竞赛试题数学(理)答案 一、选择题1-6 DCABDC 7-12 BACACB二、填空题 13. 80 14.1 15. ()6,4 16.①三、解答题17.18、解:圆C 的方程为:(x+1)2+(y ﹣2)2=2,(1)圆C 的切线在x 轴和y 轴上截距相等时,切线过原点或切线的斜率为﹣1;当切线过原点时,设切线方程为:y=kx ,相切则:,得;当切线的斜率为﹣1时,设切线方程为:y+x+b=0,由相切得:,得b=1或b=﹣3; 故所求切线方程为:或;或x+y+1=0,或x+y ﹣3=0. (2)由圆的切线长公式可得|PM|2=|PC|2﹣R 2=(x+1)2+(y ﹣2)2﹣2,由|PM|=|PO|得,(x+1)2+(y ﹣2)2﹣2=x 2+y 2,即2x ﹣4y+3=0,即x=2y ﹣,此时|P M|=|PO|====,∴当y=即P (,)时,|PO|最小. 19.(1)ΘE ,F 分别是AB ,AD 的中点,BD EF 21//∴ΘG ,H 分别是BC ,CD 上的点,且DC CH BC CG 31,31==,BD CH 31//∴ CG EF 23//∴,∴E,F,H,G 四点共面; (2)由E,F,H,G 四点共面,且CG EF 23//∴,那么延长EG ,FH 相交于点P ,∈P Θ直线EG ,故点P 在平面ABC 上,同理:点P 在平面ACD上,由公理3知,点P 在平面ABC I 平面ACD=AC ,∴三条直线FH ,EG ,AC 共点.20. 解(1)由条件设二次函数f (x )=a (x-1)2+16=ax 2-2ax+a+16,设f (x )=0的两根为:x 1,x 2,令x 1<x 2,∵图象在x 轴上截得线段长为8,由韦达定理得:(x 2-x 1)2=(x 2+x 1)2-4x 2x 1=(-2)2-4×a+16 a=64, 解得a=-1,∴函数的解析式为f (x )=-x 2+2x +15.(2)①∵f (x )=-x 2+2x+15,∴g (x )=(2-2a )x-f (x )=x 2-2ax-15,而g (x )在x ∈[0,2]上是单调增函数,∴对称轴x=a 在[0,2]的左侧,∴a ≤0.所以实数a 的取值范围是{a|a ≤0}.②g (x )=x 2-2ax-15,x ∈[0,2],对称轴x=a ,当a >2时,g (x )min =g (2)=4-4a-15=-4a-11,当a <0时,g (x )min =g (0)=-15,当0≤a ≤2时,g (x )min =g (a )=a 2-2a 2-15=-a 2-15. 综上所述:()()()min 24112g()1501502a a x a a a ⎧-->⎪-<⎨⎪--≤≤⎩21.证明:(1)060(2)ABCD PD 平面⊥ΘDC PD ⊥∴ DC PD =Θ可知PDC ∆是等腰直角三形,而E 是斜边PC 的中点 PC DE ⊥∴。
临泉一中2015届高三竞赛语文试题

• 宽容,是一种境界。海纳百川,胸 怀寰宇。不是宽泛之宽,也非放任 之容,而是心底的宽广,是兼容并 蓄的包容。 • 宁静,是一种境界。波澜不惊,宠 辱偕忘。不是苟安之宁,也非沉寂 之静,而是处世的宁帖,是明志致 高 山仰止。不是膜拜之崇,也非高傲 之高,而是人格的高标,是胸无尘 杂的高洁。 • 廉洁,是一种境界。荷花不染,冰 雪无尘。不是廉价之廉,也非真空 之洁,而是品质的廉正,是冰心玉 壶的纯洁。
21、作文
• 题目:小小的变化,理念的提升 • 观点:以人为本,人文关怀,是社会文明 的体现。以人为本,尊重他人,是文明理 念的提升。 • ①提示他人,要尊重为先; ②关怀他人, 要温馨为要; ③互相尊重,互相关爱,社 会和谐,文明程度大为提升,社会进步才 显全面。
8、上片,艺术手法,选一种,分析 • 【示例三】 • ①比喻。②把眉比作山峰,无心梳 妆,容颜憔悴,如山峰“减翠”; 把腕比作玉,形容消瘦,如美玉 “香消”。生动形象地写出了心上 人的美好和自己的强烈思念。
8、上片,艺术手法,选一种,分析
• 【示例四】 • ①叠词连用。②“淡淡”写阴霾的天 色,“潇潇”写雨淅淅沥沥绵密不歇; “暮暮”“朝朝”,一天又一天,写 阴云密雨时间之长;叠词的连用,烘 托了阴郁沉闷、迷蒙伤感的气氛,表 达了对心上人的绵绵思念。叠词运用, 富有音韵美感。
2015届高三竞赛语文试题
临泉一中 宇文劳诗制作 2014、12、29
7、翻译题(10分)
• (1)虽然,吾兵业已加鲁矣,去 而之吴,大臣疑我,奈何? • 【译文】虽然这样,(但是)我的 士兵已经奔赴鲁国了,离开(鲁国) 前去讨伐吴国,大臣怀疑我,怎么 办?
7、翻译题(10分)
• (2)今存越示诸侯以仁,救鲁伐 齐,威加晋国,诸侯必相率而朝吴, 霸业成矣。 • 【译文】如果保存越国向诸侯显示 你的仁慈,营救鲁国讨伐齐国,威 势超过晋国,诸侯必定相随朝拜吴 国,吴国就会成就了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014~2015届临泉一中高三年级竞赛试题
数学(文)试题
本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
全卷满分150分,考试时间:120分钟。
考生务必将答案答在答题卷上,在试卷上作答无效。
考试结束后只交答题卷。
第Ⅰ卷(选择题满分50分)
一、选择题(本大题共10小题,每小题5分,共50分,请将答案填涂在答题卡上)
1.集合A ={﹣1,0,1},B ={y|y =e x ,x ∈A},则A ∩B =( )
A .{0}
B .{1}
C .{0,1}
D .{﹣1,0,1}
2.已知命题p :,下列的取值能使“p ”命题是真命题的是( )
A .a ∈R
B .a =﹣2
C .a =l
D .a =0
3.若,,,且,则x =( )
A .2
B .72
C .﹣2或72
D .12或﹣72 4.直线y =kx +1与曲线y =x 3+ax +6相切于点A(l ,3),则2a+b 的值为( )
A .2
B .﹣1
C .l
D .﹣2
5.已知函数y =f (x )的定义域为{x|x ≠0},满足f (x )+ f (﹣x )=0,当x>0时, f (x )=ln x -x +1,则函数y =f (x )的大致图象是( )
6.下列命题中错误的是( )
A .如果平面α⊥平面β,那么平面α内一定存在直线平行于平面β
B .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β
C .如果平面α⊥平面γ,平面α⊥平面β,α∩β=l ,那么直线l 平面γ
D .如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
7.若正项数列{a n }满足lg a n+1 =1+lg a n 。
,且a 2001+a 2002+…+a 2010=2014,则a 2011+a 2012+…+a 2020的值为( )
A .2014·1010
B .2014·1011
C .2015·1010
D .2015·1011
8.若函数y =f (x )=sin(ωx +π3)的图象向右平移π3
个单位后与原函数的图象关于x 轴对称,则ω的最小正值是()
A .12
B .1
C .2
D .3
9.已知函数f (x ) = x 2-2x +c ,记f 1(x )= f (x ) f n+1(x )= f (f n (x )),(n ∈N *),若函数),y = f n (x )-x 不存在零点,则c 的取值范围是( )
A .c <14
B .c ≥34
C .c >94
D .c ≤94
10.已知函数f (x )=e x ,对于曲线y = f (x )上横坐标成等差数列的三个点A 、B 、C ,给出以下四个判断:①△-ABC 一定是钝角三角形;②△ABC 可能是直角三角形;③△ABC 可能是等腰三角形;④△ABC 不可能是等腰三角形.其中正确的判断是( )
A .①③
B .①④
C .②③
D .②④
第Ⅱ卷(非选择题满分100分)
二、填空题(本大题共5小题,每小题5分,共25分,请将答案填在答题卷相应位置)
11.已知A ={x |18 <2-x <12
},B ={x |log 2(x -2)<1},则A ∪B =_______________. 12.一个几何体的三视图如图所示,则该几何体的体积为________________.
13.正项数列{a n }满足:a 1=1,a 2=2,2a n 2= a n+12+ a n -12(n ∈N *,n ≥2),则a 7=______.
14.已知锐角α,β满足3tan α=tan(α+β),则tan β的最大值为________.
15.定义在R 上的偶函数f (x ),且对任意实数x 都有f (x +2)= f (x ).当x ∈[0,1]时, f (x ) =x 2,若在区间[-1,3]内,函数g (x )= f (x )-kx -k 有4个零点,则实数的k 取值范围是__________.
三、解答题:(本大题共6小题,共75分。
解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡上的指定区域内)
16.(本题12分)已知函数f (x )=3sin2x -2cos 2x -1,x ∈R .
(I)求函数f (x )的最小正周期和最小值;
(Ⅱ)在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,若c =3, f (C )=0,sin B =2sin A ,求a ,b 的值.
17.(本题12分)已知等差数列{ a n }满足:a 3=7,a 5+a 7=26,{ a n }的前n 项和为S n .
(I)求a n 及S n ;
(Ⅱ)求数列{
1S n
}妾}的前n 项和为T n .
18.(本题12分)已知函数f (x )=1 x +1 x 2+1 x 3 (I)求y = f (x )在[﹣4,﹣12
]上的最值; (Ⅱ)若a ≥0,求g (x )= 1 x +2 x 2+a x 3.
19.(本题12分)如图所示,矩形ABCD 中,AD ⊥平面ABE ,AE =EB =BC =2,F 为CE 上的点,且BF ⊥平面ACE .
(I)求证:AE ⊥平面BCE ;
(Ⅱ)求证:AE ∥平面BFD ;
(Ⅲ)求三棱锥C -BGF 的体积.
20.(本题13分)已知函数f (x )=a (x 2+1)+ln x .
(I)讨论函数f (x )的单调性;
(Ⅱ)若对任意a∈(﹣4,﹣2)及x∈[1,3)时,恒有ma-f(x)>a2成立,求实数m的取值范围.
21.(本题14分)已知函数f(x)=x2-1,设曲线y=f(x)在点(x n,y n)处的切线与x轴的交点为(x n+1,0),其中x1为正实数.
(I)用x n表示x n+1;
(Ⅱ) x1=2,若a n=lg x n+1
x n-1
,试证明数列{ a n}为等比数列,并求数列{ a n}的通项公式;
(Ⅲ)若数列{ b n}的前n项和S n=n(n+1)
2,记数列{a n·b n}的前n项和为T n,求T n.。
