北师大版五年级数学下册分数加减法及简便运算(全面)
北师大版五年级数学下册分数简便运算知识讲解

北师大版五年级数学下册分数简便运算341455341()455314314++=++=+=7212833--7212()833=-+7218=-718= 分数加减法的简便运算 加法运算定律有哪些:(1)加法交换律:a+b=b+a (2)加法结合律:a+b+c=a+(b+c) 减法运算定律有哪些:连减的性质:(1)a-b-c=a-(b+c) (2)a-(b+c)=a-b-c其他:(1)a-b+c=a+c-b (2)a-(b-c)=a-b+c (3)a-b+c-d=(a+c)-(b+d) 这些运算定律在分数的加减法简便运算中同样适用,因此,分数的加减法简便运算和整数的加减法简便运算一样。
(一)加法结合律:a+b+c=a+(b+c) (二)减法的连减:a-b-c=a-(b+c)例:练习: 234577++ 184595++ 87811516--(三)减法的连减:a-(b+c)=a-b-c (四)a-b+c=a+c-b例:511()44551144511545-+=--=-= 53274752377431414-+=+-=-=练习:1511()16162-+ 114111412512-+ 11175761276-+计算下面各题,能简算的要简算 314165+- 15415751++ )5243(107--6165910+- 13992134+- 16916723--分数乘除法的简便运算(一)乘法结合律:a ×b ×c=a ×(b ×c)例:1548375⨯⨯(二)乘法分配率:(a+b )×c=a ×c+b ×c a ×c+b ×c=(a+b )×c例: 306153⨯+)( 279132⨯-)( 76999971⨯+⨯变式题:51724 ×34 +51724 ÷4 335×+848÷43计算下面各题,能简算的要简算。
完整版)北师大版小学数学五年级下册知识点整理

完整版)北师大版小学数学五年级下册知识点整理将分数的分子相加或相减,分母保持不变即可。
这种情况下,分母相同的分数,分子越大,数值越大;分子越小,数值越小。
2)异分母分数加、减法:先将分数化为相同分母的分数,再将分子相加或相减,分母保持不变即可。
这种情况下,分母相同的分数,分子越大,数值越大;分子越小,数值越小。
3)分数加减混合运算:先将带分数化为分数,再按照同分母或异分母的方法进行加减运算,最后将结果化为带分数。
4、最终结果要化为最简分数,即分子和分母没有公因数。
七、总结分数是将单位“1”平均分成若干份后表示一份或几份的数。
分数与除法有密切关系,可以表示真分数、假分数和带分数。
分数具有基本性质,可以进行大小比较和约分。
分数和小数可以互相转化,方便比较大小。
分数的加法和减法需要注意同分母和异分母的情况,最终结果要化为最简分数。
同分母分数加减法很简单,只需要将分子相加或相减,分母不变。
计算出的结果如果能约分,就要化为最简分数。
异分母分数加减法需要先通分,将分母变为相同的数,再按照同分母分数加减法的方法计算。
在分数加减混合运算中,运算顺序与整数加减混合运算相同,要先算括号里面的,再算括号外面的,如果只含有同一级运算,应从左到右依次计算。
整数加法的交换律和结合律同样适用于分数加法。
长方体和正方体是常见的几何体,长方体有6个面,每个面都是长方形,有8个顶点和12条棱,棱分为3组,每组4条棱一样长。
正方体是特殊的长方体,每个面都是正方形,有8个顶点和12条棱,棱长都相等。
长方体的棱长总和可以通过公式计算,即(长+宽+高)×4或长×4+宽×4+高×4.如果已知棱长总和,可以通过公式计算长、宽、高的值。
长方体的高可以用公式h=L÷4-(a+b)来计算,其中L 表示棱长总和,a和b表示长和宽。
这个公式可以帮助我们计算长方体的高度。
正方体的棱长总和可以用公式L=12a来计算,其中a表示正方体的棱长。
北师大版五年级数学下册知识点详解及练习第一单元 分数加减法

北师大版五年级数学下册知识点详解及练习第一单元分数加减法在本文中,我们将详细介绍北师大版五年级数学下册第一单元——分数加减法。
这个单元包括异分母分数加减法、分数加减混合运算和分数与小数互化三个部分。
1.1 异分母分数加减法在异分母分数加减法中,我们需要注意分数单位(即分母)不同的问题。
为了解决这个问题,我们需要将分数转化成相同的分数单位后再进行计算。
具体来说,同分母分数相加减时,分母不变,只需将分子相加减即可;而分母不同的分数则需要先转化成相同的分数单位,再按同分母分数相加减的方法进行计算。
1.2 分数加减混合运算在分数加减混合运算中,我们需要注意运算的顺序和方法。
一般来说,我们先计算整数部分的加减法,再计算分数部分的加减法。
为了简化计算,我们还可以使用一些简便算法。
1.3 分数与小数互化在分数与小数互化中,我们需要理解它们之间的转化关系。
具体来说,我们可以使用小数化分数和分数化小数的方法将它们互相转化。
这样,我们就可以在不同的计算问题中灵活运用它们了。
异分母分数加减法的方法在进行异分母分数相加减时,需要先通分,将分数化成相同的分母,然后按照同分母分数相加减的方法进行计算。
最终的计算结果,如果能约分,则需要将其约分成最简分数。
1)分母互质如果两个分数的分母互质,那么它们的最小公倍数是它们的积。
为了将这两个分数的分母变成相同的数,需要将它们的分子和分母分别同乘对方的分母,然后将分子相加减。
具体来说,分母相乘作为新的分母,分子交叉相乘再相加减即可。
例如,对于分数3/4和5/8进行相加,先找到它们的最小公倍数8,然后将分母转化成8,得到:3/4 + 5/8 = 6/8 + 5/8 = 11/82)分母具有倍数关系如果两个分数的分母具有倍数关系,那么可以将其中一个分数的分母变成另一个分数的分母的倍数,然后再按照同分母分数相加减的方法进行计算。
最终的计算结果需要化简成最简分数。
例如,对于分数2/3和1/8进行相加,可以将1/8的分母变成3的倍数24,得到:2/3 + 3/24 = 16/24 + 3/24 = 19/243)分母具有相同因数如果两个分数的分母具有相同的因数,那么可以将它们的分母都变成这个因数的倍数,然后再按照同分母分数相加减的方法进行计算。
(完整版)北师大版五年级数学下册分数简便运算(可编辑修改word版)
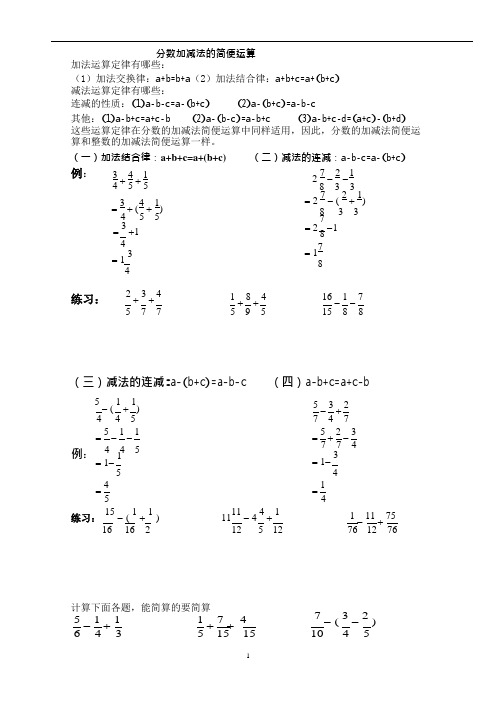
分数加减法的简便运算加法运算定律有哪些:(1)加法交换律:a +b =b +a (2)加法结合律:a +b +c =a +(b +c )减法运算定律有哪些:连减的性质:(1)a -b -c =a -(b +c ) (2)a -(b +c )=a -b -c 其他:(1)a -b +c =a +c -b (2)a -(b -c )=a -b +c (3)a -b +c -d =(a +c )-(b +d ) 这些运算定律在分数的加减法简便运算中同样适用,因此,分数的加减法简便运 算和整数的加减法简便运算一样。
(一)加法结合律:a+b+c=a+(b+c)(二)减法的连减:a -b -c =a -(b +c )例:3 +4 + 1 45 5 2 7 - 2 - 1 8 3 3 = 3 + 4 ( 4 + 1) 5 5 = 2 7 - ( 2 + 1) 8 3 3 7 = 3 +1 = 2 -1 8 4 = 1 3 4练习:2 +3 + 41 + 8 + 4 = 17 816 - 1 - 7 5 7 75 9 515 8 8(三)减法的连减:a -(b +c )=a -b -c(四)a -b +c =a +c -b5- ( 1 + 1) 4 4 5 = 5 - 1 - 1 例: 4 4 5= 1- 15 = 4 55 - 3 + 2 7 4 7 = 5 + 2 - 3 7 7 4 = 1- 34 = 1 4练习: 15 - ( 1 + 1)1111- 4 4 + 1 1 - 11 + 75 16 16 212 5 1276 12 76计算下面各题,能简算的要简算 5 - 1 + 1 1 + 7 + 4 7 - ( 3 - 2) 6 4 3 5 15 1510 4 5米的木头截去 和截去 米,剩下的部分不一样长。
(10 - 5 + 14 - 2 + 9 3 - 7 - 9 9 6 613 9 132 16 16分数乘除法的简便运算(一)乘法结合律:a ×b ×c=a ×(b ×c)例: 5 ⨯ 3 ⨯ 47 8 15(二)乘法分配率:(a+b )×c=a ×c+b ×ca ×c+b ×c=(a+b )×c 例: (3 + 1)⨯ 30 ( 2 - 1)⨯ 271 ⨯ 99 + 99 ⨯ 6 5 6 3 97 717 3 173 3 54 变式题:5 × +5 ÷4× + ÷ 24 4 248 4 8 3计算下面各题,能简算的要简算。
北师大版五年级下册数学全册知识点归纳与整理

北师大版五年级下册数学全册知识点归纳与整理北师大版五年级数学下册知识点归纳一、分数的加减、乘除法1.异分母分数相加减的步骤为先通分,化成同分母分数,再进行加减。
计算结果能约分的要进行约分。
2.将小数化为分数的方法是根据小数的意义,将小数化为分母是10、100、1000.的分数。
能约分的要进行约分。
具体方法是看有几位小数,就在1后面写几个做分母,把小数点去掉的部分做分子。
3.分数化为小数的方法是根据分数与除法的关系,用分子除以分母所得的商即可。
除不尽时通常保留两位小数。
4.分数乘法的意义是求几个相同分数的和的简便运算。
5.分数除法的意义是已知两个乘数的积和其中一个乘数,求另一个乘数的运算。
例如,25÷5=?已知两个乘数的积是25,其中一个数是5,求另一个数是多少?6.分数乘法的运算法则有两种情况。
一种是分数与整数相乘,此时分母不变;另一种是分数与分数相乘,分子与分子相乘,分母与分母相乘。
能约分的可以先约分。
7.分数除法的运算法则有两种情况。
一种是一个数除以一个整数(除外)等于这个数乘以这个整数的倒数;另一种是一个数除以一个分数等于这个数乘以这个分数的倒数。
除以一个数(除外)等于这个数乘以这个分数的倒数。
8.分数除法的意义是如果两个数的乘积是1,那么这两个数互为倒数,其中一个数是另一个数的倒数。
求一个数的倒数的方法是把这个数的分子、分母交换位置。
整数可以看成分母是1的分数,小数要先化为分数才能求倒数。
1的倒数是1,而0没有倒数,原因是0不能作除数。
9.分数乘整数的意义与整数乘法意义相同,就是求几个相同加数的和的简便运算。
10.一个数乘以分数的意义是求这个数的几分之几是多少。
11.分数的混合运算分数混合运算的顺序与整数加减混合运算的顺序相同,先算乘除法,再算加减法。
如果有括号,先算括号里面的,再算括号外面的。
整数的运算律在分数运算中同样适用。
运算定律:①乘法分配律:a×(b±c)=a×b±a×c;②乘法结合律:a×b×c=a×(b×c);③乘法交换律:a×b=b×a。
北师大版五年级数学下册分数加减法及简便运算(全面)

北师大版五年级数学下册分数加减法及简便运算(全面)五年级数学下册第一单元:分数加减法一、同分母的分数加减法在计算同分母的分数加减法中,分母不变,直接用分子相加减。
需要注意的是,如果得数不是最简分数,必须将其约分,使其成为最简分数。
例如,464/5 + 6/5 = 10/5 = 2.因为10/5不是最简分数,所以我们需要约分。
10和5的最大公因数是5,所以将分子和分母同时除以5,得到2.又如,959/10 - 542/10 = 417/10.因为417/10不是最简分数,必须约分。
4和10的最大公因数是2,所以将分子和分母同时除以2,得到209/5.回顾:如何将一个非最简分数化为最简?将一个非最简分数化为最简,需要进行约分,一直约到分子和分母互质为止。
因此,我们需要找到分子和分母的最大公因数,然后用分子和分母同时除以最大公因数。
练:1、计算7271/997 + 1/15 - 1515/1212 - 1611/1133 +1333/3333 = 8866/14442、连线:7314/997 + 2/7941 = 5588/4631/45 + 1/99 = 777/1793、判断对错,并改正:1) 4375/7714 += 6/7 - 47/7,应为4375/7714 - 6/7 + 47/72) 753/23 = 5 - 7/7,应为753/23 = 5 + 7/234、应用题:1) 一根铁丝长73米,比另一根铁丝长1212米,长了1010米;另一根铁丝长多少米?答案:2199米2) 一条路长73米,需要3天修完。
第一天修了15/73,第二天修了12/73,第三天修了1/2.问第三天修了多少米?答案:23/73米二、异分母的分数加减法在异分母的分数加减法中,可分为三种情况:分母互质关系、分母是倍数关系、分母是一般关系(既非互质也非倍数)。
例如,当分母互质且分子都为1时,可以使用以下公式进行计算:1/A + 1/B = (A+B)/AB当分母是倍数关系且分子都为1时,可以使用以下公式进行计算:1/A + 1/B = (B+A)/AB当分母是一般关系时,需要先找到分母的最小公倍数,进行通分,再进行加减。
最新北师大版五年级数学下册第1单元《分数加减法》教案

要注意:把分数化成小数的方法:用分子除以分母。不能化成有限小数的,一般保留三位小数。
牢记: =0.5, =0.25, =0.75, =
0.2, =0.125,为以后进一步学习分数、小数混合运算打下坚实的基础。
一 分数加减法
一、异分母分数的加法
异分母分数的加法的计算法则:先通分,将分母不同的分数化成分母相同的分数,再按照同分母分数相加的方法进行计算。通分时,一般是用分母的最小公倍数作公分母。
计算结果能约分的,要约成最简分数。
+ = + =
+ = + =
二、异分母Leabharlann 数的减法异分母分数的减法的计算法则:先通分,将分母不同的分数化成分母相同的分数,再按照同分母分数相减的方法进行计算。计算结果能约分的,一定要约分。
=4÷5=0.8 =1÷4=0.25 =1÷6≈0.167
2.根据小数的意义,可以把小数化成分数。
(1)小数的意义:像0.1,0.23,0.059,…这样表示十分之几,百分之几,千分之几……的数,叫作小数。一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……
(2)把小数化成分数的方法:原来有几位小数,就在1的后面写几个0作分母,把原来的小数去掉小数点作分子,能约分的要约分。
1.分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同,但为了计算简便,几个分数可以一次通分,然后按照顺序依次计算。
- + = - + = + =
2.整数加法的交换律、结合律和连减的性质对分数加法和分数减法同样适用。
加法交换律:两个数相加,交换加数的位置,和不变。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
(完整版)北师大版五年级数学下册分数简便运算(最新整理)

1
1
2、一只猴子摘了一堆桃子,第一天吃了这堆桃子的 ,第二天这堆桃子的 ,这时
7
6
还剩下 13 个桃子,这只猴子一共摘了多少个桃子?
2
5
3、广场上跳舞的小朋友的人数是唱歌的 ,踢足球的小朋友的人数是跳舞的 ,有 20 名小
3
6
朋友在踢足球。有多少名小朋友在唱歌?
4、庆“六一”计划一些做红花,小明已经做了 12 朵,小芳已经做 15 朵,小芳做 1
2.1 1 的倒数与 2 的商是( )
2
3
3.一本书看了 20 页,占全书的 2 ,这本书有多少页?把( 3
)看作单位“1”,
(
)的(
)是看了的页数,设(
)有 X页,列方程为
(
)
3
3
4、一本书第一天看了全书的 ,第二天是第一天的 ,两天共看了这本书的
8
4
( )。
二、解决问题 1.水果店运来苹果和梨共 350 千克,其中苹果占总数的 4 ,梨有多少千克? 7
1 99 99 6
7
7
17 3 17 变式题:5 × +5 ÷4
24 4 24
3×3 +5÷ 4 84 8 3
计算下面各题,能简算的要简算。
( 3 5 )×36 4 12
2×4×3 958
81 8 1 ×+×
949 4
3×3 +5÷ 4 84 8 3
23 8 ÷ 5 ×15 9 6 16
2 ÷( 2 × 5) 3 15 6
分数乘法判断题
1.一根长 1 米的木头截去 1 和截去 1 米,剩下的部分不一样长。( )
2
2
2
2.一个数(0 除外)乘分数,积一定小于这个数( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
五年级数学下册第一单元《分数加减法》 日期:一、同分母的分数加减法知识点:在计算同分母的分数加减法中,分母不变,直接用分子相加减。
注意:在计算同分母的分数加减法中,得数如果不是最简分数,我们必须将得数约分,使它成为最简分数。
例 5654+=510564=+=2 注意:因为510不是最简分数,所以得约分,10和5的最大公因数是5,所以分子和分母同时除以5,最后得数是2.例 1041059105109=-=-=52 注意:因为104不是最简分数,必须约分,因为4和10的最大公因数是2,所以分子和分母同时除以2,最后的数是52知识点回顾:如何将一个不是最简的分数化为最简?(将一个非最简分数化为最简,我们就是将这个分数进行约分,一直约到分子和分母互质为止。
所以要将一个分数进行约分,我们必须找到分子和分母的最大公因数,然后用分子和分母同时除以他们的最大公因数。
)练习: 1、计算 715 - 215 712 - 112 1 - 916 911 - 711 38 + 38 16 + 16 314 +314 34 + 342、连线19 + 49 2 7377+145 +15 1 8987+47 + 67 137 11511141+18 +78 2911 9392+2411 +511 59 2121+3、判断对错,并改正(1)47 +37 = 714 (2)6 - 57- 37ABA B AB B A B A ±±=±或11 =577 -57 -37=527 -37=5174、应用题 (1)一根铁丝长710 米,比另一根铁丝长310米,了;另一根铁丝长多少米?(2)3天修一条路,第一天修了全长的112 ,第二天修了全长的512,第三天修了全长的几分之几?二、异分母的分数加减法。
在异分母的分数加减法中,可分为三种情况。
分别是分母是互质关系、分母是倍数关系、分母是一般关系(即非互质也非倍数)例:A 代表一个分数的分母,B 代表另一个分数的分母,分母是倍数关系)(即分子都为的倍数)是或的倍数)是(、,分母互质)即分子都为或、1(1111)2(1(11)1(AB A B AB A B A B B A ABA B AB B A B A ±±=±±±=± )3(、A 和B 是一般关系,就找到A 和B 的最小公倍数,进行通分,再加减。
(一)分母是互质关系、且分子都为1的分数加减法。
知识点:如果分母是互质关系,且分子都为1,那么这两个分数相加减后的得数的分母就是互质的这两个分母的乘积,分子就为这两个互质分母的和。
例:分母是互质关系、且分子都为1的分数加法20954455141=⨯+=+ (讲解:因为4和5分别是上面两个分数的分母,且为互质关系,所以他们的公分母就为20.因为原来两个分数的分子都是1,通过分数的基本性质可知道,在通分之后这两个分数的分子分别是5和4。
因为是41加51,所以得数就是209。
例:分母是互质关系、且分子都为1的分数减法20154455141=⨯-=- (讲解:因为4和5分别是上面两个分数的分母,且为互质关系,所以他们的公分母就为20.因为原来两个分数的分子都是1,通过分数的基本性质可知道,在通分之后这两个分数的分子分别是5和4。
因为是减法,所以得数就是201。
)练习:1、计算: 3121+ 7131+ 10191+ 11151+8171-7161+8787⨯-=561-=761⨯=421=的倍数)是(的倍数)或是A B BA BB A A B A B A 1(111±±=±3121- 7131- 10191- 11151- 2、判断对错,并改正(二)分母是倍数关系、且分子都为1的分数加减法。
知识点:如果分母是倍数关系,且分子都为1,那么这两个分数相加减后的得数的分母就是这两个分母中较大的那一个,分子就为这两个分母的倍数加减1。
例:分母是倍数关系、且分子都为1的分数加法。
103101210151=+=+ (讲解:因为5和10分别为10151和的分母,且他们是倍数关系,又因为10是5的2倍,所以得数的分母是10,分子为2+1,即3.)例:分母是倍数关系、且分子都为1的分数减法。
101101210151=-=- (讲解:因为5和10分别为10151和的分母,且他们是倍数关系,又因为10是5的2倍,所以得数的分母是10,分子为2-1,即1.)练习:1、计算 4121- 15151- 511171- 4121+ 15151+ 511171+2、判断对错,并改正 2012012401201=-=- 1212121111211111=+=+ (三)分子和分母是一般关系的分数加减法。
知识点:分子和分母是一般关系的分数加减法,我们在计算的时候必须将他们的分母化为相同的数,即找到这几个分数的分母的最小公倍数,然后进行通分,最后再相加减。
例 =⨯⨯+⨯⨯=+2621343361439211121212+= 讲解:因为4和6是一般关系,所以在计算时,我们要找到4和6的最小公倍数,即12,通过分数的基本性质,所以31114612+=例 313312927464362121212⨯⨯-=-=-=⨯⨯ 讲解:因为4和6是一般关系,所以在计算时,我们要找到4和6的最小公倍数,即12,通过分数的基本性质,所以3174612-=练习:1、计算 7586- 5164- 8495- 91166- 7586+ 5164+ 8495+ 91166+2、判断对错,并改正 31214102010-== 71731421425868364242448⨯⨯+=+=+=⨯⨯ (四)分子不为1的异分母加减法知识点:在计算分子不为1的异分母加减法中,我们一般得通过以下几个步骤: (1)找到这几个分母的最小公倍数。
(2)通分(即将分母化为同一个数) (3)相加减(4)不是最简分数的必须约分。
注意:在计算分数的加减法时,得数不是最简分数的必须约分例:2334+ 例:1126+(1)找最小公倍数:3和4的最小公倍数是1 (1)找最小公倍数:2和6的最小公倍数是6(2)通分:224833412333944312⨯==⨯⨯==⨯ (2)通分:1133223611116616⨯==⨯⨯==⨯(3)相加:8917121212+= (3)相加:314666+=(4)约分44226623÷==÷ 练习:1、计算 3247+ 5264+ 8195+ 6275+ 3247- 5264- 8195- 6275-2、看图填空3、填空(1)异分母分数相加减,先(),然后按照()法则进行计算.(2)分数的分母不同,就是()不相同,不能直接相加减,要先(),化成()分数再加减.(3)分数加减法的验算方法与整数加减法的验算方法().(4)4、列式计算.(1)27与45的和是多少?(2)511减去413的差是多少?(五)含带分数的分数加减法知识点:带分数相加减,先把整数部分和分数部分分别相加减,再把所得的数合并起来。
复习:1、2、3、例1、+=()()()()()+ +例2、 例3、(分数部分不够减借1) (分数部分不够减借1)例4、(一次借2,连续减才够减)注意:在带分数减法中,从被减数的整数部分借“1”或借“2”的计算,应该说是比较复杂的,因此要多多练习,计算中要特别认真、仔细,否则容易出错。
练习:(六)分数加减法方程例1、3261=+x 例2、9172=-x 例3、9183=-x 例4、51141=+x练习:153352=-x 91121=+x 5335=-x 91175=+x(七)分数加减混合运算341455341()455314314++=++=+=知识点:分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同.没有括号的分数加减混合运算顺序是从左往右依次计算 ;有括号的分数加减混合运算的运算顺序是先算括号里面的,后算括号外面的。
注意:计算三个分数的加减法时,一般情况是先把三个分数一次通分,然后再计算。
在计算三个带分数减法时,通分后要观察是否需要从整数部分借“1”,若借“1”不够,最后一次借“2”。
例练习:三、分数加减法的简便运算加法运算定律有哪些:(1)加法交换律:a+b=b+a (2)加法结合律:a+b+c=a+(b+c) 减法运算定律有哪些:连减的性质:(1)a-b-c=a-(b+c) (2)a-(b+c)=a-b-c其他:(1)a-b+c=a+c-b (2)a-(b-c)=a-b+c (3)a-b+c-d=(a+c)-(b+d) 这些运算定律在分数的加减法简便运算中同样适用,因此,分数的加减法简便运算和整数的加减法简便运算一样。
(一)加法结合律:a+b+c=a+(b+c)例:7212833--7212()833=-+7218=-718=练习:234577++ 184595++ 1312242++ 12131744++(二)减法的连减:a-b-c=a-(b+c) 例:练习: 24312544-- 9111688-- 712633--(三)减法的连减:a-(b+c)=a-b-c例:511()44551144511545-+=--=-=练习:1511()16162-+ 2761()282814-+ 4413()557-+(四)a-b+c=a+c-b例 :53274752377431414-+=+-=-=练习:1313757-+ 114111412512-+ 11175761276-+(五)a-(b-c)=a-b+c例: 1152()2261152226526526--=-+=+=练习:311()445-- 31112(10)454-- 511()665--(六)a-b+c-d=(a+c)-(b+d)例:323345453323()()445561464442412-+-=+-+=-=-==练习:172111183183-+- 51116262-+- 841619595-+-分数加减法练习题一、口算。
=+5251 =-8385 =+3121 =-2143 =+8381 =+3195 =-10121 =+15153 =+18198 =+114117 =-3265 =-411二、填空。
(1)2个101是( ),107里面有( )个101。
(2)比3米短21米是( )米,87米比( )米长21米。
(3)分数单位是51的所有最简真分数的和是( )。
(4)()()()8242424765=+=+ ()()()()31155215=-=- (5)一个最简真分数,分子与分母相差2,它们的最小公倍数是63,这个分数是( ) ,它与721的差是( ).(6)有三个分母是21的最简真分数,它们的和是2120,这三个真分数可能是( )、( )、( )。
