第五章 无失真信源编码-习题课-2013
合集下载
第五章 信源编码-习题答案
00000000 8 0 5.6 有二元平稳马氏链，已知 p(0/0) = 0.8，p(1/1) = 0.7，求它的符号熵。用三个符号合成一个来编写二进 制哈夫曼码，求新符号的平均码字长度和编码效率。 5.7 对题 5.6 的信源进行游程编码。若“0”游程长度的截至值为 16， “1”游程长度的截至值为 8，求编码 效率。 5.8 选择帧长 N = 64 (1) 对 0010000000000000000000000000000001000000000000000000000000000000 遍 L-D 码； (2) 对 1000010000101100000000010010000101001000000001110000010000000010 遍 L-D 码再译码； (3) 对 0000000000000000000000000000000000000000000000000000000000000000 遍 L-D 码； (4) 对 10100011010111000110001110100110000111101100101000110101011010010 遍 L-D 码； (5) 对上述结果进行讨论。
x3 x4 x5 x 6 x 7 X x1 x2 5.1 设信源 P ( X ) 0.2 0.19 0.18 0.17 0.15 0.1 0.01
(1) 求信源熵 H(X)； (2) 编二进制香农码； (3) 计算平均码长和编码效率。
解： (1)
H ( X ) p ( xi ) log 2 p( xi )
K ki p( xi ) 3 0.2 3 0.19 3 0.18 3 0.17 3 0.15 4 0.1 7 0.01
李梅李亦农《信息论基础教程》-教案-第五章无失真信源编码PPT课件
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 0 s 2 11 s 3 00 s 4 11
译码
s2
11
s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
2) 非奇异码
s1 0 s 2 10 s 3 00 s 4 01
二次扩展信源符号
sj(j1,2,...,16)
s1 s1s1 s2 s1s2 s3 s1s3
二次扩展码码字
wj(j1,2,...,16)
w1 w1w1 00 w2w1w2001 w3w1w30001
s16 s4s4
w 16w 4w 4111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语
编码器输出的码符号序列 w i 称为码字；长度 l i 称为码
字长度，简称码长；全体码字的集合C称为码。 若码符号集合为X={0,1}，则所得的码字都是二元序
列，称为二元码。
将信源符号集中的每个信源符号 s i 固定的映射成某
一个码字 w i ，这样的码称为分组码。
若一个码中所有码字的码长都相等，则称为定长码； 否则为变长码。
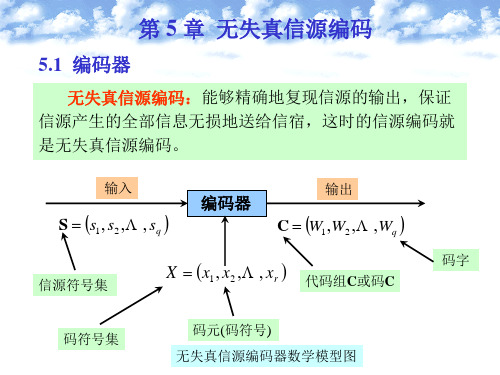
Ss1 ,s2, ,sq
编码器
C{w1,w2, ,wq}
X:{x1,x2,..x.r,}
码字 wi xi1xi2 xili
将信源符号集中的符号s （i 或者长为N的信源符号序
列）映射成由码符号x i 组成的长度为l i 的一一对应的码
符号序列w i 。
第五章：无失真信源编码
信息论基础与应用-李梅-第五章 无失真信源编码解析
s1 s1s1 s 2 s1s2 s3 s1s3 s16 s4 s4
二次扩展码码字 w j ( j 1, 2,...,16)
w1 w1w1 00 w 2 w1w2 001 w3 w1w3 0001 w16 w4 w4 111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语
编码器输出的码符号序列 wi称为码字；长度 li 称为码 字长度，简称码长；全体码字的集合C称为码。 若码符号集合为X={0,1}，则所得的码字都是二元序 列，称为二元码。
将信源符号集中的每个信源符号
si 固定的映射成某
一个码字 wi ，这样的码称为分组码。
码字与信源符号一一对应
2) 不同的信源符号序列对应不同的码字序列
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 s2 s3 s4
0 11 00 Байду номын сангаас1
译码 11
s2 s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
译码 0 0 0 1 1 0 1 1
s1s2 s3 s4
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续5）
4)
唯一可译码 1 1 0 1 0 0 1 0 0 0 0
s1 s2
1 10
1 0
1
s2 / s3 ?
s3 100 s4 1000
为非即时码
第五章：无失真信源编码
一、信源编码的相关概念
二次扩展码码字 w j ( j 1, 2,...,16)
w1 w1w1 00 w 2 w1w2 001 w3 w1w3 0001 w16 w4 w4 111111
第五章：无失真信源编码
一、信源编码的相关概念
4. 关于编码的一些术语
编码器输出的码符号序列 wi称为码字；长度 li 称为码 字长度，简称码长；全体码字的集合C称为码。 若码符号集合为X={0,1}，则所得的码字都是二元序 列，称为二元码。
将信源符号集中的每个信源符号
si 固定的映射成某
一个码字 wi ，这样的码称为分组码。
码字与信源符号一一对应
2) 不同的信源符号序列对应不同的码字序列
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续2）
例1：
1) 奇异码
s1 s2 s3 s4
0 11 00 Байду номын сангаас1
译码 11
s2 s4
奇异码一定不是唯一可译码
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续3）
译码 0 0 0 1 1 0 1 1
s1s2 s3 s4
第五章：无失真信源编码
一、信源编码的相关概念
6. 唯一可译性（续5）
4)
唯一可译码 1 1 0 1 0 0 1 0 0 0 0
s1 s2
1 10
1 0
1
s2 / s3 ?
s3 100 s4 1000
为非即时码
第五章：无失真信源编码
一、信源编码的相关概念
信息论第五章 信源编码习题答案
0
1111110
7
x8
0.0078125
1
1111111
7
(3)
香农编码效率：
费诺编码效率：
(4)
xi
p(xi)
编码
码字
ki
x1
0.5
0
0
1
x2
0.25
1
1
1
x3
0.125
2
0
20
2
x4
0.0625
1
21
2
x5
0.03125
2
0
220
3
x6
0.015625
1
221
3
x7
0.0078125
2
0
2220
100
x5
0.15
0.74
3
101
x6
0.1
0.89
4
1110
x7
0.01
0.99
7
1111110
1)
0.0 --- 0.000000
2)
0.2*2 = 0.4 0
0.4*2 = 0.8 0
0.8*2 = 1.6 1
3)
0.39 * 2 = 0.78 0
0.78 * 2 = 1.56 1
0.56 * 2 = 1.12 ki
x1
0.2
0
0
00
2
x2
0.19
1
0
010
3
x3
0.18
1
011
3
x4
0.17
1
0
10
2
x5
0.15
1
1111110
7
x8
0.0078125
1
1111111
7
(3)
香农编码效率：
费诺编码效率：
(4)
xi
p(xi)
编码
码字
ki
x1
0.5
0
0
1
x2
0.25
1
1
1
x3
0.125
2
0
20
2
x4
0.0625
1
21
2
x5
0.03125
2
0
220
3
x6
0.015625
1
221
3
x7
0.0078125
2
0
2220
100
x5
0.15
0.74
3
101
x6
0.1
0.89
4
1110
x7
0.01
0.99
7
1111110
1)
0.0 --- 0.000000
2)
0.2*2 = 0.4 0
0.4*2 = 0.8 0
0.8*2 = 1.6 1
3)
0.39 * 2 = 0.78 0
0.78 * 2 = 1.56 1
0.56 * 2 = 1.12 ki
x1
0.2
0
0
00
2
x2
0.19
1
0
010
3
x3
0.18
1
011
3
x4
0.17
1
0
10
2
x5
0.15
1
第5章-无失真信源编码-题与答案
码字中有2个“1”，错误概率：
码字中有3个“1”，错误概率：
5.9设有离散无记忆信源
码符号集 ，现对该信源 进行三元哈夫曼编码，试求信源熵 ，码平均长度 和编码效率 。
解：
满树叶子节点的个数： ， ，不能构成满树。
11
222
212
202
022
012
0003
0013
5.1有一信源，它有6个可能的输出，其概率分布如题5.1表所示，表中给出了对应的码 和 。
题表 5.1
消息
p(ai)
A
B
C
D
E
F
a1
1/2
000
0
0
0
0
0
a2
1/4
001
01
10
10
10
100
a3
1/16
010
011
110
110
1100
101
a4
1/16
011
0Hale Waihona Puke 1111101110
1101
110
a5
(1) 求码字所需要的长度；
(2) 考虑没有给予编码的信源序列出现的概率，该等长码引起的错误概率 是多少？
解：
(1)
码字中有0个“1”，码字的个数：
码字中有1个“1”，码字的个数：
码字中有2个“1”，码字的个数：
码字中有3个“1”，码字的个数：
(2)
码字中有0个“1”，错误概率：
码字中有1个“1”，错误概率：
1/16
100
01111
11110
1011
1100
111
a6
1/16
码字中有3个“1”，错误概率：
5.9设有离散无记忆信源
码符号集 ，现对该信源 进行三元哈夫曼编码，试求信源熵 ，码平均长度 和编码效率 。
解：
满树叶子节点的个数： ， ，不能构成满树。
11
222
212
202
022
012
0003
0013
5.1有一信源，它有6个可能的输出，其概率分布如题5.1表所示，表中给出了对应的码 和 。
题表 5.1
消息
p(ai)
A
B
C
D
E
F
a1
1/2
000
0
0
0
0
0
a2
1/4
001
01
10
10
10
100
a3
1/16
010
011
110
110
1100
101
a4
1/16
011
0Hale Waihona Puke 1111101110
1101
110
a5
(1) 求码字所需要的长度；
(2) 考虑没有给予编码的信源序列出现的概率，该等长码引起的错误概率 是多少？
解：
(1)
码字中有0个“1”，码字的个数：
码字中有1个“1”，码字的个数：
码字中有2个“1”，码字的个数：
码字中有3个“1”，码字的个数：
(2)
码字中有0个“1”，错误概率：
码字中有1个“1”，错误概率：
1/16
100
01111
11110
1011
1100
111
a6
1/16
信息论基础第5章无失真信源编码
进行霍夫曼编码时，应把合并后的概率总是放在 其他相同概率的信源符号之上，以得到码长方差最小 的码。
r 元霍夫曼编码步骤：
1) 验证所给 q 是否满足 q (r 1) r ，若不满足该式，
可以人为地增加 t 个概率为零的符号，满足式
n (r 1) r ，以使最后一步有 r 个信源符号；
2) 取概率最小的 r 个符号合并成一个新符号，并分别用 0， 1，…，(r 1) 给各分支赋值，把这些符号的概率相加作为该新 符号的概率；
上述不等式只是即时码存在的充要条件，而不能作为判别的依据。
需要注意的是，克拉夫特不等式是即时码存在的充要条件，而 不能作为判别的依据。后来麦克米伦（B. McMillan）证明唯一可译 码也满足克拉夫特不等式。这说明在码长选择的条件上，即时码与 唯一可译码是一致的。
【例】 对于二元码，即 r 2 ，如果 q 4 ， L1 2 ， L2 2 ，
原始信源普遍存在剩余度，香农信息论认为信源的剩余度主 要来自两个方面：一是信源符号间的相关性，二是信源符号概率 分布的不均匀性。为了去除信源剩余度，提高信源的信息传输率， 必须对信源进行压缩编码。
目前去除信源符号间相关性的主要方法是预测编码和变换编 码，而去除信源符号概率分布不均匀性的主要方法是统计编码。
《信息论基础》
第5章 无失真信源编码
第 2 章已经讨论了离散信源的信息度量—信源熵， 本章将讨论信源的另一个重要问题：如何对信源的输出 进行适当的编码，才能用尽可能少的码元来表示信源信 息，做到以最大的信息传输率无差错地传输信息呢？即 无失真信源编码，它解决的是通信的有效性问题。
本章将首先介绍信源编码器；然后从理论上阐述无 失真信源编码定理，得出“平均码长的理论极限值就是
r 元霍夫曼编码步骤：
1) 验证所给 q 是否满足 q (r 1) r ，若不满足该式，
可以人为地增加 t 个概率为零的符号，满足式
n (r 1) r ，以使最后一步有 r 个信源符号；
2) 取概率最小的 r 个符号合并成一个新符号，并分别用 0， 1，…，(r 1) 给各分支赋值，把这些符号的概率相加作为该新 符号的概率；
上述不等式只是即时码存在的充要条件，而不能作为判别的依据。
需要注意的是，克拉夫特不等式是即时码存在的充要条件，而 不能作为判别的依据。后来麦克米伦（B. McMillan）证明唯一可译 码也满足克拉夫特不等式。这说明在码长选择的条件上，即时码与 唯一可译码是一致的。
【例】 对于二元码，即 r 2 ，如果 q 4 ， L1 2 ， L2 2 ，
原始信源普遍存在剩余度，香农信息论认为信源的剩余度主 要来自两个方面：一是信源符号间的相关性，二是信源符号概率 分布的不均匀性。为了去除信源剩余度，提高信源的信息传输率， 必须对信源进行压缩编码。
目前去除信源符号间相关性的主要方法是预测编码和变换编 码，而去除信源符号概率分布不均匀性的主要方法是统计编码。
《信息论基础》
第5章 无失真信源编码
第 2 章已经讨论了离散信源的信息度量—信源熵， 本章将讨论信源的另一个重要问题：如何对信源的输出 进行适当的编码，才能用尽可能少的码元来表示信源信 息，做到以最大的信息传输率无差错地传输信息呢？即 无失真信源编码，它解决的是通信的有效性问题。
本章将首先介绍信源编码器；然后从理论上阐述无 失真信源编码定理，得出“平均码长的理论极限值就是
(信息论)第5章无失真信源编码
这就是说，每个英文电报符号至少要用5位二元符号进行 编码才能得到唯一可译码。 12
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q
N N
现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。
以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p
定长编码定理
定长信源编码定理讨论了编码的有关参数对译 码差错的限制关系
sq p s q
定理 5.3.1 设离散无记忆信源
S s1 P p s 1 p s 2 s2
的熵为H S ，其 N 次扩展信源为
S N 1 p 1 P
2 q p 2 p q
N N
现在用码符号集 X x1 , x2 ,, xr 对N次扩展信源 S N 进行长度为 l 的定长编码，对于 0, 0 ，只要满足
l H S N log r
则当 N 足够大时，译码错误概率为任意小，几乎可以实 现无失真编码。 反之，若满足
l H S 2 N log r
则不可能实现无失真编码。而当N足够大时，译码错误概 14 率近似等于1。
以上的定理5.3.1 和定理5.3.2实际上说明的是一个 问题，虽然该定理是在平稳无记忆离散信源的条件下 证明的，但它也同样适合于平稳有记忆信源，只要要 2 求有记忆信源的极限熵 H S 和极限方差 存在 即可。对于平稳有记忆信源，式(5.6)和式(5.7 ) 中 H S 应该为极限熵 H S 。
变长码(可变长度码)
2
奇异码：若码中所有码字都不相同，则称此码为非
奇异码。反之，称为奇异码。
同价码：每个码符号所占的传输时间都相同的码。定
长码中每个码字的传输时间相同。而变长码中的每个码 字的传输时间不一定相等。
表 5.1
信源符号si
信源符号出现概率 si p
信息论与编码第五章课后习题答案
第五章课后习题【5.1】某信源按43)0(=P ，41)1(=P 的概率产生统计独立的二元序列。
（1）试求0N ，使当0N N >时有01.005.0)()(≤≥−S H N I P i α 式中，)(S H 是信源的熵。
（2）试求当0N N =时典型序列集N G ε中含有的信源序列个数。
解：（1）该信源的信源熵为811.0)(log )()(=−=∑i i s p s p S H 比特/符号自信息的方差为4715.0811.04log 4134log 43)()]([)]([22222=−+=−=S H s I E s I D i i 根据等长码编码定理，我们知道δεα−≤≥−1)()(S H N I P i 根据给定条件可知，05.0=ε，99.0=δ。
而[]2)(εδN s I D i =因此[]5.19099.0*05.04715.0)(220==≥δεi s I D N 取1910=N 。
（2）ε典型序列中信源序列个数取值范围为：])([])([22)1(εεεδ+−<<−S H N N S H N G代入上述数值得451.164351.1452201.0<<×N G ε【5.2】有一信源，它有六个可能的输出，其概率分布如下表所示，表中给出了对应的码A 、B 、C 、D 、E 和F 。
表5.2消息 )(i a P A B C D E F 1a 1/2 000 0 0 0 0 0 2a 1/4 001 01 10 10 10 100 3a 1/16 010 011 110 110 1100 101 4a 1/16 011 0111 1110 1110 1101 110 5a 1/16 100 01111 11110 1011 1110 111 6a1/1610101111111111011011111011（1） 求这些码中哪些是惟一可译码； （2） 求哪些码是非延长码（即时码）； （3） 求对所有惟一可译码求出其平均码长L 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
R log M n
19
4
“码长”与“唯一可译码/即时码是否存在”之间关系
Kraft 和 McMillan不等式 q
r li 1
i 1
5
3 定长编码
唯一可译定长码的存在条件
码字需要满足的条件
r、l、q需要满足的关系
定长编码定理
ε典型序列集的性质（渐近等分割性）
这类序列出现的概率趋于1 每个典型序列接近等概分布2-NH(S) 序列数目占信源序列的比值很小
要求：平均码长必须相等
方差计算公式、方差的含义
2
q
pi
li
L
2
i 1
8
作业讲解 - 8
定长编码定理的应用
如何定义待编码的序列个数？
长度100的序列中含有3个或小于3个‘1’的序列
如何确定译码错误？
未参与编码的序列的出现概率
9
补充作业 （10分）有下列三种码字长度： 码长 l1 l2 l3 l4 l5
C1 2 1 2 4 1 C2 2 2 2 3 1 C3 1 4 6 1 1 1. 设编码符号集为X＝{0, 1, 2}，上表中哪种
码长可用来构造出唯一可译码？ 2. 对每种可用的码长，构造出一个即时码。
10
作业讲解 – 3.5
1. “消息的符号熵”就是“信源熵”
2. “平均码长”和“二进制码的熵”
4. 若每秒可以传输100个码元，则上述三种情
况对于的编码后的码元个数与传输时间如
下所示
300 3s
17
相关重要公式
返回
q
平均码长
:
L
psi
l
码符号
i
/
信源符号
i 1
编码后的信息传输率: R HX HS比特/码符号
L
编码效率 : R H S / L Hr S H S
编码器
代码组C / 码C
C W1,W2 ,,Wq
码符号集
X :{x1, x2 ,..., xr}
码元 / 码符号
r元码
码字
平均码长
Wi xi1 xi2 xili
ቤተ መጻሕፍቲ ባይዱ码长
L p si li 定长码、变长码；奇异码、非奇异码
i
4
2 分组码
分组码：将信源符号集中的每个信源符号映射成一个 固定的码字 。
S
PS
A 0.4
B 0.2
C 0.2
D 0.1
E 0.06
F 0.02
G 0.02
3. 考虑像素间的依赖关系后，根据平均码长界定定 理和香农第一定理可知：平均码长会进一步降低
另：从信源的剩余度亦可分析还存在压缩空间
信源 符号
AB
AC
AD
EC
FC
GC
概率
码字
码长
16
作业讲解 – 补充（续）
编码过程 树根在上面； 每个节点都要圈起来，圈内
标明对应的信源符号或概率值。 编码结果要给出 所得码字一定是即时码
5.3、最佳二元和三元码
Huffman码 – 最佳码、紧致码 多元Huffman编码的注意事项！
12
2
作业讲解 – 6、12
5.6、给定信源符号集
1. 信源熵、信息传输率
实际熵
实际编码，每个信源
7
符号需要的码元数
作业讲解 – 1、15
5.1、对给定信源的六种编码结果
唯一可译码、即时码如何判断
必须有过程！即时码是唯一可译码的子集！
平均码长的求解
5.15、对给定信源构造两种不同的即时码
如何构造即时码 – 树图法
只能选择叶子节点作为码字 – 杜绝前缀！
H(S) LN H(S) 1 log r N log r N
编码算法
lim LN N N
Hr(S)
Huffman - 二元/多元、Fano、香农编码
编码过程、生成码字、编码效率
H S / L Hr S H S
log r
L L *log r
信息传输率的小结
2. Huffman编码及编码效率
5.12、对Huffman编码方法的练习巩固
1. 信源熵和信源剩余度 – 第三章内容 2. 单符号信源的紧致码及平均码长 3. 对N次扩展信源生成紧致码，当N=2、3、
无穷时对应的平均码长（单符号）？ 4. N=1, 2, 3时对应的编码效率和码剩余度
l H(S)
l H (S)－2
N log r
N log r
6
1
4 变长编码方法 – 匹配编码
基本概念
最佳码/紧致码、信息传输率、编码效率、码剩余度
重要定理
平均码长界定定理
H(S) L H(S) 1
log r
log r
变长无失真信源编码定理 – 香农第一定理
log r log r
L L *log r
码剩余度 : 1
18
3
各章涉及到的“信息传输率” 返回
第四章：信道的信息传输率
R I X ;Y Rt C
第五章：信源编码后的信息传输率
定长编码
R l log r N
变长编码 R H S
L
第六章：信道编码后的信息传输率
第五章 无失真信源编码
复习、作业讲解
1.1、概述 – 编码器概论
信源编码 – 有效地表示
使信源适合于信道的传输，用信道能传输 的符号来代表信源发出的消息。
在不失真或允许一定失真的条件下，用尽 可能少的符号来传递信源消息。
信源编码目的 – 提高通信有效性
通常通过压缩信源的冗余度来实现。 采用的一般方法是压缩每个信源符号的平
均比特数。
2
1.1、概述 – 信源编码器模型
信源编码：将信源符号序列按一定的数 学规律映射成码符号序列的过程。
S s1 , s2 , , sq
X {x1, x2,, xr}
S
信源
X
X’
S’
编码器
信道
译码器
信宿
信源编码器模型
3
1.2、概述 – 基本术语
信源符号集
S s1, s2,, sq
随着参与编码的消息个数的增加 （N=2，3，……），编码输出的‘0’和‘1’ 趋近等概出现；编码后的信息传输率也 增大了，编码效率……
对于常见的对称信道，等概出现时，信 道实际传输的信息量可达到信道容量！
15
作业讲解 – 补充
1. 二进制等长编码，则 q rl l 3
2. 霍夫曼编码：信源的概率空间如下
1.6218 1.6875
0.9611
bit / 二元符号
编码后发出i‘0’、‘1’码元的无条件概率
p0
i
psi
* si 对应码字含有'0' 码元的个数
9 16
3 16
3 16
5
L2
27
149
16
作业讲解 – 5.11的说明
可以定义新信源，也可以看作原信源的 扩展信源。区别：符号的写法不同。
3. 求0、1出现的无条件概率
p0
pu0
1
pu1 1
pu2
1/
L
1 2
p1
pu1 1
pu2
2
pu3
3/
L
1 2
或者：令N个信源符号参与编码，计算按 照该编码方法编码后所获得的0和1的个 数，即可计算对应的概率。
11
作业讲解 – Huffman编码 树图法表示Huffman编码过程，要求：
唯一可译码：任意一串有限长的码符号序列只能被唯一地译
为对应的信源符号序列，则此码为唯一可译码。没有二义性
充要条件：编码的任意次扩展均为非奇异码 如何判别：
即时码：唯一可译码接收到一个完整码字后，无需参 考后续的码符号就能立即译码。
如何判别：唯一可译码 + 无前缀；单独无前缀亦可 如何构造：树图法
13
作业讲解 – 7、11
5.7、香农码 － log4 = 2
各信源符号的自信息是用于确定对应码字的长 度，不需要算出一个确切的数值。
5.11、Fano和Huffman编码
“二重延长” = 二次扩展消息
编码后的平均传输率
R H S 2 L2
2* H S psi li