第七节 驻波
驻波产生及消除

Fig. 6. Schematic diagram of the locations of the simulated four foci. The geometric focus of the phased array is located at the location, 3. The locationof sonication points, 1, 2, and 4 are [−12, −6, 6] mm from the geometric focus (3 ) on the acoustic axis, z.
Fig. 9. Comparison of the normalize pressure field measurements and sim ulation results. (a) 72 (apodization: 37.5%) element and (b) full (apodization: 100%) phased array.
Figure 4. Two-dimensional distribution of the ultrasound passing through a temporal bone fragment. The diagrams (a)–(d) are sinusoidal activation cases, and the diagrams (e)–(h) are RSBIC activation cases. The activating voltage was 50 Vpp. The other parameters are the same as those in Figure 3.
Fig. 10. Simulation results of sagittal views of the normalized pressure amplitude diቤተ መጻሕፍቲ ባይዱtribution inside the skull for eight different apodization levels when the focus is located at the geometric focus of the hemispherical phased array: (a) 12.5%, (b) 25.0%, (c) 37.5%, (d) 50.0%, (e) 62.5%, (f) 75.0%, (g) 87.5%,and (h) 100% apodization.
大学物理驻波

以柔软细绳中的横波为例
⏹波的能量密度w:波传播时,单位体积介质中所
储存的波的能量.
⏹波的能流密度I:波传播时,单位时间内通过垂
直于波的传播方向单位面积的
体积介质中所波的能量.
⏹对于简谐波,两者关系为:I=uw
简谐波的能量密度和能流密度
⏹机械波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率平方成正比.
⏹电磁波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率无关.
⏹在介质中任意一点,简谐机械波的动能与势能都是同相位振动的;在真空中传播的简谐电磁波的电场能和磁场能在任意一点都是同相位振动的.
波的叠加原理
当几列波在介质中某点相遇时,该点的振动位移是各列波单独存在时在该点引起的位移的叠加
波的叠加原理举例驻波(standing waves)
122cos cos x y y y A t u
ωω=+=1cos ()x y A t u ω=-2cos ()x y A t u
ω=+
驻波
⏹形成驻波的条件:两列简谐波
✓频率相同;
✓振幅相同;
✓振动方向相同;
✓在同一媒介中相向传播,叠加而形成逐波.⏹驻波的现象:
✓相邻波节(或波腹)的间距为二分之一波长;✓相邻波节与波腹的间距为四分之一波长;
✓相邻两波节之间各点(称为一段)同相位振动;✓相邻两段的振动相位差为π.
驻波举例
位于A,B两点的两个简谐波源的振幅相同,频率都是100Hz,相位差为π.若A,B相距30m,波速为400m/s,求AB连线上因叠加而静止的各点的位置.
波的叠加原理举例驻波(standing waves)
拍(beats)。
大学物理课件--驻波

u 2d ν 2 0.153 1 080 m s 1 330m s 1
例21.4 一只二胡的“千斤”(弦上方固定点)和“码子” (弦下方固定点)之间的距离是L=0.3m。其上一根弦的质量线密 度为l=3.8×10-4kg/m,拉紧它的张力 F=9.4N。求此弦所发的声 音的基频是多少?此弦的三次谐频振动的节点在何处?
L
2 2
n =3
三次 谐频
3 2
边界情况不同,简正模式也不同:
L= n
n
4
L
L= n
n
2
L
n=1,3… n = 1
基频Βιβλιοθήκη n=1,3… n = 1n
1
1 4
基频
1
1 2
n = 3
三次 谐频
n = 3
3 2
三次 谐频
3
3
3 3 2
末端封闭的笛中的驻波
末端开放的笛中的驻波
一般地说,对于一个驻波体系存在无限多个本征频率和 简正模式。在这一体系中形成的任何实际的振动,都可以看成 是各种简正模式的线性叠加,其中每一种简正模式的位相和所 占比例的大小,则由初始扰动的性质决定。 当周期性驱动力的频率与驻波体系的某一简正频率相同时, 就会使该频率驻波的振幅变得最大,这种现象也称为共振。利 用共振方法可以测量空气中的声速。
2
r1 )
y2 Acos[t
半波损失
2
( r1
2
)]
例题2
一列沿x轴方向传播的入射波的波函数为
t x y Acos 2 ( ) ,在x=0处反射,反射点为一节点 T
驻波

频率和振幅均相同、振动方向一致、传播方向相反的两列波叠加后形成的波。
2.驻波形成条件:
产生驻波的条件是两个反射面之间平行,而且之间的距离是半波长的整数倍,这样可以形成两列相反方向的波的叠加,平均能流密度为0
3.相干性:
振动频率相同、相同 2.振动方向相同 3.相位相同或相位差恒定
4.高斯函数
高斯函数的形式为:
其中 a、b 与 c 为实数常数 ,且a > 0.
5.法布里-珀罗干涉仪
光谱分辨率极高的多光束干涉仪。由法国物理学家C.法布里和A.珀罗于1897 年发明 。
其结构如左图,M和M'是两块具有很小楔角的平板玻璃,相对两面互相平行,并涂有高反射率涂层,两板间用殷钢环隔离并固定。这种间距固定不变的干涉仪常称作标准具。入射光在相对两面上反复反射和折射后产生多束相干反射光和透射光,透射光束在透镜 L′的焦面上叠加,形成等倾圆环状干涉条纹。
驻波

相邻两波腹距离
3.相位特点
各质点作振幅为 2 A0 cos( 2 ) ,角频率为ω的简谐运动。
2 A0 cos2x / cost y 2 A0 cos2x / cost
x
cos2x / 0 cos2x / 0
0.4 sin x sin 200t
(3)在O与P间各个波节和波腹点的坐标.
y驻 0.4 sin x sin t
波节点的坐标满足:
x k , k取整数
考虑x的范围解得:x=0,1,2,3,4,5,6 波腹点的坐标满足: x 2k 1 , k取整数 2 1 3 5 7 9 11 考虑x的范围解得: x , , , , , . 2 2 2 2 2 2
作业:P172 (6.22)(6.25)
波节 (1) 两相邻波节间的点(同一段的点)
cos(2 x
x
) 符号相同,相位相同。
驻波波形曲线 分为很多“分段” (每段长λ/2 );
(2) 波节两边的点(相邻段的点)
cos( 2
)
符号相反,相位相反。
驻波相位不传播 ---"驻"字的第二层含义。
4.能量特点 (1)动能: 当各质点同时到达平衡位置时:介质无形变,势能 为零,此时驻波能量为动能。波腹处动能最大,驻 波能量集中在波腹附近。 (2)势能: 当各质点同时到达最大位移时:动能为零,此时驻波 能量为势能。波节处形变最大,势能最大,能量集中 在波节附近。 (3)结论: 动能、势能不断在波腹附近和波节附近间相互转换, 能量交替传递。
(素材取自酷6网)
二 、驻波方程
设有两列同振幅相干波在同一直线上相向传播
驻波_精品文档
t = 5T / 8
t = 3T / 4
t = 7T / 8
t = T
驻波的形成
在同一坐标系
XOY 中
正向波
反向波
驻波
点击鼠标,观察在一个周期T 中不同时刻各波的波形图。
每点击一次,
时间步进
正向波
反向波
合成驻波
驻波方程
为简明起见,
设
改写原式得
并用
由
正向波
反向波
驻 波 方 程
注意到三角函数关系
得
(1)振动滞后时间、相位和位移;
(2)振动滞后相位、时间和位移;
(3)振动位移及滞后时间、相位;
(4)振动滞后相位、振动位移及振动滞后时间。
请在放映状态下点击你认为是对的答案
平面谐波的方程为 y = A cos ω ( t - )
u
x
则
u
x
和
分别代表
u
x
ω
y
结束选择
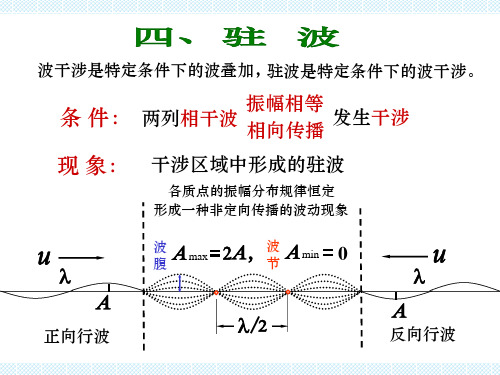
驻波
波干涉是特定条件下的波叠加,
驻波是特定条件下的波干涉。
条 件:
两列相干波
振幅相等
相向传播
发生干涉
现 象:
正向行波
反向行波
干涉区域中形成的驻波
各质点的振幅分布规律恒定
形成一种非定向传播的波动现象
max
min
0
波腹
波节
t = 0
t = T / 8
t = T / 4
t = 3T / 8
t = T / 2
驻 波 方 程
波腹、波节位置
为简明起见,
设
改写原式得
并用
由
正向波
反向波
驻 波 方 程
大学物理课件-驻波

波源的振动通过介质传递到另一 端,并被反射回来,形成驻波。
分类
按形成方式分类
可分为自由驻波和强制驻波。自由驻 波是由自由振动的波源产生的,而强 制驻波则是由外部力作用下的振动系 统产生的。
按节点数量分类
可分为一阶驻波、二阶驻波等。节点 数量越多,波形越复杂。
02
驻波的形成原理
BIG DATA EMPOWERS TO CREATE A NEW
液体和气体介质中的驻波
在液体和气体介质中,由于声速较低,驻波的波长较 长。与固体介质中的驻波相比,液体和气体中的驻波 振幅分布更加均匀,能量分布也更加广泛。
不同形状的驻波
要点一
矩形驻波
矩形驻波是指沿着传播方向上存在周期性变化的波形。在 矩形驻波中,波腹和波节的位置是固定的,振幅和相位在 空间中呈现周期性变化。
大学物理课件-驻波
BIG DATA EMPOWERS TO CREATE A NEW
ERA
• 驻波的概念 • 驻波的形成原理 • 驻波的应用 • 驻波实验 • 驻波的数学模型与计算 • 驻波的扩展知识
目录
CONTENTS
01
驻波的概念
BIG DATA EMPOWERS TO CREATE A NEW
波腹
在驻波中,有些位置的振动幅度最大,这些位置被称为波腹。波腹的位置由介质 和障碍物的性质共同决定。
弦的振动与驻波的关系
弦的振动
弦的振动可以产生驻波。当弦以一定的频率振动时,产生的 波动会在弦的两端反射,形成驻波。
弦的长度与驻波的关系
弦的长度必须是半波长的整数倍才能产生驻波。如果弦的长 度不是半波长的整数倍,则无法形成驻波。
乐器发声原理
弦乐器
七驻波·教案

七、驻波·教案教学目的1.知道驻波现象及什么是波节、波腹,驻波是一种特殊的干涉现象.2.理解驻波的形成过程,理解驻波与行波的区别,理解空气柱共鸣的条件.教具驻波演示仪、投影仪、水槽、音叉、玻璃管.教学过程●引入新课一列波在向前传播的途中遇到障碍物或者两种介质的分界面时,会发生反射,如果反射波和原来向前传播的波相互叠加,会发生什么现象呢?●进行新课【板书】*第七节驻波一、驻波【演示】如课本图10-31所示,把弦线的一端A固定在电磁打点计时器的振针上,另一端跨过定滑轮拴一个砝码盘,盘上放砝码,将弦线拉平.在靠近定滑轮的B处,用一个尖劈把弦线支起来.接通电磁打点计时器的电源,振针振动时,有一列波向定滑轮的一侧传播,并在B处发生反射.改变尖劈的位置,来调节AB的长度,当尖劈调到某适当位置时,可以看到,弦线会分段振动起来.仔细观察这时弦线振动情况(课本10-32),可以看到:【板书】1.波节——弦线上有些点始终是静止不动的,这些点叫做波节.波腹——在波节和波节之间的那段弦线上,各质点以相同的频率、相同的步调振动,但振幅不同,振幅最大的那些点叫做波腹.在相邻的两段弦线上,质点的振动方向是相反的.相邻的两个波节(或波腹)之间的距离等于半个波长,即等于λ/2.【板书】2.驻波——波形虽然随时间而改变,但是不向任何方向移动,这种现象叫做驻波.行波——驻波跟前面讲过的波形向前传播的那种波显然是不同的,相对于驻波来说波形向前传播的那种波叫行波.【板书】3.两列沿相反方向传播的振幅相同、频率相同的波叠加,形成驻波.【板书】4.振幅相同、频率相同波的叠加.课本10-33中用虚线表示两列沿相反方向传播的振幅相同、频率相同波的叠加,用实线表示这两列波叠加后形成的合成波.图中画出了每隔T/8周期波形的变化情况.由图可以看出,合成波在波节的位置(图中的“·”表示),位移始终为零.在两波节之间,各质点以相同的步调在振动,两波节之间的中点振幅最大,就是波腹(图中用“+”表示).由此可知,驻波有如下特点:【板书】5.驻波——特殊的干涉现象驻波也是一种波的干涉现象,但是一种特殊的干涉现象.其特殊性表现在两个方面:【板书】6.波源特殊驻波是由频率相同,振幅相同,振动方向相同,而传播方向相反的两列波叠加而成的.【板书】7.波形特殊波形虽然随时间而改变,但是不向任何方向移动,相邻两波节间质点运动方向一致,但振幅不同,波节两侧的质点振动方向总是相反.从上述弦线上驻波的形成来看,可以认为驻波是一种特殊的干涉现象.从驻波的振动情况来看,可以认为驻波是组成弦线的无数有相互联系的质点的一种振动模式.实际上,只要设法激起弦线的振动(弹、拉、打击等),就能在弦线上产生驻波,并在周围空气中发出声波,这就是弦乐器发声的原理.管乐器是否是这样呢?【演示】在盛有水的容器中插入一根粗玻璃管,管口上方放一个正在发声的音叉,慢慢向上提起玻璃管,当管内空气柱达到一定长度时,可以听到空气柱发出较强的声音这时,从音叉发出并进入玻璃管的声波和经水面反射回来的反射波相互叠加,在空气柱内产生驻波,玻璃管开口处为波腹,水面处为波节,空气柱的长度l=λ/4、l=3λ/4、l=5λ/4时.课本图10-34(乙、丙、丁),都会产生驻波.【板书】8.空气柱产生驻波条件l=(2n+1)/4(n=0,1,2,3……)空气柱内的驻波可看作空气柱的一种振动模式,所以上述现象可看作音叉和空气柱发生了共鸣.实际上,只要设法激起空气柱的振动(如吹奏),就能使空气柱产生驻波,并在周围空气中发出声波,这就是管乐器发声的原理.在上述实验中,如果测出空气柱的长度l,就可以测出声波的波长λ.如果已知音叉的频率f,还可测出声波的速度v=λf.【例】一玻璃管坚直插入一水槽中,在玻璃管上端有一发声音叉,频率为200Hz,上下移动玻璃管,测到相邻两次共鸣时管中空气柱的长度差为34 cm,如课本图10-34所示,试求声速.分析与解:由于玻璃管中的空气要产生共鸣,空气柱长L等于λ/4的奇数倍,因此相邻两次共鸣的空气柱长度差:△L=λ/2 根据:△L=λ/2=34cm 所以:λ=68cm=0.68m 又:v=λ/T=λf=0.68×500=340 m/s●巩固练习(1)对着一只空罐子唱歌,当唱到某一单调(即某一频率)时,声音会特别响亮,同时罐子会发生振动,这是什么缘故?(2)课本图10-34甲所示的情景中,如果音叉的频率是400Hz,管在水面上的部分至少为多长时,管内空气柱会产生共鸣?(设这时空气中的声速为340 m/s)●作业1.复习本节课文.2.课本练习五第(1)、(2)题.参考题(1)驻波的说法正确的是:[ ] A.两列向相反方向传播的波叠加就一定会产生驻波B.在驻波中有些质点始终静止不动;相邻的两个这样的质点的距离相距半个波长C.驻波各质点都有相同的振幅D.驻波中各质点的振动频率相同(2)说法正确的是:[ ] A.波节处质点始终静止B.波腹处质点的振幅最大C.波腹处质点的位移有时可能为零D.相邻的两个波节之间的距离为一个波长(3)如图10-23所示,在弦上的A、B两点间形成了如图所示的驻波,且两点间距离7.5m,则波长为:[ ] A.1mB.1.5mC.3mD.4m(4)弦ab之间某时刻形成的驻波如图10-24所示,那么经过半个周期后波形应是下图中的哪一个?[ ](5)驻波与行波的区别是[ ] A.驻波中的质点振动形式不向外传播,而行波的波形则外传播B.行波在传播过程中,质点沿波前进的方向移动,而驻波不同C.行波向外传播能量,而驻波不向外传播能量D.在形成驻波的区域内,存在着所有质点位移都为零的时刻,而行波在传播过程中不存在这样的时刻.(6)如图10-25所示,在玻璃管的上端有振动频率未知的音叉,现使音叉发声,并将玻璃管上提,当玻璃管口离水面距离为17cm,则刚好能听到空气柱共鸣(已知声音在空气中传播速度v=340 m/s),则音叉的频率为:[ ] A.200 HzB.1000 HzC.500 HzD.100 Hz说明驻波与行波的区别1.物理意义不同:驻波是两列波的特殊干涉现象,行波是一列波在介质中的传播.2.质点振动不同:相邻波节间质点运动方向一致.波节两侧质点振动方向总相反.3.波形不同:波形向前传播的是行波,波形不向任何方向传播的是驻波.天津市武清区杨村一中郎荣福。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*第七节驻波
学习目标:
1.知道驻波现象,知道波腹和波节.
2.知道驻波是怎样产生的.
3.知道驻波是一种特殊的干涉现象.
学习重点:驻波的概念及产生
学习难点:驻波的形成过程.
学习内容:
一、驻波
1.波节和波腹
(1)波节:以弦线驻波为例,弦线上始终静止不动的点叫做波节.
(2)在波节和波节之间,振幅最大的那些点叫做波腹.
2.在相邻的两波节和波节之间,质点振动方向是相反的,相邻的两个波节(或波腹)之间的距离等于半个波长.即λ/2
3.驻波:两列波沿相反方向传播的振幅相同,频率相同的波的叠加时形成的波叫做驻波.
4.驻波的形成是两列波沿相反方向传播的振幅相同,频率相同的波叠加的结果.
二、驻波是一种特殊的干涉现象
1.波源特性:驻波是由频率相同、振幅相同而传播方向相的两列波的叠加而成.
2.波形特殊:波形虽然随时间而改变,但不向任何方向移动.
三、空气柱内的驻波
1.空气柱内产生驻波的条件:空气柱的长度l跟声波波长λ间满足l=(2n+1)λ/4时,在空气柱内产生驻波.(n =0、1、2、3……)
2.利用空气柱内产生的驻波能测出声波的速度.
自我检测:
1.下列说法中正确的是()
A.弦线上的驻波其总长为半个波长的自然数倍
B.用驻波的规律可测波形的波长
C.驻波上处于波节的点位移始终为零,处于波腹的点位移始终处于最大
D.弦乐器发声使弦上形成驻波.
2.下列说法中正确的是()
A.两列和相反方向传播的波叠加就一定产生驻波
B.在驻波中有些质点始终静止不动,相邻的两个这样的质点的距离相距半个波长
C.驻波中各质点都有相同的振幅
D.驻波中两波节间各质点的振动频率相同.。
