高中数学高三综合素质测试试题 图片版
高中数学必修3 学期综合测评

数学 ·必修3
1.下面算法的功能是( ) 第一步,令 i=1. 第二步,i 除以 3,得余数 r. 第三步,若 r=0,则输出 i;否则,执行第四步. 第四步,令 i 的值增加 1. 第五步,若 i≤1000,则返回第二步;否则,算法结束. A.求 3 的倍数 B.求 1 至 1000 中 3 的倍数 C.求 i 除以 3 D.求 i 除以 3 的余数
13
数学 ·必修3
8.问题:①有 1000 个乒乓球分别装在 3 个箱子内,其 中红色箱子内有 500 个,蓝色箱子内有 200 个,黄色箱子内 有 300 个,现从中抽取一个容量为 100 的样本;②从 20 名
学生中选出 3 名参加座谈会. 方法:Ⅰ.简单随机抽样;Ⅱ.系统抽样;Ⅲ.分层抽样. 其中问题与方法能配对的是 ( )
A.r1=r2 B.r1>r2>0 C.0<r1<r2 D.r1<0<r2
5
数学 ·必修3
解析 根据题意,开始吸烟年龄(X)岁与其得肺癌的相 对危险度(Y)是负相关关系,所以 r1<0;每天吸烟(U)支与其 得肺癌的相对危险度(V)是正相关关系,所以 r2>0.即 r1<0<r2. 故选 D.
6
数学 ·必修3
10
数学 ·必修3
6.如图是一边长为 8 的正方形苗圃图案,中间黑色大
圆与正方形的内切圆共圆心,圆与圆之间是相切的,且中间
黑色大圆的半径是黑色小圆半径的 2 倍.若在正方形图案上
随机取一点,则该点取自黑色区域的概率为( )
π A.8
π B.16
C.1-π8
D.1-1π6
11
数学 ·必修3
解析 正方形面积为 82,正方形的内切圆半径为 4,中 间黑色大圆的半径为 2,黑色小圆的半径为 1,所以白色区 域的面积为 π×42-π×22-4×π×12=8π,所以黑色区域的 面积为 82-8π,在正方形图案上随机取一点,则该点取自 黑色区域的概率为 P=82-828π=1-π8,故选 C.
2023届山东潍坊高三高中学科核心素养测评数学试卷真题(含答案详解)
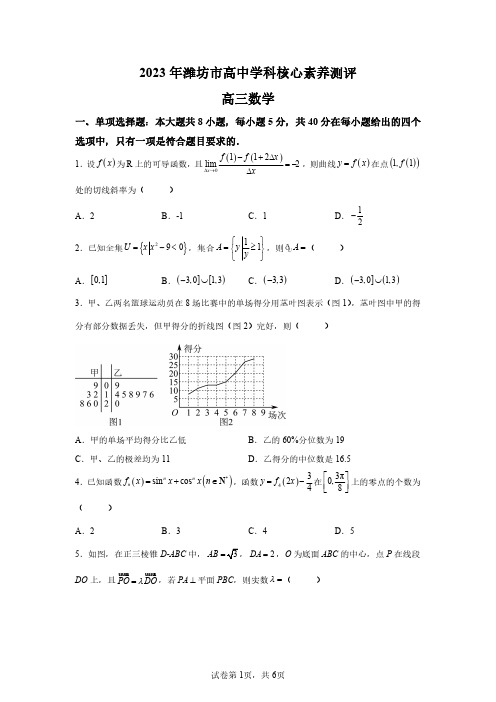
2023年潍坊市高中学科核心素养测评高三数学一、单项选择题:本大题共8小题,每小题5分,共40分在每小题给出的四个选项中,只有一项是符合题目要求的.1.设()f x 为R 上的可导函数,且()()112lim 2x f f x x∆→-+∆=-∆,则曲线()y f x =在点()()1,1f 处的切线斜率为()A .2B .-1C .1D .12-2.已知全集{}290U x x =-<,集合11A y y ⎧⎫=≥⎨⎬⎩⎭,则U A =ð()A .[]0,1B .(][)3,01,3-⋃C .()3,3-D .(]()3,01,3-⋃3.甲、乙两名篮球运动员在8场比赛中的单场得分用茎叶图表示(图1),茎叶图中甲的得分有部分数据丢失,但甲得分的折线图(图2)完好,则()A .甲的单场平均得分比乙低B .乙的60%分位数为19C .甲、乙的极差均为11D .乙得分的中位数是16.54.已知函数()()*sin cos n n n f x x x n =+∈N ,函数()4324y f x =-在3π0,8⎡⎤⎢⎣⎦上的零点的个数为()A .2B .3C .4D .55.如图,在正三棱锥D -ABC 中,AB =,2DA =,O 为底面ABC 的中心,点P 在线段DO 上,且PO DO λ=uu u r uuu r,若PA ⊥平面PBC ,则实数λ=()A .12B .13-C .4D .66.阿基米德螺线是一个点匀速离开一个固定点的同时又以固定的角速度绕该固定点转动而产生的轨迹.如图,在平面直角坐标系xOy 中,螺线与坐标轴依次交于点()11,0A -,()20,2A -,()33,0A ,()40,4A ,()55,0A -,()60,6A -,()77,0A ,()80,8A ,并按这样的规律继续下去.若四边形123n n n n A A A A +++的面积为760,则n 的值为()A .18B .19C .21D .227.已知双曲线()22122:10,0x y C a b a b-=>>的左,右焦点分别为1F ,2F ,点2F 与抛物线()22:20C y px p =>的焦点重合,点P 为1C 与2C 的一个交点,若△12PF F 的内切圆圆心的横坐标为4,2C 的准线与1C 交于A ,B 两点,且92AB =,则1C 的离心率为()A .94B .54C .95D .748.设a =0.1e b =,1ln1.1c =+,则()A .a b c>>B .c b a>>C .b a c>>D .b c a>>二、多项选择题:本大题共4个小题,每小题5分,共20分在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,选对但不全的得2分,有选错的得0分,9.假设某厂有两条包装食盐的生产线甲、乙,生产线甲正常情况下生产出来的包装食盐质量服从正态分布()2500,5N (单位:g ),生产线乙正常情况下生产出来包装食盐质量为x g ,随机变量x 服从正态密度函数()2200(1000)x x ϕ--=,其中x ∈R ,则()附:随机变量2(,)N ξμσ-,则()0.683P μσξμσ-<<+=,()220.954P μσξμσ-<<+=,()330.997P μσξμσ-<<+=.A .正常情况下,从生产线甲任意抽取一包食盐,质量小于485g 的概率为0.15%B .生产线乙的食盐质量()2~1000,100x N C .生产线乙产出的包装食盐一定比生产线甲产出的包装食盐质量重D .生产线甲上的检测员某天随机抽取两包食盐,称得其质量均大于515g ,于是判断出该生产线出现异常是合理的10.已知非零向量a e ≠,1e = ,对任意t R ∈,恒有a te a e -≥- ,则()A .a 在e上的投影的数量为1B .2a e a e +≥-r r r r C .()a a e ⊥- D .()e a e ⊥- 11.已知函数()f x 的定义域D 关于原点对称,,0m D m ∃∈>且()1f m =,当()0,x m ∈时,()0f x >;且对任意,,y D x y D x D ∈-∈∈且x y ≠,都有()()()()()1f x f y f x y f y f x +-=-,则()A .()f x 是奇函数B .()30f m =C .()f x 是周期函数D .()f x 在()2,3m m 上单调递减12.设x ∈R ,当()11Z 22n x n n -≤<+∈时,规定x n =,如1.21=, 4.54-=-.则()A .(),R a b a b a b +≤+∈B ()*N n n =∈C .设函数sin cos y x x =+的值域为M ,则M 的子集个数为32D .()*11112111N 22222n x x x x nx n n n n --+-++-+++-+=-∈三.填空题:本大题共4小题,每小题5分,共20分把答案填在答题卡的相应位置.13.已知,R a b ∈,()320233i i i a b -+=+(i 为虚数单位),则a b +=______.14.已知圆M 满足与直线:60l x -=和圆()()22:129N x y -+-=都相切,且直线MN 与l 垂直,请写出一个符合条件的圆M 的标准方程________________________.15.若0x >,0y >,则22334x yx y +++的最大值为____________.16.公元656年,唐代李淳风注《九章算术》时提到祖暅的开立圆术.祖暅在求球体积时,使用一个原理:“幂势既同,则积不容异”.“幂”是截面积,“势”是几何体的高.意思是两个同高的几何体,若在等高处的截面积相等,则体积相等.如图是某厂家生产的游泳池浮漂实物图及设计图,则h 的长度为____________cm ;利用祖暅原理可求得该浮漂的体积为____________3cm.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.将正奇数数列1,3,5,7,9…的各项按照上小下大、左小右大的原则写成如图的三角形数表.(1)设数表中每行的最后一个数依次构成数列{}n a ,求数列{}n a 的通项公式;(2)设()211n n n n b a -=+,求数列{}n b 的前n 项和n T .18.设钝角△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且()2222a b c R ab +-=,其中R 是ABC 外接圆的半径.(1)若7π12B =,求C 的大小;(2)若2CD DA = ,π2CBD ∠=,证明:ABC 为等腰三角形.19.如图,直角梯形ABCD 中,//,,22AB DC AB BC AB BC CD ⊥===,直角梯形ABCD 绕BC 旋转一周形成一个圆台.(1)求圆台的表面积和体积;(2)若直角梯形ABCD 绕BC 逆时针旋转角(0)θθ>到11A BCD ,且直线1A D 与平面ABCD 所成角的正弦值为7,求角θ的最小值.20.某校举行“强基计划”数学核心素养测评,要求以班级为单位参赛,最终高三一班(45人)和高三二班(30人)进入决赛.决赛规则如下:现有甲、乙两个纸箱,甲箱中有4个选择题和2个填空题,乙箱中有3个选择题和3个填空题,决赛由两个环节组成,环节一:要求两班级每位同学在甲或乙两个纸箱中随机抽取两题作答,作答后放回原箱.并分别统计两班级学生测评成绩的相关数据;环节二:由一班班长王刚和二班班长李明进行比赛,并分别统计两人的测评成绩的相关数据,两个环节按照相关比赛规则分别累计得分,以累计得分的高低决定班级的名次.(1)环节一结束后,按照分层抽样的方法从两个班级抽取20名同学,并统计每位同学答对题目的数量,统计数据为:一班抽取同学答对题目的平均数为1,方差为1;二班抽取同学答对题目的平均数为1.5,方差为0.25,求这20人答对题目的均值与方差;(2)环节二,王刚先从甲箱中依次抽取了两道题目,答题结束后将题目一起放入乙箱中,然后李明再抽取题目,已知李明从乙箱中抽取的第一题是选择题,求王刚从甲箱中取出的是两道选择题的概率.21.已知动点P 与两定点()12,0A -,()22,0A ,直线1PA 与2PA 的斜率之积为34-,记动点P的轨迹为曲线C .(1)求曲线C 的方程;(2)设()(),012D a a <<,E 为直线2x a =上一动点,直线DE 交曲线C 于G ,H 两点,若GD 、HE 、GE 、HD 依次为等比数列{}n b 的第m 、n 、p 、q 项,且m n p q +=+,求实数a 的值.22.已知函数()()()e ln 11R xf x k x k =++-∈.(1)当1k =时,求曲线()y f x =在点()()0,0f 处的切线方程;(2)若对任意()1,x ∈+∞,都有()0f x ≥,求实数k 的取值范围;(3)当12k ≥-时,对任意的[),0,s t ∈+∞,且s t ≠,试比较()()f s f t ''+与()()22f s f t s t--的大小.【分析】根据导数的定义,计算得到答案.【详解】()()()()()0011211211limlim 122x x f f x f f x f xx∆→∆→-+∆-+∆'==-=-∆∆.故曲线()y f x =在点()()1,1f 处的切线斜率为1.故选:C 2.D 【分析】求解全集U 以及集合A ,根据补集的定义计算补集即可求出结果.【详解】解:{}{}29033U x x x x =-<=-<<,{}11|01A y y y y ⎧⎫=≥=<≤⎨⎬⎩⎭,所以{|30U A x x =-<≤ð或}13x <<.故选:D 3.D 【分析】根据茎叶图、直方图,平均数、中位数、百分数、极差的求法判断各项的正误即可.【详解】A :由茎叶图和直方图,甲比赛得分为{}9,12,13,14,15,20,26,28,平均得分为91213141520262813788+++++++=,乙比赛得分为{}9,14,15,16,17,18,19,20,平均得分为91415161718192012888+++++++=,甲高于乙,错误;B :由860 4.8⨯=%,故乙的60%分位数为17,错误;C :甲的极差为28919-=,乙的极差为20911-=,错误;D :乙得分的中位数是161716.52+=,正确.故选:D【分析】首先求出()4f x 的解析式,即可得到()4324y f x =-,再根据余弦函数的性质计算可得.【详解】因为()()*sin cos n n n f x x x n =+∈N ,所以()()24422224sin cos sin cos si c 2n os f x x x x x x x-=+=+2111cos 4131sin 21cos 422244x x x -=-=-⨯=+,所以()4313312cos8cos844444y f x x x =-=+-=,令0y =,令1cos804x =,则π8π,Z 2x k k =+∈,解得ππ,Z 168k x k =+∈,因为3π0,8x ⎡⎤∈⎢⎥⎣⎦,所以π16x =或3π16x =或5π16x =,所以函数()4324y f x =-在3π0,8⎡⎤⎢⎥⎣⎦上的零点的个数为3个.故选:B 5.D 【分析】由正棱锥的结构特征构建空间直角坐标系,根据已知条件确定相关点坐标并求出面PBC 的法向量,结合线面平行及向量共线定理求参数λ即可.【详解】由题设,△ABC2DA DB DC ===,等边△ABC 32,在正棱锥中,以O 为原点,平行CB 为x 轴,垂直CB 为y 轴,OD为z 轴,如上图示,则11(0,1,0),,,0),(,,0),22A B C D -,且)P ,所以)AP =,1,)2PB =,CB = ,若(,,)m x y z = 为面PBC的法向量,则10220PB m x y z CB m ⎧⋅=+-=⎪⎨⎪⋅==⎩,令1z =,则(0,,1)m =,又PA ⊥平面PBC ,则AP km =且k为实数,101k k λ⎧=⎪⎪=⎨⎪≤≤⎪⎩,故6λ=.故选:D 6.A 【分析】根据四边形的特点,将四边形的面积转化为四个直角三角形的面积,即可求解.【详解】如图,四边形123n n n n A A A A +++的面积由四个直角三角形构成,得()()()()()()11111122337602222n n n n n n n n +++++++++=,()()()132131520n n n n n n ++++++++=,()()24221520n n ++=,即()()21380n n ++=,*N n ∈,解得:18n =故选:A 7.B 【分析】令12(,0),(,0)F c F c -,由题设知02p c =>且22b AB a=求得249b a =,再由内切圆中切线长性质及双曲线定义、性质确定与12F F 的切点C 的位置,进而求离心率.【详解】由题设12(,0),(,0)F c F c -,又点2F 与抛物线的焦点重合,即02pc =>,由()22222221c y a ba b c ⎧-⎪-=⎨⎪+=⎩,则2b y a =±,故2292b AB a ==,即249b a =,如下图示,内切圆与△12PF F 各边的切点为,,D E K,所以1122,,PD PE DF KF EF KF ===,又12||||2PF PF a -=,则121212()()2PD DF PE EF DF EF KF KF a +-+=-=-=,所以K 为双曲线右顶点,又△12PF F 的内切圆圆心的横坐标为4,即4a =,故29b =,则5c =,所以离心率为54c e a ==.故选:B 8.C 【分析】利用c a -、b a -的形式构造函数,应用导数研究其在(0,1)上单调性,进而比较相应函数值的符号,即可知参数的大小关系.【详解】由1ln1.1c a -=+,令()1ln(1)f x x =++01x <<,所以1()1f x x =-+'令()1g x x =-且01x <<,则()10g x =<',即()g x 递减,所以()(0)0g x g <=,故()0f x '<在(0,1)上恒成立,则()f x 在(0,1)上递减,所以()(0)0f x f <=,即(0.1)0f <,则c a <;由0.1e b a -=()e x t x =01x <<,所以()ext x '=-(0,1)上递增,故()(0)0t x t ''>=,故()t x 在(0,1)上递增,()(0)0t x t >=,即(0.1)0t >,则b a >;综上,b a c >>.故选:C 【点睛】关键点睛:应用作差法得到某种函数形式,并构造函数研究单调性判断函数值的符号即可.9.AD 【分析】根据正态分布的参数,以及结合3σ原则的参考数据,即可判断选项.【详解】由条件可知,设生产线甲正常情况下生产出来的包装食盐的质量为X ,其中()2500,5X N ,其中500μ=,5σ=,则()()10.99748530.00150.15%2P X P X μσ-<=<-===,故A 正确;B.随机变量x 服从正态密度函数()2200(1000)x x ϕ--=,可知,1000μ=,10σ=,所以生产线乙的食盐质量()2~1000,10x N ,故B 错误;C.不一定,可能小概率事件发生,生产线乙产出的包装食盐比生产线甲产出的包装食盐质量轻,故C 错误;D.()()10.99751530.00150.15%2P X P X μσ->=>+===,说明生产线甲抽到质量大于515g 的可能性很低,所以随机抽取两包质量均大于515g ,说明判断出该生产线出现异常是合理的,故D 正确.故选:AD 10.ABD 【分析】根据数量积的运算律求得a e ⋅,再根据数量积的运算,对每个选项进行逐一分析,即可判断和选择.【详解】由||||a te a e -≥- 可得2222222a ta e t e a a e e -⋅+≥-⋅+ ,又1e = ,令a e m ⋅=则上式等价于22210t mt m -+-≥,对任意的R t ∈恒成立,故()244210m m ∆=--≤,解得()210m -≤,解得1m =,即1a e ⋅= ;对A :由cos 1a e a e a e ⋅=⋅⋅= ,且1e = ,故cos 1a a e ⋅= ,即a 在e上的投影的数量为1,故A 正确;对B :222223a e a a e e a +=+⋅+=+r r r r r r r ,22222242a e a a e e a -=-⋅+=+r r rr r r r ,222a e a e ∴+≥-r r r r ,即2a e a e +≥-r r r r ,故B 正确;对C :()221a a e a a e a ⋅-=-⋅=- ,不确定其结果,故()a a e ⊥- 不一定成立,故C 错误;对D :()10e a e a e ⋅-=⋅-= ,故()e a e ⊥-,D 正确;故选:ABD.11.ACD 【分析】对于A ,令t x y =-,根据()()()()()1f x f y f x y f y f x +-=-证明()()f t f t =--即可判断;对于B ,根据()1f m =,结合()()()()()1f x f y f x y f y f x +-=-即可求得()()2,3f m f m ,即可判断;对于C ,先求出()f x m -,再根据()()2f x m f x m m -=--求出()2f x m -,即可判断;对于D ,令23m y x m <<<,先判断()(),f x f y 的符号,再根据()()()()()1f x f y f x y f y f x +-=-比较()(),f x f y 即可判断.【详解】对于A ,令t x y =-,则()()()()()()()()()()()()11f x f y f x f y f t f x y f y x f t f y f x f x f y ++=-==-=--=----,所以函数()f x 是奇函数,故A 正确;对于B ,由()1f m =,得()()()()()()()()212121212f m f m f m f m f m m f m f m f m ++=-===--,所以()20f m =,则()()()()()()()()3131230313f m f m f m f m f m m f m f m f m ++=-===--,所以()31f m =-,故B 错误;对于C ,由()()()()()1f x f y f x y f y f x +-=-,得()()()()()()()111f x f m f x f x m f m f x f x ++-==--,则()()()()()()()()()1111121111f x f x m f x f x m f x m m f x f x m f x f x ++-+--=--===-+----,则()()()142f x m f x f x m -=-=-,即()()4f x m f x +=,所以函数()f x 是以4m 为周期的周期函数,故C 正确;对于D ,令23m y x m <<<,则()()()0,,20,,20,x y m x m m y m m -∈-∈-∈,则()()()()()()211202f x f m f x m f m f x f x +-==->-,所以()0f x <,()()()()()()211202f y f m f y m f m f y f y +-==--,所以()0f y <,所以()()0f x f y >,()()()()()10f x f y f x y f y f x +-=>-,因为()()0f x f y >,所以()()10f x f y +>,所以()()0f y f x ->,即()()f y f x >,所以()f x 在()2,3m m 上单调递减,故D 正确.故选:ACD.【点睛】关键点点睛:本题考查了抽象函数的奇偶性,周期性及单调性,C 选项的关键在于根据()()2f x m f x m m -=--判断()2f x m -与()f x 的关系,D 选项的关键在于令23m y x m <<<,判断出()(),f x f y 的符号.12.BCD 【分析】结合特例,可判定A 错误;结合12n n <<+,可判定B 正确;结合正弦、余弦函数的值域,得到cos y x x =+的值域为{}2,1,0,1,2M =--,可判定C 正确;设()1111211122222n f x x x x x nx n n n -=-+-++-+++-+-- ,得到()f x 的周期为1n,证得()f x 恒为0,可判定D 正确.【详解】对于A 中,例如0.61,0.61-=--=-,则0.60.6 1.21,0.60.62--=-=--+-=-,可得0.60.60.60.6-->-+-,所以A 错误;对于B 中,由22211()42n n n n n +<++=+12n +,所以12n n <<+n =,所以B 正确;对于C 中,因为1sin 11cos 1x x -≤≤⎧⎨-≤≤⎩,可得{}{}sin 1,0,1cos 1,0,1x x ⎧∈-⎪⎨∈-⎪⎩,当5π3ππ,π,,,0444x =时,可得sin cos 2,1,0,1,2y x x =+=--,即函数sin y x x =+的值域为{}2,1,0,1,2M =--,所以集合M 的子集个数为5232=,所以C 正确;对于D 中,设()1111211122222n f x x x x x nx n n n -=-+-++-+++-+-- ,若N n *∈,可得a n a n +=+,所以11122x x +=-+,11122nx nx +=-+,则()11111()1102222f x f x x x nx nx n +-=+---++-=-=,所以()f x 的周期为1n,又当10x n≤<时,可得111112222x n -≤-<-<,此时102x -=;1111121122222x n n n -≤-+≤-+<-<,此时1102x n -+=;1111112222n n x n n ---≤-+≤-+<,此时1102n x n --+=;111222nx -≤-<,此时102nx -=,所以()0f x =1(0x n ≤<,结合周期为1n,即()f x 恒为0,所以D 正确.故选:BCD.【点睛】方法点睛:对于函数的新定义试题的求解:1、根据函数的新定义,可通过举出反例,说明不正确,同时正确理解新定义与高中知识的联系和转化;2、正确理解函数的定义的内涵,紧紧结合定义,结合函数的基本性质(如单调性、奇偶性和周期等性质)进行推理、论证求解.13.2-【分析】利用复数的乘方运算及乘法运算计算,再借助复数相等求解作答.【详解】由()320233i i i a b -+=+得:()3i i (i)a b +=+-,即3i 1i a b +=-,而,R a b ∈,则1,3a b ==-,所以2a b +=-.故答案为:2-14.()()22521x y -+-=(答案不唯一)【分析】不妨设圆M 与圆N 外切,根据直线MN 与l 垂直,可得圆M 的纵坐标,由两圆的位置关系列出横坐标和半径的等量关系,求解可得圆M 的一个方程.【详解】由条件可知:直线6x =与圆N 相离,不妨设圆M 与圆N 外切,设(),M a b ,半径为r ,因为直线MN 与l 垂直,所以2b =,则有613r a a r =-⎧⎨-=+⎩,解得:521a b r =⎧⎪=⎨⎪=⎩,所以圆M 的标准方程为:()()22521x y -+-=.故答案为:()()22521x y -+-=15.12##0.5【分析】由()()22223334133x y x yx y x y ++=+++++,再利用基本不等式即可得解.【详解】()()2222333134262133x y x y x y x y x y x y +++=≤==++++++,当且仅当21x =且233y =,即1x y ==时,取等号,所以22334x y x y +++的最大值为12.故答案为:12.16.【分析】根据设计图截面结构,结合球体轴截面的性质确定球体半径、实物高及中间柱体底面半径的关系求h ;应用祖暅原理求圆柱两端处球冠的体积,然后用球体体积减去圆柱体积、两个球冠体积即可得实物体积.【详解】由实物轴截面如下图示:O为球心,结合设计图知:5,1,2OA OB h AB ===,故21254h +=,可得h =;由题设知:若1V 为球体体积,2V 为圆柱体积,3V 为圆柱一端的球冠体积,由祖暅原理知:323321250π5[π5π]π333V =⨯-⨯⨯⨯=-,所求体积为321234500π2π5π133V V V V =--=⨯-⨯⨯-+=cm 3.故答案为:,【点睛】关键点点睛:第二空,求柱体两端球冠体积要模仿祖暅原理求球体体积的思路计算得出,然后求实物体积.17.(1)22n a n n =+-(2)1221n n +-+【分析】(1)题意三角形数表可知12n n a a n --=,利用累加法和等差数列前n 项求和公式计算可得21n a n n =+-,检验即可;(2)由(1)可得1221n n n b n n +=-+,结合裂项相消求和法计算即可求解.【详解】(1)由题意知,214a a -=,326a a -=,……,12n n a a n --=,所以,()()()213214682n n a a a a a a n --+-++-=++++L L ()()()2221223422n n n n n +-=++++==+-L ,得212n a a n n -=+-,因为11a =,所以21n a n n =+-,经检验满足题意,所以21n a n n =+-;(2)由题意得,()()1212211n n n n n b n n n n +-==-++,所以,12231122222222122311n n n n n n T n ++⎛⎫⎛⎫=++⎛⎫---=-⎪++⎝⎭+ ⎪ ⎪⎝⎭⎝⎭ .18.(1)π12C =(2)证明见解析【分析】(1)应用正余弦边角关系及三角形内角性质得π2B C =+,即可求C 的大小;(2)由(1)及题设易知ABC ADB ,则有2213c b =,应用余弦定理可得22233cos 22a b a C ab b+==,进而确定三角形形状.【详解】(1)因为()2222a b c R ab +-=,由余弦定理得:22cos Rab C ab =,所以2cos R C b =,由正弦定理得:2cos 2sin R C R B =,所以cos sin C B =,又(),,0,πA B C ∈,π2B C +≠,所以π2B C =+,又7π12B =,所以π12C =.(2)由题意得3bAD =,23CD b =,由(1)知:π2ABC C ∠=∠+,所以ABD C ∠=∠,所以ABC ADB ,则AB AD AC AB =,即2AB AD AC =⋅,即2213c b =,在ABC 中2222223cos 22a b a b c C ab ab ++-==,在Rt ABC △中3cos 2a C b =,所以2223322a b a ab b+=,解得3a b =,故3cos 22a C b ==,又()0,πC ∈,故π6C =,ππ226A C =-=,所以ABC 为等腰三角形.19.(1)表面积和体积分别为()5π,14π3【分析】(1)利用圆台的表面积、体积公式求圆台的表面积和体积;(2)构建空间直角坐标系,确定1A D、面ABCD 的一个法向量,应用空间向量夹角的坐标表示列方程求cos θ,进而可求θ的最小值.【详解】(1)由题意,直角梯形ABCD 旋转形成下底面半径为2,上底面半径为1,高为2的圆台,所以该圆台的表面积()()π12π4π5πS =+++=,该圆台的体积()1142π4ππ33V =⨯⨯+=,故所求圆台的表面积和体积分别为()5π,14π3;(2)作BM BA ⊥,以点B 为坐标原点,射线BA ,BM ,BC 为x ,y ,z 轴的正半轴,建立空间直角坐标系,如图所示,则()1,0,2D ,()12cos ,2sin ,0A θθ,即()112cos ,2sin ,2A D θθ=--uuu r,又平面ABCD 的一个法向量()0,1,0n = ,设1A D 与平面ABCD 所成的角为α,则1sin cos ,A D n α=uuu r r=,两边平方并结合22sin cos 1θθ+=,解得1cos 2θ=或1cos 14θ=-,故1cos 2θ=时所求θ的最小值为π3.20.(1)样本均值为1.2,样本方差为0.76【分析】(1)首先求分层抽取的两个班的人数,再根据两个班抽取人数的平均数和方差,结合总体平均数和方差公式,代入求值;(2)根据全概率公式和条件概率公式,即可求解.【详解】(1)一班抽取45201275⨯=人,二班抽取3020875⨯=人,一班样本平均数为1x =,样本方差为211s =;二班样本的平均数为 1.5y =,样本方差为220.25s =;总样本的平均数为12181.51.2128ω⨯+⨯==+.记总样本的样本方差为2s ,则222121(11.2)80.25(1.5 1.2)0.7620s ⎡⎤⎡⎤⨯+-+⨯+-⎣⎦⎣⎦==.所以,这20人答对题目的样本均值为1.2,样本方差为0.76.(2)设事件A 为“李明同学从乙箱中抽出的第1个题是选择题”,事件1B 为“王刚同学从甲箱中取出2个题都是选择题”,事件2B 为“王刚同学从甲箱中取出1个选择题1个填空题",事件3B 为“王刚同学从甲箱中取出2个题都是填空题”,则1B 、2B 、3B ,彼此互斥,且123B B B ⋃⋃=Ω,()24126C 2C 5P B ==,()1142226C C 8C 15P B ==,()2236C 1C 15P B ==,()158P A B =,()212P A B =,()338P A B =,()()()()()()()112233P A P B P A B P B P A B P B P A B =⨯+⨯+⨯258113135815215824=⨯++⨯=所求概率即是A 发生的条件下1B 发生的概率:()()()()()()111125658131324P B P A B P B A P B A P A P A ⨯====.21.(1)()221243x y x +=≠±(2)a =【分析】(1)设点P 坐标,依据题意列出等式,化简可求出轨迹方程;(2)依据等比数列的性质可得GD HE GE HD ⋅=⋅,代入弦长公式化简结合韦达定理可求出a 的值.【详解】(1)设动点P 的坐标为(),x y ,由题意得,3224y y x x ⋅=-+-,化简得:()221243x y x +=≠±,故所求C 的方程为()221243x y x +=≠±.(2)设()2,E a t ,0t ≠,设直线DE 的方程为:()t y x a a=-,设()11,G x y ,()22,H x y ,联立方程:()22,1,43t y x a a x y ⎧=-⎪⎪⎨⎪+=⎪⎩消去y 得()22222223484120a t x at x a t a +-+-=,所以21222834at x x a t +=+,222122241234a t a x x a t -=+,由题意得m n p q b b b b =,所以GD HE GE HD ⋅=⋅,即0GD HE GE HD ⋅-⋅=.即2212122212120t t a x a x a x x a a a ⎛⎫⎛⎫+---+--= ⎪ ⎪⎝⎭⎝⎭从而()()()()1212220a x a x a x x a -----=,所以()212122340x x a x x a -++=,即222222222412823403434a t a at a a a t a t-⋅-⋅+=++,所以22a =,又12a <<,a =22.(1)20x y -=(2)1k =-(3)()()()()22f s f t f s f t s t-''+>-【分析】(1)利用导数几何意义求切线方程;(2)由已知不等式恒成立且()00f =知()00f '=,进而求得1k =-,再代入()y f x =应用导数研究()0f x ≥恒成立,根据充要关系确定参数值;(3)设0s t >≥,构造()()()()()()2g s f s f t s t f s f t ''⎡⎤⎡⎤=+---⎣⎦⎣⎦,利用导数研究()g s 单调性,进而确定其函数值符号,即可证结论.【详解】(1)当1k =时()()e ln 11x f x x =++-,()00f =,所以()1e 1x f x x ='++,()02f '=,所以()y f x =在点()()0,0f 处的切线方程为20x y -=.(2)对()1,x ∀∈-+∞都有()0f x ≥且()00f =,而()e 1x k f x x '=++,则()010f k '=+=,所以1k =-,此时()()e ln 11x x f x =-+-,故()1()e 1x f x g x x ==-+',则()21()e 1x g x x '=++,在()1,x ∈-+∞上()0g x '>,即()()g x f x '=单调递增,且()00f '=,当()1,0x ∈-时()00f '<,()f x 单调递减,当()0,x ∈+∞时()00f '>,()f x 单调递增,所以()()00f x f ≥=,满足题意,综上,1k =-.(3)不妨设0s t >≥,令()()()()()()2g s f s f t s t f s f t ''⎡⎤⎡⎤=+---⎣⎦⎣⎦,所以()()()()()g s f s s t f t f s '''''=-+-,则()()()g s f s s t '''''=-,又()e 1x k f x x '=++,()()2e 1x k f x x ''=-+,()()32e 1x k f x x '''=++,且0x >,当12k ≥-,()()()3321e e 11x x k f x x x '''=+≥-++,而e 1x >,()3111x <+,所以()0f x '''>,故()()()0g x f s s t '''''=->,()g s '在()0,∞+上单调递增,所以()()0g s g t ''>=,所以()g s 单调递增,故()()0g s g t >=,所以()()()()()()20g s f s f t s t f s f t ''⎡⎤⎡⎤=+--->⎣⎦⎣⎦,即()()()()22f s f t f s f t s t -''+>-.【点睛】关键点点睛:第二问,根据不等式恒成立及()00f =得()00f '=求参数范围,求证所得参数范围使不等式恒成立,由充要关系确定范围;第三问,构造()()()()()()2g s f s f t s t f s f t ''⎡⎤⎡⎤=+---⎣⎦⎣⎦研究其函数值符号即可.。
2020届高三毕业班第一次综合质量检测数学(理)试题—附答案

5.
已知函数
f
(
x)
1
x x
2
sin x ,则函数 y
f (x) 的图像大致为
A.
B.
C.
D.
6.从区间 0,1随机抽取 2n 个数 x1, x2 ,, xn , y1, y2 ,, yn ,组成坐标平面上的 n 个点
(x1, y1 ) ,(x2 , y2 ) ,… (xn , yn ) ,其中到原点距离小于1的点有 m 个,用随机模拟的
A.20100
B.20200
C.40200
D.40400
12.在棱长为 4 的正方体 ABCD A1B1C1D1 中, E, F 分别为 AA1, BC 的中点,点 M 在
棱 B1C1 上, B1M
1 4
B1C1
,若平面
FEM
交
A1B1 于点 N
,四棱锥 N
BDD1B1 的五
个顶点都在球 O 的球面上,则球 O 半径为
A(3, 0, 0) , B(0, 3, 0) , S(0, 3 , 3 3 ) , C(1,0,0) , 22
上.
(1)求曲线 C 的普通方程及直线 l 的直角坐标方程. (2)求△PAB 面积的最大值.
23.(本小题满分 10 分)选修 4-5:不等式选讲
已知函数 f (x) | 2x t | ,若 f (x) 1的解集为 (1,0) . (1)求 t 并解不等式 f (x) x 2 ; (2)已知: a,b R ,若 f (x) 2a b | 2x 2 | ,对一切实数 x 都成立, 求证: a 2b 1 .
3
2
根据所给数据用事件发生的频率来估计相应事件发生的概率,估计该顾客支付的平均费用
河北省衡水市衡水中学2025届高三上学期第一次综合素养测评数学试题(含答案)

河北省衡水中学2025届高三上学期第一次综合素养测评数学试题一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.已知不等式x2−2x−3<0的解集为A,不等式x+3x−2<0的解集为B,则A∩B为( )A. [−3,3]B. (−3,3)C. [−1,2]D. (−1,2)2.已知|a|=63,|b|=1,a⋅b=−9,则向量a与b的夹角为( )A. 2π3B. 5π6C. π3D. π63.如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN= 30∘,C点的仰角∠CAB=45∘以及∠MAC=75∘,从C点测得∠MCA=60∘,已知山高BC=100m,则山高MN=( )A. 120mB. 150mC. 503mD. 160m4.已知等差数列{a n}和{b n}的前n项和分别为S n、T n,若S nT n =3n+4n+2,则a3+a7+a8b2+b10=( )A. 11113B. 3713C. 11126D. 37265.已知双曲线C:x2a2−y2b2=1(a>0,b>0)的左、右焦点分别为F1,F2,P是双曲线C的一条渐近线上的点,且线段PF1的中点N在另一条渐近线上.若cos∠PF2F1=35,则双曲线C的离心率为( )A. 53B. 54C. 2D. 56.点P(−2,−1)到直线l:(1+3λ)x+(1+λ)y−2−4λ=0(λ∈R)的距离最大时,其最大值以及此时的直线方程分别为( )A. 13;3x+2y−5=0B. 11;3x+2y−5=0C. 13;2x−3y+1=0D. 11;2x−3y+1=07.已知函数f(x)的定义域为(−3,3),且f(x)={lg 3−x 3+x +2x−3,−3<x <0,lg 3+x 3−x−2x +3,0⩽x <3.若3f[x(x−2)]+2>0,则x 的取值范围为( )A. (−3,2) B. (−3,0)∪(0,1)∪(1,2)C. (−1,3)D. (−1,0)∪(0,2)∪(2,3)8.已知x x−1≥ln x +ax 对∀x >0恒成立,则a 的最大值为( )A. 0B. 1eC. eD. 1二、多选题:本题共3小题,共15分。
2025届江南十校高三第一次综合素质检测数学试题及答案

姓名座位号(在此卷上答题无效)绝密★启用前2024年“江南十校”新高三第一次综合素质检测数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号框涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号框。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、选择题:本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合{}2log 2<=x x A ,{}4<=x x B ,=B A A .)4,(-∞B .)4,0(C .)4,4(-D .)0,4(-2.记等差数列{}n a 的前n 项和为n S ,已知863=+a a ,则=8S A .28B .30C .32D .363.已知函数1221)(+-=xx f ,则对任意实数x ,有A .0)()(=+-x f x f B .0)()(=--x f x f C .2)()(=+-x f x f D .2)()(=--x f x f 4.已知βα,都是锐角,71cos =α,1411)cos(-=+βα,求=βcos A .21B .9839C .9859D .98715.已知()nx 21+的展开式中各项系数的和为243,则该展开式中的4x 项的系数为A .5B .16C .40D .806.已知正方体1111D C B A ABCD -的棱长为3,以顶点A 为球心,2为半径作一个球,则球面与正方体的表面相交所得到的曲线的长为A .23πB .25πC .π2D .π7.某次跳水比赛甲、乙、丙、丁、戊5名跳水运动员进入跳水比赛决赛,现采用抽签法决定决赛跳水顺序,在“运动员甲不是第一个出场,运动员乙不是最后一个出场”的前提下,“运动员丙第一个出场”的概率为A .133B .51C .41D .1348.对于0>x ,0ln 12≥-x e xλλ恒成立,则正数λ的范围是A .e1≥λB .e21≥λC .e 2≥λD .e≥λ二、选择题:本题共3小题,每小题6分,共18分。
2020学年高中数学学期综合测评(二)(含解析)新人教A版必修3(2021-2022学年)

学期综合测评(二)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷 (选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知变量x与y正相关,且由观测数据算得样本平均数错误!未定义书签。
=3,错误!=3.5,则由该观测数据算得的线性回归方程可能是( )A.错误!=0.4x+2.3B.错误!未定义书签。
=2x-2.4C.错误!未定义书签。
=-2x+8.5 D.y\s\up6(^)=-0.3x+4.4答案A解析首先,因为x与y正相关,所以线性回归方程的斜率为正数,排除C,D;其次,线性回归方程应满足样本中心点(3,3.5)在直线上,将该坐标代入A,B选项验证,结果仅有A项等式成立,即3.5=0.4×3+2.3.故选A.2.阅读如图所示的程序框图,该程序框图运行的结果是( )A.-2B.2 C.-3 D.3答案C解析程序执行后:S=1,i=2;S=-1,i=3;S=2,i=4;S=-2,i=5;S=3,i=6;S=-3,i=7>6,故程序框图运行的结果是-3.ﻬ3.从某校高三年级随机抽取一个班,对该班50名学生的高校招生体检表中视力情况进行统计,其结果的频率分布直方图如图,若某高校A专业对视力的要求在0.9以上,则该班学生中能报A专业的人数为( )A.10 B.20C.8 D.16答案B解析由频率分布直方图可知,视力在0.9以上的人数为(1.00+0.75+0.25)×0.2×50=20(人),故选B.4.如图,在△ABC中,在线段AB上任取一点P,则恰好满足错误!未定义书签。
〉错误!未定义书签。
的概率是( )A.错误!B.错误!C.错误!D.错误!未定义书签。
答案D解析记△ABC的高为h,则\f(S△PBC,S△ABC)=错误!=错误!.要使错误!未定义书签。
2020学年高中数学学期综合测评(一)(含解析)新人教A版选修2-3(2021-2022学年)

学期综合测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.下列说法正确的有()①回归方程适用于一切样本和总体.②回归方程一般都有时间性.③样本取值的范围会影响回归方程的适用范围.④回归方程得到的预报值是预报变量的精确值.A.①② B.②③ C.③④ D.①③答案B解析回归方程只适用于所研究样本的总体,所以①不正确;而“回归方程一般都有时间性”正确,③也正确;而回归方程得到的预报值是预报变量的近似值,故选B。
2.6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品.已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为()A.1或3 B.1或4 C.2或3D.2或4答案D解析任意两个同学之间交换纪念品共要交换C错误!=15次,如果都完全交换,每个人都要交换5次,也就是得到5份纪念品,现在6个同学总共交换了13次,少交换了2次,这2次如果不涉及同一个人,则收到4份纪念品的同学有4人;如果涉及同一个人,则收到4份纪念品的同学有2人,答案为D.3.(错误!未定义书签。
x-1)5的展开式中第3项的系数是( )A.-20错误!未定义书签。
B.20 C.-20 D.20错误!未定义书签。
答案D解析T r+1=C错误!未定义书签。
·(\r(2)x)5-r·(-1)r,令r=2,则T3=C错误!·(错误!x)3·(-1)2=10×2错误!未定义书签。
x3,即第3项系数为202。
4.设随机变量X服从二项分布X~B(n,p),则错误!未定义书签。
等于()A.p2 B.(1-p)2C.1-p D.以上都不对答案Bﻬ解析因为X~B(n,p),(D(X))2=[np(1-p)]2,(E(X))2=(np)2,所以错误!=错误!=(1-p)2.故选B.5.若随机变量ξ~N(-2,4),则ξ在区间(-4,-2]上取值的概率等于ξ在下列哪个区间上取值的概率( )A.(2,4] ﻩB.(0,2]C.[-2,0)ﻩ D.(-4,4]答案C解析此正态曲线关于直线x=-2对称,∴ξ在区间(-4,-2]上取值的概率等于ξ在[-2,0)上取值的概率.6.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12。
2020学年高中数学学期综合测评(一)新人教A版选修2-2(2021-2022学年)

学期综合测评(一)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,共60分)1.曲线y=错误!未定义书签。
在点(-1,-1)处的切线方程为( )A.y=2x+1B.y=2x-1C.y=-2x-3 D.y=-2x-2答案A解析易知点(-1,-1)在曲线上,且y′=错误!未定义书签。
=错误!未定义书签。
,∴切线斜率k=y′|x=-1=错误!=2.由点斜式得切线方程为y+1=2(x+1),即y=2x+1。
2.若复数z满足z(2-i)=11+7i(i为虚数单位),则z为()A.3+5iB.3-5iC.-3+5i D.-3-5i答案A解析由z(2-i)=11+7i得,z=错误!未定义书签。
=错误!=错误!=3+5i。
3.定积分错误!错误!dx的值为( )A.32+ln2 B.错误!未定义书签。
C.3+ln 2 ﻩD。
错误!答案A解析错误!错误!未定义书签。
dx=错误!错误!未定义书签。
dx=错误!未定义书签。
错误!dx+错误!xdx=lnx错误!未定义书签。
+错误!未定义书签。
x2|错误!=ln2-ln 1+错误!×22-错误!未定义书签。
×12=错误!+ln2.4.如图是某年元宵花灯展中一款五角星灯连续旋转闪烁所成的三个图形,照此规律闪烁,下一个呈现出来的图形是()答案 A解析 观察图形可知,下一个呈现出来的图形是A 选项中的图形.5.已知函数f(x )在R 上的导函数为f ′(x ),若f (x )〈f′(x )恒成立,且f (0)=2,则不等式f (x )>2ex 的解集是( )A .(2,+∞)B .(0,+∞) C.(-∞,0) ﻩ D.(-∞,2)答案 B解析 由f (x )〈f′(x )得f (x )-f ′(x)〈0,则错误!′=错误!未定义书签。
〉0,所以函数y =错误!未定义书签。
