三角形框架
斯腾伯格爱情的三角形理论述评

斯腾伯格爱情的三角形理论述评斯腾伯格爱情的三角形理论述评作者:李朝旭摘要:本文介绍了美国心理学家斯腾伯格(Robert.J.Sternberg)提出的爱情三角形理论框架,分基本三角形原理、多重三角形原理和基本评价三个部分。
人类爱情包括三种成分:①亲密成分②激情成分③决定/忠守成分,它们组成了爱情三角形的三个顶点,成为对爱情进行描述的维度。
在此基础上,爱情可以分成八种类型。
而且,在基本三角形之外还有各种复杂的多重三角形,根据它们能够准确地预测关系的满意度和关系质量。
这一理论虽然有其局限性和不成熟性,但对在我国开展类似研究有借鉴意义。
关键词: 爱情爱情的三角形理论亲密激情决定忠守斯腾伯格(Robert.J.Sternberg)是当今世界上从信息加工的角度来研究智力的学者,曾提出了著名的“三重智力理论”,产生了广泛的影响,国内亦有人介绍之(李其维、金瑜,1994,1995;万明钢,1995)。
他不仅在人类智能研究领域内在需要帮助时能指望所爱的人;⑤互相理解;⑥分享一个人的自我和一个人的所有;⑦接受来自所爱的人的情感方面的支持;⑧对所爱的人提供情感方面的支持;⑨能与所爱的人进行亲密的沟通交流;⑩重视对方在自己生活中的价值。
斯氏提出的这一成分也广泛地存在于较深的友谊关系之中。
⒉激情成分(Passion) 或称“情欲成分”,指驱力,这些驱力能引起浪漫恋爱、体态吸引、性完美,以及爱情关系中的其它有关现象。
或者说,该成分就是在爱情关系中能引起激情体验的各种动机性的唤醒源以及其它形式的唤醒源。
它包括一种激烈地渴望与另外一人成为一个统一体的状态。
在爱情关系中,性的需要是引起这种激情体验的主导形式,除此之外,按斯氏的说法,诸如自尊、养育、亲合、支配、服从以及自我实现等需要也是唤醒源。
⒊决定/忠守成分(Decision/commitment) 有两层含义:①在短期方面,指一个人做出了爱另外一个人的决定;②在长期方面,指那些能维持爱情关系的承诺或担保、投入、忠心、义务感或责任心。
初中数学三角形知识框架

初中数学三角形知识框架三角形重难点:(1)三角形的边、角的关系;三角形的“三线”;重心的概念及性质(2)三角形三边的关系;三角形的的“三线”(3)三角形的三线的区分;多边形的外角一、知识框架二、知识概念1.三角形:由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系:三角形任意两边的和大于第三边,任意两边的差小于第三边.3.高:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足间的线段叫做三角形的高.4.中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线:三角形的一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性:三角形的形状是固定的,三角形的这个性质叫三角形的稳定性.7.多边形:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角:多边形相邻两边组成的角叫做它的内角.9.多边形的外角:多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.11.正多边形:在平面内,各个角都相等,各条边都相等的多边形叫正多边形.12.平面镶嵌:用一些不重叠摆放的多边形把平面的一部分完全覆盖,叫做用多边形覆盖平面13.公式与性质:⑴三角形的内角和:三角形的内角和为180°。
⑵三角形外角的性质:性质1:三角形的一个外角等于和它不相邻的两个内角的和.性质2:三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式:n边形的内角和等于(n-2)·180°。
⑷多边形的外角和:多边形的外角和为360°.⑸多边形对角线的条数:①从边形的一个顶点出发可以引(n-3)条对角线,把多边形分成(n-2)个三角形.②边形共有n(n-3)/2条对角线.。
小学美术《搭建框架》教案

5.培养学生的表达能力:鼓励学生用语言描述自己的框架设计,提高沟通表达能力。
三、教学难点与重点
1.教学重点
-框架结构的定义与作用:理解框架结构在稳定性和支撑性方面的基本原理。
-常见框架类型:掌握三角形、矩形、圆形等稳定框架的特点和应用。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解框架结构的基本概念。框架结构是由直线和节点组成的几何形状,用于支撑和稳定建筑或艺术品。它在工程和艺术领域都有着重要作用。
2.案例分析:接下来,我们来看一个具体的案例。这个案例展示了三角形框架在桥梁建设中的应用,以及它如何帮助我们解决稳定性问题。
实践活动环节,学生们分组讨论并动手搭建框架,这个过程相当热闹。我观察到他们在操作中遇到了一些问题,比如材料的选择和连接方式等。这让我意识到,在实践活动之前,我应该更加明确地讲解和演示搭建过程中可能遇到的问题和解决方法。
小组讨论时,学生们的参与度很高,大家积极发表自己的观点,这让我很高兴。但同时,我也发现有些学生在讨论中显得比较被动,可能是因为他们对自己的想法不够自信。在未来的教学中,我应该更多地鼓励和支持这些学生,帮助他们建立自信。
-搭建框架的方法:学会使用不同材料搭建框架,并了解其连接方式。
-创作与展示:能够运用所学知识创作具有个人特色的作品,并图示,强调三角形的三个角固定了三条边的位置,使得整个结构不易变形。
2.教学难点
-理解框架结构的空间概念:学生需要能够想象和构建三维空间中的框架结构。
-创新设计:鼓励学生在遵循框架稳定原则的基础上,进行独特的创意设计。
-实践操作中的问题解决:在搭建过程中,学生可能会遇到材料匹配、连接方式等实际问题,需要学会解决。
新版湘教版秋八年级数学上册第二章三角形课题三角形的基本概念教学设计

新版湘教版秋八年级数学上册第二章三角形课题三角形的基本概念教学设计一. 教材分析湘教版秋八年级数学上册第二章三角形课题三角形的基本概念是本学期数学课程的重要组成部分。
这部分内容主要介绍了三角形的定义、分类、性质以及三角形的相关概念。
通过这部分的学习,学生可以对三角形有更深入的了解,为后续的三角形相关题目打下坚实的基础。
二. 学情分析在开始本节课的学习之前,学生已经掌握了实数、平面几何的基本概念,具备了一定的逻辑思维能力和空间想象力。
但是,对于三角形的一些基本概念,如三角形的定义、分类、性质等,学生可能还不够熟悉。
因此,在教学过程中,教师需要注重引导学生理解并掌握这些基本概念。
三. 教学目标1.知识与技能:使学生了解三角形的基本概念,掌握三角形的分类,能运用三角形的性质解决一些简单问题。
2.过程与方法:通过观察、操作、思考、交流等活动,培养学生发现问题、分析问题、解决问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的团队合作精神,使学生感受到数学与生活实际的联系。
四. 教学重难点1.重点:三角形的基本概念、分类和性质。
2.难点:三角形性质的运用。
五. 教学方法1.情境教学法:通过生活实例引入三角形的基本概念,激发学生的学习兴趣。
2.启发式教学法:引导学生主动思考、发现问题、解决问题。
3.合作学习法:学生进行小组讨论,培养学生的团队合作精神。
4.巩固练习法:通过适量练习,使学生掌握三角形的基本概念和性质。
六. 教学准备1.教具:三角板、直尺、圆规等。
2.课件:三角形的相关图片、动画、PPT等。
3.练习题:针对三角形基本概念的练习题。
七. 教学过程1.导入(5分钟)利用生活实例,如电线塔、自行车三角架等,引导学生思考:这些物体为什么都要用到三角形呢?从而引出三角形的基本概念。
2.呈现(10分钟)通过PPT或板书,呈现三角形的基本概念、分类和性质。
让学生初步了解三角形的定义、分类和性质。
三边组成三角形的条件

三边组成三角形的条件篇一:嘿!同学们,你们知道三边组成三角形有啥条件不?这可有意思啦!就比如说,有三根小木棒,一根3 厘米长,一根5 厘米长,还有一根8 厘米长。
你说它们能组成一个三角形吗?这可得好好想想哟!其实呀,要想让三条边能组成一个三角形,有个很重要的规则,那就是任意两边的长度之和一定要大于第三边。
咱们就拿刚刚那三根小木棒来说吧。
3 厘米和5 厘米加起来是8 厘米,这和第三边8 厘米一样长,那能组成三角形吗?当然不能啦!这就好像跑步比赛,两个人一起跑的速度要是和第三个人一样,那怎么能比得过呀?再比如说,有三根木棒,分别是4 厘米、6 厘米和7 厘米。
那它们能组成三角形不?咱们来算算,4 厘米加6 厘米等于10 厘米,10 厘米大于7 厘米。
4 厘米加7 厘米等于11 厘米,11 厘米大于6 厘米。
6 厘米加7 厘米等于13 厘米,13 厘米大于4 厘米。
这就像搭积木,每两块积木加起来都比剩下的那块长,才能稳稳地搭起来,不是吗?那这个条件到底有啥用呢?哎呀,用处可大啦!比如说工程师叔叔盖房子的时候,要是不懂得这个条件,那房子的架子可能就搭不稳啦!还有咱们做手工,要是想做个三角形的框架,也得按照这个条件来选材料呀,不然可就做不成啦!所以说,三边组成三角形的条件可重要啦,咱们一定要记住哟!任意两边之和大于第三边,这样才能成功地组成一个三角形。
同学们,你们记住了吗?篇二:《三边组成三角形的条件,你知道吗?》嘿!同学们,今天咱们来聊聊一个超级有趣的数学知识——三边组成三角形的条件!先来说说什么是三角形吧。
三角形啊,就像是我们生活中的好多东西,比如三明治的形状,是不是三个边围起来的?还有那些漂亮的三角尺,它们也是三角形呀!那到底什么样的三条边才能组成一个三角形呢?这可大有讲究!假设我们有三条边,分别叫边A、边B 和边C。
要是这三条边能组成一个三角形,那就得满足一个重要的条件:任意两边之和大于第三边。
这啥意思呢?比如说边A 是3 厘米,边B 是4 厘米,边C 是5 厘米,那3 + 4 就得大于5 ,3 + 5 得大于4 ,4 + 5 也得大于3 。
高考数学:解三角形(复习学案)
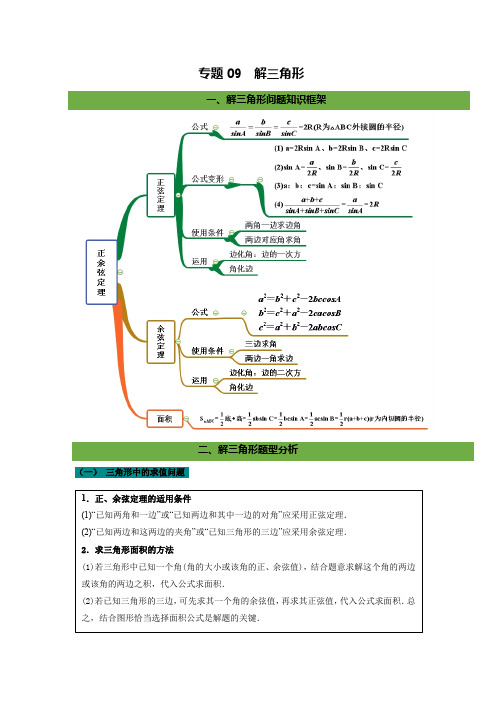
专题09 解三角形(一) 三角形中的求值问题1.例题【例1】设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若a =2,c =23,cos A =32,且b <c ,则b =( )A . 3B .2C .2 2D .3【例2】在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若1a =,cos )cos 0A C C b A ++=,则角A =( )A .23π B .3π C .6π D .56π 【例3】在ABC ∆中,角A ,B ,C 的对边分别是a ,b ,c ,4a =,b =cos (2)cos c B a b C =-,则ABC ∆的面积为______.【例4】(2017·全国高考真题(理))△ABC 的内角、、A B C 的对边分别为a b c 、、, 已知△ABC 的面积为23sin a A.(1)求sin sin B C ;(2)若6cos cos 1,3,B C a ==求△ABC 的周长.【例5】如图,在△ABC 中,∠B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC =17.(1)求sin ∠BAD ; (2)求BD ,AC 的长.2.巩固提升综合练习【练习1】(2019·全国高考真题)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A -b sin B =4c sin C ,cos A =-14,则bc =( )A .6B .5C .4D .3【练习2】(2018·全国高考真题)△ABC 的内角A , B , C 的对边分别为a , b , c ,已知bsinC +csinB =4asinBsinC ,b 2+c 2−a 2=8,则△ABC 的面积为________. 【练习3】 在ABC ∆中,已知AB 边上的中线1CM =,且1tan A ,1tan C ,1tan B成等差数列,则AB 的长为________.【练习4】在△ABC 中,已知AB =2,AC =5,tan ∠BAC =-3,则BC 边上的高等于( ) A .1 B .2 C . 3 D .2【练习5】已知圆内接四边形ABCD 的边长AB =2,BC =6,CD =DA =4,求四边形ABCD 的面积S .【练习6】 △ABC 的内角A ,B ,C 的对边分别为a ,b ,c 已知c cos B =(3a -b )cos C . (1)求sin C 的值;(2)若c =26,b -a =2,求△ABC 的面积.(二)三角形中的最值或范围问题1.例题【例1】在△ABC中,已知c=2,若sin2A+sin2B-sin A sin B=sin2C,则a+b的取值范围为________.【例2】已知在锐角ABC∆中,角A,B,C的对边分别为a,b,c,若2cos cosb Cc B=,则111tan tan tanA B C++的最小值为()A B C D.【例3】已知△ABC的外接圆半径为R,角A,B,C所对的边分别为a,b,c,若a sin B cos C +32c sin C=2R,则△ABC面积的最大值为( )A.25B.45C.255D.125【例4】在ABC∆中,角A,B,C的对边分别为a,b,c,且cos Ccos cos cos2ab Ac A B+=,ABC∆,则ABC∆周长的最小值为______.2.巩固提升综合练习【练习1】 设锐角三角形ABC 的内角,,A B C 所对的边分别为,,a b c ,若2,2a B A ==,则b 的取值范围为( )A .(0,4)B .(2,C .D .4)【练习2】 在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若bc =1,b +2c cos A =0,则当角B 取得最大值时,△ABC 的周长为( ) A .2+3 B .2+2 C .3D .3+2【练习3】已知ABC ∆1,且满足431tan tan A B+=,则边AC 的最小值为_______.【练习4】在ABC ∆中,23BAC π∠=,已知BC 边上的中线3AD =,则ABC ∆面积的最大值为__________.(三)解三角形的实际应用必备知识:实际测量中的有关名称、术语南偏西60°指以正南方向为始边,转向目标方向线形成的角1.例题【例1】在海岸A处,发现北偏东45°方向,距离A处(3-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 3 n mile的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?【例2】如图,A,B两点在河的同侧,且A,B两点均不可到达,测出A,B的距离,测量者可以在河岸边选定两点C,D,测得CD=a,同时在C,D两点分别测得∠BCA=α,∠ACD=β,∠CDB=γ,∠BDA=δ.在△ADC和△BDC中,由正弦定理分别计算出AC和BC,再在△ABC中,应用余弦定理计算出AB.若测得CD=32km,∠ADB=∠CDB=30°,∠ACD=60°,∠ACB=45°,求A,B两点间的距离.【例3】某人在点C测得塔顶A在南偏西80°,仰角为45°,此人沿南偏东40°方向前进100米到D,测得塔顶A的仰角为30°,则塔高为____________米.2.巩固提升综合练习【练习1】甲船在A处,乙船在甲船正南方向距甲船20海里的B处,乙船以每小时10海里的速度向正北方向行驶,而甲船同时以每小时8海里的速度由A处向北偏西60°方向行驶,问经过多少小时后,甲、乙两船相距最近?【练习2】如图,一艘船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这艘船航行的速度为( )A.1762海里/时B .346海里/时 C.1722海里/时D .342海里/时【练习3】某气象仪器研究所按以下方案测试一种“弹射型”气象观测仪器的垂直弹射高度:A 、B 、C 三地位于同一水平面上,在C 处进行该仪器的垂直弹射,观测点A 、B 两地相距100米,∠BAC =60°,在A 地听到弹射声音的时间比在B 地晚217秒.在A 地测得该仪器弹至最高点H 时的仰角为30°,求该仪器的垂直弹射高度CH .(声音的传播速度为340米/秒)1.在△ABC 中,角A ,B ,C 的对边分别是a ,b ,c ,若a ,b ,c 成等比数列,且a 2=c 2+ac -bc ,则cb sin B =( )A .32B .233C .33D .32.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,a =3,c =23,b sin A =a cos ⎪⎭⎫⎝⎛+6πB 则b =( ) A .1 B.2 C.3D.53.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若a =2,c =32,tan B =2tan A ,则△ABC 的面积为( ) A .2 B .3 C .32D .423.如图,在△ABC 中,∠C =π3,BC =4,点D 在边AC 上,AD =DB ,DE ⊥AB ,E 为垂足.若DE =22,则cos A 等于( ) A .223B .24C .64D .634.在锐角三角形ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若B =2A ,则2ba的取值范围是( ) A .(2,2) B .(2,6) C .(2,3)D .(6,4)5.在ΔABC 中,角A 、B 、C 所对的边分别为a ,b ,c ,a =2,B =45°,若三角形有两解,则b 的取值范围是_______.6.已知a ,b ,c 是△ABC 中角A ,B ,C 的对边,a =4,b ∈(4,6),sin 2A =sin C ,则c 的取值范围为________.7.设△ABC 的内角A ,B ,C 的对边a ,b ,c 成等比数列,cos(A -C )-cos B =12,延长BC至点D ,若BD =2,则△ACD 面积的最大值为________.8.(2019·高考全国卷Ⅱ)△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .若b =6,a =2c ,B =π3,则△ABC 的面积为________. 9.若满足3ABC π∠=, AC =3, ,BC m ABC =恰有一解,则实数m 的取值范围是______.10.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,外接圆的半径为1,且tan A tan B =2c -bb ,则△ABC 面积的最大值为________.11.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且a 2+c 2-b 2=ab cos A +a 2cos B . (1)求角B ;(2)若b =27,tan C =32,求△ABC 的面积.12.已知ABC ∆中,角A B C 、、的对边分别为a b c ,,,若cos sin a b C c B =+(Ⅰ)求B ;(Ⅰ)若2b = ,求ABC ∆面积的最大值。
三角形的重心与面积

三角形的重心与面积
在几何学中,三角形是一种基本的多边形,它由三条直线相交而成,每条边上可分别固定三个点,这三个点确定了该三角形的位置,其重心也就随之而定。
三角形的重心是三角形内点的一种特殊位置,它具有一定的特性,可以帮助我们理解三角形的几何结构,并可以作为我们在研究三角形时的参考点。
同时,重心也直接影响着三角形的面积,三角形的面积与重心位置息息相关。
首先,让我们从重心的性质入手,谈谈三角形的重心。
重心是三角形内部某一点,它位于三角形三条边的交点所形成的外接圆上,且与外接圆的圆心重合。
重心不同于其他三角形内部点,它的位置受到三角形三条边的影响,而不仅受三角形的内点的影响。
它是一种具有一定特性的位置,在研究三角形的几何性质时,可以作为参考点,可以帮助我们理解三角形结构框架。
其次,让我们来谈谈三角形的面积,它受重心的影响很大。
根据莱布尼茨三角形定理,三角形的面积可以表示为内角平分线段的乘积:面积=1/2×内角平分线段1×内角平分线段2。
而内角平分线段1和内角平分线段2又被证明与重心位置有关,因此可以得出结论:重心位置与三角形的面积是有关的。
一般来说,三角形的重心越靠近该三角形的长边,其面积也就越大;反之,三角形的重心如果靠近短边,则其面积就会越小。
最后,我们来总结总结本文的内容:重心是三角形内的一个特殊点,它不仅反映了三角形的几何性质,而且也与三角形的面积有
关,重心越靠近长边,三角形面积就越大;反之重心越靠近短边,三角形面积就越小。
三角形的重心与面积之间的关系可以作为我们在研究三角形几何性质时的重要参考。
教学论的三角形

教学论的三角形
教学论的三角形是一种比喻,用来描述教学过程中的三个基本要素及其关系。
这三个要素是教师、学生和教材,它们之间的关系构成了一个三角形的框架。
在这个框架中,教师是主导者,负责设计和实施教学活动,引导学生学习教材中的内容。
学生是参与者,需要积极参与教学过程,主动探索和学握知识。
教材则是教师和学生之间的桥梁,提供了学习的内容和资源。
教学论三角形的理论认为,这三个要素必须相互协调、相互作用,才能取得最佳的教学效果。
教师需要根据学生的特点和需求,选择合适的教材,采用适当的教学方法,激发学生的学习兴趣和动力,促进学生的学习和发展。
同时,学生也需要积极参与到教学过程中,认真听讲、思考和实践,才能真正学握知识并转化为自己的能力。
总之,教学论的三角形提供了一种理解和分析教学过程的模型,帮助教师深入思考如何有效地设计和实施教学活动,提高教学质量和效果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《做框架》:科教版六年级科学上册第四单元 第五课
设计人:王华英
房县红塔镇高碑小学
巴黎铁塔是法国最著名的建筑,该塔高320.7米,是世界上最高的著
三角形框架
三角形框架具有稳定性
三角形每条用
拉
推
四边形框架
• 四边形框架特点:不稳定
给正方形增加斜杆
• 正方形内斜杆的作用:推和拉
推 拉
斜杆的作用:
斜杆在四边形内起到“推”和 “拉”的作用,阻止了框架的倾斜、 垮塌,使框架更具稳定性。
三角形和四边形在生活中应用: 用三角形和四边形来加固框架结构, 使框架结构稳定性更强。
小结:
1.三角形、四边形是最简单、 最基本的框架。
2.框架结构的特点:稳定强,节 省材料,减少了空气对框架的阻力。
