正射影和三垂线定理PPT优选课件
合集下载
《三垂线定理》课件
垂直的判定定理,这两条直线可以是:①相交直线
注意:如果将定理中“在平面内” ②异面直线
的条件去掉,结论仍然成立吗?
定理就不一定成立
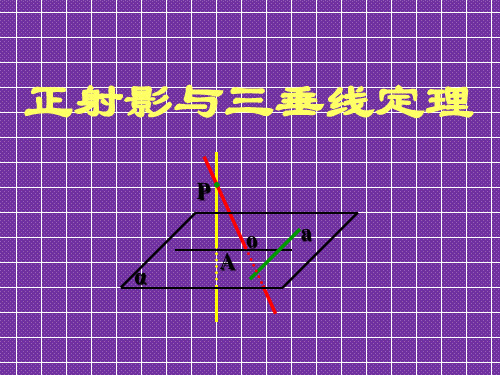
线射垂直 P
A
α
?P
Oa
A
α
线斜垂直
Oa
三垂线定理的逆定理
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。
区别 1、条件和结论上区分:线射垂直 线斜垂直 2、作用上区分:共面直线垂直 异面直线垂直
AD在平面BCD上的射影。
∵AB⊥CD,∴BO⊥CD,
同理CO⊥BD,
B
D
于是O是△BCD的垂心,
O
∴DO⊥BC,于是AD⊥BC.
C
练习:
判断下列命题的真假:
D1
⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( ×)
A1
C1 B1
⑵若 a是平面α的斜线,平面β内
的直线b垂直于a在平面α内的射
一面,四线,三垂直
①线面垂直 ②线射垂直 ③ 线斜垂直
P
P
P
A Oa
A Oa
A Oa
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
例1、 直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD
C B
AO a α
P P
C A
M B
三垂线定理解题的关键:找三垂! 怎么找?
程序:一垂、二射、三证
解 第一、找平面(基准面)及平面垂线 第二、找射影线,
注意:如果将定理中“在平面内” ②异面直线
的条件去掉,结论仍然成立吗?
定理就不一定成立
线射垂直 P
A
α
?P
Oa
A
α
线斜垂直
Oa
三垂线定理的逆定理
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。
区别 1、条件和结论上区分:线射垂直 线斜垂直 2、作用上区分:共面直线垂直 异面直线垂直
AD在平面BCD上的射影。
∵AB⊥CD,∴BO⊥CD,
同理CO⊥BD,
B
D
于是O是△BCD的垂心,
O
∴DO⊥BC,于是AD⊥BC.
C
练习:
判断下列命题的真假:
D1
⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( ×)
A1
C1 B1
⑵若 a是平面α的斜线,平面β内
的直线b垂直于a在平面α内的射
一面,四线,三垂直
①线面垂直 ②线射垂直 ③ 线斜垂直
P
P
P
A Oa
A Oa
A Oa
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
例1、 直接利用三垂线定理证明下列各题:
(1) PA⊥正方形ABCD所在平面,O为对角线BD的中点 求证:PO⊥BD,PC⊥BD
C B
AO a α
P P
C A
M B
三垂线定理解题的关键:找三垂! 怎么找?
程序:一垂、二射、三证
解 第一、找平面(基准面)及平面垂线 第二、找射影线,
正射影和三垂线定理 PPT课件 人教课标版

•
30、经验是由痛苦中粹取出来的。
•
31、绳锯木断,水滴石穿。
•
32、肯承认错误则错已改了一半。
•
33、快乐不是因为拥有的多而是计较的少。
•
34、好方法事半功倍,好习惯受益终身。
•
35、生命可以不轰轰烈烈,但应掷地有声。
•
36、每临大事,心必静心,静则神明,豁然冰释。
•
37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。
练 习 :如 图 ,A是 平 面 BCD外 一 点 ,
ABCD,ACBD.
求证: AD⊥ BC 证明:设O是A在平面BCD内的射影, A
∵AB⊥CD,AC⊥BD,
∴BO⊥CD,CO⊥BD,
(三垂线逆定理)
B
O
D
∴O是三角形BDC的垂心,
C
∴DO⊥BC,(三角形的性质)
∴AD⊥BC,(三垂线定理)
平面内的直线 和平面的一条 斜线垂直
巩固练习:
1、两平行直线在一平面内的射影不可能是(D)
A、 两平行直线 B、两点
C、一条直线
D、两相交直线
2、两直线在平面内的射影是两相交直线,则这
两直线的位置关系不是(B )
A、两异面直线; B、两平行直线
C、两相交直线; D、以上都不对 3.斜线b在面α内的射影为c,直线a ⊥c,则a
•
80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
解: 在路上取点C、D使BC垂直 于CD,且角CDB为450。 测得CD=20m
因BC是AC在地面上的射影,且 CD垂直于BC,故CD垂直于AC
CDB450,CDBC,
CD20m.BC20m.
立体几何之三垂线定理 PPT

P
A
a
O
α
三垂线定理说明(2)
• 如果平面α内得直线a垂直于斜线 OP得射影OA,那么α必垂直于斜线 OP;反之也成立
P
A
a
O
α
三垂线定理说明(3)
• 满足条件(2)得直线a必垂直于斜线 及射影所确定得平面
P
A
a
O
α
三垂线定理说明(4)
• 运用三垂线定理及逆定理得规律: 确定平面、找到斜线、找到(做出) 垂线、连成射影、查面内线
则AG BC,连结A'G则A'G BC
A'F FG 3 a A'G 6 a
4
4
即A'点到BC的距离是 6 a 4
AG 3 a, 2
A
E F D
B
C G
垂直于AB的两条相等的斜线,且分别在 AB的两侧,若AB 5cm,AC BD 8cm,
AB和平面的距离为7cm,求CD的长
A
B
C
A1 O α
B1 D
举一个例子
分析:①因为AB 平面,又因为AB AC,
A
B
AB BD,则应想AA1 BB1 7cm且AA1 所以A1B1 AB 5cm
得距离 • 求二面角得平面角
一些例子
• 判定空间中两条直线相互垂直
已知:正方体中截去以P为定点的一角得截面ABC 求证:所截得的 ABC是锐角三角形
P C
A
B
一些例子
• 判定空间中两条直线相互垂直
证明:过P作PD AB于D, ABP是Rt , PD的垂足D在AB内, 连结CD,由三垂线定理可知,CD AB, CD为 ABC中AB边上的高线且满足垂足在AB内, 同理可证 ABC中BC边、AC边上的高线的垂足也在BC、AC内 ABC的垂心在 ABC内,故 ABC为锐角三角形
三垂线定理及其典型例题ppt课件

思考:
a 如果把定理中的条a⊥AO与结 论a⊥PO互换,命题是否成立?
三垂线定理的逆定理: 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
在平面内的一条直线,如果它和这个平面的一条 斜线垂直,那么它也和这条斜线在这个平面内的 射影垂直。
三垂线定理
(1)若a是平面α的斜线、直线b垂直于a在平面
α内的射影,则a⊥b。
( ×)
(2)若a是平面α的斜线,b是平面α内的直线,
且b垂直于a在β内的射影,则a⊥b。
( ×)
强调:1°四线是相对同一个平面而言
2°定理的关键找“平面”这个参照学。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
P a
Ao α
用法:
∵PA⊥α, a α,
AO是斜线PO在平面 α内的射影, a⊥PO ∴ a⊥AO
说明:三垂线定理及其逆定理是证明线线垂
直的重要方法。
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
例题分析: 1、判定下列命题是否正确
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
复习提问:
1。直线与平面垂直的定义。 2。直线与平面垂直的判定定理。 3。证明线面垂直的方法。 4。证明线线垂直的方法。
一、射影的概念 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
三垂线定理(微课件)

斜线的射影垂直,那么它也和这条斜线垂直。
PA⊥α ①
aα
PA⊥a
AO⊥a
②
a⊥平面PAO
PO 平面PAO
③
a⊥PO
P
a
Ao α
① 线面垂直
②
③
线线垂直
线面垂直
线线垂直
性质定理
判定定理
性质定理
对三垂线定理的说明:
三垂线定理
1、三垂线定理描述的是PO(斜线)、AO(射影)、Leabharlann a(直线)之间的垂直关系。
感谢莅临指导!
再见!
P a
Ao α
用法:
∵PA⊥α, a α,
AO是斜线PO在平面 α内的射影, a⊥PO ∴ a⊥AO
说明:三垂线定理及其逆定理是证明线线垂
直的重要方法。
小结
三垂线定理
三垂线定理:在平面内的一条直线,如果 和这个平面的一条斜线的射影垂直,那么它也 和这条斜线垂直。
1°定理中四条线均针对同一平面而言 2°应用定理关键是找“基准面”这个参照系 3°操作程序分三个步骤——“一垂二射三证”
三垂线定理
P
oa
α
A
平面的斜线、垂线、射影
三垂线定理
PO是平面α的斜线, O为斜足; PA是平面α的垂线, A为垂足; P AO是PO在平面α内的射影.
oa
如果a α, a⊥AO,
α
A
思考a与PO的位置关
系如何?
结论:a⊥PO
三垂线定理:
为什么呢?
三垂线定理
在平面内的一条直线,如果和这个平面的一条
2、a与PO可以相交,也可以异面。
3、三垂线定理的实质是平面的一条斜线和
9.4.3 正射影和三垂线定理(11)名师课件

①射影相等的两条斜线段相等,射 影较长的斜线段也较长;
B
O
C
②相等的斜线段的射影相等,较长的斜线段的射影也较长;
③垂线段比任何一条斜线段都短。
二.三垂线定理
ቤተ መጻሕፍቲ ባይዱ
1.三垂线定理
在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,
那么它就和这条斜线垂直。
P
已知 :PO、PA分别是平面的垂线、
斜线,OA是PA在平面上的射
A
B
90°
C
45°
D
例2 在正方体AC1中, 求证: A1C⊥面AB1D1
C D
C1 D1
B A
B1 A1
我们要学会从纷繁的已知条件中找出 或者创造出符合三垂线定理的条件 ,怎么找?
P
解 题
α
A
Oa
回
顾 A1
C1 B1
C B
AO a α
PP
C A
M B
4. 逆定理
在平面内的一条直线,如果和这个平面的一 条斜线垂直,那么,它也和这条斜线的射影垂直。
在Rt△PBC中,PE= 4--×---6- = -1-2-42+62 13
在Rt△APE中,AE= PA2+PE 2= 3 13
B 377
三. 练习 ①课本P24. 1,2,3 ②课本P25. 5
斜线上一点与斜足间的线段 叫做这点到这个平面的斜线段。
过斜线上斜足以外的一点向平面引垂线,过垂足和斜足的 直线叫做斜线在这个平面上的射影;
垂足与斜足间的线段叫做这点到平面的斜线段在这个平面 上的射影。
斜线上任意一点在平面上的射影,一定在斜线的射影上。
3.射影长定理
正射影和三垂线定理PPT课件

已知 :PO、PA分别是平面的垂线、斜线,
OA是PA在平面内的射影。a
,a
⊥OA
。
三垂线
求证: a ⊥PA
定理
证明:PO⊥
a
PO ⊥a a ⊥ OA
P
O
a A
POPOAA==PO
a⊥平面PAO
PA平面PAO
a⊥PA
线射垂直
P
定理 逆定理
线斜垂直
P
A Oa α
三垂线定理:
A Oa α
三垂线定理的逆定理
体功能比例尺度,能符合人体使用功能上的要求,具有很高的科学性。以椅子为例,其中的弯背椅、圈椅均契合人体需要,坐感舒适。 二、造型优美 庄重典雅的红木家具,在变化中求统一,雕饰精细,线条流畅。既有简洁大方的仿明式,又有雕龙画凤、精心雕琢的仿清式,
也有典雅大方的法式等,适合不同人的审美需求。 ; / 仙游红木家具 jah31kbf
(×)
⑷若a是平面α的斜线,b∥α,直线)
P
a
AO
α
课堂小结:
1、三垂线定理是研究空间线面位置关系的关键性定理, 承上启下,涉及与“垂直”有关的几乎所有领域。 2、三垂线定理主要应用于:解决垂直问题与空间图形度量
(如角和距离)问题.
3、三垂线定理的基本模式导析
D C
P
解
题
A Oa α
回
顾 A1
C1 B1
C B
AO a α
P P
C A
M B
三垂线定理是平面
的一条斜线与平面内
回 顾
的直线垂直的判定定 理,这两条直线可以 是:
P
思
考 ①相交直线
e dc
②异面直线
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“在平面内”的条件
回 去掉,结论仍然成立 吗?
顾
思 考
直线a 一定要在平 面内,如果 a 不
在平面内,定理就
不一定成立。
α
2020/10/18
P
b
Oa
A
19
练习:
判断下列命题是否正确: ⑴若a是平面α的斜线,直线b垂直于
a在平面α内的射影,则 a⊥b ( ×)
⑵若 a是平面α的斜线,平面β内
的直线b垂直于a在平面α内的射
影,则 a⊥b
( ×)
⑶若a是平面α的斜线,直线b α
且b垂直于a在另一平面β内的射
影则a⊥b
(×)
2020/10/18
20
⑷若a是平面α的斜线,b∥α,直线 b垂直
于a在平面α内的射影,则 a⊥b (
)
P
a
AO
α
2020/10/18
21
课堂小结:
1、三垂线定理是研究空间线面位置关系的关键性定理, 承上启下,涉及与“垂直”有关的几乎所有领域。 2、三垂线定理主要应用于:解决垂直问题与空间图形度量
B
12
练习:1、正方体ABCD-A’B’C’D’ (1)找平面AC的斜线BD’在平面AC上的射影; (2)BD’与AC的位置关系如何?
DD’ ’ A’
C’ B’
D
C
O
2020/10/18
A
B
13
2.正方体ABCD-A’B’C’D’ D’
(1)求证:BD’⊥A’C’
A’
(2)求证:BD’⊥B’C
D
2
一、点在平面上的射影
自点P向平面α引垂线 l, 垂足P1叫做
点P在平面α内的正射影(简称射影)
P
l
α
P1
2020/10/18
3
二、图形在平面内的射影
如果图形F上的所有点在一平面内的射影构成的
图形 F ,则 F 叫做图形F在这个平面上的射影.
C B
A
C
B
2020/10/18
A
4
斜线 —— 与平面相交且不垂直的直线
求证:BC⊥PM.
P
2. PA⊥平面ABC,PB=PC, A M是BC的中点。 求证:AM⊥BC.
2020/10/18
C M B
11
1.PA⊥平面ABC,AB=AC,M是BC的中点。 求证:BC⊥PM.
P
2. PA⊥平面ABC,PB=PC,
M是BC的中点。
A
C
求证:AM⊥BC.
M
2020/10/18
(如角和距离)问题.
3、三垂线定理的基本模式导析
b
(1)、一面四线
c
l
2020/10/18
a
22
谢谢您的聆听与观看
THANK YOU FOR YOUR GUIDANCE.
感谢阅读!为了方便学习和使用,本文档的内容可以在下载后随意修改,调整和打印。欢迎下载!
汇报人:XXX 日期:20XX年XX月XX日
2020/10/18
1
复习提问
1、直线和平面垂直的定义是什么?
如果一条直线和一个平面相交,并且和这 个平面内的任意一条直线都垂直,则这条直 线和这个平面互相垂直。交点叫做垂足。
2、如何判定直线与平面垂直? 如果一条直线和一个平面内的两条相交
直线都垂直,那么这条直线垂直这个平面。
2020/10/18
A
C’ B’
C B
2020/10/18
14
2.正方体ABCD-A’B’C’D’ D’
(1)求证:BD’⊥A’C’
A’
(2)求证:BD’⊥B’C
D
A
C’ B’
C B
2020/10/18
15
例2:正方形ABCD 的边长为12,PA⊥平面ABCD, PA=12,O为对角线BD的中点, 求:点P到对角线BD的距离
P
a
O
A
2020/10/18
7
在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么它就和这条斜线垂直。
已知 :PO、PA分别是平面的垂线、斜线,
OA是PA在平面内的射影。a
,a
⊥OA
。
三垂线
求证: a ⊥PA
定理
证明:PO⊥
a
PO ⊥a a ⊥ OA
P
O
a A
POPOAA==PO
a⊥平面PAO
a⊥PA
PAO 2020/10/18 PA平面
8
线射垂直
P
定理 逆定理
线斜垂直
P
A Oa α
三垂线定理:
A Oa α
三垂线定理的逆定理
平面内的一条直线和 平面内的一条直线和
平面的一条斜线在平面 平面的一条斜线垂直,则
内的射影垂直,则它就 它也和这条斜线的射影垂
和这条斜线 垂直 。
直。
2020/10/18
斜足 —— 斜线与平面交点 斜线段—— 斜线上一点与斜足之间线段
斜线
A
A O α
O
B
ι
射影
2020/10/18
5
P
a
O
A
2020/10/18
6
在平面内的一条直线,如果和这个平面的一条 斜线的射影垂直,那么,它就和这条斜线垂直。
已知 :PO、PA分别是平面的垂线、斜线,
OA是PA在平面内的射影。a ,a⊥OA。 求证:a ⊥PA
P
A
D
O
B
C
2020/10/18
16
P
解
题
A Oa α
回
顾 A1
C1 B1
2020/10/18
C B
AO a α
P P
C A
M
17
B
三垂线定理是平面
的一条斜线与平面内
回 顾
的直线垂直的判定定 理,这两条直线可以 是:
P
思
考 ①相交直线
e dc
②异面直线
αA
Ob a
2020/10/18
18
注意:如果将定理中
9
三垂线定理及逆定理涉及的几何元素:
(1)一个平面;
(2)四条直线: ①平面的斜线;
②平面的垂线;
③斜线条直线.
(3)三个垂直:
①直线与平面垂直;
②平面内的一条直线与斜线在平面内的 射影垂直;
2020/③10/18平面内的一条直线与斜线垂直. 10
1.PA⊥平面ABC,AB=AC,M是BC的中点。
