苏教版八年级上学期期末复习数学试题
苏科版八年级上学期期末数学试卷 (解析版)

苏科版八年级上学期期末数学试卷 (解析版) 一、选择题1.如图,以数轴的单位长度为边作一个正方形,以原点为圆心,正方形的对角线长为半径画弧,交数轴于点A ,则点A 表示的数为( )A .12+B .21-C .2D .322.变量x 、y 有如下的关系,其中y 是x 的函数的是( ) A .28y x = B .||y x = C .1y x = D .412x y =3.对函数31y x =-,下列说法正确的是( )A .它的图象过点(3,1)-B .y 值随着x 值增大而减小C .它的图象经过第二象限D .它的图象与y 轴交于负半轴4.在平面直角坐标系中,点()23P -,关于x 轴的对称点的坐标是( ) A .()23-, B .()23, C .()23--, D .()23-,5.下列图形中的五边形ABCDE 都是正五边形,则这些图形中的轴对称图形有( )A .1个B .2个C .3个D .4个 6.若2149x kx ++是完全平方式,则实数k 的值为( ) A .43 B .13 C .43± D .13± 7.在22、0.3•、227-38( ) A .1个B .2个C .3个D .4个 8.已知一次函数y=kx+b ,函数值y 随自变置x 的增大而减小,且kb <0,则函数y=kx+b的图象大致是( )A.B.C.D.9.下列说法正确的是()A.(﹣3)2的平方根是3 B.16=±4C.1的平方根是1 D.4的算术平方根是210.点P(3,﹣4)关于y轴的对称点P′的坐标是()A.(﹣3,﹣4)B.(3,4)C.(﹣3,4)D.(﹣4,3)11.一组不为零的数a,b,c,d,满足a cb d=,则以下等式不一定成立的是()A.ac=bdB.a bb+=c dd+C.9ab-=9cd-D.99a ba b-+=99c dc d-+12.关于等腰三角形,以下说法正确的是()A.有一个角为40°的等腰三角形一定是锐角三角形B.等腰三角形两边上的中线一定相等C.两个等腰三角形中,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等D.等腰三角形两底角的平分线的交点到三边距离相等13.下列图形中:①线段,②角,③等腰三角形,④有一个角是30°的直角三角形,其中一定是轴对称图形的个数()A.1个B.2个C.3个D.4个14.如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是()A.9cm B.12cm C.15cm D.18cm15.正比例函数y=kx(k≠0)的函数值y随着x增大而减小,则一次函数y=x+k的图象大致是()A.B.C.D .二、填空题16.星期天,小明上午8:00从家里出发,骑车到图书馆去借书,再骑车回到家.他离家的距离y (千米)与时间t (分钟)的关系如图所示,则上午8:45小明离家的距离是__千米.17.在311,2π,122-,0,0.454454445…,319中,无理数有______个. 18.如图,D 在BC 边上,△ABC ≌△ADE ,∠EAC =40°,则∠B 的度数为_____.19.在平面直角坐标系中,将点()3, 2P -先向右平移2个单位长度, 再向下平移2个单位长度后所得到的点坐标为_________.20.某工厂现在平均每天比原计划多生产50台机器,现在生产600台机器所需时间比原计划生产450台机器所需时间相同,现在平均每天生产___台机器.21.一次函数1y kx b =+与2y x a =+的图象如图,则()0kx b x a +-+>的解集是__.22.如图,△ABC 中,AD 平分∠BAC ,AB =4,AC =2,且△ABD 的面积为2,则△ABC 的面积为_________.23.教材上“阅读与思考”曾介绍“杨辉三角”(如图),利用“杨辉三角”展开(1﹣2x )4=a 0+a 1x+a 2x 2+a 3x 3+a 4x 4,那么a 1+a 2+a 3+a 4=_____.24.如图,在平面直角坐标系中,点A 、B 的坐标分别为()1,4、()3,4,若直线y kx =与线段AB 有公共点,则k 的取值范围为__________.25.如图,在△ABC 中,∠C =90°,∠B =22.5°,DE 垂直平分AB 交BC 于点E ,EC =1,则三角形ACE 的面积为__.三、解答题26.甲、乙两地间的直线公路长为400千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发1小时,途中轿车出现了故障,停下维修,货车仍继续行驶.1小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离y (千米)与轿车所用的时间x (小时)的关系如图所示,请结合图象解答下列问题:(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;t 值为_______. (2)求轿车距其出发地的距离y (千米)与所用时间x (小时)之间的函数关系式并写出自变量x 的取值范围;(3)请直接写出货车出发多长时间两车相距90千米.27.已知2y -与x 成正比例,当2x =时,6y =. (1)求y 与x 的函数关系式;(2)当6y >时,求x 的取值范围.28.先化简,再求值:35(2)362x x x x -÷+---,其中53x =- 29.如图,ABC ∆中,90BAC ∠=,8AC cm =,DE 是BC 边上的垂直平分线,ABD ∆的周长为14cm ,求BC 的长.30.直角三角形ABC 中,90ABC ∠=︒,点D 为AC 的中点,点E 为CB 延长线上一点,且BE CD =,连接DE .(1)如图1,求证2C E ∠=∠(2)如图2,若6AB =、5BE =,ABC ∆的角平分线CG 交BD 于点F ,求BCF ∆的面积.31.(1)计算:203(12125(39)(45)(45);π---+⨯-(2)求x 的值:23(3)27.x +=【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【解析】【分析】先根据勾股定理求出正方形对角线的长,然后根据实数与数轴的关系解答即可.【详解】,∴点A .故选C.【点睛】本题考查了勾股定理,以及实数与数轴,主要是数轴上无理数的作法,需熟练掌握.2.C解析:C【解析】【分析】根据函数的定义:对于x 的每一个取值,y 都有唯一确定的值与之对应即可确定有几个函数.【详解】A. 28y x =,y 不是x 的函数,故错误;B. ||y x =,y 不是x 的函数,故错误;C. 1y x =,y 是x 的函数,故正确; D. 412x y =,y 不是x 的函数,故错误; 故选C.【点睛】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x ,y ,对于x 的每一个取值,y 都有唯一确定的值与之对应,则y 是x 的函数,x 叫自变量.3.D解析:D【解析】【分析】根据一次函数的性质,对每一项进行判断筛选即可.【详解】A 将x=3代入31y x =-得:3×3-1=8,A 选项错;B .一次函数k >0,y 值随着x 值增大而增大,B 选项错;C .一次函数k >0,y 值随着x 值增大而增大,当x=0时,y=-1,故此函数的图像经过一、三、四象限,C 选项错;D .当x=0时,y=-1,一次函数的图象与y 轴交于负半轴,D 项正确.故选D.【点睛】本题考查了一次函数的性质,解决本题的关键是正确理解题意,熟练掌握一次函数的性质. 4.B解析:B【解析】【分析】根据关于x 轴对称的点的坐标与原坐标横坐标相等,纵坐标互为相反数的性质解答即可.【详解】∵P (2,-3)关于x 轴对称,∴对称点与点P 横坐标相同,纵坐标互为相反数,∴对称点的坐标为(-2,-3).故答案为(-2,-3).【点睛】本题考查的是坐标与图形的变换,关于y 轴对称的点的坐标与原坐标纵坐标相等,横坐标互为相反数;关于x 轴对称的点的坐标与原坐标横坐标相等,纵坐标互为相反数;掌握轴对称的性质是解题的关键,5.D解析:D【解析】分析:直接利用轴对称图形的性质画出对称轴得出答案.详解:如图所示:直线l 即为各图形的对称轴.,故选:D .点睛:此题主要考查了轴对称图形,正确把握轴对称图形的定义是解题关键.6.C解析:C【解析】【分析】本题是已知平方项求乘积项,根据完全平方式的形式可得出k 的值.【详解】由完全平方式的形式(a±b )2=a 2±2ab+b 2可得: kx=±2•2x•13, 解得k=±43. 故选:C【点睛】本题关键是有平方项求乘积项,掌握完全平方式的形式(a±b )2=a 2±2ab+b 2是关键. 7.A解析:A【解析】【分析】根据无理数的三种形式,①开方开不尽的数,②无限不循环小数,③含有π的数,结合题意判断即可.【详解】解:在实数2、•0.3、227-中,2是无理数; •0.3循环小数,是有理数;227-是分数,是有理数;=2,是整数,是有理数;所以无理数共1个.故选:A .【点睛】此题考查了无理数的概念,解答本题的关键是掌握无理数的定义,属于基础题,要熟练掌握无理数的三种形式,难度一般.8.A解析:A【解析】试题分析:根据一次函数的性质得到k <0,而kb <0,则b >0,所以一次函数y=kx+b 的图象经过第二、四象限,与y 轴的交点在x 轴是方.解:∵一次函数y=kx+b ,y 随着x 的增大而减小,∴k <0,∴一次函数y=kx+b 的图象经过第二、四象限;∵kb <0,∴b >0,∴图象与y 轴的交点在x 轴上方,∴一次函数y=kx+b 的图象经过第一、二、四象限.故选A .考点:一次函数的图象.9.D解析:D【解析】【分析】根据平方根和算术平方根的定义解答即可.【详解】A 、(﹣3)2的平方根是±3,故该项错误;B 4,故该项错误;C 、1的平方根是±1,故该项错误;D 、4的算术平方根是2,故该项正确.故选D.【点睛】本题考查了平方根、算术平方根的定义,解决本题的关键是熟记平方根、算术平方根的定义.10.A解析:A【解析】试题解析:∵点P (3,-4)关于y 轴对称点P′,∴P′的坐标是:(-3,-4).故选A .11.C解析:C【解析】【分析】根据比例的性质,对所给选项进行整理,找到不一定正确的选项即可.【详解】 解:一组不为零的数a ,b ,c ,d ,满足a c b d=, ∴a b c d =,11a c b d +=+,即a b c d b d ++=,故A 、B 一定成立; 设a c k b d==, ∴a bk =,c dk =, ∴999999a b kb b k a b kb b k ---==+++,999999c d kd d k c d kd d k ---==+++,∴9999a b c da b c d--=++,故D一定成立;若99a cb d--=则99a cb b d d-=-,则需99b d=,∵b、d不一定相等,故不能得出99a cb d--=,故D不一定成立.故选:C.【点睛】本题考查了比例性质;根据比例的性质灵活变形是解题关键.12.D解析:D【解析】【分析】根据全等三角形的判定定理,等腰三角形的性质,三角形的内角和判断即可.【详解】解:A:如果40︒的角是底角,则顶角等于100︒,故三角形是钝角三角形,此选项错误;B、当两条中线为两腰上的中线时,可知两条中线相等,当两条中线一条为腰上的中线,一条为底边上的中线时,则这两条中线不一定相等,∴等腰三角形的两条中线不一定相等,此选项错误;C、如图,△ABC和△ABD中,AB=AC=AD,CD∥AB,DG是△ABD 的AB边高,CH是是△ABC 的AB边高,则DG=CH,但△ABC和△ABD不全等;故此选项错误;D、三角形的三个内角的角平分线交于一点,该点叫做三角形的内心.内心到三边的距离相等.故此选项正确;故选:D.【点睛】本题考查了全等三角形的判定,等腰三角形的性质,三角形的内角和,熟练掌握各知识点是解题的关键.13.C解析:C【解析】【分析】直接利用轴对称图形的性质分别分析得出答案.【详解】解:①线段,是轴对称图形;②角,是轴对称图形;③等腰三角形,是轴对称图形;④有一个角是30°的直角三角形,不是轴对称图形.故选:C .【点睛】本题考查的知识点是轴对称图形的定义,理解定义内容是解此题的关键. 14.D解析:D【解析】【分析】首先根据题意画出图形,利用勾股定理计算出AC 的长.【详解】根据题意可得图形:AB=12cm ,BC=9cm ,在Rt △ABC 中:2222=129AB BC ++(cm ),则这只铅笔的长度大于15cm .故选D .【点睛】此题主要考查了勾股定理的应用,正确得出笔筒内铅笔的最短长度是解决问题的关键.15.A解析:A【解析】【分析】根据自正比例函数的性质得到k <0,然后根据一次函数的性质得到一次函数y=x+k 的图象经过第一、三象限,且与y 轴的负半轴相交.【详解】解:∵正比例函数y=kx (k≠0)的函数值y 随x 的增大而减小,∴k <0,∵一次函数y=x+k 的一次项系数大于0,常数项小于0,∴一次函数y=x+k 的图象经过第一、三象限,且与y 轴的负半轴相交.故选A .【点睛】本题考查了一次函数图象:一次函数y=kx+b (k 、b 为常数,k≠0)是一条直线,当k >0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).二、填空题16.5.【解析】【分析】首先设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b,然后再把(40,2)(60,0)代入可得关于k、b的方程组,解出k、b的值,进而可得函数解解析:5.【解析】【分析】首先设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b,然后再把(40,2)(60,0)代入可得关于k、b的方程组,解出k、b的值,进而可得函数解析式,再把t=45代入即可.【详解】设当40≤t≤60时,距离y(千米)与时间t(分钟)的函数关系为y=kt+b.∵图象经过(40,2)(60,0),∴240060k bk b=+⎧⎨=+⎩,解得:1106kb⎧=-⎪⎨⎪=⎩,∴y与t的函数关系式为y=﹣16 10t+,当t=45时,y=﹣110×45+6=1.5.故答案为1.5.【点睛】本题主要考查了一次函数的应用,关键是正确理解题意,掌握待定系数法求出函数解析式.17.3【解析】【分析】根据无理数的定义进行判断.【详解】解:根据无理数的定义可知,,0.454454445…,为无理数,共3个.故答案为:3.【点睛】本题考查了无理数.解题的关键是掌握无解析:3【解析】【分析】根据无理数的定义进行判断.【详解】解:根据无理数的定义可知,2 ,0.4544544453个.故答案为:3.【点睛】本题考查了无理数.解题的关键是掌握无理数的三种形式:①开方开不尽的数,②无限不循环小数,③含有π的数.18.70°.【解析】【分析】根据全等三角形的性质得出AB=AD,∠BAC=∠DAE,求出∠BAD=∠EAC=40°,根据等腰三角形的性质得出∠B=∠ADB,即可求出答案.【详解】解:∵△ABC解析:70°.【解析】【分析】根据全等三角形的性质得出AB=AD,∠BAC=∠DAE,求出∠BAD=∠EAC=40°,根据等腰三角形的性质得出∠B=∠ADB,即可求出答案.【详解】解:∵△ABC≌△ADE,∴AB=AD,∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,∴∠BAD=∠EAC,∵∠EAC=40°,∴∠BAD=40°,∵AB=AD,∴∠B=∠ADB=12(180°﹣∠BAD)=70°,故答案为:70°.【点睛】本题考查了全等三角形的性质,等腰三角形的性质和三角形内角和定理等知识点,能根据全等三角形的性质得出AB =AD 和求出∠BAD =∠EAC 是解此题的关键.19.(-1,0)【解析】【分析】根据横坐标右移加,左移减;纵坐标上移加,下移减,即可得到.【详解】解:点先向右平移个单位长度, 再向下平移个单位长度后所得到的点坐标为(-3+2,2-2),即(解析:(-1,0)【解析】【分析】根据横坐标右移加,左移减;纵坐标上移加,下移减,即可得到.【详解】解:点()3, 2P -先向右平移2个单位长度, 再向下平移2个单位长度后所得到的点坐标为(-3+2,2-2),即(-1,0)故答案为:(-1,0)【点睛】此题主要考查了坐标与图形的变化-平移:向右平移a 个单位,坐标P (x ,y )得到P '(x+a ,y);向左平移a 个单位,坐标P (x ,y )得到P '(x-a ,y);向上平移a 个单位,坐标P (x ,y )得到P '(x ,y+a);向下平移a 个单位,坐标P (x ,y )得到P '(x ,y-a). 20.200【解析】【分析】【详解】设现在平均每天生产x 台机器,则原计划可生产(x ﹣50)台,根据现在生产600台机器的时间与原计划生产450台机器的时间相同,等量关系为:现在生产600台机器时解析:200【解析】【分析】【详解】设现在平均每天生产x 台机器,则原计划可生产(x ﹣50)台,根据现在生产600台机器的时间与原计划生产450台机器的时间相同,等量关系为:现在生产600台机器时间=原计划生产450台时间,从而列出方程:600450x x 50=-, 解得:x=200.检验:当x=200时,x (x ﹣50)≠0.∴x=200是原分式方程的解.∴现在平均每天生产200台机器.21.【解析】【分析】不等式kx+b-(x+a )>0的解集是一次函数y1=kx+b 在y2=x+a 的图象上方的部分对应的x 的取值范围,据此即可解答.【详解】解:不等式的解集是.故答案为:.【点解析:1x <-【解析】【分析】不等式kx+b-(x+a )>0的解集是一次函数y 1=kx+b 在y 2=x+a 的图象上方的部分对应的x 的取值范围,据此即可解答.【详解】解:不等式()0kx b x a +-+>的解集是1x <-.故答案为:1x <-.【点睛】本题考查了一次函数的图象与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=kx+b 的值大于(或小于)0的自变量x 的取值范围;从函数图象的角度看,就是确定直线y=kx+b 在x 轴上(或下)方部分所有的点的横坐标所构成的集合.22.3;【解析】【分析】过D 作DE⊥AB 于E ,DF⊥AC 于F ,由面积可求得DE ,根据角平分线的性质可求得DF ,可求得△ACD 的面积,进而求△ABC 的面积.【详解】解:过点D 作DE⊥AB 于E ,解析:3;【解析】【分析】过D 作DE ⊥AB 于E ,DF ⊥AC 于F ,由面积可求得DE ,根据角平分线的性质可求得DF ,可求得△ACD 的面积,进而求△ABC 的面积.【详解】解:过点D 作DE ⊥AB 于E ,DF ⊥AC 于F ,∵S △ABD =2∴12AB•DE=2, 又∵AB=4 ∴12×4×DE=2,解得DE=1, ∵AD 平分∠BAC ,且DE ⊥AB ,DF ⊥AC∴DF=DE=1,∴S △ACD =12 AC•DF=12×2×1=1, ∴S △ABC =S △ABD +S △ACD =2+1=3故答案为:3.【点睛】 本题主要考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键. 23.0【解析】【分析】令求出的值,再令即可求出所求式子的值.【详解】解:令,得:,令,得:,则,故答案为:0.【点睛】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.解析:0【解析】【分析】令0x =求出0a 的值,再令1x =即可求出所求式子的值.【详解】解:令0x =,得:01a =,令1x =,得:012341a a a a a ++++=,则12340a a a a +++=,故答案为:0.【点睛】此题考查了代数式求值,熟练掌握运算法则是解本题的关键.24.【解析】【分析】由直线与线段AB 有公共点,可得出点B 在直线上或在直线右下方,利用一次函数图象上点的坐标特征,即可得出关于k 的一元一次不等式,解之即可得出k 的取值范围.【详解】解:∵点A 、B 解析:443k ≤≤ 【解析】【分析】由直线y kx =与线段AB 有公共点,可得出点B 在直线上或在直线右下方,利用一次函数图象上点的坐标特征,即可得出关于k 的一元一次不等式,解之即可得出k 的取值范围.【详解】解:∵点A 、B 的坐标分别为()1,4、()3,4,∴令y=4时, 解得:4x k= , ∵直线y=kx 与线段AB 有公共点,∴1≤4k≤3, 解得:443k ≤≤. 故答案为:443k ≤≤. 【点睛】本题考查了一次函数图象上点的坐标特征,用一次函数图象上点的坐标特征,找出关于k 的一元一次不等式是解题的关键.25..【解析】【分析】由线段垂直平分线的性质可知EA =EB ,由等边对等角的性质及外角的性质可得∠AEC=45°,易知△ACE 为等腰直角三角形,可得CA 长,利用三角形面积公式求解即可.【详解】解 解析:12. 【解析】【分析】 由线段垂直平分线的性质可知EA =EB ,由等边对等角的性质及外角的性质可得∠AEC =45°,易知△ACE 为等腰直角三角形,可得CA 长,利用三角形面积公式求解即可.【详解】解:∵DE 垂直平分AB 交BC 于点E ,∴EA =EB ,∴∠EAB =∠B =22.5°,∴∠AEC =∠EAB +∠B =45°,∵∠C =90°,∴△ACE 为等腰直角三角形,∴CA =CE =1,∴三角形ACE 的面积=12×1×1=12. 故答案为:12. 【点睛】本题主要考查了线段垂直平分线的性质及等腰三角形的性质,线段垂直平分线上的点到线段两端的距离相等,等腰三角形的两底角相等,灵活利用这两个性质是解题的关键. 三、解答题26.(1)50;80;3(2)()()()8003240348056047x x y x x x ⎧≤≤⎪=≤≤⎨⎪-+≤≤⎩(3)货车出发3小时或5小时后两车相距90千米【解析】【分析】(1)观察图象即可解决问题;(2)分别求出得A 、B 、C 的坐标,运用待定系数法解得即可;(3)根据题意列方程解答即可.【详解】解:(1)车的速度是50千米/小时;轿车的速度是:()4007280÷-=千米/小时;240803t =÷=.故答案为:50;80;3;(2)由题意可知:()3,240A ,()4,240B ,()7,0C ,设直线OA 的解析式为()110y k x k =≠,∴()8003y x x =≤≤,当34x ≤≤时,240y =,设直线BC 的解析式为()20y k x b k =+≠,把()4,240B ,()7,0C 代入得:22424070k b k b +=⎧⎨+=⎩,解得280560k b =-⎧⎨=⎩, ∴80560y =-+,∴()()()8003240348056047x x y x x x ⎧≤≤⎪=≤≤⎨⎪-+≤≤⎩; (3)设货车出发x 小时后两车相距90千米,根据题意得:()5080140090x x +-=-或()5080240090x x +-=+,解得3x =或5.答:货车出发3小时或5小时后两车相距90千米.【点睛】本题主要考查根据图象的信息来解答问题,关键在于函数的解析式的解答,这是这类题的一个难度,必须分段研究.27.(1) y=2x+2 (2) 6y >时,x >2【解析】【分析】(1) 根据正比例函数的定义设y-2=kx (k ≠0)然后把x ,y 的值代入求出k ,即可求出解析式;(2)根据 (1)中的解析式,判断即可.【详解】(1)∵y-2与x 成正比例函数∴设 y-2=kx (k ≠0)将x=2,y=6 代入得,2k=6-2 k=2∴ y-2=2x∴y=2x+2(2)根据函数解析式 y=2x+2得到y 随x 的增加而增大∵ y=6时 x=2∴6y >时,x >2.【点睛】此题主要考查了待定系数法求一次函数解析式及判断函数取值范围,熟练掌握相关概念是解题的关键.28.()133x +【解析】【分析】先根据分式混合运算法则进行化简,再代入已知值求值.【详解】 解:35(2)362x x x x -÷+--- =()2345()3222x x x x x --÷---- =()239322x x x x --÷-- =()()()323233x x x x x --⨯-+- =()133x +当3x =时,原式==【点睛】考核知识点:二次根式化简求值.先根据分式性质进行化简是关键.29.10BC =【解析】【分析】由垂直平分线的性质得到BD=CD ,则得到AB+AC=14,然后求出AB ,由勾股定理即可求出BC 的长度.【详解】解:∵DE 是BC 边上的垂直平分线,∴BD=CD ,∵ABD ∆的周长为14cm ,∴AB+AD+DB=14,∴AB+AD+DC=AB+AC=14,∵8AC =,∴1486AB =-=,在Rt △ABC 中,由勾股定理,得226810BC =+=.【点睛】本题考查了垂直平分线的性质定理,勾股定理,解题的关键是掌握由垂直平分线的性质定理,求出AB 的长度. 30.(1)见解析(2)9613 【解析】【分析】 (1)连接BD ,依题意得BD=CD ,所以∠C=∠CBD ,可证明∠CBD=2E ∠,进而可得结论; (2)过点F 作FM BC ⊥,FN AC ⊥,根据已知求出CD=5,AC=10,由勾股定理求出BC=8,求出S △BCD =12S △ABC ,再根据BCD BCF CDF S S S ∆∆∆=+,即111222CD FN BC FM =⋅+⋅可求出FM ,从而可得结论. 【详解】(1)连接BD点D 为AC 中点,且90ABC ∠=︒,12BD AC CD AD ∴===, CD BE =,BE BD ∴=,BDE E ∴∠=∠,又BD CD ∴=,C DBC ∴∠=∠,2C DBC BDE E E ∴∠=∠=∠+∠=∠,(2)过点F 作FM BC ⊥,FN AC ⊥.CG 平分ABC ∠,FM FN ∴=,5BE =,5,10CD AD BE AC ∴====,又6AB =∴在Rt ABC ∆中,222AB BC AC +=,8BC ∴= BD 为ABC ∆中线,11111681222222BCD ABC S S AB BC ∆∆∴==⨯⨯=⨯⨯⨯=, 又BCD BCF CDF S S S ∆∆∆=+,111222CD FN BC FM ∴=⋅+⋅, 11581222FM FM ∴⨯⨯+⨯⨯=, 2413FM ∴=, 1124968221313BCF S BC FM ∆∴=⋅=⨯⨯=, 【点睛】此题考查了直角三角形的性质,角平分线的性质以及三角形中线的性质,熟练掌握这些性质是解题的关键.31.(1)4--2)120,6x x ==-【解析】【分析】(1)根据二次根式混合的运算、立方根、以及零指数幂的法则计算即可(2)利用直接开平方法解方程即可【详解】解:(1)原式=3511654---+=--(2)23(3)27.x +=2(3)9.x +=3 3.x +=±120,6x x ==-【点睛】本题考查了二次根式的混合运算和解一元二次方程,熟练掌握法则是解题的关键。
苏教版数学八年级上册期末试卷

17.如图所示,一次函数图象经过点A,且与正比例函数 的图象交于点B,则该一次函数的表达式为.
18.如图,已知矩形ABCD,AD在y轴上,AB=2,BC=3,点A的坐标为(0,1),在AB边上有一点E(2,1),过点E的直线与CD交于点F.若EF平分矩形ABCD的面积,则直线EF的解析式为.
,解得 ,
与 的函数关系式为 .
当 时, .
点 的纵坐标为60,
表示因故停车检修,
交点 的纵坐标为60.
把 代入 中,有 ,解得 ,
交点 的坐标为(3,60).
交点 表示第一次相遇,
乙车出发 小时,两车在途中第一次相遇.10分
八年级数学抽测试卷
时间100分钟总分150分
一、选择题:(40分)
题号
1
2
3
4
5
6
7
8
9
10
答案
1.下列图形中,是中心对称图形而不是轴对称图形的是()
A.平行四边形B.矩形C.菱形D.正方形
2.下列命题中假命题的是()
A.平行四边形对角线互相平分;B.对角线互相平分的四边形是平行四边形;
C.矩形的对角线相等;D.对角线相等的四边形是矩形;
3.在四边形ABCD中,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD中任选两个使四边形ABCD为平行四边形的选法有()
27.(1)设乙车所行路程 与时间 的函数关系式为 ,把(2,0)和(10,480)代入,得 ,解得
与 的函数关系式为 .3分
苏教版八年级数学上册期末复习

八年级数学上册期末复习1班级姓名学号一、选择题1. 下列说法正确的是( )A. 0的平方根是0B. 9的立方根是3C. 是无理数D. 比小2.如果点在第四象限, 那么的取值范围是( )A. B. C. D.3. 等腰三角形两边分别为5cm和2cm, 则它的第三边长为( )A.2cmB.5cmC.2c m或5cmD.4cm4. 点(2, -3)关于坐标原点的对称点是( )A.(-2,-3)B.(2,-3)C. (2.3)D.(-2,3)5.小明骑自行车上学,开始以正常速度匀速行驶, 但行至途中因车出了毛病,只好停下修车,车修好后,怕耽误上课,他比修车前加快了骑车速度继续匀速行驶.下面是行驶路程关于行驶时间的函数图象,那么符合这个同学行驶情况的图象大致是( )A B C D二、填空题(本大题共10小题, 每小题2分, 共20分)1. 计算: = .2. 式子中x的取值范围是 .3. 在十八大精神的鼓舞下, 东台市的财政总收入超百亿元, 达110.6亿元, 这个数据用科学计数法表示为(精确到个位)元.4. 已知点在一次函数的图象上, 则= .5. 如图, 学校有一块长方形花铺, 有极少数人为了避开拐角走“捷径”, 在花铺内踩出了一条“路”. 他们仅仅少走了步路(假设2步为1米), 却踩伤了花草.6.若不等式组的解集为, 那么的值等于 .7. 如图, 已知矩形ABCD, AB在y轴上, AB=2, BC=3, 点A的坐标为(0, 1), 在AD边上有一点E(1, 1), 过点E的直线平分矩形ABCD的面积, 则此直线的解析式为 .第5题图第7题图三、解答题1. 计算:2. 求不等式组的整数解.3. (本题满分7分)12月份文化艺术节成功演出后, 实验中学决定将演出节目刻录成电脑光盘, 若到电脑公司刻录, 每张需8元(包括空白光盘费);如果学校自刻, 除租用刻录机需120元外, 每张光盘还需要成本4元(包括空白光盘), 问至少刻录电脑光盘多少张时学校自己刻录的费用较省?。
苏教版八年级数学上学期期末考前练习卷(含答案)
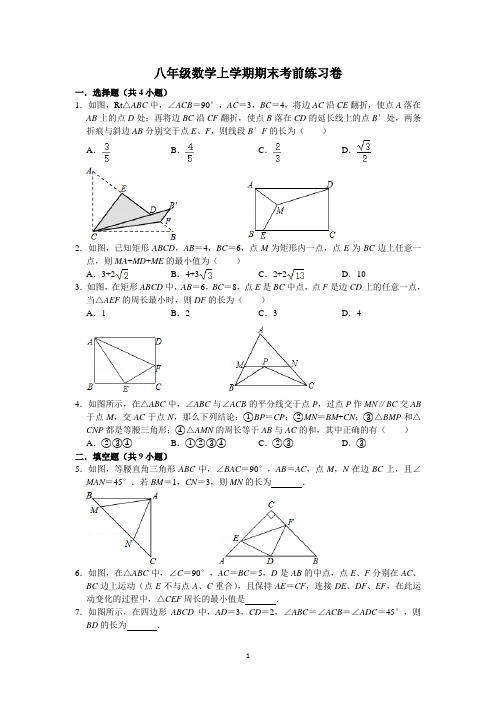
八年级数学上学期期末考前练习卷一.选择题(共4小题)1.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为()A.B.C.D.2.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为()A.3+2B.4+3C.2+2D.103.如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为()A.1B.2C.3D.44.如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点P,过点P作MN∥BC交AB 于点M,交AC于点N,那么下列结论:①BP=CP;②MN=BM+CN;③△BMP和△CNP都是等腰三角形;④△AMN的周长等于AB与AC的和,其中正确的有()A.②③④B.①②③④C.②③D.③二.填空题(共9小题)5.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为.6.如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是.7.如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为.8.若一次函数y=kx+b(k,b是常数,k≠0)的图象经过点(1,3)和点(﹣1,2),则k2﹣b2的值为.9.如图,在平面直角坐标系中,点A、B的坐标分别为(1,4)、(n,4),若直线y=2x与线段AB有公共点,则n的取值范围为.10.在平面直角坐标系中,点A坐标为(﹣3,m+2),点B坐标为(1,m﹣2),若点C(t+1,n1)和点D(t﹣2,n2)均在直线AB上,则n1﹣n2=.11.已知点A(2m﹣1,4m+2015)、B(﹣n+,﹣n+2020)在直线y=kx+b上,则k+b 值为.12.在平面直角坐标系中,点P是一次函数y=x+b图象上的一个动点,O是坐标原点,连接OP,若OP的最小值为4.8,则b=.13.如图,在平面直角坐标系中,点A的坐标为(3,1),直线l与x轴,y轴分别交于点B (﹣3,0),C(0,3),当x轴上的动点P到直线l的距离PE与到点A的距离P A之和最小时,则点E的坐标是.三.解答题(共27小题)14.如图,已知一次函数y=﹣x+b的图象与x轴交于A(﹣6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.(1)求b的值,并求出△P AB为等腰三角形时点P的坐标;(2)在点P出发的同时,动点Q也从点A出发,以每秒个单位的速度,沿射线AB 运动,运动时间为t(s)①求点Q的坐标;(用含t的表达式表示)②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.15.如图,在平面直角坐标系中,已知A(2,0),以OA为一边在第四象限内画正方形OABC,D(m,0)为x轴上的一个动点(m>2),以BD为一直角边在第四象限内画等腰直角△BDE,其中∠DBE=90°.(1)试判断线段AE、CD的数量关系,并说明理由;(2)设DE的中点为F,直线AF交y轴于点G.问:随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.16.如图,直线MN与x轴,y轴正半轴分别交于A,C两点,分别过A,C两点作x轴,y 轴的垂线相交于B点,直线y=x与直线MN交于点P,已知AC=10,OA=8.(1)求P点坐标;(2)作∠AOP的平分线OQ交直线MN与点Q,点E、F分别为射线OQ、OA上的动点,连结AE与EF,试探索AE+EF是否存在最小值?若存在,请直接写出这个最小值;若不存在请说明理由;(3)在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,请直接写出G点的坐标.17.模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.(1)求证:BE=CD;(2)模型应用:①已知直线l1:y=﹣x﹣4与y轴交于A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(﹣8,6),A、C分别在坐标轴上,P是线段BC上动点,点D是直线y=﹣2x﹣4上的一点,若△APD是不以点A为直角顶点的等腰Rt△,请求出点D的坐标.18.如图,在平面直角坐标系中,已知A(16,0)、B(16,8),C(0,8),D(0,﹣4),点E从点A出发,以每秒1个单位的速度沿AB运动到点B停止,过点E且与AD平行的直线l与y轴相交于点F,设运动时间为t秒(t>0).(1)设t=6时,求直线l的函数表达式;(2)若点E运动t秒后,直线l与x轴相交于点N,且CN=CE,求t的值;(3)记EF的中点为P,请你探求线段OP随点E运动所形成的图形,说明理由并求其面积.19.如图,已知A(a,0),B(0,b)分别为两坐标轴上的点,且a、b满足a2+b2﹣12a﹣12b+72=0,OC:OA=1:3.(1)求A、B、C三点的坐标;(2)若点D(1,0),过点D的直线分别交AB、BC于E、F两点,设E、F两点的横坐标分别为x E、x F,当BD平分△BEF的面积时,求x E+x F的值;(3)如图2,若M(2,4),点P是x轴上A点右侧一动点,AH⊥PM于点H,在BM 上取点G,使HG=HA,连接CG,当点P在点A右侧运动时,∠CGM的度数是否发生改变?若不变,请求其值,若改变,请说明理由.20.如图1,某物流公司恰好位于连接A,B两地的一条公路旁的C处.某一天,该公司同时派出甲.乙两辆货车以各自的速度匀速行驶.其中,甲车从公司出发直达B地;乙车从公司出发开往A地,并在A地用1h配货,然后掉头按原速度开往B地.图2是甲.乙两车之间的距离S(km)与他们出发后的时间x(h)之间函数关系的部分图象.(1)由图象可知,甲车速度为km/h;乙车速度为km/h.(2)已知最终乙车比甲车早到B地0.5h,求甲车出发1.5h后直至到达B地的过程中,S 与x的函数关系式及x的取值范围,并在图2中补全函数图象.21.已知甲、乙两地相距3200m,小王、小李分别从甲、乙两地同时出发,相向而行,两人相遇后立即返回到各自的出发地并停止行进.已知小李的速度始终是60m/min,小王在相遇后以匀速返回,但比小李晚回到原地.在整个行进过程中,他们之间的距离y(m)与行进的时间t(min)之间的函数关系如图中的折线段AB﹣BC﹣CD所示,请结合图象信息解答下列问题:(1)a=,b=;(2)当t为何值时,小王、小李两人相距800m?22.如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.(1)当b=3时,①求直线AB的解析式;②若QO=QA,求P点的坐标.(2)是否同时存在a、b,使得△QAC是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.23.在△ABC中,AB、BC、AC三边的长分别为、、,求这个三角形的面积.小华同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.这种方法叫做构图法.(1)△ABC的面积为:;(2)若△DEF三边的长分别为、、,请在图1的正方形网格中画出相应的△DEF,并利用构图法求出它的面积;(3)如图2,一个六边形的花坛被分割成7个部分,其中正方形PRBA,RQDC,QPFE 的面积分别为13,10,17,且△PQR、△BCR、△DEQ、△AFP的面积相等,求六边形花坛ABCDEF的面积.24.(1)如图①,在正方形ABCD中,E、F分别是BC、CD上的点且∠EAF=45°.猜测线段EF、BE、FD三者存在哪种数量关系?直接写出结论.(不用证明)结论:.(2)如图②,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是BC、CD 上的点,且∠EAF是∠BAD的一半.(1)中猜测的结论是否仍然成立?若成立,请证明;若不成立,请说明理由;25.(1)如图①,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,求线段EF、BE、FD之间的数量关系小明提供了这样的思路:延长EB到G,使BG=DF,连结AG,根据小明的思路,请直接写出线段EF、BE、FD之间的数量关系:(2)如图②,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?说明理由;(3)如图③,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.26.如图,四边形ABCD中,∠ABC=∠ADC=45°,将△BCD绕点C顺时针旋转一定角度后,点B的对应点恰好与点A重合,得到△ACE.(1)求证:AE⊥BD;(2)若AD=2,CD=3,试求出四边形ABCD的对角线BD的长.27.已知:如图,△ABC、△CDE都是等边三角形,AD、BE相交于点O,点M、N分别是线段AD、BE的中点.(1)求证:AD=BE;(2)求∠DOE的度数;(3)求证:△MNC是等边三角形.28.如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=130°,∠BOC=α,△BOC≌△ADC,∠OCD=60°,连接OD.(1)求证:△OCD是等边三角形;(2)当α=150°时,试判断△AOD的形状,并说明理由;(3)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)29.在△ABC中,AB=AC,点D是直线BC上一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连结CE.(1)如图1,当点D在线段BC上时,如果∠BAC=90°,则∠BCE=°.(2)设∠BAC=α,∠BCE=β.①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由.②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出你的结论.30.图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处.(1)①当PC∥QB时,OQ=cm;②在OB上找一点Q,使PC⊥QB(尺规作图,保留作图痕迹);(2)当折叠后重叠部分为等腰三角形时,求OQ的长.31.已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D 是OA的中点,点P在BC上运动,当△ODP是等腰三角形时.(1)求P点的坐标;(2)求满足条件的△ODP的周长最小值.(要有适当的图形和说明过程)32.已知:如图,∠BAC的平分线与BC的垂直平分线交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.(1)求证:BE=CF;(2)若AB=15,AC=9,求CF的长.33.如图,在△ABC中,AD平分∠BAC,DG⊥BC且平分BC于点G,DE⊥AB于点E,DF⊥AC交AC的延长线于点F.(1)求证:AE=AF;(2)求证:BE=CF;(3)如果AB=12,AC=8,求AE的长.34.如图,AD平分∠BAC,DG⊥BC于点G且平分BC,DF⊥AB于点F,DE⊥AC于点E.(1)求证:BF=CE;(2)求证:AB=AC+2CE.35.某培训中心有钳工20名,车工30名,现将这50名技工派往A,B两地工作,两地技工的月工资如下:钳工(元/月)车工(元/月)A地18001400B地16001500(1)若派往A地x名钳工,余下的技工全部派往B地,写出这50名技工的月工资总额y(元)与x之间的函数表达式,并写出x的取值范围;(2)若派往A地x名车工,余下的技工全部派往B地,写出这50名技工的月工资总额y(元)与x之间的函数表达式,并写出x的取值范围;(3)如何派遣这50名技工,可使他们的工资总额最高?直接写出结果.36.“低碳环保,绿色出行”的概念得到广大群众的接受,越来越多的人喜欢选择骑自行车作为出行工具.小军和爸爸同时骑车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆.小军始终以同一速度骑行,两人骑行的路程为y(米)与时间x(分钟)的关系如图.请结合图象,解答下列问题:(1)填空:a=;b=;m=.(2)若小军的速度是120米/分,求小军第二次与爸爸相遇时距图书馆的距离.(3)在(2)的条件下,爸爸自第二次出发后,骑行一段时间后与小军相距100米,此时小军骑行的时间为分钟.37.已知:如图∠ABC=∠ADC=90°,M,N分别是AC、BD的中点.(1)求证:MN⊥BD.(2)若∠BAD=45°,连接MB、MD,判断△MBD的形状,并说明理由.38.在Rt△ABC和Rt△ADC中,∠ABC=∠ADC=90°,E是AC中点(1)如图(1),求证:∠DEB=2∠DCB;(2)如图(2),上述结论是否仍然成立?若成立,请给予证明;若不成立,请说明理由.39.已知:如图,∠ACB=∠ADB=90°,E为AB中点,连接DE、CE、CD.(1)求证:DE=CE;(2)若∠CAB=25°,∠DBA=35°,判断△DEC的形状,并说明理由;(3)当∠CAB+∠DBA=45°时,若CD=12,取CD中点F,求EF的长.40.如图,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,使角的两边分别交AB、AC边于M、N两点,连接MN.①当MN∥BC时,求证:MN=BM+CN;②当MN与BC不平行时,则①中的结论还成立吗?为什么?③若点M、N分别是射线AB、CA上的点,其它条件不变,再探线段BM、MN、NC之间的关系,在图③中画出图形,并说明理由.答案与解析一.选择题(共4小题)1.如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为()A.B.C.D.【分析】根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,Rt△ABC中根据勾股定理求得AB=5,再根据三角形的面积可求得B′F的长.【解答】解:∵Rt△ABC中,∠ACB=90°,AC=3,BC=4,∴AB=5,根据折叠的性质可知AC=CD,∠A=∠CDE,CE⊥AB,∴B′D=BC﹣CD=4﹣3=1,∠DCE+∠B′CF=∠ACE+∠BCF,∵∠ACB=90°,∴∠ECF=45°,∴△ECF是等腰直角三角形,∴EF=CE,∠EFC=45°,∴∠BFC=∠B′FC=135°,∴∠B′FD=90°,∵S△ABC=AC•BC=AB•CE,∴AC•BC=AB•CE,∴CE=,∴EF=,ED=AE==,∴DF=EF﹣ED=∴B′F==.故选:B.【点评】此题主要考查了翻折变换,勾股定理的应用等,根据折叠的性质求得相等的角是本题的关键.2.如图,已知矩形ABCD,AB=4,BC=6,点M为矩形内一点,点E为BC边上任意一点,则MA+MD+ME的最小值为()A.3+2B.4+3C.2+2D.10【分析】将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,推出AM=MM’可得MA+MD+ME=D’M+MM’+ME,共线时最短;由于点E也为动点,可得当D’E⊥BC时最短,此时易求得D’E=DG+GE 的值;【解答】解:将△AMD绕点A逆时针旋转60°得到△AM’D’,MD=M’D’,易得到△ADD’和△AMM’均为等边三角形,∴AM=MM’,∴MA+MD+ME=D’M+MM’+ME,∴D′M、MM′、ME共线时最短,由于点E也为动点,∴当D’E⊥BC时最短,此时易求得D’E=DG+GE=4+3,∴MA+MD+ME的最小值为4+3.故选:B.【点评】本题考查轴对称、旋转变换、矩形的性质等知识,解题的关键是学会添加常用辅助线,构造等边三角形解决问题,学会用转化的思想思考问题,属于中考选择题中的压轴题.3.如图,在矩形ABCD中,AB=6,BC=8,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为()A.1B.2C.3D.4【分析】作点E关于直线CD的对称点E′,连接AE′交CD于点F,再根据△CE′F∽△BE′A即可求出CF的长,进而得出DF的长.【解答】解:作点E关于直线CD的对称点E′,连接AE′交CD于点F,∵在矩形ABCD中,AB=6,BC=8,点E是BC中点,∴BE=CE=CE′=4,∵AB⊥BC,CD⊥BC,∴=,即=,解得CF=2,∴DF=CD﹣CF=6﹣2=4.故选:D.【点评】本题考查的是轴对称﹣最短路线问题及相似三角形的判定与性质,根据题意作出E点关于直线CD的对称点,再根据轴对称的性质求出CE′的长,利用相似三角形的对应边成比例即可得出结论.4.如图所示,在△ABC中,∠ABC与∠ACB的平分线交于点P,过点P作MN∥BC交AB 于点M,交AC于点N,那么下列结论:①BP=CP;②MN=BM+CN;③△BMP和△CNP都是等腰三角形;④△AMN的周长等于AB与AC的和,其中正确的有()A.②③④B.①②③④C.②③D.③【分析】由平行线得到角相等,由角平分线得角相等,根据平行线的性质及等腰三角形的判定和性质.【解答】解:∵∠ABC、∠ACB的平分线相交于点P,∴∠MBP=∠PBC,∠PCN=∠PCB,∵MN∥BC,∴∠PBC=∠MPB,∠NPC=∠PCB,∴∠MBP=∠MPB,∠NPC=∠PCN,∴BM=MP,PN=CN,∴MN=MP+PN=BM+CN(②正确),∴△BMP和△CNP都是等腰三角形(③正确).∵△AMN的周长=AM+AN+MN,MN=BM+CN,∴△AMN的周长等于AB与AC的和(④正确).故选:A.【点评】本题考查了等腰三角形的性质及角平分线的性质及平行线的性质;题目利用了两直线平行,内错角相等,及等角对等边来判定等腰三角形的;等量代换的利用是解答本题的关键.二.填空题(共9小题)5.如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为.【分析】将△ABM逆时针旋转90°得到△ACF,连接NF,由条件可以得出△NCF为直角三角形,利用勾股定理就可以求出NF,通过证明三角形全等就可以MN=NF,求出NF即可.【解答】解:将△AMB逆时针旋转90°到△ACF,连接NF,∴CF=BM,AF=AM,∠B=∠ACF.∠2=∠3,∵△ABC是等腰直角三角形,AB=AC,∴∠B=∠ACB=45°,∠BAC=90°,∵∠MAN=45°,∴∠NAF=∠1+∠3=∠1+∠2=90°﹣45°=45°=∠NAF,在△MAN和△F AN中∴△MAN≌△F AN,∴MN=NF,∵∠ACF=∠B=45°,∠ACB=45°,∴∠FCN=90°,∵CF=BM=1,CN=3,∴在Rt△CFN中,由勾股定理得:MN=NF==,故答案为:.【点评】本题考查了旋转的性质的运用,勾股定理的运用,全等三角形的判定与性质,能正确作出辅助线是解此题的关键,难度适中.6.如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是5+.【分析】连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DE =DF.所以△DFE是等腰直角三角形;当E、F分别为AC、BC中点时,EF取最小值,根据三角形的中位线的性质得到EF,于是得到结论.【解答】解:连接CD;∵△ABC是等腰直角三角形,∴∠DCB=∠A=45°,CD=AD=DB;在△ADE与△CFD中,,∴△ADE≌△CDF(SAS);∴ED=DF,∠CDF=∠EDA;∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△DFE是等腰直角三角形,∵∠C=90°,AC=BC=5,∴AB=5,∴当△CEF周长的最小时,EF取最小值,∴E、F分别为AC、BC中点时,EF的值最小,∴EF=AB=,∴△CEF周长的最小值=CE+CF+EF=AE+CE+EF=AC+EF=5+;故答案为:5+.【点评】此题主要考查了全等三角形的判定与性质,等腰三角形、直角三角形性质等知识,找到EF∥BC时取最小值是解题关键.7.如图所示,在四边形ABCD中,AD=3,CD=2,∠ABC=∠ACB=∠ADC=45°,则BD的长为.【分析】作AD′⊥AD,AD′=AD,连接CD′,DD′,易证∠BAD=∠CAD′,即可证明△BAD≌△CAD′,可得BD=CD′,∠DAD′=90°,根据勾股定理可求得DD'的值,再根据勾股定理可求得CD'的值,即可解题.【解答】解:作AD′⊥AD,AD′=AD,连接CD′,DD′,如图:∵∠BAC+∠CAD=∠DAD′+∠CAD,即∠BAD=∠CAD′,在△BAD与△CAD′中,,∴△BAD≌△CAD′(SAS),∴BD=CD′,∠DAD′=90°,由勾股定理得DD′==3,∠D′DA+∠ADC=90°,由勾股定理得CD′==,∴BD=CD′=.故答案为:.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,考查了直角三角形中勾股定理运用,本题中求证△BAD≌△CAD′是解题的关键.8.若一次函数y=kx+b(k,b是常数,k≠0)的图象经过点(1,3)和点(﹣1,2),则k2﹣b2的值为﹣6.【分析】将点(1,3)和点(﹣1,2)代入解析式可求k,b的值,即可求k2﹣b2的值.【解答】解:根据题意得:解得:∴k2﹣b2=﹣=﹣6故答案为:﹣6【点评】本题考查了一次函数图象上点的坐标特征,熟练掌握图象上点的坐标满足图象解析式是本题的关键.9.如图,在平面直角坐标系中,点A、B的坐标分别为(1,4)、(n,4),若直线y=2x与线段AB有公共点,则n的取值范围为n≥2.【分析】由直线y=2x与线段AB有公共点,可得出点B在直线上或在直线右下方,利用一次函数图象上点的坐标特征,即可得出关于n的一元一次不等式,解之即可得出n的取值范围.【解答】解:∵直线y=2x与线段AB有公共点,∴2n≥4,∴n≥2故答案为:n≥2【点评】本题考查了一次函数图象上点的坐标特征,用一次函数图象上点的坐标特征,找出关于n的一元一次不等式是解题的关键.10.在平面直角坐标系中,点A坐标为(﹣3,m+2),点B坐标为(1,m﹣2),若点C(t+1,n1)和点D(t﹣2,n2)均在直线AB上,则n1﹣n2=﹣3.【分析】先求出直线AB的解析式,把点C,点D坐标代入可求解.【解答】解:设直线AB解析式为:y=kx+b解得:k=﹣1,b=m﹣1∴直线AB解析式为:y=﹣x+m﹣1∵点C(t+1,n1)和点D(t﹣2,n2)均在直线AB上,∴n1=﹣t﹣1+m﹣1,n2=﹣t+2+m﹣1,∴n1﹣n2=﹣3故答案为:﹣3【点评】本题考查了一次函数图象上点的坐标特征,熟练掌握函数图象上的点的坐标满足函数解析式是本题的关键.11.已知点A(2m﹣1,4m+2015)、B(﹣n+,﹣n+2020)在直线y=kx+b上,则k+b 值为2019.【分析】把点A(2m﹣1,4m+2015)和点B(﹣,﹣n+2020)分别代入直线y=kx+b,经过整理变形,即可得到k的值,利用代入法,可求得b的值,即可得到答案.【解答】解:把点A(2m﹣1,4m+2015)代入直线y=kx+b得:4m+2015=k(2m﹣1)+b①,把点B(﹣,﹣n+2020)代入直线y=kx+b得:﹣n+2020=k(﹣+)+b②,①﹣②得:4m+n﹣5=k(2m),k==2,把k=2代入①得:4m+2015=2(2m﹣1)+b,解得:b=2017,则k+b=2+2017=2019,故答案为:2019.【点评】本题考查了一次函数图象上点的坐标特征,正确掌握代入法是解题的关键.12.在平面直角坐标系中,点P是一次函数y=x+b图象上的一个动点,O是坐标原点,连接OP,若OP的最小值为4.8,则b=±8.【分析】线段OP的最小值,就是原点到已知直线的距离,可以根据所构建的三角形面积一样来求OP;【解答】解:如图:∵y=x+b,①当b>0时;∴它与x的交点坐标是A(,0),与y轴的交点坐标是B(0,b)∴OA=;OB=b,根据勾股定理:AB==∵S△AOB=,OP=4.8,∴解得b=8;②当b<0时;∴它与x的交点坐标是A'(,0),与y轴的交点坐标是B'(0,b)∴OA'=﹣;OB'=﹣b,根据勾股定理:A'B'==﹣∵OP=4.8,∴解得b=﹣8;故答案填:±8.【点评】本题考查一次函数的综合运用,熟练运用两点之间的距离公式以及面积法是解决本题的关键.13.如图,在平面直角坐标系中,点A的坐标为(3,1),直线l与x轴,y轴分别交于点B (﹣3,0),C(0,3),当x轴上的动点P到直线l的距离PE与到点A的距离P A之和最小时,则点E的坐标是(﹣,).【分析】作点A关于x轴的对称点A',过A'作A'D⊥l,与x轴交于点P,则A'D即为所求最小值;求出直线BC和直线A'E的解析式,联立方程组,即可求出E点坐标;【解答】解:作点A关于x轴的对称点A',过A'作A'D⊥l,与x轴交于点P,则A'D即为所求最小值;∵A的坐标为(3,1),∴A'(3,﹣1),∵B(﹣3,0),C(0,3),直线BC所在的直线解析式y=x+3,∴A'E所在直线解析式y=﹣x+2,∴,∴,∴E(﹣,),故答案为(﹣,);【点评】本题考查一次函数图象及性质,轴对称求最短距离;将所求距离通过轴对称转化为A'E,借助方程组求解是关键.三.解答题(共27小题)14.如图,已知一次函数y=﹣x+b的图象与x轴交于A(﹣6,0)与y轴相交于点B,动点P从A出发,沿x轴向x轴的正方向运动.(1)求b的值,并求出△P AB为等腰三角形时点P的坐标;(2)在点P出发的同时,动点Q也从点A出发,以每秒个单位的速度,沿射线AB 运动,运动时间为t(s)①求点Q的坐标;(用含t的表达式表示)②若点P的运动速度为每秒k个单位,请直接写出当△APQ为等腰三角形时k的值.【分析】(1)把A(﹣6,0)代入y=﹣x+b得到b=﹣2,于是得到B(0,﹣2),AO =6,OB=2,AB==,根据等腰三角形的性质列方程即可得到结论;(2)①由点Q在直线y=﹣x+b上,设Q(a,﹣a﹣2),作QH⊥x轴于H,得到QH=a+2,AH=6+a,根据勾股定理得到AQ==(a+2),列方程即可得到结论;②由题意得到AQ=t,AP=kt,根据等腰三角形的性质列方程即可得到结论.【解答】解:(1)把A(﹣6,0)代入y=﹣x+b得,b=﹣2,∴B(0,﹣2),AO=6,OB=2,AB===2,∵△P AB为等腰三角形,∴当AP=AB时,AP=2,∴P(2﹣6,0);当BP=BA时,OP=OA=6,∴P(6,0);当P A=PB时,设OP=x,则P A=PB=6﹣x,在Rt△OPB中,∵OP2+OB2=PB2,∴x2+22=(6﹣x)2,解得:x=,∴P(﹣,0);综上所述,当△P AB为等腰三角形时点P的坐标为(2﹣6,0)或(6,0)或(﹣,0);(2)①∵点Q在直线y=﹣x+b上,∴设Q(a,﹣a﹣2),作QH⊥x轴于H,则QH=a+2,AH=6+a,∴AQ==(a+2),∵AQ=t,∴t=a+2,∴a=3t﹣6,∴Q(3t﹣6,﹣t);②由题意得,AQ=t,AP=kt,∵△APQ为等腰三角形,∴当AP=AQ时,t=kt,∴k=,当AQ=PQ时,即AH=AP,∴3t=kt,∴k=6;当P A=PQ时,在Rt△PQH中,∵HP2+HQ2=PQ2,∴(3t﹣kt)2+t2=(kt)2,∴k=,综上所述,当△APQ为等腰三角形时k的值为或6或.【点评】本题考查了待定系数法求函数的解析式,勾股定理,等腰三角形的性质,正确的理解题意是解题的关键.15.如图,在平面直角坐标系中,已知A(2,0),以OA为一边在第四象限内画正方形OABC,D(m,0)为x轴上的一个动点(m>2),以BD为一直角边在第四象限内画等腰直角△BDE,其中∠DBE=90°.(1)试判断线段AE、CD的数量关系,并说明理由;(2)设DE的中点为F,直线AF交y轴于点G.问:随着点D的运动,点G的位置是否会发生变化?若保持不变,请求出点G的坐标;若发生变化,请说明理由.【分析】(1)由正方形OABC,可得BC=BA,∠ABC=90°,由等腰直角三角形BDE,可得BD=BE,∠DBE=90°,再根据∠CBD=∠ABE,即可得到△CBD≌△ABE,进而得出CD=AE;(2)过点E作PQ∥OD,分别交直线AB,AF于点P,Q,判定△ADB≌△PBE,可得AD=PB,AB=PE,判定△ADF≌△QEF,可得AD=QE,依据AP=QP,可得∠AQP=45°,依据PQ∥OD,可得∠OAG=∠Q=45°,进而得到△AOG是等腰直角三角形,进而得到G(0,2),即点G的位置不会发生变化.【解答】解:(1)AE=CD.理由:由正方形OABC,可得BC=BA,∠ABC=90°,由等腰直角三角形BDE,可得BD=BE,∠DBE=90°,∴∠ABC+∠ABD=∠DBE+∠ABD,即∠CBD=∠ABE,∴△CBD≌△ABE,∴CD=AE;(2)点G的位置不会发生变化.理由:如图,过点E作PQ∥OD,分别交直线AB,AF于点P,Q,∵∠DAB=∠P=∠DBE=90°,∴∠ADB+∠ABD=∠PBE+∠ABD=90°,∴∠ADB=∠PBE,又∵DB=BE,∴△ADB≌△PBE,∴AD=PB,AB=PE,∵F是DE的中点,∴DF=EF,∵AD∥EQ,∴∠DAF=∠Q,又∵∠AFD=∠QFE,∴△ADF≌△QEF,∴AD=QE,∴AB+BP=PE+EQ,即AP=QP,∴∠AQP=45°,又∵PQ∥OD,∴∠OAG=∠Q=45°,∴△AOG是等腰直角三角形,∴GO=AO=2,∴G(0,2),即点G的位置不会发生变化.【点评】本题主要考查全等三角形的判定和性质、等边三角形的性质、坐标与几何图形的关系、正方形的性质等知识点,解题的难点在于作辅助线构造全等三角形,运用全等三角形的对应边相等得出△APG是等腰直角三角形.16.如图,直线MN与x轴,y轴正半轴分别交于A,C两点,分别过A,C两点作x轴,y 轴的垂线相交于B点,直线y=x与直线MN交于点P,已知AC=10,OA=8.(1)求P点坐标;(2)作∠AOP的平分线OQ交直线MN与点Q,点E、F分别为射线OQ、OA上的动点,连结AE与EF,试探索AE+EF是否存在最小值?若存在,请直接写出这个最小值;若不存在请说明理由;(3)在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,请直接写出G点的坐标.【分析】(1)由AC与OA的长,利用勾股定理求出OC的长,确定出C坐标,利用待定系数法求出直线MN解析式,与y=x联立求出交点P坐标即可;(2)作出相应的图形,如图1所示,作出A关于射线OQ的对称点A′,可得OA′=OA=8,过A′作A′F⊥OA,交射线OQ于点E,角射线OA于点F,此时A′E+EF=AE+EF存在最小值,求出即可;(3)在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,分三种情况考虑:①GC=GB,此时G为线段BC垂直平分线与直线MN的交点;②GC=BC=8;③GB=BC=8,分别求出G坐标即可.【解答】解:(1)∵AC=10,OA=8,∴OC===6,∴C(0,6);设直线MN的解析式是y=kx+b(k≠0),∵点A、C都在直线MN上,∴,解得:,∴直线MN的解析式为y=﹣x+6,∵P为y=﹣x+6与直线y=x的交点.∴﹣x+6=x,解得:x=,∴p的坐标为(,);(2)如图1所示:作出A关于射线OQ的对称点A′,可得OA′=OA=8,过A′作A′F⊥OA,交射线OQ于点E,角射线OA于点F,此时A′E+EF=AE+EF存在最小值,在Rt△A′OF中,∠A′OF=45°,设A′F=OF=x,根据勾股定理得:x2+x2=82,解得:x=4,则最小值为4;(3)如图2所示:∵A(8,0),C(0,6),∴根据题意得:B(8,6),∵G在直线MN:y=﹣x+6上,∴设G(a,﹣a+6),在直线MN上存在点G,使以点G,B,C三点为顶点的三角形是等腰三角形,分三种情况考虑:①当GC=GB时,G点为BC垂直平分线与MN交点,此时G1(4,3);②当GC=BC=8时,根据两点间的距离公式得:a2+(﹣a+6﹣6)2=64,解得:a=±,此时G2(﹣,),G3(,);③当GB=BC=8时,根据两点间的距离公式得:(a﹣8)2+(﹣a+6﹣6)2=64,解得:a=,可得﹣a+6=﹣,此时G4(,﹣),则符合条件的点G有:G1(4,3),G2(﹣,),G3(,),G4(,﹣).【点评】此题属于一次函数综合题,涉及的知识有:坐标与图形性质,两点间的距离公式,待定系数法确定一次函数解析式,等腰三角形的性质,利用了分类讨论的思想,熟练掌握公式及法则是解本题的关键.17.模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.(1)求证:BE=CD;(2)模型应用:①已知直线l1:y=﹣x﹣4与y轴交于A点,将直线l1绕着A点顺时针旋转45°至l2,如图2,求l2的函数解析式;②如图3,矩形ABCO,O为坐标原点,B的坐标为(﹣8,6),A、C分别在坐标轴上,P是线段BC上动点,点D是直线y=﹣2x﹣4上的一点,若△APD是不以点A为直角顶点的等腰Rt△,请求出点D的坐标.【分析】(1)先根据△ABC为等腰直角三角形得出CB=CA,再由AAS定理可知△ACD ≌△CBE;(2)①如图2中,设直线l1交x轴于B,作BP⊥AC于P,作PE⊥OB于E,PF⊥y轴于F.首先证明四边形PEOF是正方形,求出点P的坐标,利用待定系数法即可解决问题.(3)当点D为直角顶点,分点D在直线P A的上方或下方两种情况;点P为直角顶点,显然此时点D位于直线AP的上方,由此可得出结论.【解答】(1)证明:如图1中,∵△ABC为等腰直角三角形,∴CB=CA,∠ACD+∠BCE=90°,又∵AD⊥ED,BE⊥ED,∴∠D=∠E=90°,∠EBC+∠BCE=90°,∴∠ACD=∠EBC,在△ACD与△CBE中,。
2023年新版苏教版八年级上册数学期末复习(含答案)

2023年新版苏教版八年级上册数学期末
复习(含答案)
第一部分选择题
1. 中国最古老的算盘是哪种?
A. 筹算(一种木质算盘)
B. 珠算(一种珠子计算器)
C. 算盘(一种框架式计数器)
D. 砂算(一种以铁质砂粒为标志进行计算的工具)
答案: C
2. 我国现代数学家华罗庚在哪年去世?
A. 1981年
B. 1982年
C. 1983年
D. 1984年
答案: B
3. 数轴上点 P 坐标是 -3,则其关于原点的对称点是?
A. -3
B. 3
C. -6
D. 6
答案:B
......
(以下省略)
第二部分简答题
1. 有三种色带,分别为红,黄,蓝,将它们两两搭配,能搭配出什么颜色?请列举出来。
答案:可以搭配成红、黄、蓝、橙、绿、紫。
2. 若甲、乙两人合作创业,甲投资10万元,乙资10亿元,搜索到第 7 年,共获利 2 亿元,则甲、乙收益各是多少?
答案:甲和乙的收益分别为:6800万元和132亿元。
第三部分计算题
1. 计算:$(-\frac{2}{3})\div(-\frac{1}{6})\times(-4)^3$
答案:-256
2. 计算勾股直角三角形的斜边。
已知直角边为4,另外一直角边为3,斜边为 x。
由勾股定理,得:$$x =
\sqrt{4^2+3^2}=\sqrt{16+9}=\sqrt{25}=5$$
答案:5
......
(以下省略)
期末复习题答案仅供参考,希望同学们在复习时一定要深入理解每道题目,多做练习,加强对知识点的掌握和运用,从而取得更好的成绩!。
最新苏教版八年级数学上册期末考试卷(带答案)

最新苏教版八年级数学上册期末考试卷(带答案)班级: 姓名:一、选择题(本大题共10小题,每题3分,共30分)1.﹣3的绝对值是( )A .﹣3B .3C .-13D .132.已知:将直线y=x ﹣1向上平移2个单位长度后得到直线y=kx+b ,则下列关于直线y=kx+b 的说法正确的是( )A .经过第一、二、四象限B .与x 轴交于(1,0)C .与y 轴交于(0,1)D .y 随x 的增大而减小3.成人每天维生素D 的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为( )A .74610-⨯B .74.610-⨯C .64.610-⨯D .50.4610-⨯4.已知a b 3132==,,则a b 3+的值为( ) A .1 B .2 C .3 D .275.若关于x 的一元二次方程2(2)26k x kx k --+=有实数根,则k 的取值范围为( )A .0k ≥B .0k ≥且2k ≠C .32k ≥D .32k ≥且2k ≠ 6.已知关于x 的不等式组0320x a x ->⎧⎨->⎩的整数解共有5个,则a 的取值范围是( )A .﹣4<a <﹣3B .﹣4≤a <﹣3C .a <﹣3D .﹣4<a <327.下面是一位同学做的四道题:①222()a b a b +=+;②224(2)4a a -=-;③532a a a ÷=;④3412a a a ⋅=,其中做对的一道题的序号是( )A .①B .②C .③D .④8.如图,每个小正方形的边长为1,A 、B 、C 是小正方形的顶点,则∠ABC 的度数为( )A .90°B .60°C .45°D .30°9.将一副三角板和一张对边平行的纸条按如图摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则∠1的度数是( )A .15°B .22.5°C .30°D .45°10.已知:如图,∠1=∠2,则不一定能使△ABD ≌△ACD 的条件是 ( )A .AB =AC B .BD =CD C .∠B =∠C D .∠BDA =∠CDA二、填空题(本大题共6小题,每小题3分,共18分)1.16的平方根是 .2.方程22310x x +-=的两个根为1x 、2x ,则1211+x x 的值等于__________. 3.一个正多边形的每个外角为60°,那么这个正多边形的内角和是______.4.如图,△ABC 中,CD ⊥AB 于D ,E 是AC 的中点.若AD=6,DE=5,则CD 的长等于________.5.正方形111A B C O 、2221A B C C 、3332A B C C 、…按如图所示的方式放置.点1A 、2A 、3A 、…和点1C 、2C 、3C 、…分别在直线1y x =+和x 轴上,则点n B 的坐标是__________.(n 为正整数)6.如图,在平行四边形ABCD 中,连接BD ,且BD =CD ,过点A 作AM ⊥BD 于点M ,过点D 作DN ⊥AB 于点N ,且DN =32,在DB 的延长线上取一点P ,满足∠ABD =∠MAP +∠PAB ,则AP =________.三、解答题(本大题共6小题,共72分)1.解方程:(1)2101x x -=+ (2)2216124x x x --=+-2.先化简,再求值:213(2)211a a a a a +-÷+-+-,其中a =2.3.已知关于的方程2(2)210x k x k -++-=.(1)求证:该方程一定有两个不相等的实数根;(2)若12125x x x x +=-,求k 的值.4.如图,已知AC 平分∠BAD ,CE ⊥AB 于E ,CF ⊥AD 于F ,且BC=CD .(1)求证:△BCE ≌△DCF ;(2)求证:AB+AD=2AE.5.如图1,在菱形ABCD中,AC=2,BD=23,AC,BD相交于点O.(1)求边AB的长;(2)求∠BAC的度数;(3)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A 处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF.判断△AEF是哪一种特殊三角形,并说明理由.6.2017年5月,某县突降暴雨,造成山体滑坡,桥梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,已知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1 000件帐篷与乙种货车装运800件帐篷所用车辆相等.(1)求甲、乙两种货车每辆车可装多少件帐篷;(2)如果这批帐篷有1 490件,用甲、乙两种汽车共16辆装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其余装满,求甲、乙两种货车各有多少辆.参考答案一、选择题(本大题共10小题,每题3分,共30分)1、B2、C3、C4、B5、D6、B7、C8、C9、A10、B二、填空题(本大题共6小题,每小题3分,共18分)1、±2.2、3.3、720°.4、8.5、1 (21,2) n n--6、6三、解答题(本大题共6小题,共72分)1、(1)x=1;(2)方程无解2、11a-,1.3、(1)见解析;(2)k=84、略5、(1)2;(2)60︒;(3)见详解6、(1)甲种货车每辆车可装100件帐篷,乙种货车每辆车可装80件帐篷;(2)甲种货车有12辆,乙种货车有4辆.。
苏教版八年级数学上册期末考试题及答案【汇总】

苏教版八年级数学上册期末考试题及答案【汇总】班级:姓名:一、选择题(本大题共10小题,每题3分,共30分)1.4的平方根是()A.±2 B.2 C.﹣2 D.162.如果y=2x-+2x-+3,那么y x的算术平方根是()A.2 B.3 C.9 D.±33.等式33=11x xxx--++成立的x的取值范围在数轴上可表示为()A.B.C.D.4.如果a+b<0,并且ab>0,那么()A.a<0,b<0 B.a>0,b>0 C.a<0,b>0 D.a>0,b<0 5.如图,a,b,c在数轴上的位置如图所示,化简22()a a c c b-++-的结果是()A.2c﹣b B.﹣b C.b D.﹣2a﹣b 6.如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是()A.x=2 B.x=0 C.x=﹣1 D.x=﹣37.如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为()A.1 B.1.3 C.1.2 D.1.58.下列图形中,不是轴对称图形的是()A.B.C.D.9.如图,将△ABC放在正方形网格图中(图中每个小正方形的边长均为1),点A,B,C恰好在网格图中的格点上,那么△ABC中BC边上的高是()A.102B.104C.105D.510.如图,已知在△ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是()A.AE=EC B.AE=BE C.∠EBC=∠BAC D.∠EBC=∠ABE 二、填空题(本大题共6小题,每小题3分,共18分)1.16的平方根是.2.若关于x、y的二元一次方程3x﹣ay=1有一个解是32xy=⎧⎨=⎩,则a=_____.3.分解因式6xy2-9x2y-y3 = _____________.4.如图,△ABC中,CD⊥AB于D,E是AC的中点.若AD=6,DE=5,则CD的长等于________.5.如图,△ABC 中,AB=BC ,∠ABC=90°,F 为AB 延长线上一点,点E 在BC 上,且AE=CF ,若∠BAE=25°,则∠ACF=__________度.6.如图,长为8 cm 的橡皮筋放置在x 轴上,固定两端A 和B ,然后把中点C 向上拉升3 cm 到点D ,则橡皮筋被拉长了_____ cm.三、解答题(本大题共6小题,共72分)1.用适当的方法解方程组(1)3322x y x y =-⎧⎨+=⎩ (2)353123x y x y -=⎧⎪⎨-=⎪⎩2.(1)已知x 35y 352x 2-5xy +2y 2的值.(2)先化简,再求值:222222x y x y x xy y x xy x y ⎛⎫--÷ ⎪-+--⎝⎭,其中x =221-,y =22-3.解不等式组()31511242x x x x ⎧-<+⎪⎨-≥-⎪⎩,并写出它的所有非负整数解.4.在▱ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F(1)在图1中证明CE=CF;(2)若∠ABC=90°,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若∠ABC=120°,FG∥CE,FG=CE,分别连接DB、DG(如图3),求∠BDG 的度数.5.如图,已知在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D,BC=CE.(1)求证:AC=CD;(2)若AC=AE,求∠DEC的度数.6.为了抓住梵净山文化艺术节的商机,某商店决定购进A、B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,B种纪念品6件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?参考答案一、选择题(本大题共10小题,每题3分,共30分)1、A2、B3、B4、A5、A6、D7、C8、A9、A10、C二、填空题(本大题共6小题,每小题3分,共18分)1、±4.2、43、-y(3x-y)24、8.5、706、2.三、解答题(本大题共6小题,共72分)1、(1)47xy=-⎧⎨=⎩;(2)831xy⎧=⎪⎨⎪=⎩2、(1)42,(2)13+-3、非负整数解是:0,1、2.4、(1)略;(2)45°;(3)略.5、(1)略;(2)112.5°.6、(1)A种纪念品需要100元,购进一件B种纪念品需要50元(2)共有4种进货方案(3)当购进A种纪念品50件,B种纪念品50件时,可获最大利润,最大利润是2500元。
苏教版八年级上学期期末复习数学试题

2012-2013年育青八年级数学复习题(一)一、选择题(本大题共8小题,每小题3分,共24分)1.在天气预报图上,有各种各样表示天气的符号,下列表示天气符号的图形中,既是中心对称图形又是轴对称图形的是 ( )2.如图,小手盖住的点的坐标可能为( )A (46)--,B (63)-,C (52),D (34)-, 3.下列各式中正确的是( ) A 416±= B 9273-=- C 3)3(2-=- D 211412= 4. 下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( )A 正三角形B 正方形C 正五边形D 正六边形5.顺次连结对角线互相垂直的等腰梯形四边中点得到的四边形是( )A 平行四边形B 矩形C 菱形D 正方形 6.若点),(1y a 、),1(2y a +在直线1+=kx y 上,且21y y >,则该直线所经过的象限是( )A 第一、二、三象限B 第一、二、四象限C 第二、三、四象限D 第一、三、四象限7.如图所示,把一个正方形三次对折后沿虚线剪下,则所得的图形是8. 如图,是一块在电脑屏幕上出现的矩形色块图,由6形的边长为1,那么这个矩形色块图的面积为A 142B 143C 144D 145二、填空题(本大题共10小题,每小题3分,共30分,把答案填在题目中的横线上) 9.平方根等于本身的数是 .10.把1.952取近似数并保留两个有效数字是 .11.已知:如图,E (-4,2),F (-1,-1),以O 为中心,把△EFO 旋转180°,则点E 的对应点E ′的坐标为 .12.梯形的中位线长为3,高为2,则该梯形的面积为 .13.已知点),(11y x 、),(22y x 、……、),(n n y x 都在直线53-=x y 上,若这n 个点的横坐标的平均数为a ,则这n 个点的纵坐标的平均数为 .14.等腰梯形的上底是4cm ,下底是10cm ,一个底角是60,则等腰梯形的腰长是 cm .晴 C冰雹A雷阵雨 B 大雪 D第8题 第2题 xyA B C Dy P ,则二元一次方16.在Rt △ABC 中,∠C =90°,AD 平分∠BAC 交BC 于D ,若BC =15,且BD ∶DC =3∶2,则D 到边AB 的距离是 .17.在△ABC 中,∠A=40°,当∠B= 时,△ABC 是等腰三角形.18.如图,有一种动画程序,屏幕上正方形区域ABCD 表示黑色物体甲.已知A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y = 2x + b 发射信号,当信号遇到区域甲(正方形ABCD )时,甲由黑变白.则b 的取值范围为? 时,甲能由黑变白.三、解答题(本大题共10小题,共96分,解答应写出必要的文字说明、证明过程或演算步骤)19.(本题满分8分)(1)计算:4)21(803++-- (2)已知:9)1(2=-x ,求x 的值.20.(本题满分8分)一架竹梯长13m ,如图(AB 位置)斜靠在一面墙上,梯子底端离墙5m , (1)求这个梯子顶端距地面有多高;(2)如果梯子的顶端下滑4 m (CD 位置),那么梯子的底部在水平方向也滑动了4 m 吗?为什么? 21.(本题满分8分)如图所示,每个小方格都是边长为1.(1)画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1(2)画出四边形OABC 绕点O 顺时针方向旋转90OB 旋转到OB 2所扫过部分图形的面积.22.(本题满分8分)如图,点B 、E 、C 、F 在同一直线上,=CF .请说明:(1)△ABC≌△DEF;(2)四边形ACFD 是平行四边形.23.(本题满分10分)已知一次函数y =kx +b 的图像经过点(-1,-5),且与正比例函数1y=x 2的图像相交于点(2,m ).求:(1)m 的值; (2)一次函数y =kx +b 的解析式;(3)这两个函数图像与x 轴所围成的三角形面积.24.(本题满分10分)甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如左图所示:_ B第20题 AC 第16题第18题F E DC B A 第22题(1)请填写右表;(2)请从下列三个不同的角度对测试结果进行分析:①从平均数和中位数看(谁的成绩好些);②从平均数和9环以上的次数看(谁的成绩好些);③从折线图上两人射击环数的走势看(分析谁更有潜力).25.(本题满分10分)已知有两张全等的矩形纸片。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版八年级上学期期末复习数学试题LEKIBM standardization office【IBM5AB- LEKIBMK08- LEKIBM2C】2012-2013年育青八年级数学复习题(一)一、选择题(本大题共8小题,每小题3分,共24分)1.在天气预报图上,有各种各样表示天气的符号,下列表示天气符号的图形中,既是中心对称图形又是轴对称图形的是 ( )2.如图,小手盖住的点的坐标可能为( ) A (46)--,B (63)-,C (52),D (34)-,3.下列各式中正确的是( )A 416±=B 9273-=-C 3)3(2-=-D 211412= 4. 下列图形中,单独选用一种图形不能进行平面镶嵌的图形是( )A 正三角形B 正方形C 正五边形D 正六边形5.顺次连结对角线互相垂直的等腰梯形四边中点得到的四边形是( ) A 平行四边形 B 矩形 C 菱形D 正方形6.若点),(1y a 、),1(2y a +在直线1+=kx y 上,且21y y >,则该直线所经过的象限是( )A 第一、二、三象限B 第一、二、四象限C 第二、三、四象限D 第一、三、四象限 7.如图所示,把一个正方形三次对折后沿虚线剪下,则所得的图形是8. 如图,是一块在电脑屏幕上出现的矩形色块图,由6个不同颜色的正方形组成,已知中间最小的一个正方形的边长为1,那么这个矩形色块图的面积为 A 142 B 143 C 144 D 145二、填空题(本大题共10小题,每小题3分,共30分,把答案填在题目中的横线上)晴冰雹雷阵雨大雪第8第2xyA B C D9.平方根等于本身的数是 .10.把1.952取近似数并保留两个有效数字是 .11.已知:如图,E (-4,2),F (-1,-1),以O 为中心,把△EFO 旋转180°,则点E 的对应点E ′的坐标为 .12.梯形的中位线长为3,高为2,则该梯形的面积为 .13.已知点),(11y x 、),(22y x 、……、),(n n y x 都在直线53-=x y 上,若这n 个点的横坐标的平均数为a ,则这n 个点的纵坐标的平均数为 .14.等腰梯形的上底是4cm ,下底是10cm ,一个底角是60,则等腰梯形的腰长是 cm .15.如图,已知函数y ax b =+和y kx =的图象交于点P ,则二元一次方程组,y ax b y kx=+⎧⎨=⎩的解是 .16.在Rt △ABC 中,∠C =90°,AD 平分∠BAC 交BC 于D ,若BC =15,且BD ∶DC =3∶2,则D 到边AB 的距离是 .17.在△ABC 中,∠A=40°,当∠B= 时,△ABC 是等腰三角形.18.如图,有一种动画程序,屏幕上正方形区域ABCD 表示黑色物体甲.已知A (1,1),B (2,1),C (2,2),D (1,2),用信号枪沿直线y = 2x + b 发射信号,当信号遇到区域甲(正方形ABCD )时,甲由黑变白.则b 的取值范围为? 时,甲能由黑变白.三、解答题(本大题共10小题,共96分,解答应写出必要的文字说明、证明过程或演算步骤)19.(本题满分8分)(1)计算:4)21(803++-- (2)已知:9)1(2=-x ,求x 的值.第11题yxEO FC BD 第16题y 第18题D C BA12 1 2 xO第15题P xyO -2-4 y=kxy=ax +b20.(本题满分8分)一架竹梯长13m ,如图(AB 位置)斜靠在一面墙上,梯子底端离墙5m , (1)求这个梯子顶端距地面有多高;(2)如果梯子的顶端下滑4 m (CD 位置),那么梯子的底部在水平方向也滑动了4 m 吗为什么21.(本题满分8分)如图所示,每个小方格都是边长为1的正方形,以O 点为坐标原点建立平面直角坐标系.(1)画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1,并写出点B 1的坐标是 ;(2)画出四边形OABC 绕点O 顺时针方向旋转90°后得到的四边形OA 2B 2C 2;连结OB ,求出OB 旋转到OB 2所扫过部分图形的面积.22.(本题满分8分)如图,点B 、E 、C 、F 在同一直线上,AB =DE ,∠B =∠DEF ,BE =CF .请说明:(1)△ABC≌△DEF ;(2)四边形ACFD 是平行四边形._ O _ C_ B_ D_ A 第20DA23.(本题满分10分)已知一次函数y =kx +b 的图像经过点(-1,-5),且与正比例函数1y=x 2的图像相交于点(2,m ).求:(1)m 的值; (2)一次函数y =kx +b 的解析式;(3)这两个函数图像与x 轴所围成的三角形面积.24.(本题满分10分)甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如左图所示:(1)请填写右表;(2)请从下列三个不同的角度对测试结果进行分析:①从平均数和中位数看(谁的成绩好些);②从平均数和9环以上的次数看(谁的成绩好些);③从折线图上两人射击环数的走势看(分析谁更有潜力).25.(本题满分10分)已知有两张全等的矩形纸片。
(1)将两张纸片叠合成如图甲,请判断四边形ABCD 的形状,并说明理由;(2)设矩形的长是6,宽是3.当这两张纸片叠合成如图乙时,菱形的面积最大,求此时菱形ABCD的面积.26.(本题满分10分)小明平时喜欢玩“QQ 农场”游戏,本学期八年级数学备课组组织了几次数学反馈性测试,小明的数学成绩如下表:(1)以月份为x 轴,成绩为y 轴,根据上表提供的数据在下列直角坐标系中描点;NLKHGFEDCB A图甲HGFEDCBA图乙(2)观察①中所描点的位置关系,照这样的发展趋势........,猜想y 与x 之间的函数关系,并求出所猜想的函数表达式;(3)若小明继续沉溺于“QQ 农场”游戏,照这样的发展趋势,请你估计元月份的期末考试中小明的数学成绩,并用一句话对小明提出一些建议27.(本题满分12分)如图(1),BD 、CE 分别是△ABC 的外角平分线,过点A 作AF⊥BD ,AG⊥CE ,垂足分别为F 、G ,连结FG ,延长AF 、AG ,与直线BC 相交于M 、N .(1)试说明:FG=21(AB+BC+AC ); (2)①如图(2),BD 、CE 分别是△ABC 的内角平分线;②如图(3),BD 为△ABC 的内角平分线,CE 为△ABC 的外角平分线.则在图(2)、图(3)两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况说明理由.(1) (2) (3) MN(第2728.(本题满分12分)已知直角梯形OABC 在如图所示的平面直角坐标系中,AB∥OC ,AB=10,OC=22,BC=15,动点M 从A 点出发,以每秒1个单位长度的速度沿AB 向点B 运动,同时动点N 从C 点出发,以每秒2个单位长度的速度沿CO 向O 点运动.当其中一个动点运动到终点时,两个动点都停止运动. (1)求B 点坐标; (2)设运动时间为t 秒.①当t 为何值时,四边形OAMN 的面积是梯形OABC 面积的一半; ②当t 为何值时,四边形OAMN 的面积最小,并求出最小面积;③若另有一动点P ,在点M 、N 运动的同时,也从点A 出发沿AO 运动.在② 的条件下,PM +PN 的长度也刚好最小,求动点P 的速度.MNOABC xy OA BC xy (备用(第28八年级数学参考答案一、选择题(本大题共8小题,每小题3分,共24分)二、填空题(本大题共10小题,每小题3分,共30分)9、0 10、 11、(4,-2) 12、6 13、3a -5 14、615、⎩⎨⎧-=-=24y x 16、6 17、40°、70°或100° 18、-3≤b ≤0三、解答题(本大题共10小题,共96分.)19、(1)解:原式=-2-1+2 ………3分 (2)解:由9)1(2=-x 得, =-1 ………4分 x -1=3或x -1=-3 ……6分 ∴x=4或x=-2 ……8分 20、解:(1)∵AO ⊥DO (2)滑动不等于4 m ∵AC=4m∴AO=22BO AB - ……2分 ∴OC=AO -AC=8m ……5分 =22513-=12m ……4分 ∴OD=22OC CD -∴梯子顶端距地面12m 高。
=m 10581322=- …7分 ∴BD=OD -OB=45105>- ∴滑动不等于4 m 。
……8分。
21、(1)画出四边形OA 1B 1C 1 ……1分 B 1(-6,2) ……2分(2)画出四边形OA 2B 2C 2 ……4分。
∵4062222=+=OB ……5分 且OB⊥OB 2 ……6分∴ππ10412=⨯=OB S ……8分题号 1 2 3 4 5 6 7 8 答案CADCDBCBB 1A 1C 1A 2B 2C 222、解:(1)∵BE =CF∴BE +EC =CF +EC即 BC=EF ……………2分在△ABC 与△DEF 中⎪⎩⎪⎨⎧=∠=∠=EF BC DEF B DE AB ∴△ABC≌△DEF ………………5分(2)∵△ABC≌△DEF∴AC=DF ∠ACB =∠F …………7分 ∴AC ∥DF …………9分 ∴四边形ACFD 是平行四边形.………10分 23、解:(1)把点(2,m )代入x y 21=得,m=1 ………2分 (2)把点(-1,-5)、(2,1)代入y =kx +b 得,⎩⎨⎧=+-=+-125b k b k 解得,⎩⎨⎧-==32b k∴ 一次函数的解析式为:32-=x y ………6分 (3)如图,直线32-=x y 与x 轴交于点B (23,0)……7分 与直线x y 21=相交于点A (2,1) ∴ OB=23………8分 ∴ S △OA B =431232121=⨯⨯=⋅A y OB ………10分24、解:(1) 平均数、中位数各 2分;其余各1分。
平均数中位数 命中9环以 上的次数甲 7 7 1 乙73FEDC BA 第22题xyOAB(2)①乙 …… 7分 ②乙 ………8分③从折线图的走势看,乙呈上升趋势,所以乙更有潜力。
………10分。
25、解(1)四边形ABCD 是菱形。
理由:作AP ⊥BC 于P ,AQ ⊥CD 于Q由题意知:AD ∥BC ,AB ∥CD∴四边形ABCD 是平行四边形 ……2分∵两个矩形全等∴AP=AQ ……3分∵AP ·BC=AQ ·CD ∴BC=CD ……4分∴平行四边形ABCD 是菱形 ……5分(2)设BC=x ,则CG=6-x ,CD=BC=x ……7分在Rt △CDG 中,222CD DG CG =+∴ 2223)6(x x =+- 解得 x=415 ……9分∴ S=BC ·DG=445……10分26、(1)如图 ………2分 (2)猜想:y 是x 的一次函数 ……3分 设b kx y +=,把点(9,90)、(10,80)代入得⎩⎨⎧=+=+8010909b k b k 解得⎩⎨⎧=-=18010b k ∴18010+-=x y ………5分HGFE DC B A N LH G F E D C B A 图甲 图乙PQ405060708090100211211109yxO经验证:点(11,70)、(12,60)均在直线18010+-=x y 上∴y 与x 之间的函数关系式为:18010+-=x y ……6分(3)∵ 当x=13时,y=50∴估计元月份期末考试中小明的数学成绩是50分。
