第三讲参数检验.
stata第三讲【山大陈波】

例题:利用MLE方法估计下列两个方程: 1.price=b0+b1*weight+b2*length+ε 2.price=b0+b1*weight+b2*length+b3*mpg+ε 利用wald检验和LR检验验证:b3=0
sysuse auto,clear ml model lf myprog (price = weight length) (sigma:) ml max est store r0 ml model lf myprog (price = weight length mpg) (sigma:) ml max est store r1
异方差的检验与FGLS
异方差是违背了球型扰动项假设的一种情形。 在存在异方差的情况下: (1)OLS 估计量依然是无偏、一致且渐近 正态的。 (2)估计量方差Var(b|X) 的表达式不再是 σ2(X’X)−1,因为Var(ε|X) ≠σ2I。 (3)Gauss-Markov 定理不再成立,即OLS 不再是最佳线性无偏估计(BLUE)。
参数约束检验的三大方法: Wald检验 似然比检验(LR) 拉格朗日乘数检验(LM) 注意: 1。参数约束检验不仅用于MLE中,同时可以用在其 他计量方法中。 2。由于LM检验在后面的计量模型中广泛使用,检验 过程与模型设定密切相关,因此stata没有提供单纯 使用LM进行检验的命令,只能通过手动计算的方法, 因此,在此我们重点关注前两种检验。
Stata上机实验
大样本OLS
大样本OLS经常采用稳健标准差估计(robust) 稳健标准差是指其标准差对于模型中可能存 在的异方差或自相关问题不敏感,基于稳健 标准差计算的稳健t统计量仍然渐进分布t分布。 因此,在Stata中利用robust选项可以得到异 方差稳健估计量。
参数检验原理及操作过程

参数检验一、单样本t 检验:One-Samples T Test 过程1.单样本t 检验的含义单样本t 检验是检验某个变量的总体均值与指定的检验值之间是否存在显著差异。
它是比较样本均值与总体均值的假设检验。
例如,某区商业系统对员工进行技术考核,得出员工考核的平均分为87分,该区的某个超市随机抽取了9名员工得到考核的平均技术成绩为82.67分,问该超市员工的考核的平均得分与全区是否一致?单样本t 检验的前提是要求样本来自的总体应服从正态分布或者近似服从正态分布。
2.单样本t 检验的步骤单样本t 检验作为假设检验的一种方法,它的基本步骤如下:首先,根据实际问题提出零(原)假设H 0:样本均值与指定检验值之间不存在显著差异,即H 0:μ=μ0 , H 1:μ≠μ0,其中,μ为总体均值,μ0为指定检验值。
其次,选择检验统计量。
由于抽样误差的存在,虽然样本均值呈现出差异性,但样本均值的抽样分布是可以确定的,当总体分布为正态分布X~N (μ,σ2)时,样本均值的抽样分布仍为正态分布,该正态分布的均值为μ,方差为n 2σ,即),(~2nN x σμ (1-1)其中,μ为总体均值,σ2为总体方差,n 为样本容量。
当总体的分布近似服从正态分布时,我们就选择较大样本容量的样本,由中心极限定理可知,n 较大时,样本均值近似第服从(1-1)式的正态分布。
再将样本进行标准化转换,可以构造Z 检验统计量,为:nx Z 2σμ-=(1-1)Z 统计量服从标准正态分布。
通常总体方差σ2是未知的,我们可以用样本方差S 2替代,得到的检验统计量就是t 统计量,为:nS x t 2μ-=(1-3)其中,μ用μ0代入,t 统计量服从自由度为n-1的t 分布。
第三,计算检验统计量的值和概率P 值。
SPSS 将自动计算t 值,并根据t 分布表给出t 值对应的概率P 值。
最后,给出显著性水平α,并给出结论。
如果概率P 值小于给出的显著性水平α,则拒绝H 0,认为总体的均值与检验值之间存在显著差异。
参数检验名词解释

参数检验名词解释
参数检验:参数检验是通过检查参数范围、参数类型、参数正确性等,确保参数输入的正确性,从而使程序运行正常的一种检查工作。
参数:参数是在程序运行过程中,由程序的使用者提供的变量,它影响程序的运行结果。
范围:范围是指参数的取值范围,即参数的可用取值范围。
类型:类型是指参数的数据类型,它描述了参数的存储格式和表示方式。
正确性:正确性是指参数输入与实际情况的准确度,它反映了参数是否输入正确。
参数检验名词解释

参数检验名词解释
参数检验是软件开发中的一种常用技术,它主要是为了检测来自应用程序的参数是否符合用户的预期。
参数:参数是一个被应用程序使用的值,它可以用于控制程序行为或传递信息。
它可以是字符串或数字,也可以是复杂的对象或结构体。
检验:检验是指检查程序的输入和输出,以确保程序正确地响应用户的输入。
它可以检查参数的有效性,并且可以检测参数之间的冲突。
有效性:有效性是指参数是否有效的概念,它指的是参数是否符合程序期望的格式,是否符合用户的意图,以及参数的范围是否合理。
冲突:冲突是指两个或多个参数之间的不一致性或抵触,它可能导致程序错误或失效。
第三讲_多元线性回归模型检验及stata软件应用
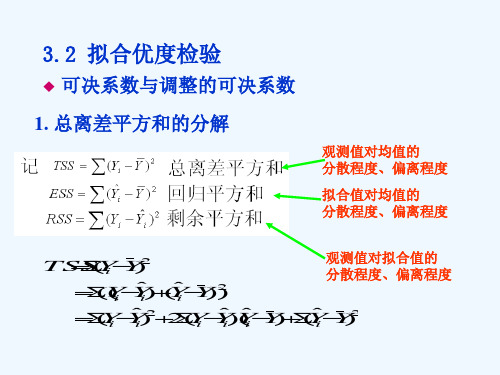
F检验的思想来自于总离差平方和的分解式: TSS=ESS+RSS
2 ˆ ESS y 由 于 回 归 平 方 和 解 释 变 量 X 的 联 合 体 对 被 解 i 是
释 变 量 Y 的 线 性 作 用 的 结 果 , 考 虑 比 值
2 ˆ ESS /RSS y i 2 e i
如果这个比值较大,则X的联合体对Y的解释程度 高,可认为总体存在线性关系,反之总体上可能不存 在线性关系。 因此,可通过该比值的大小对总体线性关系进行推 断。
**关于P值:以t统计量的观测值作为临界值,并计算该检 验的响应显著水平,这就是P值。
P值检验法(p-value test)
p 值的概念: 为了方便,将 t 统计量的值记为
பைடு நூலகம்t0
Se
j j
计算 称为p
p=P{|t|>t 0}
值(p-value )
通常的计量经济学软件都可自动计算出p 值
Excel格式数据的读取
直接拷贝,粘贴到stata中
使用Stat
transfer把其它格式的数据转成 stata格式的数据 读入ASCII格式数据文件:比较麻烦
常见数据格式
格式:dta 文本格式:txt Excel格式:xls 其它格式:sas、spss、gauss等
Stata
检验统计量2250nntn???????当用正态已知时当未知时也可用正态n用分布很小1t变量iiiibtbsb???其中1ixxsbs???12iiiixxbn????2t检验统计量给定显著性水平??可得到临界值t??2nk由样本求出统计量t的数值通过t??t??2nk或t??t??2nk来拒绝或不能拒绝原假设h0从而判定对应的解释变量是否应包括在模型中
常用参数检验方法

P111 注意数据 输入格式
P114
----------专业最好文档,专业为你服务,急你所急,供你所需------------文档下载最佳的地方
检验方法名称 卡方检验 游程检验 K-S 检验
----------专业最好文档,专业为你服务,急你所急,供你所需------------文档下载最佳的地方
----------专业最好文档,专业为你服务,急你所急,供你所需------------文档下载最佳的地方
常用参数检验方法
检验方法名 称
问题类型
假设
适用条件
抽样方法
概率计 算方法
单样本 T—检 验
判断一个总体平 均数等于已知数
总体平均数 等于 A
从总体中抽取一个
总体服从正态分布
Байду номын сангаас
样本
P110
F—检验
非参数检验方法
问题类型
假设
概率计算方法
用于检验实际观测频数与 观测频数与理论
P119
理论频数之间是否有差异 频数无差异
检验一组观测值是否有明 无明显变化趋势
显变化趋势
P121
检验变量取值是否为正态 分布
服从正态分布
P123
----------专业最好文档,专业为你服务,急你所急,供你所需------------文档下载最佳的地方
分布 2、两总体方差不相
等
1、总体服从正态分 布
2、两组数据是同一 试验对象在试验前
后的测试值
从两个总体中各抽 取一个样本
从两个总体中各抽 取一个样本
从两个总体中各抽 取一个样本
抽取一组试验对 象,在试验前测得 试验对象某指标的 值,进行试验后再 测得试验对象该指
流行病学复习资料_公式和指标

第一讲1. 发病率(incidence rate)指一定时期内,特定人群中发生某病新病例的频率。
某病发病率=某年(期)某人群中发生某病新病例数/ 同年(期)暴露人口数*KK -‰、万/万、10万/10万计算发病率应注意:观察时间、发病时间、暴露人口数、单位暴露人口必须符合两个条件:①必须是观察时间内观察地区内的人群;②必须有患所要观察的疾病的可能。
正在患病或因曾经患病或接受了预防接种而在观察期内肯定不会再患该病的人不能算作暴露人口。
在研究女性疾病时,暴露人口只限于女性。
若可能患某病的人群不易明确界定(如高血压等),则以全人群作为暴露人群。
发病密度(incidence density, ID)ID=观察期间内新发病例数/ 该期间观察人年数人年数:1人观察1年=1人×1年=1人年2. 患病率(prevalence rate)指某特定时间内总人口中某病新旧病例所占的比例。
患病率=某时间内某病新旧病例数/ 该人群同期平均人口数*K3. 死亡率(mortality rate)死亡率=某人群某年总死亡人数/ 该人群同年平均人口数*K是测量人群死亡危险最常用的指标,也是国际间比较常用的指标。
4. 病死率(fatality rate)病死率=一定时间内因某病死亡人/ 同期确诊的某病病例数反映疾病的严重程度,也可反映医疗水平和诊断能力5. 生存率(survival rate) 指观察开始至少到某时点仍处于存活状态的概率生存率=随访满n年尚存活的病例数/ 随访满n年的病例数=(总例数N –失访-死亡)/(N-失访数)常用1年和5年生存率来反映疾病严重性和预后指标生存率是指在随访期末仍存活的病例数与坚持随访的病例总数之比6. 罹患率(attack rate)罹患率与发病率一样是测量新发病例频率的指标,与发病率比较,其区别在于罹患率常用来衡量人群中在较短时间内新发病例的频率。
观察时间可以日、周、旬、月为单位,使用比较灵活,常用于疾病的流行或爆发时病因的调查。
第三讲 Sm-Nd法

4.60 Ga 参考等时线
提示: 1)检验陨石Sm-Nd等 时线年龄; 2)确定未经历过地球 地壳幔分异事件(原始 地幔)的物质储库 (CHUR)的现今SmNd同位素组成; 3)建立Nd同位素示踪 研究参数的基准点。
Sm-Nd isochron diagram for whole-rock samples of six different chondrites. SS = St Severin; MU = Murchison; GU = Guarena; PR = Peace River; ALL = Allende. JUV = new analysis of the Juvinas achondrite. The large apparent errors are due to very expanded axis scales. After Jacobsen and Wasserburg (1980).
Sm-Nd同位素体系的主要应用领域
通过对陨石系统研究,建立壳幔演化关系模型; 建立全球地壳生长模型、判别岩石圈演化过程 中的区域初生地壳加入与壳幔物质再循环机制、 对岩浆物质来源等重要地质问题进行示踪研究; 在中低级变质和高级变质条件下,对原岩形成 和变质事件进行定年研究等。
陨石Sm-Nd同位素研究的意义
almandine
GROSSULAR on DIOPSIDE
GROSSULAR
albite
monazite
apatite
hornblen
augite
olivine diopside
范例:石榴石高Sm/Nd比值与定年
扬子克拉通陆核崆岭太古宙基底岩系中约19.5亿年热改造事件的识别 (Ling WL, et al., 2001)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018/9/22
24
说明:
在SPSS软件中直接显示的是双侧检验的p-值为 Sig(2tailed),而没有显示单侧检验的p-值,因此,得到的p-值要进 行处理,处理的原则是:
单侧的P值=双侧的P值/2
因此,利用SPSS软件操作所得到的p-值,可按如下的结论来进 行决策:
双侧检验
得出接受或拒绝原假设的结论
商学院 李丽明
2018/9/22
11
假设检验中的小概率原理
1.
什么是小概率?
在一次试验中,一个几乎不可能发生的事件 发生的概率
2.
3.
在一次试验中小概率事件一旦发生,我们就 有理由拒绝原假设
小概率由研究者事先确定
商学院 李丽明
2018/9/22
12
假设检验中的两类错误
若p-值 ,不能拒绝 H0,即接受H0 若p-值 < 拒绝 H0 若p=双侧的P值/2 , 不能拒绝 H0,即接受H0 若p=双侧的P值/2 < , 拒绝 H0
2018/9/22
单侧检验
商学院 李丽明
25
假设检验步骤的总结
陈述原假设和备择假设 从所研究的总体中抽出一个随机样本 确定一个适当的检验统计量,并利用样本数据算出 其具体数值
One-Sample Test Test Value = 20 95% Confidence Interval of the Difference Lower Upper 1.5508 2.4612
29
人 均面 积
t 8.640
df 2992
Sig . (2-tailed) .000
Mean Difference 2.00596
10cn H1 : 10cn
H0 :
商学院 李丽明
2018/9/22
14
提出假设 (例题分析)
【例】某品牌洗涤剂在它的产品说明书中声称:平 均净含量不少于 500 克。从消费者的利益出发,有 关研究人员要通过抽检其中的一批产品来验证该产 品制造商的说明是否属实。试陈述用于检验的原假 设与备择假设 解:研究者抽检的意图是倾向于 证实这种洗涤剂的平均净含量并 不符合说明书中的陈述 。建立的 原假设和备择假设为 H0 : 500 H1 : < 500
μ1– μ2= 0 μ1– μ2≠0
18
显著性水平和拒绝域
(双侧检验 )
抽样分布
拒绝域 /2
置信水平
拒绝域
1-
接受域
/2
临界值
H0值
临界值
样本统计量
商学院 李丽明
2018/9/22
19
显著性水平和拒绝域 (左侧检验 )
抽样分布
拒绝域
置信水平
1- 接受域 H0值 样本统计量
临界值
商学院 李丽明
2018/9/22
20
显著性水平和拒绝域 (右侧检验 )
商学院 李丽明
2018/9/22
4
假设检验的过程 (提出假设→抽取样本→作出决策)
提出假设
我认为茶叶的净重 平均为500
作出决策
拒绝或接受 假设!
总体
抽取随机 样本
均值 X = 495
商学院 李丽明
2018/9/22
5
假设检验的步骤
提出原假设和备择假设 确定适当的检验统计量 规定显著性水平 计算检验统计量的值 作出统计决策
2018/9/22
商学院 李丽明
7
提出原假设和备择假设
1.
什么是备择假设?(Alternative Hypothesis) 与原假设对立的假设(研究者想收集证据予 以支持的假设)
2.
3.
总是有不等号:
表示为 H1
, 即< 或
>
H1: 某一数值, <某一数值,或 >某一数值 例如, H1: 500 (克), < 500(克), 或 >500(克)
2018/9/22
500g
15
商学院 李丽明
提出假设 (例题分析)
【例】一家研究机构估计,某城市中家庭拥有汽 车的比率超过30%。为验证这一估计是否正确, 该研究机构随机抽取了一个样本进行检验。试陈 述用于检验的原假设与备择假设
解:研究者想收集证据予以支持的假 设是“该城市中家庭拥有汽车的比率 超过30%”。建立的原假设和备择假设 为 H0 : 30%
2018/9/22
商学院 李丽明
13
提出假设 (例题分析)
【例】一种零件的生产标准是直径应为 10cm ,为对生 产过程进行控制,质量监测人员定期对一台加工机床检 查,确定这台机床生产的零件是否符合标准要求。如果 零件的平均直径大于或小于 10cm ,则表明生产过程不 正常,必须进行调整。试陈述用来检验生产过程是否正 常的原假设和被择假设。 解:研究者想收集证据予以证明的假设 应该是“生产过程不正常”。建立的原 假设和备择假设为:
Std. Deviation .16734
Std. Error Mean .03839
受 高等 教 育 比例
t -1.437
df 18
Sig . (2-tailed) .168
Mean Difference -.05515
One-Sample Test Test Value = 0 95% Confidence Interval of the Difference Lower Upper .6642 .8255
商学院 李丽明
H1 : 30%
2018/9/22
16
提出假设 (结论与建议)
原假设和备择假设是一个完备事件组,而且 相互对立 在一项假设检验中,原假设和备择假设必 有一个成立,而且只有一个成立
先确定备择假设,再确定原假设
等号“=”总是放在原假设上
因研究目的不同,对同一问题可能提出不同 的假设(也可能得出不同的结论)
确定一个适当的显著性水平,并计算出其临界值, 指定拒绝域
将统计量的值与临界值进行比较,作出决策 统计量的值落在拒绝域,拒绝H0,否则不拒绝 H0 也可以直接利用P值作出决策
2018/9/22
商学院 李丽明
26
第二节 一个正态总体的参数检验
一、总体均值的检验 (大样本)
商学院Байду номын сангаас李丽明
2018/9/22
商学院 李丽明
2018/9/22
8
确定适当的检验统计量
什么检验统计量? 1.用于假设检验问题的统计量 2.选择统计量的方法与参数估计相同,需 考虑 是大样本还是小样本 总体方差已知还是未知 检验统计量的基本形式为
z
x 0
n
9
商学院 李丽明
2018/9/22
规定显著性水平
1. 2.
什么显著性水平?
是一个概率值
原假设为真时,拒绝原假设的概率 被称为抽样分布的拒绝域 表示为 常用的 值有0.01, 0.05, 0.10 由研究者事先确定
2018/9/22
3.
4.
商学院 李丽明
10
作出统计决策
计算检验的统计量
根据给定的显著性水平 ,查表得出相 应的临界值Z或 Z/2 将检验统计量的值与 水平的临界值进 行比较
(决策风险)
在对原假设的真伪作判断时,由于样本的随机 性可能使决策发生下面两类错误: 第一类错误(弃真错误):原假设H0为真,但 由于样本的随机性,使样本观测值落入拒绝域 ,所下的决策是拒绝H0 ,这类错误称为第一 类错误,其发生的概率称为犯第一类错误的概率 ,也称为拒真概率α。 第二类错误(取伪错误):原假设H0为假,但 由于样本的随机性,使样本观测值落入接受域 ,所下的决策为保留H0 ,这类错误称为第二 类错误,其发生的概率称为犯第二类错误的概率 ,也称为取伪概率β 。
商学院 李丽明
2018/9/22
3
一个例子
某茶叶厂生产袋装茶叶,正常情况下每袋茶 叶净重平均为500克,标准差为13克。最近,厂 质检部门接到消费者投诉,认为该厂新投放市 场的一批茶叶似乎普遍分量不足。为此,从生 产线中随机抽取了40袋茶叶,测得其平均重量 为495克,能否认为该厂最近生产的茶叶包装分 量确实不足?(显著性水平=1%)
2018/9/22
31
两个正态总体的参数检验(两独立样本T检验)
一、两个总体均值之差的检验
(独立大样本)
商学院 李丽明
2018/9/22
32
两个总体均值之差的Z检验 (假设的形式)
研究的问题
假设
没有差异
有差异
均值1 均值2 均值1 < 均值2
均值1 均值2 均值1 > 均值2
H0 H1
商学院 李丽明
2018/9/22
案例5-2
One-Sample Statistics N 受 高等 教 育 比例 19 Mean .7448
One-Sample Test Test Value = 0.8 95% Confidence Interval of the Difference Lower Upper -.1358 .0255
2018/9/22
商学院 李丽明
17
双侧检验与单侧检验 (假设的形式)
假设
双侧检验 H0 : = 0 H1 : ≠0
单侧检验 左侧检验 H0 : 0 H1 : < 0 右侧检验 H0 : 0 H1 : > 0
